1 Introduction
Connaître la vitesse d’écoulement dans un fluide est une information cruciale dans nombre d’études de rhéologie et de mécanique des fluides. En rhéologie, ce sont les propriétés du fluide lui-même que l’expérimentateur souhaite explorer. C’est en observant comment le fluide est mis en mouvement lorsqu’il est sollicité que l’on remonte à sa loi de comportement. En mécanique des fluides, on cherche souvent à caractériser la forme d’un écoulement autour d’une géométrie particulière. Le champ de vitesse est, dans ce cas, précisément une des grandeurs que l’on veut déterminer. Par sa capacité à mesurer des champs de vitesse dans des fluides en mouvement [1,2], l’IRM s’impose aujourd’hui progressivement dans ces deux domaines.
Depuis quelques années, la vélocimétrie par IRM du proton a ainsi fait son entrée dans l’étude rhéologique des pâtes, des suspensions colloïdales et, plus généralement, de ce que l’on nomme les fluides complexes [3–5]. Elle sert à mesurer directement l’écoulement des fluides étudiés au cœur des cellules rhéométriques. On obtient ainsi une information locale sur le comportement du fluide, progrès notable puisque cette information échappe en fait au rhéomètre « classique » de laboratoire, qui ne fournit que des données moyennes sur un échantillon sollicité de manière « macroscopique ». Quelques études de suspensions colloïdales au moyen d’un rhéomètre inséré dans notre IRM ont d’ores et déjà permis d’importantes avancées dans l’observation des comportements rhéologiques de ces systèmes [5]. Les enjeux actuels au plan méthodologique sont de caractériser les écoulements dans des délais courts, sans sacrifier la qualité des mesures, afin de permettre l’étude par IRM de systèmes dont les propriétés rhéologiques évoluent rapidement au cours du temps.
Nous présentons, en première partie d’article, une approche qui nous a permis, en géométrie Couette, de gagner considérablement en rapport signal sur bruit par rapport à la méthode de vélocimétrie dite de « codage par la phase », et ce à temps d’expérience constant. Nous en exposons les principes ainsi qu’une illustration de la méthode sur une pâte de ciment à temps de relaxation très court.
Parente de la rhéologie, la mécanique des fluides se heurte également à des problèmes que la vélocimétrie par IRM peut résoudre. Pour déterminer la forme d’un écoulement autour d’une structure, deux solutions sont en effet traditionnellement mises en œuvre. Tout d’abord, la simulation numérique, méthode la plus économique, qui demande de connaître la loi d’écoulement du fluide, et de disposer d’outils numériques fiables aptes à bien prendre en compte cette loi dans un calcul. Elle n’est pas toujours applicable, car la caractérisation rhéologique d’un fluide peut être problématique, et la simulation numérique de certaines lois de comportement, par exemple pour les fluides à seuil, loin d’être un problème résolu, fait encore l’objet d’actives recherches. Une deuxième méthode consiste à réaliser des expériences, soit grandeur nature, soit sur modèle réduit. Les techniques couramment utilisées pour mesurer des cartes de vitesses ont alors elles aussi leurs propres limitations. La méthode optique de PIV [6] est capable de réaliser des cartes tridimensionnelles de champs de vitesse dans des liquides, mais elle demande d’introduire des particules traceuses dans l’écoulement, ce qui peut perturber le système, et nécessite que le fluide d’étude possède une bonne transparence optique, ce qui limite la gamme de milieux pouvant être étudiés. L’IRM, qui ne nécessite ni traceur, ni propriété optique particulière, peut donc permettre d’élargir le panel des expériences possibles [7].
Nous présentons en deuxième partie de cet article une étude de vélocimétrie IRM sur modèle réduit, dans laquelle nous avons réalisé une carte tridimensionnelle de champ de vitesse dans un fluide viscoplastique brassé par une maquette animée de malaxeur à béton. Nous montrons ainsi la compétitivité de l’IRM dans ce type d’études.
2 Rhéométrie IRM en géométrie Couette
2.1 Enjeux
Considérons un fluide cisaillé de façon uniforme entre deux plans de surface S, l’un fixe et l’autre qui se déplace à la vitesse V (Fig. 1). Le fluide a tendance à s’opposer au cisaillement, et une force F doit être appliquée au plan mobile pour maintenir le mouvement. Sur la base de cette expérience de pensée, on définit en rhéologie deux grandeurs : la contrainte de cisaillement τ et le taux de cisaillement , qui caractérisent respectivement l’effort subit par le fluide et la déformation résultante dans l’écoulement. Ils sont définis selon (1) :
| (1) |

Schéma de principe pour une expérience de cisaillement de fluide entre deux plans.
En rhéologie, on se focalise généralement sur l’étude de la relation entre τ et . À cette fin, différentes géométries de rhéomètre permettent de mettre le fluide en situation de cisaillement et de réaliser des mesures. Dans la géométrie couette (Fig. 2), le fluide est introduit dans l’entrefer de deux cylindres concentriques, le cylindre extérieur étant par exemple fixe, et le cylindre intérieur tournant sur lui-même. Les mesures consistent traditionnellement à mesurer simultanément la vitesse de rotation ω du cylindre interne et le couple résistant C qu’il reçoit de la part du fluide, au cours d’expériences dans lesquelles, soit ω, soit C sont variés – ou le cas échéant maintenus constants – selon des protocoles choisis. Il apparaît ainsi clairement que le rhéomètre ne mesure pas directement τ et au cœur du fluide – ce qui constitue pourtant l’information recherchée –, mais réalise plutôt une sorte de mesure moyenne de ces deux grandeurs, que nous noterons <τ> et , sur tout le volume d’échantillon contenu dans la cellule. Or, en faisant l’hypothèse classique que l’écoulement du fluide entre les cylindres est à symétrie cylindrique, on calcule que la contrainte locale de cisaillement dépend de la coordonnée r selon :
| (2) |
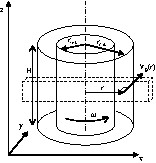
Schéma de principe du rhéomètre Couette insérable dans l’IRM. L’ordre de grandeur des rayons des cylindres intérieur et extérieur est de 4 et 6 cm, respectivement. Le barreau en pointillés indique la zone sélectionnée par la séquence IRM de mesure de vitesse.
Le champ de contrainte n’est donc pas homogène dans l’échantillon. ne sera donc lui-même généralement pas homogène. Un problème crucial en rhéologie « classique » consiste à rétablir le lien entre la grandeur globale– grandeur mesurée – et le taux de cisaillement local – grandeur d’intérêt. Une première solution qui s’offre à l’expérimentateur est de faire des postulats quant à la forme de la loi d’écoulement du fluide. Les mesures sur rhéomètres ne sont alors utilisées que pour déterminer les paramètres clés des modèles. Néanmoins, certaines suspensions colloïdales d’intérêt industriel (ciment frais, peinture, boue...) présentent des propriétés rhéologiques particulières, notamment de seuil de contrainte et de thixotropie – c’est-à-dire d’effets mémoire réversibles dans leurs propriétés d’écoulement –, dont la modélisation ne fait toujours pas l’unanimité dans la communauté des rhéologues [5].
La mesure par IRM de la composante orthoradiale Vθ(r) dans la cellule Couette en cours d’expérience permet de résoudre le problème de la mesure globale du taux de cisaillement. se calcule en effet à partir de Vθ(r) selon :
| (3) |
La donnée d’un seul profil de vitesse Vθ(r) et la mesure de couple C associée permettent donc non seulement, via les relations (2) et (3), d’avoir directement une estimation des grandeurs locales τ et , mais également, en exploitant les données pour les différentes valeurs de r, d’explorer plusieurs valeurs de ces deux grandeurs. C’est ainsi une information beaucoup plus riche et beaucoup plus précise qui est obtenue sur l’échantillon.
2.2 Méthodologie IRM et gains en rapport signal sur bruit
Les principes de la séquence RMN utilisée pour la mesure des profils de vitesses (Fig. 3) ont déjà fait l’objet de descriptions détaillées dans la littérature [5,8]. Deux impulsions radiofréquence sélectives délimitent dans l’échantillon un barreau le long d’un diamètre dans la cellule Couette. Un gradient de lecture parallèle au barreau permet de réaliser des profils complexes d’aimantation le long de celui-ci. Une paire de gradients de « codage », d’amplitude G, de durée δ et séparés par un temps Δ permettent d’introduire sur les profils un déphasage φ(r) qui dépend de la composante de vitesse Vθ(r) selon (4):
| (4) |
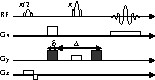
Séquence RMN utilisée pour la mesure de vitesse en géométrie Couette. Les impulsions de gradient permettant le codage de la vitesse sont en noir.
La mesure de vitesse s’effectue en réalisant deux mesures successives de profil d’aimantation, respectivement en présence et en absence des gradients de codage, et en comparant pour chaque valeur de la coordonnée r la phase des deux profils complexes obtenus. Une difficulté au niveau du traitement des données vient du fait que la phase n’est connue qu’à 2 π près. Afin de mesurer la vitesse sans ambiguïté, il faut ainsi régler la séquence de telle sorte que :
| (5) |
Nous proposons ici, pour gagner en rapport signal sur bruit sans augmenter le temps d’expérience, de passer outre à cette condition, en augmentant la valeur du produit G δ Δ. Dans l’absolu, les vitesses ne sont alors connues qu’à 2π /γ Gδ Δ près. Pour lever cette inconnue, nous faisons l’hypothèse – maintes fois vérifiées sur les systèmes étudiés au laboratoire – que le champ de vitesse est continu. Nous reconstruisons le profil de proche en proche, en partant des bords externes du rhéomètre (sur lesquels on sait que la vitesse est nulle) et en affectant à un pixel donné la vitesse la plus proche de celle trouvée au pixel précédent. Dans cette nouvelle manière de procéder, tant que le nouveau choix des paramètres G, δ et Δ n’induit pas de pertes de signal supplémentaires par relaxation ou par diffusion, l’erreur absolue Δφ sur la phase φ(r) reste inchangée. L’erreur absolue sur la mesure de vitesse ΔV = Δφ/γ G δ Δ est donc réduite de manière inversement proportionnelle au facteur G δ Δ.
2.3 Validation expérimentale et application à l’étude d’une pâte de ciment
Les expériences ont été conduites sur l’IRM Bruker Biospec 24/80 DBX du LMSGC. Il possède un aimant vertical (Magnex Scientific) de 0,5 T, soit 21 MHz en proton, accueille dans son antenne en cage d’oiseau des échantillons jusqu’à 20 cm de diamètre, et peut délivrer des gradients de 5 G cm–1 avec un temps de montée de 500 μs. Il est équipé d’un rhéomètre de type Couette insérable dans l’appareil qui permet, outre les mesures de rhéologie proprement dites, de mettre également des échantillons solides en rotation.
La variante méthodologique proposée a tout d’abord été testée sur un récipient cylindrique de 13 cm de diamètre rempli de graines de moutardes, et animé d’un mouvement de rotation solide autour de l’axe z à 63 tours par minute. La séquence de mesure était réglée de manière à sélectionner dans l’échantillon un barreau « radial » de 6 cm de hauteur (selon z) et de 5 mm de large. Les profils étaient faits avec un champ de vue de 20 cm et une résolution de 256 pixels. Les délais pour le codage de la vitesse étaient respectivement de δ = 2,5 ms et Δ = 4,8 ms. Deux mesures de vitesse ont été réalisées en utilisant respectivement des forces de gradient de 0,218 G cm–1 et 3,488 G cm–1, toutes choses étant égales par ailleurs (Figs. 4 et 5). Les profils de vitesse ont été obtenus en cumulant huit acquisitions de signal successives, en un temps total d’expérience de 8 s chacun. En prenant pour Vmax la vitesse de la surface du cylindre (de 0,408 m s–1), nous calculons pour la première valeur de gradient γ G δ Δ Vmax ≈ 3,07, ce qui respecte bien la condition (5). La deuxième valeur de gradient correspond à un codage en vitesse 16 fois plus fort. La reconstruction du profil de vitesse par continuité était ici menée en partant du centre du cylindre. Alors que l’erreur absolue de mesure relevée est de ±1,5 cm s–1 dans le premier cas (Fig. 4), l’erreur obtenue avec le gradient le plus fort n’est plus que de ±1 mm s–1 : le deuxième profil (Fig. 5) apparaît en effet très clairement moins bruité. L’excellent accord constaté avec le profil de vitesse théorique apporte, en outre, une validation au procédé de reconstruction du champ de vitesse par continuité.
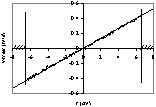
Cylindre solide tournant à 63 tr min–1. Mesure du champ de vitesse orthoradial Vθ en fonction de la coordonnée radiale r, avec un gradient de 0,218 G cm–1. Les traits verticaux indiquent la position des bords de l’échantillon. Le profil de vitesse théorique est en trait fin.
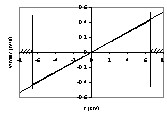
Cylindre solide tournant à 63 tr min–1. Mesure du champ de vitesse Vθ en fonction de la coordonnée radiale r, avec un gradient de 3,488 G cm–1. Les traits verticaux indiquent la position des bords de l’échantillon. Le profil de vitesse théorique est en trait fin.
La méthode a ensuite été testée sur une pâte « fraîche » de ciment blanc. La formulation de ce type de matériau fait actuellement l’objet d’intenses recherches chez les cimentiers, recherches motivées par le souhait d’adapter la rhéologie de ce système à différentes conditions de mise en œuvre sur les chantiers de construction. La pâte de ciment est un fluide qualifié de « complexe », présentant simultanément un comportement à seuil et des propriétés rhéologiques qui évoluent dans le temps, et ce même en bloquant artificiellement le phénomène de prise. L’étude de ce matériau par IRM serait donc d’un apport considérable. Nous avons mesuré sur notre échantillon des temps de relaxation RMN T1 et T2 de 30 ms et 4 ms, respectivement. Le T2 très court est un sérieux handicap pour la mesure de vitesse par IRM. Nous montrons sur la Fig. 6 le résultat d’une mesure de champ de vitesse dans le rhéomètre Couette, le cylindre interne tournant à 60 tours par minute, avec sélection d’un barreau de 5 cm de hauteur et de 1 cm de large, faite en 32 acquisitions, avec des temps δ et Δ respectivement de 1,5 et 4 ms. Le champ de vue des profils était de 15 cm, avec une résolution de 256 points, et le temps de mesure total du profil était d’environ 5 s. Les gradients de codage de vitesse étaient choisis de manière à satisfaire au plus juste la condition (5). Le profil de vitesse apparaît extrêmement bruité, et quasiment inexploitable pour le rhéologue. La durée globale de la séquence, d’environ 7 ms, est déjà ici la source d’importantes pertes de signal par relaxation T2, et ne peut être réduite, pour des raisons de temps de montée de gradients et de durée de pulses RF.

Pâte de ciment blanc cisaillée dans le rhéomètre Couette à 60 tr min–1. Mesure du champ de vitesse Vθ en fonction de la coordonnée radiale r, avec la force de gradient respectant la condition (5). Seule la zone correspondant à l’entrefer entre les cylindres est représentée. Les traits verticaux indiquent les bords de ceux-ci.
Nous avons réalisé (Fig. 7) d’autres mesures sur le même système, mais dans lesquelles la force des gradients de codage de vitesse a été augmentée d’un facteur 12 et le champ de vitesse reconstruit par continuité. Le gain en rapport signal sur bruit, d’un facteur 12 lui aussi, permet aux profils de redevenir exploitables. On peut observer, en particulier, une rupture de pente caractéristique de la rhéologie de nombreuses pâtes et milieux colloïdaux [9]. Le temps d’acquisition d’un profil de vitesse, maintenu à 5 s, nous a permis ici de suivre l’évolution des propriétés rhéologiques de l’échantillon pendant une dizaine de minutes, avec des mesures aussi instantanées que possible. À titre de comparaison, pour obtenir le même niveau de bruit sans changer la force des gradients, il aurait fallu passer de 32 à environ 4600 acquisitions, ce qui aurait pris 12 minutes par profil, et n’aurait pas permis cette observation cinétique.
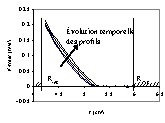
Pâte de ciment blanc cisaillée dans le rhéomètre Couette à 60 tr min–1. Mesure du champ de vitesse Vθ en fonction de la coordonnée radiale r, avec un gradient 12 fois plus fort que celui donné par la condition (5). Les quatre courbes successives correspondent à des mesures effectuées respectivement 0, 2, 5 et 10 min après que le rhéomètre fut entré en rotation.
3 Vélocimétrie tridimensionnelle dans une maquette de malaxeur à béton
3.1 Problématique
Le malaxeur est un appareil de génie civil qui permet, sur chantier, de préparer un béton en assurant le mélange de ses divers constituants – à savoir le ciment, les granulats et l’eau, additionnés, le cas échéant, d’adjudants destinés à contrôler la rhéologie de l’ensemble. Le malaxage a pour double objectif d’homogénéiser globalement le mélange, mais également de permettre aux constituants de se mettre en place les uns par rapport aux autres à l’échelle microscopique, ce dernier point conditionnant en fait la solidité du futur édifice. Or, les contraintes de production sont sévères, et imposent d’effectuer cette opération dans des temps inférieurs à la minute. Une étude a récemment été entreprise au LCPC visant à caractériser les champs de vitesse dans un malaxeur à béton [7]. Le but est, à terme, d’identifier les structures d’écoulement responsables de la qualité du malaxage, et d’obtenir des critères permettant d’optimiser a priori la géométrie de l’appareil. Aucune technique ne permet actuellement de mesurer le champ de vitesse dans un milieu aussi complexe que le béton. Par ailleurs, les propriétés rhéologiques de fluide à seuil exhibées par ce matériau [10], ainsi que la complexité de la surface libre de l’écoulement, rendent le problème difficilement abordable par voie numérique. L’orientation a ainsi été prise d’effectuer des mesures sur modèle réduit, en utilisant comme fluide d’étude un gel de carbopol, dont le comportement rhéologique est proche de celui du béton [7].
3.2 Vélocimétrie IRM 3D
Le modèle réduit (Fig. 8), construit pour l’essentiel en PMMA, est monté dans notre appareil à la place du rhéomètre. Une cuve en forme d’anneau, de 12 cm de diamètre externe et de 6 cm de diamètre interne, est remplie partiellement par le fluide à étudier sur une hauteur de 3,5 cm. Quatre pales composites fixées à un disque tournant brassent le fluide à vitesse constante. La séquence de mesure utilisée (Fig. 9) est de type « Fourier 3D » [11] et met en œuvre encore ici le principe du codage de vitesse par la phase précédemment décrit. La forme particulière des gradients d’imagerie dans les directions y et z permet une compensation de vitesse qui limite au maximum les artefacts d’imagerie dus aux mouvements de la maquette [1,2]. Une telle compensation n’est en revanche pas nécessaire dans la direction x, pour laquelle le gradient de lecture reste constant pendant toute la séquence. Quatre images sont réalisées de manière entrelacée : une image de référence faite en l’absence de gradient de codage de vitesse, et trois images où ces gradients sont ajoutés aux gradients d’imagerie dans les directions x, y, et z, successivement. Un système de synchronisation par fibres optiques permet de déclencher les séquences chaque fois que les pales reviennent à une position fixe. C’est ensuite en comparant les phases des trois images codées en vitesse à l’image de référence que sont obtenues une à une les composantes du champ de vitesse selon x, y et z, et que l’on peut dresser une carte tridimensionnelle de l’écoulement dans la maquette. À 60 tours par minute, 18 h d’expérience étaient nécessaires pour une résolution spatiale de 64 × 64 × 16 voxels.
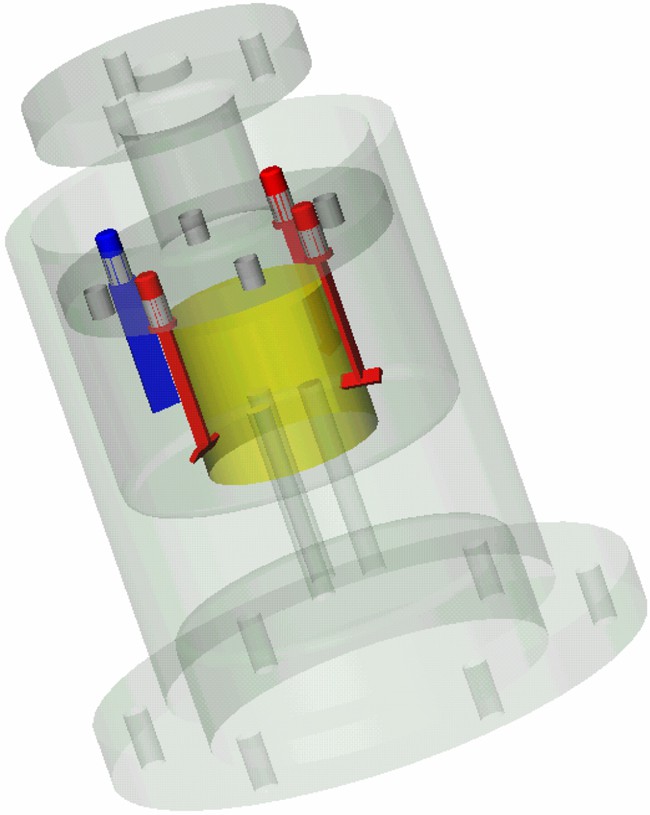
Représentation de la maquette de malaxeur à béton utilisée dans les expériences.
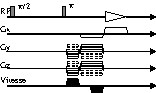
Séquence RMN utilisée pour l’imagerie 3D de champ de vitesse.
La Fig. 10 permet de visualiser la répartition du fluide et les composantes horizontales du champ de vitesse dans un plan situé au niveau du bas des pales. Les pales, qui apparaissent en noir, sont pour certaines suivies de traînées noires qui correspondent à des bulles d’air. L’IRM permet ici, non seulement de caractériser la forme de ces bulles d’air, mais également d’attester leur stabilité au cours des 18 h d’expérience (sans quoi ces zones seraient entourées d’artefacts). Les champs de vitesse mesurés font enfin clairement apparaître des structures d’écoulement en forme de tourbillons au voisinage des pales, et présentent en outre un rapport signal sur bruit d’une qualité suffisante pour être exploités numériquement.

Gel de carbopol brassé par le malaxeur à 60 tr min–1. Visualisation des composantes horizontales de la vitesse dans une coupe plane horizontale de la cuve en anneau. Sur l’image de fond, le gel apparaît en blanc. Le champ de vitesse est matérialisé par les petits vecteurs.
4 Conclusion
Les deux exemples traités dans cet article illustrent les champs d’application qui s’offrent à la vélocimétrie IRM dans les domaines de la rhéologie et de la mécanique des fluides. Grâce à des améliorations méthodologiques simples, et grâce à l’insertion de rhéomètres dans l’IRM, de nouveaux horizons s’ouvrent pour le rhéologue, qui peut étudier de manière plus détaillée et plus précise un nombre croissant de systèmes. Les possibilités présentées ici pour la réalisation d’études dynamiques devraient maintenant permettre d’approfondir l’étude des fluides thixotropes.
Vis-à-vis de la mécanique des fluides, la vélocimétrie, bien que peu répandue, se révèle également être un outil efficace pour caractériser quantitativement les écoulements stationnaires autour de géométries complexes. Cette méthode, qui présente l’avantage de ne pas utiliser de traceurs, devrait également obtenir un rôle de référence pour la validation de codes de calcul grâce à la qualité de ces mesures. Il est donc très probable que la vélocimétrie par IRM parviendra bientôt à s’imposer parmi les autres techniques de vélocimétrie 3D pratiquées couramment.
Remerciements
Les auteurs tiennent à remercier J.-S. Raynaud, pour les discussions sur les méthodes de mesure de vitesse, et J.-P. Guilbaud, pour l’aide qu’il a apportée à la conception et à la mise en place des dispositifs expérimentaux.


