1 Introduction
Les facteurs de croissance régulent l'équilibre entre la mort et la survie cellulaire nécessaire au maintien de l'homéostasie lymphoïde. Des études récentes ont montré que Akt, aussi connue sous le nom de PKB (protéine kinase B), joue un rôle central dans la survie lymphocytaire comme dans la survie d'autres types cellulaires. Akt s'illustre en tant que protéine relais d'une cascade de signalisation par laquelle une pléiade de stimuli extracellulaires, comme les facteurs de croissance et autres interleukines, répriment l'apoptose [1–3]. AKT est une cible majeure de la PI3-kinase, la phosphorylase des lipides membranaires, elle-même sous le contrôle de récepteurs tyrosine kinase sur lesquels se fixent les hormones. AKT est exprimée ubiquitairement en trois isoformes identifiées chez l'homme : Akt-1/PKBα, Akt-2/PKBβ et Akt-3/PKBγ (deux sous-classes). Il s'agit de protéines d'une soixantaine de kilo-Daltons dont la similitude de séquence est de l'ordre de 80%. Chacun des membres de cette sous-famille est constitué d'un domaine homologue à la pleckstrine (PHD) en amino-terminal, d'une boucle charnière, d'un domaine phosphorylase et d'un motif hydrophobe de régulation en carboxy-terminal. Lors de l'activation d'AKT, le PHD interagit avec des phosphoinositides phosphorylés sur la position 3' (les phosphatidyl-inositol 3,4-bisphosphate et phosphatidyl-inositol 3,4,5-trisphosphate) par la phosphatidyl-inositol-3-kinase (PI3K). Cette interaction facilite la translocation d'AKT du cytoplasme à la membrane où elle est ensuite activée.
La détermination de la structure 3D du PHD d'AKT2 (AKT2–PHD) a été entreprise au laboratoire. L'analyse d'expériences hétéronucléaires 3D triple résonance a permis d'attribuer la majorité des résonances spectrales 1H, 15N et 13C, à l'exception de celles des résidus appartenant à deux segments peptidiques (Glu59–Gln61 et Arg76–Thr87) reliés par un pont disulfure. Ces deux segments sont situés dans des boucles « variables » flexibles du PHD (Fig. 1). Nous avons pu démontrer par des expériences préliminaires que cette perte d'information n'était pas due à l'échange chimique des protons amides contre les protons du solvant. La perte des signaux correspondants pourrait être attribuée à l'existence de mouvements sur une échelle de temps intermédiaire, probablement associés à des phénomènes d'isomérisation du pont disulfure. Une autre explication pourrait être un échange (toujours sur la même échelle de temps) entre une forme monomère de la protéine et un état plus ou moins oligomérisé, impliquant les boucles concernées dans une interaction intermoléculaire. En effet, la dimérisation des PHD est un phénomène qui a déjà était observé pour d'autres protéines contenant ce motif. Afin de déterminer l'état d'oligomérisation du PHD d'AKT2 en solution, nous avons déterminé son temps de corrélation rotationnel par les méthodes de relaxation 15N ainsi que son coefficient de diffusion translationnel par la méthode RMN de DOSY 2D.

Superposition des 20 « meilleures » structures obtenues par modélisation des données RMN grâce au programme X-PLOR. Les segments colorés en vert correspondent aux deux segments peptidiques non attribués.
2 Matériels et méthodes
Les spectres RMN ont été enregistrés à 13 °C sur des échantillons d'AKT2–PHD marqués 15N à une concentration de 0,4 mM, dissout dans un tampon Tris-HCl 10 mM, NaCl 300 mM, pH 7,4 (H2O + 5–10% 2H2O pour les expériences de relaxation, 100% 2H2O pour les expériences de diffusion), et en présence de 4 mM de Ins(1,4,5)P3 (inositol-(1,4,5)-tris-phosphate), un analogue de la tête polaire des phosphatidyl-inositides. Les expériences ont été réalisées sur des spectromètres Bruker AVANCE 500 MHz (mesures de relaxation) et 600 MHz (DOSY) équipés de sondes 5 mm 1H-13C-15N triple-resonances, conventionnelles (600 MHz) ou cryogéniques (500 MHz). Les deux types de sondes sont équipés de bobines capables de délivrer des impulsions de gradient Z d'environ 50 G cm–1. Les spectres RMN ont été traités à l'aide du logiciel Gifa (version 4.4) [4].
2.1 Mesures de diffusion
Les expériences de diffusion ont été réalisées à l'aide d'une séquence d'impulsion LED [5] modifiée, utilisant des gradients bipolaires [6,7] pour prévenir les effets parasites dus aux courants de Foucault. Le signal résiduel d'HDO était supprimé par une irradiation à faible puissance pendant le délai de relaxation (1 s) et le délai de diffusion (400 ms). Pour déterminer le coefficient d'autodiffusion d'AKT2–PHD, 90 expériences 1D ont été enregistrées avec des délais de diffusion identiques et des impulsions de gradient de champ d'une durée de 2,4 ms et d'intensité variant entre 2 G cm–1 et 47,5 G cm–1 (4 à 95% de la puissance maximale de l'amplificateur de 10 A). Chaque expérience provenait de l'accumulation de 544 balayages (4 K points complexes). Le coefficient de diffusion d'AKT2–PHD a été obtenu à partir du déclin de l'intensité des pics en fonction de l'intensité des gradients par un traitement de type « maximum d'entropie » (MaxEnt) [8], avec une transformée de Laplace inverse calculée sur 128 points. Le poids moléculaire correspondant a été déduit, sans tenir compte d'aucun facteur de forme, d'une courbe d'étalonnage établie sous les mêmes conditions expérimentales à partir de protéines de poids moléculaire connu (ubiquitine : 8,5 kDa ; lysozyme : 14 kDa ; myoglobine : 16,9 kDa ; inhibiteur trypsique de soja : 24 kDa ; ovalbumine : 42,9 kDa).
2.2 Mesures de relaxation
Quand la relaxation d'un noyau 15N dépend essentiellement de l'interaction dipolaire avec un proton directement lié et de l'anisotropie de son déplacement chimique, les données de relaxation peuvent être interprétées en termes de mouvement du vecteur 15N–1H [9]. Sachant que les trois paramètres de relaxation mesurés expérimentalement (RN(Nz), RN(Nxy) et NOE) dépendent des valeurs des fonctions de densité spectrale à cinq fréquences différentes [10,11], le calcul des densités spectrales peut être approché par l'approximation des hautes fréquences permettant un échantillonnage « réduit », grâce auquel les vitesses de relaxation sont directement traduites en densités spectrales à trois fréquences [12–15] par la relation :
| (1) |
dans laquelle
où μ0 est la perméabilité du vide, h la constante de Planck, γH (2,6752 × 108 rad s–1 T–1) et γN (–2,711 × 107 rad s–1 T–1) les rapports gyromagnétiques des noyaux 1H et 15N, ωH et ωN les fréquences de Larmor 1H et 15N, rNH la distance internucléaire 15N–1H (1,02 Å), B0 l'intensité du champ magnétique et Δσ la différence entre les composantes parallèles et perpendiculaires du tenseur de déplacement chimique 15N de symétrie axiale (–170 ppm [16]). La vitesse de corrélation croisée RN(Hz → Nz) entre l'15N et le proton amide est corrélée au NOE et calculée par la relation : NOE = 1 + (γH/γN) RN(Hz → Nz)/RN(Nz). La fréquence de la densité spectrale moyenne, <J(ωH)>, a été prise égale à 0,87 ωH [12].
Les séquences d'impulsions utilisées pour déterminer les valeurs des vitesses de relaxation 15N RN(Nz) (R1), RN(Nxy) (R2), et de 15N{1H}NOE sont similaires à celles déjà décrites [10,11], et les paramètres expérimentaux utilisés ainsi que le traitement des données ont déjà été reportés en détail pour d'autres protéines étudiées au laboratoire [17,18]. La vitesse de relaxation longitudinale 15N (RN(Nz)) a été obtenue à partir de 10 expériences d'inversion–récupération, avec des délais de relaxation allant de 18 à 1026 ms. La vitesse de relaxation transverse 15N (RN(Nxy)) a été obtenue à partir de 10 expériences CPMG, avec des délais de relaxation allant de 16 à 144 ms. La valeur du NOE hétéronucléaire, 15N{1H}, a été déterminée à partir du rapport de deux expériences réalisées avec et sans présaturation des protons.
3 Résultats
3.1 Expériences de diffusion
Dans le cas d'une solution idéale et à dilution infinie, le coefficient de diffusion translationnel d'une molécule est donné par la relation de Stokes–Einstein :
Il est néanmoins possible, à partir du coefficient de diffusion, d'obtenir une information relative sur la masse d'une protéine via une courbe d'étalonnage construite à partir de mesures réalisées dans des conditions expérimentales strictement identiques sur des protéines de masse moléculaire connue. Pour des protéines sphériques et de même « compacité » (densité moyenne identique), D peut être exprimé selon :
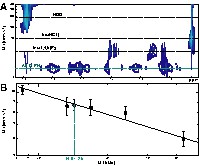
(A) Spectre 2D DOSY enregistré sur AKT2–PHD dans les conditions expérimentales utilisées pour son étude structurale (voir § Matériel et Méthodes). Les différentes espèces en présence apparaissent parfaitement séparées en fonction de leur coefficient de diffusion respectif, et sont indiquées sur des lignes horizontales. (B) Détermination de la masse moléculaire d'AKT2–PHD (rond bleu) par la courbe d'étalonnage construite à partir des coefficients de diffusion mesurés pour des protéines de masse moléculaire connue (voir § Matériel et méthodes).
3.2 Relaxation 15N
Les paramètres de relaxation ont pu être mesurés précisément pour 71 résidus d'AKT2–PHD (111 résidus, dont sept prolines et 18 résidus non attribués) et les densités spectrales correspondantes calculées en utilisant l'équation (1) (Fig. 3). Les faibles valeurs de J(0) obtenues pour les résidus N- et C-terminaux, ainsi que pour les segments peptidiques Gly16–Thr21 et Arg41–Leu52, indiquent une flexibilité accrue. Ces deux segments correspondent aux boucles variables VL1 et VL2. Dans ces régions, les faibles valeurs de J(0) sont compensées par des valeurs élevées de <J(ωH)>, en bon accord avec l'hypothèse de la conservation de l'énergie du système. Les faibles valeurs de <J(ωH)> obtenues pour le reste de la protéine indiquent une flexibilité restreinte sur une échelle de temps rapide. À 50 MHz, les valeurs de J(ω) montrent un profil inverse de celui observé pour celles de J(0) : des valeurs légèrement plus élevées sont observées pour les vecteurs NH localisés dans les boucles VL1 et VL2. Ceci démontre que J(ωN) est légèrement supérieur à la fréquence isobestique, fréquence pour laquelle les contributions à J(ω) sont indépendantes de la mobilité interne. Les valeurs de J(0) mesurées pour les résidus Thr72 et Val57 sont significativement plus élevées que la moyenne, sans pour autant être compensées par des valeurs plus faibles de J(ωN) et <J(ωH)>. Ceci indique la présence de mouvements plus lents que le temps de corrélation de la protéine, sur une échelle de temps comprise entre la micro- et la milliseconde. Ces contributions adiabatiques s'observent fréquemment autour des résidus aromatiques (Phe73 et Phe55) ou près d'un pont disulfure (Cys60–Cys77) : le déplacement des cycles aromatiques ou l'isomérisation des ponts disulfure entraînent des variations importantes de déplacement chimique, qui vont constituer des chemins de relaxation efficaces et contribuer ainsi à la relaxation transverse (terme R2ex), majoritairement représentée dans la valeur de la fonction de densité spectrale à fréquence nulle. Un mécanisme similaire peut être invoqué pour expliquer la dispersion des valeurs de J(0) observées dans l'hélice C-terminale.
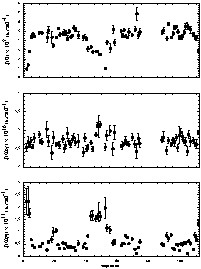
Valeurs des densités spectrales calculées via l’équation (1) à partir des temps de corrélation et des valeurs de 15N{1H}NOEs mesurées sur le domaine PH d'AKT2, en fonction de la séquence.
En analysant les données de relaxation obtenues pour différentes protéines, Lefèvre et al. [15] ont montré qu'il existait souvent une corrélation linéaire entre J(0) et J(ωN) :
| (2) |
Les données obtenues montrent que cette relation se vérifie pour AKT2–PHD (Fig. 4A). Si l'on considère que les mouvements mis en jeu dans une protéine sont limités par des mouvements purement diffusifs (Brownien) [15,19], un modèle lorentzien peut être utilisé pour décrire les densités spectrales :
| (3) |
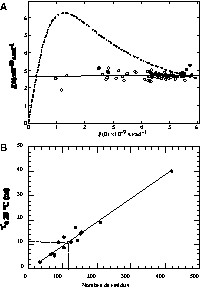
(A) Corrélation linéaire entre J(0) et J(ω) obtenu pour les vecteurs NH à partir de la mesure des temps de relaxation 15N (voir § Matériel et méthodes). La courbe est obtenue en utilisant un modèle lorentzien pour les densités spectrales. (B) Détermination du nombre de résidus d'AKT2–PHD grâce à une courbe d'étalonnage établie à 20 °C à partir de données de relaxation enregistrées sur des protéines publiées dans la littérature. La valeur du temps de corrélation obtenue à 13°C pour AKT2–PHD a été corrigée en appliquant la loi de Stokes–Einstein. Masquer
(A) Corrélation linéaire entre J(0) et J(ω) obtenu pour les vecteurs NH à partir de la mesure des temps de relaxation 15N (voir § Matériel et méthodes). La courbe est obtenue en utilisant un modèle lorentzien ... Lire la suite
La courbe théorique correspondant à ce modèle est reportée sur la Fig. 4A. Si l'on combine (2) et (3), on obtient une équation du troisième degré en τc:
| (4) |
On notera que certains points (cercles pleins : non pris en compte pour la régression linéaire) se trouvent hors ou très près de la courbe théorique : ils correspondent à des vecteurs – déjà signalés plus haut – animés de mouvements complexes (échange conformationnel...) dans un domaine de temps supérieur (μs–ms) au simple mouvement brownien (ns) de la protéine en solution. Les racines de l'équation (4) sont les temps de corrélation représentatifs des mouvements animant les vecteurs NH. Les coefficients αN et βN pouvant êtres déduits de la régression linéaire, cette équation se résout alors simplement. Une de ces racines est négative (–601 ns) et ne sera pas considérée, car elle n'a pas de sens physique. Les deux autres racines positives correspondent au temps de corrélation rotationnel de la protéine (τc = 13,81 ns) et à un temps de corrélation interne globale appelé τi [15,20] (τi = 0,70 ns). Ce temps de corrélation τi ne doit pas être considéré comme un paramètre physique. Il indique simplement l'existence d'une contribution de mouvements internes complexes au mouvement de chaque vecteur NH, sur une échelle de temps moyenne proche de la valeur de τi.
Il existe une relation empirique entre la valeur du temps de corrélation et le nombre de résidus de la protéine, établie à travers de nombreuses études de relaxation réalisées sur différentes protéines, de tailles diverses. Cette relation montre une corrélation linéaire entre le temps de corrélation et le nombre de résidus de la protéine (Fig. 4B). D'après cette relation et le temps de corrélation rotationnel précédemment déterminé, on peut déduire que le nombre de résidus d'AKT2–PHD est d'environ 117 résidus, ce qui est très proche de la taille du monomère (113 résidus).
4 Discussion
Nous avons utilisé deux méthodes RMN pour déterminer l'état d'oligomérisation d'AKT2–PHD. Ces deux méthodes reposent sur des bases physiques très différentes. La mesure du temps de corrélation rotationnel par les techniques de relaxation met en jeu des propriétés microscopiques des spins, basées sur une modulation de leurs interactions par les mouvements de la protéine en solution. La mesure du temps de corrélation translationnel par les méthodes de diffusion reposent quant à elles sur une propriété macroscopique de la molécule en solution. Les deux méthodes donnent des résultats convergents et attestent un état monomérique pour la protéine en solution, dans les conditions utilisées pour son analyse structurale. La perte d'information aux niveaux des deux segments peptidiques précédemment cités est donc due à leur dynamique particulière, incluant des mouvements sur une échelle de temps intermédiaire.
On notera que, bien que de natures a priori différentes, nous attendons bien une valeur identique pour ces deux temps de corrélation : la dilution du soluté met en jeu essentiellement le mouvement brownien et conduit à une réorientation isotrope. D'un point de vue pratique, les mesures de DOSY paraissent apporter une solution plus rapide à notre question. En fait, la diffusion des protéines en solution est très sensible aux conditions expérimentales (notamment la température et la force ionique), ce qui implique la réalisation d'une courbe d'étalonnage et, donc, augmente notablement le temps de mesure. En contrepartie, les mesures de relaxation, a priori plus fastidieuses, permettent d'accéder, en plus du temps de corrélation rotationnel, à la dynamique interne de la protéine, mais nécessitent une protéine enrichie en 15N. Enfin, la méthode des corrélations linéaires permet de s'affranchir de tout modèle pour l'analyse des mouvements.


