1 Introduction
In NMR, knowing the quadrupole coupling ωQ of a nucleus with spin I ≥ 1 allows us to determine the local symmetry of a crystallographic site in solids. Since the variation of the line intensity with a radio-frequency (RF) pulse duration depends on ωQ, the one-dimensional (1D) nutation method, which records a series of spectra for increasing RF pulse duration, allows us to extract the value of ωQ via an iterative fitting of the experimental line intensities to the theoretical curve.
The piezoelectric effect [1,2] from a ferroelectric crystal [3–5] and the ringing effect [6,7] from the NMR probe head tuned for low gyromagnetic ratio nuclei introduce spurious signals when the one-pulse sequence (Fig. 1A) is used to excite the spin system. Experimentally, a suitable modification of the NMR probe head [8] or the application of a two-pulse Hahn echo sequence [9] can cancel these spurious signals. Recently, we have applied a composite-pulse sequence [10], consisting of three pulses (Fig. 1B) with the same duration (t1 = t2 = t3), to cancel the ringing effect from the probe head in the spectra of 131Xe (I = 3/2) physisorbed on NaY zeolite [11,12]. The main advantages of this sequence over the above two methods are the use of a standard NMR probe head and the simplicity for optimising the line intensity. The Hahn echo sequence requires optimisation of three parameters: the two durations of pulses and that between these two pulses. On the other hand, there is only one parameter to determine for the composite-pulse sequence: the three pulses have the same duration.

(A) One-pulse sequence with duration t1 and (B) composite-pulse sequence consisting of three pulses without any delay between them. We used three pulses of the same duration (t1 = t2 = t3). Due to the acquisition delay d, the FID acquisition starts at point A.
The LiNbO3 crystal is a ferroelectric and piezoelectric oxide with a great variety of applications. It is used, in the undoped form, for acoustic-optic, piezoelectric, linear and non-linear optical applications, and in the doped form, for laser action in bulk samples and in wave-guide structures [13,14]. In fact, the centre of gravity of the positive charges in the LiNbO3 crystal does not coincide with that of the negative charges, resulting in a macroscopic electric dipole (ferroelectric property). When the one-pulse sequence is applied to 7Li (I = 3/2) in LiNbO3 crystal, spurious (or piezoelectric) signals are observed [15]. These signals are due to the vibration of the macroscopic electric dipole of the crystal, caused by the electric field associated with the RF magnetic field B1 during the excitation of the spin system (piezoelectric property).
The present paper proposes the composite-pulse sequence to cancel the piezoelectric signals from a LiNbO3 single crystal. The 1D nutation method with the one-pulse sequence has already been applied by Shin and co-workers [16] for the study of the electric quadrupole interaction of the 7Li nucleus in LiNbO3 crystals. Unfortunately, the spin–lattice relaxation time of 7Li in the LiNbO3 crystal is unknown, but certainly more than 100 s. As a result, the line intensities are not quantitative. This fact prevents us from determining ωQ by fitting the line intensities against the pulse duration of the one-pulse sequence or that of the composite-pulse sequence with the theoretical curve.
2 Java applets
In theoretical NMR studies of half-integer quadrupole spins, usually only the static first-order quadrupole interaction HQ(1) is taken into account during the RF pulses. This interaction represents the coupling of the nuclear electric quadrupole moment eQ with the electric-field gradient (EFG) generated by the surroundings of a nucleus. The two terms HQ(1) and ωQ are related as:
In the condition of high magnetic field B0, the central line of a half-integer quadrupole spin system in a powder is featureless. As a result, lineshape analysis is not suitable for determining the two quadrupole parameters: QCC and η. The NMR line intensity, which depends on the various interactions involved during the RF pulses, is proportional to the amplitude of the first sampled point of a free-induction decay (FID) or the integrated area of the corresponding spectrum. The 1D nutation method allows the determination of ωQ for a single crystal or QCC and η for a powder. In other words, the line intensity depends not only on the RF pulse duration, but also on the ratio of ωQ to the amplitude ωRF of the RF pulse for a single crystal, or the ratio of QCC to ωRF for a powder. However, there is an upper limit to these ratios, above which the line intensity does not change any more for a given RF pulse duration.
Java applets, which calculate 1D nutation line intensities and extract the value of ωQ in a single crystal or those of QCC and η in a powder, are available in our website www.pascal-man.com. They are software programs that execute via a browser such as Internet Explorer, Netscape, Opera or HotJava, regardless of the computer used (PC, Mac, mainframe...). The four half-integer quadrupole spins (I = 3/2, 5/2, 7/2, and 9/2) can be excited by various RF pulse sequences (one-pulse, Hahn echo, MQ-MAS, Solomon echo...). First, the Java applet associated with a specific sequence calculates the theoretical nutation line intensities of the central transition with experimental parameters (the spin I, the amplitude ωRF, the variable pulse duration and its increment) and estimated values for ωQ or QCC and η. Then, it extracts the value of ωQ or that of QCC by fitting your experimental central line intensities with the theoretical curve. One application of these Java applets is the quantification of EFG in the supercage of Y zeolites by means of a 131Xe NMR experiment [17].
3 Experimental
The size of the LiNbO3 crystal is 5 × 5 × 20 mm3. The 7Li NMR was performed with a Bruker MSL300 multinuclear high-power spectrometer, where the resonance frequency of 7Li is 116.6 MHz. The static probe head was equipped with a solenoid coil 10 mm in diameter and 35 mm in length. Two series of experiments were performed with increasing t1 from 4 to 20 μs by steps of 2 μs: one with the one-pulse sequence and the other with the composite-pulse sequence where t1 = t2 = t3. These pulse sequences also include CYCLOPS in their phase cycling. The other acquisition conditions are: a recycle delay of 100 s, an acquisition delay d of 8 μs, and 48 scans. The pulse program of the composite-pulse sequence can be found on our website.
4 Results and discussion
Fig. 2 presents two series of 7Li FIDs for the LiNbO3 crystal for increasing t1 of the one-pulse sequence, observed in the two detection channels u (Fig. 2A) and v (Fig. 2B) of the receiver with quadrature detection. Each curve shows a complex FID superimposed on that of the spin system. This complex FID expresses the piezoelectric effect of the LiNbO3 crystal and its duration is about 0.6 ms. The latter is comparable to that observed with 23Na (I = 3/2) NMR in a NaNO2 crystal by Pandey and Hughes [18], which is about 0.4 ms. However, it is much longer than that of the complex FID from the ringing effect in the case of 131Xe physisorbed on NaY zeolite, where its duration is about 0.08 ms [11,12,17].

FIDs of 7Li in a single crystal of LiNbO3 following the one-pulse sequence for t1 increasing from 4 to 20 μs in steps of 2 μs and for the two detection channels u (A) and v (B) of the receiver with quadrature detection.
It should be mentioned that when the piezoelectric oxide is in powder form, the centre of gravity of the positive charges from all the crystallites of the powder coincides with that of the negative charges. In other words, the macroscopic electric dipole does not exist in a powder. Therefore, the piezoelectric effect is not observed with the one-pulse sequence.
Figs. 3A and 3B show the 7Li FIDs of the LiNbO3 crystal observed in the two channels u and v of the receiver and for increasing t1 of the composite-pulse sequence. The complex FIDs (Fig. 2) observed with the one-pulse sequence were cancelled whatever the duration t1 of the composite-pulse sequence. Only the FID of the spin system remains and its duration is about 0.2 ms, which is shorter than that of the complex FID. In fact, this composite-pulse sequence cancels the ringing and the piezoelectric effects even when the durations of the three pulses are not identical (t1 ≠ t2 ≠ t3); however, the variation of line intensity will be changed. This variation can be predicted with the Java applets.
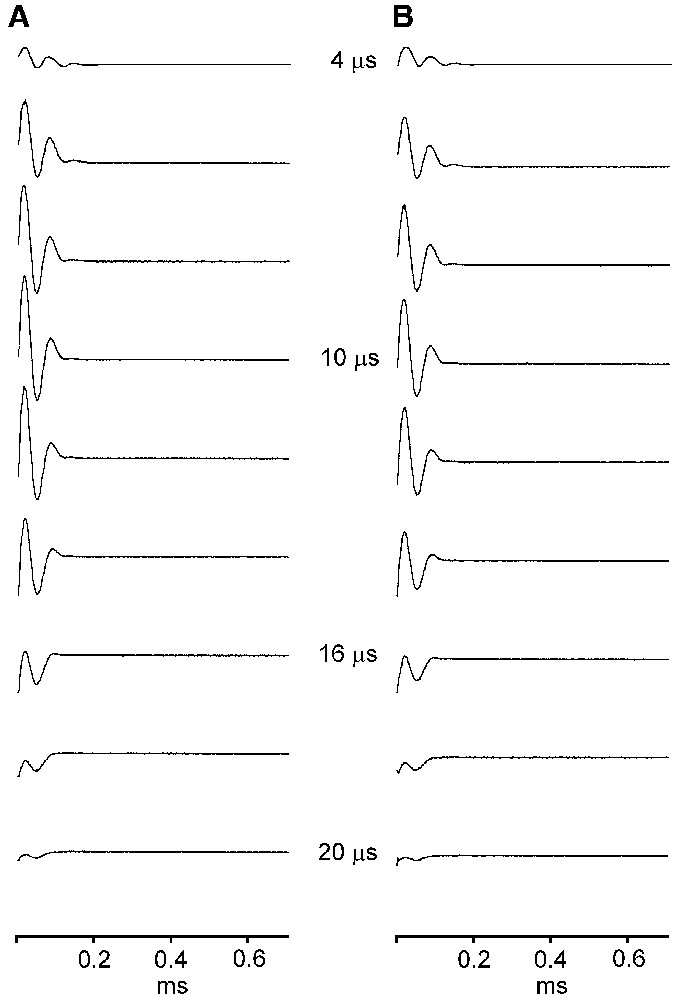
FIDs of 7Li in a single crystal of LiNbO3 following the composite-pulse sequence for t1 = t2 = t3 increasing from 4 to 20 μs in steps of 2 μs and for the two detection channels u (A) and v (B) of the receiver with quadrature detection.
Fig. 4A shows the Fourier transform of the one-pulse FIDs of Fig. 2. The spectra consist of sharp lines from the piezoelectric effect on both sides of those of 7Li located around 0 ppm. The spectrum of 7Li should consist of a central line and of two equally spaced satellite lines. However, the splitting of these three lines is not sufficient due to the small value of ωQ, resulting of an overlapping of these lines. Fortunately, the piezoelectric effect on the spectrum is less dramatic than on the FID, since it generates sharp lines outside those of 7Li. In comparison, the ringing effect distorts the baseline of the spectrum so efficiently that the NMR line of the nucleus becomes difficult to recognise [17]. Since the spin–lattice relaxation time of 7Li in this crystal is much longer than the recycle delay used, we did not attempt to extract the value of ωQ from our nutation experiments by means of an iterative fitting of the line intensities with our Java applets.

7Li (A) one-pulse spectra and (B) composite-pulse spectra of LiNbO3 crystal corresponding to Figs. 2 and 3, respectively.
Fig. 4B presents the Fourier transform of the composite-pulse FIDs of Fig. 3. These spectra are those of 7Li without the sharp lines due to the piezoelectric effect, as shown in Fig. 4A. For a pulse duration t1 shorter than 12 μs, the central line and the two equally spaced satellite lines of 7Li are observed. The 7Li spectra in Fig. 4B differ from those of Fig.4A. This is due to the different spin dynamics involved in the excitation of the spin system by the two sequences. Since the resonance frequency of satellite lines depends on the orientation of the crystal relative to the static magnetic field B0, whereas that of the central line does not [19], it would be necessary to study the crystal with different orientations in the solenoid coil to obtain a better resolution.
5 Conclusion
We have extended our investigation on the cancellation of spurious signals that are not generated by the spin system. The composite-pulse sequence suppresses not only the ringing effect from the NMR probe head tuned for low gyromagnetic ratio nuclei, as shown previously [12], but also the piezoelectric effect due to the vibration of the macroscopic electric dipole in a ferroelectric single crystal. These effects are cancelled whatever the duration of each of the three RF pulses. From a practical point of view, for a featureless central lineshape of a half-integer quadrupole spin system in a powder, the 1D nutation method associated with Java applets should be used to determine QCC and η.
Acknowledgements
We are very grateful to Mrs Jocelyne Maquet (‘Laboratoire de chimie de la matière condensée’, CNRS UMR 7574, Paris, France) for her technical assistance and for the access to the MSL300.


