1 Introduction
The on-going interest in boron carbonitrides with general composition BxCyNz arises from the difficulty to obtain new materials for abrasives, heat sinks and protective coating applications. Ternary systems with a diamond-like structure in which some of the carbon atoms are replaced with nitrogen and boron are expected to show the same interesting properties found in diamond and cubic boron nitride, such as large hardness, wide band gap and high melting points. As a consequence their possible applications could be found in several mechanical and electronic devices [1–3]. Moreover, the low oxidation resistance of diamond, which is one of the most important drawbacks for its applications, might be improved in the boron-based hard materials. As a matter of fact diamond can only be used at around 870 K in air, while cubic boron nitride avoids the oxidation up to 1370 K [4,5]. As a first ternary ‘BCN’ system we have investigated BC2N: Graphitic BC2N was prepared in the late eighties [6–9] by Chemical Vapour Deposition (CVD) or diamond anvil. Since then several efforts have been made [1–3,10–12] to modify graphitic phases (2D) into more dense covalently bonded 3D systems. Some researchers claimed limited solubility [13,14], while others have shown segregation in a mixture of diamond and cubic-BN (c-BN) [2,10,11]. As a result the physical properties are not well characterised and the atomic structure not well defined experimentally. Our former theoretical investigations in the framework of the density functional theory have led to characterise the stability and the hardness of six novel BC2N structures obtained from a full geometry relaxation of the substituted diamond [15,16].
2 The concept of hardness
Many theoretical predictions on the hard materials have been made in the last two decades by looking at the magnitude of the bulk modulus, B0 [17,18]. But the shear modulus, G0, which defines the resistance to reversible deformation upon shape change, might be another predictor of the hardness. More recently, Teter [19] showed that for a wide variety of materials the shear modulus is actually better correlated to the Vickers hardness than the bulk modulus. However the computation of G0 calls for an accurate determination of the elastic constants cij, which are symmetry dependent, i.e. their number becomes increasingly high when the lattice symmetry is lowered. In this work we rely on a preliminary discrimination of the hardness of model two and tri-dimensional (2D, 3D) phases within the criterion of the bulk modulus B0.
Bulk modulus values in the order of B0 ~ 400 GPa were found to be in-between the calculated values for diamond B0 ∼ 464 GPa and c-BN (B0 ~ 397 GPa). Besides BC2N recently prepared by Solozhenko et al. [8,9] and simultaneously computationally announced by Mattesini et al. [15,20], to our knowledge no other stoichiometry within the BCN system is proposed in the literature. However a recent investigation of systems prepared from organic reactants has led to propose boron cyanide ‘B(CN)3’, for which model structures were proposed and investigated by IR and EELS spectroscopies [16]. The relevant feature is that upon heating the linearly connected B-(CN)-B precursors, a 2D network similar to that of graphitic C3N4 [21] was found. The authors claim that the C3N3 hetero-cycles were connected by trigonal planar boron with B–C connections. Further in view of the extension of the experimental investigations to an element belonging to the 3rd period, namely Ga [22] we develop trends for the evolutions of the physicochemical properties along the B, Al and Ga column by an investigation of XC3N3 stoichiometries (X = B, Al and Ga).
As a consequence the aim of this paper in the same framework as formerly described [15,16] is twofold:
- • (i) to provide a description of the structure and of the electronic properties for the model XC3N3 tricyanides;
- • (ii) to propose model 3D phases likely to be obtained under high pressure (and temperature) conditions.
3 Computational details
Calculations of the electronic states were carried out in the framework of Density Functional Theory (DFT) [23]. We particularly use the VASP package in which the interactions between the ions and the electrons are described by using ultra soft Vanderbilt pseudo potential (US–PP) [24,25] and the electron-electron interaction is treated within the LDA by the Ceperley–Alder exchange-correlation potential [26]. In the plane wave pseudo potential approach, the rapid variation of the potential near the nuclei is avoided by substituting the all electrons Hamiltonian with a smoother pseudo-Hamiltonian that reproduces the valence energy spectrum. The rapid variations of the wave functions near the nucleus, characterising the core states are removed. The PP allows a considerable reduction of the necessary number of plane waves per atom for transition metal and first row elements, thus force and full stress tensor can be easily calculated and used to relax atoms into their ground state. In our computational scheme the conjugate-gradient algorithm [27] is used to relax the ions of the BC3N3 system into their ground state. Optimisation of the structural parameters is performed until the forces on the atoms are less than 0.02 eV Å–1 and all stress components are less than 0.003 eV Å–3. The calculations were performed by using an energy cut-off of 434.8 eV for the plane wave basis set. The tetrahedron method with Blöchl corrections [28] as well as a Methfessel–Paxton scheme for conducting systems was applied for both geometry relaxation and total energy calculations. Brillouin-zone integrals were approximated using the special k-point sampling of Monkhorst and Pack [29]. Furthermore from US–PP calculations we obtain a qualitative picture of the electron localisation through real space electronic structure plots of the electron localisation function ELF according to Becke and Edgecombe [30].
4 Results and discussion
4.1 2D systems
In formerly investigated graphitic-like C3N4 forms [31], nitrogen chemically belongs to two different sites: Aromatic like Naro within the C3N3 hetero cycle and tertiary nitrogen Nter that connects the cycles to build the graphitic like network (see Fig. 1a for a schematic representation of the C3N3X layers). From this and from the experimental observations [16], BC3N3 is obtained as a model structure by substituting Nter by B. Preliminary tests with hetero cycles connected via B–N bonds led to a large energy destabilisation of more than 2 eV. This confirms a posteriori the assumption made experimentally on B–C connecting hetero-cycles [16].

Extended graphitic-like network of BC3N3. Carbon atoms are in red, nitrogen atoms are in blue and boron atoms are in green (c-axis is orthogonal to the figure).
Similar substitutions were carried out with Al and Ga in order to establish trends within the system; further we added the results formerly obtained for graphitic C3N4 [31]. The resulting structural setups were then fully geometry optimised (lattice constants and atomic positions) using the US–PP method described above. The results are summarized in Table 1.
Geometry optimisation for the 2D XC3N3 systems (X = N, B, Al, Ga)
| System/Property | Volume (Å3) | Energy (eV) | B0 (GPa) | Atomic radius rX (Å) [32] | a (Å) | c (Å) | dC–N (Å) | dX–C (Å) |
| BC3N3 | 63.16 | –62.123 | 236 | 0.98 | 5.00 | 2.92 | 1.33 | 1.55 |
| AlC3N3 | 84.91 | –57.835 | 32 | 1.43 | 5.67 | 3.04 | 1.33 | 1.96 |
| GaC3N3 | 85.27 | –57.065 | 27 | 1.41 | 5.66 | 3.07 | 1.33 | 1.96 |
| C3N4 | 65.86 | –64.876 | 209 | 0.92 | 4.73 | 3.40 | 1.33 | 1.45 |
For all systems minimum energy at convergence was observed for a coplanar structure with a preserved C3N3 hetero cycle in shape and non variant interatomic distance of dC–N = 1.33 Å. The change is observed for the intercycle connection which undergoes a lengthening: dB–C = 1.55 Å, while dAl–C = 1.96 Å and dGa–C = 1.96 Å. The little change for the two latter distances is due to similar covalent radii of Al and Ga. Compared with dN(ter)–C = 1.45 Å in C3N4, the larger magnitude of dB–C = 1.55 Å can be related to the larger electronegativity of nitrogen with respect to boron. From this the equilibrium volume increases in the B, Al Ga series with contributions from a,b in-plane parameters and from the c value changes. We note that with respect to C3N4 these c values are smaller due to the absence of repulsion arising form N non bonded electrons between planes when N is replaced by a IIIrd-column element with two less electrons. This leads to a strengthening of the magnitude of the bulk modulus for graphitic BC3N3. Furthermore we notice a drastic decrease of the bulk modulus within the Al and Ga members, which can be explained on the one hand by the increase of their atomic radii with respect to rB, and by the loss of covalence upon going down the 3rd-group column on the other hand.
In order to test furthermore the mechanical properties we have simulated non isotropic compressions of graphitic BC3N3. This can be done by changing the volume through selectively modifying in the hexagonal lattice the ‘a,b’ distances while ‘c’ is kept constant, i.e. isoplanar compression then by varying ‘c’ while ‘a,b’ are constant, i.e. axial compression. The E(V) results are shown in Fig. 2. The resulting bulk moduli magnitudes are B0(c) = 41 GPa and B0(a,b) = 340 GPa. The bulk modulus values were obtained from the fit of the E(V) curves using a 2nd-order Birch equation of state [17].

Energy versus volume curves for isotropic and anisotropic compression of graphitic BC3N3.
This result, which situates the isotropic B0 at an intermediate value (Table 1) can be used to propose that upon compressing BC3N3 one should firstly reduce the c parameter then at higher pressures the a,b spacings should start to change. Lastly the mean value of the two anisotropic bulk moduli gives an average <B0> ≈ 240 GPa close to the isotropic B0 magnitude (236 GPa). It should be noticed that this result is due to the lack of correlation between x,y dimensions (a,b plan) and z dimension (c axis).
An insight into the real space electronic structure around the different atomic species can be obtained by the electron localisation function (ELF) for a layer the 2D structure. We show as an example the plots for BC3N3 [30]. The ELF values range from 1 (highest localisation) to 0 (lowest localisation) with 0.5 representing the electron gas. Fig. 3a shows the ELF for graphitic plan of BC3N3 including full hetero cycle. On the one hand within the C3N3 heterocycle, maxima are observed between the C–N bonds (ELF > 0.9) as well as at Naro where one expects the lone pair, on the other hand between cycles where B–C connections show high ELF indicating strong covalent bonding. While this agrees with the experimental observations claiming B–C connections [16], it underlines the stabilisation of the extended network in this structure and leads to actually propose it as a precursor for more dense 3D materials. In Fig. 3b and c we show the interplanar electron localisation for BC3N3 and C3N4 respectively. While there is a vanishing interplanar electron localisation between C and Nter in the carbonitride, there is a non negligible localisation between B and C. This is due to the reduced repulsion along c in the carbonitride, leading to the larger c parameter (Table 1).


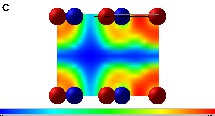
ELF plots for graphitic XC3N3. BC3N3: (a) (a,b) plan including one full C3N3 hetero cycle, (b) for an orthogonal plan including B and C in BC3N3, and (c) C3N4 for an orthogonal plan including Nter and C (see text). The density scale (between 0 and 1) is given below the graph. Note that the legend for the atoms is the same as in Fig. 1 for (a) and (b) panels, while in panel (c) the colours are inverted, where red and blue spheres refer respectively to N and C.
4.2 3D systems
The former investigations of C3N4 phases with 3D networks have led us [33] and others [3] to propose different symmetries besides the well-known β-phase. We elect here to build 3D model structures of BC3N3 starting from the latter (hexagonal) and from the tetragonal structure proposed by Teter (P–42m No111) [19]. Like in previous section the obtained geometries were fully relaxed using US–PP and a large mesh of k points for energy convergence in the respective Brillouin zones.
4.2.1 β-phase
Fig. 4 shows the β-C3N4 structure in which boron replaces nitrogen at two sites which are planar coordinated within the a,b plane. The B–C coordination can be seen to be reminiscent of the graphitic like structure studied above. The geometry optimisation did not lead to a change of the overall crystal symmetry, however due to the large B–C distances as compared to C–N ones in pristine carbonitride (a = 6.402Å, c = 2.404 Å [33]), the a lattice constant is obtained larger, whereas the c axis is shorter (a = 6.717 Å, c = 2.358 Å). The decrease of the c lattice constant is explained, like in previous section, by the fact that between two cells the boron-boron contact does not involve a repulsion as it is the case for nitrogen-nitrogen in β-C3N4 due to the lone pair of nitrogen. In fact the c axes in these hexagonal phases mirror these distances. As a consequence the bulk modulus of β-BC3N3 (B0 = 333 GPa) is found lower than that of β-C3N4 (B0 = 427 GPa [21,31]). We can note here that the bulk modulus of β-AlC3N3 amounts to a much lower magnitude of B0 ≈ 122 GPa. This can be explained ain the same framework as the assessments on size and electron repulsion considerations used in the graphitic low B0 values.

β-BC3N3 structure as optimised from β-C3N4 (colour scheme is the same as in Fig. 1).
4.2.2 Rhombohedral phase
A second 3D model structure was proposed on the basis of tetragonal C3N4 (2m [19]), which is actually a pseudo cubic structure. In this case the replacement of one nitrogen by one boron led, upon geometry optimisation, to a distorted structure for which a rhombohedral space group (R3m; No. 160) could be assigned. The crystal structure parameters were: a = 3.45 Å, α = 87.5° (ahex = 5.07 Å, chex = 5.43 Å). Fig. 4 shows the obtained structure in which the C3N3 hetero cycle of the graphitic structure is now shown in a ‘chair-like’ conformation. Further the B–C connections are shown to be maintained albeit in a tetrahedral-like (i.e. not coplanar) configuration. From total energies this phase is stabilised by 1 eV per formula unit with respect to the β-phase (Fig. 5).

Rh-BC3N3 structure (colour scheme is the same as in Fig.1.).
The bulk modulus for the new structure obtained in the same manner as above is found to be B0 = 358 GPa. Its slightly larger magnitude as compared to β-BC3N3 can be explained on the basis of the tetrahedral arrangement of the atoms. Further the stabilisation energy favours the new rhombohedral structure. Turning to the Al member we find B0(AlC3N3) ≈ 325 GPa with a 3–eV energy stabilisation with respect to the β-phase. With a magnitude of energy stabilisation three times that of 3D BC3N3 phases, the large energy stabilisation of rhombohedral AlC3N3 makes the β-phase a true intermediate metastable structure when pressure is increased from the 2D precursor system. This is due to the fact that Al is rarely found in a planar coordination such as in the β-structure. The small magnitude of the β-phase bulk modulus is equally related to this instability. This can be equally connected to the electronic structure of the 3D systems, which shows a passage from metallic (2D) to semi-conducting behaviour of 3D phase (rhombohedral) [34].
5 Concluding remarks
This work which starts from well established ideas of systematic search for new candidates for ultra hard materials complying with isoelectronic rule with carbon [41] is opening a new route for finding new binary and ternary systems with a departure from this rule. The extension of our investigations to the XC3N3 series with X = B, Al, Ga has led to establish chemical trends for the role of the substituting elements. Other precursors could equally be selected either by completing the III rd-column elements or from the 4th period (Ga, As, etc.) for the sake of providing a complete picture for this new interesting class of materials. In this context the search for new hard materials could be the non unique objective in as far as the chemical role of the studied elements can lead to further understand the possibilities of phase preparations (2D, 3D) as well as 2D→3D phase transitions.
Acknowledgements
Computational facilities of the intensive numerical calculations scientific pole M3PEC of the University Bordeaux-1 are gratefully acknowledged. One of us (R.W.) thanks the Training and Mobility of Researchers (TMR) Network: Synthesis, structure and properties of New Carbon based Ultrahard Materials for a 6-month scholarship at the ICMCB–CNRS in 2002.
One of us (E.B.) acknowledges the Aquitaine Régional Council for its financial support.


