1 Introduction
Many photochemical and photophysical studies continue to be dedicated to transition metal clusters, owing to their potential application as site-selective photocatalysts under mild reaction conditions or as building blocks in the design of supramolecular assemblies [1]. Time resolved infrared (TRIR) spectroscopy is a particularly suitable experimental technique to investigate the behavior of carbonyl derivatives, since the carbonyl stretching frequencies serve as a very efficient probe to detect any chemical or electronic change in the surroundings of the CO ligands. The combination of UV–vis flash photolysis with TRIR detection allows the investigation of clusters in excited states, short-lived transient species and photoproducts by means of their IR absorption. Recent developments in experimental techniques have led to the detection of species with increasingly shorter lifetimes. Initially, mononuclear transition metal carbonyl complexes (Cr, Mo [2], Ru, Os [3], Co [4]) were studied by picosecond TRIR spectroscopy. Other TRIR studies followed, addressing both dinuclear [M2(CO)10] (M = Mn [5], Re [6]) as well as trinuclear species, such as [Ru3(CO)12] [7], [Ru3(CO)8(μ-CO)2(4,4′-dimethyl-2,2′-bipyridine)] [8], and [Os3(CO)10(cyclohexa-1,3-diene)] [9]. For [Ru3(CO)12], the ps TRIR experiments showed the formation of a short-lived transient species containing a CO bridge, in agreement with the open-core transient structure proposed in the literature [5]. In contrast to this, no CO-bridged species was detected for the analogous cluster [Os3(CO)12]1. The ps TRIR experiments on the clusters [M3(CO)12] revealed the need for updating the available computational studies in order to explain the observed differences in the reactivity. They prompted us to reexamine the bonding situation in [M3(CO)12] (M = Ru, Os), as well as the nature and energies of their frontier orbitals and electronic transitions, using DFT [10] and TD-DFT [11] calculations. A new interpretation of the experimental photochemical data are presented in the light of the theoretical results obtained.
2 Results and discussion
2.1 Structures
The first step of the work consisted of a full geometry optimization of the two [M3(CO)12] clusters (M = Ru, 1; Os, 2). Although this problem has been addressed in an earlier publication [12], and the results were satisfactory for the ruthenium complex, the same did not apply to [Os3(CO)12], as all the calculated Os–Os distances were systematically too long. The availability of new basis sets including polarization functions for the metals, as well as an improved treatment of relativistic effects, which cannot be neglected for osmium derivatives, led to a much better quality of the calculated structures [9]. In contrast to the earlier work, full optimizations (ADF [13] program), without any symmetry constraints, have led to two slightly different geometries [14]: a so-called ‘D3h’ geometry, where the carbonyl groups either lie in the equatorial M3-plane, or are perpendicular to it, and a less symmetric arrangement, where one of the M(CO)4 fragments has rotated. The two geometries, as well as their M–M distances, are shown in Fig. 1 for [Ru3(CO)12] and [Os3(CO)12].
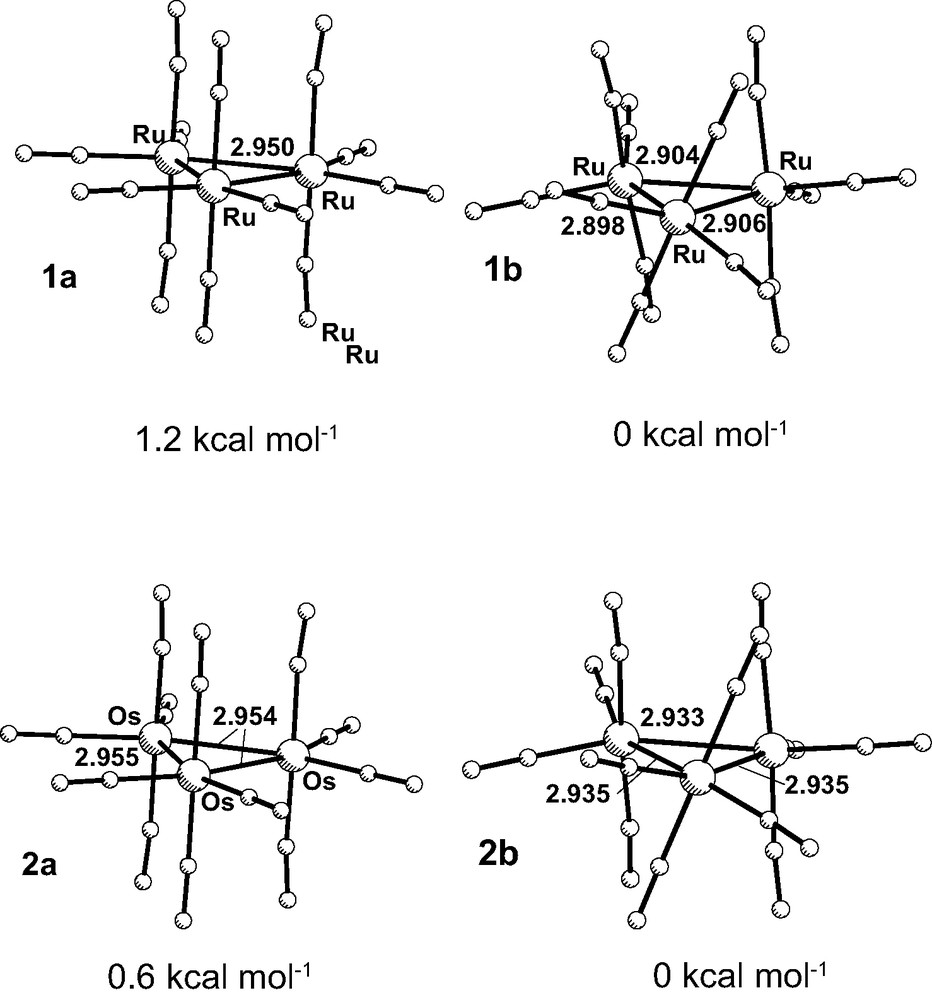
Optimized (ADF) structures of [M3(CO)12], with ‘D3h’ symmetry (1a/2a, left) and without symmetry (1b/2b, right), and M–M distances (Å).
The less symmetric arrangement 1b is more stable by 1.2 kcal mol–1, while for osmium the difference is only 0.6 kcal mol–1, the most stable form being again the rotated one (2b), compared to the ‘D3h’ one (2a). As ADF frequency calculations would take too long to run, the two geometries were used as input to run a B3LYP [15] optimization, with Gaussian 98 [16]. Only one geometry was found (the less symmetric one, 1bg), regardless of the starting geometry, and it was a minimum. In the available X-ray structures of the two clusters, the D3h arrangement is always observed for both Ru and Os [17]. Several structures obtained at different temperatures, have been reported for both [M3(CO)12] clusters, as disorder, resulting from the fluxionality of the carbonyl ligands, is a frequent problem. However, the energy difference between the symmetric and the rotated arrangements, calculated with ADF, can be easily overcome by crystal packing forces. On the other hand, for the mixed-metal cluster [Ru2Fe(CO)12] [18], the rotated geometry has been found in the crystal structure. The calculated Ru–Ru distances in 1b are the shortest (2.898, 2.904, 2.906 Å), and thus most closely reproduce the experimental parameters (2.85, 2.85, and 2.86 Å), regardless the difference in the carbonyl arrangements. In 1bg, the calculated distances range between 2.911 and 2.913 Å. The agreement can be considered good in any of the calculations.
A similar situation is found for [Os3(CO)12]. As noted above, the rotated form (2b) is more stable than the ‘D3h’ geometry (2a) by 0.6 kcal mol–1 (Fig. 1), while according to a B3LYP calculation, only one minimum is found (2bg). The calculated Os–Os distances are 2.933, 2.935, 2.935 Å (2b, ADF), 2.954, 2.954, 2.955 Å (2a, ADF), 2.957, 2.959, 2.960 Å (2bg), comparing well with the experimental values (2.87, 2.88, 2.88 Å). Again, the best agreement is provided by the 2b geometry.
2.2 Frontier orbitals
The frontier orbitals were calculated (ADF) for both geometries of the Ru and Os clusters and there are no significant differences, neither in energy nor localization. As the orbitals are, however, much easier to visualize in the more symmetric structures 1a and 2a, the most relevant frontier orbitals of these two structures are shown in Figs. 2 and 3, for the [Ru3(CO)12] and [Os3(CO)12] clusters, respectively. Their compositions are given in Tables 1 and 2, respectively.
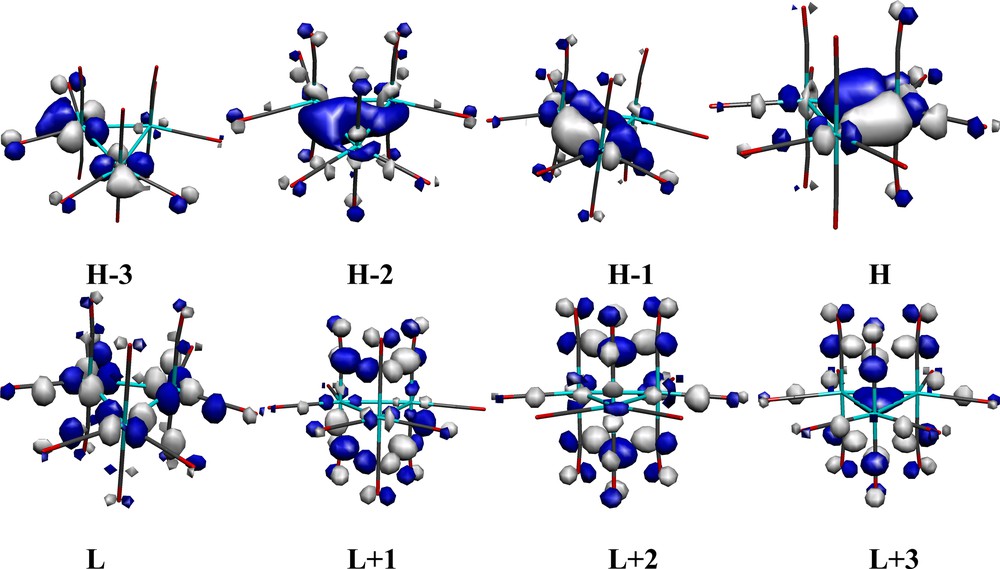
Frontier orbitals of [Ru3(CO)12] (1a) in a Molekel [19] representation.
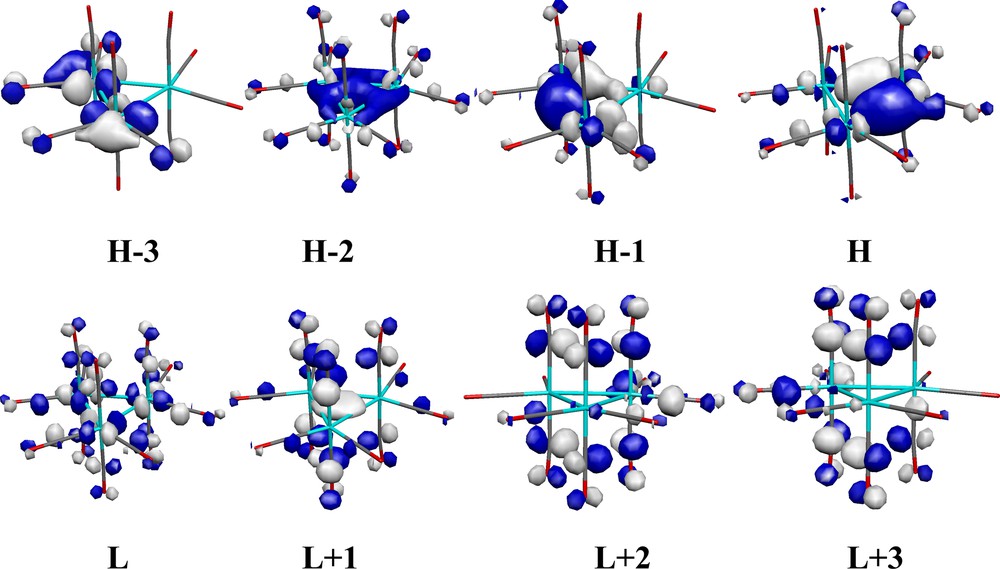
Frontier orbitals of [Os3(CO)12] (2a) in a Molekel [19] representation.
Composition (%) and energies (eV) of frontier molecular orbitals of [Ru3(CO)12] (1a) (L = LUMO, H = HOMO)
| Orbital | E | Ru1 | Ru2 | Ru3 | CO | |
| 81a | H – 3 | –7.29 | 44.3 | 24.3 | 4.0 | 27.4 |
| 82a | H – 2 | –6.40 | 18.5 | 20.0 | 14.3 | 47.2 |
| 83a | H – 1 | –6.40 | 26.6 | 27.8 | 10.1 | 35.5 |
| 84a | H | –6.39 | 15.7 | 12.8 | 36.3 | 35.2 |
| 85a | L | –3.69 | 15.9 | 16.5 | 15.9 | 51.7 |
| 86a | L + 1 | –3.04 | 4.2 | 4.5 | 5.6 | 85.7 |
| 87a | L + 2 | –3.04 | 4.3 | 5.5 | 4.5 | 85.7 |
| 88a | L + 3 | –2.82 | 4.9 | 4.1 | 4.8 | 86.2 |
Composition (%) and energies (eV) of frontier molecular orbitals of [Os3(CO)12] (2a) (L = LUMO, H = HOMO)
| orbital | E | Os1 | Os2 | Os3 | CO | |
| 101a | H – 4 | –7.34 | 6.8 | 18.6 | 41.3 | 33.3 |
| 102a | H – 3 | –7.34 | 37.7 | 25.9 | 3.2 | 33.2 |
| 103a | H – 2 | –6.70 | 16.3 | 16.3 | 16.1 | 51.3 |
| 104a | H – 1 | –6.55 | 28.3 | 25.0 | 8.4 | 38.3 |
| 105a | H | –6.55 | 12.8 | 16.0 | 32.9 | 38.3 |
| 106a | L | –3.50 | 10.3 | 10.8 | 10.3 | 68.6 |
| 107a | L + 1 | –3.09 | 4.5 | 5.1 | 4.9 | 85.5 |
| 108a | L + 2 | –3.08 | 2.3 | 3.1 | 1.0 | 93.6 |
| 109a | L + 3 | –2.62 | 2.0 | 2.2 | 2.9 | 92.9 |
While the HOMO (H) of 1a is more localized at Ru3, H – 1 and H – 3 are more localized at Ru1 and Ru2, and H – 2 is spread over the three ruthenium centers, being a highly symmetrical Ru–Ru σ-bonding orbital. The three highest occupied orbitals shown are Ru–Ru bonding, but H – 3 is π-bonding between Ru and the equatorial CO ligands, and Ru–Ru π* antibonding. The LUMO (L) has a localization close to 50% on the Ru3-core, and is both Ru–CO (π*) and Ru–Ru (σ*) anti-bonding. In contrast, L + 1, L + 2 and L + 3 show a much larger localization on the carbonyls and are Ru–CO π* antibonding.
The main difference between the Ru and Os clusters is the much smaller participation of the Os centers in the unoccupied orbitals compared to Ru (with the exception of L + 1). Indeed, in the LUMO of 2a, the three osmium centers only contribute with ca. 31%. This trend becomes more marked for L + 2 and L + 3, where the participation of osmium becomes negligible.
Note also that the L + 1 orbital of [Os3(CO)12] resembles the L + 3 orbital of the Ru cluster, both being M3-core bonding. The latter orbitals do not participate (for symmetry reasons) very much in the allowed low-lying electronic transitions.
2.3 Electronic transitions
TD-DFT [11] calculations were performed on both [M3(CO)12] clusters. Despite the similarities between the frontier orbitals of the forms a and b, the different symmetry gives rise to slightly different excitation energies, as the mixing between the individual electronic transitions is not exactly the same for both cases. The calculated excitation energies, their characters and oscillator strengths are given in Tables 3 and 4, for [Ru3(CO)12] (1a) and [Os3(CO)12] (2a), respectively.
Calculated low-energy singlet excitation energies, wavelengths, and oscillator strengths (OS) for [Ru3(CO)12] (1a)
| Composition | Energy (eV) | Wavelength (nm) | λmaxa (nm) | OS (× 103) |
| 66% (H→L), 11% (H – 1→L + 1) | 3.095 | 400 | 392 | 0.038 |
| 64% (H – 1→L), 15% (H→L + 2) | 3.096 | 400 | 0.038 | |
| 3.556 | 348 | 0.030 | |
| 3.568 | 347 | 0.031 | |
| 73% (H→L + 3) | 3.662 | 338 | 0.012 |
a Observed absorption maximum for [Ru3(CO)12] (1) in isooctane at 298 K [20].
Calculated low-energy singlet excitation energies, wavelengths, and oscillator strengths (OS) for [Os3(CO)12] (2a)
| Composition | Energy (eV) | Wavelength (nm) | λmaxa (nm) | OS (× 103) |
| 3.366 | 368 |
| 0.037 |
| 3.367 | 368 | 0.037 | |
| 80% (H→L + 1) | 3.520 | 352 | 0.007 | |
| 3.522 | 352 | 0.007 | |
| 3.641 | 340 | 0.028 | |
| 3.641 | 340 | 0.028 | |
| 75% (H – 2→L + 2) | 3.716 | 333 | 0.009 |
a Observed absorption maxima for [Os3(CO)12] (2) in methylcyclohexane at 293 K [21].
The band of [Ru3(CO)12] observed experimentally at 392 nm has previously been ascribed [20] to “a transition from a delocalized metal–metal bonding orbital to an anti-bonding one in this regard”, i.e. σσ*. According to the values in Table 3 and Fig. 2, the two allowed transitions at 400 nm start from H or H – 1 (Ru–Ru σ-bonding orbitals) and end mainly in L, which is strongly Ru–Ru σ* and Ru–CO anti-bonding. Therefore, both transitions have, indeed, essentially a σσ* character. On the contrary, the transitions at 347 and 348 nm originate from H – 2 (also mainly Ru–Ru σ-bonding), H – 3 and H – 4 (mainly Ru–COeq π bonding) and have their end mostly in L + 1 or L + 2 (π* CO), although the LUMO also contributes.
For [Os3(CO)12], two fairly intense bands at 368 and 340 nm, respectively, were calculated (Table 4). The first one has major components from H and H – 1 to L transitions, directed mainly to the Os–Os σ* anti-bonding LUMO and much less to the mainly π* CO levels L + 2 and L + 3. The band at 340 nm comprises transitions that start from the same type of levels (H and H – 1, Os–Os σ bonding), but are not directed to the LUMO. Instead, their end point is always one of the higher energy levels (L + 1, L + 2, L + 3), in which the participation of Os is very small and which therefore exhibit a non-bonding carbonyl nature.
The simulated SWizard spectra [22] for the ‘D3h’ geometry and the rotated geometry of the [M3(CO)12] clusters (Fig. 1) are shown, together with the experimental UV–vis spectra, in Figs. 4a (Ru) and 4b (Os). Owing to the comparable intensities and the energy difference, reproduced by the TD-DFT calculations, the Ru band at 392 nm and the Os band at 330 nm should be equivalent, belonging to the lowest-energy allowed transitions with the dominant H-to-L and H – 1-to-L components (Tables 3 and 4). These transitions differ more than the higher-lying sets, reflecting the difference in the Ru and Os LUMO. The best fit has been obtained for the calculated ‘D3h’ geometries reproducing the crystal structures of the [M3(CO)12] 1 and 2.

Simulated SWizard [23] spectra of [Ru3(CO)12], 1 (top), and [Os3(CO)12], 2 (bottom), for the ‘D3h’ (a) and rotated (b) geometries, together with the experimental electronic spectra recorded in hexane at 298 K.
The intense electronic transitions calculated at 348–338 nm (Ru) and 340 nm (Os) probably lie in the experimental spectra below 300 nm, contributing to the UV absorption in this region. By comparison with a situation frequently encountered in [Os(2,2′-bipyridine)3]2+-type complexes [23], the most plausible assignment of the shoulder at 385 nm in the experimental spectrum of cluster 2 considers a triplet character of the corresponding lowest-energy electronic transition(s), partially allowed due to a strong spin–orbit coupling. In agreement with this assignment, there is no apparent analogous absorption band in the electronic spectrum of [Ru3(CO)12] (1), despite the similar nature and intensities of the electronic transitions calculated for both clusters. For ruthenium, the spin–orbit coupling is much weaker and the low-intensity absorption band, equivalent to the Os shoulder at 385 nm, may be covered by the dominant Ru band at 392 nm, in the unresolved tail between 450–550 nm.
2.4 Reactivity and transient species
For [Ru3(CO)12], irradiation into the higher-lying absorption bands (λirr < 300 nm) results in CO-loss reactions. This reactivity is not discussed here, even though [Ru3(CO)11] could be seen with ps TRIR, following partial irradiation (λirr = 400 nm) into the tailing higher energy band (shoulder between 300 and 350 nm; see Fig. 4 (top) and [20]). Although the higher energy transitions were not calculated, the intense electronic transitions calculated at 348–338 nm have tentatively been assigned to contribute to this band.
The Ru band at 392 nm has previously been assigned to a metal–metal bonding to anti-bonding (σ→σ*) transition [20]. Irradiation at this wavelength was argued to cause heterolytic Ru–Ru bond cleavage and formation of an open-core transient with a CO-bridge [7]. This species can bind two-electron donor π-acids (CO, PR3, olefins), resulting in fragmentation (via the associative pathway) or CO substitution, or converts back to the ground-state geometry. Although the previous assignment of the band at 392 nm to a single electronic transition is an oversimplification, our results indicate that occupied orbitals with a strong Ru–Ru σ-bonding character (H and H – 1) are involved in all transitions contributing to this band. Therefore, depopulation of these orbitals should indeed lead to weakening of the Ru–Ru bond, despite the nature of the levels being populated, though the partial population of the LUMO (Ru–Ru σ*) may be decisive for the ultimate bond cleavage.
The [Os3(CO)12] cluster generally shows the same reactivity pattern as [Ru3(CO)12]. Again, short-wavelength excitation (λirr < 300 nm) leads to CO dissociation, while irradiation into the 330-nm band causes photoreactivity (substitution, fragmentation) via a presumed open-core CO-bridged transient. The photoreaction quantum yields are generally lower compared to Ru, which was ascribed to stronger Os–Os bonding. Besides, as described above (Figs. 2 and 3), the LUMO of [Ru3(CO)12] has some M–M σ* character, while the contribution of the Os centers to the LUMO of [Os3(CO)12] is much smaller. In contrast to Ru, no apparent photoreactivity of [Os3(CO)12] is observed upon irradiation into the shoulder at 385 nm (λirr = 436 nm). This third band was therefore believed to have a σ*σ* character, the populated σ* orbital being anti-bonding with regard to the metal–equatorial carbon bonds [20]. Other authors have considered this lowest-energy transition to originate from a highly delocalized HOMO (mixed Os–CO π-bonding, Os–Os bonding and Os–CO σ-antibonding contributions) to an empty orbital of largely axial π*(CO) character [21], which is close to our interpretation.
According to our TD-DFT data, the lowest electronic transitions for both Ru and Os clusters, with significant H→L and H – 1→L contributions, have a similar, mixed σπ*/σσ* character, which agrees with the shift of the CO-stretching wavenumbers to smaller values for the lowest-energy excited states as observed in the ps TRIR experiments [7]2. The H, H – 1, and H – 2 orbitals are basically M–M σ-bonding regarding specific Os–Os bonds or the whole cluster core, and they contribute all to the lowest electronic transitions. It is therefore expected that depopulation of the bonding orbitals upon visible excitation is highly delocalized and hardly any specific M–M bond is weakened. The LUMO, strongly involved in the lowest electronic transitions, is more M–M anti-bonding (σ*) for the Ru cluster, and this may decide about the reactivity. For Ru, a transient containing a CO-bridge is observed with ps TRIR, which favors the existence of an open-core photoproduct (provided the Ru–Ru bond is indeed opened and not merely significantly weakened). For Os, the perturbation of the Os–Os bonds is minor and the observed transient (primary photoproduct), following irradiation at 400 nm into the lowest-energy band ([3] σσ*/σπ*, see above), lacks the CO bridge. Unfortunately, in the course of the ps TRIR measurements, it was not possible to excite with 300–350 nm light into the corresponding [1] σσ*/σπ* transition, which might favor CO-bridge formation by heterolytic Os–Os bond cleavage. It should be also added at this point that the formation of CO-bridged species in binary Os-carbonyl clusters is electronically very unfavorable.
As described above, UV–vis flash photolysis (λirr = 400 nm) of [Ru3(CO)12] resulted in the detection of a transient, exhibiting a ν(CO) band in the bridging carbonyl region. Aiming at a further characterization of this transient species, we used DFT to search for possible structures containing CO bridges, similar to those proposed for the transient species formed upon irradiation of [Os3(CO)10(cyclohexa-1,3-diene)] [9]. A low-energy isomer (1c) was found, in which one of the Ru–Ru bonds is spanned by two bridging carbonyl ligands (Fig. 5, left). This structure is the most stable one and is also the experimentally observed for the [Fe3(CO)12] analogue [24]. The IR spectrum of the latter cluster exhibits two CO-stretching bands at 1834 and 1865 cm–1 in n-hexane. The bands for the bridging carbonyls in the related cluster [Fe2Ru(CO)12] are observed at 1826 and 1859 cm–1 in the same solvent [25].
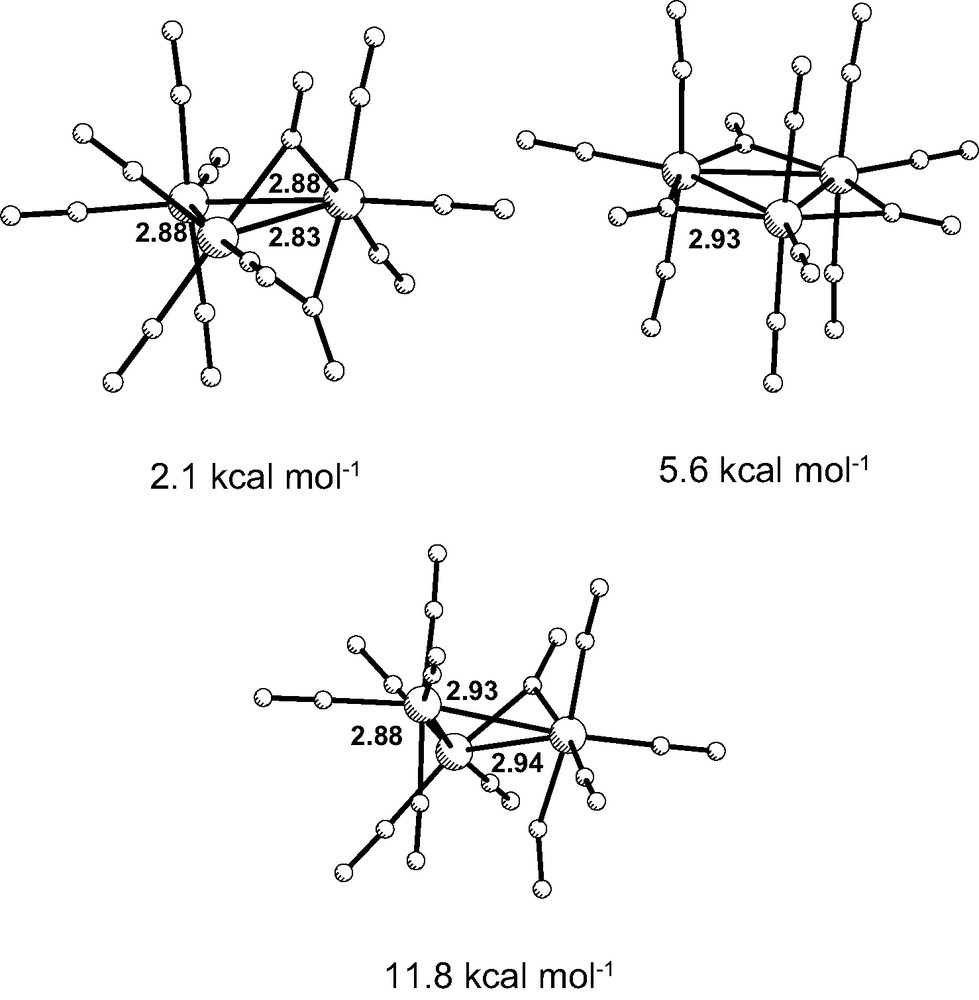
Optimized structure of CO-bridged [Ru3(CO)12], with ‘C2v’ symmetry (1c, top left, ADF), with ‘D3h’ symmetry (1d, top right, ADF), and the transient (1e, bottom, G98), together with the Ru–Ru distances (Å). The energies are relative to 1a.
Isomer 1c, which will be called ‘C2v’, although it was obtained without any symmetry constraints in the calculations, has an energy only 2.1 kcal mol–1 higher than 1b. It represents a higher energy isomer of the ground-state structure and can be invoked as an intermediate to explain carbonyl scrambling [26]. Notice that the shortest bond (2.83 Å) is spawned by the two bridging carbonyls and is the weakest, as indicated by the lowest Mayer index [27] (0.306), compared to that of the other two bonds (0.503). Another structure, with even higher energy, 1d, has approximate ‘D3h’ symmetry. All the Ru–Ru bonds carry CO bridges and are comparatively weakened (Mayer indices of 0.392). The Ru–Ru distances in 1d are the longest, from all the species 1a–1d. Still, the energy is compatible with participation in carbonyl scrambling mechanisms in solution.
Imposition of some constraints in the calculations (see computational details), led to the third structure, 1e (Fig. 5, right). Isomer 1e closely resembles 1c, except for the fact that 1e has one bridging carbonyl (Ru–C distances 2.078 and 1.975 Å), and a semibridging one (Ru–C distances 2.206 and 2.488 Å), since the latter distance is too long for a bond. The energy of 1e is 11.8 kcal mol–1 higher than that of 1bg. This species exhibits a νC≡O band at 1851 cm–1, assigned to the stretching of the bridging carbonyl ligand, which agrees surprisingly well with the band characterizing the transient in the ps TRIR spectra of [Ru3(CO)12] (1850 cm–1). All the other calculated CO-stretching frequencies appear close to 2000 cm–1 and involve the terminal carbonyls. The Ru–Ru bond bridged by the carbonyl is relatively long (2.94 Å). The bond order, however, is relatively low (Wiberg index of 0.079, compared to 0.174 and 0.207 for the other two bonds), suggesting that it may be considered broken. It is noteworthy that 1e, which we tentatively assign as the transient observed in the ps TRIR experiments, shares several structural features with another transient, proposed to be formed upon visible irradiation of the cluster [Os3(CO)10(cyclohexa-1,3-diene)] [9].
3 Conclusions
The frontier orbitals of the two [M3(CO)12] clusters (M = Ru, Os), obtained from DFT calculations, have been analyzed. While the HOMO and the next lower-lying occupied orbitals are mainly M–M (σ) bonding, with contributions from different M–M bonds, the LUMO is M–M (σ*) and M–CO (π*) anti-bonding. The higher-lying group of empty orbitals is largely formed by the CO (π*) orbitals, with an almost negligible contribution from the metal centers in the Os cluster, and a more significant one for Ru. The nature of these empty orbitals, which participate in the excitation processes, is the main difference between the two metal clusters. Experimentally, the Os cluster exhibits a low-energy shoulder at 385 nm not observed for Ru, being probably obscured in the latter case by the strong band at 392 nm. The typical reactivity pattern is related to the loss of a carbonyl, with possible coordination of a two-electron donor π-acid, if present. A transient was detected in ps TRIR spectra recorded for [Ru3(CO)12] and thought to contain a bridging CO ligand. The weakening or cleavage of the Ru–Ru bond in this primary photoproduct is still a matter of debate. The overall picture is thus complex and further studies are needed. This work is a first step towards a more objective description of the bonding properties and reactivity of this type of binary carbonyl clusters.
4 Computational details
Density functional theory (DFT) calculations [10] were carried out with the Amsterdam Density Functional (ADF-2002) program [13]. Vosko et al. [28] local exchange-correlation potential was used. Gradient-corrected geometry optimizations [29] were performed, using the generalized gradient approximation (Becke's exchange [30] and Perdew's correlation [31] functionals). Relativistic effects were treated with the ZORA approximation [32]. The core orbitals were frozen for Os ([1–4]s, [1–4]p, [3,4]d), Ru ([1–3]s, [1–3]p, 3d), and C, O (1s). Triple ζ Slater-type orbitals (STO) were used to describe the valence shells of C, O (2s and 2p), Os (4f, 5d, 6s), and Ru (4d, 5s). A set of two polarization functions was added: C, O (single ζ, 3d, 4f), Os (single ζ, 6p, 5f), and Ru (single ζ, 5p, 4f). Full geometry optimizations were performed without any symmetry constraints on clusters based on the crystal structures of [Os3(CO)12] and [Ru3(CO)12]. Geometry optimizations were also performed at the DFT/B3LYP [15a,b] levels using Gaussian 98 [16]. This functional includes a mixture of Hartree–Fock exchange with DFT exchange-correlation, given by Becke's three parameter functional [15b] with the Lee, Yang and Parr correlation functional [15a], which includes both local and non-local terms. The Stuttgart/Dresden (SDD) [33] ECPs were used for Os and Ru plus an f polarization function (0.886 for Os; 1.235 for Ru) [34]. The 6-31G* basis set [35] was used for the other atoms (C, O). The geometry optimization of the photoproduct [Ru3(CO)11(μ-CO)] (1e) was carried out with Gaussian 98 constraining one carbonyl group to remain bridging. IR frequencies were calculated.
Time-dependent DFT calculations (TD-DFT) [11] in the ADF implementation were used to determine the excitation energies. In all cases the lowest ten singlet-singlet excitation energies were calculated using the optimized geometries.
Mayer indices [27] were calculated with the ADF densities using the MAYER program [36]. A natural population (NPA) analysis [37] was performed and Wiberg indices [38] (using the B3LYP density) were evaluated and used as bond strength indicators. The UV–vis spectra were calculated using the SWizard program, revision 3.7 [22], using the Gaussian model. The half-band widths, Δ1/2,I, were taken to be equal to 3000 cm–1, the default value in the program. Three-dimensional representations of orbitals were obtained with Molekel [19].
Acknowledgements
This work has been undertaken as a part of a European collaborative COST project (D14/0001/99). P.J.C. acknowledges FCT for a grant (SFRH/BD/10535/2002).
1 The ps TRIR experiments with [Os3(CO)12] were performed using the PIRATE facility at the Rutherford Appleton Laboratory in Didcot, United Kingdom, as described for excitation of Ru3(CO)12 elsewhere [7]. The ps TRIR spectra were recorded in dichloromethane at several pump-probe delays between 0 and 1000 ps after 400 nm excitation. Although the resulting transient spectra showed similar spectral changes in the terminal CO-stretching region as depicted for [Ru3(CO)12] [7], the presence of a bridging carbonyl ligand could not be established.
2 See footnote 1


