Pathways for proton migration over the surface of a metal-cyclotriphosphorus cluster

Massimo Di Vaira; Piero Stoppioni

doi:10.1016/j.crci.2004.10.032

Pathways for proton migration over the surface of a metal-cyclotriphosphorus cluster

Massimo Di Vaira ¹ ; Piero Stoppioni ¹

¹ Dipartimento di Chimica, Università di Firenze, via della Lastruccia 3, 50019 Sesto Fiorentino, Firenze, Italy

Comptes Rendus. Chimie, Volume 8 (2005) no. 9-10, pp. 1535-1542.

Résumés

Anglais
Français

In order to rationalize the fluxionality on the NMR time scale of the [(triphos)Co(P₃H)]⁺ complex cation, where triphos is a tripod-like phosphine, paths for motion of the proton over the CoP₃ core have been investigated by quantum-mechanical procedures. Possible pathways for such motion have been identified, although alternative processes, involving limited H participation to the overall motion, have also been found and appear to be competitive. .

Dans le but de rationaliser la fluctionnalité à l'échelle de temps de la RMN des cations du complexe [(triphos)Co(P₃H)]⁺, où la phosphine est un ligand tripodal, les déplacements du proton autour du cœur CoP₃ ont été étudiés par la mécanique quantique. Des chemins possibles pour de telles migrations ont été identifiées, bien que des procédés alternatifs, mettant en jeu une participation limitée de H dans l'ensemble du déplacement, aient été trouvés et semblent être compétitifs. .

Métadonnées

Reçu le : 2004-04-15
Accepté le : 2004-10-04
Publié le : 2005-04-15

DOI : 10.1016/j.crci.2004.10.032

Keywords: Density functional, Fluxional system, Proton migration, Transition states
Mots clés : Fonctionnelle de densité, Système fluctionnel, Migration de protons, État de transition

Affiliations des auteurs :

Massimo Di Vaira ¹ ; Piero Stoppioni ¹

¹ Dipartimento di Chimica, Università di Firenze, via della Lastruccia 3, 50019 Sesto Fiorentino, Firenze, Italy

@article{CRCHIM_2005__8_9-10_1535_0,
     author = {Massimo Di Vaira and Piero Stoppioni},
     title = {Pathways for proton migration over the surface of a metal-cyclotriphosphorus cluster},
     journal = {Comptes Rendus. Chimie},
     pages = {1535--1542},
     publisher = {Elsevier},
     volume = {8},
     number = {9-10},
     year = {2005},
     doi = {10.1016/j.crci.2004.10.032},
     language = {en},
}

TY  - JOUR
AU  - Massimo Di Vaira
AU  - Piero Stoppioni
TI  - Pathways for proton migration over the surface of a metal-cyclotriphosphorus cluster
JO  - Comptes Rendus. Chimie
PY  - 2005
SP  - 1535
EP  - 1542
VL  - 8
IS  - 9-10
PB  - Elsevier
DO  - 10.1016/j.crci.2004.10.032
LA  - en
ID  - CRCHIM_2005__8_9-10_1535_0
ER  -

%0 Journal Article
%A Massimo Di Vaira
%A Piero Stoppioni
%T Pathways for proton migration over the surface of a metal-cyclotriphosphorus cluster
%J Comptes Rendus. Chimie
%D 2005
%P 1535-1542
%V 8
%N 9-10
%I Elsevier
%R 10.1016/j.crci.2004.10.032
%G en
%F CRCHIM_2005__8_9-10_1535_0

Massimo Di Vaira; Piero Stoppioni. Pathways for proton migration over the surface of a metal-cyclotriphosphorus cluster. Comptes Rendus. Chimie, Volume 8 (2005) no. 9-10, pp. 1535-1542. doi : 10.1016/j.crci.2004.10.032. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2004.10.032/

Version originale du texte intégral

1 Introduction

The propensity of the pseudotetrahedral MP₃ core in the [(triphos)MP₃] compounds [1,2] [triphos = 1,1,1-tris(diphenylphosphinomethyl)ethane; M = Co, Rh, Ir] to undergo addition reactions, e.g. by metal carbonyls [3,4] or by the CH₃⁺ group [5], on the electron-rich phosphorus atoms of the P₃ ring has been extensively probed in the recent past. Attack by the isolobal HgCH₃⁺ species [6] or the bare proton, H⁺ [7], yielded different results, leading to incipient insertion into a P–P bond of the cyclotriphosphorus unit in the former case [6] and to insertion into a metal-phosphorus bond of the CoP₃ core of [(triphos)CoP₃] in the latter [7]. The nature of the H⁺ insertion product, proposed on the basis of an X-ray investigation [7], was substantiated by a theoretical analysis at DFT-LDA level with symmetry constraints [8]. The NMR data show that the above H⁺ derivative, similarly to many other products of the reactions performed on a MP₃ core [9], is fluxional, presumably due to easy configurational rearrangements undergone within the CoP₃H⁺ moiety and/or to changes in its orientation with respect to the triphos ligand. We were interested in investigating the possible paths for such rearrangements, a task too difficult to pursue at the time of the previous study, that now has been made possible by advances in computer technology and, on the theoretical side, by the availability of new and powerful computational algorithms.

2 Computational procedures

Calculations were performed on the [(triphos)Co(P₃H)]⁺ system and its neutral parent [(triphos)CoP₃] with the GAUSSIAN98 [10] suite of programs, at the B3LYP/6-31G(d,p) level [11,12] unless specified otherwise, with LANL2DZ valence functions and effective core potential (ECP) [13] for the metal atom. Transition states were searched and identified by application of the synchronous transit-guided quasi-Newton procedure [14]. The nature of stationary points as true minima or first-order saddle points, the latter characterized by one imaginary frequency, was checked by frequency calculations and unscaled ZPE corrections were applied to the energy values. Intrinsic reaction coordinate calculations [15] and subsequent geometry optimizations were performed to verify the expected connections of the first-order saddle points with local minima on the potential energy surface. NBO analyses [16] were performed as an aid in the interpretation of the results. For comparison purposes, few calculations were performed according to the PCM polarizable continuum model [17–19] in order to account for solvation effects, in dichloromethane solution. For graphics Molden [20] and CACAO [21] were employed. Atomic coordinates for the reported stationary states may be obtained by the authors on request.

3 Results and discussion

Calculations were performed on simplified models of the [(triphos)Co(P₃H)]⁺ system, where the phenyl groups of the triphos ligand were replaced by hydrogen atoms (the name ‘triphos’ will nevertheless be applied hereafter to the simplified model ligand). It was expected that the simplification of peripheral parts of the ligand would not affect considerably the prediction of properties and transformations essentially restricted to the CoP₃ core. Indeed, the computed values of bond distances and angles about the metal for the similarly simplified model of the neutral [(triphos)CoP₃] parent compound were found to be in reasonable agreement with the experimental values [1]. The largest deviations in bond lengths were found for the P_P3–P_P3 bonds (this notation will be used hereafter for atoms of the P₃ unit and the symbol P_tr will be used for the triphos phosphorus atoms), whose values exceeded by ca. 0.04 Å those of the experimental structure; this might be ascribed in part to the apparent shortening of such bonds in the X-ray structure [1], due to thermal motion effects. The largest deviations in bond angles about the metal (0.5°) were found for the P_tr–Co–P_tr angles. The experimentally detected threefold symmetry of the molecule was substantially verified, although it was not imposed in the calculations.

An exhaustive search of minimum energy configurations, without symmetry constraints, was performed in the gas phase for the [(triphos)Co(P₃H)]⁺ system, as a prerequisite to the investigation of transition states for proton migration. This part of the study represents an extension of the previous work [8], performed with ADF procedures [22], under symmetry constraints and with triphos-mimicking PH₃ groups in fixed orientations. With the present investigation four distinct minimum energy arrangements have been identified. These, denoted 1–4, are shown in Fig. 1; their energies relative to the lowest energy model 1 are: 11.26 (2), 9.85 (3) and 9.42 (4) kcal mol^–1. In the present approach, in which the triphos ligand backbone has not been neglected, contrary to the previous study, none of these models possesses symmetry elements higher than C₁. However, if the aliphatic part of the ligand chains is ignored, 1 and 2 may be considered to possess substantially C_s symmetry, about a plane passing through the Co, H and the H-carrying P_P3 atom (in both cases the symmetry plane bisects the P_P3–P_P3–P_P3 angle with vertex in the above P_P3 atom). Also 4 has approximate C_s symmetry, however, about a plane passing through the Co and H atoms, and bisecting the P_P3–H–P_P3 angle. Models 1, 2 and 4 correspond to previously investigated species [8] and their energy ordering matches that found with the previous ADF approach, although there is considerable disagreement in energy differences. On the other hand, the arrangement of the present relative minimum 3, possessing C₁ symmetry, could not be detected before, due to the symmetry constraints imposed with that study.

Fig. 1
Views of geometries attained by the [(triphos)Co(P₃H)]⁺ system in correspondence of the global energy minimum 1 and of the relative energy minima 2–4. Values of important distances (Å) and relative energy values (for 2–4 from 1, kcal mol^–1) are given. Carbon and hydrogen atoms are not labeled for clarity. 1: values in parentheses, both in the figure and in this caption, are from Ref. [7]. The P_tr–Co–P_tr bond angles (°) are in the range: 90.4–95.6 (90.9–94.8). The P_P3–Co–P_P3 angle formed by the P₃ atoms not bound to H is 56.1 (55.1). The other two P_P3–Co–P_P3 angles measure 53.6 (53.7, average). Co–H–P_P3 = 100.8. 2: angles at the H-carrying phosphorus atom are Co–P_P3–H 172.1 and P_P3–P_P3–H 120.4 (average of two essentially equal angles). The angle (α, hereafter) between the P_P3–H vector and the normal to the P₃ plane is α = 36.0. 3: angles at the H-carrying phosphorus atom are Co–P_P3–H 115.7, P_P3–P_P3–H 107.0 and 68.0 (with obvious assignment of the last two values, from the figure). α = 64.4. 4: P_P3–P_P3–H angles are 92.0 and 43.2 (both are averages of two practically identical values; the latter angle involves the pair of P_P3 atoms bound to H); P_P3–H–P_P3 = 93.6. The dihedral angle (δ hereafter) between the plane defined by the latter three atoms and the plane of the P₃ unit is δ = 139.2. α = 63.4 (two identical values).

Best agreement with the experimental arrangement of the non-hydrogen atoms [7] is provided, as before [8], by the lowest energy model 1, confirming that in solid state conditions the hydrogen atom should reside in bridging position between the metal and a P₃ phosphorus atom. However, with the pertaining Co–P_P3 distance, for the H-capped edge of the CoP₃ pseudotetrahedron (Fig. 1), predicted to be ca. 0.10 Å longer than the experimental value of 2.396(2) Å, the present model 1 does not improve over the picture (Co–P = 2.43 Å) of the previous approach [8]. Recourse to the B3LYP/6-311*G(d,p) level of theory (avoiding the use of a Co pseudopotential), better than the level generally adopted in this study, yielded only a small improvement (Co–P_P3, 2.484 Å). It could not be excluded that part of the disagreement is due to the effects of a small amount of disorder in the position of the H atom in the solid sample, where such effects would combine with those already mentioned for the parent compound, due to thermal motion. According to the NBO analysis, the occupancies of both the bonding and the antibonding orbitals within the P₃ group in 1 do not differ significantly from those calculated for the same grouping in the [(triphos)CoP₃] neutral parent, neither do the occupancies of the Co–P_P3 bonds in the two models (there are only two bonds of this type in 1, since no orbital interaction between the H-carrying phosphorus and the metal is revealed by the NBO analysis).

No comments will be devoted here to the geometries of 2 and 4, for which the data accompanying the representations should be sufficient. The newly detected relative minimum 3 (Fig. 1) fits well between 2 and 4, forming with them and with symmetry-related sets of stationary states, in the C_3v symmetry of the bare CoP₃ moiety, a sequence of relative minima that trace a possible path for proton migration along the periphery of the P₃ ring. However, as reported below, lower energy pathways consistent with the fluxional behavior appear to exist. Still about the 2–4 sequence, it should be noted that those relative minima belong to a region of very slowly varying energy values and the detailed geometry of the intermediate 3 might be rather sensitive to the choice of basis set (particularly as far as the orientation of the P_P3–H bond, in terms of the α angle defined in the caption of Fig. 1, is concerned). The NBO occupancies of the P_P3–H bond in 1–4 increase on going from 4 to 1, to 3 and to 2, i.e. in the order of decreasing bond length.

It should be noted that attempts to locate a stationary state geometry for proton approach along the normal to the P₃ ring, in a capping position on the triangular face, were unsuccessful, since a geometry of type 2–4 was invariably reached. Scans performed with geometry constraints along the normal to the ring revealed the presence of a minimum, limitedly to that constrained path, characterized by 1.7 Å P–H distances and very high relative energy (ca. 35 kcal mol^–1).

The main purpose of this study was investigating the transition pathways between the minimum energy stationary states. The following transition states (TS) have been detected, and their connections with pairs of the above minima in configuration space have been verified:

a) TS between a pair of type 1 minimum energy configurations, i.e. for a path consisting in the proton transfer from the H-bridging condition in correspondence of a Co–P_P3 edge to the analogs condition involving a different Co–P_P3 edge. This transition state will be denoted Tsa;
b) TS (TSb) between minima of type 1 and 2. This belongs to a substantially C_s-symmetry path, such symmetry being possessed to a good approximation by both limiting geometries, as pointed out above;
c) TSc, for a possible path connecting the stationary states 1 and 4;
d) One or more TS's for a path spanning the periphery of the P₃ ring. The reason for the implied ambiguity is detailed below;
e) TS's for rotational motion of the whole P₃H moiety with respect to the (triphos)Co one, or for rotation of the only P₃ group with respect to the rest of the structure.

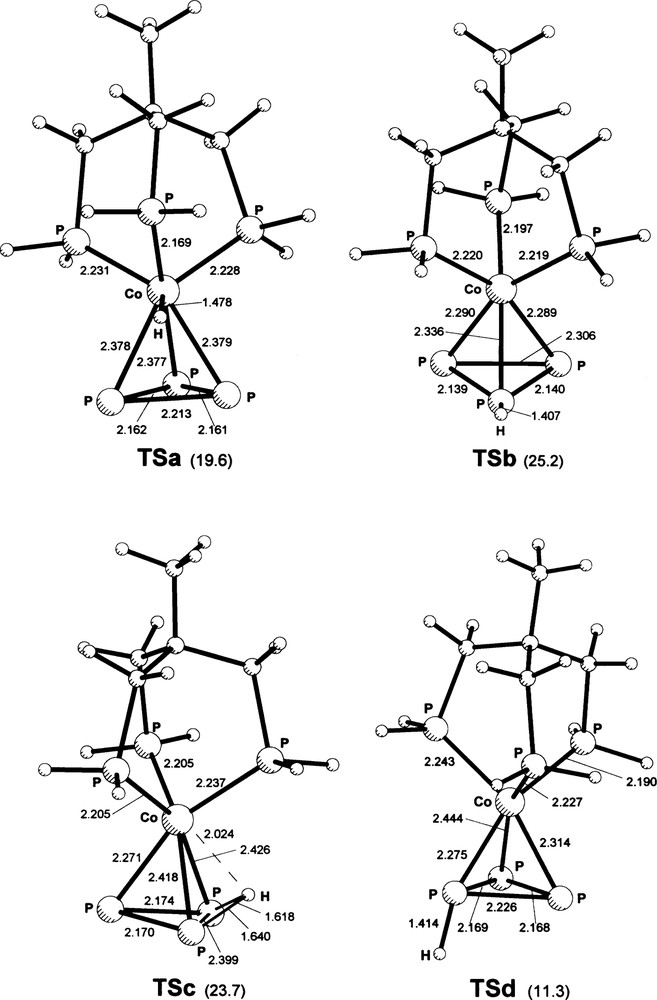
The geometries of these TS's are shown in Figs. 2 and 3.

Fig. 2
Geometries of **TSa**–**TSd** transition states for H migrational motion. **TSa**: transition state geometry along the path joining two minima of type 1. Angles (°) at the metal, formed by H and the three closest P atoms are P_P3–Co–H 64.4 and 65.9, P_tr–Co–H 64.8. **TSb**: transition state connecting minima 1 and 2. Co–P_P3–H = 109.2, P_P3–P_P3–H = 144.2 (average of two closely similar values). **TSc**: transition state connecting minima 1 and 4. P_P3–H–P_P3 = 94.8, Co–P_P3–H = 55.8; α = 64.8 (each of the last two entries is the average of two closely similar values). δ = 141.0. **TSd**: transition state connecting minima 2 and 3. Angles at the H-carrying phosphorus atom are Co–P_P3–H 156.5, P_P3–P_P3–H 122.0 and 102.1; α = 74.5.

Fig. 3
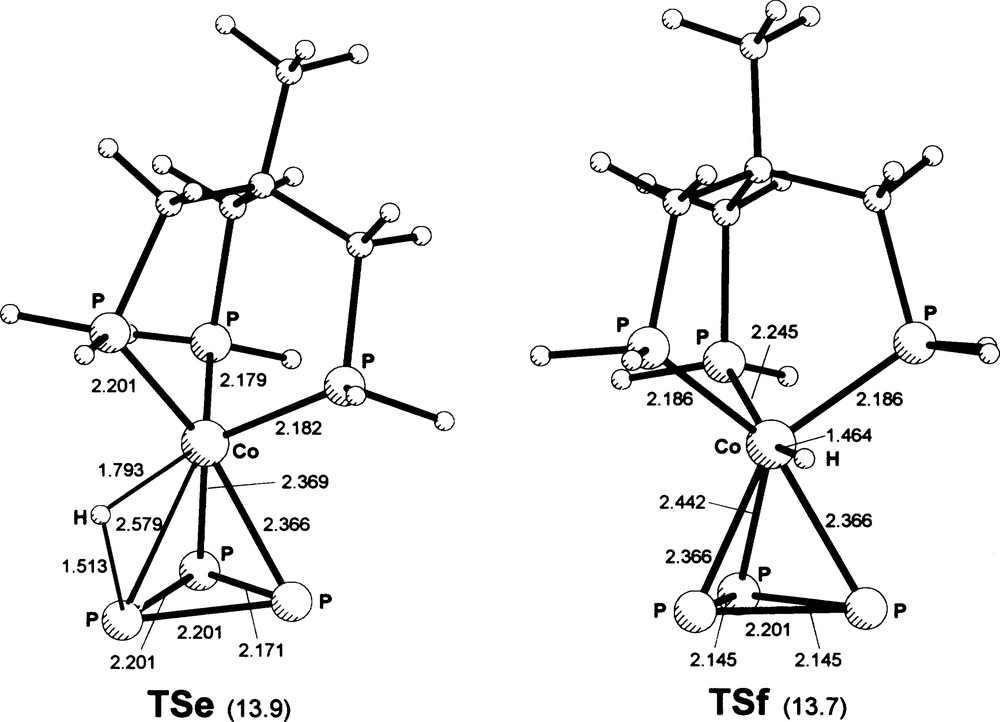
Geometries of transition states for predominantly rotational motion of [(triphos)Co(P₃H)]⁺ moieties around an axis passing through the metal atom. **Tse** (for relative rotation of the triphos and P₃H moieties; joins two type 1 geometries): the P_P3–Co– –P_P3 angle (°) between Co-bound P_P3 atoms is 54.6; P_P3–Co– –P_P3 = 52.6 (two identical values for angles with common Co–P_P3 edge); Co–H–P_P3 = 102.2. **TSf** (for mainly rotational motion of the P₃ group, between two geometries of type 1): the P_tr–Co–P_tr angles are 103.8 between P_tr atoms close to H and 87.3 otherwise. Angles at the metal formed with H by the P_tr and P_P3 atoms close to H are P_tr–Co–H 80.2 and P_P3–Co–H 77.3 (two identical values in each case).

TSa (Fig. 2) connecting two type 1 lowest energy geometries, is also the lowest one in energy among TS states of the first three kinds listed above, namely those not involving H motion around the periphery of the P₃ ring or relative rotation of large moieties. Its energy is 19.6 kcal mol^–1 higher than that of the absolute minimum 1. TSa is characterized by an H position closer to the metal than in 1 and almost equidistant from three phosphorus atoms (one of these being a phosphine donor atom). In spite of the short distance from Co, the H atom is not strongly linked to it, according to the Lewis-bond picture of the NBO analysis, probably due to its position with respect to nodal surfaces: rather, it appears to be “carried” over the barrier essentially via a linkage to the triphos P atom (although this is weakened by the build-up of P_tr–H antibonding density due to interactions with several filled orbitals and lone pairs of the CoP₃ cage. Overall, the H atom does not seem to be involved in other particularly important (non-electrostatic) interactions, as is indirectly revealed by the smaller deformations of the CoP₃ cage than is found for other stationary states. In the symmetry-constrained approach of the previous study [8] the present TSa appeared as a relative minimum.

TSb, along a path with C_s local symmetry for proton transfer from 1 to 2, is on top of a higher barrier (25.2 kcal mol^–1 above 1) than that of TSa and does not seem to provide a favorable route for H motion. TSc, connecting two configurations, 1 and 4, both with the H atom in a bridging position, is at slightly lower energy than TSb (23.7 kcal mol^–1 above 1), but it still presents a higher barrier than TSa. The hydrogen in TSc may be considered to establish comparable acceptor interactions, at second order perturbation theory level (NBO), with the electron densities of one P_P3–P_P3 and two Co–P_P3 bonds.

The situation is less clear-cut for the relative minima and transition states for H motion along the periphery of the P₃ ring, due to the smallness of energy differences involved. TS's are found, with relatively small (absolute value) imaginary frequencies, between 2 and 3 as well as between 3 and 4, the former TS lying only 0.4 kcal mol^–1 above 2 (1.7 kcal mol^–1 above 3) and the latter 0.3 and 0.2 kcal mol^–1, respectively, above 3 and 4. Indeed, the characterization of the stationary state 3 is based on the identification of those TS's. However, such small barriers (especially the second one) are practically zeroed by the application of zero-point energy corrections, a situation not unusual with soft modes, which is not improved by conventional ZPE scaling [23]. Moreover, the features of those TS's might be significantly affected by alternative choices of basis set; therefore, only the geometry of the first of them (TSd) is shown in Fig. 2. Overall, it is evident that there are no major obstacles to H motion around the P₃ ring. However, such path involves stationary states belonging to an energy plateau lying ca. 10 kcal mol^–1 above the absolute minimum of 1; moreover, a TS at least as high as TSc has to be passed in order to reach that plateau from 1.

An alternative to all of the previous paths is represented by a sort of rotational motion of the whole P₃H group, with relative positions of the H and P_P3 atoms substantially fixed, around the pseudo-threefold axis of the model; this may also be viewed as relative rotational motion of the (triphos)Co and P₃H moieties. A motion of this type is well established for the parent unprotonated complex and related species [9]. It may rationalize the observed fluxionality of the present compound, except for the absence of P–H coupling in its NMR spectrum. A representation of this TS (Tse), which lies 13.9 kcal mol^–1 above 1 and is connected on the two sides with type 1 minima, via ±60° rotations of the whole P₃H group as specified above, is given in Fig. 3. The relative orientations of the triphos and P₃ moieties in TSe should be compared with those of 1 in Fig. 1.

Finally, the rotational mode of the only P₃ group around the molecular axis, with the metal-bound hydrogen substantially fixed with respect to the (triphos)Co frame, has been probed. This yielded the TSf stationary state (Fig. 3), lying 13.7 kcal mol^–1 above 1, which is, again, connected on the two sides to type 1 minima. Similarly to the previous TSe, but at variance with all of the other TS's, TSf is characterized by a pseudo-prismatic arrangement of the P_tr and P_P3 triads; on the other hand, it is the only stationary state for which an effective Co–H bond is present according to the NBO description (as a result of the overall arrangement, rather than of a particularly short Co–H distance). The last two types of intramolecular rearrangement, characterized by the comparatively low barrier heights of Tse and TSf, appear to be good candidates to account for the fluxionality of the system; the second of the two is also consistent with the absence of P–H coupling in the NMR spectrum of the compound.

Attempts were made to verify to what extent changes in the model would affect the overall picture. Sets of single-point energy calculations were performed in correspondence of each of the above stationary state geometries, employing the B3LYP functional and a basis set augmented by (a) a diffuse function for the migrating H atom, or (b) a diffuse function for each atom of the P₃H moiety. Another set (c) of single-point calculations was at the same B3LYP/6-31G(d,p) + ECP level generally employed (hereafter, level A), however, within the PCM approach [17–19], in order to simulate the effects of a solvent environment. Relative energies (ΔE) were calculated including in all cases ZPEs from the frequency analyses performed at the level A of computation. Only limited changes in relative energies were found, by far the largest one being a 1.6 kcal mol^–1 increase in the ΔE of 4 in the set (c) of calculations. In addition, the geometries of the representative stationary states 1 and TSf were again optimized: (d) assigning a diffuse function to each of the P₃H atoms, on top of the level A basis set, for gas phase conditions, (e) within the PCM approach, at level A, and (f) at the full-electron B3LYP/6-311*G(d,p) level (gas phase), performing in this case new frequency analyses for ZPE contributions, (results for 1 from calculations of the latter type have been mentioned above). Changes in geometries, with respect to those reported in Fig. 1 for 1 and Fig. 3 for TSf, were generally small, consisting of maximum 0.003, 0.015, or 0.024 Å shortenings in Co–P_P3 distances, respectively, for the (d), (e), or (f) calculations. As for the relative energy of TSf, its change from the (level A, gas phase) 13.7 kcal mol^–1 value was negligible for the computational model (d) and small (0.3 kcal mol^–1 increase) for (e). Calculations (f) yielded a rather substantial decrease, of 1.3 kcal mol^–1, in the TSf ΔE, suggesting that significant (but computationally intensive) improvements in the level of theory may lead to estimates of barrier heights better in line with values expected for processes occurring in solution at room temperature.

4 Conclusions

This investigation has been addressed to the search of possible pathways for proton migration over the CoP₃ cluster, without the aim of obtaining very accurate energy values, also in view of the fact that energies are likely to be affected by solvation effects, possibly to a larger extent than can be mimicked by polarizable continuum models. The existence of several accessible pathways has been verified, with the indication that the pathways characterized by minima and saddle points with the hydrogen residing in proximity of the metal atom should possess overall lower energies than those with the hydrogen localized on the P₃ far side. The fluxionality of the system on the NMR time scale appears to be best rationalized in terms of processes consisting of relative rotations of the triphos and P₃H, or simply P₃, parts around an axis passing through the metal atom. If such types of motion actually prevail, the proton would just participate to the overall configurational changes, rather than being the nucleus most extensively involved in the motion over a relatively fixed frame. However, it should not be ignored that the last two processes reported, which appear to be favored among those investigated with gas phase models, may be restrained more than the competing processes by solvation effects, since they imply rather extensive motion of large moieties.

Acknowledgements

We acknowledge financial support by the Italian Ministero dell'Istruzione, dell'Università e della Ricerca. We are grateful to Dr. Andrea Ienco of ICCOM, CNR, Florence, for advice with graphic procedures.

Bibliographie

[1] C.A. Ghilardi; S. Midollini; A. Orlandini; L. Sacconi Inorg. Chem., 19 (1980), p. 301

[2] C. Bianchini; C. Mealli; A. Meli; L. Sacconi Inorg. Chim. Acta, 37 (1979), p. L543

[3] M. Di Vaira; M. Ehses; M. Peruzzini; P. Stoppioni Inorg. Chem., 39 (2000), p. 2199

[4] S. Midollini; A. Orlandini; L. Sacconi Angew. Chem. Int. Ed. Engl., 91 (1979), p. 93

[5] G. Capozzi; L. Chiti; M. Di Vaira; M. Peruzzini; P. Stoppioni J. Chem. Soc. Chem. Commun. (1986), p. 1799

[6] M. Di Vaira; D. Rovai; P. Stoppioni Polyhedron, 20 (1990), p. 2477

[7] M. Di Vaira; P. Stoppioni; S. Midollini; F. Laschi; P. Zanello Polyhedron, 10 (1991), p. 2123

[8] A. Bencini; M. Di Vaira; P. Stoppioni; M. Uytterhoeven Theor. Chim. Acta, 91 (1995), p. 187

[9] M. Di Vaira; P. Stoppioni Coord. Chem. Rev., 120 (1992), p. 259

[10] J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; V.G. Zakrzewski; J.A. Montgomery; R.E. Stratmann; J.C. Burant; S. Dapprich; J.M. Millam; A.D. Daniels; K.N. Kudin; M.C. Strain; O. Farkas; J. Tomasi; V. Barone; M. Cossi; R. Cammi; B. Mennucci; C. Pomelli; C. Adamo; S. Clifford; J. Ochterski; G.A. Petersson; P.Y. Ayala; Q. Cui; K. Morokuma; D.K. Malick; A.D. Rabuck; K. Raghavachari; J.B. Foresman; J. Cioslowski; J.V. Ortiz; A.G. Baboul; B.B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R. Gomperts; R.L. Martin; D.J. Fox; T. Keith; M.A. Al-Laham; C.Y. Peng; A. Nanayakkara; C. Gonzalez; M. Challacombe; P.M.W. Gill; B. Johnson; W. Chen; M.W. Wong; J.L. Andres; C. Gonzalez; M. Head-Gordon; E.S. Replogle; J.A. Pople Gaussian 98, Revision A.7, Gaussian, Inc., Pittsburgh, PA, 1998

[11] (a) A.D. Becke, J. Chem. Phys. 98 (1993) 1372; (b) A.D. Becke, J. Chem. Phys. 98 (1993) 5648; (c) C. Lee, W. Yang, R.G. Parr, Phys. Rev. B 37 (1988) 785.

[12] J.S. Binkley; J.A. Pople; W.J. Hehre J. Am. Chem. Soc., 102 (1980), p. 939

[13] P.J. Hay; W.R. Wadt J. Chem. Phys., 82 (1985), p. 270

[14] C. Peng; P.Y. Ayala; H.B. Schlegel; M.J. Frisch J. Comp. Chem., 17 (1996), p. 49

[15] G. Gonzales; H.B. Schlegel J. Chem. Phys., 90 (1989), p. 2154

[16] (a) NBO Version 3.1, E.D. Glendening, A.E. Reed, J.A. Carpenter, F. Weinhold; (b) J.P. Foster, F. Weinhold, J. Am. Chem. Soc. 102 (1980) 7211.

[17] S. Miertus; E. Scrocco; J. Tomasi J. Chem. Phys., 55 (1981), p. 117

[18] M. Cossi; V. Barone; R. Cammi; J. Tomasi Chem. Phys. Lett., 255 (1996), p. 327

[19] M.T. Cances; V. Mennucci; J. Tomasi J. Chem. Phys., 107 (1997), p. 3032

[20] G. Schaftenaar; J.H. Noordik Molden: a pre- and post-processing program for molecular and electronic structures, J. Comput. Aided Mol. Des., Volume 14 (2000), p. 123

[21] (a) C. Mealli, D.M. Proserpio, J. Chem. Educ. 67 (1990) 399; (b) C. Mealli, A. Ienco, D.M. Proserpio, Abstracts XXXIII ICCC, Florence, Italy, 1998, p. 510.

[22] ADF, release 1.0.2 Department of Theoretical Chemistry, Vrije Universiteit, Amsterdam, 1993.

[23] A.P. Scott; L.R. Radom J. Phys. Chem., 100 (1996), p. 16502