1 Introduction
Many of today's life comforts are based in the silicon technology mainly because of electronics. This makes the Si(100) surface, used in electronic devices production, one of the most important surfaces from a technological point of view [1]. Moreover, with the relatively recent advent of nanodevices and nanotechnology as well as the recent efforts to produce smaller and more sensible sensors for organic, inorganic and biological molecules, or even the possibility of using the Si(100) as a molecular reagent [2,3], the effort to study and understand the processes involved in the adsorption of large molecules to the silicon surface has become of the utmost importance. Even though the Si(100) surface has already been the subject of numerous articles, the computational power available even today is still not enough to perform this kind of studies when large molecules are involved.
The theoretical study of any surface is usually very difficult because it cannot correctly represent its almost infinite characteristic. However, two approximations are currently in use when considering this kind of system. These are known as the cluster and slab approaches [4]. The cluster approach uses just a few atoms both from the surface and from the bulk crystal, and assumes that those are enough to represent the local characteristics of the surface. The slab approach uses a unit cell that is reproduced in all the directions so that the surface is really infinite. Both have problems as all approximations do. Steckel et al. [4] have applied both these approaches when studying the hydrogen desorption from the Si(100) surface, and provide a good comparison of their use in this kind of systems. While the slab methodology achieves better results overall, it cannot represent an infinite dilution adsorption and is computationally tougher. This makes it inappropriate to study the adsorption of large molecules both due to the large area of interaction between the adsorbed molecules and to the incomputable large unit cells required. Furthermore, the adsorption of molecules on the silicon surface does not allow for long-range interactions to be taken into account. However, a large number of theoretical works, mainly older ones, have been accomplished using just a Si9H12 cluster to represent the reconstructed silicon surface and the adsorption of a small molecule on top of a unique dimer [5–7]. Even the adsorption of larger molecules (e.g. benzene or naphthalene) has been accomplished using just two surface dimers [8]. Even though these older studies claim success, Penev et al. found that only a three-dimer cluster (Si21H20) could show similar results to the slab calculation when studying the H2 adsorption and that the one and two-dimer clusters (Si9H12 and Si15H16, respectively) were inappropriate [9–11]. Even taking all this into consideration, the real problem starts when we want to study much larger molecules, as, e.g. fullerenes [12] or other complex monolayer organic coatings and films on the surface [13], or even protein [14] and DNA/RNA adsorptions [15], where a larger surface area needs to be represented (even considering only localized effects).
One other problem with the cluster method is the representation of the geometry restrictions, naturally imposed by the bulk crystalline structure, which simple valence-compensating hydrogen atoms or geometrical restrictions cannot correctly simulate [16]. Authors usually achieve that by fixing the few bulk atoms represented in their clusters at their perfect crystalline positions, or by optimizing a larger cluster and then fixing the central smaller cluster atoms in their optimized positions. Any of these strategies cannot really represent the real effects that exist when the second, third and more sub-surface layers relax throughout the adsorption process, which many times involves the conversion of a dimer from the buckled geometry to the symmetric one.
This present work tries to address both these problems and resolve them by simply using larger clusters with quantum mechanical/quantum mechanical (QM/QM) hybrid methods and that has proved to be very successful.
ONIOM, is a method that allows for the study of different groups of atoms using different calculation methods [17]. The idea behind it is to maintain the computationally expensive methods in the important areas of a cluster, e.g. the area of adsorption, and use other more inexpensive methods to study the less important areas farther from the important center, although still contributing to the geometry and the electronic density of the relevant part of the system.
We have investigated the capability of the ONIOM method when applied to the Si(100) surface cluster approach, using Hartree–Fock (HF) [18,19] and B3LYP [20] with several different basis-sets to study the relevant central part of the surface, and AM1 [21] semi-empirical methods to study the rest of the cluster. While this approach may seem relatively obvious, no one has tried to use it in this system until now, even though it has been showing some good results when applied to proteins [22]. Some problems not encountered in protein applications do show up when we apply this QM/QM method to the crystalline structure of the Si(100) surface. Here, we present, discuss and test some solutions to those problems.
We have looked also at the computational effort associated with this method and ab initio methods currently being used.
2 Methodology
The Gaussian98 software package [23] was used to perform all the calculations made. The manipulation and creation of the structures was carried out using GaussView [23], Molden [24] and Molekel [25].
Since we are dealing with a periodic structure, the form and size of the cluster is not a trivial matter. To find the best cluster model that would be both the smallest possible while correctly representing the surface structure, we have investigated several cluster sizes and models using AM1, HF and B3LYP and the two hybrid QM/QM (ONIOM) combinations AM1/HF and AM1/B3LYP.
Previous works [26] have shown that the B3LYP functional is appropriate to represent the Si(100) surface, and therefore we have used this functional to calculate the central part of the cluster, while the HF and AM1 should only be adequate to represent the atoms in the cluster not directly in contact with the adsorbed molecule [16,27]. Nevertheless, we ran and tested several combinations using various basis-sets to understand how compatible would be the methods used in each of the QM/QM layers.
It was found that generating a cluster structure above a certain size, mainly dictated by how good the total geometry was, would yield a non-converging minimization irrespective of the method used. Eventually we carried out partial optimizations by columns, optimizing each dimmer column, in the lower level, at a time. This provided very good results.
3 Results and discussion
The scope of this paper is to provide a system sufficiently big to represent reality, and a method reliable and fast enough to study it. To accomplish that we have studied several silicon clusters (the smallest one Si9H12, and the biggest Si252H100), using several calculation methods and basis-sets. The smaller the system the greater the number of calculations performed onto them. For each system, at least three types of calculations were carried out at different theoretical levels: semi-empirical (AM1), Hartree–Fock (HF) and hybrid quantum mechanical (HF/AM1 and/or B3LYP/AM1, with ONIOM). The chosen basis-set for the two latter methods was SHC [28], which proved fairly reliable.
Throughout the years, the Si(100) surface dimer structure has been the subject of much discussion. Initially, the scientific community would not agree whether the dimer was buckled in a c(4 × 2) symmetry arrangement or whether it was the symmetric, unbuckled p(2 × 1) arrangement, that was the minimal energy structure. However, presently there are many studies both theoretical [29,30] and experimental [31–33] concerning the geometry of the Si(100) surface, which is now well established. The dimer is indeed buckled with an angle of around 19–20°, and with a dimer bond length (presenting a larger variance) of 2.25–2.37 Å. Due to the very small energy difference between the buckled and unbuckled states, the optimized geometry obtained with a theoretical method is sensitive to the quality of that same method. Therefore, it is possible to infer if a certain methodology is acceptable or not when applied to the Si(100) surface representation using geometry only results. In our work we used the dimer angle and dimer distance as geometrical standards. This way, we can compare our results with previous experimental and theoretical works and judge how reliable the representation of our surface is when using a certain method. A nice discussion and presentation of all those previous works and results can be found in chapters 2 and 3 of Ref. [1] and references within.
3.1 One, two and three-dimer clusters
The one (Si9H12), two (Si15H16) and three-dimer (Si21H20) clusters can be visualized in Fig. 1.
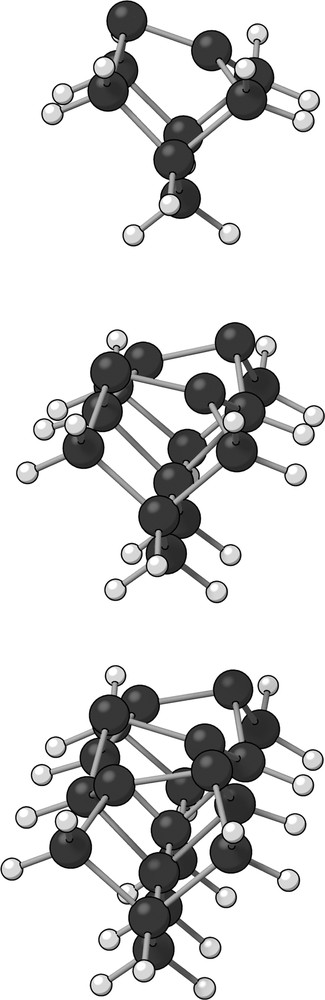
The three small clusters. From top to bottom: Si9H12 (one-dimer); Si15H16 (two-dimers) and Si21H20 (three-dimers). Large dark spheres represent silicon atoms while lighter small spheres represent hydrogen atoms. The structures shown are optimized geometries obtained with B3LYP/6-311G, B3LYP/6-31 + G(d) and B3LYP/6-311G, respectively.
Table 1 is self-explanatory, showing the cluster size in the first column, the theoretical level in the second, the used basis-set in the third, the final optimized energy of the cluster in the fourth column, the atomic distance between silicon atoms in the dimer in the fifth column, and the angle of tilt of the dimer, relative to the surface, in the last column. These two last measurements correspond only to the central dimer in the case of the three-dimer cluster. Lateral dimers typically and understandably present worst geometrical values.
One-, two- and three-dimer clusters calculation results using both HF and DFT/B3LYP with several basis-sets. Columns refer to the cluster size, theoretical level, basis-set, final optimized energy, dimer Si–Si distance and tilt of the dimer relative to the surface, respectively
| Cluster size | Theoretical level | Basis-set | Energy (keV) | Si–Si (Å) | Tilt (°) |
| Si9H12 | HF | 3-21G | –70.57471 | 2.198 | 0.0 |
| 6-311G | –70.94304 | 2.214 | 0.0 | ||
| LANL2DZ | –1.10602 | 2.169 | 0.0 | ||
| SHC | –1.10126 | 2.210 | 0.0 | ||
| DFT/B3LYP | 3-21G | –70.72235 | 2.236 | 0.0 | |
| 6-311G | –71.09517 | 2.252 | 0.0 | ||
| LANL2DZ | –1.14601 | 2.213 | 0.0 | ||
| SHC | –1.14098 | 2.265 | 0.0 | ||
| Si15H16 | HF | 3-21G | –117.56275 | 2.197 | 0.0 |
| 6-311G | –118.17596 | 2.212 | 0.0 | ||
| LANL2DZ | –1.78081 | 2.166 | 0.0 | ||
| SHC | –1.77318 | 2.207 | 0.0 | ||
| DFT/B3LYP | 3-21G | –117.80650 | 2.235 | 0.0 | |
| 6-311G | –118.42726 | 2.301 | 11.1 | ||
| 6-31 + G(d) | –118.42688 | 2.264 | 12.2 | ||
| LANL2DZ | –1.84512 | 2.210 | 0.0 | ||
| SHC | –1.83700 | 2.262 | 0.0 | ||
| Si21H20 | HF | 3-21G | –164.55079 | 2.199 | 0.0 |
| 6-311G | –165.40889 | 2.212 | 0.0 | ||
| LANL2DZ | –2.45558 | 2.169 | 0.0 | ||
| SHC | –2.44547 | 2.460 | 16.7 | ||
| DFT/B3LYP | 3-21G | –164.89068 | 2.237 | 0.0 | |
| 6-311G | –165.75942 | 2.363 | 15.1 | ||
| 6-31 + G(d) | –165.75869 | 2.298 | 15.3 | ||
| LANL2DZ | –2.54423 | 2.209 | 0.0 | ||
| SHC | –2.53324 | 2.419 | 16.1 | ||
| SHC* | –2.54610 | 2.330 | 16.4 |
To start analyzing these results, we should remember the experimental and theoretical values for the buckled dimer state presented in the previous section, i.e. 2.25–2.37 Å for the Si–Si dimer bond length and 19–20° for the dimer tilt angle [29–33].
General trends are readily seen both in bond length and tilt angle. As expected, values get better with bigger clusters and added dimers. We also see better results when DFT/B3LYP is used, when in comparison to the HF theoretical level.
The one-dimer cluster, regardless of the theoretical level and basis-set used, cannot represent the dimer buckling effect. It is only when we get to the two-dimer cluster using DFT/B3LYP that we see the buckling effect and even then the values obtained, around 11–12°, are still low when compared to the expected values of 19–20°. The Hartree–Fock level, in this case, still does not present any buckling angle. The use of the three-dimer cluster, continues the trend and values get better, to around 15–16°. Once again, DFT/B3LYP presents better results than HF.
In the case of the dimer bond length, we can see again the same trend formerly observed for the case of the tilt angle. Larger clusters usually present better results and HF behaves worse than DFT/B3LYP.
So, until now, everything is as expected and coherent with previous works [16,26,27]. Still, there are some specific points that should be noted. First, one of the two pseudo-potential basis-sets (LanL2DZ) used turned out to be completely unusable in what concerns the Si(100) surface. On the other hand, the SHC basis-set, especially with polarization functions employed (SHC*), presented very good results when the three-dimer cluster was used. These results were comparable to the much bigger and time-consuming 6-311G basis-set. Therefore, the SHC* basis-set turned out to be the best basis-set in terms of results quality per computation time required.
3.2 Larger clusters
Table 2 shows the results of selected calculations performed in clusters using the ONIOM methodology [17]. Both for this table and the previous one, we carried out a larger number of calculations but, for simplicity, we decided to present only part of the results that not affecting any of the conclusions still exemplify the main points of interest.
Results for QM/QM clusters calculations. Columns refer to the cluster size, theoretical level, basis-set, final optimized energy, central dimer Si–Si distance, tilt angle of the central dimer relative to the surface, and the number of high-level/low-level/sulfur atoms, respectively
| Cluster size | Theoretical level | Basis-set | Energy (keV) | Si–Si (Å) | Tilt (°) | H/L/S |
| Si57H40 | AM1 | – | 0.01976 | 2.138 | 0 | |
| B3LYP/AM1 | SHC | –1.82630 | 2.335 | 13.9 | 15/82/0 | |
| Si83H48 | AM1 | – | 0.02716 | 2.148 | 0 | |
| B3LYP/AM1 | SHC | –3.64126 | 2.535 | 17.6 | 31/100/0 | |
| Si87H52 | AM1 | – | 0.02594 | 2.164 | 0 | |
| B3LYP/AM1 | LANL2DZ | –3.93569 | 2.235 | 0 | 33/106/0 | |
| B3LYP/AM1 | SHC | –3.91919 | 2.689 | 19.9 | 33/106/0 | |
| Si121H64 | AM1 | – | 0.03889 | 2.149 | 0 | |
| B3LYP/AM1 | SHC | –10.75735 | 2.506 | 21.9 | 50/135/18 | |
| Si197H84 | AM1 | – | 0.06019 | 2.168 | 0 | |
| HF/AM1 | SHC | –10.84118 | 2.568 | 17.8 | 83/198/6 | |
| B3LYP/AM1 | SHC | –11.20485 | 2.543 | 18.2 | 83/198/6 | |
| Si252H100 | AM1 | – | 0.05537 | 2.155 | 0 | |
| HF/AM1 | LANL2DZ | –3.76883 | 2.185 | 0 | 33/319/0 | |
| B3LYP/AM1 | SHC | –3.87969 | 2.547 | 19.5a | 33/319/0 | |
| B3LYP/AM1 | SHC* | –3.89982 | 2.400 | 18.6a | 33/319/0 | |
| B3LYP/AM1 | 6-31 + G(d) | –260.37656 | 2.364 | 17.5a | 33/319/0 | |
| B3LYP/AM1 | 6-31 + G(d) | –165.70446 | 2.364 | 17.3a | 21/331/0 |
a Angular restrictions applied to the peripheral dimers calculated with AM1.
With these calculations, we have tried to verify the applicability of this QM/QM methodology to these systems, and investigated the problems that could arise when using it.
In comparison to the previous table, Table 2 has one added column. This refers to the number of atoms present in the ONIOM high layer (H), low layer (L) and the number of valence-compensating sulfur atoms (S) in the layers interface, respectively. This brings us to one of the problems encountered. These sulfur atoms were needed in a few cases, i.e. when an interface atom belonging to the low layer was connected to two high layer atoms. The default hydrogen atom used by ONIOM did not let the calculations converge and so we tried to substitute it by a sulfur atom, which is the most similar in size to silicon while still allowing for the formation of the two needed bonds. Although this may seem a reasonable approach in comparison to the default hydrogen substitution, the truth is that it only worked partially. The calculations did start to converge much more easily after we started to use the sulfur atoms, but the optimized geometries were heavily distorted. This was caused by the simple fact that even small differences in the bond length between the bulk atoms originate a sizeable distortion in a large volume of crystalline structures. In the case of the sulfur atoms the optimized bulk Si–Si distance increased by about 0.2 Å, from the 2.35 Å bulk distance that AM1 correctly represents, to about 2.55 Å. These distortions turned out to be unacceptable and so we abandoned this strategy. Instead, we opted to define the high layer atoms in such a way that there were no two interface atoms connected to the same low-level atom. This is trivial but limitative. Fortunately, by selecting only a column of dimers, such problem is avoided. When more than just one column of dimers is to be optimized, we found that the best strategy was to optimize them one by one restricting the others (only dimer angles restricted), in a self-consistent way, until the optimization is achieved in just one iteration.
Interestingly enough the bond length issue was more important than we initially thought it would be. AM1 gave good results in relation to the optimized bulk Si–Si bonds where the correct distances were found (not shown in the table). This was very good news since it allowed us to use AM1 without any major reservations in the treatment of the bulk atoms. However, on the high-level part, both HF and B3LYP type calculations were not coherent and presented some variation in the Si–Si bond lengths. This posed some problems equivalent to the previously described sulfur atoms case. As the lower layer always surrounds the higher one, if they do not fit correctly, the occurrence of distortions in the whole cluster is inevitable. The worst case was that in which we tried to use B3LYP/LanL2DZ in an ONIOM calculation. This resulted consistently in the higher layer being too large in relation to the AM1 part. This poses a further restriction in the definition of the initial system as one has now to know what is the most compatible ab initio calculation in relation to the AM1 part. We found that a good and relatively fast ab initio method was the B3LYP/SHC combination. Besides of giving acceptable results and being computationally fast, as already discussed earlier, it did also quite well in the ONIOM calculations.
The AM1 method, though, is completely inadequate to represent the Si(100) surface, as can be seen in all calculations (totally unrestricted ones) made using the AM1 method alone, where not even once we obtained the tilted dimer geometry. Fortunately, we found that when restricting the angles around the silicon atoms involved in the surface dimers treated with AM1 (usually lateral columns), the Si–Si bond length in the dimers was adequate (around 2.37 Å). The angles were the ones resulting from the partial optimizations performed in each column separately using the high-level method (around 19°). The cases where this was applied are marked with footnote (a) in Table 2.
As for the computation times, it is not very easy to compare them as many times the number of steps required to optimize a geometry is very different between different methods. Nevertheless, we can say that the AM1 part only took between 5% and 15% of the total computation time. The high-level part though is affected by the low-level one and usually takes longer to compute when ONIOM is used. On the other hand, due to the rigidity imposed by the low-level part, these calculations optimized in fewer steps and so the final computation times of the QM/QM clusters, when compared to the DFT only clusters, were not significantly higher, while still giving better results. For instance, the optimization of the biggest cluster (Si252H100) representing five surface dimers, using B3LYP/AM1 and SHC*, took less than 2 days in a typical low-end desktop computer (Pentium® 4 @ 1.5 GHz and 256 Mb of RAM), which is quite acceptable.
In the end, having solved the several problems encountered, we achieved a very good surface representation as can be seen in the last four results of Table 2 and the larger cluster created was the one with 252 silicon atoms and shown in Fig. 2. This cluster contains 15 surface dimers aligned in three columns, is 10 silicon layers thick and contains almost no surface distortion. Moreover, we can create even larger clusters with different high layer central parts that can be appropriate for the adsorption of large molecules.

The largest ONIOM cluster Si252H100. Large spheres represent the high-level atoms while the low-level ones are represented as sticks. The central high-level part contains an entire column with five-dimers. The B3LYP/AM1 output using the SHC* basis-set is shown.
4 Conclusion
We have applied the ONIOM methodology to the study of silicon (100) surfaces. The method allows for a big improvement in the representation of surface properties, while keeping the calculation times relatively low. However, while the CPU time is not much higher than an ab initio only calculation using a much smaller cluster, ours can represent a much larger number of atoms and present a good electronic description of the central part of the clusters surface. Consequently, a large number of new studies that formerly could not be done because of the small size of the clusters used until now can now be performed. Moreover, these studies can be carried out fast, initially, and afterwards a further refinement of the structures can be made by just increasing the number of high-level atoms and/or using a better basis-set.
We found that the SHC or the SHC* basis-sets were very good to reproduce the surface characteristics and very fast to compute. The results are a little worse than the ones obtained with big Gaussian type basis-sets, but the CPU time is inferior by about 10-fold. So, as a starting point for these silicon studies, these basis-sets are a good choice.
We also found out that there is a marked effect of the dimer neighborhood in its final geometry. The results improved while we kept increasing the system size. Even better was the fact that the use of the AM1 low-level part in the system also helped improving the dimer representation while the CPU time increased only slightly.
The other objective that we had in mind was also accomplished since we now have a cluster that can relax realistically, making it possible to account for the sub-surface relaxation effects when a molecule adsorbs at the surface.
In the end, we think that we have created a good working system for future studies that involve the use of larger surface areas as is the case of the adsorption of large molecules.


