Emission spectroscopy of metal-to-ligand-charge-transfer states of HRe(CO)<sub>3</sub>(H-dab), model system for α-diimine rhenium tricarbonyl complexes

Sébastien Villaume; Chantal Daniel

doi:10.1016/j.crci.2004.10.037

Résumés

Anglais
Français

The emission and absorption theoretical spectra of HRe(CO)₃(H-dab) (H-dab = 1,4-diaza-1,3-butadiene), model system for a broad class of transition metal carbonyls α-diimine compounds, have been obtained by means of wave packet propagations on the V(q) (q = [Re–H]) CASSCF/MRCI potentials calculated for the electronic ground state and the ¹MLCT (metal-to-ligand charge-transfer) absorbing state corresponding mainly to a 5d_Re → π*_H-dab excitation. The simulated spectra reproduce the main features of the experimental spectra of this class of complexes, namely one intense absorption band between 20 000 and 25 000 cm^–1 assigned to this MLCT state and one strong emission band shifted to the red. The contribution of the low-lying bound MLCT triplet states or dissociative sigma-bond-to-ligand-charge-transfer (SBLCT) state is not taken into account in these preliminary simulations. Indeed the main goal is to understand the contribution of the absorbing MLCT state to the radiative process which may compete with the homolytic cleavage of the rhenium–hydrogen bond via the ³SBLCT state coupled to the absorbing state by spin-orbit (SO). The theoretical time-resolved emission spectrum simulated by wave packet propagation on the same potentials (absorbing ¹MLCT state and electronic ground state) is also presented. .

Les spectres d'émission et d'absorption théoriques du complexe HRe(CO)₃(H-dab) (H-dab = 1,4-diaza-1,3-butadiene), système modèle pour toute une classe de composés α-diimine de métaux de transition, ont été construits par propagation de paquets d'ondes sur le potentiel V(q) (q = [Re–H]) calculé au niveau CASSCF/MRCI pour l'état fondamental et l'état absorbant ¹MLCT (metal-to-ligand charge transfer) correspondant principalement à une excitation 5d_Re → π*_H-dab. Les spectres issus de ces simulations comportent les principales caractéristiques des spectres expérimentaux couramment observés, c'est-à-dire une bande d'absorption intense située entre 20 000 et 25 000 cm^–1, attribuée à cet état MLCT, et une bande d'émission correspondante, décalée vers le rouge. La contribution des états triplets dissociants (sigma-bond-to-ligand charge transfer ou ³SBLCT) et liés (³MLCT) n'est pas prise en compte dans ces simulations préliminaires, dont le but est de comprendre la contribution de la transition ¹MLCT (absorbant) vers l'état fondamental dans le spectre d'émission expérimental. Ce processus peut entrer en compétition avec la rupture homolytique de la liaison Re–H via l'état ³SBLCT couplé par spin orbite à l'état absorbant. Enfin, le spectre d'émission théorique résolu en temps accessible expérimentalement par des expériences laser pompe/sonde pour ce type de molécules est présenté. .

1 Introduction

Emission from (L) Re (CO)₃(α-diimine) complexes (L = axial ligand = halide, alkyl, benzyl, metal fragment) often provides the first indication of the character of the low-lying excited states. Moreover, detailed experimental studies of emission spectroscopy have played a central role in the understanding of their photochemical reactivity and photophysical properties [1]. This class of molecules is characterized by significant electronic delocalization effects on the three chemical centers determined by the metal atom, the α-diimine group and the ligand L [2]. Depending on these chemical centers irradiation into the visible may lead to a variety of important applications such as ultra-fast dissociation of a carbonyl ligand or homolytic cleavage of the Re–L bond with formation of di-radicals initiators of polymerization [3]. The molecules may also behave as strong luminophore or as precursors of electron/energy transfer.

The photoreactivity and excited states dynamics of this class of molecules have been investigated in details by means of accurate quantum chemical calculations completed by wave packet propagations for the HM(CO)₃(H-dab) complexes (M = Mn, Re) [4,5]. Whereas a complete and ultra-fast direct dissociation of the CO ligand (in less than 500 fs) has been put in evidence by the theoretical study for the manganese complex a rather slow (beyond the ps time scale), non total and indirect homolysis of the Re–H bond occurs through ¹MLCT → ³SBLCT intersystem crossing in HRe(CO)₃(H-dab). This later reaction may certainly compete with the emission process either from the ¹MLCT absorbing state or from the low-lying ³MLCT states, according to the schematic view of the potential energy curves (Scheme 1).

This is corroborated by the experimental quantum yield of the Re–L bond homolysis which may vary between 10^–2 (L = methyl) to nearly 1.0 (L = ethyl or benzyl) [6,7] in these molecules.

The purpose of the present theoretical investigation is to simulate the absorption/emission spectra of HRe(CO)₃(H-dab) by means of wave packet propagation on the one-dimensional potentials V(q) (q = [Re–H]) calculated for the MLCT (5d_Re → π*_H-dab) and the electronic ground state. The low-lying ³SBLCT and ³MLCT states are not included in this preliminary study.

2 Computational details

The potential energy curves corresponding to the electronic ground state ¹A' (σ_Re–H)²(5d_x²_–_y²)²(5d_yz)²(5d_xz)²) and low-lying ¹MLCT absorbing state (5d_Re → π*_CO) were obtained by calculating the potential energy as a function of the Re–H bond length, keeping all other coordinates frozen at the idealized geometry depicted in Fig. 1.

Fig. 1
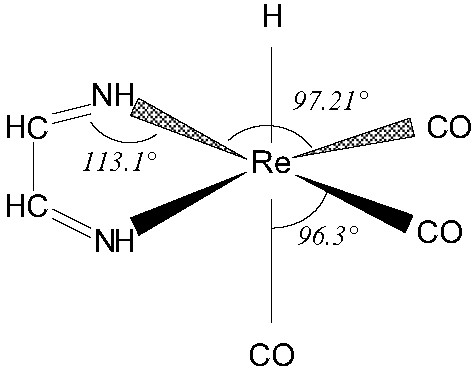
Idealized geometry of HRe(CO)₃(H-dab) [5].

The details of the quantum chemical calculations are reported elsewhere [5].

The molecule has been modeled as a pseudo diatomic with the hydrogen on one side and the rest of the complex on the other side. The Re–H bond distance q is the only degree of freedom; all other coordinates were remained fixed and were decoupled from q.

The photo-absorption and emission dynamics were obtained by solving the time-dependent Schrödinger equation,(1)

i ℏ \frac{\partial}{\partial t} Ψ_{k} (q, t) = [T_{n u} + V_{k}] Ψ_{k} (q, t)

where k denotes the electronic state, with the following initial conditions for the absorption,(2)

Ψ_{k} (q, t = 0) = {μ_{GS \to abs}}_{} Φ (q, E_{k}, n = 0)

and the following initial conditions for the emission,(3)

Ψ_{k} (q, t = 0) = μ_{em \to GS} Φ (q, E_{k}, n)

where the subscripts abs and em stand for absorbing and emitting states, respectively. μ_{GS → abs} (μ_{em → GS}) is the electronic transition moment between the electronic ground state and the absorbing (emissive) b¹MLCT state and Φ (q, E_k, n) represents the vibrational wave function of the electronic state k in the vibrational levels n (n = 0, 1, 2) evaluated through the Fourier grid Hamiltonian method. The parameters of the one-dimensional grid are: Δq = 0.01 a.u. for q between 1.2 and 8.0 a.u.

The kinetic part of the Hamiltonian of the system is given by:(4)

T_{nu} = - \frac{ℏ^{2}}{2 μ} \frac{\partial^{2}}{\partial q^{2}}

where μ is the reduced mass corresponding to the coordinate q. The time-dependent Schrödinger equation is solved using the second order propagation scheme (SOD) with Δt = 0.5 fs.

The absorption and emission spectra are obtained by evaluation of the cross sections within the weak field approximation [8,9](5a)

σ_{abs} (ω) \propto ω \int_{- \infty}^{+ \infty} e^{i (E_{0} + ω) t} S (t) d t

(5b)

σ_{em} (ω) \propto ω^{3} \int_{- \infty}^{+ \infty} e^{i (E_{0} ω) t} S (t) d t

where ω is the frequency of the radiation, E₀ represents the energy of the initial wave packet on the electronic state k and S(t) is the autocorrelation function(6)

S (t) = 〈 Ψ_{k} (0) | Ψ_{k} (t) 〉

The time-dependent emission spectrum is simulated by the ¹A′ (GS) → b¹MLCT absorption (see above), the $Ψ_{a b s} (q, t)$ wave packet developed on the absorbing state being transferred on the electronic ground state at each step of the propagation on the upper state.

3 Absorption/emission spectra of HRe(CO)₃(H-dab)

The CASSCF/MRCI potential energy curves calculated as a function of the Re–H bond elongation in HRe(CO)₃(H-dab) [5] for the electronic ground state, the low-lying MLCT states and the ³SBLCT dissociative state are represented in Fig. 2. A detailed study of the theoretical absorption spectrum based on wave packet propagations on two-dimensional potential energy surfaces (PES) taking into account several low-lying singlet electronic states has been published elsewhere [5].

Fig. 2
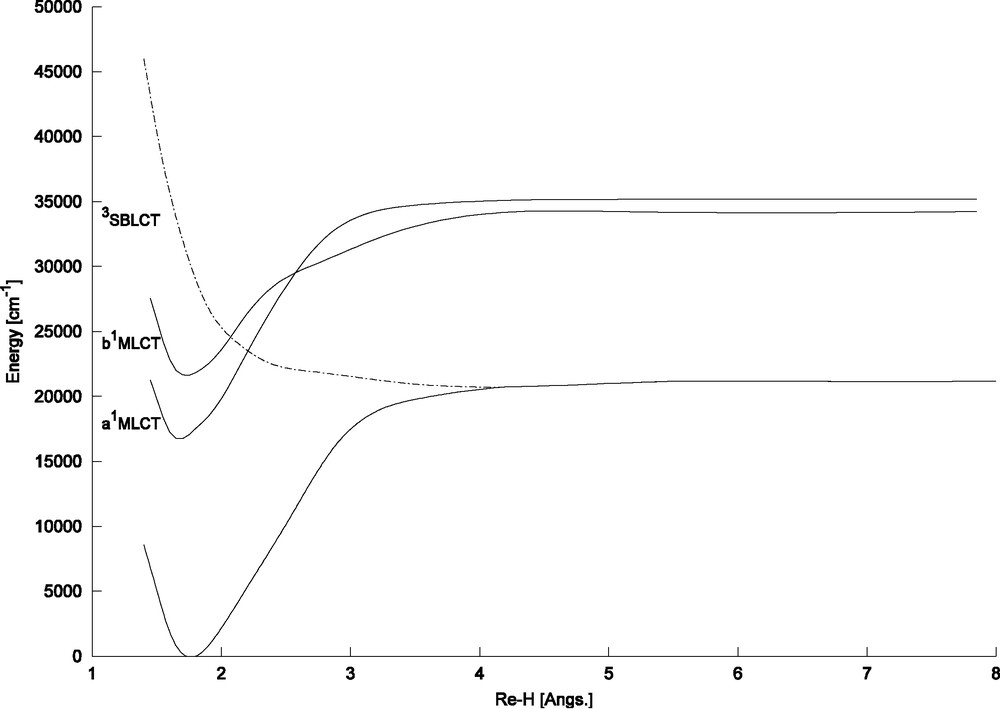
CASSCF/MRCI potential energy curves of HRe (CO)₃(H-dab) calculated as a function of the Re–H bond elongation under C_s symmetry constraint [5] corresponding to the low-lying a¹MLCT, b¹MLCT (absorbing state) and ³SBLCT.

The goal of the present simulation based on a simple one-dimensional scheme including only the low-lying b¹MLCT (the only one with a significant oscillator strength of 0.38) is to recover the main features of this absorption spectrum and to reproduce the characteristics of the corresponding emission spectrum originated from the absorbing state. The simulation should serve as a reference for the limiting case of a pure radiative decay. For this purpose the electronic ground state potential has been shifted by 0.4 a.u. to the short Re–H bond distances and the initial wave packet (Eq. (2)) prepared on the electronic ground state has been propagated on the upper MLCT state. The theoretical absorption spectrum is depicted in Fig. 3.

Fig. 3
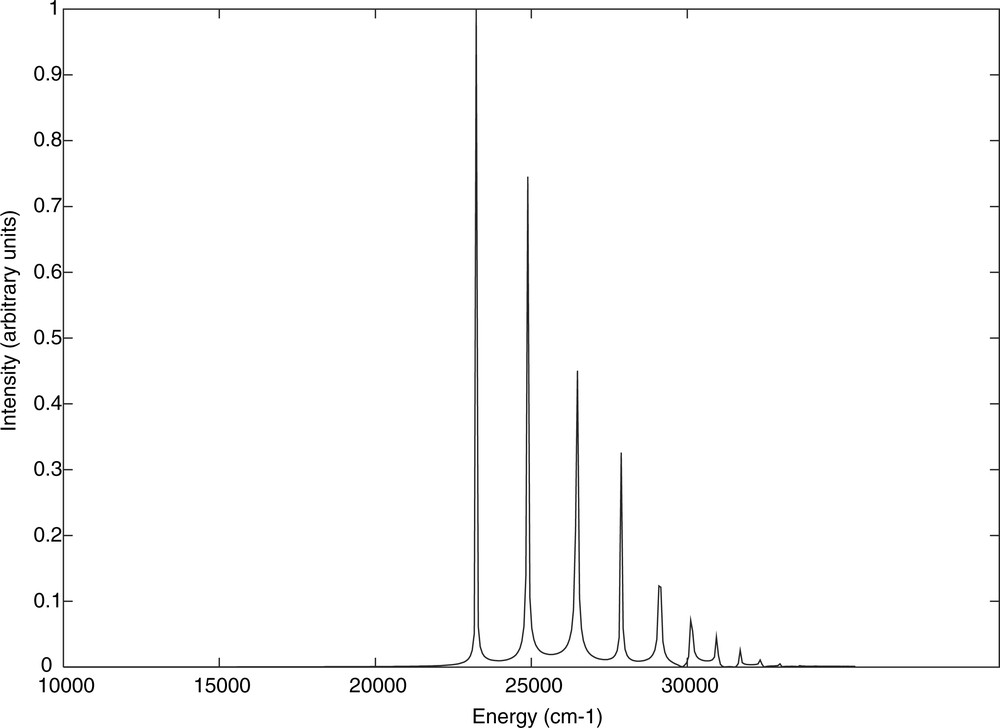
Theoretical absorption spectrum of HRe (CO)₃(H-dab) corresponding to the electronic ground state → b¹MLCT transition.

The simulated spectrum exhibits an intense peak at 23 200 cm^–1 in agreement both with the experimental spectrum recorded for this class of molecules [10] and the published theoretical spectrum [5]. The shoulder at 35 000 cm^–1 and the weak absorption at 15 000 cm^–1 obtained in our previous simulation [5] do not appear in Fig. 3 since the corresponding low-lying singlet states are not included in the simulation. In order to compare the fine structure of the absorption and emission spectra we did apply a multiplication factor exp (–Γt, Γ = 0.10) necessary to get the envelope of the spectrum.

The induced emission spectrum built on the basis of the propagation of initial wave packets prepared on the absorbing state and defined by Eq. (3) is represented in Fig. 4. This emission signal reflects the structure of the absorption spectrum and is shifted to the red. The intense peaks between 20 000 and 25 000 cm^–1 originate from the contribution of the initial Φ (q, E_k, n = 0) vibrational wavefunction corresponding to the vibrational ground state of the absorbing state (|0 > → |0 > at 23 200 cm^–1). The initial Φ (q, E_k, n = 1) and Φ (q, E_k, n = 2) wave packets corresponding to excited vibrational levels lead to minor contributions of 0.5% and 0.01%, respectively, between 15 000 and 22 000 cm^–1.

Fig. 4
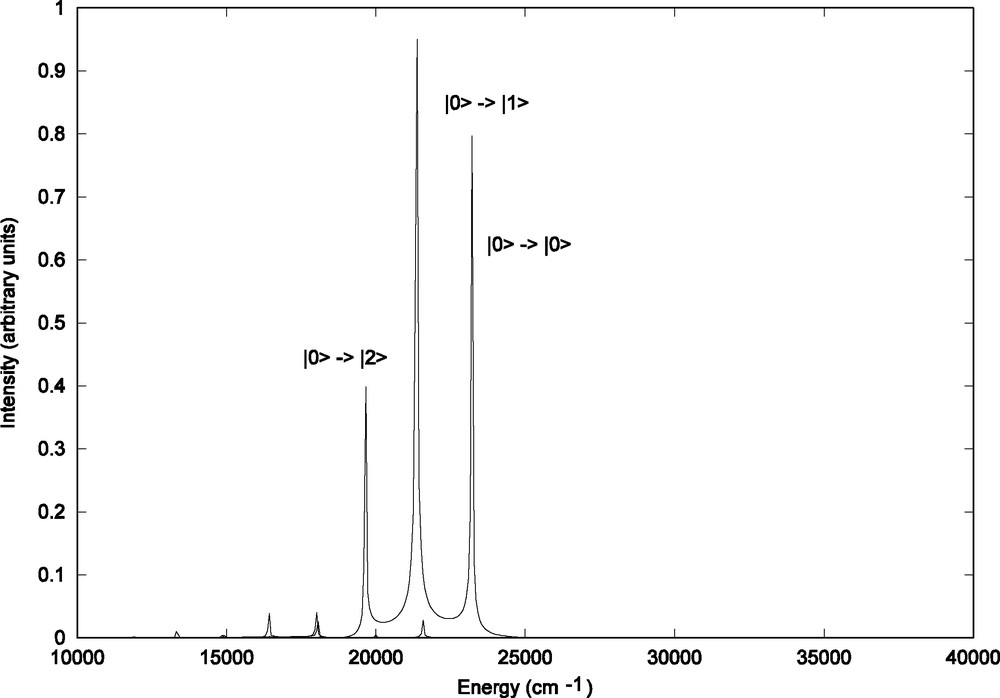
Total theoretical emission spectrum of HRe (CO)₃(H-dab) corresponding to the b¹MLCT → electronic ground state transition.

The structures of the partial contributions to the total emission spectrum are depicted in Fig. 5a–c. The contribution of the emission from the vibrational ground state (n = 0) of the b¹MLCT electronic state (Fig. 5a) can be superposed to the total emission spectrum (Fig. 4) with three peaks corresponding to the $| 0 〉 \to | 0 〉, | 0 〉 \to | 1 〉$ and $| 0 〉 \to | 2 〉$ transitions.

Fig. 5
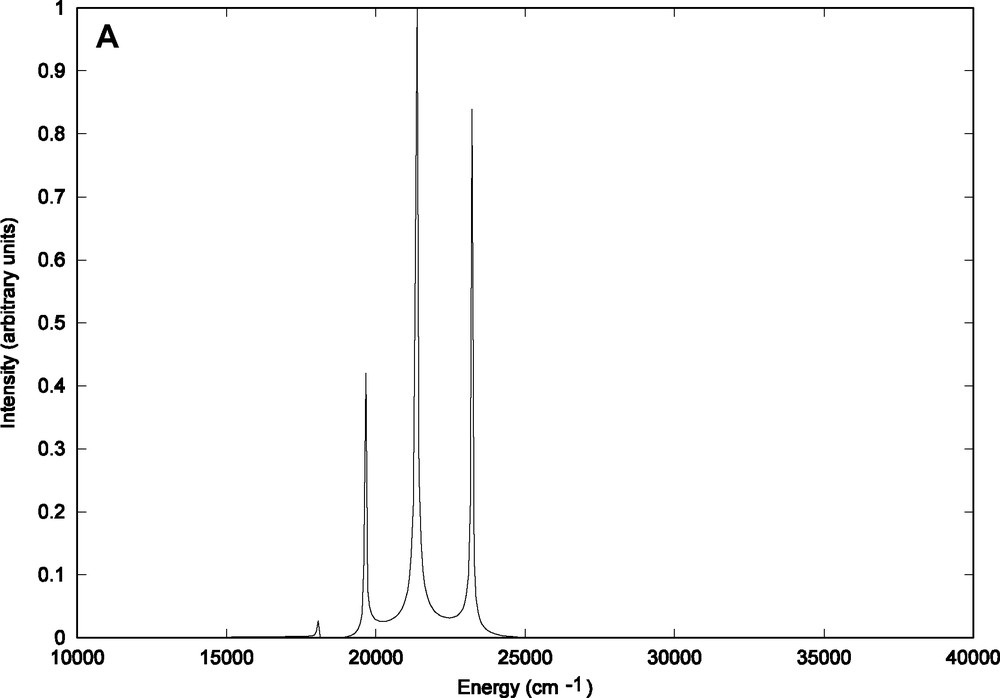
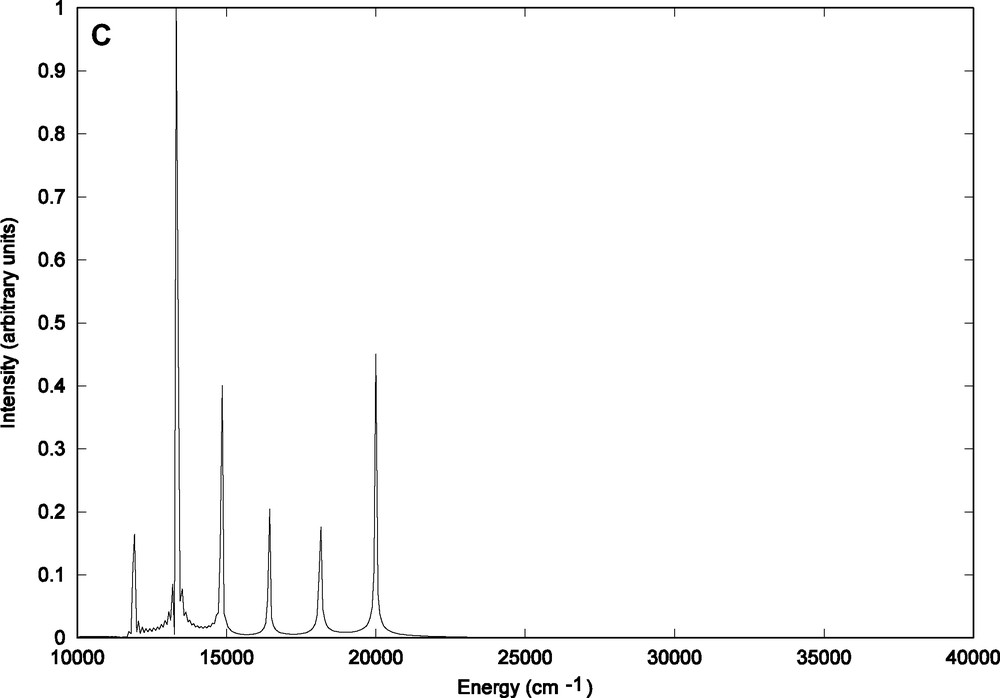
Contributions to the theoretical emission spectrum of HRe (CO)₃(H-dab) from (A) the vibrational ground state (n = 0) of the b¹MLCT state (B) the vibrational state (n = 1) (C) the vibrational state (n = 2).

Indeed this contribution does account for nearly 98% in contrast to the minor contributions reported in Fig. 5b (n = 1) and Fig. 5c (n = 2) which reveal very weak fine structures coming from transitions occurring from the initial Φ (q, E_k, n = 1) and Φ (q, E_k, n = 2) wave packets propagated on the upper potential (b¹MLCT) to the various vibrational bound states of the electronic ground state.

4 Time-resolved emission spectrum of HRe(CO)₃(H-dab)

The time-dependent emission spectrum simulated for the b¹MLCT → electronic ground state transition in HRe(CO)₃(H-dab) within a three-dimensional picture is represented in Fig. 6. In our simulation the laser promotes the initial state Φ (q, E_k, n = 0) multiplied by the corresponding transition dipole moment instantaneously to the upper b¹MLCT absorbing state.

Fig. 6
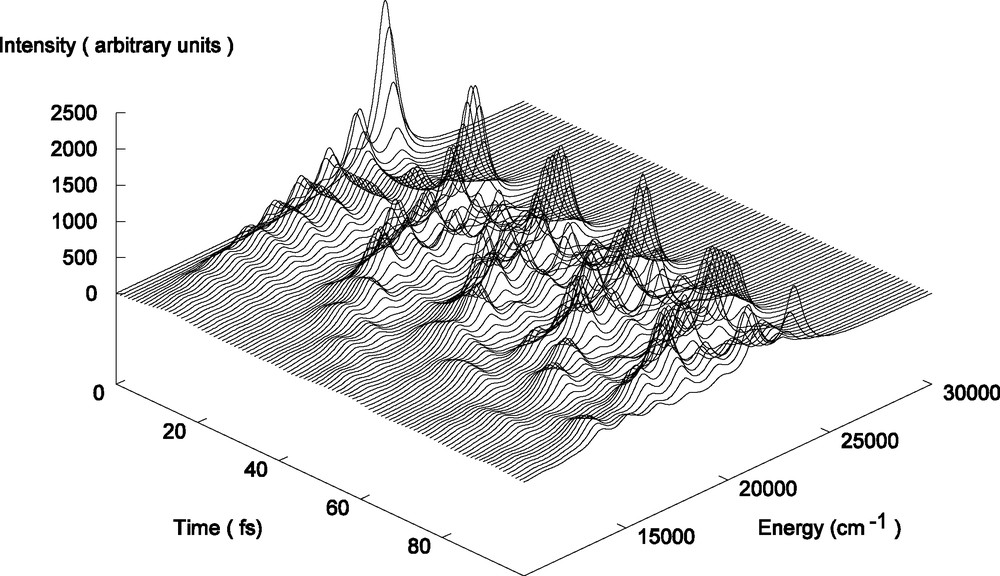
Time-dependent emission spectrum of HRe(CO)₃(H-dab) simulated for the b¹MLCT → electronic ground-state transition.

Under the influence of the Hamiltonian of the corresponding potential it starts to move and to accumulate overlap with all excited vibrational wavefunctions of the electronic ground state. The shape of the time-dependent emission spectrum points to the presence of an intense single peak at 23 210 cm^–1 at the initial time which illustrates the Franck–Condon principle, namely the instantaneous nature of the electronic transition back to the ground state. In the few tens of femtoseconds the oscillatory motion of the wave packet in the potential well of the absorbing state leads to the formation of new lines to the lower energies corresponding to the population of the low-lying vibrational states of the emitting state. Within the same time scale a decrease in intensity of the initial peak is also observed which corresponds to the decay of the autocorrelation function S(t) as a function of time. After 40 fs the complicated pattern of the spectrum due to the ‘interference’ of the dynamics in the upper b¹MLCT state and electronic ground state is difficult to analyze.

5 Conclusion

The absorption/emission spectra of [HRe(CO)₃(H-dab)], model system for α-diimine rhenium carbonyls complexes, have been simulated by wave packet propagations on the one-dimensional potentials V(q = [Re–H]) calculated for the electronic ground state and the b¹MLCT absorbing state. The main features of the absorption/emission spectra recorded for this class of molecules, namely an intense absorption peak in the visible and a corresponding emission band shifted to the red have been recovered. The emission spectroscopy has been simulated within the limiting case of a pure radiative decay, the other competing processes such as intersystem crossing, dissociation or vibrational relaxation in the medium being neglected. The time-resolved emission spectrum has been obtained by simulating the whole absorption/emission process on the basis of the decomposition of wave packet into a superposition of vibrational eigenstates v′, each with different phases. A sufficiently long time of propagation has been chosen in order to ensure the validity of the autocorrelation function Fourier Transform approach. In order to study the competition between the ¹MLCT emission and the rhenium–hydrogen bond homolysis in [HRe(CO)₃(H-dab)] it will be necessary to go beyond the present theoretical model based on the generalization of the Kramers–Heisenberg expression to the continuous spectrum [11].

Acknowledgements

The authors are grateful to Professor A. Strich and Professor J. Manz for helpful discussions. The simulations have been carried out at the IDRIS (Orsay, France) through a grant of computer time from the Conseil Scientifique.