1 Introduction
The chemistry of transition metal complexes with pyrrolyl (pyr = NC4H4−), or substituted pyrrolyls (pyr′), has been poorly developed, specially when compared with the isoelectronic and geometrically related cyclopentadienyl ligand (Cp = C5H5−). In fact, cyclopentadienyl has been present since the very beginning of organo-transition metal chemistry, in ferrocene, and from then on complexes with Cp or substituted derivatives of this ligand (Cp′) have grown to form an important part of organometallic chemistry [1], with applications ranging from catalysis [2] to cancer therapy [3,4]. Two reasons can be invoked to explain the differences between the history of pyrrolyl and cyclopentadienyl organometallic chemistry. On the one hand, there is the mentioned historical relevance of the Cp ligand and, on the other hand, the instability of the pyrrolyl metal complexes [5–7].
Two alternative and extreme coordination modes are known for pyrrolyl ligands (Fig. 1). A π coordination, with the entire π system of the pyrrolyl ligand involved in the bond (π-pyr), and a N-σ mode, with the nitrogen lone pair establishing the pyr−metal bond. A search on the Cambridge Structural Database (CSD) [8] reveals that π-pyr complexes with determined X-ray structure are rare, and most pyrrolyl transition metal complexes fully characterized, from the structural point of view, correspond to σ-pyr′ species. This is also true for group-4 metal complexes. Only very recently has been reported the first series of Zr complexes with π-coordinated pyr′ ligands [9]. In the π-pyr′ species the five atoms of the pyrrolyl ring bind the metal, corresponding to a pentahapto coordination (η5) of that ligand. However, the geometry of the pyrrolyl ligand normally found in the π-pyr′ complexes corresponds to a distorted η5 coordination, since the nitrogen atom tends to be closer to the metal. This bonding geometry of pyr′ is sometimes considered an intermediate coordination between η5 and η3 [10].
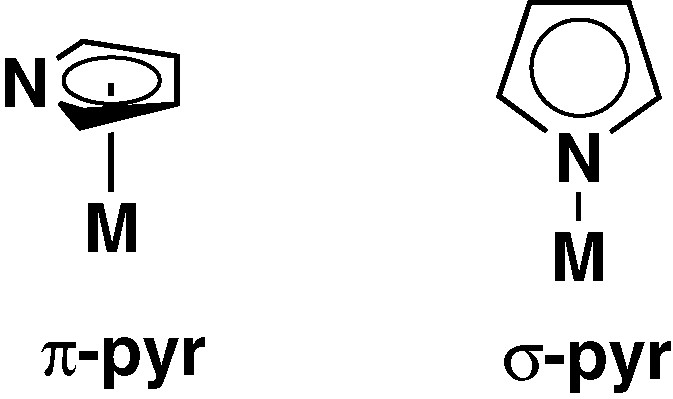
Coordination modes of the pyrrolyl ligand.
In the course of a continued interest of our group in pyrrolyl transition metal chemistry [10–13], recent NMR results were obtained suggesting fluxonality between π- and σ-coordination of pyr′ ligands in group 4 metal complexes [14]. Similar processes have been experimentally observed in a meso-octaethylporphyrinogen Zr(IV) complex, based on 1H NMR data [15], and suggested as the possible mechanism for the rac/meso isomerization of group 4 metal complexes with asymmetric phospholyl ligands (PC4PhMe2H−) [16,17].
A DFT [18] study on zirconium pyrrolyl complexes have been the subject of a previous publication [19]. In this work we extend this study to the other group 4 metals (M = Ti, Hf) by using ab initio [20] and DFT calculations to investigate the coordination structure and bonding of π-pyr′ and σ-pyr′ in monopyrrolyl complexes, [M(pyr′)Cl3], as well as the interconversion mechanism between the two coordination modes. Two pyrrolyl ligands are addressed (Fig. 2): pyrrolyl (pyr) and 2,5-dimethylpyrrolyl (dmp).
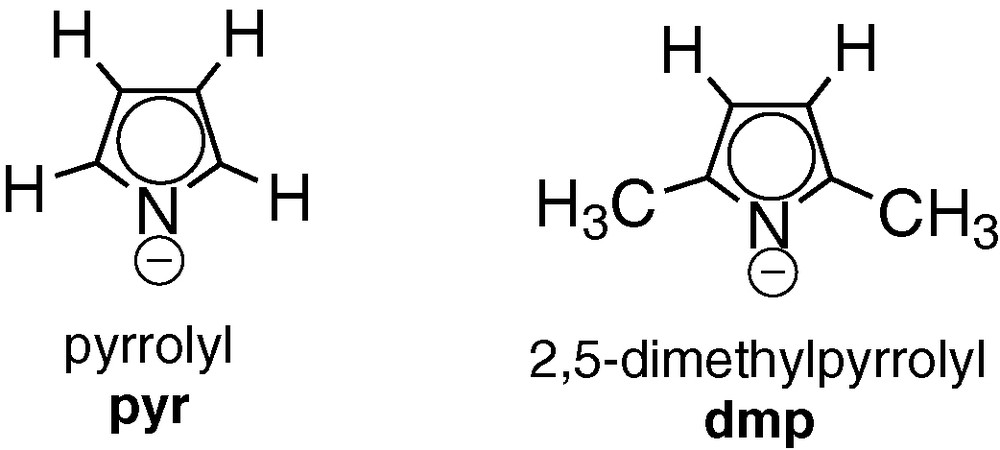
Studied pyrrolyl ligands (pyr′).
2 Results and discussion
The relevant orbital interactions associated with the two coordination modes (π and σ) of pyr in a [M(pyr)Cl3] model complex are depicted in Fig. 3 in a schematic and simplified way, based on Extended Hückel (EH) calculations [21,22]. A more detailed analysis have been published before for tungsten bispyrrolyl complexes, [W(pyr′)2(CH3)2] [13].
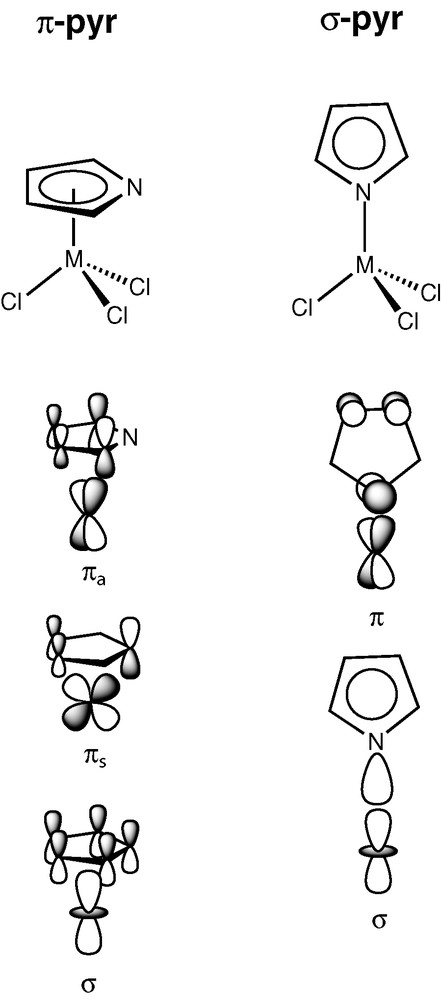
More relevant orbital interactions for the two pyr′ coordination modes.
There are three relevant interactions in a π-coordination of a pyr′ ligand, σ, πs and πa. These are represented on the left side of Fig. 3, and the labels ‘s' and ‘a' denote symmetric and antisymmetric character with respect to Cs symmetry plane. Thus, in a π-pyr complex the pyrrolyl bonding to the metal results from the combination of the metal d orbitals and the pyr π orbitals with the right symmetry. The overall bond can be view as the sum of three two-electron donations from the pyrrolyl to the metal, in close relation to what is well known for a η5-Cp ligand [23]. For σ-pyr the bond is mostly based on a strong σ interaction between the nitrogen lone pair and the metal dz2 orbital. The second interaction represented on the right side of Fig. 3, denoted as π, corresponds to a pyr–M π donation, being of comparatively small importance due to the poor overlap between the intervening fragment molecular orbitals. The overall (σ-pyr)–M bond results formally from two-electron donations from the pyrrolyl to the metal. In a comparison between the two coordination modes, an electronically richer metallic fragment should exist in the π-pyr complex, but the overall pyr–M bond strength is roughly the same for the two coordination modes. Overall, similar pyr–metal bonds are obtained when the pyr coordination is based on one strong and one weak interaction (σ-coordination), and when it is based on three interactions of intermediate strength (π-coordination).
The geometrical characteristics of a π-coordinated pyr′ ligand are important to evaluate the bonding of this ligand to the metal. Several geometrical parameters have been proposed to characterize the distortion of a C5 ring π-coordinated to a metal [24], and their use can be easily extended to a pyrrolyl ligand. Two such parameters are the slip parameter, Δ, and the folding angle, Ω (see Fig. 4). The slip parameter, Δ, can be defined as the difference between the mean distance from the metal to the β ring carbons, and the mean distance from the metal to the nitrogen and the two α carbons. A perfect η5 coordination corresponds to Δ = 0, and higher values indicate an increase of the M–Cβ/β′ bond lengths and a shortening of the M–N distance, that is, a slipped η3 coordination. The second parameter, Ω, is the angle between the mean plane of the four carbon atoms, and the plane of the nitrogen and the two adjacent carbons (α). This angle measures the degree of folding of the ring, being 0° for a perfect η5 coordination while higher values denote a tendency towards a folded η3 coordination. Finally, the tilt angle, δ, defined as the N–X–M angle (X is the ring centroid), has also been used to characterize the slippage degree of a NC4 pyrrolyl ring [10]. In the case of a slippage from a η5-pyr′ to an ideal σ-coordination of this ligand, δ decreases from 90° to 0°.
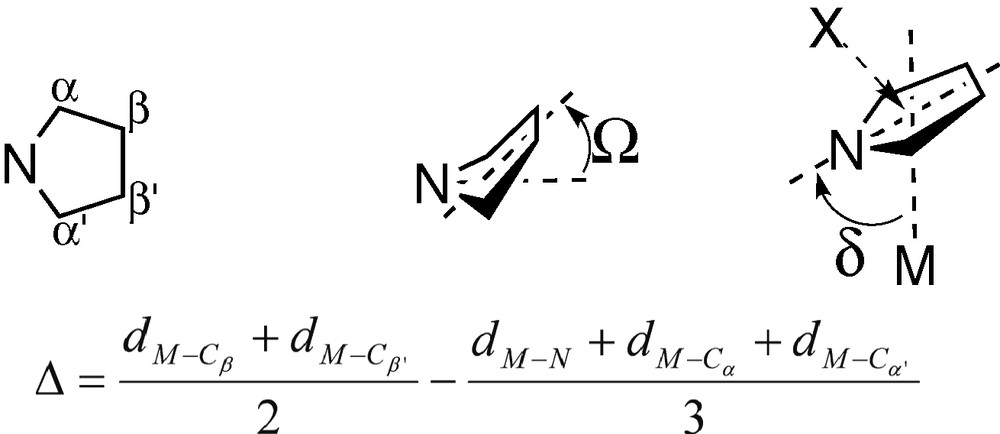
Parameters used to characterize the pyr′ coordination geometry.
The optimized geometries of the π and the σ isomers of the [M(pyr′)Cl3] complexes, as well as the corresponding transition states for the interconversion between the two, are presented in Fig. 5 for Ti and Hf, with pyrrolyl (pyr = NC4H4–) and 2,5-dimethylpyrrolyl (dmp = NC4Me2H2–). The pyr′ coordination parameters are also shown. Although there are no available X-ray structures to test the optimized geometries, the performance of method and basis set used (see Section 4) is well established with tungsten [13] and zirconium complexes [9,19].
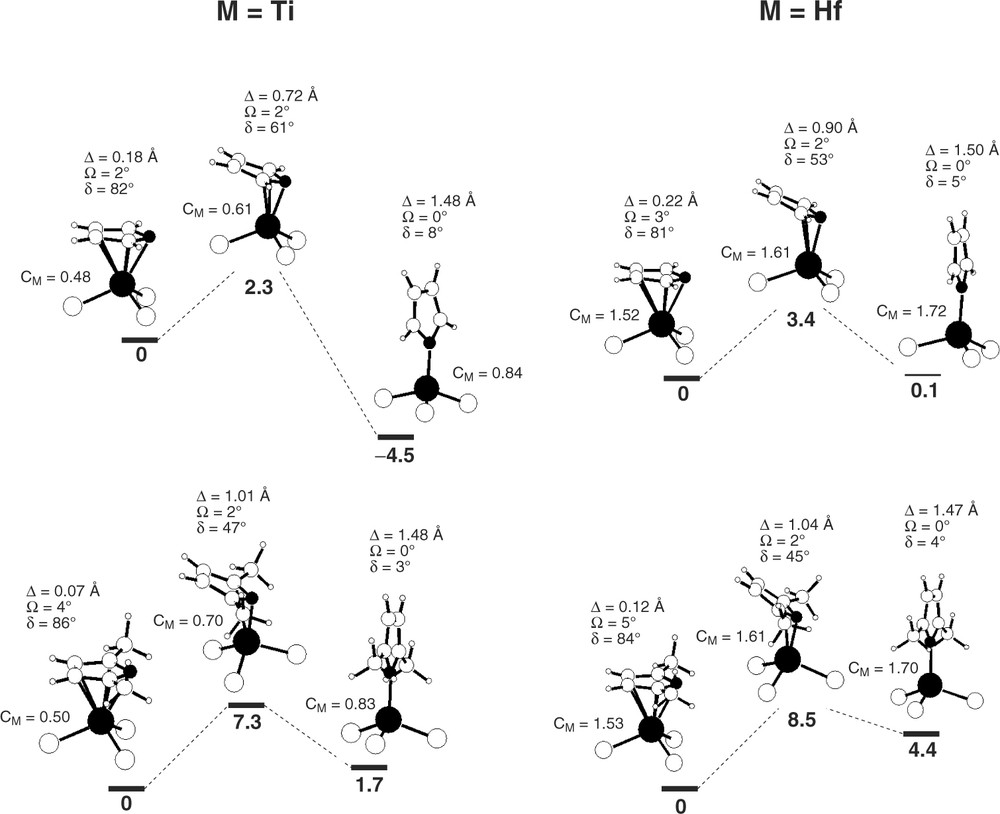
Optimized geometries (B3LYP) of the π and the σ complexes, [M(pyr′)Cl3], and of the transition states for the interconversion between the two, for M = Ti (left) and Hf (right) with pyr′ = pyr (top) and dmp (bottom). The relative energies (bold, kcal mol–1), the metal NPA charges (CM) and the pyr′ coordination parameters are presented. The metal and N atoms are shaded.
Starting with the titanium complexes, represented on the left side of Fig. 5, a first aspect deserving some attention is the comparison between the geometries obtained for the two pyr′ ligands under study. The geometries calculated for the pyrrolyl species are very similar to the ones obtained for the dmp complexes with a maximum deviation of 0.07 Å and 5° for the bond distances and angles around the metal coordination sphere. The π complexes present a typical piano stool geometry with X–Ti–Cl angles between 112° and 117° (X being the NC4 ring centroid) and Ti–Cl distances of 2.20–2.21 Å. The pyr′ ligands coordinate in a π fashion with the five ring atoms involved in the bond to the metal, as shown by Ti–N/C distances, dTi–N = 2.23, 2.29 Å and dTi–C = 2.32–2.47 Å, well within the bonding values. The result is a slightly slipped η5 coordination of the pyr′ ligand with tilt angles (δ) of 82° and 86° for the pyr and the dmp complexes, respectively, and slip parameters (Δ) of 0.18 and 0.07 Å, by the same order. The increased slippage of the pyr′ ring in [Ti(π-pyr)Cl3], when compared with its dmp analog, is probably due to the stereochemical effect of the methyl substituents in dmp, preventing further approach of the nitrogen and the two α carbon atoms to the metal. In fact, the mean distance from Ti to the five atoms is the same (2.36 Å) in both [Ti(π-pyr)Cl3] and [Ti(π-dmp)Cl3] showing that the overall pyr′ coordination is similar in the two species, at least from a geometrical point of view. Despite the slightly distorted η5 coordination found for pyr′ in the π complexes, a rather flat ring is observed for all the species presented in Fig. 5 (not only the Ti ones), the maximum folding angle (Ω) obtained being 5° for [Hf(π-dmp)Cl3]. This indicates that the interconversion process between the π and the σ isomers of these complexes occurs via ring slippage without significant ring folding.
Interestingly, the coordination geometry calculated for [Ti(dmp)Cl3] compares rather well with the X-ray structure of [Ti{π-NC4(CH3)4}Cl3] [10] (δ = 82°, Ω = 4°, Δ = 0.17 Å, dTi–N = 2.18 Å, dTi–C = 2.28–2.43 Å), specially taking into account the differences between the species.
The titanium σ complexes of Fig. 5 present slightly distorted tetrahedral geometries with N–Ti–Cl angles between 108° and 113° and distances around the metal coordination sphere well within the bonding range (dTi–N = 1.88, 1.89 Å, dTi–Cl = 2.17–2.19 Å). The pyrrolyl ligands coordinate in a clearly σ mode, as stated by the large values of the slip parameter, Δ close to 1.5 Å, and by tilt angles approaching zero, δ = 8° and 3° for the pyr and the dmp complexes, respectively.
One interesting aspect arising from the comparison between the pyrrolyl coordination geometry in the π and the σ isomers is the shortening of the Ti–N distance from 2.23–2.29 Å in a π-pyr′ to 1.88–1.89 Å in a σ bonding. This is a direct consequence of the σ interaction between the nitrogen lone pair and the metal dz2 orbital, obtained in a σ coordination, as previously discussed while addressing the qualitative nature of the pyr–M bond (see Fig. 3). The electronic base of this effect is confirmed by the calculated Wiberg indices (WI) [25] for the Ti–N bonds in the various species. These bond strength indicators raise from 0.3 in the π-pyr′ complexes to 0.9 in the σ isomers, showing that the shortening of the Ti–N bond length corresponds to an intrinsic strengthening of the bond. As anticipated by the EH calculations, the reinforcement of the Ti–N is balanced by an electron poorer metal in the σ complex, as shown by the charges represented in Fig. 5, obtained by means of a Natural Population Analysis (NPA) [26–33].
The Ti–Cl coordination is also different in the two isomers of Fig. 5. There is a slight shortening of the Ti–Cl bonds, going from the π (2.20–2.21 Å) to the σ complexes (2.17–2.19 Å). However, this tendency is not reflected in the WI obtained for those bonds in the two types of complexes (1.18–1.21 for the π species, and 1.16–1.24 for the σ isomers), suggesting that this geometrical change is of stereochemical rather than electronic nature, resulting probably from a less crowded metal coordination sphere in the σ complexes. This is further shown by the Cl–Ti–Cl mean angles, rising from 103° in the π complexes to 109–111° in the σ species. The stereochemical relieve around the metal when the pyr′ ligand adopts a σ coordination allows a relaxation of the three piano stool ‘feet' corresponding to an opening of 6°–8° in the Cl–Ti–Cl angles.
The transition states calculated for the slippage from a π to a σ coordination of the pyr′ ligands in the Ti complexes present geometrical and electronic parameters that are intermediate between the ones obtained for the two types of species. The geometry of the pyr′ ligands is flat (Ω = 2°), but considerably slipped, as shown by the corresponding parameters, δ = 61° and 47°, Δ = 0.72 and 1.01 Å, for pyr and dmp, respectively. The distance from the metal to the β carbons of the pyrrolyl ring is long (3.0–3.5 Å) indicating that the M–Cβ/β′ bond breaking is practically completed in the transition state. The Ti–N bond is shorter (2.01 Å for pyr, and 1.96 Å for dmp) and stronger (WI = 0.55 and 0.65 for pyr and dmp, respectively) than the ones existing in the π-pyr′ complexes (see above), and the M–Cα/α′ interaction can be classified as a weak bond, longer (2.38–2.78 Å) and weaker (WI = 0.14–0.28) than the ones existing in the π species (dTi–Cα/α′ = 2.32–2.35 Å, and WITi–Cα/α′ = 0.25–0.34).
The optimized geometries for the Hf species (right side of Fig. 5) are similar to the ones found for the Ti complexes, reproducing all the geometrical and electronic features, discussed above for M = Ti. The main difference corresponds to a systematic increase in the metal–ligand distances. For the Hf π complexes the mean distance from the metal to the five pyr′ atoms is 2.49–2.50 Å (compared with 2.36 Å in the Ti complexes), while the Hf–Cl distances are 2.33–2.34 Å (2.20–2.21 Å in the Ti species). The same happens in the σ complexes with longer M–N and M–Cl for M = Hf (2.02–2.03 and 2.32–2.33 Å, respectively) than for M = Ti (1.88–1.89 and 2.17–2.19 Å, by the same order). On the other hand, the optimized geometries obtained for the Hf complexes are very similar to the ones calculated for the equivalent Zr complexes, using the same method [19]. In this case, a mean deviation of 0.02–0.03 Å is observed, corresponding to the well known lanthanide contraction, with metal–ligand distances systematically shorter for Hf than for Zr. Taking, for example, the σ-pyr complex, [M(σ-pyr)Cl3], the Hf–N bond length is 2.02 Å, while the Zr–N distance is 2.04 Å, the same trend being found for the M–Cl distances: 2.32 Å for Hf, and 2.34–2.35 Å for Zr.
Comparing the energy profiles for the two pyrrolyl ligands represented in Fig. 5, pyr and dmp, a systematic destabilization of the σ complexes with respect to the corresponding π isomers, is found for the dimethylpyrrolyl complexes, when compared to the pyr analogs. This means that a σ coordination of the pyr′ ligands is disfavored when substituents are present on the pyrrolyl α carbons, confirming an empirically well known fact [9,10]. This is reflected in the activation energy for the slippage process, with higher values (by ≈ 5 kcal mol–1) for the dmp ligand. The nature of the transition states is another consequence of this result, being much closer to the σ isomer in the case of dmp than in that of pyr. This can be seen both in energetic terms, as shown by the energy differences between the transition state and the σ complexes, as well as geometrically, since the transition states for dmp have narrower tilt angles (δ) and higher slip parameters (Δ), than the transition states for pyr.
The small values obtained for the activation energy associated with the slippage process represented in Fig. 5 (2.3–8.5 kcal mol–1) suggest that fluxionality between the two isomers may occur in solution, specially for the pyr complexes. The existence of 13C NMR data, in solution at room temperature, for the [Ti(dmp)Cl3] complex [14] allowed us to probe for the possibility of such fluxional process in the case of that complex. This was done through the calculation of the C chemical shifts by means of the gauge independent atomic orbitals (GIAO) method [34–38], an approach previously used for W [13] and Zr [19] pyrrolyl complexes. Fluxionality between the two coordination modes of dmp can be tested by the comparison between the experimental 13C chemical shifts and the values calculated for the two isomers, [Ti(π-dmp)Cl3] and [Ti(σ-dmp)Cl3]. The calculated chemical shifts for the π complex are 162 ppm for the α carbons, and 130 ppm for the β carbons of dmp. In the case of the σ isomer the mean values obtained were 146 (Cα) and 110 ppm (Cβ). Since the experimental values are 157 (Cα) and 127 ppm (Cβ), and a slight overestimation is expected in the calculated values [19], these seem to correspond to the π complex, [Ti(π-dmp)Cl3], giving no indication to the occurrence of fluxionality between the to isomers in solution for this system, at least at room temperature, to which the experimental NMR data is referred. This corroborates the activation energy of 7.3 kcal mol–1, calculated for the slippage in this complex.
The shift from a π-pyr′ to a σ-pyr′ corresponds, normally, to a destabilization of the complex since it brings an electronic depletion on the metal, which is not fully balanced by the reinforcement of the M–N bond that follows the pyr′ slippage. Thus, this is an endothermic process in most cases. On the other hand, given the destabilization of the σ coordination mode for α substituted pyrrolyl ligands, such as dmp, a larger energy difference is obtained between the two isomers of the complexes with these ligands, corresponding to higher ΔE values for the slippage process. This was verified in all the Zr pyrrolyl complexes [19], and is also the case for most of the species in Fig. 5. The slippage process is endothermic for the Ti and Hf dmp complexes, and the two isomers are practically isoenergetic in the case of [Hf(pyr)Cl3]. However, for the Ti pyr complex, [Ti(pyr)Cl3], a clearly more stable σ complex is found, corresponding to an exothermic process for the slippage from the π to a σ coordination mode. In fact, the energy variation for this process has the highest absolute value among all that are represented in Fig. 5. So, our calculations predict that the most stable structure for [Ti(pyr)Cl3] has a σ coordination of pyrrolyl. In our opinion, testing this conclusion can be an interesting challenge to the experimental community.
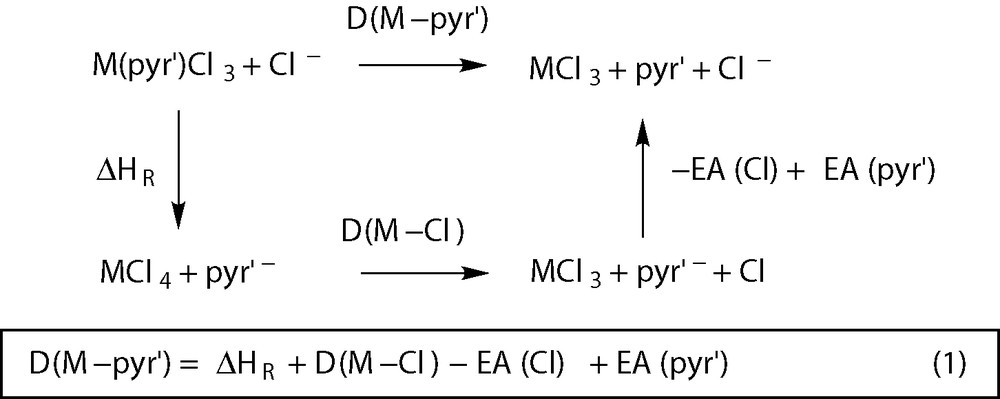
The shifting of the energy balance between the two isomers in the case of [Ti(pyr)Cl3] can be due to an increased stabilization of the σ isomer in this case, or to a special destabilization of the π isomer. Or to a conjugation of both effects, of course. A stabilization of the σ complex should be directly related to the Ti–N bond strength, while a destabilization of the π species can derive from the stereochemical constraints existent in this geometry, when compared to the σ-pyr complexes. Both effects are addressed above in the discussion of the optimized geometries of the Ti complexes. In order to investigate if the M–N bond in the σ-pyr complexes is significantly stronger for Ti than for the other elements of group 4, explaining, thus, an enhanced stability of [Ti(σ-pyr)Cl3], we need estimates of the M–pyr′ bond energies. In fact, since only relative energy values are provided in Fig. 5, that is, the energy difference for the two isomers of each species, a comparison for the three metals of group 4 is not possible, based on those values alone. The thermochemical cycle of Fig. 6 can be used to estimate M–pyr′ bond dissociation enthalpies for the different [M(pyr)Cl3] complexes, requiring published experimental data and calculations on closed shell species only, which are easier to treat from the computational point of view. The tetrachloro complexes, MCl4, and the free ligands were optimized using the same method applied to the pyr′ complexes (see Section 4). The M–pyr′ bond dissociation enthalpy, in each complex, can be estimated using equation (1) in Fig. 6, with the experimental values for EA(Cl) [39], EA(pyr′) [40] and D(M–Cl)1, and the calculated enthalpy variation, ΔHR, for the exchange ligand reaction between [M(pyr)Cl3] and MCl4. The electron affinity of dmp was assumed equal to the one published for pyr.
The method used for the enthalpy calculations proved well in the determination of Ir–halogen bond enthalpies [42], but even if the absolute values of Table 1 may be affected of some systematic uncertainty, the trends should be reliable. On the other hand, given the value used for the electron affinity of dmp, assumed equal to EA(pyr), any comparison between the M–pyr′ bond dissociation enthalpies for the two pyrrolyl ligands, should be taken with caution. Not withstanding, the data in Table 1 show that Ti–pyr′ bonds are clearly weaker than the ones formed by the heavier elements, Zr and Hf, for both ligands, and in the two coordination modes (by 24–31 kcal mol–1). Thus, a stronger Ti–N bond in [Ti(σ-pyr)Cl3] is certainly not the reason for the reverse stability between the two isomers, found in this system. In fact, the Ti–pyr bond in the σ complex is weaker than the Zr one by 24 kcal mol–1, and than the Hf one by 27 kcal mol–1. The obtained stability difference is probably related to an increased destabilization of the Ti π complex, [Ti(π-pyr)Cl3], when compared with its Zr and Hf analogs, due to the interligand repulsion. In fact, a more crowded metal coordination sphere exists in the π complexes and the corresponding destabilization should be more effective in the Ti complex, since for this metal all the M–ligand bond distances are shorter. This may be seen, for example, in the mean Cl–M–Cl angle for the three [M(π-pyr)Cl3] complexes: 103° (Ti), 105° (Zr), and 104° (Hf). An increased repulsion between the π-coordinated pyrrolyl and the three Cl ligands pushes these further away from pyr, and closes the Cl–M–Cl angles.
Bond dissociation enthalpies (in kcal mol–1), D(M–pyr′), for the [M(pyr′)Cl3] complexesa
| Ligand and coordination mode (pyr = NC4H4, and dmp = NC4Me2H2) | ||||
| Metal (M) | π-pyr | σ-pyr | π-dmp | σ-dmp |
| Ti | 67 | 71 | 69 | 67 |
| Zr | 98 | 95 | 99 | 92 |
| Hf | 99 | 98 | 99 | 94 |
There is one aspect of Table 1 data that deserves further discussion. While the Ti–pyr′ bonds are systematically weaker than the ones formed by Zr and Hf, much smaller differences are found between the two heavier elements. This corroborates the practically equal geometrical parameters of [M(pyr′)Cl3], obtained for the two metals (discussed above), and also the similar energy profiles calculated for the slippage process. The energy profiles for the Hf species are presented in Fig. 5 and, for the Zr complexes, an energy variation of 2.6 kcal mol–1, and an activation energy of 4.6 kcal mol–1 were obtained for pyr′ = pyr, while for dmp the corresponding values are ΔE = 6.8 kcal mol–1, and Ea = 9.7 kcal mol–1 [19]. The data in Table 1 explain not only the similarities between the Zr and the Hf system, but also the subtle differences. The M–pyr′ bond enthalpies are essentially the same (within 1 kcal mol–1) for the π complexes, while in the σ isomers the Hf–pyr′ bonds are slightly stronger than the Zr ones (by 2–3 kcal mol–1). Thus, equally strong bonds are found for the π coordination of pyr′ with both metals, but when it comes to the σ-pyr′ species, the M–pyr′ bonds are slightly but systematically stronger for Hf. In other words, the σ isomers are more stabilized, with respect to the π complexes in the case of Hf, and the energy difference between the two isomers should be smaller. This is exactly what is observed by comparing the Zr values referred above with the Hf ones, presented in Fig. 5. The stability of the corresponding transition states follows the same trend, the same happening with the activation energies for the slippage process.
3 Conclusions
The geometry of the pyrrolyl ligand in the π-pyr′ complexes, corresponds to a slightly distorted η5 coordination with the nitrogen closer to the metal, while in a σ-pyr′ the metal–pyr′ bond is essentially a M–N σ interaction based on the nitrogen lone pair. The slippage of a pyr′ from a π to a σ coordination mode results in an electronically poorer metal center and this process is, normally, associated with a destabilization of the complex. This destabilization is partially compensated by a stronger M–N bond in the σ-pyr′ complex. Stereochemical effects play an important role in the balance for the relative stability of the two coordination modes. For example, substituents in the pyr′ α carbons disfavor the σ coordination, and the stereochemical repulsion between the ligands destabilize the π-pyr′ species. The latter effect is specially relevant in [Ti(pyr)Cl3], resulting in a more stable σ complex in this case.
The small values obtained for the activation energy of the interconversion between the two coordination modes of the pyrrolyl rings in all complexes (Ea < 9 kcal mol–1) suggest that fluxionality may occur in solution. The π–σ isomerization process corresponds to a ring slippage, with no significant folding of the NC4 ring. In the corresponding transition state, the pyr′ ligand has a coordination geometry intermediate between the π and the σ modes: a flat η3 coordination based on one strong M–N bond and two weak interactions between the metal and the two α carbon atoms of the ring.
Calculated M–pyr′ bond enthalpies show an increasingly stronger bond going down group 4 from Ti, to Zr and to Hf. A direct relationship was found between the M–pyr′ bond strength and the relative stability of the two isomers, for the different metals.
4 Computational details
All calculations were performed using the Gaussian 98 software package [43], and the B3LYP hybrid functional. That functional includes a mixture of Hartree–Fock [20] exchange with DFT [18] exchange-correlation, given by Becke's three parameter functional [44] with the Lee, Yang and Parr correlation functional, which includes both local and non-local terms [45,46]. The LanL2DZ basis set [47–50] augmented with a f-polarization function [51] was used for the metals, and a standard 6-31G(d,p) [52–56] for the remaining elements. Transition state optimizations were performed with the Synchronous Transit-Guided Quasi-Newton Method (STQN) developed by Schlegel et al. [57,58]. Frequency calculations were performed to confirm the nature of the stationary points, yielding one imaginary frequency for the transition states and none for the minima. Each transition state was further confirmed by following its vibrational mode downhill on both sides, and obtaining the minima presented on the energy profiles. All geometries were optimized without symmetry constraints and the energies were zero-point corrected. The enthalpies were obtained at 298.15 K, by conversion of the electronic energies with the thermal energy corrections based on the calculated structural and vibrational frequency data. A NPA [26–33] and the resulting WI [25] were used for a detailed study of the electronic structure and bonding of the optimized species. NMR shielding tensors were calculated using the GIAO method [34–38] at the Hartree–Fock level using the same basis set for the metals and a 6-311+G(2d,p) [59–65] for the remaining elements.
Acknowledgements
APF acknowledges FCT for the PRAXIS XXI/BD/13348/97 scholarship.
1 The metal–chlorine bond dissociation enthalpies in MCl4 can be derived from the enthalpies of formation of gaseous MCl4 and MCl3. These data are available for M = Ti, Zr (M.W. Chase Jr., NIST–JANAF Thermochemical Tables; fourth ed., American Chemical Society and the American Institute of Physics for the National Institute of Standards and Technology; Washington, DC, and New York, 1998). The value for M = Hf was estimated from the trend observed for the M–Cl mean bond dissociation enthalpies in MCl4 [41].