1 Introduction
The bis-6-methylpyridine-substituted bispidine ligand L (L = 3,7-dimethyl-2,4-di-(6-methyl-2-pyridyl)-9-diol-3,7-diazabicyclo[3.3.1]nonane-1,5-dicarboxylate dimethylester, Fig. 1) is, in terms of the tertiary amine donors, a highly preorganized and very rigid ligand; the two pyridine donors are rotated away from the coordination site by approximately 180° but this torsion has a low energy barrier and, consequently, transition metal complexes with bispidine ligands generally are very stable [1,2]. However, due to a high elasticity of the coordination sphere, 3,4 bispidine ligands in general are less selective than might have been expected [1,3]. As a result of the elasticity a number of strikingly different structures of bispidine complexes have been observed, and these may be related to distortional isomerism [4–6]. A particularly interesting case is that of the hexacoordinate copper(II) complexes of a pentadentate bispidine derivative (two tertiary amine and three pyridine donors, the third pyridine donor is a substitutent of N3, acetonitrile as monodentate co-ligand), where two of the three possible directions of tetragonal elongation (along N7–Cu–Npy3 and Npy1–Cu–Npy2) could be trapped and structurally characterized [5]. Here, we report single crystal structures, solid state and solution UV–vis–NIR and EPR data and a preliminary analysis, based on DFT, ligand field and force field calculations, of an example, where all three ‘Jahn–Teller isomers’ can be trapped. While, in the previous case [5], the reason for stabilization (destabilization) of one of the two minima was attributed to steric interactions excerted by the substituent at N7, in the example reported here, the relative stability of the three isomeric forms (with respect to the Cu(L)-fragment) is due to the mono- or bidentate co-ligand (NCCH3, OH2, Cl–, NO3–), and steric as well as electronic effects may contribute to the stabilization of one of the three possible minima on the ‘Mexican hat’ potential energy surface.

(a) Structure of the bispidine ligand L, (b) (plot of the X-ray structure as the 9-keto derivative, hydrogen atoms omitted, N3···N7 = 2.867 Å [7].
2 Experimental structural data
Two of the five structures discussed here (Fig. 2 and Table 1), i.e. [Cu(L)(NCCH3)](BF4)2·2CH3CN (co-ligand trans to N3, elongated Cu–N7 bond) and [Cu(L)(Cl)](Cl)·CH3CN (co-ligand trans to N7, Cu–N3 ≥ Cu–N7) have been reported before [7], that of [Cu(L)(OH2)](BF4)2·H2O also has the co-ligand trans to N7, and the two independent hexacoordinate structures with a chelating NO3– ([Cu(L)(NO3](NO3) have elongated Cu–NMepy bonds. The rigidity of the adamantanoide ligand backbone is shown by the constant N3···N7 distance of approximately 2.9 Å and an N3–Cu–N7 angle of approximately 85°. While these parameters are in the expected ranges [4], it appears that the bispidine ligands in the NO3–-structures, with the elongation along the NMepy1–Cu–NMepy2 axis, have a slightly larger than usual distortion. This seems to be an elegant way to compensate for an electronically enforced large NMepy1···NMepy2 distance by distribution of strain over a large part of the bispidine backbone. As shown below (Section 3) and in Table 1, the structural adjustment is primarily by low energy torsional distortions, and this leads to a minimum loss of energy. A considerable and unusual distortion is also observed for the structure with NCCH3 as co-ligand, which has the quite generally observed square pyramidal geometry with the co-ligand in-plane and N7 as the axial donor. In order to minimize van der Waals repulsion with the 6-methyl substituents the NCCH3 group is slightly bent up and the two pyridine rings are bent down. This is nicely shown in the two torsional angles reported in Table 1. Due to the steric bulk of the pyridine methyl substituents, larger co-ligands (Cl–, OH2) are coordinated in the electronically less favorable position trans to N7 (see below and [8,9]). In the case of the bidentate NO3– there seems to be a subtle compromise between steric and electronic effects: the bidentate coordination mode does not allow for an elongation trans to N7 (note that significantly longer bonds trans to N7 than trans to N3, such as seen here in the NO3– structures, are generally observed and not only for Jahn–Teller-active systems [10,11]); therefore, the Cu–N7 bond is also relatively short (i.e. N7 is an in-plane donor, together with the other tertiary amine and the relatively weak oxygen donors of the chelating NO3–), and NMepy1–Cu–NMepy2 is the resulting Jahn–Teller axis. This also leads to relief of steric strain between the methyl substituents of the pyridine donors and the bidentate NO3– ligand.
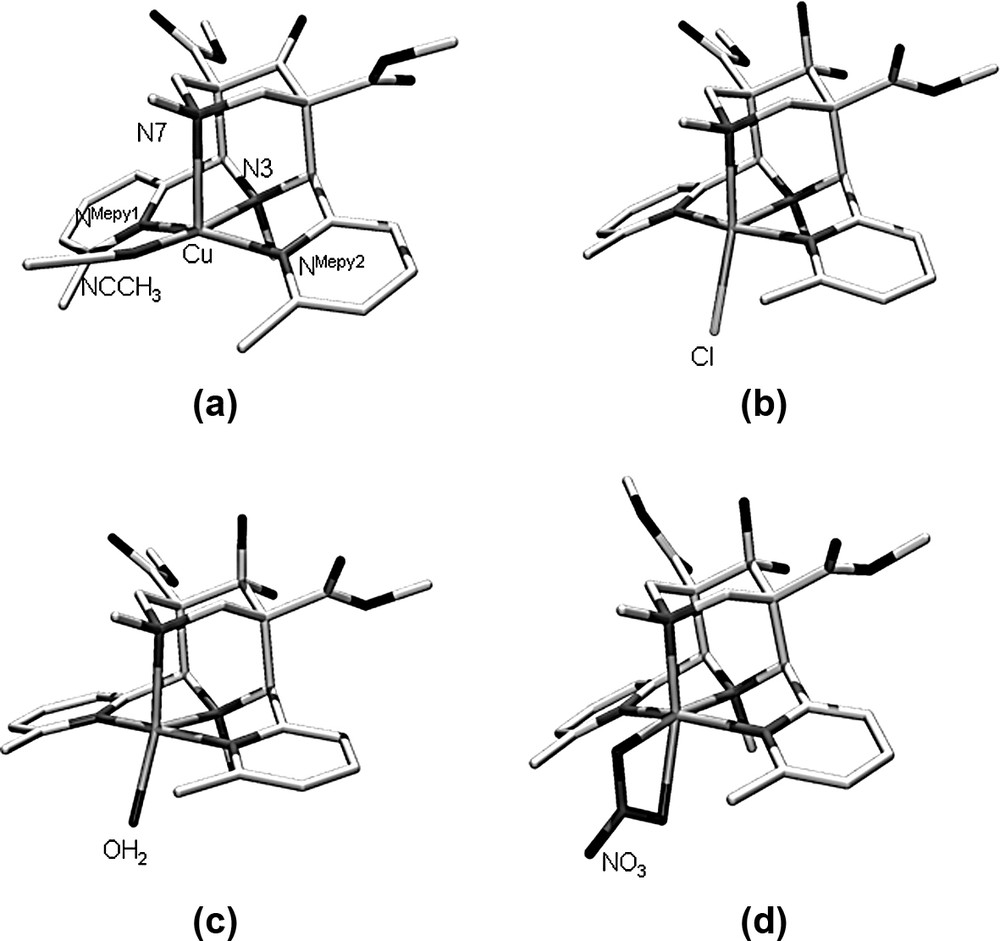
Plots of the molecular cations of (a) [Cu(L)(NCCH3)](BF4)2 · 2 CH3CN [7], (b) [Cu(L)(Cl)]Cl·CH3CN [7], (c) [Cu(L)(OH2)](BF4)2 · H2O, (d) [Cu(L)(NO3)]NO3 (hydrogen atoms omitted).
X-ray structural data of [Cu(L)X1X2]n+
| [Cu(L)(NCCH3)](BF4)2 · 2CH3CN (a) | [Cu(L)(Cl)]Cl · 2CH3CN (b) | [Cu(L)(OH2)]2+ (BF4)2 · H2O | [Cu(L)(NO3)]NO3 (c) | |
| Cu–N3 | 2.004 (0.004) | 2.1474(0.0033) | 2.1325(0.0012) | 1.9763 (0.0015), 1.9866 (0.0016) |
| Cu–N7 | 2.376(0.004) | 2.1200 (0.0033) | 2.0869 (0.0012) | 2.0919 (0.0015), 2.0318 (0.0016) |
| Cu–NMepy1 | 2.075 (0.004) | 2.0614 (0.0033) | 2.0293 (0.0012) | 2.2586(0.0015), 2.3774(0.0018) |
| Cu–NMepy2 | 2.052 (0.004) | 2.0640 (0.0032) | 2.0153 (0.0012) | 2.3467(0.0017), 2.3757(0.0018) |
| Cu–X1 (eq) | 1.950 (0.005) | – | – | 1.9638 (0.0016), 1.9819 (0.0015) |
| Cu–X2 (ox) | – | 2.2208 (0.0015) | 1.9907 (0.0012) | 2.2828 (0.0019), 2.1391 (0.0018) |
| N3···N7 | 2.928 | 2.930 | 2.930 | 2.853, 2.834 |
| Cu–N3/Cu–N7 | 0.84 | 1.01 | 1.02 | 0.94, 0.98 |
| N3–Cu–N7 | 83.68 (0.14) | 86.71 (0.12) | 87.94 (0.04) | 89.00 (0.06), 89.69 (0.06) |
| N3–Cu–X1 | 174.32 (0.17) | – | – | 171.32 (0.06), 169.66 (0.06) |
| N7–Cu–X2 | – | 160.3 | 161.60 (0.05) | 159.49 (0.06), 163.35 (0.07) |
| N7–Cu–X1 | 90.9 | – | – | 99.63 (0.06), 100.56 (0.07) |
| NMepy1–Cu–NMepy2 | 155.62 (0.16) | 163.82 (0.13) | 165.60 (0.05) | 155.61 (0.06), 152.54 (0.06) |
| N3–C–C–NMepy1 | 29.9 | 45.2 | 43.1 | 41.9, 41.7 |
| N3–C–C–NMepy2 | 26.1 | 46.0 | 40.0 | 42.2, 44.8 |
3 Force-field calculations
Molecular mechanics was used to analyze the steric strain induced on the ligand by the electronically enforced elongation of one or two copper-donor bonds, and also for an analysis of the steric repulsion between the co-ligands (NCCH3, OH2, Cl–, NO3–) and the bispidine backbone (primarily the 6-methyl substituents of the pyridine donors) in the three isomeric chromophores. Due to the use of a not fully refined ad-hoc copper–bispidine force field [4] and a number of additional approximations (see below), the results discussed here are not used for a quantitative assessment.
For the analysis of the ligand distortion the experimentally observed structures of [Cu(L)X]n+ with OH2, NCCH3 and NO3– as co-ligands X were simplified (replacement of the ester groups at C1 and C5, and of the OH groups at C9 by hydrogen atoms; replacement of the co-ligands OH2 and NCCH3 by amine nitrogens, and of the bidentate NO3– by an NCN chelate) and optimized1. The agreement between the experimental and optimized structures is acceptable, with respect to the ligand structures it is excellent. The co-ligands and copper(II) centers were then removed and the strain energies of the three optimized structures of the metal-free ligand, which correspond to the isomeric copper(II) chromophores, were determined by single-point calculations. These three steric energies of the ligand are similar; that resulting from the structure with the Jahn–Teller axis along NMepy1–Cu–NMepy2 (NO3– structure) is lowest (normalized to 0 kJ mol–1), that with the elongation along Cu–N7 (NCCH3-structure) is less stable by 2.8 kJ mol–1 and that with the co-ligand trans to N7 (Cl–, OH2) and the elongation along Cu–N3 is the highest in energy (4.5 kJ mol–1). As described above (Section 2), the similarity in terms of the steric energy was expected, and the bond stretch and valence angle distortions are minimal (e.g. the CMepy–C2(4)–C1(5) angles are all within the range of 110.0–110.7°, i.e. practically constant and very close to the ideal sp3 angle).
The major structural differences which emerge from Fig. 3 are, for the NCCH3-type structure (elongated Cu–N7 bond), a rotation of the pyridine rings such that the co-ligand lies above the pyridine planes and, more importantly, above the pyridine methyl substituents, and, for the NO3–-type structure with an elongation along the NMepy1–Cu–NMepy2 axis, a tilt of the bispidine backbone around the C2···C4 axis, coupled with the low-energy-barrier-adjustment of some torsional angles. Thus, primarily the structural changes of the Cu(L) chromophore involve a translation of the copper center within the bispidine cavity and the concomitant adjustment of the orientation of the pyridine donors by torsional distortions. Therefore, it is not unexpected that the strain induced onto the ligand in the three structures is small. This is also in agreement with the general observation with bispidine ligand complexes, that the potential energy surfaces are flat and, therefore, the coordination geometries are highly elastic [3–5,12].
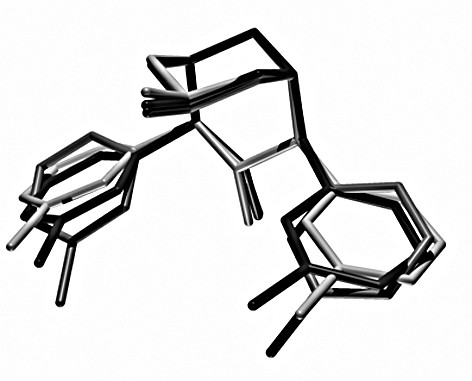
Overlay plot of the three structural forms of the ligand L, optimized by strain energy minimization of [Cu(L)(X)]n+ (see text); dark: Cl–, OH2-structure, middle: NCCH3-structure, light: ONO2–-structure.
The steric repulsion between co-ligands (NCCH3, OH2, Cl–, NO3–) and the pyridine methyl substituents in the three isomeric forms was probed by addition of these donors to the three optimized isomeric Cu(L)-fragments in the crystallographically determined positions and orientations, followed by single-point calculations of the steric energies. For the two isomers with elongated Cu–N7 or Cu–N3 and short Cu–NMepy bonds the experimentally observed coordination sites for the corresponding ligands (NCCH3 trans to N3, OH2 and Cl– trans to N7) lead to the smallest van der Waals repulsion energies in the corresponding set of structures (<40 kJ mol–1), repulsion in the other sites is considerably higher (>50 kJ mol–1; the only structural parameters which were allowed to adjust in these calculations were rotations of the methyl groups). Interestingly, the geometry with an elongated NMepy1–Cu–NMepy2 axis tolerates not only NO3– but also the other co-ligands (NCCH3, OH2, Cl–) with similar or even significantly lower repulsion than in the experimentally observed structural types (only large donors, such as Cl–, when coordinated trans to N3 in this isomer lead to a significant but not excessive build-up of van der Waals repulsion). While the isomer with a long NMepy1–Cu–NMepy2 axis is the expected minimum energy structure for steric reasons, this is not what is observed experimentally (see Section 2). This suggests that there are electronic factors which destabilize this geometry. This also emerges from the observation that the only other examples where this mode of distortion has been detected are hexacoordinate copper(II) complexes [1,5].
It appears that relatively strong axial donors, such as tertiary amines or pyridines, in particular when copper-donor bond elongation is restricted, as in examples where these apical donors are part of five-membered chelate rings or where hexacoordination requires long axial bonds, lead to a quenching of the Jahn–Teller stabilization [5,6,9]. From experimental thermodynamic data (stability constants and redox potentials) [1,2,9,13] and model DFT calculations [8] the partial quenching of the Jahn–Teller stabilization is believed to lead to a loss of approximately 5–15 kJ mol–1 [6]. With a chelating NO3– there seems to be a subtle balance between two electronically unfavorable ground states, as well as repulsive forces between the two methyl groups and the co-ligand.
4 Experimental spectroscopic data
Diffused reflectance electronic spectra of [Cu(L)(OH2)](BF4)2·H2O, [Cu(L)(NO3)]NO3 and [Cu(L)(Cl)]Cl·CH3CN as well as solution spectra in various media are shown in Fig. 4. The solution spectra recorded in pure H2O and, in particular, those at high Cl– and NO3– concentration seem to indicate that the structures in these solutions are identical to those of the [Cu(L)(OH2)]2+, [Cu(L)(Cl)]+ and [Cu(L)(NO3–)]+ molecular cations, which are known from experiment. The electronic transitions of these chromophores and those in other solvent/salt mixtures, also shown in Fig. 4, are listed in Table 2. Solution EPR spectra of [Cu(L)(OH2)]2+ in various media are presented in Fig. 5; the corresponding spin Hamiltonian parameters are also given in Table 2.
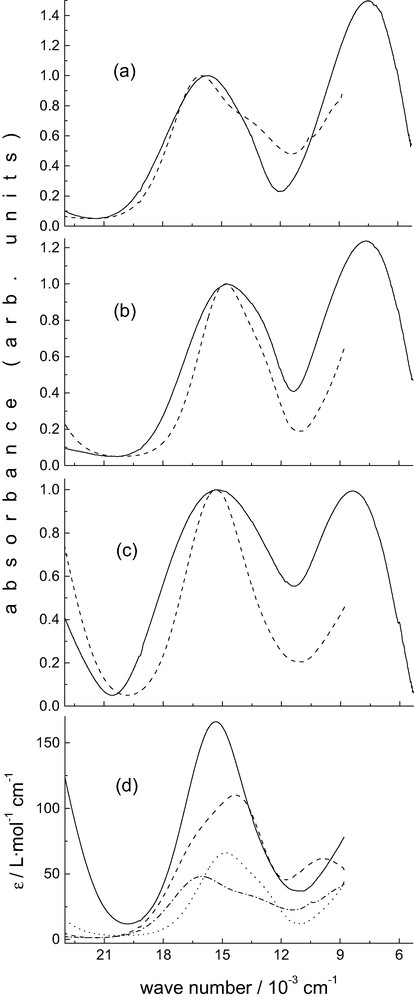
Electronic spectra of [Cu(L)(X)]n+. (a) X = H2O, — solid, --- solution (pure H2O); (b) X = NO3–, — solid, --- DMF, 0.25 M N(Bu)4NO3; (c) X = Cl, — solid, --- solution DMF, 0.25 M N(Bu)4Cl; (d) — X = Cl–: DMF, 0.25 M N(Bu)4Cl; --- X = CH3CN: pure CH3CN; ··· X = NO3–: DMF, 0.25 M N(Bu)4NO3; ·-·-·- X = H2O: pure H2O.
Experimental electronic and EPR spectra of [Cu(L)(NCCH3)]2+, [Cu(L)(Cl)]+, [Cu(L)(OH2)]2+ and [Cu(L)(NO3)]+
| Electronic transitions (cm–1) | gx, y | gz | Az (10–4 cm–1) | ||
| [Cu(L)(NCCH3)]2+ | 16 300 (sh) | 14 300 | 2.062 | 2.245 | 165 |
| 2.082 a | 2.185 a | 145 a | |||
| [Cu(L)(Cl)]+ | 15 300 | 2.040 | 2.242 | 162 | |
| 2.062 a | 2.196 a | 145 a | |||
| [Cu(L)(OH2)]2+ | 16 100 | 13 700 (sh) | 2.055 | 2.255 | 172 |
| 2.066 | 2.322 | 142 | |||
| [Cu(L)(NO3)]+ | 14 800 | 13 100 (sh) | 2.066 | 2.320 | 142 |
| 2.095 a | 2.254 a | 165 a |
a Minor component; simulation of these additional features is not unambiguous but they fit the observed spectra accurately (see Fig. 5).
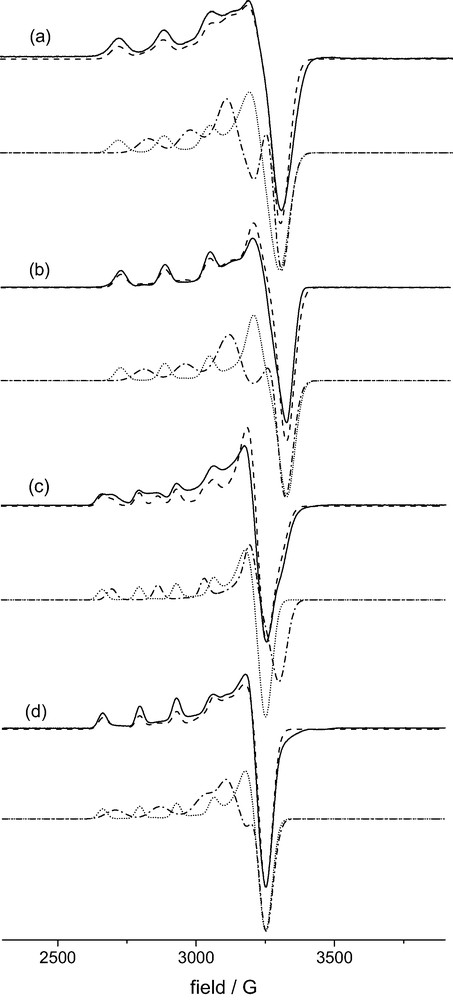
Frozen solution EPR spectra of [Cu(L)(X)]n+ (X-band, T ~ 100 K). (a) X = NCCH3, CH3CN/CH3CH2CN, 1:1; (b) X = Cl–: DMF, 0.2 M N(Bu)4Cl; (c) X = OH2, H2O/DMF, 1:1; (d) X = NO3–, DMF, 0.25 M N(Bu)4NO3; ___ experimental, --- simulation, ·-·-·- , ····· simulation of the two components each.
The experiments in solution were complicated by the necessity to use specific solvent mixtures for the EPR spectra, in order to obtain good glasses and anisotropic spectra with well resolved hyperfine coupling; for comparison identical solvent mixtures were also used for electronic spectroscopy. From the usual DMF/H2O mixed solvent at various ratios it became clear that DMF coordination may also be involved2. EPR spectra were also recorded in dry methanol and various solvent mixtures with methanol, H2O, CH3CN, C2H5CN and DMF in various ratios. From this series of experiments it emerges that the spectra presented in Fig. 5 only involve one co-ligand X each (NCCH3, OH2, Cl–, NO3–). From the spectrum with X = H2O in particular it therefore appears that two species are involved. The spin Hamiltonian parameters for both were obtained by spectra simulations [14,15] and these are given in Table 2, the simulated spectra are also presented in Fig. 5. From this it emerges that the solution electronic spectrum in Fig. 4a (X = OH2) is not due to the same single species as that of the solid. However, due to the fact that the electronic transitions are broad, as usual, it is not possible to attribute specific features in the UV–NIR spectra to specific and different species in solution. The minor components of the other EPR spectra (X = CH3CN, Cl–, NO3–) are less well defined, and, consequently, the corresponding spin Hamiltonian parameters are less accurate and not unambiguous.
Tetragonal ligand fields in copper(II) (square pyramidal or elongated octahedral) split the d-orbitals such that there is a ground state (unpaired electron in the orbital). In the AOM (angular overlap model) formalism [16] this is at an energy of 3eσ (in-plane donors). The lowest energy transition may be assigned to that from the orbital at eσ. The energy of this orbital is decreased by configurational interaction with the Cu 4s-orbital (ds-mixing, eσ – eds, eds ~ eσ/4) [17], and increased by the coordination of axial ligands (eσ – eds + eσaxial). Therefore, in the bispidine complexes discussed here, with strong axial interactions, the transition is expected at relatively low energies. From the solid state spectra it follows that the energy of this transition is in the order NO3– ~ OH2 < Cl– << NCCH3, and this is as expected since in the NCCH3 structure the axial donor (N7) has the smallest interaction (longest axial bond, see above, the NO3-structure has two axial donors) in the whole set of structures. The dxy, xz, yz set of orbitals are only influenced by π-interactions (dxy: 4eπ; dxz, yz: 2eπ + 2eπaxial). Therefore, with axial donors with little or no π-interaction the two highest energy transitions (, ) are expected to be split when in-plane π-donors are present, with axial π-interactions, this is reduced.
From the EPR spectra it appears that there are two sets of structures, i.e. those with relatively large A|| hyperfine coupling (approximately 160–170·10–4 cm–1; X = NCCH3, Cl–, OH2 first component, NO3– minor species) and those with relatively small A|| values (approximately 140·10–4 cm–1, X = NO3– major species, OH2 second component, minor species in spectra with NCCH3, Cl–). There are semi-empirical methods to relate the hyperfine parameters to the in-plane and axial ligand fields [17], and corresponding qualitative predictions are in agreement with the observation that the chromophore with X = NO3– (weak in-plane interactions, two relatively short bonds to axial pyridine donors) has a small A|| value; from the electronic spectra (see Fig. 4 and Table 2) it emerges that with the two oxygen donors in the highly distorted basal plane this complex has the smallest ligand field in the series. The fact that the second component in the spectrum with X = OH2 has similar EPR parameters suggests that this is due to an isomer with OH2 trans to N3 and a concomitant elongation of the NMepy1–Cu–NMepy2 axis (this probably leads to the coordination of a second OH2-donor trans to N7 to complete the in-plane donor set). This also is in agreement with the molecular-mechanics-based analysis of the steric energies (see above). The minor species detected in the EPR spectra of solutions with X = NCCH3 and X = Cl– might also be due to chromophores with elongated copper–pyridine bonds, that with X = NO3– might have one or two monodentate NO3– donors. Note, however, that the simulation of these minor EPR signals is not unambiguous.
5 Ligand-field calculations
While the structural, computational and spectroscopic data discussed so far lead to a consistent picture, they rely on a rather speculative assignment of the spectroscopic parameters. Therefore, these were supported with AOM model calculations. While ligand field parameters are not strictly transferable, it has been shown that the calculation of electronic transition energies with a constant set of ligand field parameters, adjusted to differences in metal-donor distances by 1/r6, leads to reasonably accurate predictions, in particular for copper(II) systems [17]. Parameters for Cu–Namine and Cu–OH2 were used before in similar studies [17–21], those for Cu–NMepy and Cu–Cl were adapted from published spectroscopic studies [22,23]; for the structures with X = NO3– Cu–O parameters of OH2 were adapted to 1.3 the value for H2O (note that this might underestimate the π-interactions), those for Cu–NCCH3 were extrapolated from the parameters of amines and water, assuming that acetonitrile is a π-acceptor, and fitted to the electronic spectrum. While fine-tuning of all the parameters on the basis of a larger set of spectroscopic and structural data might lead to more accurate predictions [17,21], the main purpose of the present study is to assign the electronic transitions to specific isomeric forms of the copper(II)–bispidine chromophores, and this is possible with the present ad-hoc parameter set (see Table 3). There are also methods to compute the g-tensor parameters with reasonable accuracy [17], but the experimentally determined g-values are not well enough defined in all structures (see above), and their variation is relatively small (see Table 2) and, therefore, this is not pursued here. The structural parameters for the AOM calculations are from the crystallographically determined coordinates, for those of [Cu(L)(OH2)2]2+ (‘second isomer’) the copper and bispidine-donor coordinates were from the experimental structure with X = NO3–, and the two OH2 donors were set trans to N3 and N7 with Cu–O = 1.98 and 2.10 Å, respectively. This structural assumption is confirmed by the experimental structural data of [Cu(L)(OH2)]2+ (see above) and by a DFT structure optimization (see below).
Calculated electronic spectra (experimental data in brackets) of [Cu(L)(NCCH3)]2+, [Cu(L)(Cl)]+, [Cu(L)(OH2)]2+ and [Cu(L)(NO3)]+
| Electronic transition (cm–1) | ||||
| [Cu(L)(NCCH3)]2+ | 16 500 (16 300) | 15 000 13 600 | (14 300) | 10 400 (10 000) |
| [Cu(L)(Cl)]+ | 14 800 (15 300) | 14 000 13 100 | – | 7100 (8300) |
| [Cu(L)(OH2)]2+ a | 15 500 (16 100) | 14 200 13 500 | (13 700) | 7100 (7600) |
| 14 400 (13 700) | 14 000 12 900 | 5700 | ||
| [Cu(L)(NO3)]+ | 14 500 (14 800) | 14 000 13 100 | (13 100) | 6000 (7700) |
a Computed with two OH2 donors in-plane with Cu, N3 and N7, Cu–O = 1.98 and 2.21 Å, respectively, elongated NMepy1–Cu–NMepy2 axis.
As expected and observed experimentally, the chromophore with X = NCCH3 has the strongest ligand field and the highest energy transition. The calculated transition energies for [Cu(L)(Cl)]+ and [Cu(L)(OH2)]2+ are similar since the two complexes have similar structures and the two monodentate co-ligands have similar ligand field parameters. Two cis-disposed in-plane O-donors (NO3– structure) lead to a very low ligand field with a small splitting within the set of transition originating from the dxy,xz,yz orbitals (π-interactions with NO3– lead to an increase of this energy difference). Based on this analysis, the shoulder in the spectrum of the aqua complex at 13 700 cm–1 is primarily attributed to [Cu(L)(OH2)2]2+.
6 DFT calculations
For the structure optimizations based on approximate density functional theory a model was used, where the ester groups at C1 and C5 were replaced by hydrogen atoms, and the C(OH)2 at C9 was replaced by C=O. The latter modification is based on the ligand originally used in the synthesis (the hydration product is usually observed when hydrous solvents are used [5,13], and it is known that the ketone leads to a decrease of the nucleophilicity of the amine donors [4,13,24]; this might be one of the reasons why all copper(II)–bispidine-donor bonds reported here are overestimated). Table 4 is a summary of the calculated structural parameters. The DFT calculations are able to qualitatively reproduce the experimental structures. Exceptions are the generally observed overestimated bond distances (see above) and the fact that the Jahn–Teller elongation is not well reproduced in two of the structures (see below). For the chromophores with X = Cl– and, specifically, for X = OH2 the potential energy surface was searched in order to localize all local minimum structures and compare their stability. The corresponding data are also included in Table 4.
Computed structures (DFT, B3LYP) of [Cu(L)(X1)(X2)]n+ a,b
| [Cu(L)(NCCH3)]2+ | [Cu(L)(Cl)]+ c | [Cu(L)(OH2)]2+ d | [Cu(L)(NO3)]+ | |
| Cu–N3 | 2.029 | 2.209, 2.056 | 2.143, 2.013, 2.054 | 2.054 |
| Cu–N7 | 2.376 | 2.216, 2.398 | 2.239, 2.355, 2.105 | 2.106 |
| Cu–NMepy1 | 2.145 | 2.048, 2.205 | 2.017, 2.138, 2.481 | 2.480 |
| Cu–NMepy2 | 2.145 | 2.048, 2.204 | 2.017, 2.138, 2.481 | 2.480 |
| Cu–X1 (eq) | 2.012 | – , 2.212 | – , 2.032, 2.050 | 2.005 |
| Cu–X2 (ax) | – | 2.262, – | 2.190, –, 2.277 | 2.118 |
| N3···N7 | 3.029 | 3.024, 3.019 | 3.080, 3.028, 2.932 | 2.933 |
| Cu–N3/Cu–N7 | 0.85 | 1.00, 0.86 | 0.95, 0.86, 0.98 | 0.98 |
| N3–Cu–N7 | 86.5 | 86.2, 85.0 | 89.3, 87.4, 89.6 | 89.6 |
| N3–Cu–X1 | 179.1 | – , 179.7 | – , 179.9, 173.4 | 170.2 |
| N7–Cu–X2 | – | 166.9, – | 163.5, –, 169.7 | 163.0 |
| N7–Cu–X1 | 92.6 | – , 95.3 | – , 92.5, 97.0 | 100.1 |
| NMepy1–Cu–NMepy2 | 148.7 | 164.9, 146.9 | 166.2, 152.0, 149.6 | 149.7 |
| N3–C–C–NMepy1 | 28.3 | 45.6, 26.2 | 43.3, 30.6, 44.2 | 44.1 |
| N3–C–C–NMepy2 | 28.3 | 45.6, 26.2 | 43.3, 30.6, 44.2 | 44.1 |
a Distances in Å, angles in °.
b Underlined bond distances are the Jahn–Teller-elongated bonds observed experimentally.
c Two isomers; C1 trans to N7, trans to N3.
d Three isomers; OH2 trans to N7, trans to N3 (OH2)2.
The structure with X = NCCH3 is the only one which experimentally is observed with X trans to N3 and an elongated Cu–N7 bond. This is in good agreement with the DFT-based predictions. Specific distortions are also well reproduced, primarily the N3–C–C–NMepy torsional angles that allow the co-ligand X to move away from the pyridine–methyl substituents (this emerges also from the angular geometry of the chromophore, although these distortions are generally a little underestimated in the computed structures due to the overestimated bond distances). The good agreement between the computed and experimental structure is visualized in Fig. 6 (the difference in orientation of the NCCH3 ligand is due to enforced Cs symmetry).
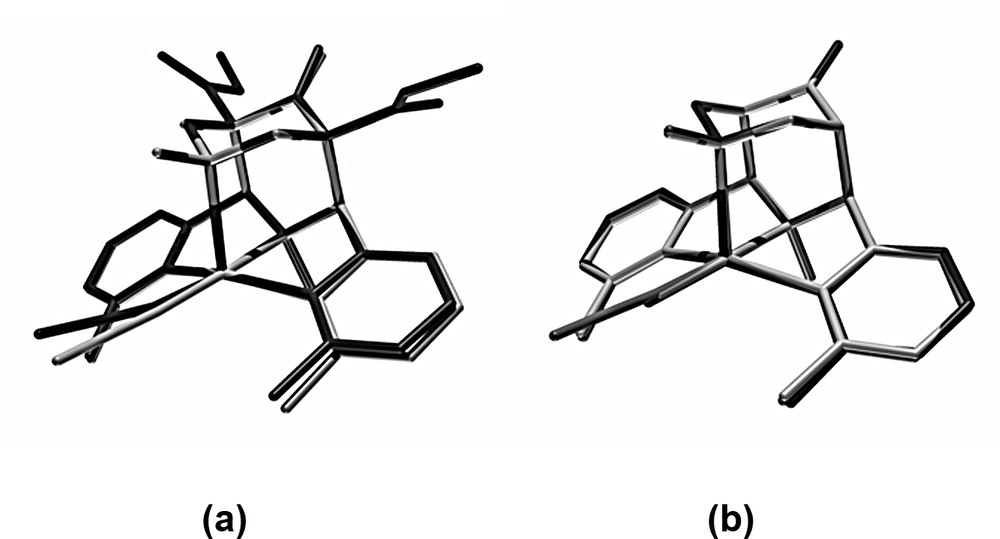
Overlay plots of (a) the experimental and computed structures of [Cu(L)(NCCH3)]2+ (dark: experimental, light: computed) and (b) the computed structures of [Cu(L)(X)]n+ with an elongated Cu–N7 bond (X trans to N3) with X = NCCH3, middle, OH2, dark, Cl–, light.
Local minima which correspond to the observed structure with X = NCCH3 have also been found with the co-ligands X = Cl– and OH2. The three computed structures with elongated Cu–N7 bonds and in-plane co-ligands (X = NCCH3, Cl–, OH2) are very similar to each other and confirm that these local minima are realistic (see Fig. 6). Molecular mechanics (see above) indicated that bulkier ligands than NCCH3 lead to a build-up of steric strain (repulsion of the pyridine–methyl groups and the co-ligand). In agreement with this the DFT structures indicate that, for X = Cl specifically, this strain leads to an elongation of the Cu–NMepy bonds see (Table 4). Spectroscopically, we have observed that, due to the resulting destabilization of this structural form, a switch to a second local minimum emerges, i.e. that with the Jahn–Teller axis along NMepy1–Cu–NMepy2. Probably, an additional OH2 is then coordinated to complete the in-plane ligand field. This hexacoordinate structure with X = OH2 has also been optimized with DFT (see Table 4). It is similar to that with the bidentate NO3– co-ligand and confirmed spectroscopically and by the AOM-computed transition energies (see above). The third structural form is that observed experimentally with X = Cl– and OH2 (see Table 1), with the monodentate co-ligand trans to N7 and an elongated Cu–N3 bond. The Cu–N3/Cu–N7 ratios in these structures are not well reproduced in the DFT-optimized geometries. Apart from some obvious and not unexpected deficiencies with respect to the energetics of the orbitals with large d-contributions (overestimated covalency of B3LYP calculations) this might also partially be due to the generally overestimated copper-donor bond distances (see above) and because N3 is part of a rigid five-membered chelate ring with little freedom to be significantly elongated. Energetically, the two five-coordinate local minimum structures (apical Cu–N7 or Cu–N3) are of similar stability with an energy difference of 5–10 kJ mol–1 and the experimentally observed structure being less stable in both cases. With the relatively small energy differences and the structural inaccuracies discussed above the conclusion is that the two minima are close to degenerate and, as outlined above, this is in agreement with the spectroscopic data (e.g., EPR spectra of the aqua complex). This also confirms the general observation that bispidine-coordination compounds are highly elastic, i.e. they have flat potential energy surfaces with various local minima (three in the systems discussed here, and all have been found experimentally and localized by DFT calculations) [3–5,13].
7 Conclusions
Recently we have presented the first example of copper(II) complexes with asymmetrical ligands, where two of the three isomeric structures of the chromophore along a Jahn–Teller vibrational mode could be trapped [5]. We now are able to present an example where all three possible Jahn–Teller elongated structures are trapped and structurally as well as spectroscopically fully characterized. While in the earlier example, which also is based on bispidine ligands, the stabilization/destabilization of one of the two close to degenerate minima of the ‘Mexican hat’ potential energy surface was due to steric interactions (size of the substituent at N7) [5,25], in the [Cu(L)X]n+ systems presented here, the stability of either of the three minima is due to the size (steric interactions) and electronic properties of the co-ligand X. Experimentally determined solid state molecular structures and a combination of solid state and solution electronic and frozen solution EPR spectroscopy, combined with ligand field calculations and spectra simulations have helped to characterize the structural variation. Empirical force field and DFT calculations were used to determine the steric influence, and spectroscopy, ligand field and DFT calculations helped to analyze electronic influences. While each method alone has some deficiencies and weaknesses which lead to ambiguities, from the combination of all the data we arrive at a consistent picture.
8 Experimental section
8.1 Materials
Reagents and solvents were used without purification; L was prepared as described in [7]. [Cu(L)(NCCH3)](BF4)2 and [Cu(L)(Cl)]Cl·H2O were obtained as described before [7]. Solvents with quality grade ‘purum’ or ‘puriss’, tetrabutylammonium chloride (purum, ≥ 97%) and tetrabutylammonium nitrate (puriss, ≥ 99%) were used for spectroscopic measurements.
8.2 Syntheses
8.2.1 [Cu(L)(NO3)](NO3)
Cu(NO3)2·3 H2O (0.78 g, 3.2 mmol) in water (10 ml) was added slowly to a suspension of L (1.5 g, 3.2 mmol) in methanol (30 ml). The resulting blue solution was put in a diethylether diffusion bath. After several days, blue crystals, suitable for X-ray diffraction precipitated from the solution (yield: 1.8 g, 2.7 mmol, 83%). C25H32N6O12Cu (672.10): Calcd. C 44.68, H 4.80, N 12.50; found C 44.27, H 4.81, N 12.25.
8.2.2 [Cu(L)(OH2)](BF4)2·H2O
[Cu(L)(NO3)](NO3) (1.2 g, 1.8 mmol) in water (0.5 l) was sorbed onto a SP-Sephadex C-25 cation exchange column (Na+ form). The column was washed with water (1 l), and the complex was eluted with 0.2 mol l–1 NaBF4. The eluate was concentrated to 25 ml and cooled to room temperature. The product was collected on a filter, washed with ethanol and dried in air (yield: 1.3 g, 1.7 mmol, 96%). C25H36N4O8CuB2F8 (757.73): Calcd. C 39.63, H 4.79, N 7.39; found C 39.66, H 4.81, N 7.36. Crystals suitable for X-ray diffraction were obtained by slow evaporation of the aqueous solution, saturated with NaBF4.
8.3 Measurements
UV–vis–NIR spectra were measured on a Cary IE spectrophotometer (solutions) or a JASCO V-570 UV/VIS/NIR instrument (diffused reflectance, polytetrafluoroethylene pellets). EPR spectra were obtained with a Bruker ELEXSYS E500 spectrometer (X-band) from frozen solutions (110 K), the same solutions were also used for UV–vis–NIR spectroscopy. The EPR spectra were simulated by XSophe (Bruker) [14,15].
8.4 Crystal structure determination
Reflections of single crystals were measured with a Bruker AXS SMART 1000 diffractometer with Mo Kα radiation (λ = 0.71073 Å) and operating in the ω-scan mode. The absorption correction was applied in all cases. The structures were solved by direct methods (SHELXS86) and refined by full-matrix, least-squares methods based on F2 (SHELXL97), with use of anisotropic thermal parameters for all non-hydrogen atoms. Crystallographic data for the new structures in this paper are reported in Table 5 and the structural data have been deposited at the Cambridge Crystallographic Data Center (CCDC 243386, 243387, 243388).
Crystallographic data of the X-ray diffraction studies
| [Cu(L)(OH2)](BF4)2·H2O | [Cu(L)(NO3)]NO3 | [Cu(L)(NO3)]NO3·1/2(CH3OH) | |
| Empirical formula | C25H36B2Cu F8N4O8 | C25H32Cu N6O12 | C25.50H34Cu N6O12.50 |
| Formula weight | 757.74 | 672.11 | 688.13 |
| Temperature | 103 (2) | 298 (2) | 103 (2) |
| Crystal system | Triclinic | Monoclinic | Triclinic |
| Space group | P | P21/c | P |
| a (Å) | 11.3822 (6) | 16.1439 (7) | 11.4300 (4) |
| b (Å) | 11.7737 (7) | 13.3029 (6) | 12.1400 (5) |
| c (Å) | 12.1129 (7) | 13.6704 (6) | 13.3298 (5) |
| α | 105.9270 (10) | 90 | 78.773 (7) |
| β | 97.7390 (10) | 93.3430 (10) | 64.815 (7) |
| γ | 92.9380 (10) | 90 | 62.433 (7) |
| V (Å3) | 1540.08 (15) | 2930.9 (2) | 1483.78 (10) |
| Z | 2 | 4 | 2 |
| dcalc (g cm–3) | 1.634 | 1.523 | 1.540 |
| Absorbance coefficient (mm–1) | 0.812 | 0.818 | 0.811 |
| F(000) | 778 | 1396 | 716 |
| Crystal size (mm) | 0.33 × 0.24 × 0.09 | 0.40 × 0.35 × 0.19 | 0.35 × 0.35 × 0.20 |
| Theta max | 32.02 | 30.50 | 32.00 |
| Reflections | |||
| Collected | 27,387 | 25,781 | 17,698 |
| Independent | 10 465 [0.0303] | 8909 [0.0289] | 9826 [0.0205] |
| Parameters | 603 | 525 | 473 |
| GOF on F2 | 1.043 | 1.015 | 1.044 |
| R1 [I > 2σ(I)] | 0.0362 | 0.0400 | 0.0518 |
| wR2 (all data) | 0.0993 | 0.1200 | 0.1566 |
| Largest difference in peak/hole (e Å–3) | 0.821/–0.673 | 0.464/–0.295 | 1.711/–0.592 |
Molecular mechanics calculations were done with the MOMEC program [26] and force field [27]; specific parameters for copper(II) bispidine complexes were as used before [1,4]; for Cl– the following van der Waals parameters were used: rvdw = 1.800, ɛ = 0.090. Note that all copper–bispidine parameters are not fully refined.
Ligand field calculations (AOM) were done with CAMMAG [28] and a transferable parameter set (adjusted by 1/(Cu–L) [16], based on normalized Cu–N and Cu–O distances), developed for copper(II) tetramines [17–20]. Parameters for copper(II)–pyridine, copper(II)–acetonitrile and copper(II)–nitrate were adapted from Refs. [22,23] and/or qualitatively fitted to the spectra ( = 6200, = 930 (for Cu–pyridine = 2.029 Å); = 5030, = 900 (for Cu–Cl = 2.260 Å), = 4400, = –100 (for Cu–NCCH3 = 1.95 Å), = 1417, = 250 (for Cu–NO3 = 2.440 Å), eds = 1/4 eσ).
DFT-calculations were performed with Gaussian03 [29], using the three-parameter hybrid exchange and correlation functional B3LYP [30,31]. This combination has been demonstrated to provide accurate geometries for a wide range of systems [32] and to perform well with transition metals [33]; various studies have shown it to be a reliable method for copper in all its oxidization states [34–37]. For the geometry optimizations a combination of the 6-311G+(d) basis set (as defined in Gaussian03) for heavy atoms and the 6-31G basis set for H atoms was used (note that the 6-311G command in Gaussian03 corresponds to a combination of basis sets, the Wachters–Hay all electron basis set for the first transition metal row (i.e. Cu) [38,39], using a scaling factor (with diffuse functions added) [40], the (12s, 9p) (621111, 52111) basis set [41,42] for the second-row main group atoms (i.e. Cl) and the 6-311G basis set [43,44] for first-row atoms (i.e. C, N, O, F)). Wavefunction stability tests were run on selected optimized structures. Frequency calculations were performed on all optimized structures to verify their status as true minima on the potential energy surface. For [Cu(II)(L)(Cl)]+, a single-point energy calculations was performed on the optimized geometry at the B3LYP/6-311G+(3df,2pd) level. This increase in size of the basis set and in the number of polarization functions was found to have a minimal effect on the energy and the energies for the remaining compounds were therefore calculated at the same level of theory as for the geometry optimizations. All energies discussed here are those calculated with the 6-311+G(d) (heavy atoms)/6-31G (H) combination.
Acknowledgements
Generous financial support by the Deutsche Forschungsgemeinschaft (DFG) is gratefully acknowledged.
1 An optimization is required to reach the energy minimum on the potential energy surface, defined by the force field, which corresponds to the conformation given by the starting coordinates.
2 DMF coordination is not discussed here in detail; even in dry DMF there are at least two species present, and these could be ‘Jahn–Teller isomers’, but probably linkage isomerism is also involved.


