1 Introduction
The frictional properties of an interface between polymers are strongly influenced by the presence of interfacial bridging chains. Disentanglement and pull-out of these chains during sliding is then expected to play an important role in energy dissipation [1,2], as for instance in problems of wall slip of polymer melts [3].
In order to probe in details the mechanisms responsible for frictional dissipation at such interfaces, we revue here two series of experimental investigation of friction at polydimethylsiloxane/polydimethylsiloxane brush interfaces. In the first set of experiments, the brush is put into contact with a PDMS melt, and full interdigitation is achieved prior to shearing. The local velocity within a molecular distance from the grafted surface is then measured by Near-Field Laser Velocimetry techniques, along with the shear force transmitted by the bulk polymer to the surface. The fluid–solid friction can thus be determined without assuming any rheological model for the fluid. Different friction regimes are observed depending on both shear velocity and molecular parameters of the grafted layer, such as surface grafting density and grafted chain length, and can be qualitatively understood in terms of progressive disentanglement of the grafted chains from the bulk, under the effect of friction forces. In the second set of experiments, similar grafted PDMS layers are put into contact with a crosslinked PDMS elastomer, which is translated under controlled load, at low slip velocities such that the grafted chains are able to at least partly penetrate into the elastomer. The evolution of the friction force with the grafting density and molecular weight of the tethered chains are quantitatively interpreted in the framework of a friction model based on arm retraction relaxation of the grafted chains.
2 Friction and slip at the wall: Near-Field Velocimetry techniques
When a fluid is sheared along a solid wall, one usually assumes that the velocity at the wall is zero (Fig. 1a). The situation could be quite different in complex fluids for which the range of the interactions can be much larger, as suggested by de Gennes [4] for entangled polymer melts without interactions with a solid surface, as schematically presented in Fig. 1b. Depending on the fact that the fluid–solid interactions are weaker or stronger than the interactions within the liquid, the extrapolation length of the velocity profile to zero, b, can be either below the surface (positive b) or above the surface (negative b). In a simple fluid, it is usually admitted that the perturbation introduced by the presence of the interface cannot produce effects over a range much larger than that of the molecular interactions. The slip length, b is thus expected to be comparable to a molecular size (Fig. 1a), while for complex fluids, such as high molecular weight polymers, b may reach micrometer sizes.
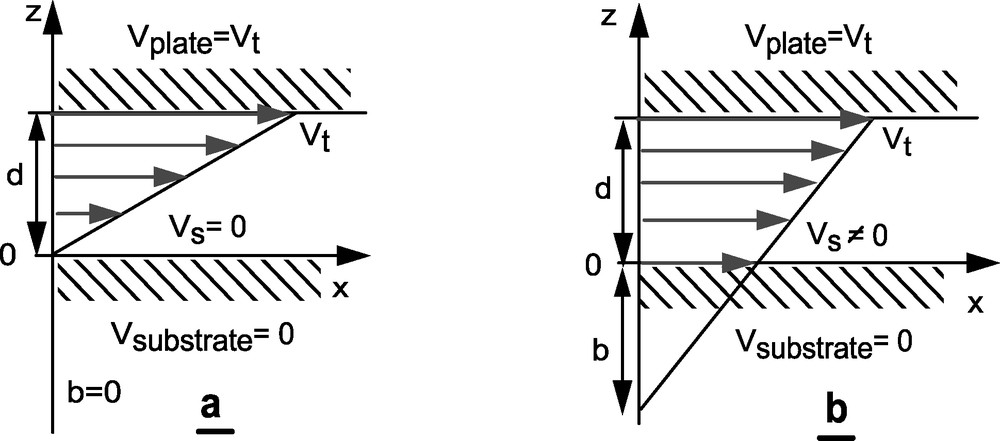
Schematic representation of a no slip (a) or a slip (b) boundary condition for the fluid velocity at the solid wall. For the sake of simplicity, the top and bottom surfaces are assumed to be different and to lead to different boundary conditions for the flow velocity at the wall. Such a situation can be achieved experimentally by treating the two surfaces in a different manner, as it will be detailed in the presentation of the experimental results.
In fact, b is directly related to the friction coefficient between the fluid and the surface. This can be easily seen by evaluating the friction force transmitted to the solid by the sheared liquid. The friction force can be estimated either as the product of the interfacial velocity Vs by a friction coefficient, k, or as the product of the fluid viscosity by the velocity gradient at the interface, i.e. , where η is the bulk fluid viscosity. The friction coefficient k is thus inversely proportional to the slip length. Any direct information on the local velocity profile close to the solid wall can be translated in terms of surface friction, provided the viscosity close to the wall is known. If one suspects that the viscosity close to the wall could differ from the bulk one, the friction coefficient can be determined without any further assumption by simultaneous measurements of the friction force and of the local velocity Vs.
The above remark points out the interest of direct measurements of the fluid velocity at the fluid–solid interface. However, to decrease the spatial resolution from the wall down to molecular sizes is a particularly difficult challenge. To reach this goal we have developed the Near-Field Laser velocimetry technique (NFLV) which allows to increase significantly the spatial resolution, down to 50 nm, i.e. much lower than what is obtained with conventional velocimetry techniques [5] (even laser velocimetry). Furthermore the flow tracers are fluorescent molecules with a size comparable to that of the fluid molecules, avoiding any disturbance of the distribution of the flow velocity. This new technique has been used to measure the velocity of a polymer melt at the interface with a solid wall [3,6–10], and also to demonstrate that a simple fluid can exhibit significant slip on a smooth solid surface [11,12]. We focus here on the polymer case.
The NFLV technique has been described in details [13], we only briefly recall here its principle. It is based on fluorescence recovery after photobleaching and evanescent wave induced fluorescence. Fluorescent molecules chosen so that they easily photobleach under intense illumination are used as flow tracers. They are produced by a local intense illumination of the sample (writing period of the experiment). The way they are then transported by the flow is monitored through the evolution with time of the fluorescence intensity, under attenuated illumination so that no further photobleaching occurs during the reading period of the experiment. The confinement of the investigated volume close to the solid – fluid interface is achieved by the use of optical evanescent waves for reading the fluorescence and eventually also to produce the photobleached probes. Detailed descriptions of the experimental set up and of the data analysis of the fluorescence recovery after photobleaching in order to extract the interfacial velocity are reported in [6,9,13]. For the polymer experiments, the fluorescent probe is chemically attached to the extremities of a few chains in the fluid (5% in weight of labeled chains). The diffusion of the photobleached probes is then very slow, and the evolution with time of the photobleached pattern printed in the sample is essentially due to convection by the flow. The re-entry of fluorescent probes in the illuminated volume can then be directly related to the average velocity in a slab of fluid close to the wall with a thickness comparable to the penetration depth of the evanescent wave, Λ, used to read the fluorescence. A typical order of magnitude of that penetration depth is in the range 30–100 nm, i.e. comparable to the size of a polymer chain. NFLV thus gives a direct access to the fluid velocity at the interface, averaged over a thickness comparable to a molecular size.
3 Friction and slip at polymer melt–solid interfaces
3.1 Newtonian polymer melt in contact with grafted polymer layers
In a first step high molecular weight polymers well in their Newtonian fluid regime have been investigated by NFLV. In order to gain information on the molecular mechanisms of friction at such interfaces, model systems for which the molecular parameters could be varied in a controlled manner have been used. They were made of low polydispersity polydimethylsiloxane (PDMS) melts in contact with smooth silica surfaces, covered with controlled densities of end grafted PDMS chains of various molecular weights. The choice of surfaces covered with end tethered chains was dictated by the fact that in practical situations where a polymer melt is sheared on a solid surface, the most probable situation is that corresponding to the spontaneous formation of a layer of surface anchored chains (even weak monomer – surface interactions result in strong polymer surface interactions, as a polymer chain has on the average monomers in contact with the surface, with N the polymerization index of the chain). The melt molecular weight was chosen so that all experiments were in the Newtonian regime, with , with TR the reptation time of the melt chains.
The important general result is that when the polymer melt is sheared against a surface on which polymer chains are strongly attached, with a surface density Σ, (the number of surface anchored chains per unit area is ν = Σ/a2, with a the size of the monomer) three different friction regimes are observed when increasing the shear rate, provided the surface chains are able to entangle with the bulk polymer ones. This non-trivial friction behavior is illustrated in Fig. 2, which presents velocity measurements at an interface between silica and a PDMS melt, the silica being covered with chemically end grafted PDMS chains, at low surface coverage (see caption for details). Details on the grafting procedure can be found in [11]. In order to ensure a constant chemical composition of the surface layer, whatever the state of elongation of the long surface grafted chains, the surface layer was a bimodal brush made of a dense layer of PDMS chains with a molecular weight shorter than the molecular weight between entanglements, among which a few long chains, also grafted to the surface were mixed. Σ is the surface density of long grafted chains. In order to prevent slip at the second wall, the top surface is covered with longer end grafted PDMS chains, with an adjusted surface coverage. Slip is always observed: the measured velocity, which is an average of the velocities within the optical penetration depth, Λ, from the surface, is always larger than what would be obtained with a no slip boundary condition, shown as the lower dashed line in Fig. 2a. At low top plate velocities the corresponding slip length is small (b ~ 1 μm) and constant (Fig. 2b), meaning that Vs is proportional to Vt. At intermediate Vt values, Vs increases more rapidly than linearly with Vt to finally reach a value close to Vt at high shear rates (quasi-plug flow; Vs = Vt is the upper dashed line in Fig. 2a). In this intermediate regime, b appears proportional to Vs (see the log–log plot of Fig. 2b). As b is inversely proportional to the friction coefficient, this is a non linear friction regime, with a friction coefficient inversely proportional to the interfacial velocity. In the high shear rate regime Vs becomes again proportional to Vt and b is constant (linear friction regime), of the order of 100 μm, implying a friction coefficient two orders of magnitude smaller than in the initial low-shear-rate regime. The striking feature is that, all through the intermediate regime, the shear rate experienced by the polymer, (d is the cell thickness) remains constant, a fact which has been confirmed by direct measurements of the shear stress transmitted by the polymer fluid to the solid. If the solid surface is covered with short PDMS chains having a molecular weight smaller than the average molecular weight between entanglements, only the low friction regime is observed, confirming that entanglements between surface anchored and bulk chains are indeed the source of the non trivial friction behavior in these systems [10,14].
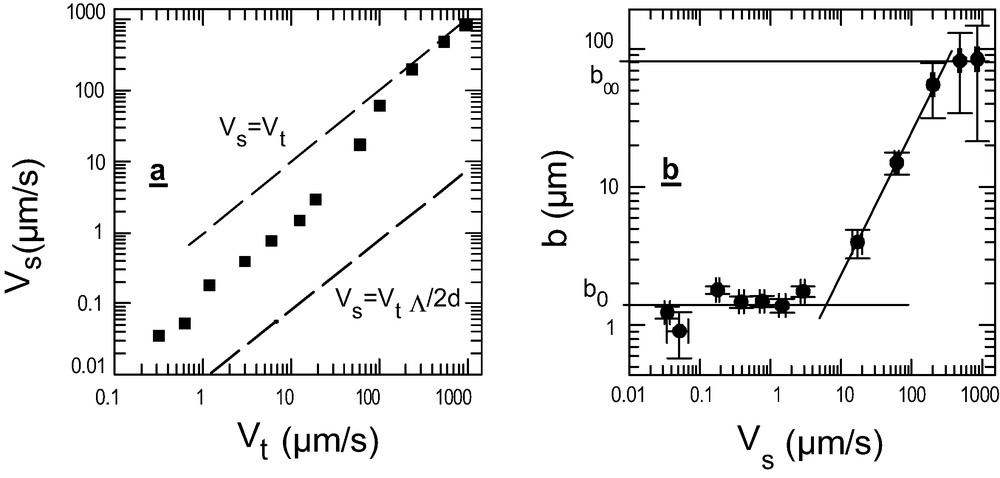
Typical results for (a) the slip velocity and (b) the slip length, for a PDMS melt (molecular weight Mw = 970 kg/mol (Mw/Mn = 1.14)), flowing against a silica surface covered with end grafted PDMS chains with Mw = 96 kg/mol (Mw/Mn = 1.1) and a surface density, Σ = 0.00025. (the surface density Σ is related to the average number of grafted chains per unit surface, ν, through ν = Σ/a2, with a the size of a monomer, a = 0.5 nm for PDMS). The top surface is treated by grafting the same PDMS chains with a larger grafting density, in order to prevent slip at the top surface.
3.2 Molecular modeling
A molecular model describing how a weak density of polymer molecules end grafted on a solid surface (surface chains independent of each other) and entangled with the bulk polymer affect the boundary condition for the velocity at the polymer–solid interface have been developed by de gennes and coworkers [15–17]. The theoretical predictions agree qualitatively with the NFLV results obtained for PDMS with low surface densities of surface chains. This model takes into account the fact that, due to entanglements, the surface chains act as obstacles to the flow of the bulk chains. These entanglements produce a large friction between the melt and the surface at low shear rates, and suppress the huge slip at the wall expected for ideal surfaces [4]. Surface chains are not however, rigid objects. Under the effect of the friction force, they can deform, and an elastic restoring force develops. In steady state, elastic and friction forces balance each other. Increasing the shear rate increases the friction force and the elongation of the surface chains. The initial high friction regime has to stop when the elongation of the surface chains becomes large enough so that the elongated chains are at the limit of disentangling from the melt. A distinct friction regime, called the marginal regime, is then encountered. The surface chains keep the limiting elongation corresponding to the limit of disentanglement for a large range of slip velocities (i.e. a range of imposed Vt), because if elongated more, the surface chains would disentangle from the melt, the friction force would strongly decrease and would no longer balance the elastic restoring force. The surface chains would then re-entangle. In the marginal regime the shear force is thus fixed and independent of the slip velocity, implying a friction coefficient inversely proportional to Vs. This marginal regime is thus the intermediate constant shear rate regime of the experiments. The marginal regime ends when the frequency at which the surface chains is solicited by the flow to entangle/disentangle from the melt becomes larger than their relaxation frequency [16,17]. The surface chains then get fully disentangled, the melt dynamically de-couples from the surface, and the friction becomes constant and low, with a slip length b∞ independent of Vs and comparable to what would be obtained on an ideal surface.
In all the three friction regimes the shear force per surface chain (which is independently measured in the experiment) remains always much smaller than the force necessary to break a hydrogen or a covalent bond [14]. The observed transition from low to high slip at the wall is thus not due to tearing off of the surface chains. For PDMS melts with lower molecular weights mixed with glass beads [18] a slip transition has been observed and attributed to de-sorption of the PDMS chains from the glass surface. This may not be contradictory. The low- to high-slip transition is in fact the signature of a dynamic de-coupling between the surface and the bulk polymer. Depending on the physico-chemical conditions, this de-coupling may take place through different modes: tearing off of the surface chains under the shear stress, if the bonding force is weak, or elongation and disentanglement of surface and bulk chains when the bonding force is large. Only the disentanglement mechanism is associated with the existence of a marginal regime extending over several decades in slip velocities, with a fixed shear rate whatever the shearing velocity (inside the range of the marginal regime).
We have experimentally characterized situations with larger surface densities, as shown in Fig. 3, where the critical shear rate all through the marginal regime is reported as a function of the surface density of grafted chains. At low surface densities, the linear regime is characteristic of surface chains acting independently of each other for the friction. Above a given surface density, the critical shear rate decreases, indicating that the decoupling between the bulk polymer and the surface layer becomes easier than for lower surface densities. This can qualitatively be related to the fact that for high enough surface densities, one expects that the bulk chains can no longer fully penetrate into the surface layer [19]. The number of mutual entanglements should thus become a decreasing function of Σ, and the critical shear rate too. At present, we have however no detailed theoretical description, at molecular level, of this high density regime, in which the surface chains are no longer independent of each other. The experiments and models described above give however precise lines of thought to design surfaces with adjusted friction properties.
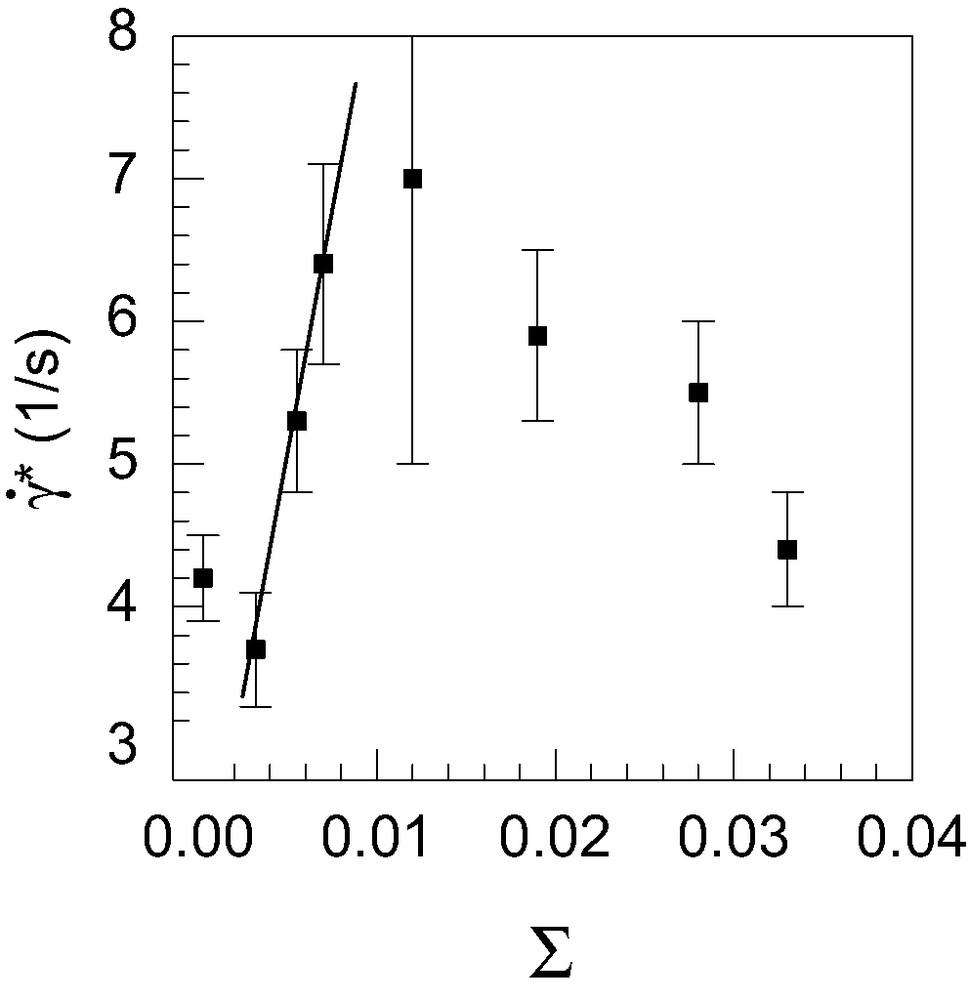
Evolution of the critical shear rate at the onset of the marginal regime as a function of the surface density of the grafted surface layer, Σ, for a PDMS melt with a molecular weight 970 kg/mol, and surface chains with a molecular weight 96 kg/mol. For small surface densities, increases linearly with Σ, indicating that the surface chains contribute to the friction independently of each other. Above a surface density Σ = 0.01, a collective behavior of the surface chains shows up.
3.3 Friction in case of non Newtonian polymer melt
The case of non-Newtonian polymer fluids has also been investigated experimentally, using NFLV, and appears more complicated [20]. The experiments show the onset of a decoupling between the surface layer of anchored chains and the bulk polymer, but which can be accompanied by a non stationary regime with stick–slip interfacial motion, as shown in Fig. 4 where data taken with another polymer (styrene–butadiene copolymer, SBR) are reported. The average distance between entanglements is smaller in SBR than in PDMS, so that for comparable molecular weights the reptation time, TR, is much longer and the limit can be easily reached in the shear rate range of the experiment. The effect of such a long reptation time is easily seen in Fig. 4, as it characterizes the duration of the initial transient regime after starting to shear the sample. In the case of all PDMS investigated, such a transient was hardly visible because too short compared to the time resolution of the stress measurement. For SBR, the transient was fully visible, with a static friction force overshoot as soon as the shear velocity was large enough to cross .
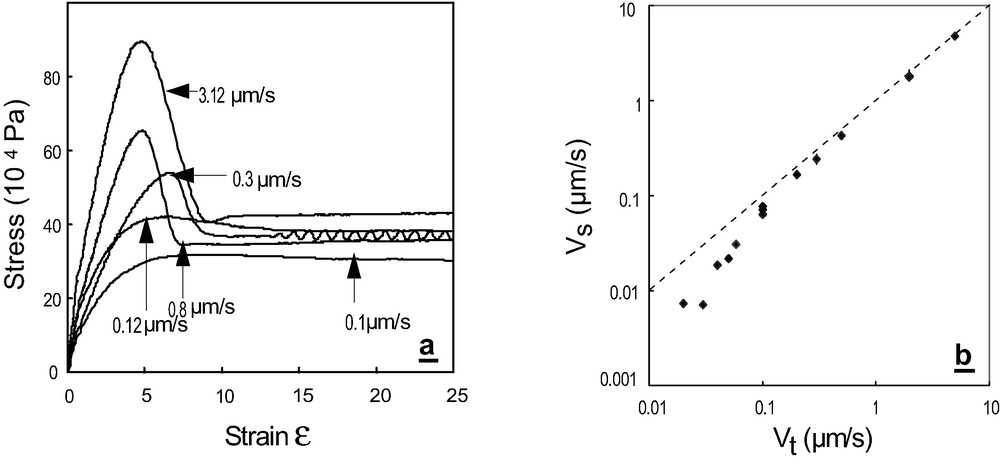
Typical results for: (a) the shear stress as a function of the displacement of the top surface of the sample for different velocities of that top surface displacement. The polymer is a SBR melt with a weight average molecular weight 135 kg/mol. The surface under investigation bears an adsorbed layer of SBR molecules with a weight average molecular weight 50 kg/mol, and a surface density Σ = 0.005. A stick–slip oscillatory regime clearly appears at intermediate shear rates; (b) slip velocity as a function of top plate velocity for the same SBR melt as in (a), but in contact with a surface covered by a thin layer of PDMS, incompatible with SBR so that no entanglements between surface and bulk chains exist. High slip and a quasi-plug flow is observed for the whole range of shear velocities investigated (the dashed line corresponds to Vs = Vt (plug flow)).
We have yet no full molecular explanation for the behavior shown in Fig. 4. In Fig. 4b, we show that in the absence of entanglements between the surface layer and the bulk at the beginning of the experiment, only the high slip, low friction regime develops, at least in the central shear rate range of the experiment. The data presented at the low shear rate end of the curve are at the limit of sensitivity of the velocity measurement, and the observed decrease in slip velocity compared to plug flow could reveal the presence of a few SBR surface anchored chains, adsorbed on the silica surface through imperfections of the PDMS layer. Indeed the shear rate corresponding to appearance of this decrease was sample dependent. We were not able to quantify by any means the possible amount of these SBR adsorbed chains, and theses experiments do demonstrate how sensitive friction is with respect to tiny physico-chemical modifications of the interface.
4 Friction at elastomer-grafted layer interfaces
In order to better understand the role of elasticity in these systems, we have undertaken a second series of experiments with the same PDMS-grafted layers put into contact with a crosslinked PDMS elastomer [21]. In order to measure the friction force when the layer was translated at a chosen low velocity in front of the elastomer, we have developed a JKR like test, adapted for friction force measurements, and schematically presented in Fig. 5. The experiment involves the contact between a lens of poly(dimethylsiloxane) (PDMS) elastomer and a ‘bimodal’ brush – i.e. made of chains of two different lengths – grafted on a flat substrate. The principle of force measurements is the following (Fig. 5): a contact of given diameter (d = 200–400 μm) is formed between a small elastomer lens and a brush-bearing substrate. This substrate is then translated through a spring driven at constant velocity, 3 nm s−1< V <300 μm s−1. The measurement of the spring bending gives access to the friction force F, typically in the range 50 μN–50 mN, while the contact area S is monitored optically during sliding. We must emphasize that contrary to the previous Near-Field Laser Velocimetry experiments, we here impose the relative velocity between the elastomer and the surface layer, and can only measure a friction stress. This stress measurement is however much more reliable than the corresponding one in the melt experiments, because in the case of the melt, spacers were necessary to maintain the fluid thickness (and thus specify the shear geometry). We had only access to the total friction stress, including the contribution of the friction on the spacers, which in most cases was comparable to the friction due to the melt. A strong interest of the elastomer experiment is to allow for direct measurement of the friction force, and thus a determination of the friction force per grafted chain as soon as the surface density of grafted chains is known.
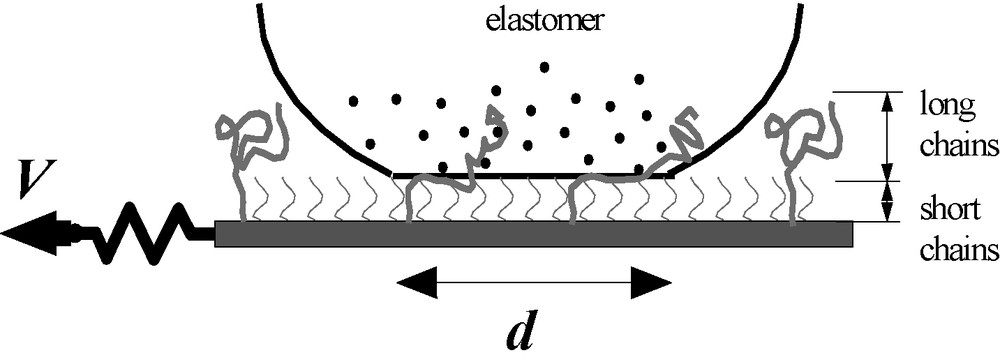
Sketch of the JKR like experimental setup designed for the measurement of the friction at elastomer–solid interface.
Elastomer lenses are obtained from droplets of a melt of divinyl end-capped PDMS chains (Mw = 9 kg mol−1, I = 1.14), crosslinked by Pt-catalyzed hydrosilation of the vinyl ends with a tetrafunctional H-terminated crosslinker. The ratio of hydride to vinyl is chosen in order to optimize the network connectivity, crosslinking is made at 110 °C for 12 h, and elastomers are then washed in toluene for ten days to extract all unreacted species [22].
Bimodal brushes are made by hydrosilation between monovinyl-terminated chains and an H-functionalized silicon wafer, following a method described in details elsewhere [23]. They are formed of a dense layer of short chains (Mw = 5 kg.mol−1) grafted at an areal density Σshort = 0.4 nm−2, in which are present long ‘connectors’ of molecular weights ranging from 27 to 114 kg.mol−1. The grafting density of these long chains can be adjusted in the range Σ = 0–0.08 nm−2.
We present in Fig. 6 typical results obtained in steady sliding for the friction stress σ = F/S as a function of slip velocity V.
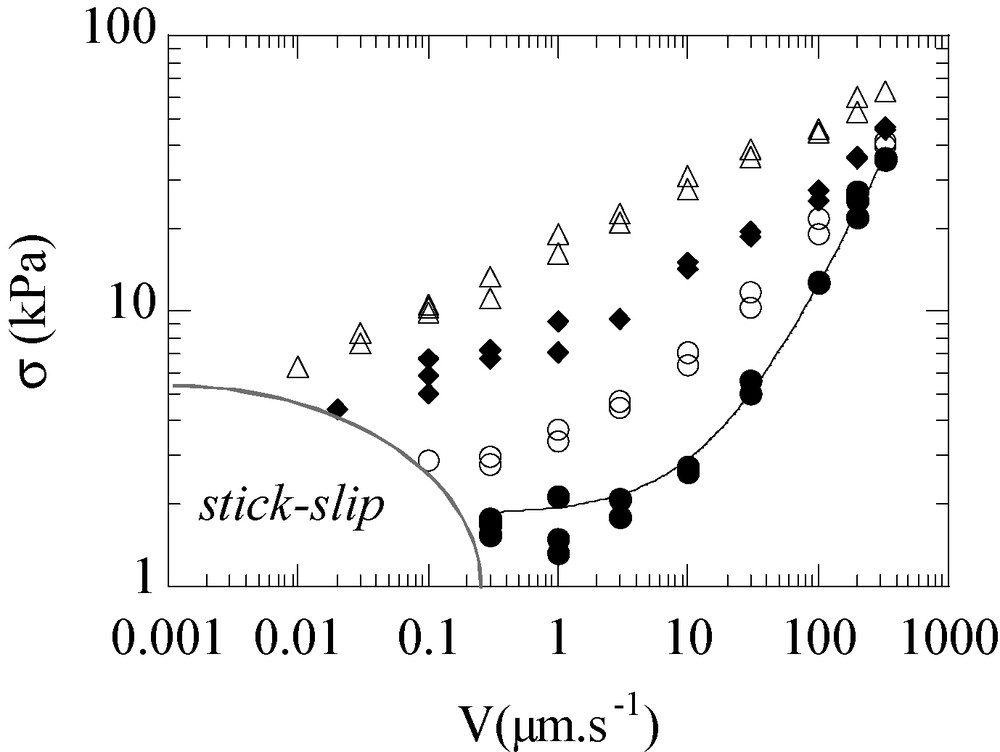
Shear stress s versus sliding velocity V, for connectors with Mw = 114 kg mol−1. (●): Σ = 0; (○): Σ = 0.0016 nm−2; (◊):Σ = 0.0076 nm−2; (△): Σ = 0.021 nm−2. The solid line is a fit of the Σ = 0 data with σ = σ0 + k V.
4.1 Friction on short-chain brushes
Without long connectors, we find that the friction stress increases linearly with velocity, after a low-velocity plateau. The data obey a relation of the form σshort = σ0 + k V, with σ0 = 2 kPa, and k = 108 Pa s m−1. Steady sliding is observed down to a critical velocity Vc ≈ 0.3 μm s−1 below which sliding is unstable and stick–slip oscillations are observed.
4.2 Friction induced by connectors
Whatever their molecular weight, long connectors have the following effects on friction:
- • the sliding stress σ depends non-linearly on velocity, and eventually grows as a weak power law of V at high grafting density of connectors (see Fig. 6);
- • the sliding stress increases quasi-linearly with the grafting density Σ, up to Σ0 ≈ 0.025 nm−2, above which σ reaches a plateau value and becomes independent of Σ, as shown in Fig. 7;
- • the critical velocity Vc at which stick–slip appears decreases with the grafting density. It varies typically from 0.3 to 0.003 μm s−1 when Σ goes from 0 to 0.05 nm−2 for connectors of Mw = 114 kg mol−1.
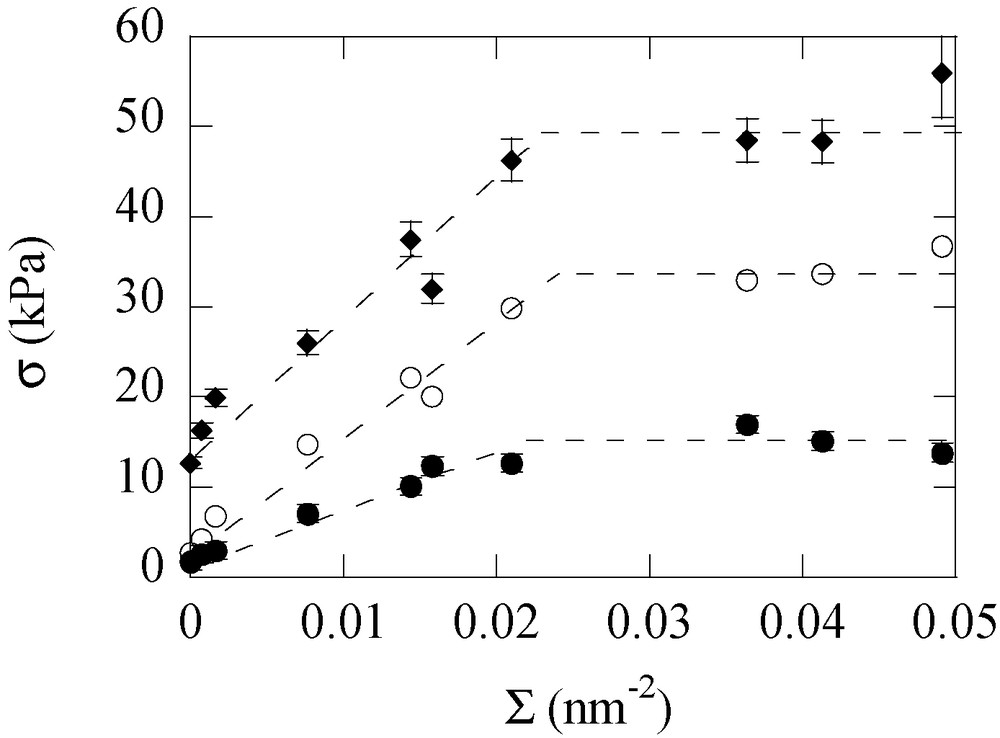
Shear stress s versus grafting density Σ for connectors with Mw = 114 kg mol−1. (●): V=0.3 μm s−1 ; (○): V = 10 μm s−1 ; (♦): V = 100 μm s−1.
4.3 Molecular-weight effects
At a given surface density, we observe that:
- • the friction stress increases when the length of the connectors increases, as illustrated in Fig. 8;
- • at high grafting density, the exponent α of the σ(V) power law increases from 0.2 to 0.5 when Mw goes from 114 to 27 kg mol−1.
- • the critical velocity Vc is lower for longer connectors.
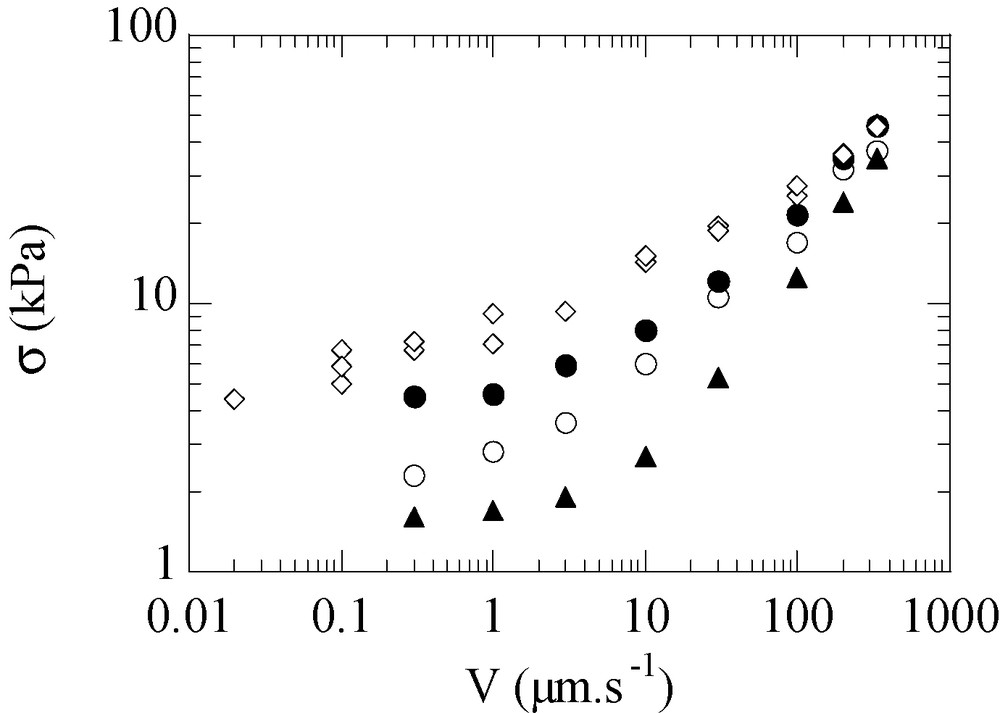
Shear stress s versus sliding velocity V for Σ = 0 (▲), and Σ = 0.01 nm−2 of connectors Mw = 27 kg mol−1 (○); Mw = 35 kg mol−1 (●); Mw = 114 kg mol−1 (◊).
4.4 Discussion
When the elastomer slides on a dense brush of short chains only, the friction is expected to be close to that between two surfaces of densely packed monomers, i.e. σ = ς1V/a2, where ς1 is a monomeric friction coefficient and a is the size of a monomer. Estimating ς1 = k a2 from the experimental value of k, we find, with a = 0.5 nm, ς1 = 2.5 10−11 N s m−1. This value is fully consistent with what is deduced from self-diffusion measurements [24]. The saturation stress σ0 and the occurrence of stick-slip can be attributed to the presence of very-small-scale defect coverage of the brush.
The increase of the friction stress in the presence of long connectors and the dependence of σ on their grafting density are in good agreement with previous studies of friction or adhesion on similar rubber/brush interfaces [2,3]. The characteristic time scale of the experiment is given by De/V, where De ≈ 5 nm is the mesh size of the elastomer, and ranges from 10−2 to 10−5s when V increases from 0.3 to 300 μm s−1. This is larger than τR≈10−5 s, the longest Rouse time of the connectors used in this study, and indicates that the grafted chains are always able to partially penetrate into the network, over distances on the order of or larger than the mesh size of the elatomer, as predicted by numerical simulations [25]. The penetrated part of the grafted chains may thus contribute to friction enhancement in two ways:
- • it acts as an anchor and allows to stretch the portion of chain which remains confined out of the elastomer,
- • it has to be pulled out of the network.
The first mechanism, i.e. the rheology of a thin layer confined outside the elastomer, probably governs friction at high grafting density, in the regime where the stress is quasi independent of Σ and grows as σ ~Vα. Indeed, if we consider that a PDMS layer of thickness h = 10 nm (typical dry thickness of a brush with Mw = 114 kg mol−1 and Σ = 0.04 nm−2) is sheared at a rate = V/h, we evaluate an effective viscosity ηeff = σ/, which decreases as V–0.8 and stays 10 to 1000 times larger than the bulk viscosity of a melt made of chains of comparable length. Both this strong increase of viscosity and the shear-thinning behaviour observed are in good agreement with recently reported results on rheology of strongly confined PDMS melts [26].
Focussing now on the results obtained at very low grafting densities, where tethered chains are independent, we can analyze the contribution of chain pull-out only (mechanism (ii) mentioned above). We do so in the framework of a model proposed by Rubinstein et al. [27], which suggests that friction at a rubber/brush interface is controlled by arm retraction of the grafted chains. This model predicts that, in the range of velocity covered in our study, a grafted chain is composed of a ‘ball-shaped’ part relaxed in the network and of a stretched part outside the network. Qualitatively, the friction force on a chain is predicted to increase weakly with V, from a constant value k T/De, and the velocity dependence is expected to be weaker for shorter chains.
In order to compare these predictions with our results, we extract the friction force per chain from our data, assuming that the total stress σ(V) = σshort + Σ Fc. The force Fc thus deduced is plotted in Fig. 9 as a function of velocity and for different molecular weights of the tethered chains.
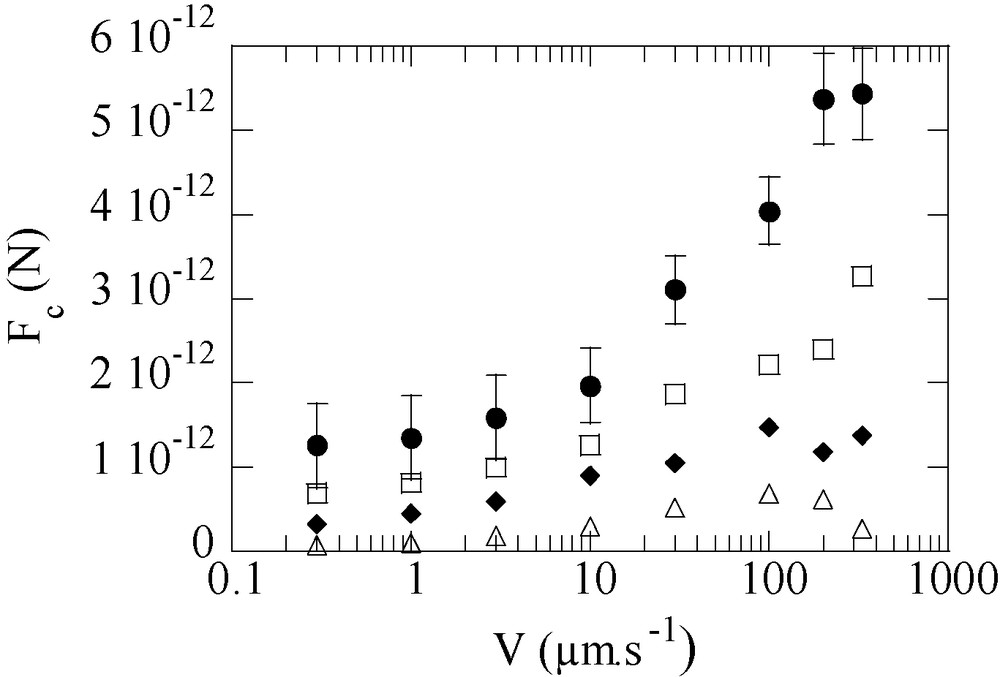
Friction force per connector chain, Fc, versus sliding velocity V: (●) Mw = 114 kg.mol−1; (□): Mw = 89 kg mol−1; (♦): Mw = 35 kg mol−1; (△) Mw = 27 kg mol−1.
We can see in Fig. 9 that:
- • the force per chain increases weakly with the velocity;
- • Fc is lower for shorter connectors;
- • the low-velocity value of Fc varies between 10−13 and 10−12 N when Mw increases from 27 to 114 kg.mol−1.
These three points are in good agreement with the theoretical predictions: the low velocity value of Fc is consistent with k T/De ≈ 8 × 10−13 N (with De≈5 nm), and the model predicts both a velocity (Fig. 10a) and a molecular weight (Fig. 10b) dependence of the friction force which are, without any fitting parameters, in satisfactory agreement with the data.
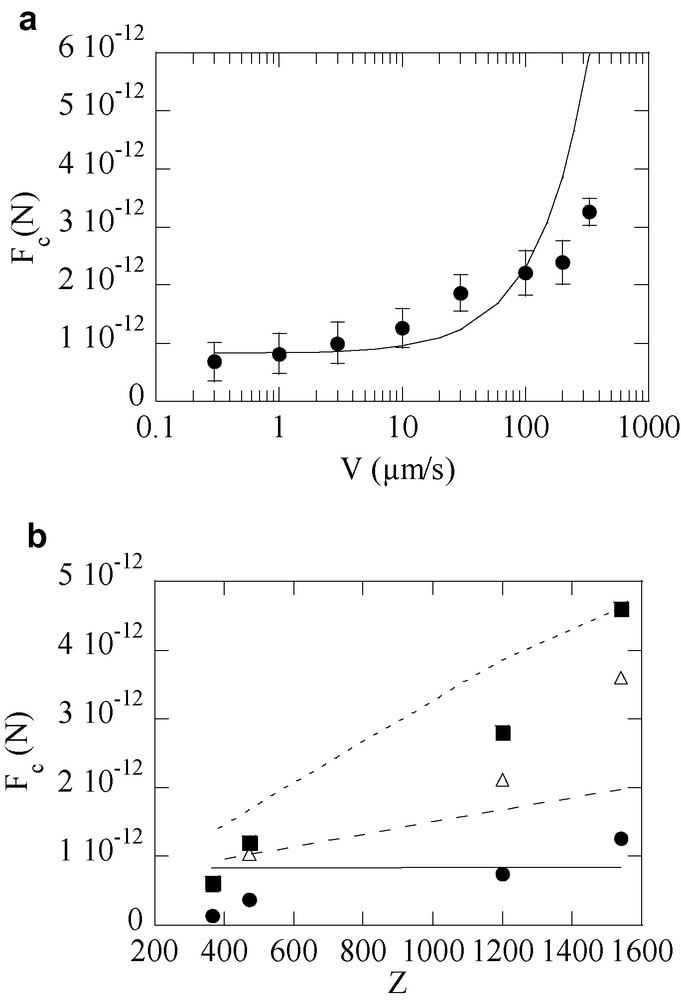
(a) Theoretical predictions for Fc versus V. (—): Z = 1200 monomers. Symbols: exp. data for Z = 1200 from Fig. 9. (b) Fc versus polymerization index Z of connectors. Symbols are experimental data and lines theoretical predictions at V = 1 μm s−1 (●) and (—); V = 60 μm s−1 (△) and (– – –); V = 200 μm s−1 (■) and (- - -).
However, discrepancies exist between experimental and theoretical results:
- • the model does not account for the systematic decrease of Fc with the molecular weight observed at low velocities;
- • once scaled by their value at 0.3 μm s−1, the Fc(V) experimental curves show that the relative force increase over the 3 decades of velocity is the same whatever the molecular weight of the connectors, whereas the model predicts a weaker relative increase for shorter chains (Fig. 10a).
These discrepancies might arise from the fact that the data for the shortest connectors correspond to a situation where only weak entanglement exists between the network and the grafted chains, which may be close to the limit of validity of the model.
5 Conclusion
From two series of experiments conducted on model systems made of surface anchored polymer layers of end grafted chains put into contact with either a polymer melt or a crosslinked elastomer in which the surface chains are able to interdigitate, we have been able to characterize the molecular mechanisms responsible for friction at such polymer–solid interfaces. In both cases, we have shown that the surface anchored chains, which are not rigid objects, but may be deformed under the effect of the friction forces, were responsible for friction forces varying non linearly with the velocity. These non linear friction regimes are the signature of the whole dynamical response of the surface chains when solicited by the shear deformation, dynamical response that governs both the aptitude of the surface chains to interdigitate into the bulk polymer and their extraction, which is necessary to allow slip motion. This entanglements driven friction appears in good quantitative agreement with molecular models. It thus appears possible to manipulate friction at such interfaces by adjusting the molecular parameters of the system.


