Outline
Comptes Rendus
no. 7-8

Account / Revue
Photoinduced intermolecular electron transfer and energy transfer of C60 dendrimers
Yasuyuki Araki1; Ryouta Kunieda1; Mamoru Fujitsuka1; Osamu Ito1 ; Jiro Motoyoshiya2; Hiroshi Aoyama2; Yutaka Takaguchi3
1 Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Kaahira, Aoba-ku, Sendai 980-8577, Japan
2 Faculty of Textile Science and Technology, Shinshu University, Ueda, Nagano 386-8567, Japan
3 Graduate School of Natural Science and Technology, Okayama University, Tsushimanaka, Okayama 700-8530, Japan
Comptes Rendus. Chimie, Volume 9 (2006) no. 7-8, pp. 1014-1021.

Abstract

Photoinduced intermolecular electron-transfer and energy-transfer processes of the fullerodendrimers with two poly(amidoamine)dendron groups of 0.5-th, 1.5-th and 2.5-th generations have been investigated by laser flash photolysis. The rate constants and quantum yields of photoinduced electron transfer with the added aromatic amine donors in PhCN tend to decrease with the dendron generation, indicating that the bulky dendron groups act as barriers for the donor molecules to approach the C60 moiety in the center of the dendrimers. The decreases in the rate constants of triplet energy transfer processes vs. O2 and β-carotene with the dendron generation are smaller than those of electron-transfer process, probably because effective encounter radii for energy transfer are larger than those for electron transfer; hence, less sensitive to dendrimer generation. A kinetic model for intermolecular electron-transfer and energy-transfer of fullerodendrimers was proposed. .

Metadata
Received:
Accepted:
Published online:
DOI: 10.1016/j.crci.2005.09.008
Keywords: Fullerene, Dendrimer, Electron-transfer, Energy-transfer, Laser flash photolysis

Yasuyuki Araki 1; Ryouta Kunieda 1; Mamoru Fujitsuka 1; Osamu Ito 1; Jiro Motoyoshiya 2; Hiroshi Aoyama 2; Yutaka Takaguchi 3

1 Institute of Multidisciplinary Research for Advanced Materials, Tohoku University, Kaahira, Aoba-ku, Sendai 980-8577, Japan
2 Faculty of Textile Science and Technology, Shinshu University, Ueda, Nagano 386-8567, Japan
3 Graduate School of Natural Science and Technology, Okayama University, Tsushimanaka, Okayama 700-8530, Japan 
@article{CRCHIM_2006__9_7-8_1014_0,
     author = {Yasuyuki Araki and Ryouta Kunieda and Mamoru Fujitsuka and Osamu Ito and Jiro Motoyoshiya and Hiroshi Aoyama and Yutaka Takaguchi},
     title = {Photoinduced intermolecular electron transfer and~energy transfer {of~C\protect\textsubscript{60}} dendrimers},
     journal = {Comptes Rendus. Chimie},
     pages = {1014--1021},
     publisher = {Elsevier},
     volume = {9},
     number = {7-8},
     year = {2006},
     doi = {10.1016/j.crci.2005.09.008},
     language = {en},
}
TY  - JOUR
AU  - Yasuyuki Araki
AU  - Ryouta Kunieda
AU  - Mamoru Fujitsuka
AU  - Osamu Ito
AU  - Jiro Motoyoshiya
AU  - Hiroshi Aoyama
AU  - Yutaka Takaguchi
TI  - Photoinduced intermolecular electron transfer and energy transfer of C60 dendrimers
JO  - Comptes Rendus. Chimie
PY  - 2006
SP  - 1014
EP  - 1021
VL  - 9
IS  - 7-8
PB  - Elsevier
DO  - 10.1016/j.crci.2005.09.008
LA  - en
ID  - CRCHIM_2006__9_7-8_1014_0
ER  - 
%0 Journal Article
%A Yasuyuki Araki
%A Ryouta Kunieda
%A Mamoru Fujitsuka
%A Osamu Ito
%A Jiro Motoyoshiya
%A Hiroshi Aoyama
%A Yutaka Takaguchi
%T Photoinduced intermolecular electron transfer and energy transfer of C60 dendrimers
%J Comptes Rendus. Chimie
%D 2006
%P 1014-1021
%V 9
%N 7-8
%I Elsevier
%R 10.1016/j.crci.2005.09.008
%G en
%F CRCHIM_2006__9_7-8_1014_0
Yasuyuki Araki; Ryouta Kunieda; Mamoru Fujitsuka; Osamu Ito; Jiro Motoyoshiya; Hiroshi Aoyama; Yutaka Takaguchi. Photoinduced intermolecular electron transfer and energy transfer of C60 dendrimers. Comptes Rendus. Chimie, Volume 9 (2006) no. 7-8, pp. 1014-1021. doi : 10.1016/j.crci.2005.09.008. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2005.09.008/

Version originale du texte intégral

Fullerene functionalized dendrimers have recently been studied extensively, because they are very interesting in structural and synthetic chemistry [1–4]. The studies on syntheses and properties of various fullerodendrimers have been reported, showing various possibilities to apply to the field of supramolecular chemistry and material science [1,5–12]. Fullerene-based dendrimers have been revealed to be effective for application to artificial photosynthesis systems [13–17]. In general, introduction of dendritic branches to fullerene can improve solubility and easy fabrication into nanoparticles [16,17] and films [18]. Furthermore, by the introduction of additional functionalities to the dendrons, these new fullerodendrimers have high possibilities to be widely applied as new materials. However, there are a few reports on photochemical and photoinduced intermolecular kinetics of fullerodendrimers [19–21]. It has been revealed in our previous report that photoinduced bimolecular processes such as photoinduced electron transfer are much affected by the dendron generation [22]. This feature was beneficial to control the reactivity of the unstable states of the fullerene core such as triplet excited state, radical anion, and anion of the C60 moiety. Therefore, it is interesting to reveal further the dendrimer effects on photochemical and photophysical properties of fullerodendrimers.

In the present study, we studied fullerodendrimers in which C60 is attached to poly(amidoamine)-type dendrons through the sulfide bonds as shown in Fig. 1; fullerodendrimers are represented as C60–(GnB)2 (n = 0.5, 1.5, and 2.5). For C60–(GnB)2, since the dendron groups do not contain aromatic rings, it is expected that the dendron groups are very flexible covering the C60 core.

Fig. 1

Molecular structures.

Photoinduced electron transfer of the fullerodendrimers with the aromatic amine donors such as N,N′-tetramethylbenzidine (TMB) and N,N′-tetramethyl-p-phenylenediamine (TMPD) was investigated to disclose the dendrimer effects on bimolecular electron transfer processes. As for energy transfer, the triplet energy transfer from the fullerodendrimers to O2 and β-carotene has been studied. For these investigations, nanosecond laser flash photolysis techniques measuring the near-IR transient absorption spectra have been effectively used to follow the kinetic behavior of the triplet states of the fullerenes [23].

Fullerodendrimers, C60–(GnB)2 (n = 0.5, 1.5, 2.5), were prepared by the photochemical reactions between C60 and five equivalent disulfide derivatives of the dendron group under photoirradiation (> 300 nm) in the presence of five equivalent diphenyldiselenide in dichloromethane [12].

Optimized molecular structures of C60–(GnB)2 were calculated by the molecular dynamics at 300 K by using OPSL-AA force field in the MacroModel package [24]. In general, molecular dynamics using the OPSL-AA force field gave the fluctuation among the possible molecular structures with flexible substituents. Thus, in Fig. 2 (left side), each typical structure selected among the possible molecular structures found in the calculation is depicted for each fullerodendrimer. In C60–(G0.5B)2, most part of C60 moiety is exposed from the dendron extending in one direction. For C60–(G1.5B)2, the C60 moiety is appreciably exposed from the dendrons, which covers the C60 moiety as an umbrella. In C60–(G2.5B)2, the C60 moiety is almost covered with the dendron and the exposed part of the C60 moiety is quite small. By the fluctuations with time at room temperature, the exposed parts of the C60 moiety are further decreased as shown in Fig. 2 (right side), in which 200 structures are superimposed keeping the gravity of the C60 moiety at the same position. These fluctuated structures also suggested that the radii of C60–(GnB)2 increase with the generation of dendron group. The maximal radii (Rtotal) from the center of the C60 moiety to the edge of the dendron were evaluated to be 1.5, 1.8, and 2.1 nm for C60–(G0.5B)2, C60–(G1.5B)2, and C60–(G2.5B)2, respectively, from Fig. 2.

Fig. 2

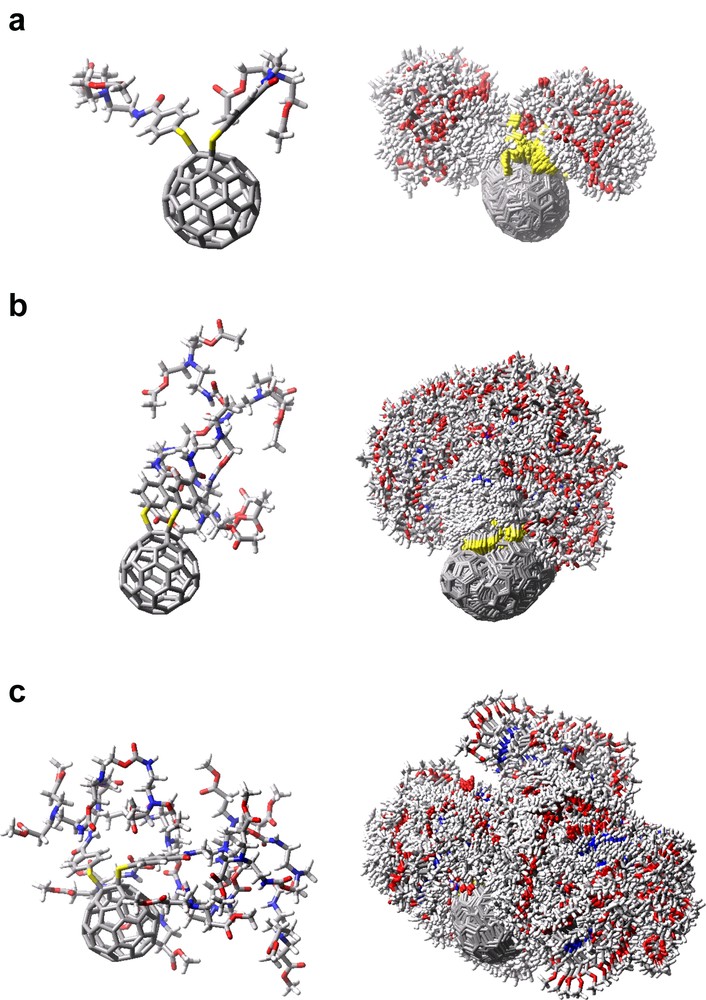
Left: Typical structures of (a) C60–(G0.5B)2, (b) C60–(G1.5B)2, and (c) C60–(G2.5B)2 founded in molecular dynamics calculation at 300 K by using OPSL-AA force field. Right: Superposition of 200 optimized structures of C60 dendrimers by molecular dynamics calculation.

Fig. 3a shows the transient absorption spectra observed by the excitation of C60–(G1.5B)2 with the laser light at 532 nm in the presence of TMPD in toluene. The transient absorption bands at 600, 730, and 1050 nm are attributed to TMPD●+, 3C60*–(G1.5B)2, and C60●––(G1.5B)2, respectively [25–30]. The absorption intensities of the bands at 600 and 1050 nm increased with concomitant decay of the band at 730 nm (inset of Fig. 3a). This observation indicates that the radical ions are generated by the electron transfer via 3C60*–(G1.5B)2. The same phenomena were also confirmed for other dendrimers and donors in toluene. Thus, the electron transfer process is described as Eq. 1, in which the radical ion–pair states between C60●––(GnB)2 and Amine●+ may depend on the solvent polarity and size of dendrimers:

C60*3-(GnB)2+Amine→kET(amine)C60● --(GnB)2+Amine●+(1)

Fig. 3

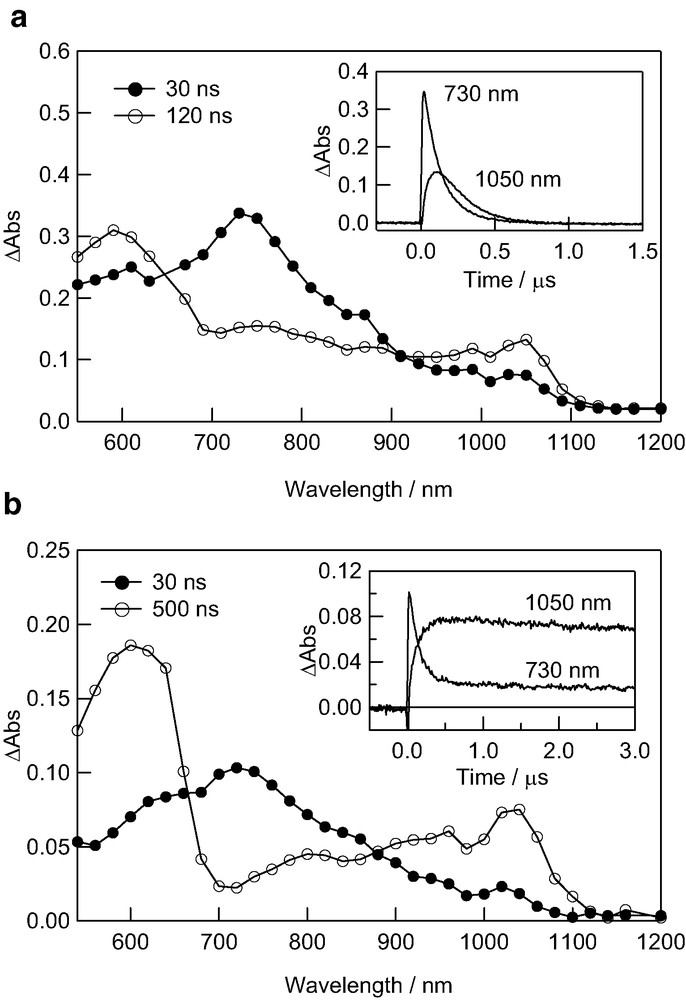
Transient absorption spectra C60–(G1.5B)2 (0.1 mM) observed by excitation with 532 nm laser light in the presence of TMPD (2.0 mM) in (a) toluene and (b) PhCN. Inset: Absorbance-time profiles.

In toluene, after reaching a maximum, the generated C60●––(G1.5B)2 begins to decay within 0.6 μs. Compared with time profiles of the pristine C60●– and 3C60* in toluene [26] in which C60●– decayed within 0.1 μs because C60●– forms the contact ion-pair with Amine●+, the observed rise and decay of C60●––(G1.5B)2 and 3C60*–(G1.5B)2 were quite slow (Fig. 3a). Thus, the bulky dendrimers may separate the radical ion–pairs, slowing down the decay of C60●––(G1.5B)2. Thus, this is one of the characteristics of the dendrimers electron-transfer systems; that is, the radical ions are present as looser radical ion-pair even in nonpolar toluene, whereas contact radical ion-pairs are present for pristine C60●– in toluene [25,26].

In PhCN (Fig. 3b), quick rise of C60●––(G1.5B) was observed with the decay of 3C60*–(G1.5B)2, although the decay of C60●––(G1.5B)2 was slower than that in toluene. In PhCN, only 10% of C60●––(G1.5B)2 decayed during 3 μs, suggesting that C60●––(G0.5B)2 and TMPD●+ are separately solvated in PhCN behaving as free radical ions, which need time to encounter longer than 100 μs in the rate of a diffusion controlled limit in PhCN under their low concentrations.

From the pseudo-first-order relation between the decay rates of 3C60*–(GnB)2 and the excess concentrations of aromatic amine donors, the bimolecular quenching rate constants (kq(amine)) were estimated as summarized in Table 1 (PhCN). In toluene, the kq(amine) values are in the region of (1–3) × 109 s–1; the variation with the dendrimer generation was quite small.

Table 1

Quenching rate constants (kq(amine)), quantum yields (ΦET(amine)), rate-constants (kET(amine)) of electron-transfer processes between 3C60*–(GnB)2 and amines, and back electron-transfer rate-constants (kBET2nd) in PhCN

C60–(GnB)2Amineskq(amine) (M–1 s–1)ΦET(amine)kET(amine) (M–1 s–1)kBET2nd/M–1 s–1
C60–(G0.5B)2TMB6.6 × 1091.006.6 × 1094.6 × 109
C60–(G0.5B)2TMPD3.7 × 1090.803.0 × 10919 × 109
C60–(G1.5B)2TMB3.5 × 1090.792.8 × 1094.3 × 109
C60–(G1.5B)2TMPD2.5 × 1090.601.5 × 10915 × 109
C60–(G2.5B)2TMB1.6 × 1090.851.4 × 1093.8 × 109
C60–(G2.5B)2TMPD1.4 × 1090.689.5 × 10830 × 109

The quantum yield of electron transfer (ΦET(amine)) via 3C60*–(GnB)2 can be evaluated from the ratio of the maximal concentration of C60●––(GnB)2 to the initial concentration of 3C60*–(GnB)2 at the amine concentrations higher than 1.0 mM (Fig. 4). Thus, the kET(amine) values were estimated by the relation of kET(amine) = ΦET(amine) × kq(amine). These values for TMB and TMPD are listed in Table 1. In toluene, appreciable changes were not observed for the ΦET(amine) values.

Fig. 4

Relations between [C60––(GnB)2]/[3C60*–(GnB)2] values and concentrations of TMPD in PhCN. (○): C60–(G0.5B)2, (■): C60–(G1.5B)2, (◊): C60–(G2.5B)2, respectively.

In PhCN, the kq(amine) values tend to decrease with an increase in the dendron generation of C60–(GnB)2 (Table 1 and Fig. 5), indicating that the dendron groups prevent the amine molecules from approaching to the C60 core, acting as a barrier [22]. For aromatic amines such as TMB and TMPD, the ΦET(amine) values of 3C60*–(G2.5B)2 are larger than those of 3C60*–(G1.5B)2, suggesting that the dendrons spreading widely act as nets catching the donor molecules. Finally, the kET(amine) values tend to decrease monotonously with the dendrimer generation as shown in Fig. 5.

Fig. 5

Variations with dendron generation of (a) kq, (b) ΦET, and (c) kE for aromatic amines in PhCN.

Since the oxidation potential of TMB is lower than that of TMPD in polar solvents [31], the electron-donor ability of TMB is expected to be higher than that of TMPD. In each 3C60*–(GnB)2, the kq(amine), ΦET(amine), and kET(amine) values obey this order in PhCN.

After the photoinduced electron transfer, back electron transfer occurs as shown in time profiles in Fig. 6. For C60●––(GnB)2 and TMPD●+ in toluene, the decay of the radical ions obeyed first-order kinetics within 0.2 μs (Fig. 6a), indicating that the radical ions are present as contact ion-pairs (Eq. 2):

(C60●--(GnB)2,  Amine●+)ion pair→kBET1stC60-(GnB)2+Amine(2)

Fig. 6

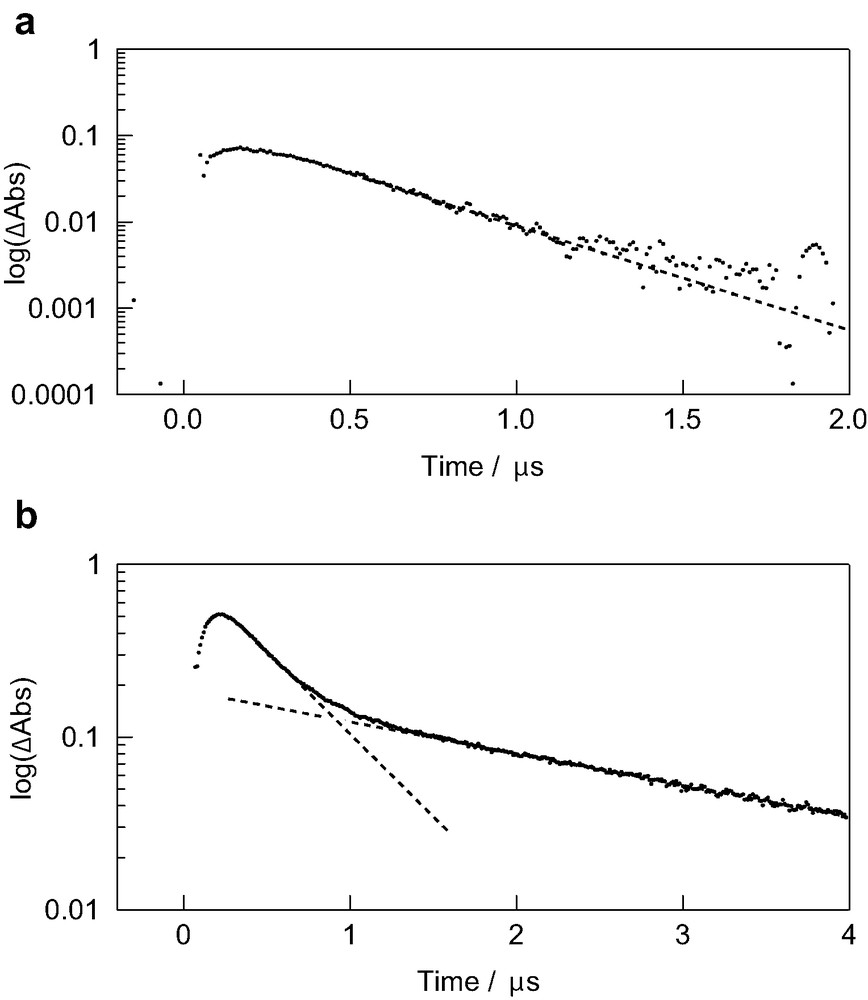
First-order plots of absorption time profiles at 1030 nm of C60––(G2.5B)2 for (a) TMPD●+ and (b) TMB●+ in toluene.

On the other hand, in the case of the radical ions of C60●––(G2.5B)2 and TMB●+ in toluene, the decay time-profile can be curve-fitted with bi-exponential functions (Fig. 6b), indicating that two kinds of the radical ion-pairs are present; one may be contact radical ion-pair and the other may be loose radical ion-pair. The variation of the kBET1st values for contact radical ion-pair with dendrimer generation was quite small, probably because the back electron transfer taking place within the oppositely charged species within the contact ion-pairs may not be affected by the size of the dendrons.

In PhCN, the decays of C60●––(GnB)2 and Amine●+ obey second-order kinetics, indicating that the back electron transfer takes place after the radical ions were solvated as free ions (Eq. 3):

(C60●--(GnB)2)solv+(Amine●+)solv→kBET2ndC60-(GnB)2+Amine(3)

The second-order rate constants (kBET2nd) were evaluated as ratio of the ε values of the absorption bands of the radical ions; by employing the reported ε values [28,32,33], the kBET2nd values were calculated as listed in Table 1. Although the evaluated kBET2nd values for the systems of C60–(GnB)2 and TMB in PhCN are smaller than those for TMPD, the dendrimer generation effect is small. The back electron transfer between the oppositely charged species may occur in the long-range over the dendrons. Furthermore, the oppositely charge species are possible to encounter with high directivity, avoiding the dendrons.

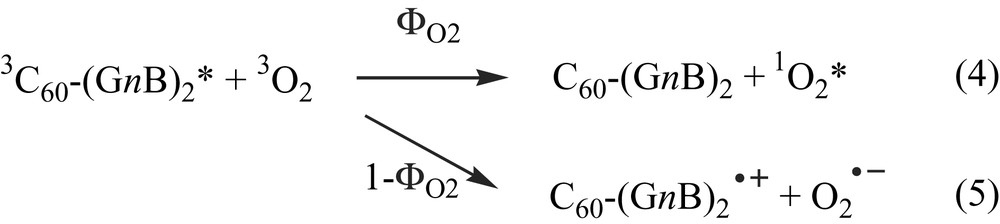
In the presence of O2, 3C60*–(GnB)2 was quenched very fast; 1O2* would be expected to be generated as Eq. 4 in nonpolar solvents, whereas electron transfer also contributes to the quenching of 3C60*–(GnB)2 in polar solvents (Eq. 5):

The bimolecular quenching rate-constants in the presence of O2 (kq(O2)) were estimated from a pseudo-first-order relation between the decay rates of 3C60*–(GnB)2 and the O2 concentrations, as listed in Table 2. The kq(O2) values in toluene are larger than the corresponding values in PhCN. In each solvent, the kq(O2) values are almost the same even by changing the dendron generation, indicating that approach of small O2 molecule to the C60 moiety is not practically hindered by the dendron. The quantum yields for the production of 1O2* (ΦO2) were determined by the comparison of the 1O2* emission with that of the pristine C60 as a standard (Fig. 7). The ΦO2 values in PhCN are smaller than those in toluene, indicating that 3C60*–(GnB)2 was partly quenched by the electron-transfer process competitive with the energy-transfer process (Eq. 4). Total quantum yields of energy-transfer and electron-transfer processes are probably constant irrespective of the dendrimer generation for small O2 molecule. With increasing the dendrimer generation, the ΦO2 values decrease causing slight decrease in the kEN(O2) values, which were obtained by kq(O2) × ΦO2 as listed in Table 2. Dendrimer generation-dependences of both ΦO2 and kEN(O2) values are smaller than those for electron transfer, indicating that the energy-transfer process is not much affected by the dendron crowding.

Table 2

Rate constants (kq(O2) and quantum yields (ΦO2) of energy transfer between 3C60*–(GnB)2 and O2

C60–(GnB)2Solventkq(O2) (M–1 s–1)ΦO2kEN(O2) (M–1 s–1)
C60–(G0.5B)2Toluene1.8 × 1090.991.8 × 108
C60–(G0.5B)2PhCN1.3 × 1090.771.0 × 109
C60–(G1.5B)2Toluene1.7 × 1090.901.5 × 108
C60–(G1.5B)2PhCN1.2 × 1090.750.9 × 109
C60–(G2.5B)2Toluene1.7 × 1090.801.4 × 108
C60–(G2.5B)2PhCN1.2 × 1090.630.8 × 109
Fig. 7

1O2* emission spectra obtained by 514-nm laser irradiation to pristine C60 and C60–(GnB)2 (0.1 mM) in (a) toluene and (b) PhCN. Absorption intensity at 514 nm was matched in each sample.

3C60*–(GnB)2 was also quenched by β-carotene as transient absorption spectra and time profiles for 3C60*–(G1.5B)2, shown as an example in Fig. 8. With the decay of 3C60*–(G1.5B)2 at 700 nm, the characteristic absorption band of 3β-carotene* increased at 520 nm. These transient absorption spectra and inserted time profiles indicate the energy transfer process from 3C60*–(GnB)2 to β-carotene as shown in Eq. 6:

C60*3-(GnB)2+β-Carotene→kENT(β-carotene)C60-(GnB)2+β-Carotene*3(6)

Fig. 8

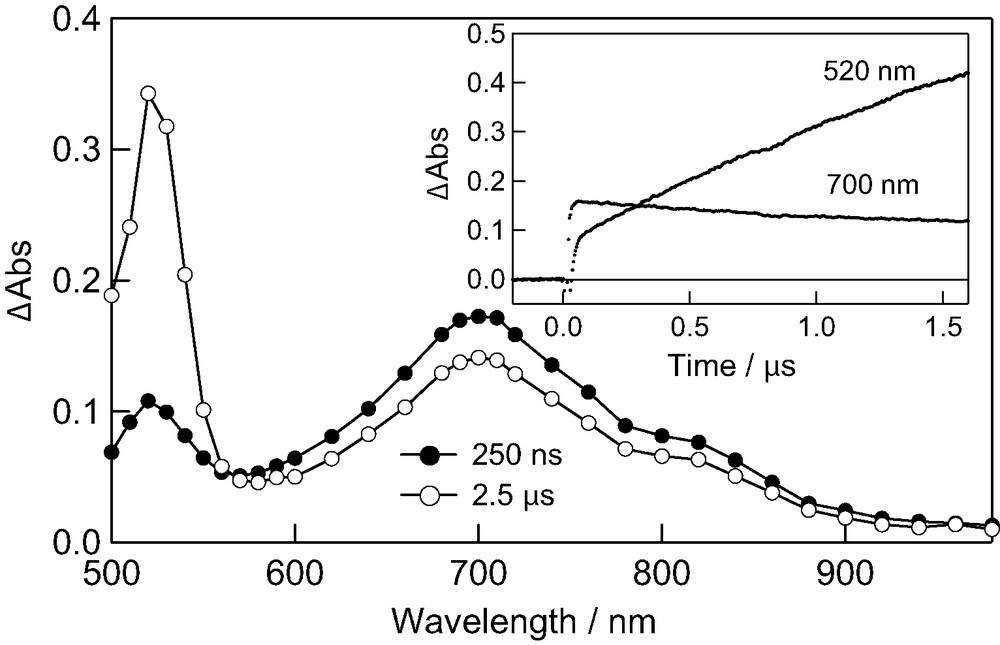
Transient absorption spectra of C60–(G1.5B)2 (0.05 mM) observed by excitation with 532 nm laser light in the presence of β-carotene (1.0 mM) in toluene. Inset: Absorbance-time profiles at 520 and 700 nm.

The bimolecular triplet-energy quenching rate-constants in the presence of β-carotene (kq(β-carotene)) were estimated from a psuedo-first-order relation between the decay rates of 3C60*–(GnB)2 and the β-carotene concentrations to be (1.7–2.9) × 108 M–1 s–1 as listed in Table 3. In both toluene and PhCN, the kq(β-carotene) values tend to decrease on going from 3C60*–(G0.5B)2 to 3C60*–(G1.5B)2, while the change was not appreciable from 3C60*–(G1.5B)2 to 3C60*–(G2.5B)2. In PhCN, photoinduced electron transfer between 3C60*–(GnB)2 and β-carotene occurs simultaneously with energy transfer as reported in our previous report for pristine C60 and β-carotene, since the radical cation of β-carotene (β-carotene●+) appeared at 960 nm in addition to the radical anion of C60 (C60●–) in the transient absorption spectra [34]. The variation of the kq(β-carotene) values with the dendrimer generation is larger than that of the kq(O2) values, probably because of the larger molecular size of β-carotene than that of O2.

Table 3

Rate constants kq(β-carotene), and kENT(β-carotene)) and quantum yields (ΦENT (β-carotene)) of energy transfer between 3C60*–(GnB)2 and β-carotene

C60–(GnB)2Solventkq(β-carotene) (M–1 s–1)ΦENT (β-carotene)kENT (β-carotene) (M–1 s–1)
C60–(G0.5B)2Toluene2.9 × 108(100)2.9 × 108
C60–(G0.5B)2PhCN2.4 × 1080.802.0 × 108
C60–(G1.5B)2Toluene2.0 × 108(100)2.0 × 108
C60–(G1.5B)2PhCN1.8 × 1080.841.5 × 108
C60–(G2.5B)2Toluene1.9 × 108(100)1.9 × 108
C60–(G2.5B)2PhCN1.7 × 1080.861.4 × 108

The quantum yields of electron transfer from 3C60*–(GnB)2 to β-carotene (ΦET(β-carotene)) were evaluated from the ratio of β-carotene●+ to 3C60*–(GnB)2, as listed in Table 3, by employing the observed transient absorption intensities and reported ε values [34]. In PhCN, the ΦENT(β-carotene) values, which are equal to (1 – ΦET(β-carotene)) [34], increase slightly with the dendrimer generation. Then, the rate constants for energy transfer (kENT(β-carotene)), which can be evaluated by Eq. 7, decrease with the dendrimer generation, although the change between 3C60*–(G1.5B)2 and 3C60*–(G2.5B)2 is small.

kENT(β-carotene)=ΦENT(β-carotene)×kq(β-carotene)(7)

When energy transfer is predominant, the variation of the observed kq(β-carotene) values with the dendrimer generation is smaller than that of the kq(amine) values in PhCN. These trends suggest that energy transfer may be carried out not only by the collision with short distance (Dexter mechanism) [35], but also by the long collisional radii with the dipolar interaction (Förster mechanism) [36].

As a first approximation, the quenching rate constants (kqpred1) of 3C60*–(GnB)2 by the encounters with molecules can be thought to be proportional to the frequency factor (Z) as represented by Eq. 8 [21];

kqpred1αZ≈σ μ-1/2(8)
where σ refers to the cross-section proportional to the square of the radius of 3C60*–(GnB)2 (σ α Rtotal2) and μ refers to the reduced mass. From molecular dynamic calculations, the ratio of the Rtotal values for 3C60*–(GnB)2 was roughly estimated as 1:1.2:1.4 for n = 0.5:1.5:2.5. The ratio of μ1/2 was calculated to be 1:1.02:1.03 for the system of 3C60*–(GnB)2 and TMPD. Therefore, the ratio of the kqpred1 values for 3C60*–(G0.5B)2 : 3C60*–(G1.5B)2 : 3C60*–(G2.5B)2 was evaluated to be 1.00:1.41:1.90. However, this ratio evaluated from Eq. 8 cannot reproduce the observed decreasing trend of the kq values for 3C60*–(GnB)2 and TMPD with the dendrimer generation. Therefore, it is necessary to introduce calibration factor (f) by fitting the calculated kqpred1 values with the observed kq(amine) as shown in Fig. 9(a); the f values can be evaluated to be 1:0.48:0.20 for 3C60*–(G0.5B)2 : 3C60*–(G1.5B)2 : 3C60*–(G2.5B)2. The f values may be explained by the exposed volume of C60 (VC60) from the dendrons. The shielding volumes of the dendrons, Vshield, can be roughly estimated by the cubic of the exclusive distance Re (= Rtotal – RC60) as defined in Fig. 10. The ratio, VC60/Vshield, was calculated to be 1:0.49:0.27 for 3C60*–(G0.5B)2 : 3C60*–(G1.5B)2 : 3C60*–(G2.5B)2, which are in good agreement with the f values evaluated from Fig. 9a. Comparing two ratios, the ratio of VC60 can be evaluated to be 1.0:0.98:0.74 for 3C60*–(G0.5B)2:3C60*–(G1.5B)2:3C60*–(G2.5B)2, which seems to match with the MD result shown in Fig. 2.

Fig. 9

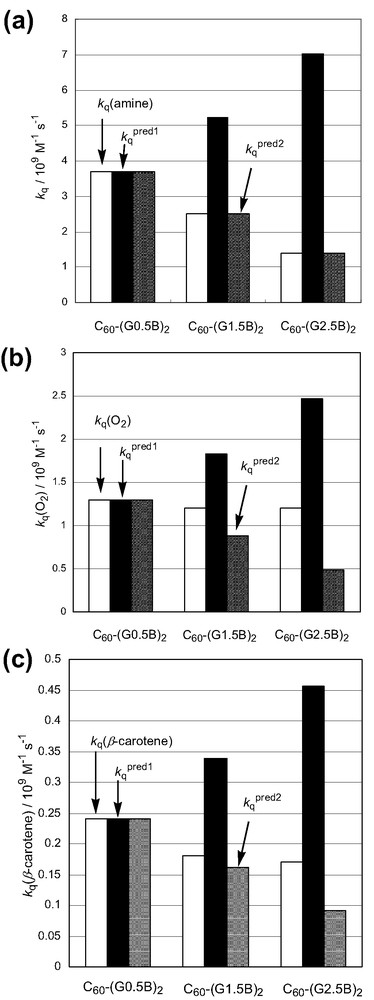
Relative reactivities for (a) kq(TMPD), (b) kq(O2), and (c) kq(β-carotene) in PhCN.

Fig. 10

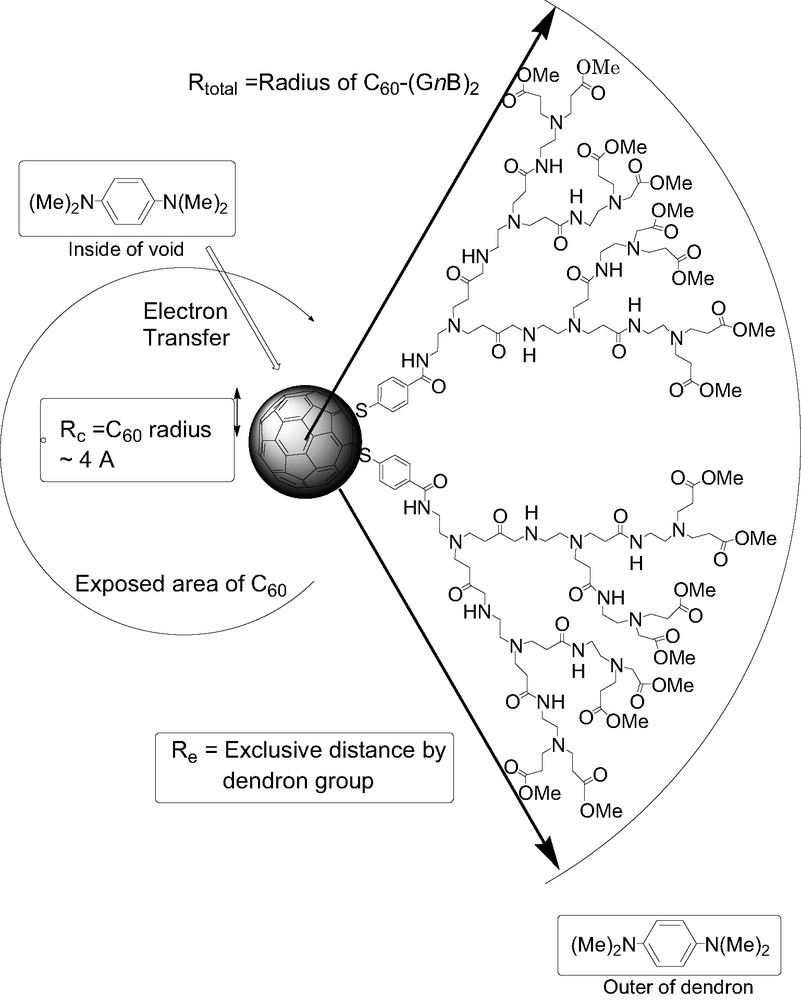
Definition of radii and exclusive distance.

By using the f values, we can predict the quenching rate constants of 3C60*–(GnB)2 with other electron donors and energy acceptors by the kqpred2 values defined by Eq. 9:

kqpred2∝kqpred1×f(9)

For electron transfer with TMB, quite good agreement was obtained between the kqpred2 values and the observed kq(TMB) values. For energy-transfer process, the results are shown in Fig. 9b and c. The ratios of the kqpred2 values were not fitted well to those of the observed kq(O2) and kq(β-carotene) values, which may be caused by the difference between the effective encounter radii of the electron-transfer process and the energy-transfer process. As mentioned before, the energy transfer from 3C60*–(GnB)2 to O2 or β-carotene may be induced by not only Dexter mechanism, but also Förster mechanism. In the latter case, energy donor and acceptor are not necessary to counter each other, resulting in the inconsistency of the kqpred2 due to the slight decrease in the ratio of the f values.

As conclusion, we revealed dendrimer generation effect on the photoinduced processes of the triplet states of fullerodendrimers, C60–(GnB)2 (n = 0.5, 1.5, and 2.5) by the nanosecond laser flash photolysis observing the transient absorption spectra in the visible and near-IR regions. Bimolecular processes such as electron transfer and energy transfer were affected by the dendron generation. In most cases, the bulky dendrons act as barrier for the reactant to approach the C60 core in fullerodendrimers. Sometimes, the dendrons act as net catching the donor molecules. From these kinetic data, the models for the bimolecular reactions of fullerodendrimers and reactants are proposed.

Acknowledgements

The authors are grateful to a financial support by a Grant-in-Aid on Scientific Research for Priority Aria (417) from the Ministry of Education, Culture, Sports, and Science.

References

[1] J.-F. Nierengarten Chem.: Eur. J., 6 (2000), p. 3667

[2] M.G. Nava; S. Setayesh; A. Rameau; P. Masson; J.-F. Nierengarten New J. Chem., 26 (2002), p. 1584

[3] J.-F. Nierengarten; N. Armaroli; G. Accorsi; Y. Rio; J.-F. Eckert Chem.: Eur. J., 9 (2003), p. 36

[4] M. Gutierrez-Nava; G. Accorsi; P. Masson; N. Armaroli; J.-F. Nierengarten Chem.: Eur. J., 10 (2004), p. 5076

[5] B. Dardel; D. Gullion; B. Heinrich; R. Deschenaux J. Mater. Chem., 11 (2001), p. 2814

[6] J.-F. Eckert; J.-F. Nicoud; J.-F. Nierengarten J. Am. Chem. Soc., 122 (2000), p. 7467

[7] C.J. Hawker; K.L. Wooley; M.J. Fréchet J. Chem. Soc., Chem. Commun., 8 (1994), p. 925

[8] A. Herzog; A. Hirsch; O. Vostrowsky Eur. J. Org. Chem., 1 (2000), p. 171

[9] F. Diederich; R. Kessinger Acc. Chem. Res., 32 (1999), p. 537

[10] J.-F. Nierengarten; J.-F. Eckert; Y. Rio; M.P. Carreon; J.-L. Gallani; D. Guillon J. Am. Chem. Soc., 123 (2001), p. 9743

[11] M. Schwell; N.K. Wachter; J.H. Rice; J.-P. Galaup; S. Leach; R. Taylor; R.V. Bensasson Chem. Phys. Lett., 339 (2001), p. 29

[12] Y. Takaguchi; K. Saito; S. Suzuki; K. Hamada; K. Ohta; J. Motoyoshiya; H. Aoyama Bull. Chem. Soc. Jpn, 75 (2002), p. 1347

[13] D. Kuciauskas; P.A. Liddell; S. Lin; S.G. Stone; A.L. Moore; T.A. Moore; D. Gust J. Phys. Chem. B, 104 (2000), p. 4307

[14] D.M. Guldi; A. Swatz; C. Luo; R. Gomez; J.L. Segura; N. Martín J. Am. Chem. Soc., 124 (2002), p. 10875

[15] M.-S. Choi; T. Aida; H. Luo; Y. Araki; O. Ito Angew. Chem., Int. Ed. Engl., 42 (2003), p. 4060

[16] T. Sasabe; P.V. Kamat; M.A. Absalom; Y. Kashiwagi; J. Sly; M.J. Crossley; K. Hosozumi; H. Imahori; S. Fukuzumu J. Phys. Chem. B, 108 (2004), p. 12865

[17] T. Hasobe; P.V. Kamat; V. Troiani; N. Solladie; T.-K. Kim; S.-K. Kim; D. Kim; A. Kongkanand; S. Kuwabata; S. Fukuzumi J. Phys. Chem. B, 109 (2005), p. 19

[18] C. Hirano; T. Imae; S. Fujima; Y. Yanagimoto; Y. Takaguchi Langmuir, 21 (2005), p. 272

[19] I. Texier; M.N. Berberan-Santos; A. Ferorov; M. Brettreich; H. Schonberger; A. Hirsch; S. Leach; E. Bensasson J. Phys. Chem. A, 105 (2001), p. 10278

[20] M. Martin; S. Atalick; D.M. Guldi; H. Lanig; M. Brettreich; S. Burghardt; M. Hatzimarinaki; E. Racvanelli; M. Prato; R. van Eldik; A. Hirsch Chem. Eur. J., 9 (2003), p. 3867

[21] X. Luo; M.-S. Choi; Y. Araki; O. Ito; T. Aida Bull. Chem. Soc. Jpn, 78 (2005), p. 371

[22] R. Kunieda; M. Fujitsuka; O. Ito; M. Ito; Y. Murata; K. Komatsu J. Phys. Chem. B, 106 (2002), p. 7193

[23] A.S.D. Sandanayaka; K. Ikeshita; N. Watanabe; Y. Araki; Y. Furusho; N. Kihara; T. Takata; O. Ito Bull. Chem. Soc. Jpn, 78 (2005), p. 1008

[24] F. Mohamadi; N.G.J. Richards; W.C. Guida; R. Liskamp; M. Lipton; C. Gaufield; G. Chang; T. Hendrickson; W.C. Still J. Comput. Chem., 11 (1990), p. 440

[25] O. Ito; Y. Sasaki; Y. Yoshikawa; A. Watanabe J. Phys. Chem., 99 (1995), p. 9838

[26] Y. Yahata; Y. Sasaki; M. Fujitsuka; O. Ito J. Photosci., 6 (1996), p. 117

[27] M. Fujitsuka; O. Ito; T. Yamashiro; Y. Aso; T. Otsubo J. Phys. Chem. A, 104 (2000), p. 4876

[28] C. Luo; M. Fujitsuka; A. Watanabe; O. Ito; L. Gan; H. Huang; C.-H. Huang J. Chem. Soc., Faraday Trans., 94 (1998), p. 527

[29] B. Ma; Y.-D. Sun; S.-K. Kim J. Am. Chem. Soc., 114 (1992), p. 4429

[30] D.M. Guldi; M. Prato Acc. Chem. Res., 33 (2000), p. 695

[31] A.S.D. Sandanayaka; Y. Araki; C. Luo; M. Fujitsulka; O. Ito Bull. Chem. Soc. Jpn, 77 (2004), p. 1313

[32] K.H. Hausser; J.N. Murrell J. Chem. Phys., 27 (1957), p. 500

[33] G.J. Kavarnos; N.J. Turro Chem. Rev., 86 (1986), p. 401

[34] Y. Sasaki; M. Fujitsuka; A. Watanabe; O. Ito J. Chem. Soc., Faraday Trans., 93 (1997), p. 4275

[35] D.L. Dexter J. Chem. Phys., 21 (1953), p. 836

[36] T. Förster Naturwissenschaften, 33 (1946), p. 166

Comments - Policy

Articles of potential interest

Photoinduced electron-transfer and magnetic field effects on the dynamics of the radical pair in a C60 cluster–phenothiazine system

Hiroaki Yonemura; Norihiro Kuroda; Shinya Moribe; ...

C. R. Chim (2006)

Photoinduced electron-transfer and magnetic-field effects on the decay rates of photogenerated biradicals in a phenothiazine-C60 linked compound with six methylene groups: temperature dependence

Shinya Moribe; Hiroaki Yonemura; Sunao Yamada

C. R. Chim (2006)

Spin-labeled fulleropyrrolidines

Carlo Corvaja; Fosca Conti; Lorenzo Franco; ...

C. R. Chim (2006)