1 Introduction
Polynuclear transition-metal complexes (PTMCs) are the focus of very active research and have been studied for many decades. During the last decade research concerning PTMCs has been intensified after the observation of exciting magnetic properties in some of those [1]. In general the magnetic behavior of isolated PTMCs is governed by the Heisenberg–Dirac–van Vleck isotropic exchange Hamiltonian [2]:
| (1) |
However, non-Heisenberg interactions such as single-ion anisotropy, dipolar interactions, etc. have prominent role in modulating the magnetic behavior of a PTMC. For instance single-ion anisotropy is the main factor responsible for the energy barrier for the reversal of magnetization observed in single molecule magnets [3].
Among the simplest PTMCs with nuclearity higher than the trivial case of 2 are the trinuclear clusters of the general formula {M3O}n+ where M = FeIII (S = 5/2), CrIII (S = 3/2), CuII (S = 1/2). Their magnetic properties have been the subject of extensive studies over decades [4]. In the following, we briefly outline the main conclusions drawn from these studies. Their magnetic properties are governed by the Heisenberg–Dirac–van Vleck isotropic exchange Hamiltonian (Eq. (1)) with i, j = 1, 2, 3. In many cases the room-temperature structure reveals an equilateral configuration with the metal ions in a common octahedral environment and equal metal–metal distances. Straightforward magnetostructural correlations would suggest that the exchange coupling constants Jij in Hamiltonian (Eq. (1)) are all equal. Unexpectedly, however, it was soon realized that in order to interpret the magnetic susceptibility versus temperature measurements at least two different Jij's are required [4].
For a coupled system comprising three half-integerspin centers there are two states which are characterized by total spin St = 1/2. In the case of equilateral configuration these two states are degenerated and constitute the ground state of the system. The non-equivalence of Jij's lifts this degeneracy leading to a separation of the two St = 1/2 states. Separation of these two states has been observed by inelastic neutron scattering experiments in many {M3O}n+ clusters [5] further justifying the necessity for a lower than D3 symmetry. The possibility of a magnetic Jahn–Teller effect has been proposed, in which a small structural distortion occurring in the ground state of any antiferromagnetially coupled trinuclear complex removes the 3-fold symmetry [6]. Distributions of exchange coupling constants, implying dynamic or static structural distortions were also shown to lead to an apparent lowering of the D3 symmetry [7].
Electron paramagnetic resonance (EPR) spectroscopy was also used in the study of trinuclear clusters. One interesting finding in the case of Fe [8], Cr [9] and recently Cu [10] complexes is that the St = 1/2 ground state is characterized by a remarkable anisotropy. This anisotropy is not expected within the isotropic exchange coupling of Eq. (1). In order to account for these effects Hamiltonian (Eq. (1)) was enhanced by the antisymmetric exchange interaction [8–10].
| (2) |
Trinuclear clusters may be viewed as the lowest nuclearity members of the superfamily of antiferromagnetic rings. The magnetic properties of this class of molecules have attracted a great deal of interest during the last years. In some even-numbered rings based on Cr and Fe, interesting phenomena were observed such as repulsion of energy levels by the application of external magnetic fields [11]. The involvement of antisymmetric exchange interactions was investigated as a possible origin for these effects. Although these even-numbered rings are characterized by integer spin whereas the trinuclear complexes are half-integer spin systems, the study of the latter may be used in order to obtain estimations of the magnitude of |d| by applying appropriate techniques.
Recently we reported on the magnetic properties of a complex with the general formula [Fe6Na2O2(O2CPh)10(pic)4(EtOH)4(H2O)2](ClO4)2·2EtOH (1) containing two non-interacting {Fe3O}7+ cores [12]. The ferric sites in the triangles are not equivalent. Two iron sites have an O5N coordination whereas one has an O6 environment. From this point of view, this cluster has a lower than D3 symmetry and non-equivalent Jij constants are anticipated. Along with bulk magnetic susceptibility measurements we applied Mössbauer spectroscopy in the presence of external magnetic fields and X-band EPR spectroscopy in frozen solutions at liquid helium temperatures in order to describe the magnetic structure of 1 in the ground state. The results have been interpreted by a combination of distribution of the exchange interaction constants and the presence of antisymmetric exchange interaction.
In the present manuscript, we analyze the X-band EPR spectra of powdered solid samples of 1. Furthermore, we discuss on the effects of AE on the Mössbauer spectra. Finally, we use the model based on distributions in Jij's in order to reproduce the magnetically perturbed Mössbauer spectra from 1 in the solid state.
2 Materials and methods
Details for the synthesis of compound 1 are given elsewhere [12]. For the magnetic measurements, and X-band EPR and Mössbauer spectroscopic studies, powdered samples were used.
X-band EPR measurements were performed with a Bruker ER 200D instrument equipped with ESR-9 Oxford cryostat and an Anritsu microwave frequency counter. Mössbauer spectra were recorded with the constant acceleration method. For liquid helium temperatures, an Oxford cryostat equipped with a superconducting magnet allowing application of 0–6 T fields perpendicular to the γ-rays was used.
Simulations of the EPR spectra were performed with software provided to us by Prof. Michael P. Hendrich and with home-written routines. Simulations of the Mössbauer spectra were performed with the software WMOSS from WEB Research and with home-written routines.
3 Results
3.1 Description of the structure
Details for the synthesis and crystallographic characterization of 1 are reported elsewhere [12]. In this section we provide a short structural description focusing on the {Fe3O}7+ core (Fig. 1). The complex cation is centrosymmetric, and contains two symmetry-related {Fe3O(O2CPh)5(pic)2(H2O)} subunits, connected by two sodium cations, through two μ3:η1:η2:η2 and two μ:η1:η2:η2 bridging chelating picolinate anions. The two subunits are related to each other by an inversion center (−x, −y, 1 − z), situated between the two sodium atoms. Inside each subunit, the three iron atoms are held together by one μ3-oxide and five syn:syn μ-benzoate bridges, like in simple ‘basic iron carboxylates’.
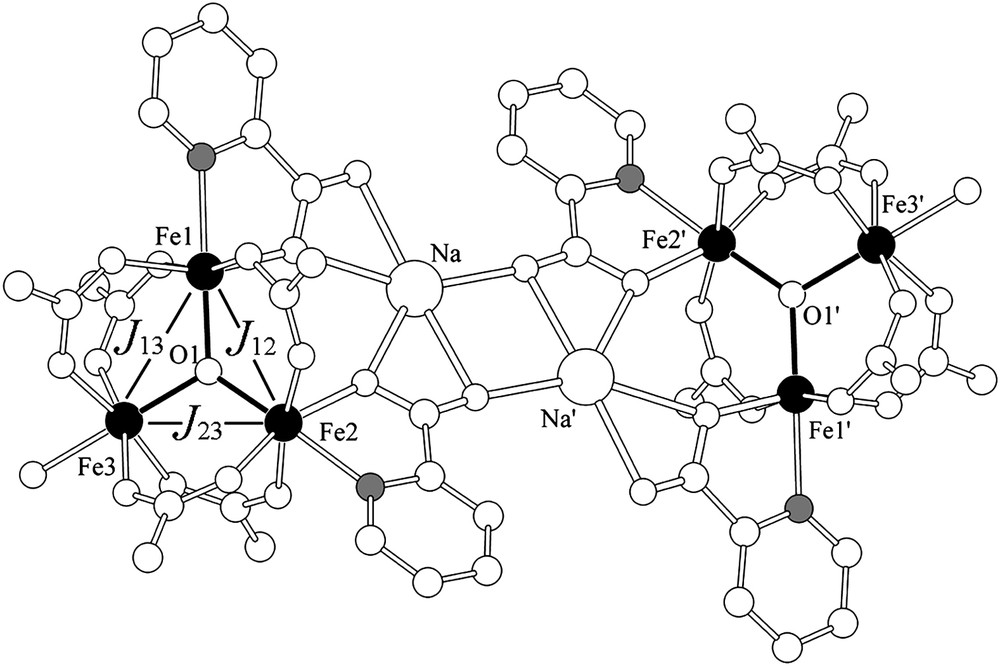
Simplified structure of 1. Black spheres represent the ferric ions. The nitrogen atoms attached to the two ferric ions in each core are shown in gray.
The iron cations are in distorted octahedral coordination environments with NO5 donor sets for Fe(1) and Fe(2) and a O6 donor set for Fe(3). The Fe–L bonds are in the range 1.917(12)–2.203(13) Å for Fe(1), 1.897(7)–2.185(7) Å for Fe(2) and 1.933(9)–2.098(9) Å for Fe(3). The shortest bonds are the Fe–O(1)oxo ones, whereas the longest ones are those in trans position to O(1) (trans effect). The Fe3O core is planar, with a sum of Fe–O–Fe angles equal to 359.26°.
3.2 Magnetic measurements
Magnetic susceptibility versus temperature measurements were performed on a powdered sample of 1 in the 2.0–300 K temperature range [12]. Here we briefly present the main findings. Although the compound contains two [Fe3O]7+ cores per molecule, and in agreement with their large separation (∼10 Å), the magnetic data were well analyzed with two independent trinuclear units. For each one the Heisenberg–Dirac–van Vleck isotropic exchange Hamiltonian Eq. (1) was considered:
| (3) |
The fitting procedure yielded two sets of Jij triads that reproduced the data. Solution A yields J12 = J13 = J = −27.4 cm−1 and J23 = J′ = −20.9 cm−1 and solution B J23 = J12 = J = −22.7 cm−1 and J13 = J′ = −31.6 cm−1. The existence of two minima in the fitting process of the magnetic susceptibility data from trinuclear clusters was recognized early [7,13]. The obtained average value of ca. −25 cm−1 falls in the range of {Fe3O}7+ clusters [4].
We mention here that efforts to simulate the data with an equilateral model (three equal Jij values) do not yield satisfactory results. In the present case the existence of at least two different values for the exchange constants may be anticipated since the ferric sites have two different environments in a 2:1 ratio. It is reminded, however, that in trinuclear clusters with an almost perfect D3 symmetry, analysis of the magnetic susceptibility data requires an isosceles configuration rather than an equilateral one [4]. Incorporation of a rhombic model, with three non-equivalent Jij values also yields satisfactory simulations for the bulk magnetic susceptibility measurements. Involvement of three different Jij constants constitutes an over-parameterization for the analysis of the bulk magnetic susceptibility measurements. Also, possible distributions of these constants cannot be discriminated by such bulk measurements, while they are revealed by the spectroscopic methods presented below.
3.3 X-band EPR spectroscopy
In Fig. 2 we show an X-band EPR spectrum from a powdered sample of 1 at 4.2 K. The spectrum exhibits a signal at g ∼ 4.3. Its temperature dependence follows approximately a Curie law (not shown) and it is attributed to high-spin ferric impurities. The Mössbauer spectra presented below indicate that the contribution of ferric impurities do not account for more than 2%. Of more importance is a strong signal at g ∼ 2.0. We attribute this signal to the St = 1/2 ground state of the complex in consistency with the analysis of magnetic susceptibility measurements. The signal is asymmetric and shares similarities with EPR signals from other antiferromagnetically coupled triferric complexes (especially Ref. [8b]) with St = 1/2 ground states.
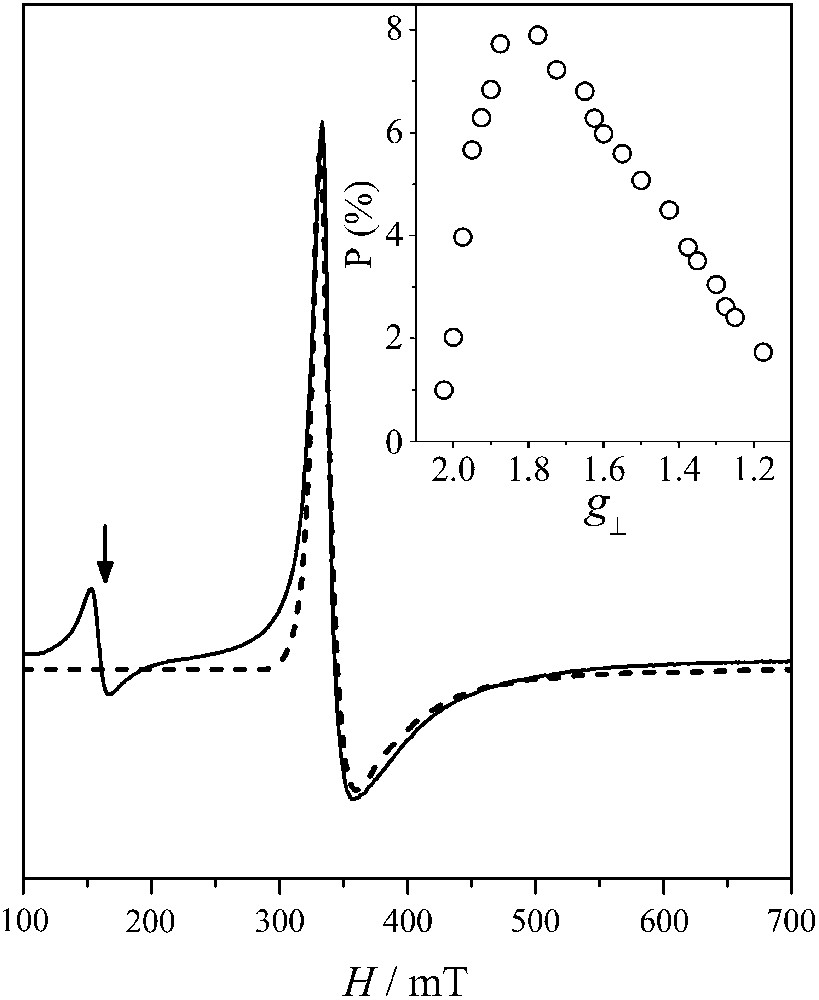
X-band EPR experimental and theoretical spectrum of powdered sample of 1 at 4.2 K. The arrow indicates the position of a g ∼ 4.3 signal attributed to ferric impurities. EPR conditions: microwave power, 2 mW, mod. ampl. 10 Gpp, microwave frequency, 9.41 GHz. Inset: the distribution of the axial species resulting from the simulation procedure described in the text.
In order to reproduce the spectrum we assume an S = 1/2 system with axial anisotropy, namely g∥ = g1 ≠ g2 = g3 = g⊥. We further assume a distribution of such species by calculating a large number of axial spectra with g∥ = 2.01 and g⊥ < 2.0. Then, we determine the contribution of each spectrum to the experimental one. The results are shown in Fig. 2 with the contribution of each axial species shown in the inset. A relatively broad maximum is observed at g ∼ 1.80–1.70.
In the case of FeIII (S = 5/2) trimers, since the intrinsic g-tensor is isotropic (close to 2.00) the anisotropy in the ground state of the exchange-coupled trimer originates from non-Heisenberg exchange interactions and single-ion zero-field splitting (ZFS) terms. The non-Heisenberg interactions include dipolar and pseudo-dipolar exchange interactions and antisymmetric exchange. Qualitative arguments indicate that the latter is more important [12]. The effect of this term is to induce axial anisotropy (gx = gy = g⊥ < gz = g∥). It is found that g∥ is, to first order, independent of |d| whereas g⊥ depends on the parameters |d| and the energy difference σ of the two lowest St = 1/2 states. For an isosceles configuration σ = 6 |J − J′| In the case of well isolated St = 1/2 states an analytical expression has been derived [8a]
| (4) |
| (5) |
In order to reproduce the line-shape of the spectrum we used an effective distribution of the g⊥ values. We attribute this behavior to distributions in the parameters |d| and Jij. The presence of such distributions is consistent with the Mössbauer results to be presented below. We also studied the EPR spectra from frozen acetone solutions of 1 [12]. A strong, highly anisotropic S = 1/2 was observed, which was characterized by a well-defined g∥ feature and a broad distribution in g⊥. Frequently, intermolecular interactions result in distortions of the EPR spectra in the solid state. Therefore, the different line-shapes of the EPR spectra from solid state and acetone glass samples may indicate such interactions. Moreover, the distributions of the parameters σ and |d| may be affected upon dissolution resulting in different distributions profiles for g⊥.
3.4 Mössbauer spectroscopy
Mössbauer spectra recorded from powdered samples of 1 in zero magnetic field and in the 4.2–300 K temperature range give rise to a relatively broad, asymmetric quadrupole-split doublet with an average isomer shift, δ = 0.50 mm s−1 and an average quadrupole splitting, ΔEQ = 0.60 − 0.70 mm s−1. These parameters are typical of FeIII (S = 5/2) in an octahedral environment with N/O ligands. Fig. 3 shows the Mössbauer spectra recorded in the presence of external magnetic fields applied perpendicular to the γ-rays. The spectra cannot be reproduced assuming isolated ferric FeIII (S = 5/2) ions. In such a case a characteristic sextet is expected spanning a large spectral region with characteristic outer peaks well outside the region of the observed spectra. Moreover, from the Mössbauer spectra, we estimate that monomeric ferric impurities cannot account for more than 2% of total iron.
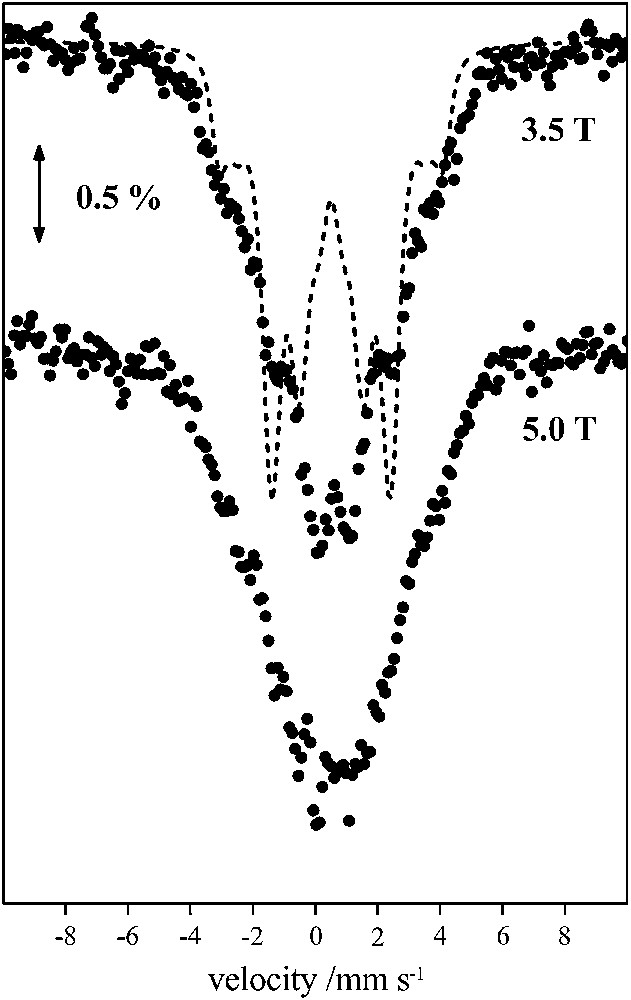
A 4.2 K Mössbauer spectra of 1 in the presence of external magnetic fields applied perpendicular to the γ irradiation. The solid line superimposed in the 3.5 T spectrum is the theoretical spectrum obtained for ω = 1.0 (see text).
The Mössbauer properties of coupled trinuclear FeIII complexes have been discussed earlier [14]. For each iron site, the total magnetic field is given by the relationship
| (6) |
| (7) |
In the context of the isotropic HHDvV Hamiltonian, Aiso,i depends on ci and this parameter depends on the relationship between the Jij values and more specifically on the parameter ω [15]:
| (8) |
In Fig. 4 we plot the dependence of Aiso,i on ω for ai = −30 MHz. In principle determination of the hyperfine values through analysis of the Mössbauer spectra and use of the plot of Fig. 4 may lead to the determination of ω, and the relationship between the Jij values may be obtained through Eq. (8).

The dependence of Aiso,i on the parameter ω. The solid lines are obtained for ai = −30 MHz. The labelling corresponds to the case with Jij < 0, and J23 > J12 > J13.
The fitting of the magnetic susceptibility data yielded two sets of triads for the parameters Jij. These two sets of exchange interactions correspond to ω = 0 and ω = 1.0. The corresponding effective hyperfine tensors Ai for the three ferric sites are (+20, −70, +20) MHz for ω = 0 and (+50, −40, −40) MHz for ω = 1, respectively. In Fig. 3 superimposed on the experimental 3.5 T spectrum is a theoretical one assuming three ferric sites with isotropic hyperfine tensors with values derived for ω = 1. Clearly this approximation fails to reproduce the experimental spectrum. Similar results are obtained for the other limiting case, with ω = 0 and these observations apply for the 5.0 T spectrum as well.
A closer examination of the spectra reveals an enhanced absorption for velocities close to 0 indicating that a particular ferric site should be characterized by a relatively small value of the effective hyperfine tensor. Examination of Fig. 4 reveals that small hyperfine values (|A| < 10 MHz) correspond to ω values in the 0.2–0.5 region for site 3, and from Eq. (8) it is inferred that the isosceles model with two equal Jij values is not appropriate. Therefore, qualitatively the Mössbauer spectra favor a rhombic configuration for the triangular complex with three non-equal Jij values. With such a model the main features of the spectra, such as the position of the lines may be reproduced. However, unreasonable line-widths (Γ ∼ 1.00 mm s−1) are required to reproduce the line-shapes of the spectra.
In order to reproduce the Mössbauer spectra we have considered two different models. In the first model, we assume that the ferric sites are characterized by anisotropic hyperfine tensors. In the second model we assume a distribution of the exchange coupling constants. The results from the two models are presented separately.
3.4.1 Anisotropic hyperfine tensors
The line-shapes of the spectra may be reproduced if we allow for anisotropic effective hyperfine tensors. Because three sets of triads (Aix, Aiy, Aiz) for the hyperfine tensors are required, within the present experimental accuracy a unique solution cannot be obtained. An indicative set of parameters that reproduces the spectra [12] is (+20, +46, +44) Hz, (−41, −78, −80) MHz and (+0.8, +5, +3) MHz.
Although indicative, these values give an estimate for the degree of anisotropy of the effective hyperfine tensor required to reproduce the spectra. Such an anisotropy is not expected for a coupled system comprising high-spin ferric sites within the context of isotropic exchange interactions. Non-Heisenberg interactions induce such anisotropies through mixing of the St = 1/2 ground state with states with St ≥ 1/2. As in the case of EPR we consider only the case of antisymmetric exchange.
The role of AE in the Mössbauer spectra from trinuclear clusters was examined theoretically [16] and implemented experimentally in the case of [3Fe-4S]1+ clusters encountered in enzymes [15]. Through the mixing of the pure St states, AE induces an anisotropy on Ai. It is found that this anisotropy is of axial character with |Ax| = |Ay| = |A⊥| > |Az| = |A∥|. We have calculated the anisotropy induced on the Ai values by using a home-written program, which numerically diagonalizes the Hamiltonian of Eq. (5) taking into consideration the manifolds with St up to 5/2. In Fig. 5 we plot the dependence of the components of the Ai tensors on the parameter |d| for a representative Jij triad.
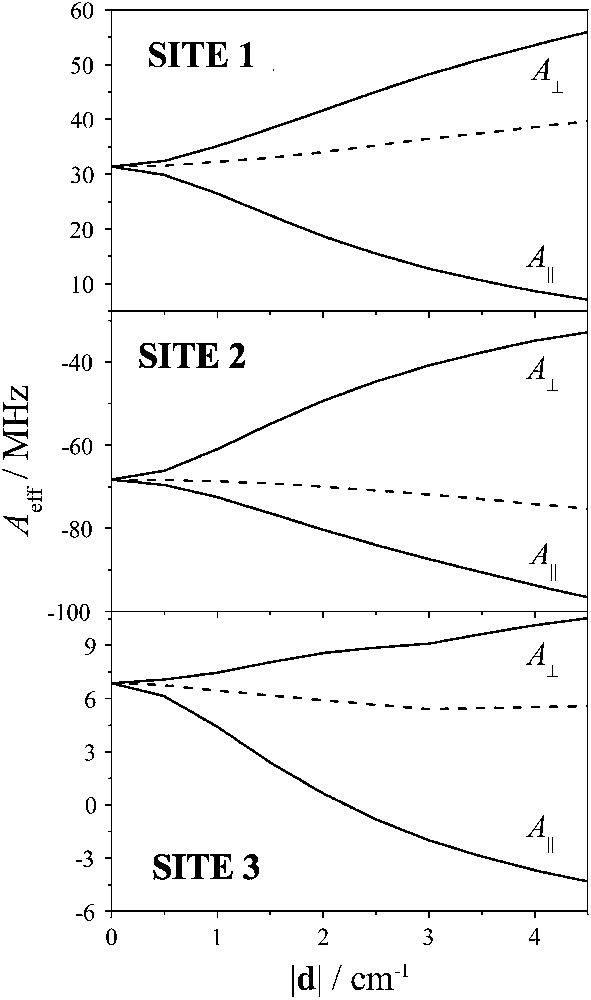
Dependence of anisotropy of the effective hyperfine tensors for each ferric site on the antisymmetric exchange parameter |d| for Jij = (J12, J13, J23) = (−22.5, −27.4, −20.9) cm−1. Dotted lines represent the dependence of Aiso,i.
In the same plot we have included the dependence of the parameter Aiso,i = (2A⊥,i + A∥,i)/3. We see that the dependence of this parameter on |d| is less pronounced. This has the consequence that the obtained Aiso,i values may be used through the plot of Fig. 4 to estimate quite safely the parameter ω.
Of special importance regarding Mössbauer spectroscopy is the fact that AE induces also a “canting” of the local magnetic moments for each site with respect to the external magnetic field because in this case the expectation value of the local spin operators along directions perpendicular to the external magnetic field is non-zero [16]. It is noted here that only AE (Eq. (2)) has such an effect in isolated PTMCs. This canting would have severe effects on the Mössbauer spectra. These effects, however, would be hardly discernible in the present case with overlapping sub-spectra from three ferric sites.
3.4.2 Distribution of isotropic hyperfine tensors
In this model we assume that the compound is characterized by inhomogeneities with the triangles adopting a variety of geometries. This inhomogeneity results in distributed Jij triads and this leads to a distribution of the ω values. For each ω value there is a certain set of three hyperfine tensors (Fig. 4) and the magnetically perturbed Mössbauer spectra consists of the superposition of the sub-spectra corresponding to each case. We therefore calculated a number of theoretical spectra for 1 ≥ ω ≥ 0.5. Next, we determined the appropriate distribution of these spectra that better reproduce the experimental ones. The simulations obtained in this way are shown in Fig. 6 and the resulting distribution in Fig. 7.
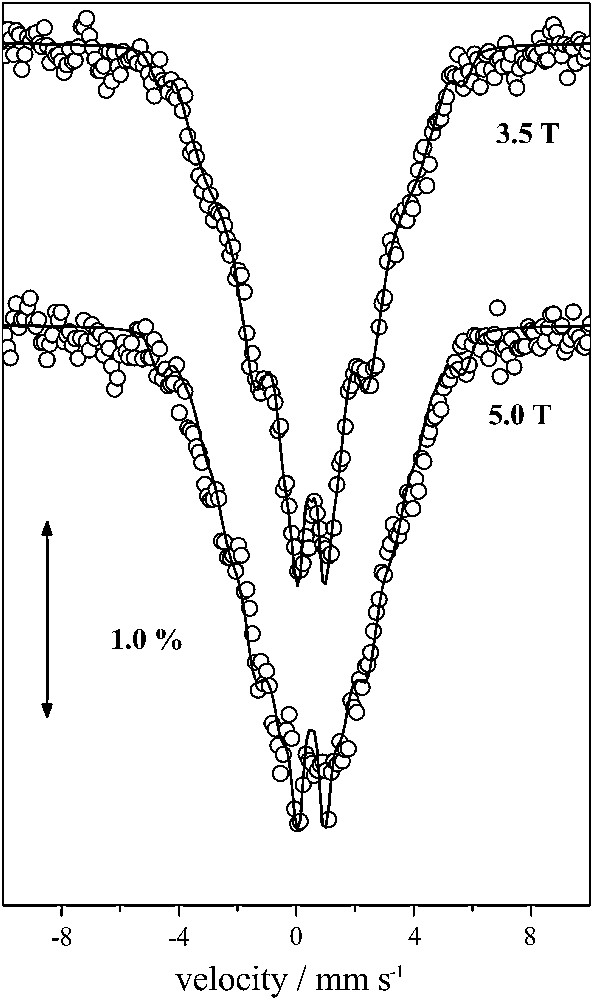
Simulations of the magnetically perturbed Mössbauer spectra at 4.2 K obtained by the model of distributed hyperfine tensors.

Distribution of the sub-spectra corresponding to various values of the parameter ω used to obtain the simulations of Fig. 6.
The profile of this distribution illustrates that the Mössbauer spectra cannot be reproduced by a well-defined value of parameter ω. In such a case a relatively narrow peak at a single value of ω is expected. On the contrary, Fig. 7 indicates a significant distribution for this parameter. The profile indicates the existence of two broad maxima at 0.1 and 0.35. It appears also that species with values larger than 0.5 do not contribute to the distribution.
4 Discussion
In the present work we compare the results from three different techniques in the study of the magnetic properties of a compound containing the {Fe3O}7+ core. All of these techniques indicate an St = 1/2 ground state for this system. Each technique, however, is sensitive to different parameters regarding the magnetic structure. (a) The magnetic susceptibility measurements are consistent with isosceles configurations with J23 = J12 > J13 or J13 = J12 < J23. (b) EPR in the solid state and in frozen solutions indicates remarkable anisotropy for the ground state accompanied by a significant degree of inhomogeneity. (c) The Mössbauer spectra in the presence of external magnetic fields are consistent with either anisotropic hyperfine interactions or with distributions of the hyperfine tensors.
Clearly, the combination of the results from these techniques has to be considered in order to obtain a more accurate and consistent description of the magnetic behavior of trinuclear complexes. First, we note that from the magnetic susceptibility data the magnitude of the average isotropic exchange interactions may be determined quite precisely. These measurements are also helpful in discriminating an equilateral configuration (with equal Jij constants) from lower symmetries. These measurements, however, cannot discriminate the existence of rhombic geometries (three different Jij values) or distributed J values.
The presence of non-Heisenberg exchange interactions with an order of magnitude smaller than the isotropic exchange interactions cannot be determined from routine magnetic susceptibility measurements. EPR spectroscopy is very useful since such interactions result in anisotropic effective g-values. Especially in the case of iron or chromium compounds the induced anisotropy exceeds significantly the intrinsic anisotropy of the g-tensor of the individual ions. The determination of non-Heisenberg interactions can therefore be attained by EPR measurements.
In the case of {Fe3O}7+ compounds Mössbauer spectroscopy may be used in order to monitor the local fields on each ferric site. These fields depend critically on the relationship between the isotropic exchange interactions (Eq. (8) and Fig. 4) and from this point of view, Mössbauer spectroscopy can complement the magnetic susceptibility measurements. For the present compound the results from this technique indicate that rhombic geometries are more appropriate. This feature cannot be identified from the magnetic susceptibility data. The details of the Mössbauer spectra can be reproduced by either a J-strain mechanism or anisotropic interactions. Incorporating the results from EPR spectroscopy leads to conclude that both mechanisms are present.
In the present work we have discussed the effects of the antisymmetric exchange on the EPR and Mössbauer spectroscopic behavior of trinuclear {Fe3O}7+ clusters. Our results show that the most sensitive technique to probe the presence of AE is EPR. EPR spectroscopy has revealed the role of AE in other triferric clusters [8], in trinuclear clusters of CrIII [9] and recently of CuII [10]. The role of AE has been revealed by EPR spectroscopy in other coupled systems especially dimers [17]. For such dimeric systems, however, the ground state is paramagnetic rendering them suitable for conventional EPR studies. Recently, AE has been assumed to play an important role in the energy level repulsion observed in antiferromagnetic rings in the presence of external magnetic fields. Direct evidence for the presence of this interaction is, however, missing. Since the ground state of such structures is diamagnetic, conventional X-band EPR spectroscopy is not appropriate for this purpose. However, in the case of ferric compounds, Mössbauer spectroscopy in the presence of external magnetic fields would be suitable. This has been demonstrated in the case of the diferric center of the hydroxylase component of the protein methane monooxygenase and of a synthetic analog [18]. In that case application of external magnetic fields of up to 8 T induced special features in the Mössbauer spectra that were indicative of canting of the local magnetic moments demonstrating thus the presence of antisymmetric exchange interaction.



Vous devez vous connecter pour continuer.
S'authentifier