1 Introduction
The geochemical behaviour of actinides have been extensively studied for understanding uranium and thorium ore deposits, and more recently for assessing the environmental impact of the possible disposal of wastes that contain Pa, Np, Pu, Am or Cm. Starting with uranium [1], the Thermochemical Data Base project of the Nuclear Energy Agency (NEA-TDB) organised the reviewing of published experimental data relevant for modelling aqueous chemistries and solubilities of the most important radionuclides. The results of the NEA-TDB project are now well accepted as a reference critical review, essentially for aqueous chemistry and solubility at room temperature, but these reviews proposed data only when convincing experimental validations were published. There is therefore a gap between this restricted set of quantitative validated thermochemical data and qualitative chemical knowledge.
However, besides selected numerical values, the NEA-TDB reviews also provide qualitative information [2,3], which we used together with analogies for estimating the hydrolysis constants and standard potentials [4] needed for drawing Pourbaix' diagrams of actinides [5]. The present paper aims at testing such rough estimates for complexation.
Rules of thumb are currently used by chemists for checking the possible formation of hypothetical chemical species in specific chemical conditions, when these chemical species are not in databases. This might typically be the case for the environmental aqueous chemistry of An(IV), the actinide elements at the +4 oxidation state (An = Th, U, Np and Pu) in the presence of S-containing inorganic ligands; for this reason it is also an aim of the present paper to estimate the stabilities of An(IV) complexes with sulfoxy-anions.
For storing radioactive wastes, several projects are looking for geological sites that are well isolated from surface waters. These often correspond to anoxic conditions, where U, Np and Pu are expected to be stable in the +4 oxidation state [2,4]. Interestingly, chemical analogues are Ce(IV) and Th, and probably Zr and Hf. Selected NEA-TDB equilibrium constants and redox potentials [2] are adequate for reliable modelling of uranium chemistry in most equilibrated groundwaters. Uranium is predicted to be stable in anoxic waters in the form of the U(OH)4(aq) aqueous species in equilibrium with uraninite, UO2(s), a compound of low solubility [2,5,6]. Similar behaviour is expected for Np and Pu, even though Pu3+ might also be stable [4–7].
In natural under-ground-waters , the carbonate anion is often the dominating ligand among the inorganic ligands (for actinide cations). However, carbonate complexes are predicted to be of little important for An(IV) [2,4,7]. Nevertheless, many complexes have been proposed, but no reliable values could be validated for most of the corresponding formation constants [2,4], for which maximum possible values have been estimated from experimental observations, that also confirmed the similar behaviour of Th, U(IV), Np(IV) and Pu(IV) in carbonate/bicarbonate aqueous solutions [4,5,8]. Values have recently been proposed for the formation constants of several complexes in an attempt to interpret a solubility study of ThO2(s) [8,9], but the species were not included in the interpretation, even though we shall see it should not be completely negligible according to the NEA-TDB data [4]. For probing such competition between the HO− and ligands, the relative stabilities of the corresponding 1:1 complexes of An4+ will be compared. In this framework, the stability of will be estimated: its existence has never been demonstrated, since it is always hidden by hydrolysed species. This over-stabilisation of hydrolysis is specific to the +4 oxidation state: the 1:1 carbonate complexes are well known, and their stabilities were well established for An(III), An(V) and An(VI) (it is not known for Pa(V), which is known to have a very different aqueous chemical behaviour from the other An(V)).
Several other inorganic hard anions are quite reactive toward actinide cations, specially those of high charge , of small size (F−), or polydentade : depending on their content in groundwaters they might form complexes with actinide cations. For example, it was recently proposed that the pore-waters of Callovo–Oxfordian clay minerals, where an underground research laboratory is being built to study the feasibility of a deep geological repository for radioactive wastes in France [10], contain quite large amounts of . The pore-water composition is approximately at the frontier point (Fig. 1). Although the most stable aqueous sulfur species - those bolded on Pourbaix' diagrams - are sulfide (HS−) and sulfate , some other sulfoxy-anions are often detected in natural environments, typically as thiosulfate and sulfite ions. For example, about 25% of the total S content has been reported to be in a reducing groundwater [11], and even in more oxidizing conditions [12]. Sulfoxy-anions are also suspected to form in the course of the oxidative dissolution of pyrite (FeS2) [13], a mineral often associated with the redox regulation of ground-waters. For this reason, we focus on sulfoxy-anion ligands, specially on .
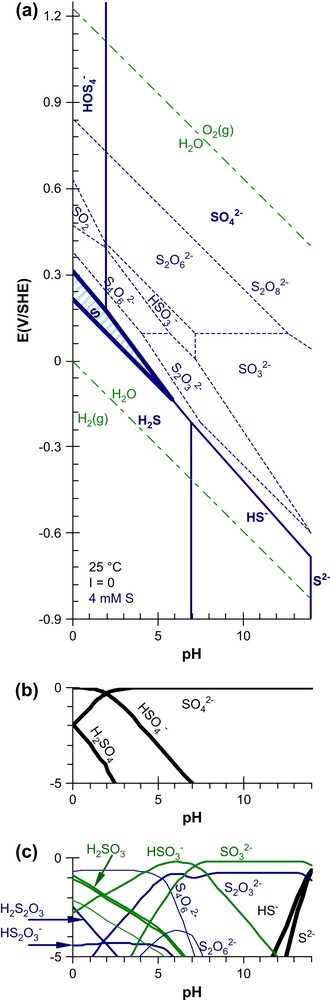
Pourbaix diagram of sulfur. (a) The names of the major species (HS−, H2S, and solid S) are in bold, and their predominance domains are drawn with thick lines. The domains (thin dashed lines) of the other (minor sulfur) species are obtained by suppressing and H2SO4. (b and c) The speciation of each species is represented for two kinetic assumptions (see text) in redox conditions corresponding to line B of Fig. 6.
Grenthe et al. have selected complexing constants for U(VI) complexes with these anions [2], but they wrote in their review that confirmation is needed: “The only quantitative information about aqueous uranium thiosulfate complexes is the study by Melton and Amis […] This review tentatively accepts [their] value, (although confirmation of the results from another study would be useful)”. Furthermore: “The solid formed seems to be a mixture indicating decomposition of thiosulfate into sulfite and elemental sulfur. This review finds no reliable evidence for the formation of solid uranium thiosulfate compounds.” This decomposition might very well be the result of redox reactions (disproportionation), since both uranium and sulfur have a wide range of possible oxidation states, and their stability domains are not well established in mixtures of uranium and sulfur. This might in fact be a problem for other uranium compounds and complexes with sulfur-containing ligands. Unfortunately the NEA-TDB reviews could not validate such data for the Th and Zr analogues [14,15]. Since the NEA-TDB review has selected data for a thiosulfate complex of U(VI) [2], one might very well expect thiosulfate complexes of U(IV) in more reducing conditions – unless thiosulfate is strongly reduced, when U(IV) is formed – because the U4+ hard cation is usually more reactive (than ) toward oxygen-donor ligands. Based on the same hardness rule, thiosulfate should bind to hard cations via the O rather than the S atom of the sulfoxy-anion ligands. The same problem holds for the system: the NEA-TDB review has selected data for sulfite complexes of U(VI); but not for U(IV): “Formation of aqueous uranium(IV) sulfite complexes was reported in a qualitative study by Rosenheim and Kelmy. However, no experimental chemical thermodynamic data on these species are available.” As a probe for ligand competition (between and typically OH− or ), we shall estimate the formation constants of the corresponding 1:1 An(IV) complexes, namely .
Various methods are commonly used for estimating equilibrium constants, typically as empirical correlations with physical (or phenomenological) parameters (atomic radii and charges, solvent interactions…). They can also be obtained from molecular modelling methods. Indeed we recently estimated an uncertainty of 10 kJ mol−1 on ΔrG for Pa(V) hydrolysis [16], which is about 20 times higher than the uncertainty of the experimental determinations of equilibrium constants and standard redox potentials in aqueous solutions. Furthermore, such methods need caution, when using calculated energies [17]. After others [18,19] (with a comment in Ref. [7]) we also tested empirical correlations, which appear to work surprisingly well for some of them: they actually help in putting numbers for quite encyclopedic qualitative knowledge. It is also a way to check such knowledge and corresponding chemical intuition. We use such correlations here, hoping this special issue will help such rules of thumb used by actinide chemistry specialists to become less mysterious. The rough estimates are only guidelines, which need experimental confirmation. They often originate in geometrical and electrostatics reasoning. Indeed, the chemical stabilities of hard cations are often correlated with the charge2/radius ratios of the reactants. Nevertheless, we shall see that the best correlations are not specially with the atomic charges; correlations between measured equilibrium constants will often appear to fit better: several physical contributions probably cancel out in those cases.
The present paper is organised as follows. First, definitions are given, together with features and explanations of methodologies from the NEA-TDB reviews. Results are first reported for correlations between U(VI) (or analogous An(VI)) 1:1 (1 cation with 1 ligand) complexes and protonation of the corresponding ligands, two types of reactions for which many published data are available. In a next step, such correlations are extended to An(III) and An(V). There are virtually no reliable published 1:1 complexing constants of An(IV), since An4+ hydrolysis usually overcomes complexation. Consequently we shall estimate An(IV) 1:1 complexing constants. We shall also consider the position of Pa(V) in our correlations, since its chemical behaviour is an exception as compared to that of the other An(V): this comparison will be based only on hydrolysis data, since there are very few other published equilibrium constants for Pa(V) aqueous complexes. Prior to this comparison, we shall examine the impact of our estimated complexing constants on the geochemical behaviour of U(IV).
2 Methods
2.1 Equilibrium constants
For consistency, we used reaction data – i.e. ΔrG° (equivalently standard equilibrium constants and potentials of redox couples) – they were preferred to formation data (ΔfG°) [2].
| (1) |
| (2) |
values were plotted as a function of , for example when is the formation constant of , is the protonation constant of . We observed
| (3) |
| (4) |
Since bx did not seem to strongly depend on X, we finally used the same bx (=b) value for all the oxidation states; in that case, for comparing An(X) complexes with An(VI) ones, we used:
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
2.2 Activity coefficients
For ionic strength corrections, we used γi, the molal activity coefficient of ion i calculated with the “Specific Interaction Theory”, the SIT formula [2,4]. The corresponding ɛij empirical (pair interaction) coefficients are taken from the NEA-TDB reviews [4]:
| (10) |
| (11) |
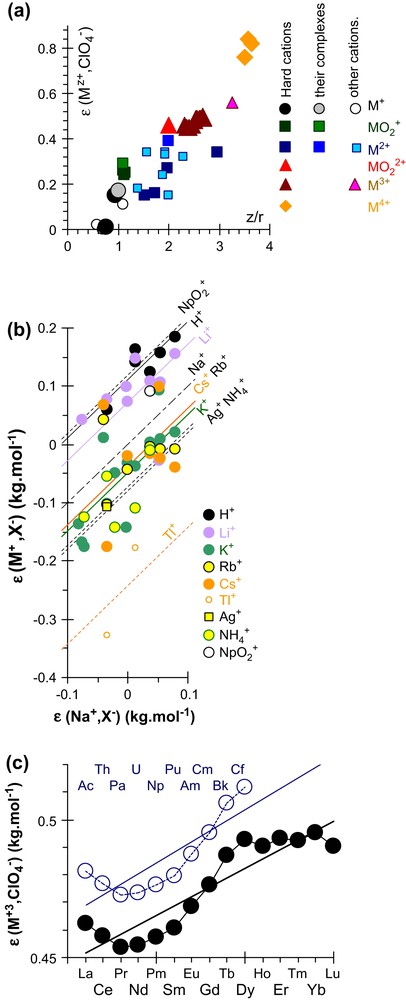
Empirical correlations for estimating SIT ion pair coefficients.
Unknown ɛij numerical values can be estimated by analogy with ions of same charge and similar sizes [3,4]. In that case it was proposed to increase the ɛij uncertainties by ±0.05 kg mol−1 [4]. Moreover, we observed a reasonable linear correlation between interaction coefficients and the charge/radius ratios (Fig. 2(a)). For this correlation we used the formal charge of the cation (or the complex), which is indeed the charge seen by the (ClO4−) counter-anion at large distance. Unfortunately this assumption does not hold for high ionic strengths, the only conditions where the ɛij mj term cannot be neglected. Indeed some data for cations are not in the middle of the correlation cloud, indicating that the relevant phenomenological charge might be higher (than the formal one). Conversely, the corresponding points are moved to the other side of this correlation plot (not represented on the figure), when using the atomic charge (Section 2.3) of An (in , for this reason, we also plotted other correlations without using the charges (Fig. 2(b) and (c))).
2.3 Quantum calculations
In our hydrolysis correlation study, we used the formal charges of An3+ (3) and An4+ (4), while we used the atomic charge of An(X) in (X = 5 or 6). This latter was deduced from quantum (DFT) calculations performed at the same calculation levels (ECP and basis sets) as in our recent previous works [17,20], from which we extracted NPA atomic charges [21,22]. Note that in Gaussian98 and 03, these NPA charges are calculated with the NBO software, which is known to consider the 6d orbitals as Rydberg orbitals, despite the final result gives the 7s5f6d electronic configuration. This overestimates the U atomic charge by 0.50 electron. For this reason we recalculated the NPA charge assuming the 6d to be valence orbitals for all the oxy actinide cations.
For the ligands (alone) closed-shell ab initio calculations were performed at the MP2/6-311+g(2df,2p) level; open-shell calculations are not needed, as checked at the B3LYP/6-31+g(d,p) level. All the quantum calculations were done with the Gaussian98 and 03 suites of programs [23,24].
ΔrE, the ab initio energy, was calculated for the protonation reaction corresponding to the pKa equilibrium (Fig. 3). pKa represents pH1/2; similarly, when adding the entropic contribution to ΔrE, it represents , the H+ partial pressure: the hydration energy of H+ is related to the slope in the ΔrE plot as a function of pKa (Fig. 3), while the intercept rather reflects the hydration energy change between the reactants and products. Since the slope is much greater than 1, the E scale had to be contracted, which means that the final correlation is quite poor. Slope ≠ 1 also means it is not equivalent to use pKa or ΔrE for our estimates of complexing constants: pKa appeared to be better correlated with measured complexing constants. Furthermore pKa represents a marginal value of ΔrE, which already is a marginal part of the DFT calculated electronic energy: the experimental pKa values are more reliable for our purpose and more accurate than the ΔrE ones obtained from quantum calculations in the gas phase.
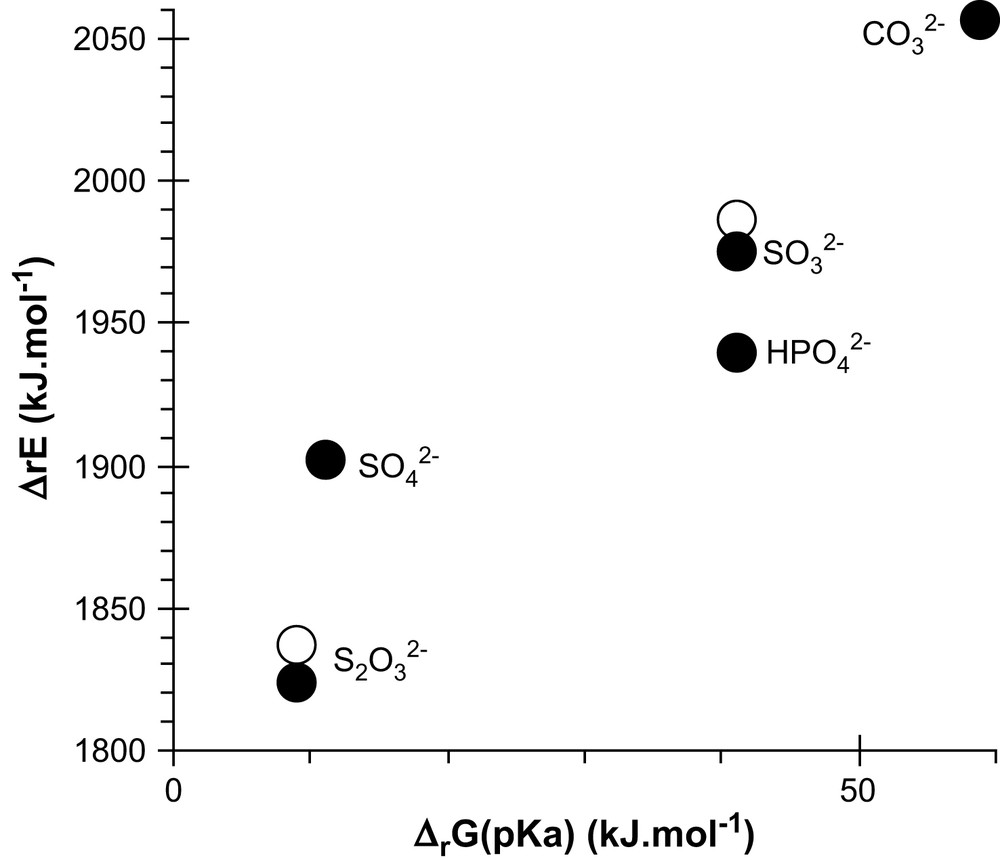
Protonation reactions of ligands in the gas phase and in aqueous solutions. The pKa (in pure liquid water at 25 °C) are converted to kJ mol−1 (ΔrG = −RTpKa) and compared to the energy of the corresponding reaction ab initio calculated (with neither matrix nor temperature correction), where the protonation is on an O (black points) or S (white points) atom.
3 Results and discussions
3.1 Comparing the affinities of hard anions for H+ and
We first examined U(VI) aqueous complexation and hydrolysis data, since a sufficiently large set of complexing constants is available. Positive correlations are observed, and even linear correlations appear to fit the data reasonably well. The plot appeared to be less scattered when restricted to the consistent set of data selected by the NEA-TDB reviews (Fig. 4): we finally used these (NEA-TDB) consistent sets of data for the figures and numerical correlations given in the present paper with the following exceptions. For An(VI) we did not use the NEA-TDB PuO2CO3(aq) formation constant based on only ( [26] and 9.3 ± 0.5 [27]) two experimental determinations that are not consistent (within uncertainties). The latter value (that we published ourselves) is closer to the U(VI) and Np(VI) ones (Table 1) [2,4], but it is rather a maximum possible value corresponding to the detection limit of our solubility measurements. For this reason, we also do not rely on the 9.5 ± 0.5 similar value more recently updated by the NEA-TDB review [16].
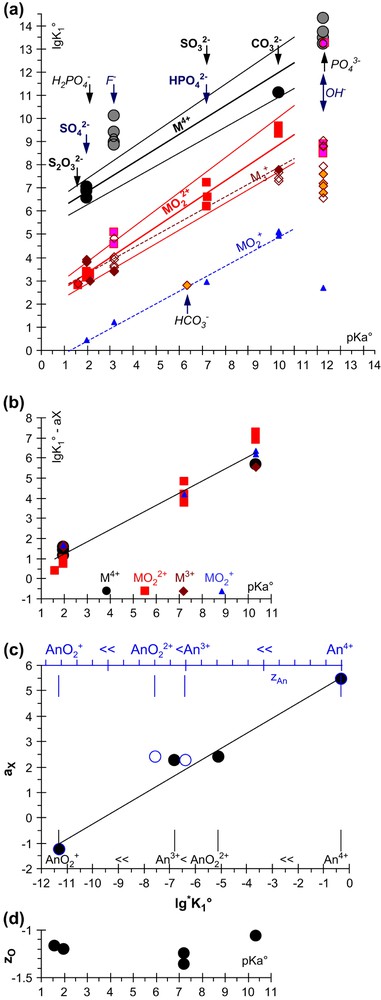
Proton and other cation affinities for ligands. is the standard formation constant of the complex, and is the protonation constant of the ligand written on the figure (Table 1). Since all the () lines are virtually parallel for all the (X) oxidation states (a). We also used the same (bx = 0.62 ± 0.16) slope in regressions for the ligands, and shifted the curves by ax (b): (Eq. (5)), where is the constant for the exchange equilibrium (Eq. (6a)) for = An3+, An4+ or For An at the oxidation state can be used as a definition of a quantitative scale for the (up to now qualitative) series (y axis of (c)). It is compared (black filled symbols) with the hydrolysis constant (*K1) scale on the x axis (of (c)), and zAn, the An atomic charge (blue open symbols corresponding to the top scale). zO, the atomic charge of O in is not specially correlated with its pKa (d).The x-axes are the same for (a), (b) and (d): the names of the ligands are only written on (a).
Formation constants used to draw Fig. 4: pKa° of ligands and corresponding formation constantsc with cations of f-block elements [2–4,16]
| pKab | c | c | c | c | |
| 1.59 | 6.6 ± 0.8a | 2.8(U) | |||
| 6.58(U) | 3.15(U) | ||||
| 1.98 | 3.85(Am) | 6.85(Np) | 0.44(Np) | 3.28(Np) | |
| 3.91(Pu) | 6.89(Pu) | 3.38(Pu) | |||
| 7.212 | 9.5 ± 2.3a | 2.95(Np) | 7.24(U) | ||
| 6.2(Np) | |||||
| 7.22 | 9.5 ± 2.3a | 6.6(U) | |||
| 10.329 | 7.7 ± 0.3(Am) | 11.1 ± 3.2a | 4.962(Np) | 9.67(U) | |
| 7.8 ± 0.2(Eu) | 5.12(Pu) | 9.32(Np) | |||
| 5.1(Am) | |||||
| ad | 2.2 | 5.8 ± 0.4 | −0.7 | 2.0 ± 0.3 | |
| bd | 0.55 | 0.51 ± 0.27 | 0.54 | 0.665 ± 0.085 | |
| axe | 2.253 ± 0.075 | 5.444 ± 0.249 | −1.236 ± 0.489 | 2.408 ± 0.453 | |
| −0.16 ± 0.5 | 3.04 ± 0.5 | −3.64 ± 0.5 | 0 | ||
| −1.7 | 4.81 | −6.2 | 0 |
a Value estimated in the present work.
b pKa of the ligand.
c is the standard constant of equilibrium for Mz+ = Anx+ (X = 3 or 4) or (X = 5 or 6) from published data (see text) [2–4,7].
d a and b, the coefficients of the linear regression are fitted for a given oxidation state, X.
e while ax is the (fitted) intercept of a similar regression, but with the same (0.62 ± 0.16) slope for all the oxidation states:
The tri-anion is out of the correlation, while the F− mono anion could probably be included into the correlation, but HO− cannot (Fig. 4). When restricting the correlations to potentially bidentate oxygen-donor ligands, virtually the same value is observed for a given ligand with for An = U, Np, Pu or Am: the variations along this series are only slightly higher than experimental uncertainties. is obtained for these cations. Adding not critically reviewed values gives similar regression coefficients with increased uncertainties, namely (2.6 ± 0.8) instead of (2.0 ± 0.3), and (0.58 ± 0.08) instead of (0.665 ± 0.085).
3.2 AnO2RO2/ exchanges for = An3+, An4+ or
Similar correlations and observations (as for , Section 3.1) are made for the An3+ and , cations, while there are too few data for M4+. For the M3+/ systems, we used our own complexing constants (Table 1) [28], is an outlier, in part due to the stabilisation of H2CO3 as CO2(aq): the measured pKa (of the couple) is not the relevant parameter for our correlations. For we found values in the order , a classical order for the reactivity of actinide cations toward hard anions. However, is often written (instead of ). Here the available data for An3+ appear to be within the correlation lines of . The atomic charge of U in is 2.8 electron, which compares with the charge of Am3+. Nevertheless, using atomic charges in the correlations gave poorer results (see below and Fig. 4(c)). We obtained for An3+ and for .
There are too few data for a statistical evaluation of all the uncertainties. Nevertheless, it seems that bx, the slopes (of every correlations) are the same within uncertainties. Indeed a reasonable fit is obtained when fixing bx = bVI (=0.665), namely for all the oxidation states. We finally fitted the slope (and ax) on all the data, and obtained with aIII = 2.253 ± 0.075, aIV = 5.444 ± 0.249, aV = −1.236 ± 0.489 and aVI = 2.408 ± 0.453 fitted values, where uncertainties are 1.96σ (the maximum errors on was +0.9 for UO2CO3 and −0.8 for ). Since there are not enough data for a meaningful statistical analysis, we finally increased the uncertainties: (Fig. 4(b)). The standard deviation of the fit is 0.5 (it represents less than 3 kJ mol−1), a value only a little higher than that of many direct experimental determinations in aqueous solutions, and of the order of magnitude of the variations of the values among the series of the analogous cations considered here. However, when a slope is fitted for each oxidation state, a small systematic deviation can be inferred, namely the slopes seem slightly different for each type of central cation (, An3+ and ). On the other hand, this difference is small as compared to the scatter in the available data, and it is not specially correlated with the charge of the cation.
Since the (0.62 ± 0.16) slope does not depend on X, (Eq. (5)), the shift between the lines in Fig. 4(a) is related to the following equation:
| (6a) |
We also attempted to force b = 1 in the fits, but without success: the correlations cannot simply be interpreted with Eq. (4).
Similarly, hydrolysis equilibria were compared using (Eq. (8)), the constant of a hydrolysis competition equilibrium (Eq. (7)) between actinide ions at oxidation states X and +6: , and for Np [4]. These results give nearly the same qualitative scale (Fig. 4(c)), and the linear correlation.
3.3 Estimating the stabilities of complexes
We now want to estimate missing complexing constants for U(IV), namely with the and anions. For this we could not use the same type of correlations as those observed for and the other cations (Section 3.2), because reliable formation constant has been published for only one type of 1:1 An(IV) complexes, namely for the complexes: [2], 6.85 [4], 6.89 [4] and 7.04 [15]. When using this single datum and the (0.62 ± 0.16) slope value estimated above, the ( line is drawn, from which , (10.1 ± 1.4), (6.8 ± 0.5) and (6.6 ± 0.5) are calculated for the An(IV) complexes of , and , respectively. The value of aIV = 5.6 ± 0.2 was chosen to fit the 6.58 , 6.85 and 6.89 data by giving less weight to , because the +4 oxidation state is more difficult to stabilise for uranium, even if more experimental studies of U(IV) are available. However, the (=6.6 ± 0.5) value is close to the fixed point (of the correlation). Therefore it does not depend sensitively on the value estimated for the slope (of the linear correlation). Consequently the uncertainties are relatively small for (the estimate of) . Conversely the biggest uncertainty is for the most stable complex, since appeared to be the most reactive ligand we studied: it is one of the endpoints of the correlation lines. For this reason, we estimated an upper bound for the value of from experimental data: we re-interpreted available published experimental solubilities of actinides(IV) by using the same methodology as in Refs. [4,5,29]. We obtained formation constants consistent with the original interpretation (by the authors of Ref. [9]). However, for consistency we added the known stabilities of An(CO3)i4−2i (i = 4 and 5), and we tested many possible complexes for which we also estimated maximum possible stabilities (Table 2) for sensibility analysis; our purpose was essentially to estimate a value for . As expected from pH vs predominance diagrams [7,26,28], the most restrictive conditions were found for published solubilities of An(IV) measured at low pH and high CO2 partial pressure, namely in Refs. [9,30]. In both cases we obtained virtually the same values: for the complex. Using this value (and the sulfate data), is calculated, from which , 9.5, 6.8 and 6.6 are calculated for the An(IV) complexes , , and , respectively. These values are within the uncertainties of the previous estimates above. The value of 11.1 is identical as, or slightly smaller (by 0.9 ± 1.9) than the central value (12.0 ± 1.9) of the above estimate, and the same trend was observed for : it was overestimated by 0.8 log10 unit when using the same slope (0.62) for all oxidation states. This correlation predicts under-stabilisation of the complexes (X = 3 or 4) as compared to the systems (X = 5 or 6): it might be attributed to the planar structure of , which offers a better fit to the geometry of the coordinating equatorial plane of the actinyl cations. Unfortunately, such an explanation would also hold for the (quasi-) planar ligand (Fig. 5), which is not specially confirmed (Fig. 4). For consistency with our estimate, , we prefer the last correlation , where we increased the uncertainties to encompass the previous correlation: from which we obtain for for , 9.5 ± 2.3 for and 6.6 ± 0.8 for , where uncertainties are increased take into account the lack of experimental data.
Stabilities of An(IV) carbonato complexes
| a, [5] | a, [9] | a,b | |
| AnOH3+ | 13.2 | ||
| ≤11.1 | |||
| AnCO3OH+ | <21.1 | ||
| An(CO3)2 | <20.8 | ||
| AnCO3(OH)2 | <<42 | 27.0 | <30.1 |
| An(OH)4 | <<47.9 | 38.5 | |
| An(CO3)2OH− | <<40.5 | <29.4 | |
| <<47.7 | 34.8 | ≤38.5 | |
| <<37.6 | <27.5 | ||
| <<46.2 | 33.3 | ≤36.8 | |
| <<51.8 | 37.4 | ≤39.9 | |
| <<42 | ≤34 | ||
| <<50.5 | <39.2 | ||
| 37 | 29.9 | ||
| <41 | <37.6 | ||
| <40.5 | <37.9 | ||
| <39 | 34.4 | 35.4 | |
| 35.6 | 28.4 | ||
| <37 | <36.4 | ||
| <38.5 | <39.3 | ||
| <36 |
a is the standard constant of equilibrium .
b Maximum possible values from the experimental data of Ref. [9]; these estimations are consistent with the original interpretation (by the authors of Ref. [9]), but the known stabilities of are here added in the fits for i = 4 and 5; our purpose was essentially to estimate a value for (see text) and to outline sensitivity analysis.
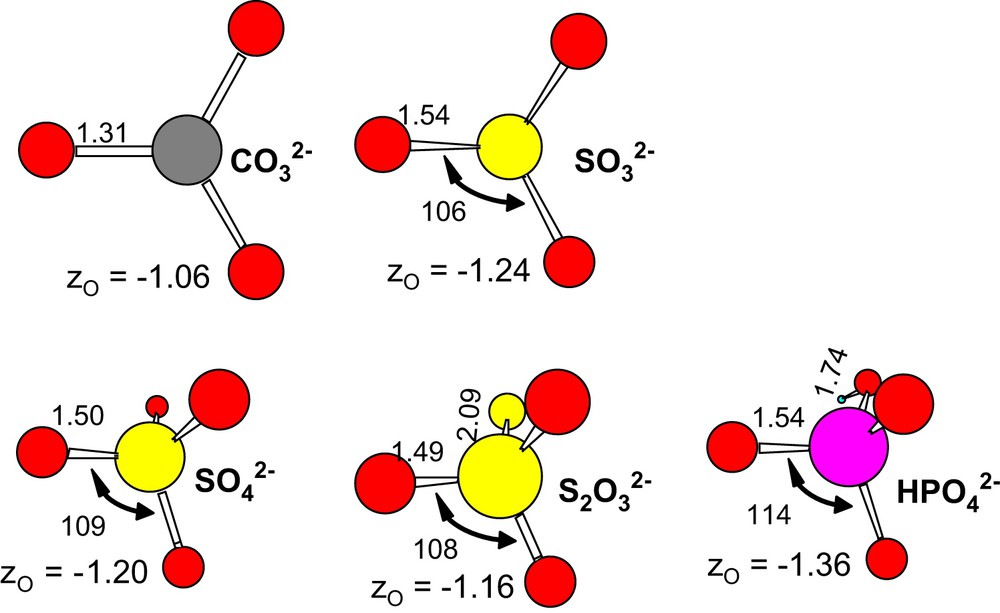
Geometry of ligands optimized in the gas phase. R–O bond distances (Å), angles (°) and zO, the atomic charge of O are written on the figure.
, the value estimated for is quite similar to those for the complexes: 6.58 , 6.85 and 6.89 . This is consistent with the molecular structures of these ligands: and both have a tetrahedral structure (Fig. 5) – an O atom (of ) being replaced by an S atom (in ) and similar pKa values. has a different structure, a higher pKa, and a higher estimated value of the complexation constant. Unfortunately, it does not seem easy to draw any simple explanation just from zO, the atomic charge of the free ligand in vacuum (Fig. 4(d)).
3.4 Uranium geochemistry
In non-complexing aqueous solutions, the solubility of uranium is controlled by uraninite (UO2(s)) in reducing conditions, and by schoepite (UO3(s)) in oxidizing and neutral conditions, as illustrated in Fig. 6(a) for 1 μM [U]t. Besides those minerals, aqueous U(VI) species are predominant in a large E–pH domain, while aqueous U(IV) is stable only in reducing conditions, and is mostly hydrolysed.
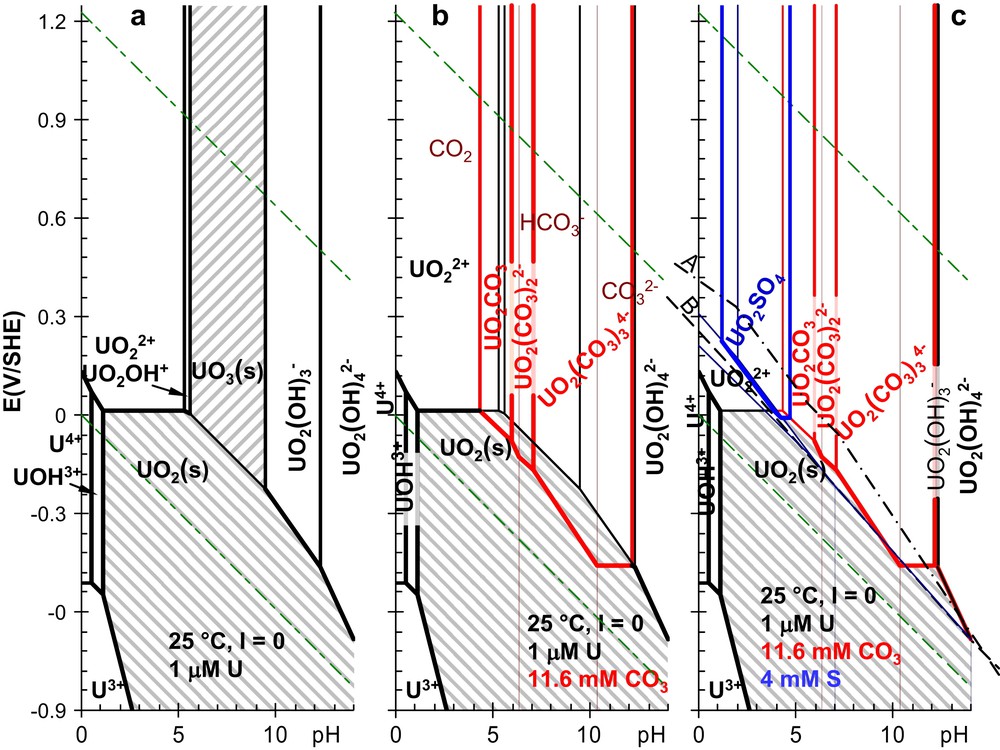
Pourbaix' diagrams of uranium. The predominance domains of the major soluble species are shown as a function of pH and E, the redox potential of the solution in (a) non-complexing media, (b) adding the influences of carbonate ions and (c) sulfur species for a typical ([CO3]t = 11.6 mM and [S]t = 4 mM) composition of underground waters [11]. pH is taken into account for carbonate speciation (), but its reduction -typically into CH4(g)- is not. The mixed dashed line (A) represents redox conditions in Fig. 7. The long dashed line (B) represents redox conditions for Fig. 1(c).
On adding carbonate ions at a typical concentration of underground waters, aqueous U(VI) carbonate complexes prevail between pH 4 and 12 (Fig. 6(b)), UO3(s) is totally dissolved, and the UO2(s) stability domain is reduced. We have ignored the reduction of the carbonate ions, since this reaction is usually very slow. Nevertheless, no carbonate complex of U(IV) appears on the Pourbaix diagrams. These complexes would predominate only at higher carbonate concentrations than those studied here. Rai and Ryan have already proposed that carbonate complexation of actinide(IV) ions in environmental conditions can be neglected [8].
Among the main sulfur species, prevails over a large (E–pH) domain in oxidizing to slightly reducing equilibrium conditions. For high pH values, this domain even extends to reducing conditions (Fig. 1). H2S, HS− and S2− prevail in reducing conditions, but their complexing properties are not significant for the (hard) cations of the f-block elements. UO2SO4(aq) is the only predominating sulfur species in our typical underground water conditions (Fig. 6(c)), even when introducing the 1:1 complexing constants estimated above (Section 3.3, Table 1) for and . The ligands are protonated in acidic conditions, which decreases their concentrations: the corresponding 1:1 complexing equilibria are actually the
| (4a) |
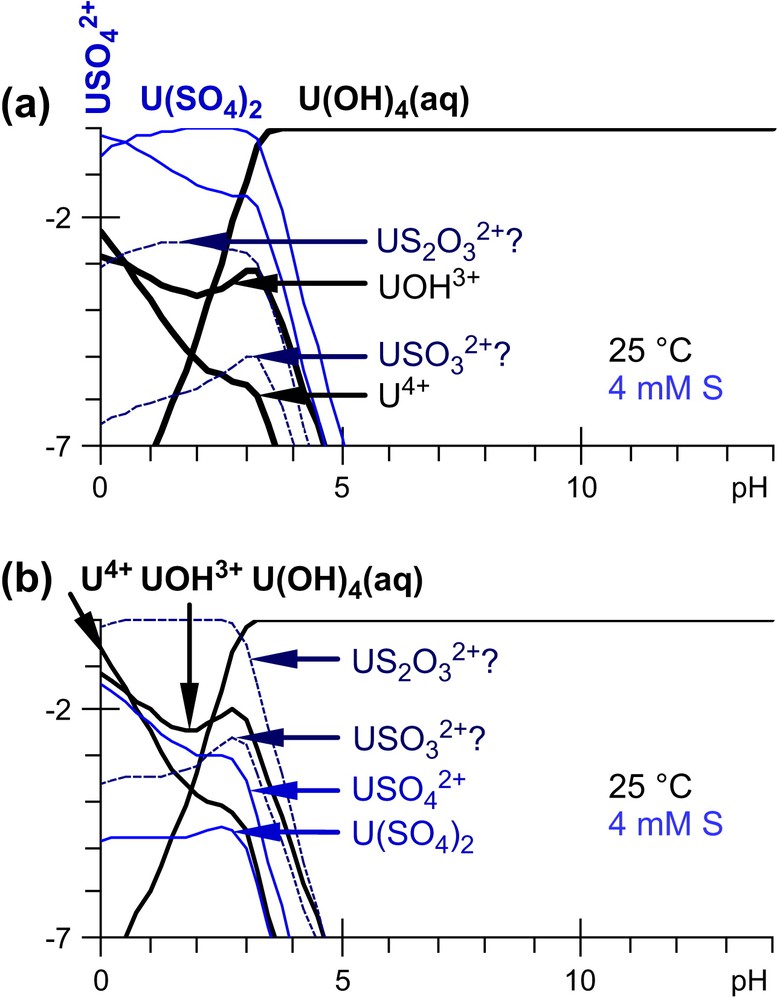
Distribution of aqueous U(IV) species. lg(|A|/|U(IV)|) is plotted as a function of pH, where |A| is the activity of an aqueous U(IV) species. The conditions are the same as in Fig. 6(c) except for E, the redox potential of the solution: (a) or (b) are assumed to be the major S species. (mixed dashed line A in Fig. 6(c)). corresponding to different kinetic assumptions.
In a first simulation we assumed that the major S species are in the +6 oxidation state (namely ), and that , which corresponds to much higher concentrations than in equilibrium conditions (for kinetic reasons). The and U(SO4)2 sulfate complexes still appear to be U(IV) major species in acidic conditions (pH < 3.2), while nearly 1% of can be formed (Fig. 7(a)). Yet might be a kinetic intermediate, since uraninite is often associated with pyrite (FeS2); indeed is an intermediary product of its oxidative dissolution [14]. and have similar reactivities (Fig. 4), but (in our hypothesis) the concentration is higher (than the one), which explains why the sulfate complexes dominate. Although the ions are more reactive, the complex is negligible in that simulation, since the reduction of (Fig. 1) decreases its concentration and consequently its complexing ability.
In a second simulation we assumed that is not formed at all (still for kinetic reasons). Therefore is now the dominating S aqueous species (Fig. 1). is the major U(IV) species, and up to a few percent of is formed at pH less than 3.0 (Fig. 7(b)).
Even if sulfoxy-anions complexes of U(IV) are certainly not stable in equilibrium conditions, these simulations indicate that they might be formed as kinetic intermediates typically in the course of uraninite and pyrite oxidative dissolutions, or the interaction of aqueous uranium (including U(VI)) with pyrite surfaces [31,32]. Of course, this statement needs experimental confirmation, specially in less acidic to basic conditions, where higher and mixed complexes may form. Furthermore, at pH > 3, U(OH)4(aq) is the dominant species in equilibrium reducing conditions, and the formation of S-containing complexes is less favourable, specially in the usual pH conditions of equilibrated natural under-ground-waters.
3.5 Hydrolysis of actinide ions
We now consider where protactinium should be placed in the above correlations. There is little experimental published information on Pa aqueous chemistry. We first used the available information on its aqueous species in non-complexing (acidic) solutions and its hydrolysis. Although Pa is known to be an f-block element [17], Pa(V) aqueous chemistry is closer to that of d elements (in the same – the 5th- column of the periodic table) than to the chemistry of trans-protactinian actinide cations. Here is a strong indication that is not the dominating aqueous Pa species.
Jaussaud et al. recently reviewed previous measurements of the Pa(V) hydrolysis constants [33–35]. They are essentially based on liquid–liquid extraction measurements, for which they pointed out many experimental difficulties: side reactions of the organic chemicals, sorption of Pa(V) on vessels and unwanted side reactions. Surprisingly most of the published studies are only based on measurements at trace concentrations of Pa(V), while sorption reactions are classically made negligible by using (non-radioactive) chemical analogues at macro-concentrations. The hydrolysis behaviour of Nb(V) seems similar to that proposed for Pa(V): we calculated the hydrolysis constants of Nb(V) by interpreting the aqueous solubility of Nb2O5 (Table 3) [25]. We re-interpreted the (Pa) experimental measurements at 25 °C by giving more weight to the data for which systematic errors seemed the lowest according to Jaussaud's observations and comments: the measurements at high ionic strength and low (TTA = thenoyltrifluoroacetone) extractant concentrations. This essentially confirmed the original interpretation given by the authors, but increased uncertainties and suppressed an inconsistency (Table 3). Namely, classical slope analyses of the raw experimental data imply a Pa species of charge +1 in 0.1 M NaClO4 aqueous solutions, and +2 at higher I (3 M), consistent with the PaOOH(OH)+ and PaOOH2+ stoichiometries [17] in nearly the whole pH range studied (0 < pH < 4). Indeed, high I usually stabilizes the species of higher charges. There is no clear evidence for neutral and tri-cationic species, due to the scattering of the data (Fig. 8). A neutral Pa species is certainly formed, but it is clearly stabilized by increasing [TTA]t, the total TTA concentration (results not reproduced in Fig. 8 for clarity), which suggests the corresponding aqueous Pa(V) species might include ionised deprotonated TTA ligands, which would hide the formation of PaOOH(OH)2 (equivalently written PaO(OH)3 or Pa(OH)5). The formation of PaO3+ is not proposed in the original interpretation of the authors, and indeed needs confirmation. Finally, the most reliable published Pa(V) standard hydrolysis constant is certainly [34], a value consistent with our re-interpretation (−1.44 ± 0.71) (Fig. 8 and Table 3), and with the Nb(V) value of −(1.65 ± 0.2). We also propose and , giving no credit to the (−(7.15 ± 0.4) [34] and −(7.03 ± 0.15) [33,35]) published interpretations from the same experimental data, because the corresponding hydrolysis species could not be detected in the experimental conditions used in this work (pH ≤ 4 corresponding to a maximum value of about 10−7+4 = 0.1% for the concentration of the hydrolysis species to be compared with the 100.71 uncertainty in the measurements of ), even though they might provide a reasonable value: the Nb(V) value of −4.95 ± 0.2 might also be used as a rough estimate. These constants are actually the hydrolysis constant of PaO3+, but the existence of this species has not clearly been demonstrated, and for this reason only the second stepwise experimental determination seems reliable, while the first one needs confirmation. The value is only a little larger than that of : the two first hydrolyses of Pa(V) would be nearly simultaneous. This is also observed for the other actinide aqueous species.
Pa(V) hydrolysis constants
| I (M) | e | e | e | |
| 3 | −2.0 ± 0.15 | −5.8 ± 0.3b | [33–35] | |
| 3 | −0.35 ± 0.29 | −1.75 ± 0.91 | <−3.5 | [33]a |
| 1 | −1.7 ± 0.2 | −6.9 ± 0.6b | [33–35] | |
| 1 | ≥−0.38c | −1.50 ± 0.56 | <−0.98b | [33]a |
| 0.5 | −1.6 ± 0.2 | −6.9 ± 0.6b | [33,35] | |
| 0.5 | −1.49c | [33]a | ||
| 0.1 | −1.5 ± 0.2 | −7.0 ± 0.6b | [33–35] | |
| 0.1 | −1.80 ± 0.34 | [33]a | ||
| 0.1 | ≥−0.75c | −1.65 ± 0.2 | −4.95 ± 0.2 | Nb(V)d [36]a |
| 0 | −1.24 ± 0.02 | −7.03 ± 0.15b | [33,35] | |
| 0 | −1.26 ± 0.15 | −7.15 ± 0.4b | [34] | |
| 0 | −0.04 ± 0.36c | −1.44 ± 0.71 | <−3.6c | [33]a |
a Graphically interpreted in the present work, and (last line) extrapolated to I = 0. See Fig. 8.
b Inconsistent value: since the measurements were performed at pH < 4, it is not possible to fit (from them) a log Ki value less than about −4.
c There is no clear experimental evidence of the corresponding reaction.
d Nb(V) value fitted from solubility data [36], and here tabulated for comparison.
e Ki,m is the constant of equilibrium PaO.
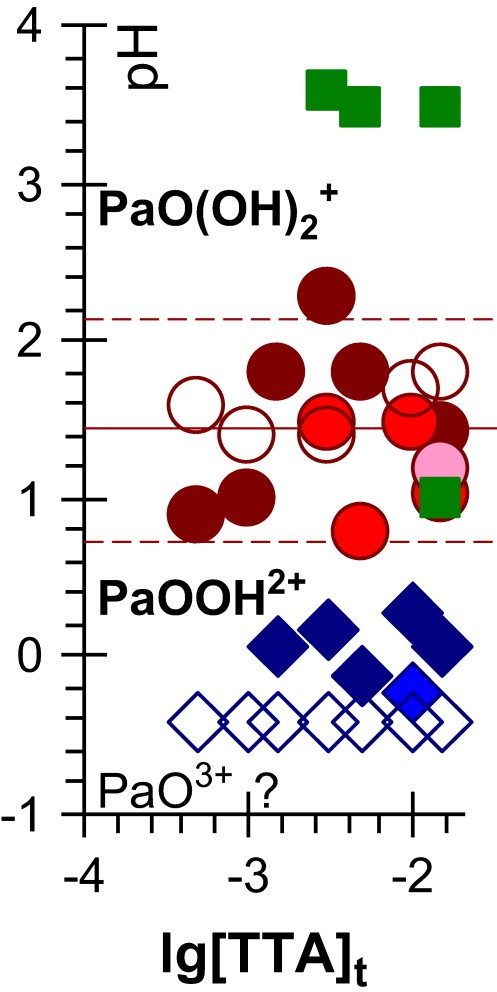
Predominance diagram of Pa(V) hydrolysis species. The hydrolysis constants ( correspond to the pH value at the half-point reaction) have been re-interpreted (Table 3) from the experimental data (and extrapolated to I = 0 with the SIT formula) of Ref. [30] in 0.1 (open symbols) to 3 (filled symbols of the same colour) mol L−1 NaClO4 aqueous solutions for the successive formations of species of charges 2 (dark blue diamonds), 1 (brown circles) and 0 (green squares). The intermediate colours are for 1 and 0.5 mol L−1. For higher [TTA] values (not represented), a systematic deviation is observed. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
A linear regression correlates reasonably well , the logarithm of the hydrolysis constant and z, the charge of the Mz+ cation for Mz+ = Ra2+, Am3+, Pu4+ (brown dotted line in Fig. 9(a)): . Adding other An3+ and An4+ cations gives virtually the same correlation (brown dotted line in Fig. 9(b)): . The actinyl ions such as , and are below this correlation line. This stabilisation of their hydrolysed species might be originated in an An–Oyl (intramolecular) charge transfer induced on approaching equatorial water molecules to [21], an inductive effects of Owater, which is expected to be more important for HO− equatorial ligands (where Oyl is an O atom of an actinyl cation, while Owater is an O atom of a water equatorial ligand of the actinyl). Nevertheless, the actinyl cations are not far from the correlation lines: including and but excluding Ra2+ (black lines in Fig. 9); , and adding other and : , while extrapolating (blue dashed lines in Fig. 9) the and data give (blue dashed) lines (in Fig. 9) that are between the PaO3+ and PaOOH2+ data. Namely, PaO3+(aq) would be intermediate between the bare actinide hard cations (Anx+, X = 3 or 4), and the usual actinyl cations (AnO2(x−4)+, X = 5 or 6, An = U, Np, Pu or Am), whose polarization by equatorial ligands essentially results in the intramolecular charge transfer between An and Oyl. Note that despite this polarization is still a hard cation for the equatorial ligands – i.e. negligible charge transfer from the equatorial ligands – we may wonder whether assuming this concept of (equatorial) hardness/(intra-actinyl) softness is still relevant for such a behaviour. However, the set can as well be considered as a series of actinide oxo-cations on their own line (approximately the blue dashed one in Fig. 9). As a result of their polarizability, these oxo-cations are below the (brown dotted) line of the bare Mz+ cations. This polarizibility probably decreases zAn, the An atomic charge (in the oxo-cation) by inductive effect. This inductive effect would increase with zAn: this can explain the quite surprisingly low calculated atomic charges of U (in ) and Pa (in PaO3+), which would therefore be at the origin of the more negative slope for the actinide oxo-cation line (as compared to that of the bare cations). However, this proposition needs confirmation, since the Pa(V) experimental results are neither very accurate, nor validated, and since physical explanations cannot be proven by only such empirical correlations: it is a limit of such correlations, rather than problems in the (very few) experimental data. According to this interpretation, two correlation lines are expected, one for the bare Anx+ cations, and the other one for the di-oxo-cations, while the PaO3+ mono-oxo-cation would fall between these lines, as we actually observed.
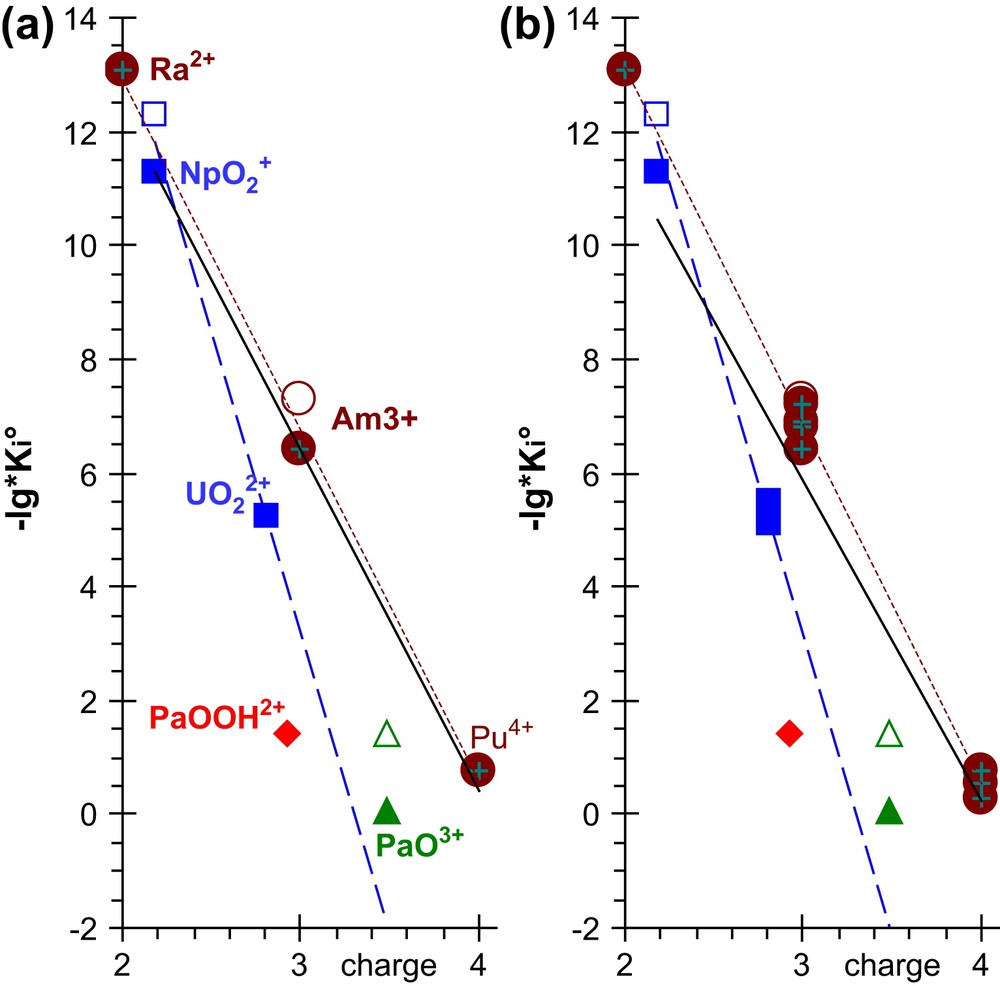
Hydrolysis constants of actinide aqueous ions: (filled symbols) and (open symbols). The lines represent the linear regressions for (black line) all the points plotted on the figures excepted Pa(V) ones, only for the (Ra2+, Am3+, Pu4+) set (brown dotted line), or only for the ( and ) set (blue dashed line). The (atomic NPA) charges of the bare An cations (written in Fig. 9(a)) were obtained from DFT quantum calculations in gas phase. Data and corresponding lines are plotted by adding similar cations in Fig. 9(b). Two possible stoichiometries of “the” Pa(V) aqueous species are represented. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The experimental hydrolysis data already indicated that PaOOH2+ should be only a little less reactive than Pu4+. Finally, it can still be under debate whether it is better to consider PaO3+ or PaOOH2+, or both, as the Pa(V) aqueous species. Using atomic charges here gave unexpected correlations, as compared to the other chemical studies reviewed in the present paper. Nevertheless, it is not a convincing proof that PaO3+ can be an important aqueous species (i.e. it is not a confirmation of the above estimate of its value).
Our DFT calculations give pictures confirming that PaOOH2+(aq) is a logical species, similar to while is easily protonated. PaOOH2+ is merely protonated [17]. However, our continuing DFT calculations for interpreting published EXAFS measurements clearly indicate that the PaO3+ geometry exists in the Pa(V) species formed in concentrated H2SO4 aqueous solutions, since none of the other tested model geometries reproduced the shortest experimental distance, including PaOOH2+: it thus dissociates in complexing media, to give aqueous sulfate complexes of PaO3+.
4 Concluding remarks on analogies
() correlations fit experimental data surprisingly well (Fig. 4(a)) for An(III to VI) complexes, with the exception of Pa(V), with 5 anionic potentially bidentate and oxygen-donor ligands: in the order of their reactivities for the actinide cations. Furthermore, the correlations were found to be linear for each oxidation state, and the (0.62) slope of these H+/An(X) correlations are approximately the same for all the oxidation states (X). This, of course, means that the An(X)/An(VI) correlations deduced are linear with slope 1: ax, the intercept, is interpreted in terms of the half-reaction point, namely (Eq. (5)) is the constant of the exchange equilibrium (Eq. (6a)), which takes (approximately) the same value (Table 1) for all the ligands and for a given oxidation state. This provides ax-based numerical values for the (up to now qualitative) scale (Fig. 4(c)). The ax values are also qualitatively correlated with z, the atomic charges of the An cations; but using z instead of ax gives a poorer correlation (Fig. 4(c)). Note that measured energies of reactions, namely the hydrolysis constants of Pa(V), show clearly that it is not an analogue of the other An(V); quantum calculations give a chemical explanation of the destabilization of by hydration, typically resulting in clear apical H-bonded water molecules [17]. The two approaches are complementary: the experimental energies of reactions are more accurate, while quantum calculations provide geometries and other physical data that can be interpreted in terms of usual chemical concepts (atomic charges, bounds and their covalency…) for explaining the observed chemical reactivity.
All the correlations we used are totally empirical. They are probably the result of various effects, some of them more or less cancel out in the correlations, and they are probably all linked to z, the atomic charge of the cation. However, using z gave poorer linear correlations than comparing only experimental equilibrium constants. For this reason it is certainly better to interpret the correlations with chemical concepts than with any unproven physical explanation. Nevertheless, intramolecular charge transfers are deduced from quantum calculations for (possibly protonated) actinyl cations. These charge transfers can be related to the slightly different trends observed between the hydrolysis behaviours for these three types of cations (Anz+, PaO3+ and ). This effect would be a little less important for PaO3+ than for the cations where there are more covalent bounds (which promote intramolecular charge transfer). Charge transfers might as well be at the origin of the over-stabilisation of the aqueous An(IV) hydroxides as compared to complexation. These predictions are restricted to similar complexes: the linear regression numbers cannot be extended to all types of complexes without validations. Indeed such approaches exist in literature, overestimating the stabilities of several hypothetical chemical species, whose existences have never been confirmed; such numbers are not considered in the NEA-TDB reviews [2–4].
We have in fact used several levels of analogy giving different rules of thumb (although some have similar mathematical equations), which might indicate that it is hopeless to develop more general empirical formulae. The strongest analogy is typically for M(X), the series of An and other cations with the same charge, geometry and oxidation state, X: they form soluble complexes and hydroxides with the same stoichiometries, and with stability constant values that hardly differ by more than the experimental uncertainties. For different (X) oxidation states, linear correlations were found with slope 1, which defines a second type of analogy: considering the exchange, a solution of activity has the same reactivity (for the ligand) as a solution of activity of
In a third type of analogy, the (b) slope of the linear correlation is no longer 1 (b ≠ 1), as found here for H+/ exchanges (b is not correlated with zM, so it is better not to consider the (zM H+)/ exchange); , as its equilibrium constant is no longer a relevant parameter for the analogy: analogue solutions should instead be based on the parameter whose interpretation is less intuitive.
Similarly when comparing protonation energies in aqueous and gas phases, the slope of the energy correlation is determined by the ratio of the H+ activity scales in both phases. It is far from 1 (Fig. 3), corresponding to differences in the orders of magnitude (of the energies of reactions) in each phase. The intercept is related to the balance of the hydration energies (it can be shifted by changing the reference state).
Finally the rules of thumb are often characterized by the value of the (fitted) slopes in linear correlations of equilibrium constants, or equivalently by the value of the corresponding exponent in ratios of activities, the ideal concentrations.


