Towards the prediction of NMR relaxation rates in proteins from their structure by a network of coupled rotators

Gabrielle Nodet; Geoffrey Bodenhausen; Daniel Abergel

doi:10.1016/j.crci.2007.08.008

Résumés

Anglais
Français

During the past decades, NMR spectroscopy of isotopically labelled proteins has emerged as a unique tool for the study of internal protein dynamics in solution. The possibility of measuring spin relaxation rates in proteins has motivated numerous theoretical and methodological developments aiming at the interpretation and the prediction of their internal dynamics. In this article, we discuss the possibility of predicting ¹⁵N relaxation rates using a Network of Coupled Rotators to describe internal motions of a protein starting from its three-dimensional structure, and illustrate the approach by the example of the protein calbindin.

Au cours de ces dernières décennies, la spectroscopie de résonance magnétique nucléaire s'est révélée un outil de choix pour l'étude de la mobilité interne des protéines en solution. La possibilité de mesurer les vitesses de relaxation de spin dans les protéines a motivé nombre de développements théoriques et méthodologiques visant à l'interprétation et à la prédiction de leur dynamique interne. Dans cet article, nous discuterons la possibilité de prédire les vitesses de relaxation des noyaux ¹⁵N l'aide d'un réseau de rotateurs couplés utilisé pour décrire la dynamique interne des protéines à partir de leur structure tri-dimensionnelle, et nous illustrerons cette approche par l'exemple de la protéine calbindin.

1 Introduction

Over the past decades, the crucial role of internal dynamics for the function of a protein has emerged and has motivated many studies. Beyond the well-known structure–function relationship, there is compelling evidence that internal motions in proteins take part in their mechanism of action at the atomic level. The issue of the relationships between structure and mobility therefore arises, and has been tackled in various ways [1–3].

Nuclear magnetic resonance (NMR) has proven to be a unique tool to provide detailed descriptions of internal motions in proteins, and a vast NMR panoply of techniques, relying mainly on spin relaxation measurements, has been developed to access internal mobility in proteins over time scales ranging from picoseconds to milliseconds. Fast motions on the sub-nanosecond time scale involve rotations, vibrations and librations of chemical bonds, and can be related to conformational entropy and other thermodynamical quantities [4,5]. For instance, binding with a ligand or another macromolecule may be associated not only with a local reduction of conformational degrees of freedom in the vicinity of the interaction site [4,5], but also with an increase of entropy in remote parts of the protein, possibly leading to a global favourable entropic contribution to binding [6,7].

Spin relaxation is essentially caused by molecular motions [8–10]. In an attempt to interpret and predict NMR relaxation experiments, we have recently developed an NMR-oriented model for internal protein dynamics, based on a Network of Coupled Rotators (NCR). In this model the protein is represented by an assembly of vectors (defined by selected chemical bonds) that undergo rotational diffusion in a harmonic potential. This potential is defined as a superposition of pair potentials that couple the network vectors to each other and can be thought of as resulting from the combination of various physical interactions (electrostatic, van der Waals, etc.). One of the main features of this approach is that the potentials only depend on the deviation from equilibrium of angles subtended by pairs of vectors, rather than on the position of atoms. In this sense, it is NMR-adapted, as it depends on the orientation of vectors. In previous studies, we have demonstrated the ability of this simple model to predict parameters obtained from NMR relaxation experiments, in particular the so-called generalized model-free order parameters S² and effective correlation times [11,12]. In this article, we extend our previous findings and demonstrate that the NCR approach allows one to predict NMR relaxation rates.

2 Brief outline of the theory

In the NCR approach, each member of an ensemble of bond vectors u_i is assumed to undergo a diffusional “wobbling” motion in a potential $U = \sum_{i < j} U_{i j}$ that results from the superposition of coupling potentials U_ij between pairs of vectors u_i and u_j such that the angle θ_ij between them fluctuates about an equilibrium value $θ_{i j}^{eq}$ defined by the (average) equilibrium structure of the protein. The shape of the coupling potential U_ij is thus like a well with a minimum at $θ^{i j} = θ_{i j}^{eq}$ :

U_{i j} = ρ_{i} ρ_{j} κ_{0} f (θ_{i j} - θ_{i j}^{eq})

(1)

where κ₀ is an adjustable parameter that is common to all pairs of vectors. In the currently preferred implementation of the model, the function f(x) = −P₂(cos x) = −(3cos² x − 1)/2 is the second-rank Legendre polynomial. In order to account for local packing in the protein [2,3], each pair potential U_ij (Eq. (1)) is also made proportional to the product of the local densities ρ_i and ρ_j in the vicinity of chosen ‘reference atoms’ associated with the coupled vectors u_i and u_j. These local densities are defined as the number of atoms in a sphere of radius R_c. Moreover, the coupling between the vectors is only taken into account for reference atoms separated by less than a cut-off distance R_c. Finally, the choice of the vectors that constitute the network may depend on the case at hand. To predict ¹⁵N relaxation rates, as in the present work, it is necessary to include vectors

u (N_{i} H_{i}^{N})

that are collinear to the amide NH bonds. When the motions of the vectors u_i are assumed to have small amplitudes, which amounts to a harmonic approximation, the evolution equations governing the dynamics of the network can be expressed in terms of the vector components in a local molecule-fixed Cartesian frame (a_i, b_i, c_i), such that c_i = 〈u_i〉 [13,14].

The calculation of the amide ¹⁵N NMR relaxation rates of a residue i in a protein requires the knowledge of the Fourier transforms J_ii(ω) of the auto-correlation functions C_ii(t), if we neglect interference effects [15]. The longitudinal and transverse ¹⁵N relaxation times, R₁ and R₂, and the ¹⁵N{¹H} heteronuclear Overhauser enhancement factors (η_NH) are given by:

R_{2 i} = d^{2} (2 J_{i i} (0) + \frac{3}{2} J_{i i} (ω_{N}) + \frac{1}{2} J_{i i} (ω_{H} - ω_{N}) + 3 J_{i i} (ω_{H}) + 3 J_{i i} (ω_{H} + ω_{N})) + c^{2} (\frac{4}{3} J_{i i} (0) + J_{i i} (ω_{N}))

(2)

R_{1 i} = d^{2} (3 J_{i i} (ω_{N}) + J_{i i} (ω_{H} - ω_{N}) + 6 J_{i i} (ω_{H} + ω_{N})) + 2 c^{2} J_{i i} (ω_{N})

η_{NH i} = 1 + \frac{γ_{H}}{γ_{N}} \frac{d^{2}}{R_{1}} (6 J_{i i} (ω_{H} + ω_{N}) - J_{i i} (ω_{H} - ω_{N}))

where

d^{2} = (μ_{0}^{2} ℏ^{2} / 16 π^{2}) ({(γ_{H} γ_{N})}^{2} / 10 r_{NH}^{6})

and

c^{2} = {(γ_{N} B_{0} Δ σ_{N})}^{2} / 15

. In these expressions, r_NH is the average NH distance, γ_H and γ_N are the H and ¹⁵N gyromagnetic ratios, μ₀ is the vacuum magnetic susceptibility, ℏ is the reduced Planck constant, and Δσ_N = σ_∥ − σ_⊥, where σ_∥ and σ_⊥ are the parallel and perpendicular components of the ¹⁵N chemical shift tensor assumed to be axially symmetric. For molecules undergoing isotropic global rotational diffusion, where global and internal motions can be considered to be statistically independent, the local correlation functions C_ii(t) can be factorized [11,12,16]:

C_{i i} (t) = C_{0} (t) C_{i i}^{I} (t) = \exp (- t / τ_{g}) C_{i i}^{I} (t)

(3)

where C₀(t) and

C_{i i}^{I} (t)

are the correlation functions relative to the overall tumbling of the molecule and to the internal motions of the vector

u (N_{i} H_{i}^{N})

and τ_g is the overall tumbling characteristic time. It can be shown that, owing to the harmonic approximation [13,17], the internal auto-correlation function

C_{i i}^{I} (t)

of a vector u_i can be written in the local reference frame in terms of its transverse components only:

C_{i i}^{I} (t) = S_{i i}^{2} + 3 〈 u_{i x} (t) u_{i x} (0) + u_{i y} (t) u_{i y} (0) 〉

(4)

where the order parameter is defined as:

S_{i i}^{2} = 1 - 3 〈 u_{i x}^{2} + u_{i y}^{2} 〉

(5)

Since correlation functions

C_{i i}^{I} (t)

can be obtained from approximate analytical solutions of the rotational Langevin equations that govern the dynamics of the vectors in the network [13,17], relaxation rates can also be predicted directly from our model. Indeed, the correlation functions of the components of the N vectors u_i in the network are described by the vector [13,17]:

V (t) = ⅇ^{A t} V (0)

(6)

where A is the matrix:

A = (\begin{matrix} (D_{1} a_{1}^{x x} - 2 D_{1}) & D_{1} a_{1}^{x y} & D_{1} f_{12}^{x x} & D_{1} f_{12}^{x y} & \dots & \dots & D_{1} f_{1 N}^{x x} & D_{1} f_{1 N}^{x y} \\ D_{1} a_{1}^{x y} & (D_{1} a_{1}^{y y} - 2 D_{1}) & D_{1} f_{12}^{y x} & D_{1} f_{12}^{y y} & \dots & \dots & D_{1} f_{1 N}^{y x} & D_{1} f_{1 N}^{y y} \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ D_{N} f_{N 1}^{x x} & D_{N} f_{N 1}^{x y} & \dots & \dots & \dots & \dots & (D_{N} a_{N}^{x x} - 2 D_{N}) & D_{N} a_{N}^{x y} \\ D_{N} f_{N 1}^{y x} & D_{N} f_{N 1}^{y y} & \dots & \dots & \dots & \dots & D_{N} a_{N}^{x y} & (D_{N} a_{N}^{y y} - 2 D_{N}) \end{matrix})

(7)

The coefficients

a_{i}^{x x}

f_{i j}^{x x}

, etc. in A are defined by the average structure of the molecule through the potential U, and D_i is the diffusion coefficient of the vector u_i [13]. In the NCR model, the diffusion coefficients D_i determine the time base of internal dynamics. For simplicity they can all be assumed to be equal to a common value D. In Eq. (6), V(t) represents the auto- and cross-correlation functions of the x- and y-component of the vectors u_i and a given u_j:

V {(t)}^{T} = [〈 u_{1 x} (t) u_{j β} (0) 〉, 〈 u_{1 y} (t) u_{j β} (0) 〉, \dots, 〈 u_{N x} (t) u_{j β} (0) 〉, 〈 u_{N y} (t) u_{j β} (0) 〉]

(8)

with β = x or y and j can take any of the values j = 1,…, N. The vector V(0) is calculated along with order parameters

S_{i i}^{2}

[13].

3 An example: ¹⁵N relaxation rates of apo-calbindin

In this section, we focus on the case of the calcium-binding protein calbindin and compare our predictions with experimental measurements [18] performed on the apo-form of the molecule [19]. Calbindin D9k contains two EF hand motifs composed of helix–loop–helix sequences. Each of these motifs can accommodate a calcium ion Ca²⁺. It was shown that in the absence of calcium, both these loops and the linker region between the EF hand motifs exhibit higher mobility than the rest of the protein, as attested to by lower model-free parameters S² [18]. This feature can be predicted by the NCR model [13,14]. We will be concerned here with the prediction of experimentally observed R₁, R₂ and ¹⁵N{¹H} NOE relaxation rates, rather than variables such as order parameters or effective correlation times that are meant to approximately model the spectral density functions as Lorentzians. Relaxation of amide ¹⁵N nuclei is mainly driven by the dipolar interaction and by ¹⁵N chemical shift anisotropy (CSA), and interference effects will be disregarded in the following.

For dipolar relaxation, the relevant correlation function is the one involving the vector $u (N_{i} H_{i}^{N})$ defining the amide NH bond. In addition, the same correlation function will describe CSA relaxation in this case, as the principal axis of the (axially symmetric) ¹⁵N CSA tensor is approximately colinear to the NH bond.

Thus, implementing the strategy described in our previous work, the equilibrium values V(0) were calculated, and using Eqs. (3)–(8), the correlation functions $C_{i i} (t) = \exp (- t / τ_{g}) [S_{i i}^{2} + 〈 u_{i x} (t) u_{i x} (0) + u_{i y} (t) u_{i y} (0) 〉]$ involved in backbone ¹⁵N dipolar and CSA relaxation were predicted. The network was defined using four types of vectors: NH, C_αH_α, C_βC_γ (or any other heavy atoms located at this position in the residue) and terminal vectors of lateral chains (LEU: C_γ–C_δ1 and C_γ–C_δ2; MET: S_δ–C_ε; GLU: C_δ–O_ε1; GLN: C_δ–O_ε1; LYS: C_ε–N_ζ; ARG: C_ζ–N_η1; TYR: C_ζ–O_η). Global parameters were adjusted to the following values: R_c = 6.5 Å, κ₀ = 2, and D = 2.08×10⁸ rad² s⁻¹. The overall tumbling is described by a characteristic time τ_g = 4.1 ns obtained from the ratios R₂/R₁ of experimental relaxation rates [18]. Numerical values of Δσ_N = 160 ppm for the ¹⁵N CSA and r_NH = 1.02 Å for the ¹⁵N–¹H distance were used. After numerical Fourier transformation of C_ii(t) giving the spectral density functions $J_{i i} (ω) = \int_{0}^{∞} C_{i i} (t) \cos (ω t) ⅆ t$ , the rates $R_{1 i}^{NCR}, R_{2 i}^{NCR}, η_{NH i}^{NCR}, i = 1, \dots, N$ , for the N residues of the protein, were obtained.

Results are presented in Fig. 1. Relaxation rates were calculated for the set of M = 33 structures of apo-calbindin deposited in the Protein Data Bank [19]. The structural differences amongst this set of structures are responsible for the different values of the predicted rates. Thus, for each residue i in the sequence, a predicted relaxation rate averaged over the set of structures, $Γ_{i}^{NCR} = \sum_{j = 1}^{M} Γ_{i}^{NCR (j)}$ , with Γ = R₁, R₂, η_NH, was obtained. The comparison with experiment was achieved by computing rank order (Spearman) ρ_s and linear ρ_l correlation coefficients [20], as well as the root mean square deviation $σ_{i} = \sqrt{(1 / N) \sum_{i} {(Γ_{i}^{NCR} - Γ_{i}^{exp})}^{2}}$ . The results are quite satisfactory, with values of ρ_s and ρ_l ≈ 0.8, as shown in Table 1. However, there are clear discrepancies between predicted and experimental transverse relaxation rates, attested to by significantly lower values of ρ_s and ρ_l. A model-free analysis of experimental relaxation rates [18] has shown that there is an exchange contribution R_ex to the apparent experimental R_2exp for a number of residues. Adding this contribution to the predicted $R_{2 i}^{NCR}$ and comparing the quantities $R_{2 i}^{NCR} + R_{ex i}$ and $R_{2 i}^{exp}$ greatly improves the result (see Table 1). This is easily explained by noticing that NMR relaxation is sensitive to internal motions that occur on time scales that are shorter than the overall tumbling time τ_g of the molecule. In contrast, exchange contributions to the transverse relaxation rates in proteins originate from chemical shift modulations that take place on the μs time scale or longer. R_ex terms cannot be predicted by our model, which is only designed to describe fast internal motions.

Fig. 1
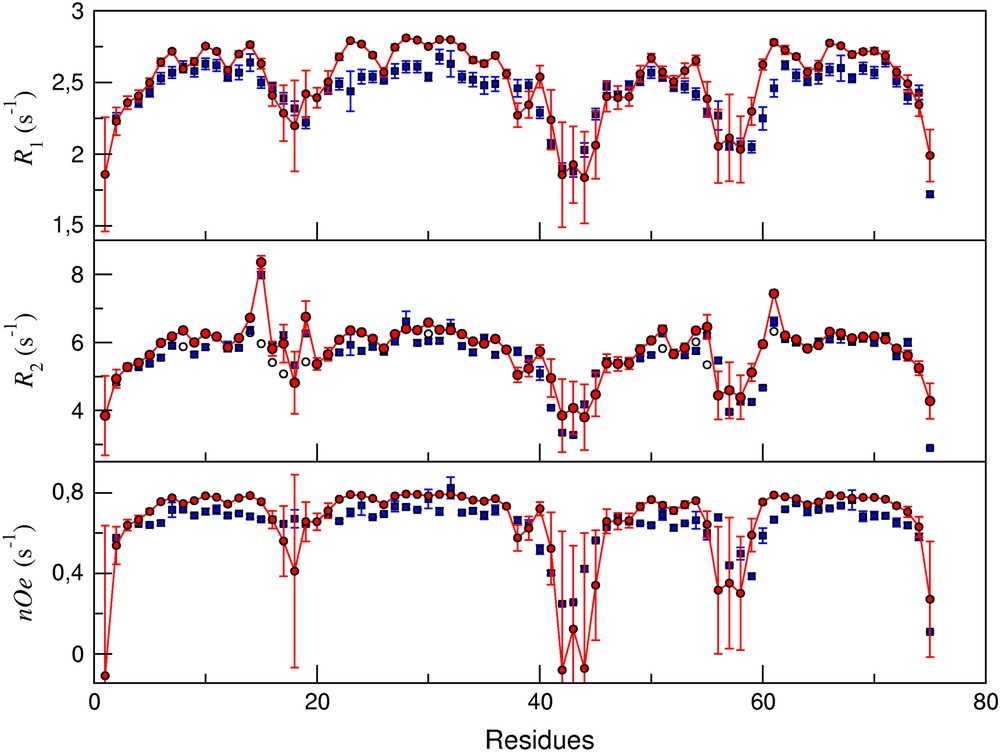
From top to bottom: predicted (circles) and experimental [18] (squares) values of amide ¹⁵N R₁, R₂, and η_NH relaxation rates in apo-calbindin. In the case of transverse relaxation rate, empty circles indicate predicted raw rates, whilst filled circles denote the value $R_{2 i}^{NCR} + R_{ex}$ , where R_ex is the exchange contribution to the transverse relaxation rate.

	ρ_s	ρ_l	σ
$S_{i}^{2 NCR} vs S_{i}^{2 exp}$	0.85	0.82	0.10
$R_{2 i}^{NCR} vs R_{2 i}^{exp}$	0.65	0.72	0.63
$(R_{2 i}^{NCR} + R_{ex i}) vs R_{2 i}^{exp}$	0.84	0.85	0.45
$R_{1 i}^{NCR} vs R_{1 i}^{exp}$	0.84	0.85	0.13
$η_{NH i}^{NCR} vs η_{NH i}^{exp}$	0.77	0.76	0.18

One of the most popular methods used in protein NMR is the so-called model-free approach introduced by Lipari and Szabo [11,12], which is based on the assumption that the internal correlation function in Eq. (3) can be approximated by a mono-exponentially decaying function towards the finite limit $S_{i i}^{2}$ :

C_{i i}^{I} (t) = S_{i i}^{2} + (1 - S_{ii}^{2}) ⅇ^{- t / τ_{e}}

(9)

The effective correlation time τ_e of the model-free correlation function sets the time scale of the internal processes. This simple model has been extended [21] to account for more complex processes where internal motions are better described by two time scales, rather than one. As an alternative, the spectral density mapping (SDM) [22,23] analysis of relaxation data consists in extracting the values of the spectral density function only at the frequencies that contribute to the relaxation rates [8]: J_ii(0), J_ii(ω_N), J_ii(ω_H), J_ii(ω_H ± ω_N). However, since it is not possible to extract five unknowns from only three independent measurements, a reduced spectral density mapping approach has been introduced, where high frequency contributions are assumed to be equal [24–26]: J_ii(ω_H) ≈ J_ii(ω_H ± ω_N). Within this reduced SDM approach,

J_{i i}^{SDM} (0)

J_{i i}^{SDM} (ω_{N})

, and

J_{i i}^{SDM} (ω_{h})

, the approximate value of the spectral density function evaluated at high frequencies, can be extracted from ¹⁵N relaxation measurements:

{\begin{cases} J_{i i}^{SDM} (ω_{h}) = \frac{R_{1 i}}{5 d^{2}} \frac{γ_{N}}{γ_{H}} (η_{NH i} - 1) \\ J_{i i}^{SDM} (ω_{N}) = \frac{R_{1 i}}{3 d^{2} + 2 c^{2}} (1 - \frac{7 γ_{N}}{5 γ_{H}} (η_{NH i} - 1)) \\ J_{i i}^{SDM} (0) = \frac{1}{4 (3 d^{2} + 2 c^{2})} (6 R_{2 i} - R_{1 i} (3 + \frac{18 γ_{N}}{5 γ_{H}} (η_{NH i} - 1))) \end{cases}

(10)

An SDM analysis of amide ¹⁵N relaxation measurements performed on apo-calbindin [18] can be compared to the spectral density functions predicted by the NCR approach (Fig. 2). $J_{i i}^{SDM} (ω_{h})$ is compared to $J_{i i}^{NCR} (ω_{h})$ defined by $J_{i i}^{NCR} (ω_{h}) = 6 J_{i i}^{NCR} (ω_{H} + ω_{N}) - J_{i i}^{NCR} (ω_{H} - ω_{N}) / 5$ . The agreement between values of the spectral densities at ω = 0, ω_N and ω_h, obtained either by NCR predictions, $J_{i i}^{NCR}$ , or by spectral density mapping, $J_{i i}^{SDM}$ , for all residues i = 1,…, N in the protein, is measured by the correlation coefficients given in Table 2. Discrepancies between values of $J_{i i}^{NCR} (0)$ and $J_{i i}^{SDM} (0)$ are noted for some residues, in particular when exchange contributions $R_{ex i}$ are significant. The correlation between $J_{i i}^{NCR}$ and $J_{i i}^{SDM}$ is thus very similar to the correlation between predicted and experimental relaxation rates $Г_{i}^{NCR}$ and $Г_{i}^{exp}$ , and therefore illustrates that both approaches are consistent with experiment to the same level of accuracy. Interestingly, the quantities calculated in the present work yielded significantly higher correlation with experiment than the comparison performed in previous work between the effective correlation time τ_e obtained either by a model-free analysis or predicted by the NCR approach on the same protein (correlation coefficients ρ_s and ρ_l ≈ 0.6) [14]. Altogether, these observations suggest that in this case the correlation and spectral density functions predicted by a network of coupled rotators provide a more relevant picture of internal dynamics than the one afforded by a model-free analysis.

Fig. 2
From top to bottom: spectral density functions J(ω) at frequencies ω = 0, ω_N, ω_h, obtained by reduced spectral density mapping from experimental relaxation rates [18] (squares) and by our NCR approach (circles). For J(0), open squares correspond to an analysis of the raw experimental data, whilst filled squares represent the values obtained after subtraction of the exchange contribution $R_{ex i}$ from the experimental transverse relaxation rate $R_{2 i}^{exp}$ .

	ρ_s	ρ_l
$J_{i i}^{NCR} (0) vs J_{i i} (0)$	0.62	0.69
$J_{i i}^{NCR} (0) vs J_{i i} (0) using R_{2 i}^{exp} - R_{ex i}$	0.78	0.80
$J_{i}^{NCR} (ω_{N}) vs J_{i i} (ω_{N})$	0.84	0.84
$J_{i}^{NCR} (ω_{h}) vs J_{i i}^{SDM} (ω_{h})$	0.67	0.72

4 Conclusion

In this article, we have discussed new implications of a model introduced recently to describe internal dynamics of proteins. This approach is based on the approximate solutions of the rotational Langevin equations for a network of coupled rotators. This model does not rely on molecular dynamics simulations and permits one to predict ¹⁵N NMR relaxation rates, as illustrated for the protein calbindin.

1 Introduction

2 Brief outline of the theory

3 An example: 15N relaxation rates of apo-calbindin

4 Conclusion

3 An example: ¹⁵N relaxation rates of apo-calbindin