1 Introduction
Many tissues and cell organelles present three-dimensional architectures which are closely related to those observed in liquid crystals, with their specific geometries and symmetries. Cell membranes and chromosomes are liquid crystalline, since they are often fluid and show an orientational order of molecules. The structure of many other biological materials is undeniably related to that of liquid crystals, despite they are not at all fluid. They are considered as stabilized analogues of liquid crystals and examples are numerous among the extracellular matrices of skeletal tissues. Myofibrils also in muscle cells show structures related to those of liquid crystals. It was tempting to consider all these analogues as produced by cells in the state of a polymer liquid crystal, which was first fluid and further stabilized by chemical cross-links. Liquid crystalline self-assembly was observed in concentrated solutions of the main polymers extracted and purified from these materials: chitin, cellulose, collagen, actin filaments, some nucleic acids, etc. Recent advances were obtained in this direction, and today liquid crystals appear to be involved in most physical aspects of biological morphogenesis, with their specific defects and textures which also have to be considered in the detailed organization of cells and tissues.
To illustrate these analogies between such biological materials and liquid crystals, let us have a first look to four micrographs in Fig. 1. We compare a thin section of the fibrous material present in a crab carapace (Fig. 1a) and a drop of cholesteric liquid crystal observed between slide and coverslip (Fig. 1b), both pictures showing superposed series of nested arcs. The two other micrographs correspond to a thin section of collagen fibrils in the dermis of a frog (Fig. 1c), and to the patterns produced by a liquid crystal during a phase transition (Fig. 1d). These pictures show two preferred directions alternating in successive layers, and lying at right angle or almost. These comparisons were purely morphological and could be simply incidental, but today it can be asserted that these patterns draw their origin from properties of liquid crystals, mainly geometrical. This was not immediately obvious, for many reasons, and particularly the fact that the considered materials were not at all fluid. We first recall our initial approach of these problems.
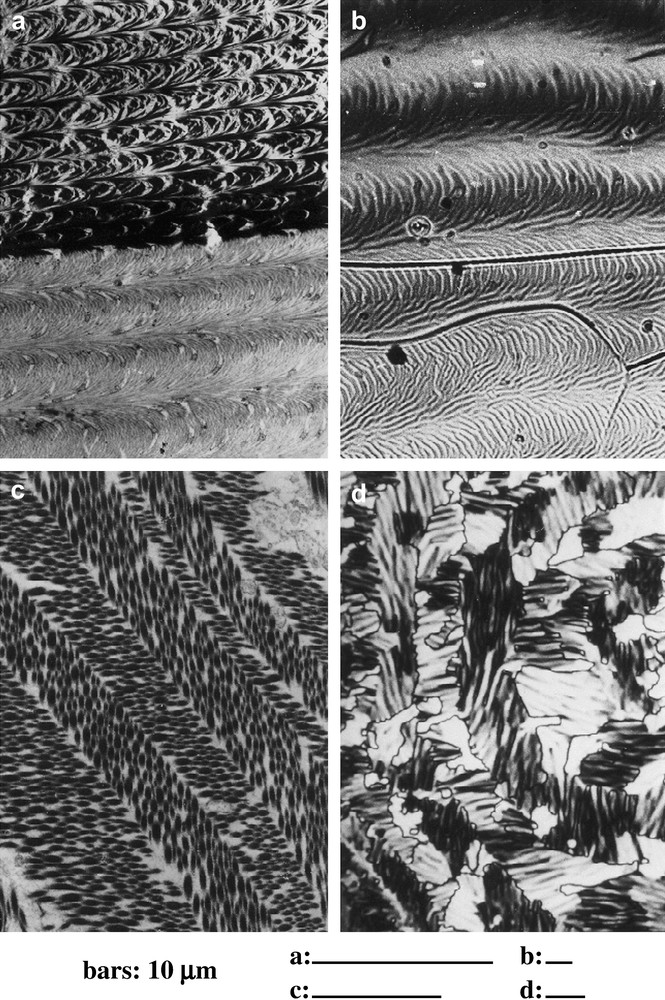
Arcs and chevrons in fibrous biomaterials and in liquid crystals. (a) Series of arcs in an oblique section of a demineralized crab carapace (Carcinus maenas L.), observed in transmission electron microscopy (TEM). The fibrous material is much denser, and less ordered in the upper series deposited before the moult, than in the lower one deposited after the moult. (b) Series of arced patterns in a mixture of cholesterol benzoate and MBBA (4′-methoxybenzylidene-4-butylaniline), a cholesteric phase observed in polarizing microscopy (crossed polars). (c) Chevrons patterns (= herring-bone patterns) in a section of frog epidermis (courtesy of Dr. Lechaire). The collagen fibrils show elliptical contours due to the section obliquity. The preferred orientations of fibrils alternate in layers, and follow two directions at right angle (TEM). (d) In a liquid crystal, passing from a blue phase to a cholesteric one, stripes directions alternate also in successive bands (PM, crossed polars).
2 Arced aspects in systems of straight fibrils
Certain patterns are very common in thin sections of biological tissues, obtained by microtomy, but their classical representations in three dimensions were often very far from being correct. As underlined by Elias [1], ‘misinterpretation of flat images can lead to perpetuated errors’. Most people (and scientists) identify a section with reality. For instance, a flat section through a large folded sheet is a long stripe, which is easily confused with a bent fiber. New stereological methods were introduced to establish more genuine three-dimensional restitutions and also to discuss their physiological implications. Most works were due to Weibel and Elias [2,3]. Here we shall recall another story, that of straight fibrils which were believed to be bent.
The “arced fibrils” were first described in carapaces of arthropods, mainly insects and crustaceans [4–7]. The crab carapace also called cuticle is strongly mineralized, and samples must be decalcified in general before dehydration, embedding and microtomy. Diverse methods are used (acid solutions, chelators, ammonium citrate, etc.), and one obtains a supple fibrous matrix, which is purely organic and can be prepared for microtomy. Insect carapaces are poorly mineralized and can be directly dehydrated and embedded. The thin sections of both materials (insects and crustaceans) showed a fibrous material made of superposed lamellae, each one being made of a long series of nested arcs, with concavities oriented along a common direction (Fig. 1a and further illustrations). The fibrils are made of chitin, a nitrogenous polysaccharide, associated with diverse proteins. We also found papers describing similar patterns superposing parallel series of arcs, in thin sections of certain fish eggshells [8], in compact bones also [9] and in chromosomes of dinoflagellates, an important group of unicellular algae [10]. This was rather surprising to observe a similar organization in so distant biological materials, differing by their chemical composition (chitin, collagen, DNA), their function and their phylogenetic position.
All these parallel series of arcs were interpreted as systems of bent fibrils present in each lamella. Such models were proposed for carapaces of crustaceans [11] and insects [6], for fish eggshells [8], and also for chromosomes [12,13]. Consequently, each lamella of carapace or bone was considered as the result of a secretion cycle, forcing cells to complex movements in order to produce the arced fibrils, and a new secretion cycle was necessary for each new lamella. Applied to chromosomes, such models led to inextricable situations at the time of duplication and cleavage [13,14].
We decided to use serial sections and goniometric methods to analyse these patterns, mainly in crab carapaces, but also in dinoflagellate chromosomes, and finally we found the origin of these nested arcs, as shown in Fig. 2 [15–17]. The arcs were an effect due to the obliquity of sections through a precise 3D-distribution of rectilinear fibrils aligned within each very thin layer, the fibril direction being regularly rotated, when one passes from one layer to the adjacent one, so that one has a system of Cartesian coordinates x, y, z, where the components of the local unit vector n parallel to fibrils can be written as follows:
| (1) |

Model of the origin of arcs in oblique sections of a regularly twisted fibrous system. A pyramidal trunk superposes a series of rectangular cards of constant thickness. Parallel straight lines are drawn on each card and their direction changes by a small and constant angle from one card to the following one. The twist is chosen left-handed, as in most biological materials of this kind. Some arcs were underlined on the oblique face, on the left. The width of the arc series depends on the obliquity and one also observes the opposite orientations of the arc concavities on the left and on the right.
It also appeared that arcs were absent from sections lying at right angle to layers and observed with the section plane rigorously normal to the optical axis of the microscope. Indeed, when such a section was tilted with respect to this optical axis, the arced patterns generally reappeared, oriented either along one direction, or along the opposite one, according to the tilt direction, as shown in Fig. 3, for a crab carapace section observed with the help of a goniometric stage. This was a way to refute the models based on arced fibrils. For certain directions of tilt, the arced patterns ceased to be symmetrical. All these goniometrical results were presented in a work on crab carapaces and dinoflagellate chromosomes [18]. We present here three unpublished views of a bacterial nucleoid, due to J.-P. Gourret, which show superposed series of arcs (Fig. 4). As in crab cuticle, and also in dinoflagellate chromosomes, sections which are normal to layers can be tilted with a goniometric stage and the concavities of arcs can be changed by the appropriate tilt.

A thin section of a demineralized matrix of crab cuticle, oriented normally to layers (C. maenas L., TEM). This section was tilted obliquely with respect to the optical axis of the microscope, in two opposite directions, at two equivalent angles of nearly 40°, in (a) and (b), with a goniometric stage. The slope orientations are specified by the position of the upper and lower sides of the section. At first view the two micrographs seemed to be similar, with oblique white areas corresponding to clefts present in the fibrous network, and forming the same patterns in both pictures. However, the fibrous arcs point in two opposite directions, in (a) and in (b). This effect of opposite tilts on the concavities of arcs was explained in Refs. [17,18] (Courtesy of Dr. M.-M. Giraud-Guille).
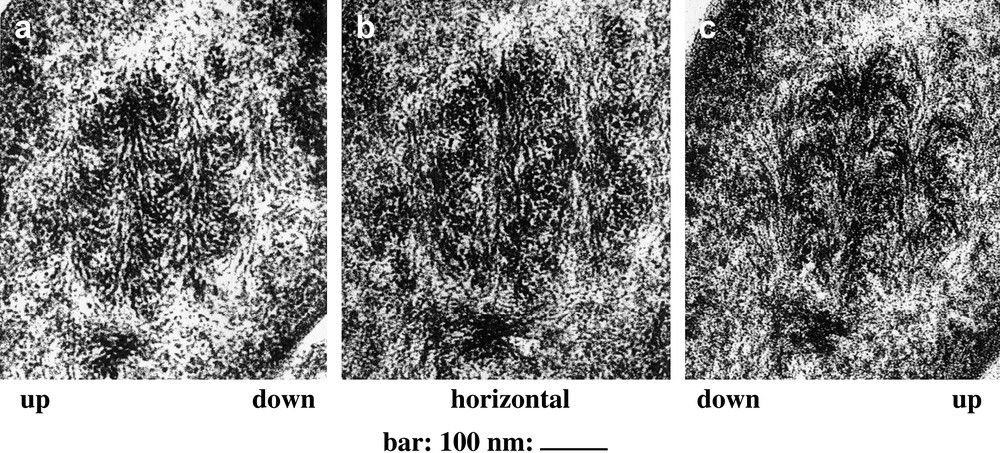
Dense nucleoid of Rhizobium in root nodules of the Leguminosae Sarothamnus scoparius. The same nucleoid is cut normally into layers and observed under three different angles. When the section is tilted, we indicate “up” and “down” to specify the oblique orientation of the tilt. The level lines lie parallel to the direction of the series of nested arcs. (a) The section is tilted at 40° and the arc concavities are oriented upwards. (b) The section is horizontal and the arcs are absent. Filaments in longitudinal view alternate with filaments in cross-section or in oblique section. (c) The section is retilted by 40° in the opposite direction, and the concavities of arcs are oriented downwards (Courtesy of Dr. J.-P. Gourret).
3 Diversity of arced patterns
The distribution of fibrils is much less regular than expected from Eq. (1), as can be seen in Fig. 1a. In each small volume of fibrous material (small enough relative to p/2), a mean direction could be defined with a standard deviation around it, and even an order parameter [17]. This was not an easy problem to define clearly these parameters, since we observed thin sections, with fibrils seen either in longitudinal view, or in oblique view or in nearly cross-section, and goniometric observations were required. In crab carapaces for instance, aggregates were present in the fibrous material and were more extended in upper layers deposited before the moult, whereas the order seemed to be “better” in layers secreted later, after the moult. The helicoidal pitch p also varies with z, so that the thickness of lamellae changes, as in Fig. 1a, and the width of arcs depends on two factors: the section obliqueness and the pitch. Note also that fibrils are made slightly sinuous (instead of straight) owing to the presence of very elongated fingers of cytoplasm penetrating vertically through the matrix.
With this continuously twisted model, the question of repeated cell cycles was simply ruled out for the secretion of distinct lamellae [15,16,19]. The positions of the two limiting planes of each lamella and its series of arcs depend on the orientation of the oblique section plane, as shown in Fig. 2, so that the lamellae do not exist as separable structures and the secretion process is continuous, without any kind of periodic modulation, as required by the ancient models. Many authors admitted that lamellae presented chemical differentiations at their median level, but this was never demonstrated in the biochemical studies, particularly in the lamellar bone [20]. The apparent alternance of clear lamellae alternating with dark ones was due to a microtomy artefact, which created alternating zones of different thickness in the sections [19,21,22].
Each lamella with a series of arcs corresponds to a vertical distance of p/2, a translational period of the structure, and the width L of the arcs depends on the section obliqueness defined by the angle θ separating the section plane from the layer plane and one has L = p/(2 sin θ).
Examples of these arced patterns were found in diverse tissues of animal and plant groups, mainly extracellular matrices, connective and skeletal tissues, but also in several intracellular differentiations [19]. Variations are considerable within these materials, simply in the same crustacean carapace for instance, according to the position in the body and also according to the distance from the outer surface. This is an aspect of biodiversity, with considerable changes also between species. Research will be necessary in this field, and the list of these twisted fibrous materials needs to be completed: the presence of fibrils is often masked but some appropriate methods, as chemical treatments, staining and use of contrast agents can make the arcs visible [23,24]. Polarizing microscopy also is essential to detect these structures.
4 Plywood-like architectures in animal and plant tissues
A common variation observed in these fibrous systems is the differentiation of domains of preferred direction, where the twist is locally excluded. This leads in many cases to an organization closely related to that of “plywoods”, a human invention which was preceded by nature at a microscopic scale, since very similar structures are present in most carapaces, bones and teeth, in many tissues of invertebrate animals and also in plant cell walls. A plywood is a mechanically resistant material, which associates several wood sheets, stuck together, with the grain of adjacent layers lying at right angle to each other, so that the fibers follow two alternating directions.
One easily conceives other plywoods associating more directions of fibrils, three for instance, separated by 60° angles, or four with 45° angles, and even more, as represented in the model of Fig. 2, apparently devised to resist forces in all directions of the plywood plane. Plywoods with two orthogonal or quasi-orthogonal directions of fibrils are present in the compact bone [9] and many other materials. A plywood with three main directions was observed in some crustacean carapaces (copepods) by Haeckel, a very long time ago [25]. More complex arrangements, with right angles alternating with 45° angles, were described in some beetle cuticles [5,26,27], and this topic was later reviewed by Neville in his book on arthropod cuticles [28]. The domains of preferred orientation are often thick layers limited by clear-cut horizontal boundaries, so that the angle α is a simple staircase function of z, which is discontinuous [29]. This was observed in many insects' carapaces, in coleoptera for instance [27,28]. Layers of constant orientation can also alternate with layers of constant twist, and α(z) is then represented by a continuous broken line, with horizontal segments separated by oblique ones of constant slope [28,29].
In the very elongated tibias of locust legs, after a moult, continuously twisted layers are mainly deposited during the night, and alternate with daily growth layers of constant orientation, with fibrils lying parallel to the long axis of the tibia [19,28]. Experiments were realized to test constant illumination versus prolonged darkness, in order to verify this effect and to detect the efficient wavelengths in the ultraviolet range. Temperature also influences these phenomena [28]. Some plywood arrangements associate layers of fibrils which themselves gather numerous aligned subfibrils, a situation found in fish scales [30] and in worms (annelids) [31,32].
Similar plywood structures are present in cell walls of plants, where built mainly with cellulose fibrils, or in cell walls of mushrooms, where fibrils are made essentially of chitin. These natural “plywoods” are either continuously twisted, or show several directions of preferred alignment [24,33].
5 Liquid crystalline self-assembly of twisted fibrous materials
When my first results were published on the fibrous structure of crab carapaces [15,16], I received separates and a letter from Dr. C. Robinson, explaining that my twisted model was similar to the structure recognized in liquid crystals prepared from concentrated solutions of polybenzyl-l-glutamate (PBLG), a synthetic polypeptide and also from concentrated solutions of DNA in water [34]. However, the carapaces were very hard and not at all fluid, in contrast with these liquid crystals. Since the fibrous materials present in carapaces were produced by epidermal cells, it was tempting to consider them as first secreted in a fluid state normally expected in a polymer liquid crystal, this secretion being further stabilized by chemical cross-links, without changing the twisted distribution of polymers. Biomineralization occurred later, increasing the hardness of a carapace comparable to a fiber-reinforced composite [35,36].
All that suggested that the biological materials presenting a twisted fibrous structure could be stabilized analogues of liquid crystals and this also introduced the idea of a process of liquid crystalline self-assembly, occurring within the secreting cells or at their close contact. These ideas were supported by the discovery of liquid crystalline phases in concentrated solutions of polypeptide and nucleic acids [34], and this was later confirmed by several studies on the main polymers extracted and purified from these twisted materials: chitin, cellulose, collagen, nucleic acids, etc [37–42]. Most recent advances were obtained in this direction, mainly by Livolant, Giraud-Guille and their coworkers, as recalled in several reviews presented in this issue.
Research on self-assembly of biological macromolecules was very active for years, from 1950 to 1970 mainly, as illustrated by excellent articles from the Scientific American during this period. Macromolecular subunits assemble into larger systems of definite shape, such as bacterial flagella, actin and myosin filaments, microtubules etc, and even the reconstruction of viruses was obtained from their separated capsomers, nucleic acids and other components [43]. In such assemblies, each subunit remains at a given place in the lattice. On the contrary, in liquid crystals, there is a ceaseless diffusion of molecules. Liquid crystalline assembly was mainly studied in the case of membranes, from their main components, after they had been chemically separated, the best illustrations of such experiments being possibly due to Nageotte in 1936 [44]. One knows that fluid “myelin figures” form spontaneously when water is added to lecithins and some other amphiphilic molecules; these figures, being made of fluid cylindrical bilayers, wrapped more or less concentrically. Other components such as cholesterol and membrane proteins easily intercalate within these fluid bilayers. It was clear very early that membranes were liquid crystalline [45,46], long before that they were recognized as simply fluid [47].
It became obvious that most structures of cells and tissues were either liquid crystals or stabilized analogues [46]. Cells are made up of fluid membranes, external or internal, which are liquid crystalline, with the exception of stabilized areas. The liquid crystallinity of dinoflagellate chromosomes [17,19] could be extended to bacterial nucleoids also, and to the eukaryotic chromatin and chromosomes, as suggested by works on liquid crystalline phases of nucleosomes cores, as presented in this issue by Leforestier et al. In muscle cells, the contractile myofibrils also were compared to liquid crystals, but partially stabilized, as reviewed in Refs. [48–50]. Liquid crystalline assembly of actin filaments was attested to recently [51]. In most skeletal tissues, the extracellular matrices are made up of fibrils which also are stabilized analogues of either nematic or cholesteric liquid crystals, as recalled above and in Refs. [19,48–50].
All these liquid crystals or stabilized analogues represent a mass of matter which could be more than the half dry mass of the body. In plants, the organic matter within cells is mainly liquid crystalline, whereas the plant cell walls lying at the periphery of cells are stabilized analogues of nematic and cholesteric liquid crystals. All these points suggest that a great part of the organic matter of biological materials is or has been liquid crystalline, even briefly before stabilization, and this could be an essential step of differentiation. This passage through a genuine liquid crystalline phase is studied on the example of collagen by Mosser et al. [52]. It is worth remembering that liquid crystals produce spontaneously very complex and reproducible shapes, and this is an essential point to consider about biological morphogenesis, when liquid crystals are involved [53].
6 Defects and textures in liquid crystals and analogues
Perfect crystals are rare or even do not exist, whereas the presence of defects in crystals strongly facilitates their growth. Such faults in the lattice are well known: interstitials, vacancies, edge- and screw-dislocation, walls, etc. Defects also exist in liquid crystals, but the system being fluid, these defects move more rapidly and reach more easily the positions minimizing the elastic energy. Defects arrange therefore into regular distributions, which are called textures and show remarkable geometries and topologies. Similar defects were observed in stabilized analogues, such as arthropod carapaces, and clearly, their distribution appeared to be closely related to the external morphology [15,19,27]. Therefore, it was essential to study the origin of defects in liquid crystals and their collective arrangements [54–56].
All along this work on defects and textures in liquid crystals themselves, I received a considerable help from several physicists, mainly Friedel, Kléman, Cladis, Williams, Toulouse [57–60]. About the biological counterpart of this study, the collaboration of F. Livolant was essential in the study of dinoflagellate chromosomes, and those of Giraud-Guille, Gaill, Lepescheux, Besseau and Moser [18,29–32,52,61] for many examples of extracellular matrices showing strong analogies with liquid crystals. We only published small pieces of our results on defects and textures in these works, since they needed to be confirmed by much more observations, but we can summarize our two main conclusions in this field: the geometry of defects in biological analogues of liquid crystals is close to that of the corresponding defects observed in fluid liquid crystals, whereas the textures strongly differ, mainly at the level of the defect lattice. We suppose that cells maintain a control at the time of the liquid crystalline secretion, mainly by the faculty of changing molecular orientations, through the interactions between the cytoskeleton and the extracellular matrices, across some specialized areas of cell membranes. We think also that these forces exerted by cells on fibrils can be prolonged, when the secretion is slightly gelated. A tentative model of these interactions was presented in Ref. [62]. This represents a considerable domain, far from being explored, and progress will come from studies on fibrillogenesis in numerous biological materials, and from new techniques of image processing. Fibrils are well recognizable in section, but their 3D directions and their connections are less easily established.
7 Image analysis in fibrous systems
Several concepts introduced in the study of liquid crystals can be transposed to their fibrous analogues, the director n for instance and the three curvatures called splay, twist and bend (two scalars and a vector):
The series of nested arcs obtained in oblique sections of a simply twisted fibrous system allow one to understand the two main mistakes encountered in the 3D-interpretations deduced from the 2D-pictures of fibrous structures considered in preparations of cells and tissues. Between two series of arcs, the fibrils seem to diverge, so that the twist is interpreted as a splay. On the contrary, in the median region of a series of arcs, the fibrils seem to be bent. This indicates how a twist is easily confused either with a splay or with a bend.
It would be useful to record automatically the goniometric data, mainly the mean direction, the three different curvatures s, t, b, the order parameter, the local thickness of the section, and to map these data onto the micrograph itself, the section lying in its usual position, normally to the optical axis of the microscope. All that supposes that fibrils are well resolved, with their two extremities well recognizable at the two cutting levels.
It is worth remembering that, for such works, we cannot ignore the numerous artefacts introduced by each step of the preparation techniques: sampling, fixation, dehydration, embedding, etc. Very interesting artefacts occur later, during sectioning, along the fracture which precedes the knife edge progression [19]. Filaments or fibrils can be displaced in the course of this process and each section is limited by two successive cutting planes. One problem is that these “cutting planes” are not strictly planar. Longitudinal streaks are due to small notches along the knife edge, or some particles attached to it. There are also fibrils with changing directions, as in our twisted fibrous systems, and the knife could be slightly deviated from its progression plane. Our carapaces present a periodic distribution of filaments, so that the knife edge oscillates, and ripples form in the section plane. These ripples were easily evidenced at the surface of thin sections, by the use of simple shadowing techniques [21]. Since these ripples are present at the two faces of sections, and do not strictly coincide, they give alternating stripes of higher thickness and contrast. This artefact produces remarkable patterns which are reproducible, and a theory can be proposed [22] and improved. This would be a way to investigate the micromechanical properties of these fibrous tissues and composites. It is worth noting also the presence of long-range deformations of sections, which make them non-planar, so that, here and there, they are observed obliquely with respect to the electron beam.
Briefly, the image analysis of fibrous structures is far from being simple and not limited to questions of contrast and resolution, since the ideal section limited by two parallel planes does not really exist and that diverse aggregated states of fibrils are observed, being natural or artificial, the latter due to fixatives and other preparation techniques. There are also displacements of fibrils (translational or rotational) due to the cutting process, or at the early steps of the sample preparation. Other problems concern the chemical evolution of materials, from fixation to embedding, and the damages produced by the electron beam in the microscope.
Despite these difficulties, remarkable images were obtained, and for instance, the reversal of arc concavities in Fig. 3a and b. Other image effects can be detected by the use of a goniometric stage, mainly dissymmetries of arcs and changes in the position where concavities change in some arc series. The examination of stereoviews is essential, but it would be better to create precise techniques to process the quantitative informations available from goniometry, with the appropriate representations of fibrils in sections.
The improvements of image analysis in fibrous systems could be extremely useful. There are complex situations, which superpose several different distortions. As recalled above, the arcs are often asymmetrical and this can be due to different effects: certain oblique tilts of sections [18], or a microtomy artefacts [22], or simply the presence of preferred orientations in a continuously twisted system [19], exactly as in a true liquid crystal, when an external field is applied in a cholesteric liquid, within the plane of layers (a magnetic field for instance, if the liquid shows a positive diamagnetic anisotropy). We met a similar situation in the study quoted above, on the locust tibias, but here the magnetic field was replaced with a biomechanical stress [19]. During the day, the fibrils were deposited parallel to the length of the tibia, whereas during the night the added layers were continuously twisted, but the direction corresponding to the long axis remained preferred, and asymmetric arcs were observed in certain section planes [19]. However, in this situation, the asymmetric arcs were not confused with a microtomy artefact or any tilt effect of the section. The improvement of techniques in image analysis of fibrous systems would provide a great help in the study of such complex situations, to precisely distinguish what is due to the self-assembly only, what is the result of a biomechanical action under cell control, and what is artefactual.
Another example of complex fibrous structure was that of the bacterial nucleoid, well known to be closely related to that of dinoflagellate chromosomes, mainly for two reasons: (1) nucleosomes are absent from nucleoids and from dinoflagellate chromosomes; (2) similar parallel series of fibrous arcs are present in nucleoids, but in some rare cases only. In these conditions, the reversal of arc concavities was obtained in such nucleoids (Fig. 4), by Gourret, with a goniometric stage, indicating a left-handed twist [63,64], exactly as in dinoflagellate chromosomes [17,18,65]. In general, these arcs are absent for the simple reason that the dimensions of the nucleoid are smaller than the half helical pitch p/2, so that, in most sections, one has less than one series of arcs. We can conjecture that in all bacterial nucleoids, the twist is left-handed, since liquid crystalline DNA seems to be always left-handed, with rare exceptions, due to some defects, which induce a very local right-handed twist as in some defects of left-handed cholesteric liquid crystals [54]. Here also the improvements of image analysis in fibrous systems would be of considerable help to ascertain this conjecture.
8 Stabilization of ordinary liquid crystals and biological fibrillogenesis
A general problem of morphogenesis within a fluid medium is that of the pattern persistence after its differentiation. We know some non-biological examples of liquid crystals which transform into solid resins, by a process associating a polymerization and a reticulation. In such conditions, defects and textures become as “fossilized” and can be studied on thin sections obtained by microtomy from samples of such resins. For instance, mono- and diacrylates of molecules which form liquid crystalline phases were synthesized [58]. These new molecules also gave liquid crystals, nematic or cholesteric, at temperatures around 180 °C, and also the liquid isotropic phase at higher temperatures. These fluid phases, liquid crystalline or isotropic, polymerized into polyacrylates and the diacrylates produced cross-links between the polymers themselves, so that one passed from initial groups of aggregated polymers to a reticulated system. Viscosity first increased and the system transformed into a solid resin.
Polymerization and reticulation did not change the initial molecular orientations, so that the resin of the isotropic phase remained isotropic, whereas that of the liquid crystal remained birefringent [58]. The precise arrangements of textures were not visibly altered by these transformations and, in polarizing microscopy, the thin sections of such stabilized cholesteric resins showed several patterns very similar to those obtained from thin sections in the organic matrix of crab carapaces.
Such solid resins obtained from liquid crystals are not to be confused with those as araldite or epoxy-resins used for electron microscopy of biological materials. After fixation, washing, dehydration and embedding in araldite or epoxy-resins, which polymerize and reticulate at temperatures from 40 to 50 °C, thin sections can be prepared by ultramicrotomy, as in Figs. 1a,c and 3–5.
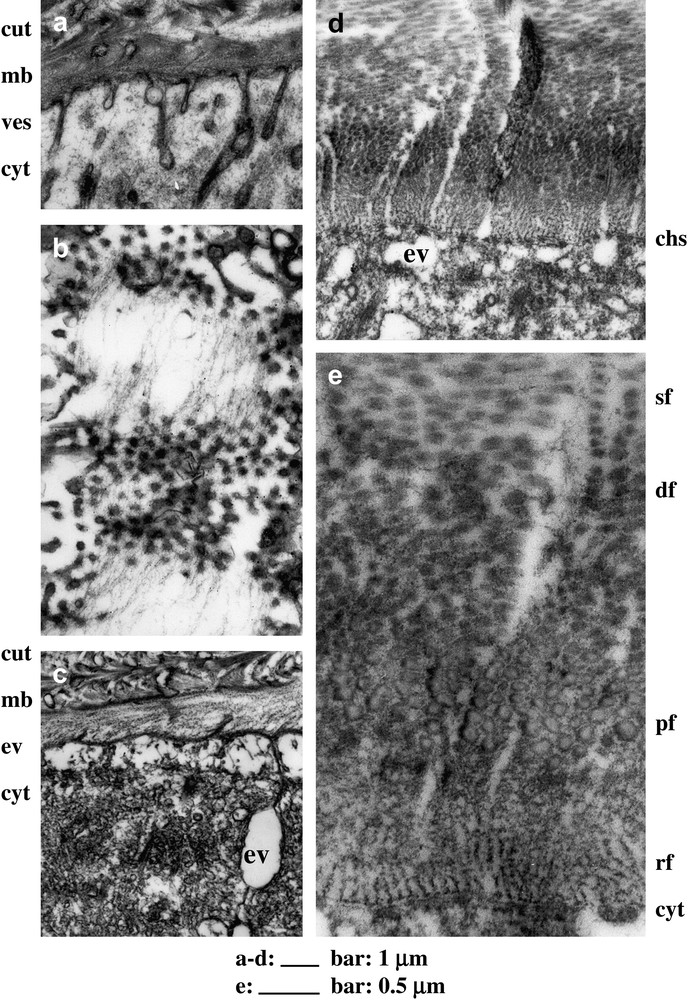
Filaments secretion and fibrillogenesis in C. maenas L.; but the proposed interpretations are still conjectural, mainly about the function of vesicles, about the so-called chitosomes, and about the complex process of fibril assembly. (a) Cuticle (cut) production some days before the moult, vesicles (ves) present in the cytoplasm (cyt) coalesce here and there with the apical membrane (mb), between chitosomes, each one forming a small protuberance containing a dark dot, possibly a set of enzymes, chitin synthetase and other ones, supposed to produce chitin filaments. (b) The same stage of secretion in tangential view, at the level of the apical membrane. Aligned thin filaments lie in the extracellar compartment, joining the protruding chitosomes which appear there as small dots, which are quasi-equidistant in their distribution. (c) Just before the moult, the putative chitosomes seem to be absent, at the level of membrane (mb) between the cytoplasm (cyt) and the cuticle (cut) with the last deposited filaments. Apparently empty vesicles are present and could be involved in the mineralization which will follow the exuviation (or moult). (d) Some days after moult, the secretion of the fibrous matrix is very active and chitosomes (chs) are present, but do not insert within membrane protuberances. The newly deposited filaments are observed in cross-section, so that the arcs are not visible, but the twist is recognizable, since fibrils at the top of the micrograph are in oblique section. Empty vesicles (ev) are present at this stage of active mineralization. (e) An enlarged view of a similar section shows some steps in the transformations of chitin filaments into fibrils and their stabilization, not long after secretion. The initial parallel filaments touch the membrane separating them from the cytoplasm (cyt). These filaments arrange into ribbons (rf), which form polymorphic fibrils (pf) of variable diameter, and further transform into dense fibrils (df), which get thinner and clearly separated (sf).
In crustaceans and in other arthropod cuticles, the fibrous matrix is produced by a secretion which is a highly concentrated solution of chitin and proteins. Thin filaments which associate these two components differentiate at the surface of the apical membrane of epidermal cells, and align in this plane (Fig. 5). This corresponds to an ordered secretion which is liquid crystalline, since alignment and fluidity are realized at the close contact of epidermis. The parallelism of filaments with the epidermis involves also that of cholesteric layers themselves with this epidermis. It appears therefore that cell membranes create strong boundary conditions, with a considerable influence on textures. The cuticle layers lie parallel or nearly parallel to the epidermis and rapidly the shape of the epidermis is maintained by the cuticle itself. But clearly all that needs to be restudied in great detail.
The problem today is to apprehend the differentiation of biological analogues of cholesteric liquid crystals, what comes from liquid crystallinity of the initial secretion, and what is controlled by cells. Progress in this direction can be expected from recent research on another remarkable material, the liquid crystalline phases of collagen.
Classically, collagen is extracted from tendons which are first dissociated mechanically and washed. An acetic acid solution (0.5 M) is added to dissolve collagen and is clarified by centrifugation. The supernatant is reprecipitated in NaCl, 0.7 M, resolubilized and centrifuged, to have a final solution adjusted to 5 mg/ml, for instance. In such collagen solutions, a neutral or an alkaline pH is well known to induce fibrillogenesis.
A glass chamber was devised by Mosser et al. for the examination of collagen solutions in polarizing microscopy. The chamber was first filled by this solution, and this was continued slowly by a syringe to counteract water evaporation, so that the collagen concentration was progressively increased, from 5 to 800 mg/ml or more [52].
These solutions were transparent and isotropic at concentrations ranging from 5 to 50 mg/ml, whereas cholesteric droplets appeared, floating in the isotropic phase, at higher concentrations, from 50 to 400 mg/ml, with long helical pitches. From 400 to 800 mg/ml or more, the solutions were fully cholesteric, showing a much smaller helical pitch, and so tight in some areas, that the cholesteric periodicity was not resolved.
To stabilize these solutions into gels, fibrillogenesis was induced by ammonia vapors [66,67], since a reprecipitation by a NaCl solutions would have generated a strong dilution. A dialysis against NaCl was not really compatible with the experimental constraints, in a glass chamber devised for microscopical observation. Despite this “ammoniacal fibrillogenesis” was far from natural, the images showed similarities with those of thin sections in natural collagen matrices, those of compact bone for instance [68], with some differences, so that these pictures deserved a detailed analysis [52].
As in the liquid crystalline resins considered above [58], the stabilization process worked in both types of collagen solutions, the isotropic ones and the liquid crystalline ones. These solutions transformed into gels showing their collagen fibrils well recognizable in transmission electron microscopy, by their characteristic cross-striations. These fibrils were randomly distributed in the stabilized isotropic phase, whereas they formed superposed series of nested arcs in the stabilized cholesteric phase, and this strongly suggested that fibrils developed along the local directions of molecular alignment, within the liquid crystalline phase (see the contribution due to Giraud-Guille et al. in this issue).
The fibrils were longer and thicker in the diluted isotropic phase, whereas they were much thinner in highly twisted cholesteric areas [52]. This result was expected, since the twist corresponds to a non-alignment of elongated molecules, arranging obliquely with respect to some of their first neighbours, whereas they are aligned within each fibril, according to a crystalline array.
At first view, the pictures of these cholesteric gels, in artificially precipitated collagen, resembled those observed in thin sections of the collagen matrix in compact bones [68], after the removal of the mineral fraction. One observes either regular series of nested arcs or chevrons patterns, which correspond to the two geometries expected in sections of either regularly twisted systems, or plywood-like systems with two preferential orientations.
However, in bones, the collagen fibrils keep a rather constant diameter from 300 to 1200 Å, in both geometries, either in the arced patterns or in the chevrons, whereas in the “ammoniacal gels” of collagen, the fibril diameter varies from 100, in the highly twisted regions, to 5000 Å in less twisted ones and possibly to some micrometers in isotropic zones. In bones, the thick layers of chevrons systems show a preferred orientation of fibrils of equal diameter, close to that observed in continuously twisted layers. This makes an essential difference between these artificial gels and bone matrices. Similar chevrons patterns, with isodiametric fibrils, are observed in dermis of numerous vertebrates, in many fish scales and in the frog dermis, as in Fig. 1c.
Collagen fibrils of extracellular matrices are known to be surrounded by a continuous coat made of proteins and polysaccharides, called proteoglycans. This coat is a quasi-fractal construction, associating long chains of hyaluronic acid, with attached globular and linear proteins, and also second-order lateral chains of chondroitin and keratan sulfates. These branched structures can be arranged to form a cylindrical protection, a sort of felt coat around each collagen fibril [69]. This was possibly selected as being well devised to stop the assembly of collagen molecules at a given diameter of fibrils. This might be also a way to have equal interdistances between fibrils and therefore an even distribution of minerals between fibrils, as required in fiber-reinforced composites. These proteoglycans could be involved in the cell control of fibril direction. This direction is initiated by the liquid crystalline self-assembly, but might be modulated by links associating the cytoskeleton with integrins, fibronectins and finally this proteoglycan coat and the collagen itself [69]. The presence of similar proteoglycan coats around fibrils is very likely in most arthropod carapaces, insects and crustaceans [70], and this could be the origin of the examples of epidermal control on fibril direction, as it was discussed above, about locusts for instance in paragraph 4. The complex transformations of filaments after their secretion by the epidermis in crab cuticle are illustrated in Fig. 5 and suggest the presence of associated macromolecules which could be involved in the control of fibril diameters and of their diverse associations.
9 Problems of growth and form in biological analogues of liquid crystals
Two different types of growth were considered by ancient naturalists [36]. The accretive growth is well known in crystals and in mollusc shells and proceeds by peripheral additions of new materials, which often show concentric growth lines, corresponding to contours at successive steps of development. Things are different in liquid crystals, since diffusion is essential in these fluid media. The intercalary (or intussusceptive) growth is very general in living beings, where new molecules can insert between other ones as in liquid crystals, but does not occur in classical crystals, since most atoms, ions or molecules forming the lattice remain attached at fixed positions, even if some other atoms, ions or molecules can diffuse, because they are less strongly attached. Intercalary growth was also studied in stems and roots of growing plants. Both types of growth, accretive and intercalary, cooperate in the development of bones and in several types of skeletal tissues. The mechanisms of intercalary growth are less easily conceived, since their full description is much more complex than for crystal growth.
The role of liquid crystals and of their more or less stabilized analogues is certainly essential in the study of intercalary growth, but this is still a rather unexplored domain. Paradoxically, useful information about this problem comes also from crab carapaces, which are unable to grow in their two main dimensions, though an accretive thickening of the carapace matrix is observed after each moult, and this is an undeniable growth process.
Such solid carapaces are cast away at definite times of development [4,71], which correspond to the successive moults. Each old carapace is replaced with a new one, first secreted as a thin film deposited by the epidermis, after a process initiated long before the moult itself, and this is the case of all arthropods, in particular crustaceans and insects [5]. The epidermis is made of a single layer of cells, which first detach from the ancient carapace or cuticle. The epidermal cells divide [71], so that the area of the epidermis is strongly increased and numerous folds appear below the ancient carapace. This epidermis secretes a new cuticle, very thin, supple, and purely organic, because not at all mineralized. This new cuticle is folded, since attached to the folded epidermis, and more extended than the ancient carapace. The folds themselves are distributed more or less randomly at the surface of the body.
The first secreted layer is the epicuticle, which is only some micrometers thick, and will be reinforced by fibrils forming the twisted layers of a cholesteric analogue, progressively deposited by the epidermis. This cuticle secreted before the moult is inextensible under the forces which can be exerted in the physiological conditions, and even under much higher forces, if not exceedingly strong. The epicuticle has the precise shape received from a mould which is the external surface of the folded epidermis, at the beginning of the secretion process, and this will be also the form of the crab after the moult, with all the correct metrical details, when this supple cuticle will be completely unfolded, due to a progressive swelling of the body, by water penetration through the gills, and through the oesophagus. This swelling facilitates the ancient carapace to be cast away and all this process is complex.
This series of events takes days or weeks or even months, depending on the body size [4]. After moult (or exuviation), a new set of twisted layers is secreted, and the unfolded cuticle is mineralized. All that leads to a solid carapace, a true sculpture, with specific morphologies and precise details at definite positions, such as bristles, secretory pores, etc. The problem is for geometers that this extremely accurate shape was moulded over a living sheet, the semi-fluid epidermis which was folded more or less randomly. This means that the metrical properties were controlled very locally by the epidermis and the question is to know which can be the cell tools for such a work.
The epidermal cells are prismatic and form a polygonal mosaic in the local epidermis plane. The polygonal contours of cells are reinforced by a grid of belt desmosomes and tight junctions, which correspond to highly stabilized areas of membranes [69]. These belts adhere along the membranes of adjacent epidermal cells, so that they form a grid, which lies just below the outer surface of the epidermis and actually imposes the outer shape of the epidermis. These junctional belts are observed also in most epithelia. The grid of belt junctions in crabs is rehandled at each mitotic crisis, but the epidermis shape is globally maintained from one moult to the following one, with only slight changes, but very precise, as shown by allometric studies. The rehandling of each junction belt by a mitosis requires their opening at two diametrically opposite points and the production of new junction components, in order to close the two resulting belts, just after the separation of the two daughter cells.
The length of each junctional belt is controlled by each cell, and the precise distribution of these lengths creates the local shape of the epidermis. Clearly, some aspects of the genetic control in morphogenesis are involved at this level and occur in a context of transport within cell membranes, which are liquid crystalline or stabilized analogues at the level of junctions. Local destabilization, return to liquid crystallinity, and restabilization of membranes are unavoidable in the rehandling of belt junctions, to position the newly synthesized components, proteins and other ones.
10 The geometric interplay of cells and liquid crystalline assembly
As recalled in Section 5, the main polymers present in biological analogues of liquid crystals can be separated and purified. Then replaced in solution, in the suitable in vitro conditions and in the absence of living cells, these polymers spontaneously align to form a cholesteric phase, so that the alignment direction is given by this process. In the case of collagen considered in Section 8, the fibrillogenesis is obtained in vitro without living cells, and fibrils lie parallel to the molecular alignment given by the liquid crystalline phase. The fibril diameter also depends on the concentration of collagen in the liquid crystalline phase. Accordingly, without living cells, this type of self-assembly suffices to impose fibril diameters and directions [52].
However, in Sections 8 and 9 it was shown that, in extracellular matrices, the fibril directions and diameters can be strongly modulated by cells. These points are not contradictory, but simply indicate that several forces add or interfere in the course of tissue differentiation in situ, but today, the control mechanisms do not seem to be really studied.
A consequence of the interplay between cells and self-assembled matrices is the constant parallelism observed between membranes of secreting cells and the last deposited fibrils. It can be shown geometrically that this suffices to give a layered organization to numerous extracellular matrices, which lie parallel or almost parallel to the membrane plane, with systems of parallel surfaces, separating layers of aligned fibrils. Examples are numerous in animal skins and in plant cell walls [24,27,28,33].
Specific morphologies are produced by systems which superpose fluid layers of constant thickness such as smectic and cholesteric phases, particularly the textures named fans, focal conics, and planar textures [54–56]. The orientation of molecules along the main interfaces is essential in the determination of textures. Diverse tissues also form sets of superposed layers of constant thickness [72], which arrange concentrically in organs, with precise morphologies, often related to those of liquid crystals. The fluidity of cell membranes and of cells themselves explains such morphological similarities, whereas the differences could be due to stabilization, and to boundary conditions imposed by cells and epithelia to give at their contact precise orientations to the self-assembled materials.
Some geometrical properties of parallel surfaces have considerable consequences on morphogenesis. Lets us consider “good surfaces”, which are smooth with a tangent plane. The local shape of a surface S at point M is that of a small disc D of this surface, centered of M. The contour of the disc is chosen so that the geodesic distance r between M and any point of the contour is constant. One says that a surface is locally elliptic when the perimeter p of D is less than 2πr and hyperbolic, if p > 2πr (r very small). This simply means, in the first case, that the surface is like any part of an egg surface, whereas in the second case the surface resembles a horse-saddle. Over surfaces, one often recognizes domains of ellipticity corresponding to convex or concave areas, generally separated by saddle areas or hyperbolic zones. This concept of a disc perimeter which is longer or shorter than the perimeter of a flat disc of the same radius is useful in the study of the above-considered grids of belt junctions in epidermis and in other epithelia. Statistically, hexagonal cells predominate in such grids, but there are also heptagonal and pentagonal cells with some other polygons. Around a pentagon one has a ring of five cells, which is generally shorter than the ring of six cells around an hexagon, which in turn is shorter than the ring of seven cells around an heptagon. Pentagons are found mainly in elliptic zones.
A closely related concept can be introduced when curved surfaces are parallel, so that they maintain constant distances and have common normals. At each point M of a surface S corresponds a point M′ of another surface S′ and MM′ is normal to each surface of the family, at point M″ of a third surface S″, for instance. A small disc D of centre M in S has an image D′ in S′ and D″ in S″. Now consider the areas a, a′, a″ of D, D′, D″ and the distances separating these surfaces. You can deduce the two main curvatures, which fully define the local shape, from the four following parameters: a′/a, a″/a and the two distances e separating S from S′ and e′ separating S′ from S″ [73]. Cells are able to control these four parameters, in several systems where such three parallel layers are realized: cell membranes, most epithelia, and many extracellular matrices: crab carapaces for instance.
Cell membranes show very different shapes: spherical, ellipsoidal, cylindrical, conical, biconcave, toroidal etc. Locally these forms reduce mainly to those of “hats” (or cups) and “saddles”, plus some special cases as cylindrical and conical for instance [74]. In the saddle situation, the paraffinic layer occupies an area which is larger than the mean area of the two associated levels of polar heads, whereas one has the opposite situation for hats [73]. In cylindrical membranes, as in microvilli, the situation is that of equality. Examples concern the plasma membrane itself, and the internal membranes involved in the structure of cell organelles.
Similarly, one finds three recognizable levels in the construction of most epithelia, made up of a single layer of cells. Well-defined areas can be measured at each level: that of apical membranes, that of basal membranes, and that of belt junctions, characterized by the belt length of each cell, to which corresponds a defined area, when these belts are fully extended [69]. Polygons formed by these belts are mainly hexagons, but pentagons and heptagons also exist and positions of hats, saddles, folds, villi, and possibly the preferred orientations of mitoses depend on the distribution of these singular polygons. The extension of these areas and the height of cells depend on the amounts of materials synthesized for the basal membrane, for the belts and for the specific coat of the apical membrane. The heights of cells have also a metabolic control.
In the cuticle deposited before the moult in crabs, one also finds three stabilized levels: (1) the epicuticle; (2) a set of two or three cholesteric layers which are stabilized by a strong reticulation of fibrils, so that fibrils form a multiconnected system, with room for the future mineral in an available space which also is multiconnected, and the system will give after the moult, a bicontinuous arrangement of fibrils and mineral; (3) last layers of the twisted fibrous matrix deposited just before the moult are multiconnected also, with little room available for mineralization. In between these three layers, the fibrils are thinner and much less reticulated, so that the cuticle could be more or less extensible at these levels, and this is an essential point for the unfolding of the cuticle after the moult.
Clearly, to control shapes, living systems use several mechanisms, but among them, two are essential and involve a liquid crystalline machinery. There are the grids of belt junctions, which correspond to stabilized membranes, but their rehandling is required for growth and morphogenesis, involving local destabilizations and new synthesized components, which are transported to precise sites, via the liquid crystalline bilayers of membranes.
There are also the three-layered systems in membranes, in epithelia and in certain extracellular matrices, which build shapes by a control of their relative areas and thickness of these parallel layers.
The genetic controls and regulations involved in morphogenesis are present at these two levels, and at many other ones, but we still do not know the precise mechanisms involved in the context of liquid crystals. Some recent papers consider gene mutations with considerable impact on cuticle structure in embryos of Drosophila melanogaster. The main examples are the gene CS-1 of chitin synthetase-1 [75], and that of rtv, an extracellular protein anchored in membrane and which might bind to chitin [76]. Much progress is expected from cloning such genes, mutated or not, and other ones involved in the production of the main components of cuticle, because the self-assembly experiments reported above are still based on preparation techniques which remain very far from the physiological conditions [37,38]. The newly synthesized filaments in cuticle lie at the surface of the apical membrane of the epidermis, and proteins such as rtv are possibly responsible for the orientational effects discussed above, in Section 4 for instance.
11 Applied perspectives
Liquid crystals are mainly used for their ability to deform under very low external fields, a property used in diverse displays, to produce pictures, a technical aspect of morphogenesis. Today, instead of creating new molecules, numerous scientists prefer to associate them to obtain some unprecedented structures and shapes, which could be useful for diverse nanotechnologies. For instance, there are considerable works on mesoporous materials, devised with lyotropic liquid crystals used as templates [77]. Hexagonal fluid phases given by the alignment of cylindrical micelles, associating the suitable amphiphilic molecules, are mixed with amorphous silica or precursors, which penetrate between the micelles and surround them, to form a honeycomb pattern at the nanoscales. After a passage in an oven at high temperature, the organic part disappears, but the silica resists, forming a porous material. New ceramics were prepared with such techniques, mainly for nanoelectronics, and also a “mesoporous chloroplast” was created [rev. in [77,78]].
Pharmaceutical research also uses liquid crystals, mainly lyotropic phases, to conceive targeted drug carriers or simply to prolong the bioavailability of the active principles. The preparation techniques of such organized micro- and nanoparticles use liquid crystalline phases and also represent an essential chapter in morphogenesis. The main problem is to discover the precise path to follow in a phase diagram in order to reach the interesting phase, which often is metastable (rev. in [78] and see also Saulnier et al. in this issue). Here we considered mainly the cholesteric liquid crystals, stabilized or not, which are scarcely considered in applied biology, but there are considerable perspectives, since we know the liquid crystalline properties of double helical nucleic acids and their remarkable liquid crystalline polymorphism in the presence of nucleosome basic proteins [79]. Proteins such as collagen and many polysaccharides, mainly cellulose and chitin also present highly differentiated phases and textures (see several reviews in this issue). New mineralized biocomposites could be created to serve as implants, with their organic part corresponding to stabilized liquid crystals. Plywood-like organizations are common in cells and tissues, and will be reproduced in new materials. Self-assemblies often work alone, without cells, but cells are able to govern them, mainly when they are fluid, as in the case of liquid crystalline assembly, and to help the process to develop along the appropriate orientations, with the suitable dimensions, as can be shown from examples of fibrillogenesis compared in situ and in vitro without cells.
The future of research on biological liquid crystals will depend on our perception of the three-dimensional organization of living matter and its inner dynamics. Among the new materials that we create, many can interfere with the living matter, and particularly those which are liquid crystals or close analogues. Some of these materials will be devised for such interactions, whereas many others will not, and this could be a considerable source of problems. Most side effects are undesirable, but recent advances in microscopy might facilitate these studies. Image and texture analyses of complex fibrous systems could lead to the conception of new devices close to those invented by nature in the course of biological evolution.


