1 Introduction
Spin crossover between a low-spin (LS) state and a high-spin (HS) state in transition metal compounds is a well-known phenomenon [1]. Especially several octahedrally coordinated iron(II) compounds show a transition between an S = 0 and an S = 2 state which can be induced by temperature or light irradiation. Whereas in diluted systems (e.g. in solution) the spin crossover is essentially monomolecular and the conversion is therefore very gradual, in the solid state the conversion can be much more abrupt and a hysteresis can occur if the intersite interactions are strong enough [1–4].
To obtain compounds with large hysteresis, the cooperativity of the systems, i.e. the intermolecular interactions in the crystal lattice needs to be strong, which can be achieved either by covalent bonding [2] or by noncovalent interactions between the ligands, e.g. stacking of aromatic rings [3,4]. Concerning this latter approach, we have investigated a family of compounds [Fe(PM–L)2(NCS)2], where PM is N-2′-pyridylmethylene and the aromatic subunit L is, respectively, 4-aminoterphenyl [TeA], 4-(phenylazo)aniline [AzA], 4-aminobiphenyl [BiA] and 4-(phenylethynyl)aniline [PEA] [2,3,5]. The members of this family show different spin-crossover behaviours that range from very smooth and incomplete for [Fe(PM–TeA)2(NCS)2], smooth with almost no hysteresis for [Fe(PM–AzA)2(NCS)2], exceptionally abrupt for [Fe(PM–BiA)2(NCS)2] and abrupt with a very large hysteresis (37 K) for [Fe(PM–PEA)2(NCS)2].
The crystal structures of the above [Fe(PM–L)2(NCS)2] complexes have been largely depicted and structural modifications due to thermal [3,5,6], piézo- [7] and photo-induced [8] spin crossover as well as effects of metal substitution and solvent inclusion [9] have been already studied. Direct correlations between structural and physical properties were also drawn and used as a basis for general structure–property correlations in Fe(II) spin-crossover materials [10]. In particular, intermolecular contacts involving S atoms have been identified as directly responsible for the cooperativity in these complexes since the gradual character of the magnetic curve depends almost linearly on the length of this contact [11]. Elsewhere, for these complexes, the temperature of the thermal transition, T1/2, seems to decrease almost linearly when the distortion of the FeN6 octahedron increases [12].
Our aim in the present work is to modify the acetylenic ligand and study the influence on the spin-crossover regime, in particular whether the cooperativity could be further enhanced. To this aim we have synthesized the [Fe(PM–NEA)2(NCS)2] complex where PM–NEA is the N-(2-pyridylmethylene)-4-(naphthalene-1-ethynyl)aniline ligand (Scheme 1). The magnetic susceptibility, the diffuse reflectivity, and the crystal structure at both temperatures 298 K (HS spin state) and 120 K (LS state) will be reported. We will also present the LIESST (light-induced excited spin state trapping) properties recorded at low temperature. This new [Fe(PM–L)2(NCS)2] complex will also be used to validate, or not, the previously reported structure–property statements.
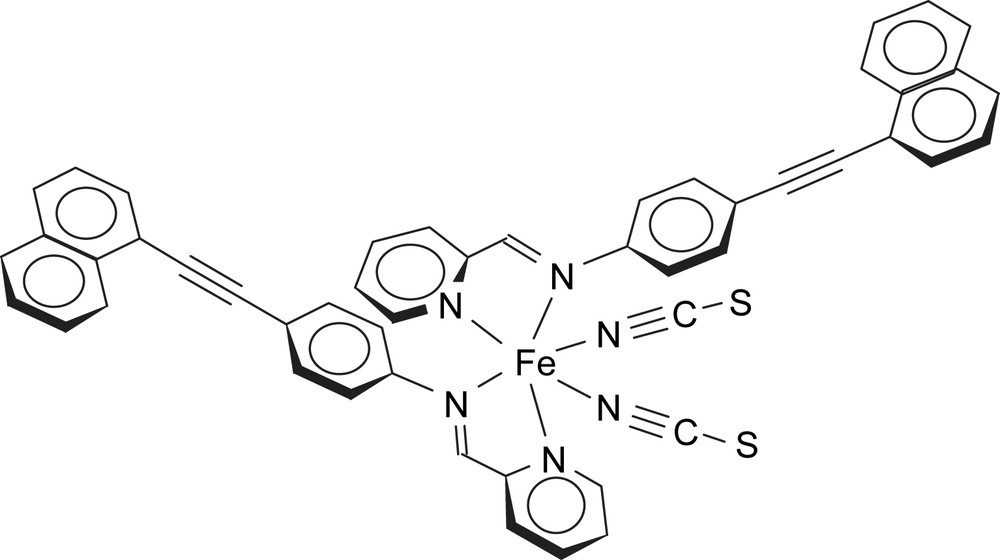
Molecular diagram of [Fe(PM–NEA)2(NCS)2] complex.
2 Experimental
2.1 Materials
[Fe(PM–NEA)2(NCS)2] complex, cis-bis(thiocyanato)bis(N-(2-pyridylmethylene)-4-(naphthalene-1-ethynyl)aniline)-iron(II), was prepared from a solution of the PM–NEA ligand in CH2Cl2 and a methanolic solution of Fe(NCS)2, in analogy to the procedure described in Ref. [3a]. Anal. calcd for C30H32N6FeS2: C, 71.77; H, 3.85; N, 10.04; Fe, 6.67; S, 7.66. Found: C, 70.61; H, 3.97; N, 10.01; Fe, 6.69; S, 7.36.
The Schiff's base PM–NEA was synthesized from 2-pyridinecarbaldehyde and 4-(naphthalene-1-ethynyl)aniline (NEA). The synthesis of NEA unit involves the preparation of the acetylenic amine. For this purpose we have chosen to use p-ethynylaniline as an intermediate which can be coupled with aromatic halide using standard Pd-coupling chemistry [3a,13]. p-Ethynylaniline was synthesized from p-iodoaniline by coupling MEBYNOL with p-iodotrifluoroacetanilide and subsequently deprotecting simultaneously both functional groups [14]; this procedure yielded a pure product that can be conveniently stored at −20 °C without decomposition. p-Ethynylaniline was then coupled to the corresponding aromatic iodide in diethylamine using Pd(PPh3)2Cl2 and CuI as a catalyst [14].
N-(2-Pyridylmethylene)-4-(naphthalene-1-ethynyl)aniline (PM–NEA): the corresponding amine and 2-pyridinecarboxaldehyde were refluxed in ca. 100 ml of benzene with a few drops of acetic acid as a catalyst for 4 h. The solution was neutralized with K2CO3, filtered and the solvent evaporated. The residue was extracted with diethyl ether and evaporated to yield the products as brown oils. 1H NMR (CDCl3): 8.74 (d, 1H, J = 4.4 Hz), 8.65 (s, 1H), 8.46 (d, 1H, J = 8.1 Hz), 8.23 (d, 1H, J = 8.9 Hz), 7.89–7.77 (8m, 4H), 7.72 (m, 2H), 7.64–7.45 (m, 3H), 7.43 (m, 1H), 7.34 (m, 2H). 13C NMR (CDCl3): 88.2, 94.1, 120.9, 121.4, 121.8, 122.0, 125.3, 126.2, 126.4, 126.8, 128.3, 128.8, 130.4, 132.7, 133.2, 133.2, 136.7, 149.8, 150.8, 154.4, 161.0.
(4-Naphthalene-1-ethynyl)aniline (NEA): 585 mg (5 mmol) of p-ethynylaniline and 5 mmol of aryl iodide were dissolved in 50 ml of diethylamine under a nitrogen atmosphere. About 0.1 mmol of bis(triphenylphosphin)palladium(II)chloride and 0.2 mmol of CuI were then added and the mixture was stirred for 20 h at room temperature (TLC control silica/CH2Cl2). The solvent was evaporated in vacuo and the residue extracted three times with diethyl ether. After evaporation, the product was purified by column chromatography (silica/CH2Cl2) and recrystallized using CH2Cl2/petroleum ether. Yield: 740 mg (60%, 3.05 mmol). IR (KBr): 2200 (CC). 1H NMR (CDCl3): 3.85 (s, 2H), 6.69 (m, 2H), 7.44–7.62 (m, 5H), 7.73 (m, 1H), 7.80–7.88 (m, 2H), 8.47 (m, 1H). Anal. calcd for C18H13N: C, 88.86; H, 5.39; N, 5.75. Found: C, 88.74; H, 5.40; N, 5.82.
2.2 Magnetic and photomagnetic measurements
The magnetic susceptibility measurements were obtained with an MPMS-55 Quantum Design SQUID magnetometer. Photomagnetic experiments were carried out by using the light source of a Spectra Physics Series 2025 Kr+ laser (λ = 647 nm, optical power adjusted to 5 mW cm−2) coupled via an optical fibre to the cavity of the SQUID magnetometer. Photomagnetic samples consisted of a very thin layer of the compound. Its weight was obtained by comparing its thermal spin-crossover curve with the curve recorded with a heavier and accurately weighed sample of the same compound. The procedure to measure the T(LIESST) temperature was as previously published [3b,15].
The measurement of the diffuse absorption spectra and reflectivity signal was performed by using a custom-built set-up equipped with an SM240 spectrometer (Opton Laser International). Under illumination with broad band source, this equipment allows us to record both the diffuse absorption spectra within the range of 500–900 nm at a given temperature and the temperature dependence (5–290 K) of the reflectivity signal at a selected wavelength (±2.5 nm). The diffuse reflectance spectrum was calibrated with respect to activated charcoal (Merck) as black standard and barium sulfate (BaSO4, Din 5033, Merck) as white standard.
2.3 X-ray diffraction
The needle-shaped dark single crystals of the title compound show a poor diffraction pattern with no Bragg peaks at high θ angle. After preliminary selection by X-ray, the best sample was mounted on a Bruker–Nonius κ-CCD diffractometer, Mo Kα radiation (0.71073 Å) at 293 K and a data collection was run by means of ϕ scans, 2° per rotation frame, 600 s per frame and a crystal–detector distance of 26.0 mm. The same sample was then cooled at a rate of 2 K min−1 to 120 K where the diffraction pattern proved to be slightly better, and a larger data collection was run by means of mixed ϕ and ω scans, 2° per frame and 300 s per frame. The structural determination by direct methods and the refinement of atomic parameters based on full-matrix least squares on F2 were performed using the SHELX-97 programs [16] within the WINGX package [17]. Hydrogen atom positions were all calculated. The twin law (1 0 0, 0 −1 0, 0 0 −1) has been introduced for the atomic parameters' refinement in both high- and low-temperature crystal structures. This twin law was applied using two twin components with about the same final refined relative weights. Moreover, due to the vicinity of the unit cells to a higher symmetry, orthorhombic and tetragonal (low-temperature) solutions were tested but gave no acceptable solution. Results are summarized in Table 1. Full experimental and crystal data can be obtained with the supplementary crystallographic data for this paper, numbers CCDC-681125 and CCDC-681126.
X-ray diffraction experimental and crystal data for [Fe(PM–NEA)2(NCS)2]
| Formula | FeC50H32N6S2 | |
| Spin state | HS | LS |
| T (K) | 293 | 120 |
| System | Monoclinic | |
| Space group | P21/c | |
| Space group_Z | 4 | 4 |
| Formula_Z | 4 | 4 |
| a (Å) | 16.489(5) | 16.510(5) |
| b (Å) | 15.732(5) | 15.540(5) |
| c (Å) | 16.016(5) | 15.550(5) |
| β (°) | 90.30(1) | 90.10(1) |
| V (Å3) | 4155(2) | 3990(2) |
| ρcalc (g/cm3) | 1.338 | 1.393 |
| μ (Mo Kα, mm−1) | 0.507 | 0.528 |
| Crystal size (mm3) | 0.30 × 0.10 × 0.10 | |
| θmax for data collection (°) | 21.07 | 24.99 |
| Completeness (%) | 95.1 | 99.4 |
| Collected reflections | 15 870 | 26 559 |
| Unique reflections | 4283 | 6992 |
| Observed reflections | 3611 | 5556 |
| Rint | 0.040 | 0.070 |
| Parameters | 533 | 533 |
| Refinement on | F2 | F2 |
| S | 1.05 | 0.96 |
| Robs (Rall) | 0.043 (0.056) | 0.056 (0.080) |
| wR2obs (wR2all) | 0.108 (0.119) | 0.154 (0.174) |
3 Results and discussions
3.1 Magnetic and photomagnetic properties
The variation in the magnetic susceptibility of [Fe(PM–NEA)2(NCS)2] with temperature is shown in Fig. 1. It can be seen that at 300 K the χMT product, where χM is the molar magnetic susceptibility and T the temperature, is near to 2.73 cm3 K mol−1, suggesting that approximately 80% of the iron(II) metal centres behave as in the quintet HS state. On cooling, the magnetic signal drops gradually and reaches a minimum value close to 0.06 cm3 K mol−1, as predicted for a singlet LS ground state. The warming curve shows no thermal hysteresis. The measurement of a gradual SCO transition indicates that the degree of cooperativity between the iron metal centres in the [Fe(PM–NEA)2(NCS)2] complex is weak.
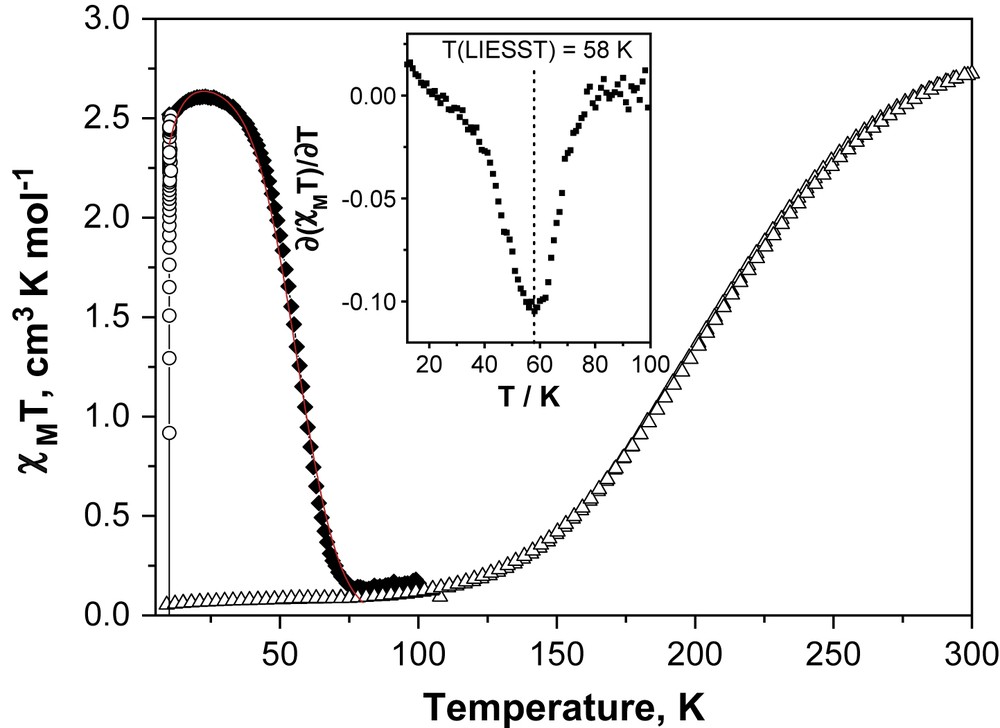
Temperature dependence of χMT. Δ = Data recorded in cooling and warming modes without irradiation; ○ = data recorded with irradiation at 10 K; ♦ = T(LIESST) measurement, data recorded in warming mode with the laser turned off after irradiation for 1 h. The solid line through the T(LIESST) measurement shows the fit generated from the deduced experimental thermodynamic parameters (k0 = 6.5 × 10−5 s−1, Ea = 200 cm−1, k = 0.12 s−1 and σ = 64 cm−1). The insets show the derivate of the dχMT/dT curves, whose minimum corresponds to T(LIESST).
The thermal spin-crossover behaviour can also be monitored by following the visible spectrum of the sample as a function of the temperature, measured by diffuse reflectance (Fig. 2). The broad diffuse absorption band at 800–870 nm corresponds to a d–d transition of the HS iron(II) centre, while the absorption in the 500–750 nm region can be assigned to both d–d and MLCT (Metal to Ligand Charge Transfer) transitions of the LS iron metal centre. Consequently, any change in the signal can be directly used to monitor the thermal SCO transition at the surface of the sample. The increase in the diffuse absorption in the 600–700- nm range from room temperature down to 100 K corresponds to the increasing population of the LS state following thermal SCO. The same reflectivity experiment can also monitor any light-induced phenomena occurring at the surface of the sample. When the temperature is sufficiently low that relaxation of the photo-induced high-spin state is slow, the light intensity at the surface of the sample can be used to tune the spin state of the complex. In this sense, the diffuse absorption bands (Fig. 2), which decrease (or increase) along the thermal spin transition and reversely increase (or decrease) at lowest temperature, from 100 K to 10 K, are a clear indication that the LIESST phenomenon occurs. The occurrence of a photo-induced effect is also evidenced by following the change in the reflectivity signal recorded at 617 nm (Fig. 3). The diffuse reflectivity signal, which decreases along the thermal spin transition, reversely increases at lower temperatures. Moreover, from the comparison of the signal recorded at 10 K and the one recorded at room temperature, it is suggested that the photo-excitation at the surface is almost quantitative.
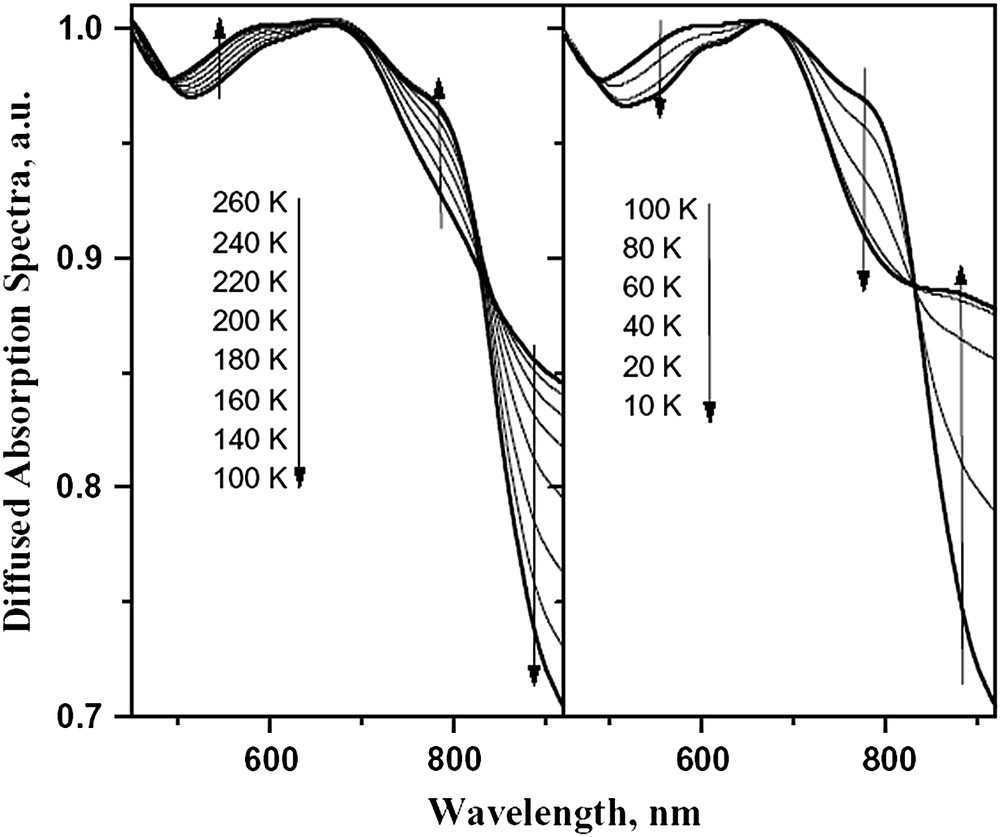
Diffused absorption spectra of [Fe(PM–NEA)2(NCS)2] complex over 290–100 K for the thermal SCO (left) and 100–10 K (right) for the LIESST effect.
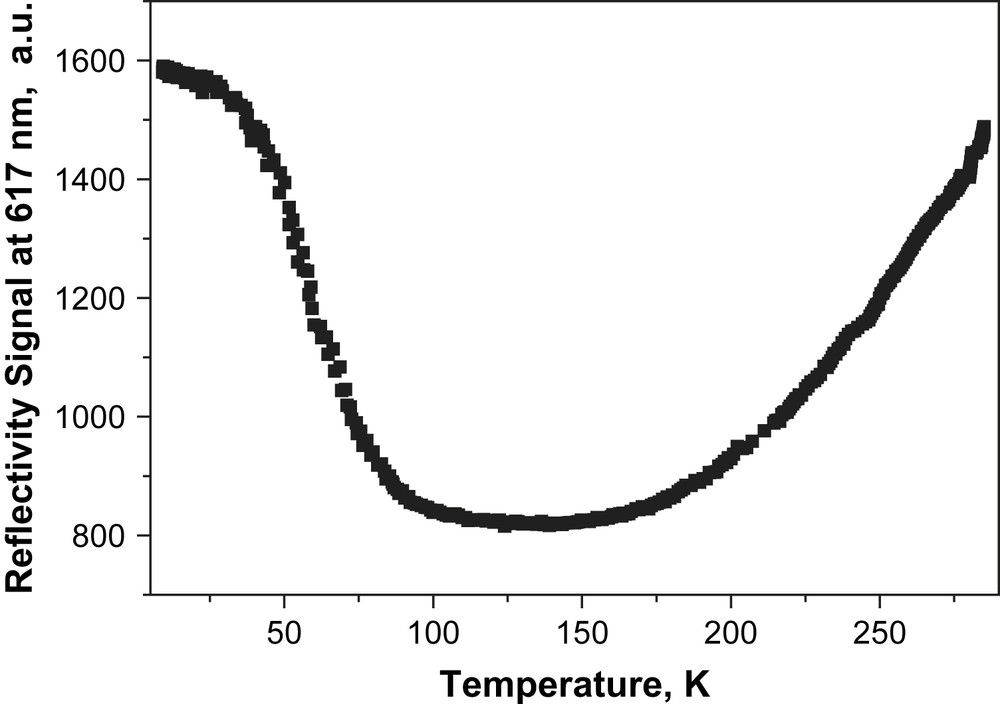
Evolution of the diffused reflectivity signal recorded at 617 nm (i.e. related to the d–d and MLCT bands of the LS state) upon cooling and upon laser irradiation.
We have then decided to study the LIESST effect in bulk condition, using a SQUID magnetometer coupled to an optical source. Fig. 1 shows the photomagnetic behaviour of [Fe(PM–NEA)2(NCS)2]. At 10 K, irradiation results in a sharp increase in χMT. The magnetic signal reaches saturation under light irradiation at a value close to 2.51 cm3 K mol−1. As the temperature is increased in the dark to 0.3 K min−1, χMT initially increases slightly before reaching a plateau and then decreases sharply to recover the magnitude before irradiation. The small increase in the magnetic signal recorded at low temperatures corresponds to the anisotropy of the HS iron(II) ion in octahedral surroundings, also known as zero-field splitting. The χMT of the plateau is nearly identical to that observed at room temperature, suggesting an almost quantitative conversion of the LS state to the metastable HS state on irradiation. The almost zero value recorded at high temperature indicates the occurrence of complete relaxation from the metastable HS state to the LS state. The T(LIESST) values were estimated to be 58 K.
Fig. 4 displays the decay kinetics for the metastable LIESST state recorded in the 10–60 K temperature range, i.e. up to the highest temperature where the decay of the metastable state can be satisfactorily monitored with a SQUID set-up. The most striking feature of these relaxation curves is the strong deviation from single exponential with a marked stretched exponential behaviour, with a fast component at earlier times and a long decay process at infinite times. Such stretched exponential behaviours have already been mentioned in disordered systems, like an iron(II) spin-crossover complex dispersed into a polymer matrix [18] or organized on a surface by the Langmuir–Blodgett technique [19], or even pure iron(II) materials [20]. For reproducing this type of curves, Hauser et al. [18] used a distribution of relaxation rates at a given temperature with a Gaussian distribution of the activation energy. Following this procedure, the relaxation curves of the [Fe(PM–NEA)2(NCS)2] complex can be satisfactorily fitted as illustrated by the solid lines in Fig. 4. The apparent activation energy, Ea (= 203 cm−1), and the apparent pre-exponential factor, k∞ (= 0.12 s−1) of the activated region are calculated from the straight line of the ln kHL(T) vs. 1/T plot (Fig. 5). The standard deviation of the activation energy in a Gaussian approach is 64 ± 8 cm−1.
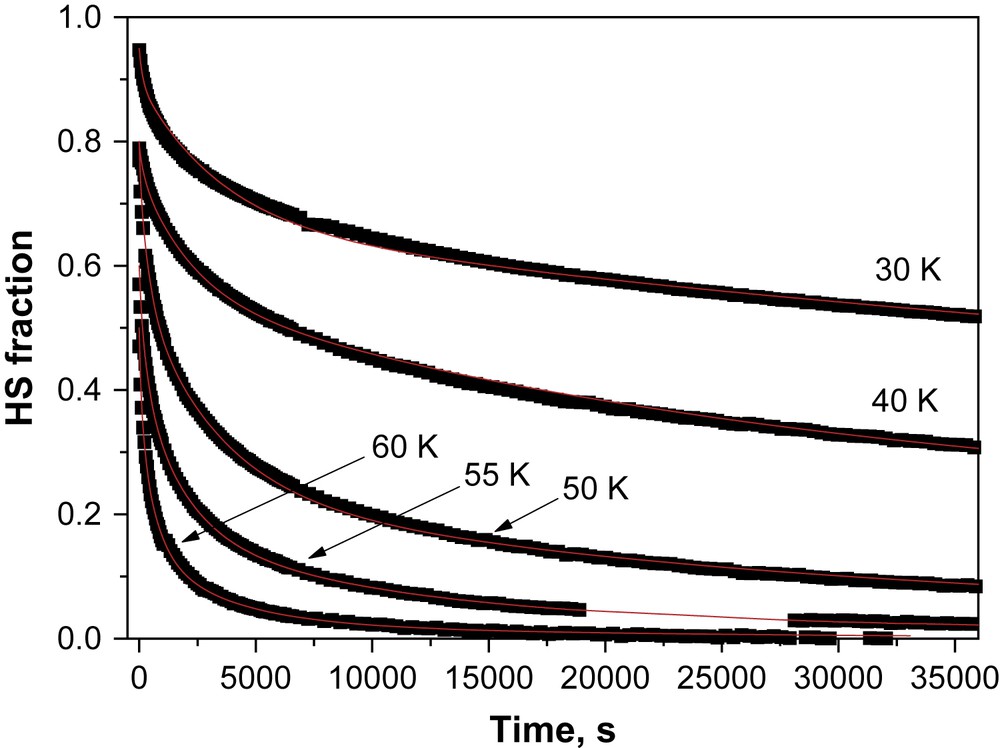
Time dependence at various temperatures of the high-spin molar fraction generated by light irradiation at 10 K. Each point represents the high-spin fraction deduced from the magnetic response measured within the SQUID magnetometer for 30 s. The relaxation curves are fitted according to stretched exponential model (Table 2).
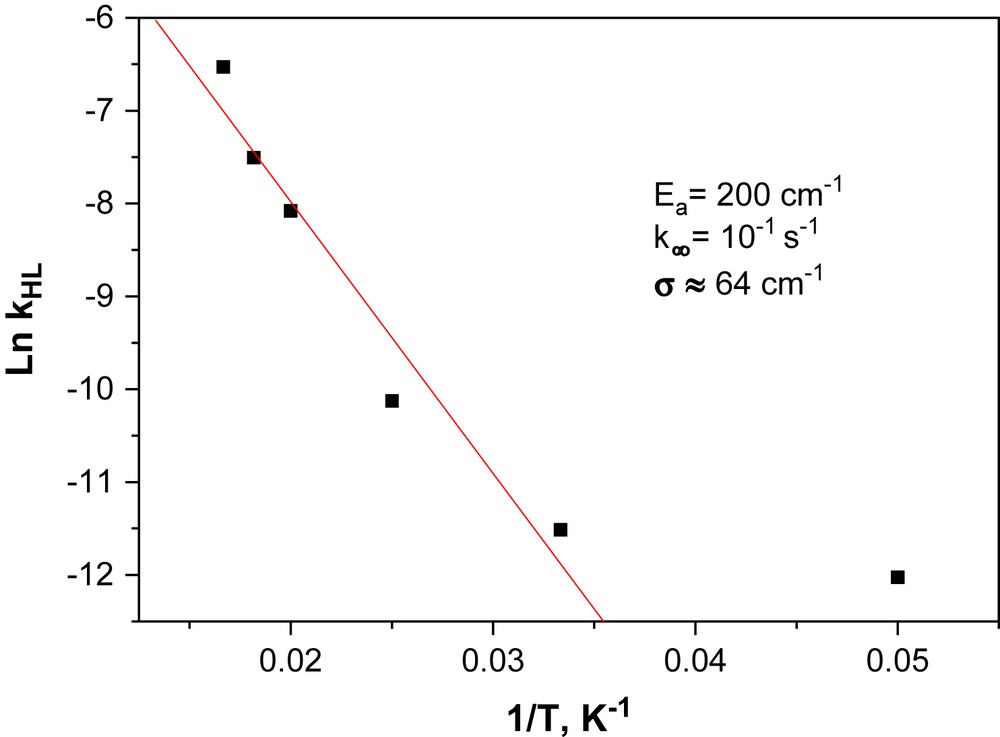
Logarithm of the rate constant kHL vs. 1/T plot of [Fe(PM–NEA)2(NCS)2] complex used for estimating the activation energy (Ea), the pre-exponential factor (k∞) and the distribution width of the activation energy in the Gaussian approach (σ).
An elegant way to account for the kinetic parameters is to use them for reproducing the experimental T(LIESST) curve [15,21]. Briefly, it is now well established that the T(LIESST) curve combines the relaxation of both the tunneling and the thermally activated regions, and we have demonstrated that for a non-cooperative spin crossover, the time dependence of the HS fraction at temperature Ti can be obtained by the following Eq. (1) [15,20,21]:
| (1) |
The rate constant k0 [i.e. kHL(T → 0)], which characterizes the relaxation in the quantum mechanical tunneling region, is estimated as an upper limit from the last complete kinetic measurement recorded at low temperature, i.e. at 40 K (Table 2). Another difficulty arises from the fact that the relaxation process of [Fe(PM–NEA)2(NCS)2] complex does not follow a purely exponential behaviour, as expressed by Eq. (1), but a marked stretched exponential behaviour with a Gaussian distribution of the activation energy. We have then decided to simulate the T(LIESST) curve as a Gaussian distribution of individual T(LIESST) curves with different activation energies [20a]. Based on this, and by using the deduced experimental parameters we have calculated the T(LIESST) curve (solid line) in Fig. 1. The agreement between the calculated and the experimental T(LIESST) curves is very good, which confirms that both the experimental kinetic parameters used in this simulation as well as the fitting procedure are adequate.
Kinetic parameters of the photo-induced HS → LS relaxation process with kHL the rate constant at a given temperature (T) and σ the standard deviation in activation energy according to a Gaussian distribution
| T (K) | 20 | 30 | 40 | 50 | 55 | 60 |
| kHL (s−1) | 6 × 10−6 | 1 × 10−5 | 4 × 10−5 | 3.1 × 10−4 | 5.5 × 10−4 | 1.46 × 10−3 |
| σ (cm−1) | 50 | 65 | 70 | 72 | 64 | 65 |
3.2 Crystal structures' description
3.2.1 General description
Up to now, there are only two kinds of crystal packing encountered in [Fe(PM–L)2(NCS)2] complexes, since some of them crystallise in the orthorhombic space group Pccn while the others crystallise in the monoclinic space group P21/c. In both cases, however, the unit cell contains four molecules. In the orthorhombic packing, the iron complexes lie on a two-fold axis and are thus aligned. Within the ab plane the neighbouring molecules are symmetrical about the screw axis and so lie in an antiparallel orientation. The monoclinic description is very close except that the iron complexes are not anymore aligned and the centres of adjacent molecules form a zigzag. The packing appears relatively compact in all cases and is driven by π–π interactions and short hydrogen-like intermolecular contacts. [Fe(PM–NEA)2(NCS)2] belongs to the monoclinic description in both HS and LS states.
3.2.2 Metal coordination sphere and molecular geometries
Examination of the geometry of the coordination sphere allows us to know the spin state of the complexes in the determined crystal structures (Table 3). The metal ligand bond lengths correspond to an HS at 293 K and to a pure LS state at 120 K. The variation in the average Fe–N distances from HS to LS (−0.186 Å) appears lower than the usual value for the FeN6 octahedron (−0.20 Å) [10,22]. This is due to a slightly shorter Fe–Npyr distance in HS than the usual values in the [Fe(PM–L)2(NCS)2] series. Note that only one of the Fe–Npyr distance (Fe–N5 = 2.196(5) Å) is relatively short in comparison with the usual value (∼2.26(2) Å), since its corresponding Fe–N distance on the other ligand is a typical one (Fe–N4 = 2.251(4) Å) (Fig. 6). The spin state of the complex in both crystal structures is confirmed by the distortion Σ parameter values that correspond to the value of the HS and LS states, respectively [7a]. This parameter shows that the iron coordination sphere goes from a strongly distorted octahedron, almost a trigonal prism, in HS to a slightly distorted octahedron in LS. The polyhedron volume decreases by 25% at the transition. The modification of the geometry of the coordination sphere in [Fe(PM–NEA)2(NCS)2] at the spin crossover confirms thus the usually observed effects of the spin crossover on a FeN6 octahedron.
FeN6 octahedron geometry in [Fe(PM–NEA)2(NCS)2]
| T (K) | Spin state | dFeN (Å) | Σ (°) | Vp (Å3) | Θ (°) |
| 293 | HS | 2.146 | 77 | 13.0 | 221 |
| 120 | LS | 1.959 | 47 | 10.1 | 137 |
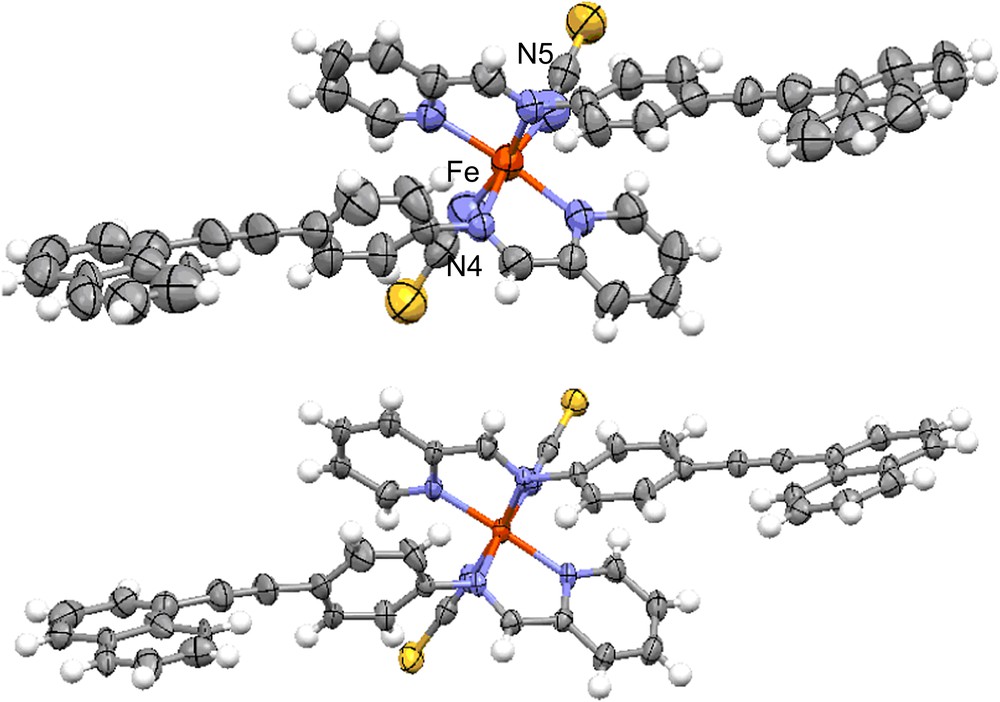
ORTEP diagram with thermal ellipsoids cut at the 50% probability level for non-H atoms in [Fe(PM–NEA)2(NCS)2] at 293 K in HS (high) and at 120 K in LS (low). For visualizing colours, see the web version for this article.
The atoms of the molecule and particularly the naphthalene rings are affected by a strong disorder at 293 K that has almost disappeared at 120 K, confirming its dynamical nature (Fig. 6). The molecular geometry pointed up by angles between ligand rings demonstrates a strong dissymmetry of the complex at 293 K in HS (Fig. 7). The large disparity shown by the angles between the phenyl and naphthalene rings of each ligand (ϕ1 = 48.6° and ϕ2 = 10.3°) is the main feature of this dissymmetry. When the ϕ angle between phenyl and naphthalene rings is high, pyridylmethylene rings appear almost orthogonal (α1 = 89.5°) and when phenyl and naphthalene rings are almost coplanar, the angle between pyridylmethylene rings decreases (α2 = 64.2°). Naphthalene rings of the two ligands within the molecular complex are almost coplanar (ω = 7.6°). The spin crossover has almost no effect on the molecular dissymmetry, since the differences between each ligand side remain despite these angles being slightly modified at 120 K in LS (ϕ1 = 56.0° and ϕ2 = 12.8°; α1 = 83.0° and α2 = 74.6°; ω = 7.9°).
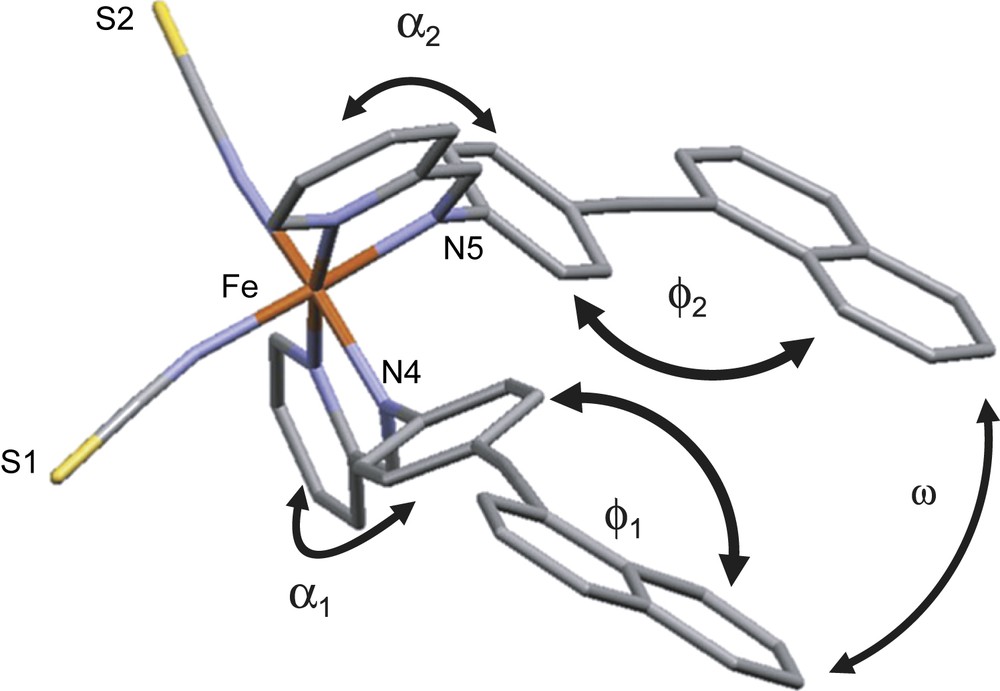
View of the molecular complex [Fe(PM–NEA)2(NCS)2] and nomenclature of the angles between rings of the ligands discussed in the text. Angles are understood as angles between the average planes defined by all the atoms of the corresponding ring. For visualizing colours, see the web version for this article.
3.2.3 Unit cell parameters
The modification of the unit cell volume from 293 K to 120 K is ΔV = 165 Å3, i.e. ΔV = 4%. Note that this value also corresponds to the modification of the macroscopic sample volume by definition in the case of a single crystal and if there is no change of unit cell choice to describe the crystal network. This value, however, takes into account both thermal contraction and spin-crossover contributions. The former is known to be of about 2% in this temperature range for this kind of complexes [6a,9a]. The modification of the unit cell volume and thus of the macroscopic sample volume due to the sole spin crossover is then ΔVSC ∼ 2%, which perfectly matches the usual value for discrete structures based on mononuclear Fe(II) complexes [10].
The modification of the unit cell parameters is highly anisotropic. From 293 K to 120 K, the a unit cell parameter remains almost constant (+0.13%), while the b and c parameters strongly decrease (−1.22% and −2.90%, respectively). Since the a parameter matches the length of the PM–NEA ligands, b almost matches the –NCS ligand line and c matches the long axis of the naphthalene rings, the anisotropic character of the unit cell contraction must correspond to the modifications of the intermolecular interactions.
3.2.4 Naphthalene rings and intermolecular interactions
The intermolecular contact network as described for other complexes of the series [5] is still present in [Fe(PM–NEA)2(NCS)2], even though it appears less compact with longer intermolecular contacts.
Let us see the effect of the presence of the naphthalene rings within the crystal packing. First, the introduction of naphthalene rings does not produce voids in the crystal packing that could host a solvent molecule, contrary to what usually happens for this series when using relatively long L ligand [5] and in particular in [Fe(PM–PEA)2(NCS)2] [9b]. At 293 K in HS, no π–π interaction is formed between naphthalene rings of neighbouring molecules. Only four intermolecular contacts per complex considered as short involve the naphthalene rings. Three of these contacts, denoted D, E and F, correspond to hydrogen-like contacts and the fourth one, G, corresponds to a π–π interaction (Fig. 8). The D and G contacts concern the naphthalene ring that forms a high angle with the phenyl group while E and F concern the naphthalene that is almost coplanar with the phenyl group. The intramolecular dissymmetry described above is thus extended to the crystal packing, since the nature of the intermolecular contacts is different on both sides of the molecule. Only one of the naphthalene rings, i.e. one of the molecule extremity, is indeed involved in π–π interactions. Hydrogen-like contacts on each side of the molecule are also different in nature, since D involves one S atom of the neighbouring molecule while E and F involve one carbon atom of the neighbouring molecule (Table 4). At 120 K in LS, this dissymmetry remains. From 293 K to 120 K the intermolecular D, E and F contacts are shortened by roughly the same ratio (Table 4). The G type π–π contact is the most affected since it is strongly shortened from 293 K in HS (C⋯C = 3.526 Å) to 120 K in LS (C⋯C = 3.373 Å).
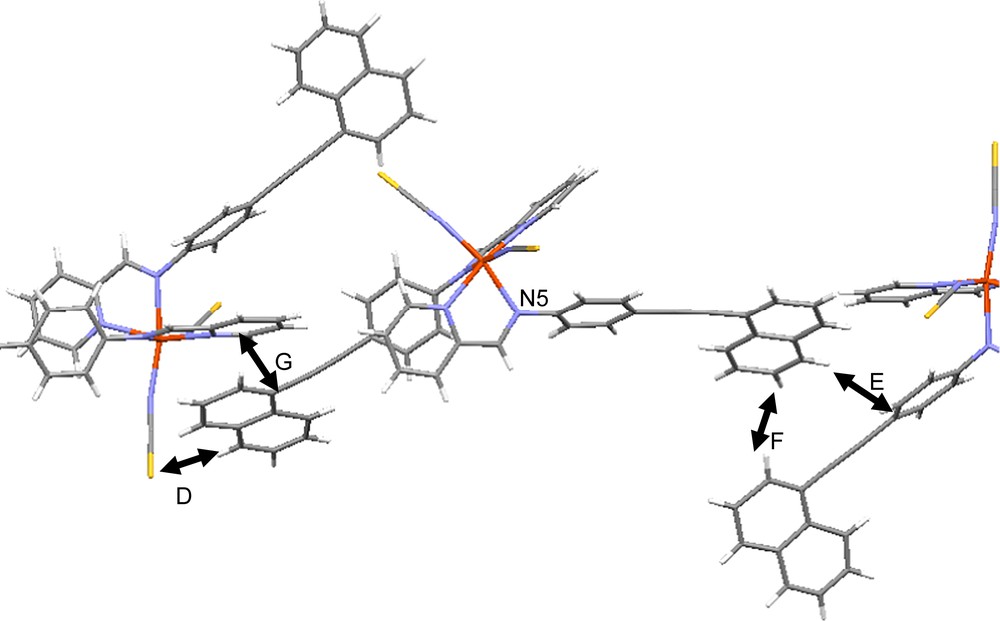
View and labels of the shortest intermolecular contacts that involved the naphthalene rings in the [Fe(PM–NEA)2(NCS)2] crystal packing. For visualizing colours, see the web version for this article.
Hydrogen-like intermolecular contact parameters involving the naphthalene rings in [Fe(PM–NEA)2(NCS)2] for HS at 293 K and LS at 120 K
| Contact type | M⋯C(H) (Å) | M⋯H–C (Å) | M⋯H–C (°) |
| D, HS | 3.809 | 2.884 | 172.7 |
| D, LS | 3.762 | 2.840 | 170.9 |
| E, HS | 3.751 | 2.898 | 153.3 |
| E, LS | 3.656 | 2.814 | 151.1 |
| F, HS | 3.779 | 2.915 | 155.3 |
| F, LS | 3.690 | 2.835 | 153.4 |
The intermolecular interactions involving S atoms through hydrogen-like contacts have proven to be of crucial importance for the propagation of the spin crossover along the solid within the [Fe(PM–L)2(NCS)2] series [11]. At 293 K in HS for [Fe(PM–NEA)2(NCS)2], this S⋯C contact is short for one of the S atoms (S2⋯C8 = 3.438 Å) and rather long for the other one (S1⋯C4 = 3.818 Å). At 120 K in LS, the dissymmetry character slightly decreases since one contact length increases (S2⋯C8 = 3.445 Å), whereas the other one decreases (S1⋯C4 = 3.745 Å). While intermolecular contacts are perfectly symmetric in orthorhombic structures of this series, the dissymmetry of the S⋯C intermolecular hydrogen-like contact is less pronounced for the other monoclinic compounds such as [Fe(PM–AzA)2(NCS)2] (3.487 Å and 3.722 Å) and [Fe(PM–BiA)2(NCS)2] polymorph II (3.540 Å and 3.750 Å).
To sum up the main difference due to the introduction of the naphthalene rings into the crystal network typical for [Fe(PM–L)2(NCS)2] complexes is the presence of a notable dissymmetry at the molecular and intermolecular levels. This asymmetry is probably responsible for the small cooperativity of this material.
3.3 Structure–properties correlation
3.3.1 Hydrogen bonds and cooperativity
It has been previously shown in the [Fe(PM–L)2(NCS)2] series that the cooperativity is directly connected with the hydrogen-like contact involving the S atoms [11]. Let us recall that cooperative systems lead to abrupt spin transition and poor cooperative ones lead to smooth spin transition. We defined the width of the magnetic transition as the temperature gap needed for a given complex to undergo a thermal transition from 80% HS to 80% LS directly calculated from SQUID magnetic curves. The smaller the width the more cooperative is the system. In the case of [Fe(PM–L)2(NCS)2] this width linearly decreases as the shortest intermolecular S⋯C distance in HS increases, showing a direct connection between one well-identified intermolecular interaction and the magnetic properties.
Present data for [Fe(PM–NEA)2(NCS)2] do not fit this previously drawn structure–property correlation (Fig. 9). The shortest S⋯C contact appears shorter than the one expected for the observed magnetic curve. One of the reasons is certainly that other intermolecular contacts, especially the ones corresponding to π–π interactions, are longer for this complex than for the other one, which, in a sense, compensates the short S⋯C contact. Another reason is probably the unusual dissymmetry of the intermolecular interactions, including the S⋯C ones, observed for [Fe(PM–NEA)2(NCS)2].
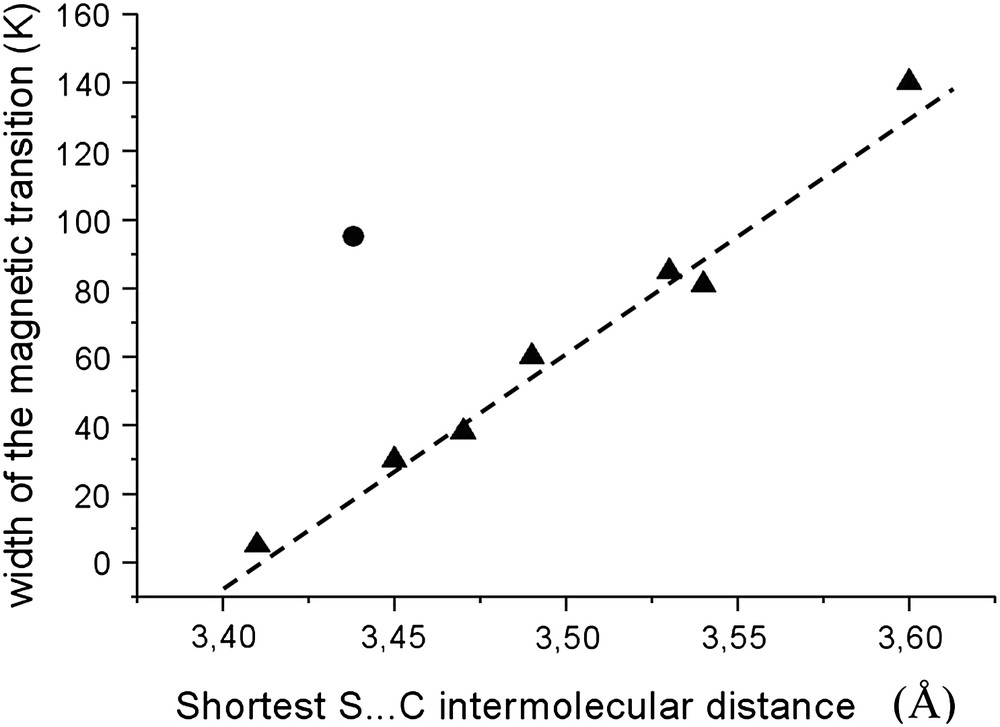
Plot of the width of the magnetic transition as a function of the shortest S⋯C intermolecular contacts in [Fe(PM–L)2(NCS)2] complexes. The former comes from SQUID measurements and the latter are issued from the X-ray crystal structures. Triangles are for the already studied and reported complexes [11] and the circle shows the [Fe(PM–NEA)2(NCS)2] complex.
3.3.2 Octahedron distortion and T1/2
In general, FeN6 octahedron goes from a trigonal prism in HS to a regular octahedron in LS [10,23]. The temperatures of spin crossover are directly influenced by the distortion of the metal coordination sphere [12]. In particular, the temperature of the thermal transition, T1/2, decreases almost linearly when the distortion of the FeN6 octahedron increases. The distortion used to account for this structure–property feature has been defined as the sum of the deviations from 60° of the 24 possible trigonal twist angles and denoted Θ. The variation of this angle from HS to LS, denoted ΔΘ, is then directly connected to the T1/2 value (Fig. 10).
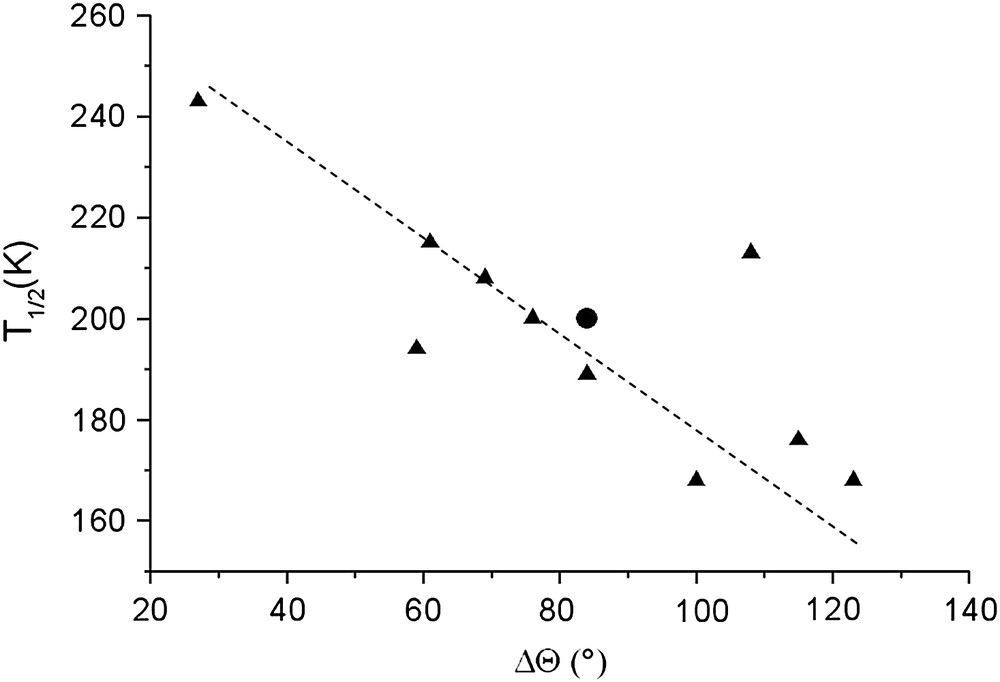
Plot of the temperature of spin crossover, T1/2, as a function of the FeN6 octahedron trigonal distortion parameter ΔΘ for the already studied [Fe(PM–L)2(NCS)2] complexes (triangle) [12] and the [Fe(PM–NEA)2(NCS)2] complex (circle).
In the case of [Fe(PM–NEA)2(NCS)2], the HS and LS Θ values lay in the range expected for iron complexes (Table 3). The ΔΘ value perfectly fits the previous correlation (Fig. 10). This clearly confirms that the temperature of the spin crossover is mainly connected to the metal coordination geometry since notable differences in the crystal packing have not affected the correlation between T1/2 and the distortion of the FeN6 octahedron.
4 Conclusion
In this work, the structural, the magnetic and the photomagnetic properties of a new member of the [Fe(PM–L)2(NCS)2] spin crossover series, namely [Fe(PM–NEA)2(NCS)2], have been presented. The title complex shows a thermal spin crossover at T1/2 = 204 K, with a smooth feature and no hysteresis. The latter is coherent with the relatively low cooperative character shown by the crystal packing, which originates in a strong dissymmetry of the intermolecular interactions due to the naphthalene rings. Furthermore, structure–property correlations confirm the direct dependence of T1/2 on the distortion of the metal coordination sphere from HS to LS; the higher the octahedron distortion the lower the T1/2. Elsewhere, an LIESST effect has been evidenced by means of diffuse reflectivity and carefully described in bulk condition with SQUID measurements, the T(LIESST) value being estimated to be 58 K. The corresponding HS-to-LS relaxation has been fitted with a stretched exponential behaviour, as expected from the small cooperativity of the system.
The [Fe(PM–NEA)2(NCS)2] complex was initially designed to obtain a stronger cooperative behaviour than in the previously reported complexes of [Fe(PM–L)2(NCS)2] series. If spin thermal and photo-induced spin crossover has indeed been observed, the cooperative character appears, however, very low in comparison to what was expected. This result illustrates the difficulty in designing efficient spin crossover materials even though a rational approach, using structure–property relationship for instance, is applied to achieve the design of materials with spin crossover properties à la carte (i.e. under request), which was one of the dreams of Prof. Olivier Kahn to the memory of whom this article is dedicated.
Acknowledgements
The authors would like to thank the bilateral DFG/CNRS action, the ANR Fast-switch (NT05-3_45333) and the Aquitaine Region for supporting the platform of photomagnetism.


