1 Introduction
A most conspicuous feature of several nonionic surfactants and polymers is the fact that, from being highly miscible with water at lower temperature, these systems phase separate into one water-rich and one water-poor phase at higher temperature; the macroscopic phase separation is preceded by a strong turbidity of the solution commonly referred to as “clouding” [1]. The phenomenon is not only scientifically intriguing but has, in view of ubiquitous applications of these systems, received a considerable attention from applied sciences. The present authors have for a long time been concerned with both experimental and theoretical studies of nonionic surfactants and polymers containing oxyethylene groups and one of us (GK) has presented a theory [2], considered to provide a thorough molecular understanding as well as being useful in designing industrial formulations. The extension of the model to nonionic carbohydrates in general has also been briefly indicated and supported by experimental observations.
In spite of extensive work, the area has, however, remained largely controversial for aqueous systems of oxyethylene compounds (here abbreviated EO; simple nonionic surfactants with m EOs being abbreviated CnEm). Furthermore, the extension of the concepts to important polymer systems like cellulose derivatives has remained largely unnoticed. In view of this situation, taken together with a steadily increasing role of EO-based polymers and surfactants, as well as nonionic cellulose derivatives, in applications, it was deemed appropriate to review the situation emphasizing some recent developments. The literature in the field grows rapidly; therefore, we restrict references to a few selected studies as well as previous reviews giving additional literature.
Temperature anomalies of nonionic oxyethylene surfactants and polymers are ubiquitous.
There is an extensive literature on temperature dependent effects of these surfactants and polymers. We will here only give a limited list illustrative for our discussion and in the next section a few illustrations.
Temperature effects include the following:
- - Phase behaviour: Clouding [3–7];
- - Solubility: Nonionic surfactants are water soluble at low T but oil soluble at high T [4];
- - Surfactant critical micelle concentation (cmc) decreases with T [4];
- - Opposite temperature dependences of cmc in oil and water [4];
- - Micelle size may increase strongly with T [8–10];
- - Surfactant self-assembly aggregates undergo dramatic shape changes with T [11];
- - Microemulsions undergo striking structural change with increasing T (from oil-in-water to water-in-oil via bicontinuous) [10];
- - Emulsions: Nonionic surfactants stabilize oil-in-water emulsions at low T but water-in-oil at high T; at intermediate T emulsions are highly unstable [4,12];
- - Soil removal by surfactants: Maximum as a function of T, maximum shifted to higher T for a longer oxyethylene chain [13,14];
- - Intermicellar interactions change from repulsive to attractive with increasing T;
- - Surface forces change from repulsive to attractive with increasing T [15];
- - Polymer and surfactant adsorption: higher T gives increased adsorption and more compact adsorbed layers [16];
- - Polymer incompatibility: The compatibility with a second polymer changes strongly with T [17,18];
- - There is a decreased hydration with increasing T [19];
- - Polymer–surfactant interactions are strongly T dependent [20–23];
- - Block copolymer cmc decreases strongly with increasing T and self-assembly structures undergo dramatic changes [24].
2 Textbook examples for nonionic surfactants
2.1 Surfactant self-assembly structures
Extensive studies of the phase behaviour of nonionic oxyethylene surfactants have been performed [11,25]. They show a very rich pattern, however, with the systematic changes with the number of oxyethylene groups and temperature as schematically illustrated in Fig. 1.
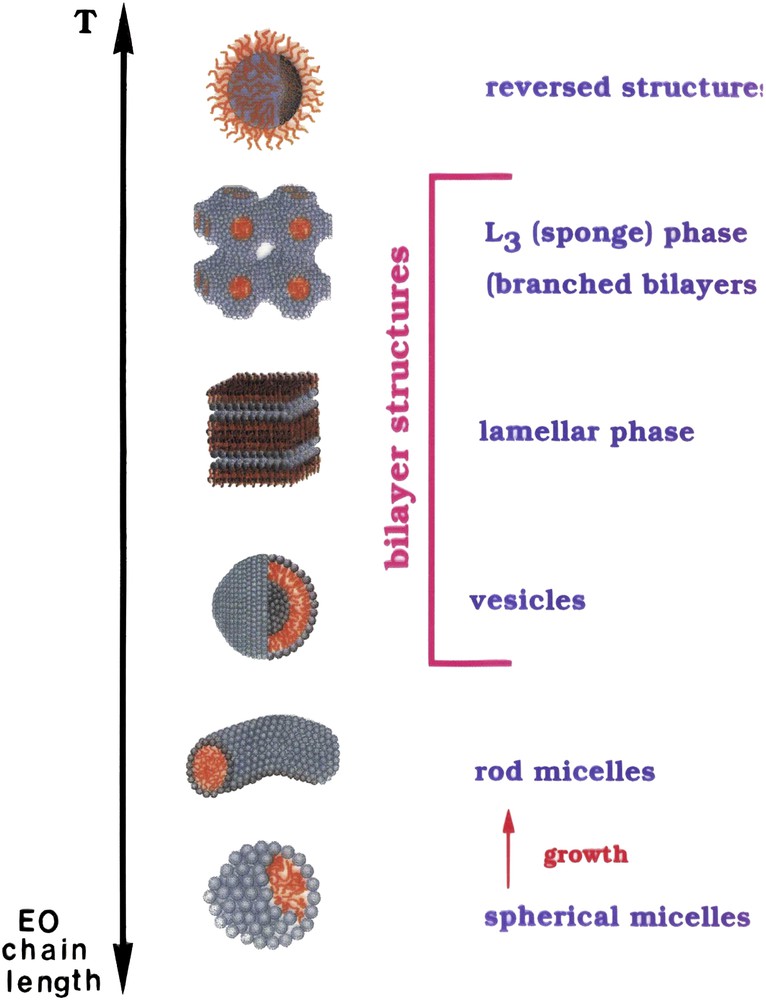
Aggregates of nonionic oxyethylene-based surfactants change with temperature and head-group size. (By the courtesy of Ulf Olsson.)
In terms of a conventional surfactant packing model, we infer that the area per head-group increases with an increasing number of EOs which is an expected behaviour. The temperature dependence of self-assembly is, on the other hand, in important respects opposite to that for other surfactants. The only reasonable conclusion is that the area per head-group decreases with increasing temperature. This can be understood in terms of a less favourable water–EO interaction at higher temperature, thus a decreased hydration, which is in line with other observations [19].
2.2 Surfactant adsorption
As illustrated in Fig. 2, surfactant adsorption increases strongly with increasing temperature [26]. Such data can be converted into a strongly decreased area per head-group with increasing temperature.

The temperature dependence of (a) the adsorption of a nonionic surfactant on PMMA latex and (b) the cross-sectional area per surfactant molecule; adapted from Ref. [26].
2.3 Soil removal
These nonionic surfactants show an excellent cleaning performance. However, soil removal is strongly temperature dependent as exemplified in Fig. 3 [27].
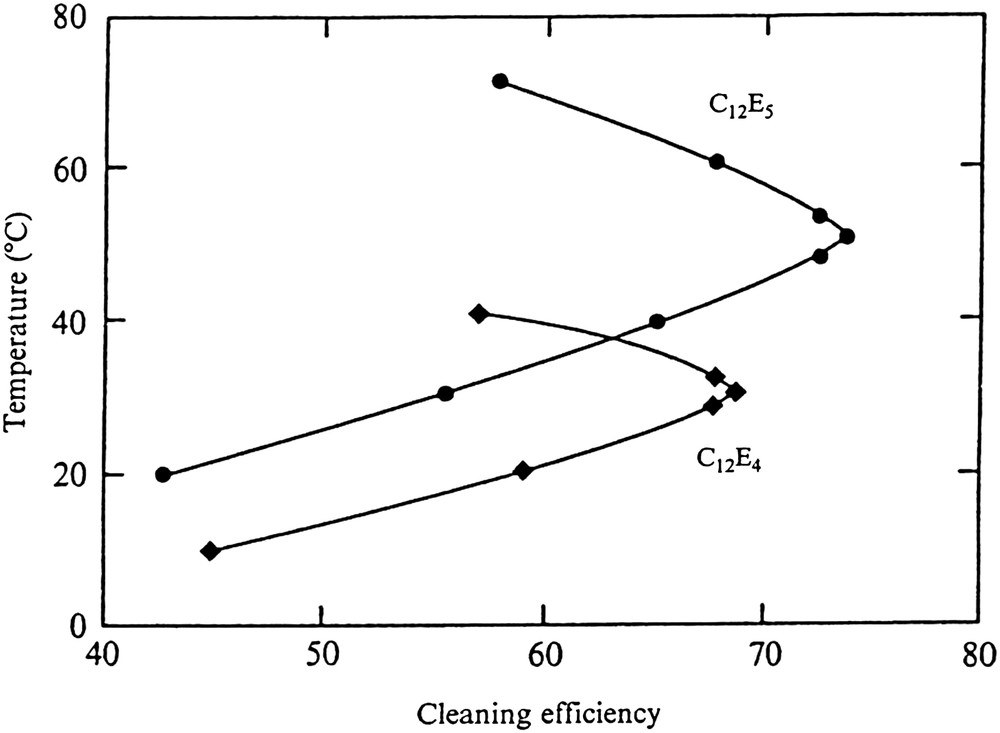
Temperature depedenence of the cleaning efficiency of nonionic surfactants; from Ref. [27].
3 Theoretical aspects
Having listed a number of intriguing observations for the oxyethylene-based surfactants and polymers we aim at identifying a general mechanism. Important parts in such an undertaking would be, firstly, to examine the breadth of these phenomena; in particular it would be important to see if we observe the same type of phenomena for other solvents than water and if there is an extension to other classes of solvents. Secondly, the underlying mechanisms can only be established by molecular level studies, mainly by spectroscopic studies. We will return to these issues after considering some general theoretical principles, mainly addressing temperature dependences of solubilities.
The thermodynamic quantity, which determines the miscibility of two substances is the free energy of mixing. In simple theories, like the regular solution theory, and the adaptation of this theory to polymers, the Flory–Huggins model, there are two contributions, an entropic and an energetic one. The interested reader is referred to standard textbooks for more information about these types of models. In these simple models, the entropic contribution, which originates from the mixing of the different types of molecules, is always favoring mixing and the energetic one may favor or disfavor mixing depending on if the interaction between the different types of molecules is more or less attractive than the average interaction between the two types of molecules that are mixed. Normally this is formulated in terms of an effective interaction parameter , where the indexes 1 and 2 refer to the two substances that are mixed. The effective interaction parameter is defined through the equation
| (1) |
| (2) |
| (3) |
| (4) |
The mixing entropy favors also in this case mixing of the two components and since this term is multiplied with the absolute temperature T, when the contribution to the free energy is evaluated
| (5) |
The probably most studied polymeric system, which shows a reversed solubility is the PEO (polyethyleneoxide) or PEG (polyethyleneglycol)–water system and actually all three possibilities to achieve the reversed solubility have been suggested as the mechanism behind the behavior.
The first explanation was given by Kjellander [28,29], who suggested that water (the solvent) could be organized in two different ways, one highly structured hydrogen-bonded way with low internal entropy and low energy, which was the dominating structural element at low temperatures, and a less structured high entropy and energy organization that became more abundant as the temperature increased. He further assumed that the PEG or PEO polymer interacted favorably with the low temperature water structures and less favorably with the high temperature forms of water. He never gave any mathematical dress to the ideas but we will for the sake of completeness do this below. To start we will introduce a two-state model of the liquid (water). This model will then be linked to a polymer using a Flory–Huggins description of a polymeric solution. To start we will assume that water can interact in two different ways, a hydrogen-bonded way and a non-hydrogen-bonded way. The probability for a hydrogen-bonded interaction will be labeled p and the probability for a non-hydrogen-bonded interaction will consequently be (1 − p). The model will also need information about these probabilities at a very high temperature where the system entropy dominates the behavior. What is actually required is the relative volume of phase space for the hydrogen-bonded interaction and the non-hydrogen-bonded interactions. Without loss of generality we can assume the first volume to be 1 and the volume of the non-hydrogen-bonded part of phase space to be Q. We will label the strength of the hydrogen-bonded interaction with wh and the corresponding value for a non-hydrogen-bonded interaction with wn. The energetic expression for water in this model would be
| (6a) |
| (6b) |
| (7) |
| (8) |
A water solution described as above can show reversed solubility properties at elevated temperatures if we assume that the interaction between the solute and the hydrogen-bonded water is more favorable than the interaction with the non-hydrogen-bonded water or as said by Kjellander [28,29], the solute fits into the hydrogen-bonded structure. If we add a polymer to water described with Eq. (8) using the Flory–Huggins model we obtain
| (9) |
This type of model will capture the solution behavior for molecules that have a minimum of their solubility at temperatures between 0 and 50–60 °C, like benzene. In this temperature regime, we may expect that the destruction of the hydrogen-bonded network of water gives a significant contribution to the mixing free energy.
An alternative explanation to the reversed solubility is given by Goldstein [30]. He assigns it to a breakdown of the hydrogen bonds between the solvent and the solute. His formulation of the theory is built on the partition function of the system and that one gets separate contributions from hydrogen and non-hydrogen-bonded interactions between the solvent and the solute. One can formulate the same theory using expressions like the one in Eq. (9). One then obtains
| (10) |
The meaning of the parameters in the equation is now slightly different. p is no longer the probability for hydrogen-bonded water molecules but instead the probability for hydrogen-bonded interaction between the solvent and the solute. In the same way, Q now measures the relative importance of hydrogen and non-hydrogen-bonded interactions between solvent and solute at very high temperatures. Goldstein used the model to describe the phase behavior of the PEO–water system.
Finally one of us has suggested that a reversed solubility can be obtained if the polymer can adopt different types of conformations, and that these conformations interact with the solvent in different ways [2,31]. Note the similarities between this model and the one suggested by Kjellander. In Kjellander's model one assumes that the solvent can exist in two different forms while in this last model we assume that the polymer can exist in different conformations. At higher temperatures the form that disfavors solubility becomes more abundant in both models. This results in a reduced solubility. The formal free energy of mixing for the last model can be written
| (11) |
An analysis of Eqs. (9)–(11) shows that they are effectively able to give the same type of phase behavior and that is not possible to determine which of the proposed mechanisms that are the explanations of the observed behavior by comparing theoretical and experimental observations. It may well be that the actual behavior in a real system is influenced by all three mechanisms.
It is, however, clear that the solubility minimum observed for hydrocarbons like benzene at low temperature does not have the last two mechanisms as its origin.
It is also clear that there is overwhelming experimental data for EO-containing molecules that indicates that their polarity decreases with increased temperature.
This gives strong support for the idea that the last mechanism is important for these systems.
4 Analogous conformational effects are expected for polysaccharides
We have in a number of applications used the model described above for EO-containing compounds to describe also the phase behavior of modified celluloses [17,18,32]. The obvious reason for this is that these systems contain structural elements that are identical to the one building the PEO polymer (Fig. 4). We have previously pointed out that not only celluloses, that are modified with ethylene oxide groups contain this structural element, but that it is also frequently appearing in other cases like methylcellulose [33,34].
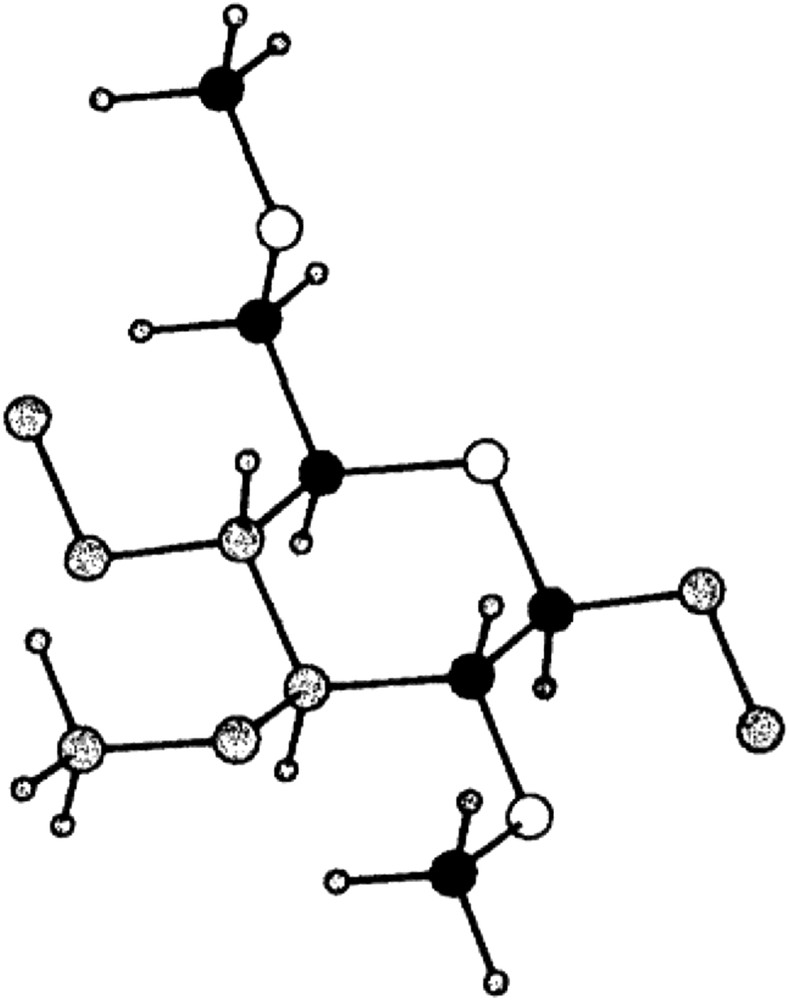
Structural element of polysaccharides.
Nonionic cellulose derivatives show a phase behaviour in water, that is quite analogous to that of poly(ethylene glycol) and its copolymers. However, striking temperature effects are seen in almost all macroscopic properties. As illustrated in Fig. 5, nonionic cellulose derivatives show a strongly temperature dependent adsorption [16].
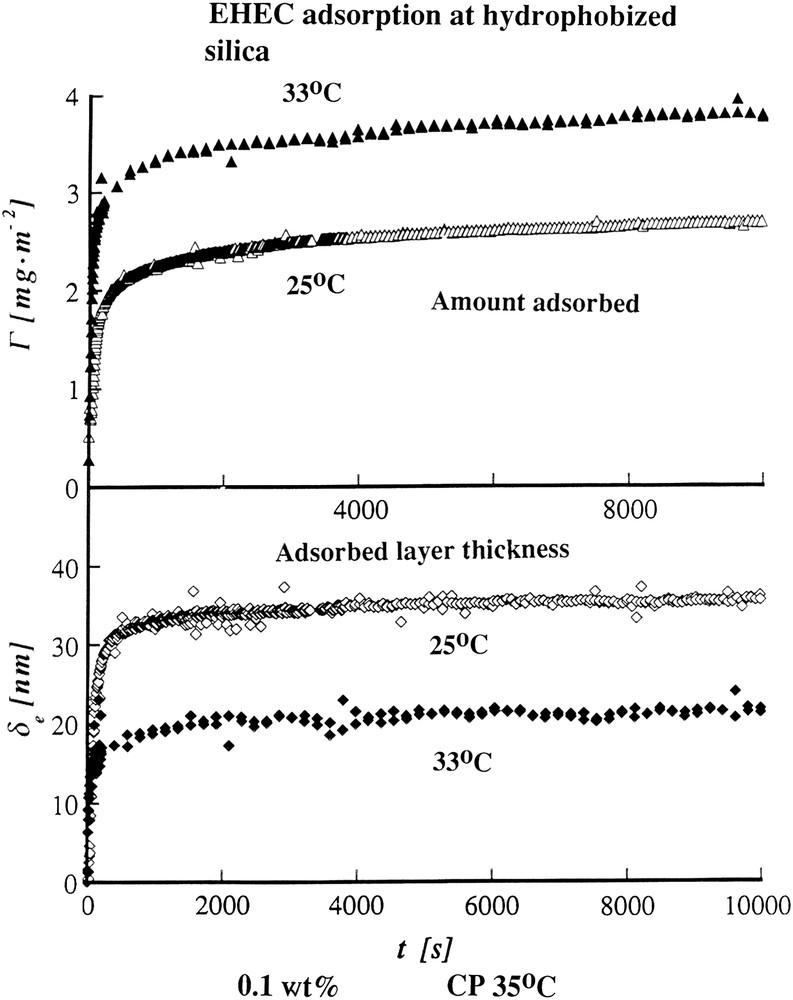
Adsorbed amount and adsorbed layer thickness from ellipsometry ethyl hydroxyethyl cellulose adsorbed from 0.1 wt% solution onto hydrophobized silica at 25 °C (open symbols) and 33 °C (filled symbols); from Ref. [16].
As can be inferred a relatively minor temperature increase leads to a markedly increased adsorption. However, at the same time as the adsorption increases the thickness of the adsorbed layer decreases strongly. This corresponds to a strong compaction of the adsorbed layer, which arises naturally in the conformational model. Thus a change over, to less polar states leads to a decreased hydration, and, consequently, to a contraction of the polymer chains.
Another striking feature of the nonionic cellulose derivatives is that with increasing temperature there is an enhanced interaction with all types of surfactants [17,18,21,35]. As this enhanced interaction is displayed by all classes of surfactant, leading to effects such as a decreased critical association concentration (cac), thermal gelation and associative phase separation, it must be ascribed to a hydrophobic effect, again supporting the notion that these polymers become more hydrophobic at higher temperature. We illustrate the behaviour in Fig. 6 by the phase diagram of an aqueous system of a nonionic cellulose derivative and a nonionic surfactant [18].
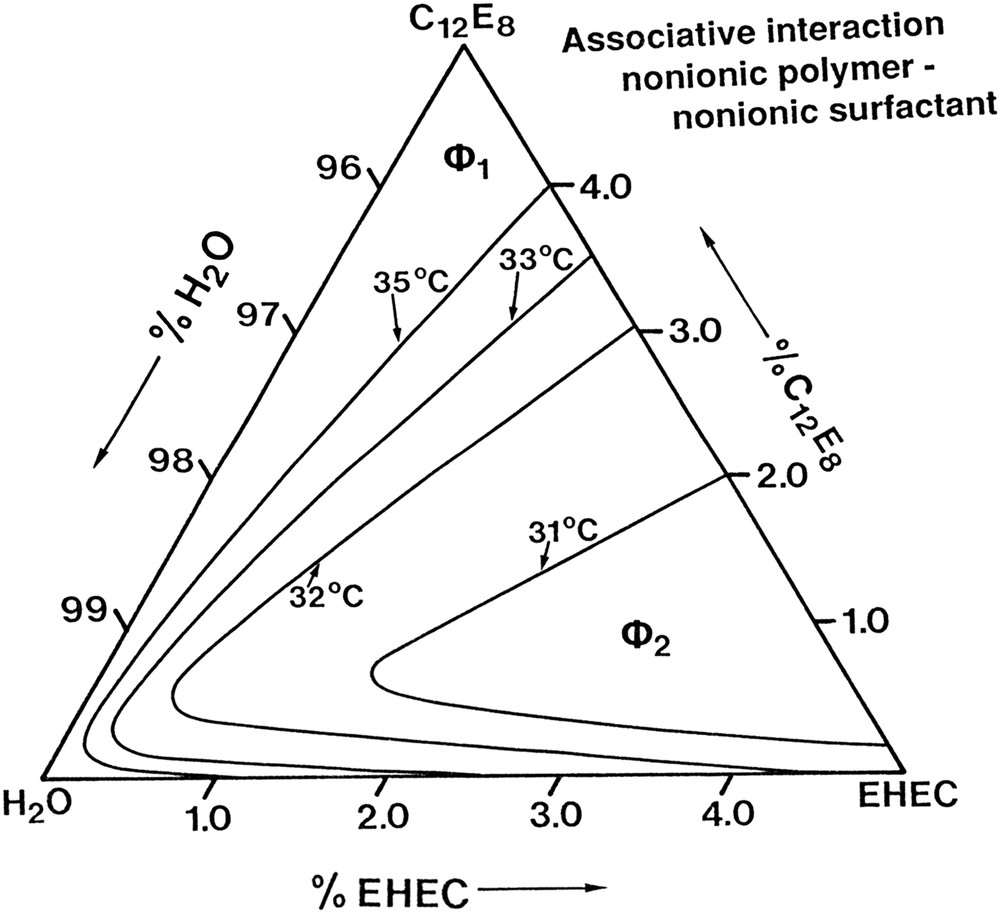
Phase diagram of an aqueous system of a nonionic polymer, ethyl hydroxyethyl cellulose, and a nonionic surfactant, C12E8; from Ref. [18].
As can be seen, as a function of increasing temperature, an associative phase separation is induced. With increasing temperature it becomes more and more extensive.
5 Temperature anomalies are not restricted to aqueous systems
We have above found some compelling evidence in favour of the conformational model. In order to test alternative models further we will consider results obtained using other solvents than water. As noted quite some time ago by Shinoda [3,4,12], a striking effect of nonionic EO-based surfactants is that while their aqueous solubility decreases strongly with increasing temperature their solubility in hydrocarbons increases. Thus in a water-oil two-phase sample there is with increasing temperature a transfer of dissolved surfactant from the aqueous to the oil phase.
Another piece of direct evidence against models based on water structure or hydrogen-bonding comes from observations of clouding and other related effects in non-aqueous systems. Thus studies of nonionic surfactants and polymers in formamide [36–39] have established clouding phenomena fully analogous to those in water and it has also been observed that clouding of poly(ethylene glycol) occurs in t-butylacetate [40], a non-hydrogen-bonding liquid. Furthermore, great analogies between water and formamide have been found for oil/surfactant/polar solvent systems. Furthermore, it was found that different salts influence the phase behaviour of EO-containing substances in water and formamide in a similar way. All these observations are naturally explained by the two-conformation model.
6 Experiments confirm the predicted conformational effects
The conformational model suggests that the EO-chain conformation is very significant for the interaction with solvent molecules. This assumption gained support from quantum mechanical ab initio calculations and statistical mechanical simulations as well as phase diagrams calculated based on predicted conformational changes [2,31].
Spectroscopic measurements are, of course, needed to further probe this issue. Based on measurements of NMR spin–spin coupling constants of 1,2-dimethoxymethane, as well as its dielectric properties, it was concluded in the beginning of the 70s that the EO segments change their average conformation from being more polar at low temperatures to being less polar at high temperatures [41]. Carbon-13 NMR chemical shifts [42] are particularly illustrative in this respect. For the ethylene oxide chains in nonionic surfactants, the chemical shifts suggest that a trans conformation around the C–C bond becomes more stable when the temperature is increased or if the environment is made less polar [43]. On the other hand, the ordinary up-field shift, corresponding to an increasing population of gauche conformers, was observed for the nonpolar part at higher temperature. In a similar study for EO copolymers, analogous results were obtained [44]. It was also possible to theoretically rationalize the observed carbon-13 chemical shifts as a function of temperature and solvent composition using the conformational model. This study also showed that qualitatively the same conformational effects occur for other solvents than water and also for liquid neat poly(ethylene glycol).
With the development of the NMR technique it has become possible to get deeper insight as well as to investigate phases that were previously not amenable to investigation. Recently, the lamellar liquid crystalline phase of a nonionic surfactant was investigated with respect to 13C–1H dipolar couplings applying a two-dimensional recoupling method [45]. For the hydrophobic tails, the population of gauche conformers was found to increase with temperature corresponding to a decreased order parameter. For the hydrophilic part, strikingly an increased dipolar splitting, corresponding to an increased order parameter, is found as temperature is increased. A corresponding behaviour was found in the 13C chemical shifts in the lamellar phase, as, with increasing temperature, the chemical shifts of the head-group carbons decrease while for the alkyl chains an increase was observed.
Raman spectroscopy may also provide a direct insight into conformational states and several EO compounds were investigated by Matsuura et al. [46–49], who found that the most stable conformation of a OCCO segment in surfactant and polymer molecules is trans–gauche–trans. With increasing temperature in the liquid state, the fraction of trans conformations around the CC bond increases. These results were confirmed for nonionic surfactant solutions [50].
Acknowledgements
The authors are supported by a Linné Award from the Swedish Research Council. Dr. Dan Lundberg is thanked for valuable assistance in this work.


