1 Introduction
Self-organization of building blocks in 1D, 2D and 3D is one of the fundamental processes in nature. A well-known example is the opal made of silica particles (few hundreds of nanometers) that self-assemble in a 3D highly ordered structure. The colour of these precious stones can be tuned by varying the silica particle size [1]. Another interesting example is the Fe3O4 nanocrystals (few tens of nanometers) fabricated by the magnetotactic bacteria. Because these magnetosomes are aligned inside the bacteria, they are sensitive to the magnetic field of the earth [2]. In fact, the organization process is present in many different systems (inorganic, organic and biological) at various length scales and gives rise to specific intrinsic physical properties. This concept has been mimicked by different groups and artificial solids as the photonic crystals made with several micrometer building blocks have been obtained [3]. At the nanometric scale, the particles are smaller by one or two orders of magnitude compared to the building blocks described above. The first self-organizations made with particles having few nanometers (<10 nm) were discovered 10 years ago [4,5]. Then, several groups showed that a rather large number of nanocrystals can short-scale organize [4–15]. In order to study the effect of the mesoscopic ordering on the physical properties, the nanocrystals have to be long-range ordered. Relatively few groups have been able to make 3D superlattices composed of several hundred layers, i.e., to grow supra-crystals. This was successfully obtained with silver [16,17], CdSe [5,18], cobalt [19,20] and gold [21] nanocrystals. This new generation of materials offers an intermediate system, whose physical properties are between those of nanocrystals and the bulk phase. For example, with silver, it was recently discovered that vibrational coherence in Raman scattering is observed when these nanocrystals are ordered in an fcc supra-crystal; this behavior is absent in a disordered 3D assembly [22]. On a similar note, a change in photoluminescence properties has been shown to depend on the order of CdSe nanoparticles in a 3D assembly [18].
Here we describe the growth of 2D and 3D long-range self-organizations of Co nanocrystals. Then, we report the various intrinsic physical properties (structural, magnetic and mechanic) due to the nanocrystal ordering. From this study, we show that an analogy emerges between nanocrystals ordered in the supra-crystal and atoms in the bulk phase or in the nanocrystal.
2 2D self-organizations of cobalt nanocrystals
2.1 Synthesis of cobalt nanocrystals: control of the size dispersion
The synthesis and characterization of cobalt nanocrystals coated with dodecanoic acid have been described in a previous paper [23]. The synthesis takes place in pure reverse micelles of Co(AOT)2, the size and form of which are controlled by the water content [24–26], defined here as w = [H2O]/[AOT] = 32. The cobalt ions are reduced by the addition of sodium borohydride, NaBH4, to the micellar solution. Its content is defined as R = [NaBH4]/[Co(AOT)2] and varies from 0.5 to 8. The addition of a low volume of NaBH4 (R < 1) maintains the stability of the reverse micelles, which play the role of nanoreactors in which the nucleation and growth of nanocrystals take place. In the supersaturated regime, that is R ≥ 1, micelles are destroyed because of the limiting water concentration, w [24]. In such a case, an additional population composed of bulk phase is obtained. Whatever the R values are, the nanocrystals are extracted from the AOT surfactant by adding dodecanoic acid molecules C11H23COOH, that covalently bond to the metallic surface. After being washed with ethanol, the nanocrystals are dispersed in hexane. In the supersaturated regime, the system is centrifuged to precipitate bulk Co and larger nanocrystals, and we recover only the smaller nanoparticles. The entire synthesis is carried out in a nitrogen glove box. The transmission electron microscopy (TEM) investigation shows an increase in the mean diameter of the nanocrystals from 6 to 8 nm when R increases from 0.5 to 8. More surprisingly, the size dispersion drastically drops from around 30% to 8%. Such a behavior is related to the yield of the reduction and nucleation processes that increases with the concentration of NaBH4. It clearly appears that the concentration of reducing agent is one of the key parameters in controlling the size dispersion of Co nanocrystals. Whatever the R value is, the electron diffraction pattern of Co nanocrystals shows three diffuse diffraction rings indicating a very low crystallinity with few small fcc domains (Fig. 1C).

A) TEM image of 7.5 nm cobalt nanocrystals long-range self-organized in a hexagonal network. B) Contrast profile made over the line marked 1. C) Electron diffraction pattern.
2.2 Key parameters involved in the growth of 2D self-organizations of cobalt nanocrystals
2D assemblies of Co nanocrystals are prepared by drop wise deposition of approximately 150 μl of the colloidal solution (5.5 × 10−7 M) on a copper grid coated with amorphous carbon. The TEM investigation shows quantitatively the influence of the size dispersion [23]. Indeed, when σ > 13%, the nanocrystals locally order whereas when σ ≤ 13%, they order over long-scale in a 2D hexagonal network. As well expected, lower the size dispersion, higher the coherence length in the 2D superlattice. The long-range ordering of the nanocrystals is due to their low size dispersion (≤13%) combined to a size segregation process occurring during the solvent evaporation [22]. To further confirm the ability the Co nanocrystals have to self-organize; the deposition of a colloidal solution obtained at R = 6 is made on a copper grid covered with a thin layer of highly oriented pyrolytic graphite (HOPG). The average diameter and size distribution of the nanoobjects are 7.5 nm and 9.4% respectively. The use of a flat substrate is required in order to favor the diffusion of the nanocrystals and then their ordering. In these conditions, Fig. 1A shows that Co nanocrystals self-organize in a 2D hexagonal network with an increase coherence length compared to the same deposition made in amorphous carbon [19]. The same behavior is also observed with Ag nanocrystals [17] whereas it is the opposite for Ag2S [4]. That clearly indicates that the key parameters involved in the ordering of metallic nanocrystals are not only the size dispersion coupled to the size segregation but also the particle–particle and particle–substrate interactions [27]. The profile technique (Fig. 1B) gives an interparticle distance (Di–p) and center-to-center distance (Dc–c) equal to 2.5 ± 0.4 nm and 10.3 ± 0.4 nm respectively. The high stability of these native organizations against coalescence and oxidation is related to the interdigitation of the dodecanoic acid chains surrounding the nanocrystals. This coating, attached to the metallic nanocrystal by a covalent bond between the Co surface and the O atom of the acid group, plays a key role in maintaining the integrity of the mesoscopic organization and consequently prevents coalescence.
2.2.1 Control of the crystallinity of cobalt nanocrystals
After deposition on TEM grid coated with a thin layer of HOPG, the 2D organizations are placed in a closed quartz ampoule with a nitrogen atmosphere and are annealed in a furnace at various temperatures (250, 300, 350 °C) for 15 min [28]. After annealing at 250 °C, the diffraction pattern (Fig. 2B) shows that most of the rings correspond to hcp cobalt, however, an additional weak ring corresponding to the (200) reflection of an fcc structure is observed. After annealing at 300 and 350 °C (Fig. 2D and F), we detect only the rings corresponding the hcp reflections. At 350 °C, the second-order reflections are also observed indicating an increase in the coherence length. The high-resolution TEM image (Inset of Fig. 2F), clearly illustrates the formation of monocrystals with the (002) planes of hcp Co [29,30]. Then, such a thermal treatment allows the nanoparticles to transform from fcc polycrystals to hcp monocrystals. Note that no ɛ-Co phase is detected conversely to what has been reported elsewhere [31,32]. Additionally to the increase in the particle crystallinity and conversely to what has been observed by other groups [33,34], the thermal treatment does not induce any damage in the 2D organizations that remain ordered without no coalescence (Fig. 2A, C and E) neither oxidation of the Co nanomaterial (Fig. 2B, D and F) [28]. The high thermal stability of these 2D superlattices is related to the dodecanoic acid molecules that remain bond to the metallic surface of the nanocrystals during the annealing step.

TEM images of 7.5 nm cobalt nanocrystals ordered in an hexagonal network in situ annealed at A) 250 °C, C) 300 °C and E) 350 °C. B, D and F, corresponding electron diffraction patterns. Insert of F, HRTEM of a Co nanocrystal.
2.2.2 Structural intrinsic property due to 2D hexagonal order of cobalt nanocrystals
When the 2D self-organized hcp Co nanocrystals are exposed to air for few hours, the building blocks are characterized by a fairly well contrast core/shell structure (Fig. 3A and C) with an average shell thickness of ≈2 nm and an average core diameter of ≈5 nm [30]. This gives a total average particle diameter ≈ 9 nm larger than that observed for non-oxidized hcp Co nanocrystals (7.5 nm). This difference is explained by a change of material density. Indeed, the electron diffraction pattern clearly shows both the signature of hcp Co and cubic CoO. The high-resolution TEM image (Fig. 3E) shows a core characterized by regular lattice planes with a typical distance of 2.00 Å corresponding to the (002) planes of hcp Co and a shell with a lattice distance of 2.46 Å attributed to CoO. Very surprisingly, when the same nanocrystals are in a disordered fashion or isolated on the substrate and subjected to the same exposure to air, they present a more diffuse contrast (Fig. 3A and D), which is attributed to a full oxidation in CoO [35]. Some of these nanocrystals tend to coalescence. The HRTEM image shown in Fig. 3F confirms the CoO structure of these nanocrystals through the visible lattice planes of approximately 2.46 Å. Hence, nanocrystals ordered in an hexagonal network are less sensitive to oxidation than the same nanocrystals disordered or isolated on the substrate. This claim is confirmed by the elemental mapping technique where a reference corresponding to a zero-loss map is considered (Fig. 4A). The cobalt map obtained using the Co-L edge (Fig. 4B) mainly shows the core of nanocrystals ordered in the regular network made of cobalt metal. At the O-K edge, the oxygen signal originates mainly from the shell, the gap between the core/shell structures in the ordered array and from the poorly contrasted isolated nanocrystals (Fig. 4C). This oxygen signal indicates either formation of CoO or presence of O2 molecules. The resulting colour map (Fig. 4D) clearly shows that there is a large Co core region (in red (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)) in the ordered array, whose size tends to decrease as we move towards the edges whereas Co material is no longer detected for the surrounding isolated nanocrystals. The lack of Co metal is replaced by the CoO oxide (in blue). The detection of oxygen between core–shell nanocrystals in the 2D array attests to the presence of molecular oxygen still trapped in the alkyl chain of the dodecanoic acid molecules. All these results clearly show that nanocrystals in a 2D hexagonal network are more resistant to oxidation than those isolated on the substrate or in a disordered fashion. This is explained in terms of interdigitation of the alkyl chain [35]. From these data, it is reasonable to conclude that the nanocrystal oxidation process mainly depends on the nanocrystal ordering. An analogy with atoms could be controversial. However, let us consider an isolated atom and bulk material. We know that the isolated atoms can be highly oxidized whereas in the bulk material this takes place only at the surface.
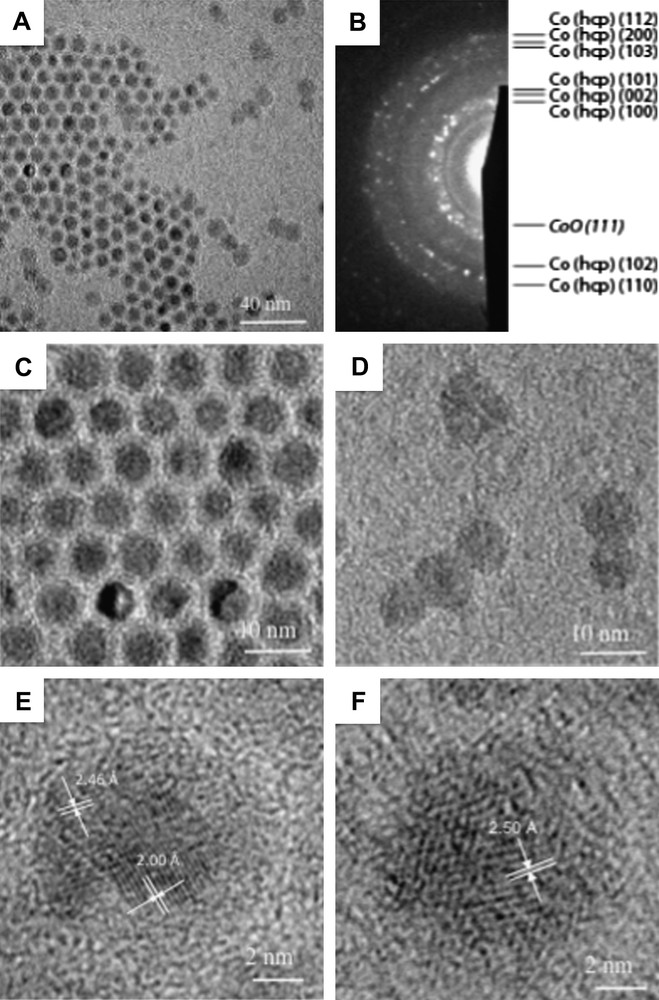
A) TEM image showing ordered nanocrystals and disordered or isolated nanocrystals after annealing at 350 °C and exposure to air. B) Corresponding electron diffraction pattern showing both Cohcp rings and a characteristic CoO {111} ring. C) Higher magnification image of nanocrystals from ordered zone showing core/shell structure. D) Higher magnification image of nanocrystals from disordered zone showing structures with a smaller core and/or with absence of contrast. E) HRTEM image of a nanocrystal from ordered zone showing core Co hcp lattice planes and shell CoO lattice planes. F) HRTEM image of a nanocrystal from disordered zone without contrast showing CoO lattice planes.
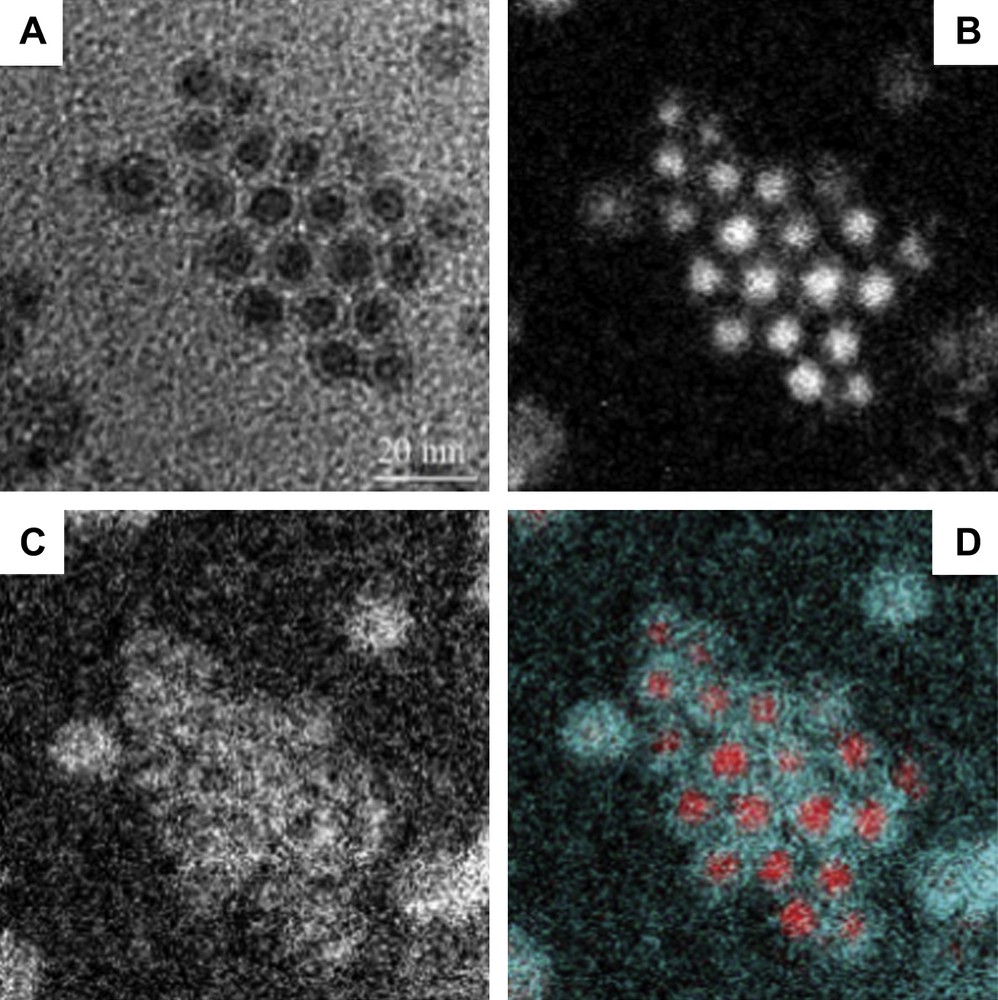
EFTEM maps of Co nanocrystals after oxidation showing: A) Zero-loss map, B) Cobalt map, C) Oxygen map, D) Colour map.
3 3D supra-crystals of cobalt nanocrystals
3.1 Control of the mesoscopic order
When cobalt nanocrystals are able to long-range self-ordered in 2D hexagonal network (Fig. 1), they can also regularly ordered in 3D superlattices i.e., in 3D supra-crystals (Fig. 5C, E and G). [16–20]. For this aim, an HOPG substrate is immersed in 200 μl of a colloidal solution (5.5 × 10−7 M), the solvent evaporates under nitrogen and the order is controlled by the substrate temperature which varies from 25 to 45 °C [20]. At room temperature (Fig. 5C), the film is characterized by cracks, and the resulting domains have an average area and thickness of 400 μm2 and 5 μm respectively, they are composed of several hundred layers of nanocrystals. The GISAXS study clearly indicates an fcc mesoscopic structure [19]. As can be shown from the diffractogram (Fig. 5D), the (111) reflection is intense and nearly resolution-limited indicating a long-range ordering out of the plane. The minimum value for the coherence length is found equal to 140 nm. The interparticle distance is found around 3 ± 0.5 nm. This gives a mean chain interdigitation of 1 nm (6 C–C distances) against 1.5 nm (9 C–C) for the 2D superlattice. The difference is attributed to the residual solvent molecules (hexane) that are still trapped in the 3D structure leading to a hindering in the interdigitation whereas in 2D the solvent is more easily evaporated. By increasing the temperature from 25 to 45 °C, the domain area increases (Fig. 5C, E and G). The (111) peak width decreases, its intensity drastically increases while the second-order reflection appears (Fig. 5D, F and H). This behavior clearly indicates an increase in both size and ordering of the fcc supra-crystals. Now, in order to determine the influence of the nanocrystal ordering on the physical properties of the 3D supra-crystals, we need to produce disordered 3D assemblies. This can be achieved by decreasing the temperature deposition. Indeed, at 10 °C, the deposition gives rise to the formation of a thin film coexisting with aggregates (Fig. 5A) and the GISAXS pattern, though a low intense and broad peak indicates the absence of long-range ordering (Fig. 5B). Hence, with the same batch of nanocrystals, we are able to tune the 3D ordering from disordered assemblies to highly ordered fcc supra-crystals. From these results, it is claimed that, even if the involved forces are not the same, nanocrystals are able to behave as atoms with formation of either disordered or crystalline phases as this is the case for the carbon that can grow to give rise either to amorphous carbon or diamond. Other structures of nanocrystals such as rings, fingers, etc. are governed by Marangoni instabilities [6] and mainly depend on the temperature gradient induced during the solvent evaporation process and not on the parameters described above.

SEM images obtained by depositing cobalt nanocrystals on HOPG substrate at various temperatures; A) 10 °C, C) 25 °C, E) 35 °C, G) 45 °C. B, D, F and H, corresponding diffractograms.
3.2 Magnetic intrinsic properties due to long-range 3D fcc order of cobalt nanocrystals
A general feature characterizing single magnetic nanocrystals is their superparamagnetic behavior. The magnetocrystalline anisotropy energy in axial symmetry depends mainly on both the particle volume, V, and its anisotropy constant, K. In the superparamagnetic regime, the anisotropy energy barrier, Eb = KV, is usually of the same magnitude as the thermal energy. Then the magnetization vector fluctuates among the easy directions of magnetization. This process is called superparamagnetic relaxation. When a magnetic material is subjected to an increasing magnetic field, the spins within the material tend to align with the field. Its magnetization increases and reaches a maximum value called the saturation magnetization, Ms. As the magnitude of the magnetic field decreases, spins cease to be aligned with the field, and the total magnetization decreases. Now, if the sample is cooled at low temperature (5 K) and then a magnetic field is applied (20 Oe), the increase in the temperature induces a progressive increase in the magnetization that reaches a maximum called blocking temperature (TB). Above TB, the behavior is superparamagnetic and the magnetization decreases with increasing temperature. This measurement is called the zero field cooled (ZFC) magnetization versus temperature.
Fig. 6 shows the ZFC magnetization versus temperature curves normalized to TB for both the ordered (red) and disordered (black) 3D assemblies composed of 7.5 nm cobalt nanocrystals [36–38]. The ZFC peak is significantly narrower for the ordered sample. The width of the ZFC peak is related to the distribution of energy barriers, Eb, in the system: a larger distribution gives a broader peak. The energy barriers involved are the anisotropy energy, Ea = kaV (where ka is the anisotropy constant and V is the particle volume) and the dipole–dipole interaction energy which depends on the interparticle distance [39]. As the ordered and disordered samples are made with the same batch of nanocrystals, the change in the width of the ZFC peak cannot results the volume distribution or the anisotropy of the nanocrystals. We therefore explain the difference in the distribution of Eb by the change in the structural environment of the Co nanocrystals. As pointed out, dipolar forces have a strong directional dependence and, consequently, dipolar interactions in the assembly should be sensitive to the detailed geometrical arrangement of the nanocrystals. In the fcc supra-crystals, characterized by a long-range coherence length, the geometric environment of the nanocrystals is fairly uniform. Conversely, in the disordered 3D assembly, we have a mixture of small fcc domains and amorphous domains. Therefore, we expect the distribution of Edd (and hence Eb) in the supra-crystal sample to be lower than in the disordered sample, leading to the observed narrowing of the ZFC peak. We acknowledge that this effect of order is fairly subtle, however, we have found that it is highly reproducible. The first magnetic intrinsic property due to the ordering is observed [36–38].
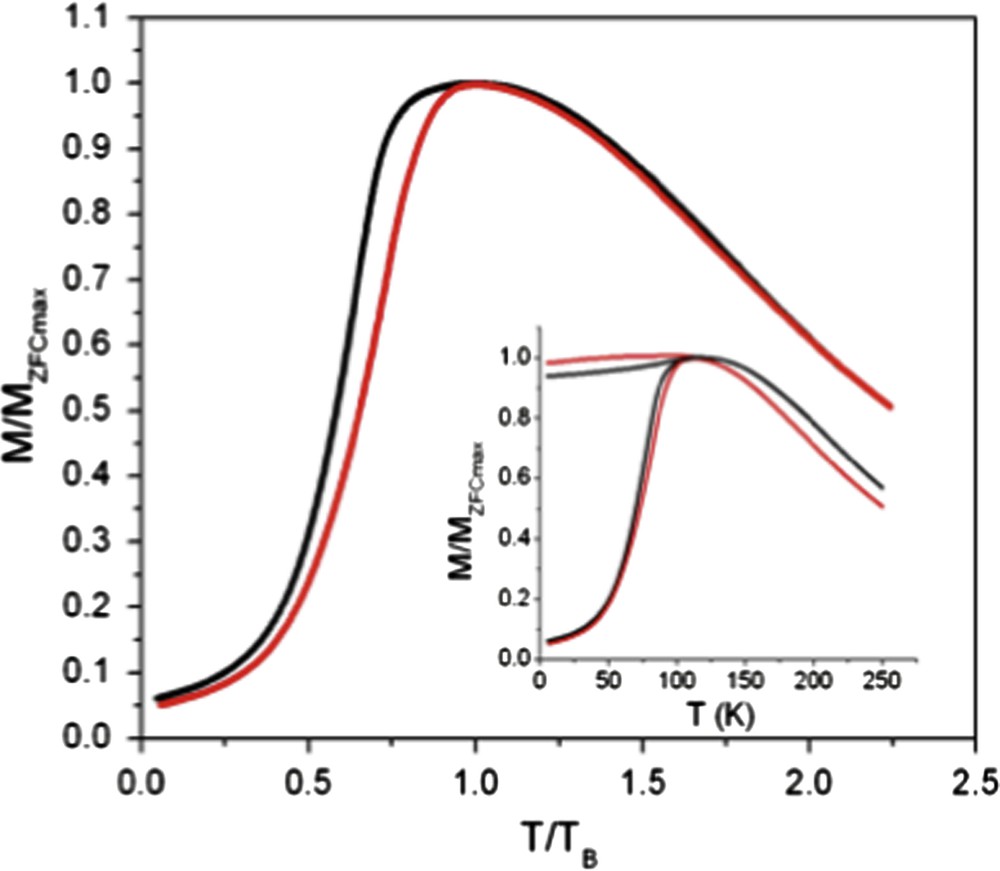
ZFC M versus T/TB curves of disordered (black line) and ordered (red line) 3D assemblies. Insert: The raw ZFC (dashed line) and FC (full line) M versus T/TB curve. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.).
3.3 Analogy between the magnetic behavior of nanocrystals 3D ordered in a supra-crystal and atoms in the bulk phase
Here, we compare the high field magnetic response of ordered and disordered samples. Fig. 7 shows the magnetization versus field curves obtained at 5 K for both the samples. Whatever the mesoscopic ordering is, saturation is reached at around 1.5 T and hysteresis is observed. The approach to saturation for the supra-crystal appears to be slower compared to the disordered assembly. The difference in the approaches to saturation is explained by considering the model of amorphous ferromagnets proposed by Chudnovsky et al. [40,41]. In this model there is only short-range structural order that leads to a local random anisotropy with a short-range correlation length. The randomness of this local anisotropy leads to a very small uniform anisotropy in the sample, referred to a coherent anisotropy. The model predicts an approach to saturation in these materials given by ΔM ≈ 1/H1/2, which has been confirmed experimentally [42]. This was extended to disordered nano-crystallized films [43] where a 1/H1/2 approach to saturation is also observed. In addition, the authors show that increasing the anisotropy in these films leads to a deviation from 1/H1/2 to 1/H2 on approaching saturation, which would apply in the case of a perfect uniaxial system. By analogy to what is observed in Fig. 7, it is concluded that in the disordered assembly, the direction of anisotropy randomly fluctuates from one magnetic nanocrystal to another and leads to an extremely small uniform local anisotropy with a square root magnetization law in approaching saturation. For supra-crystals, due to long-range mesoscopic order, the total anisotropy is rather large with inter-nanocrystals coupling energies leading to a smoother magnetization curve on approaching saturation. This clearly shows that, from a magnetic point of view, the ordered and disordered assemblies of nanocrystals [36] behave similarly to highly crystallized and amorphous materials. Similarly, as predicted, the coercive field increases for supra-crystals (900 Oe) compared to disordered assembly (600 Oe). Again, as above, this agrees with a change in the local anisotropy with the nanocrystals ordering [42]. From this comparison between both the approach to saturation magnetization and the coercive field of either amorphous material or highly crystallized supra-crystals, it is reasonable to conclude that there is a similarity in the magnetic behavior between disordered assemblies or highly ordered supra-crystals as in amorphous and highly crystalline materials of atoms. To go further and to a first approximation, we could assume that the magnetic behavior of atoms and nanocrystals is similar in a given order.
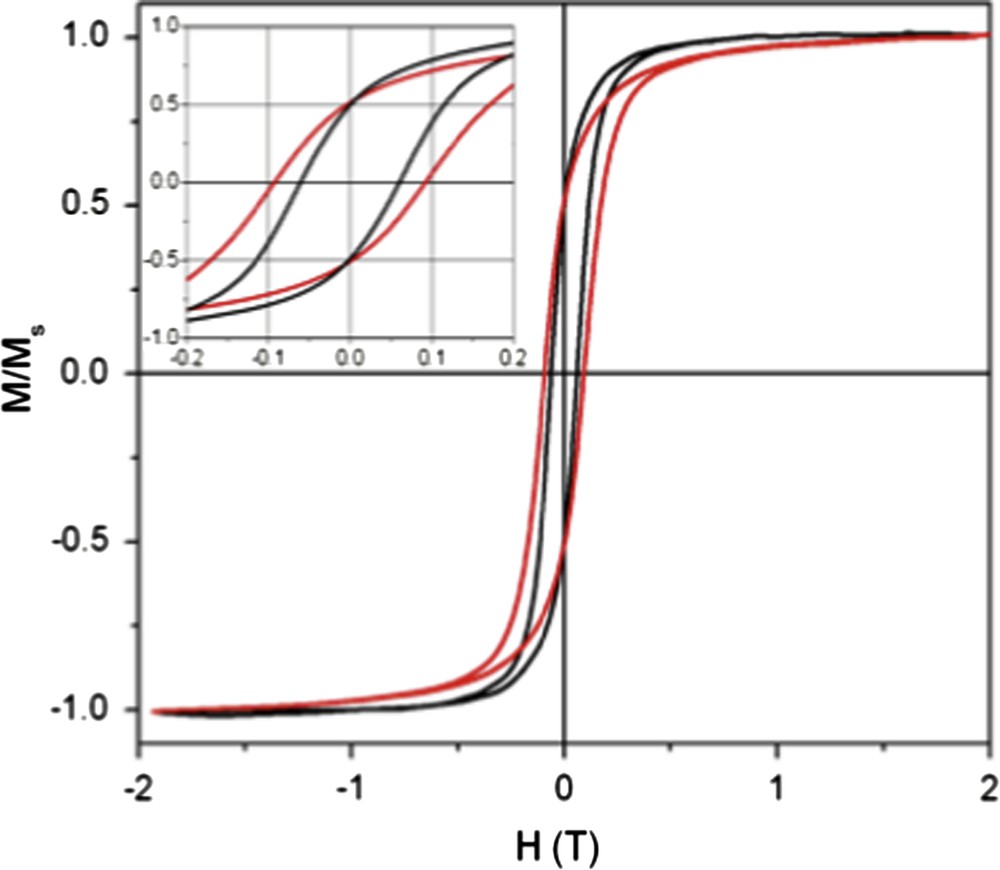
M versus H curves of disordered (black line) and ordered (red line) 3D assemblies. Insert: Enlargement of the low field region. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.).
3.4 Structural intrinsic properties due to long-range 3D fcc order of cobalt nanocrystals
By applying a magnetic field perpendicular to the substrate during the evaporation process of 5.7 nm cobalt nanocrystals dispersed in hexane and characterized by a low size dispersion (13%) [44–46], we mainly favor the formation of dots (columns), which are either fallen or upright on the substrate (Fig. 8A and the insets). Conversely, when nanocrystal size dispersion is rather large (18%) and keeping a similar average diameter (5.9 nm), the formation of a large number of flower-like is observed. These structures are due to coalescence of either upright or fallen columns inducing either worm-like or labyrinths (Fig. 8B and the insets). The major difference between these structures is due to the size dispersion of nanocrystals: The proposed mechanism of pattern formation is as follows: During the evaporation process, a liquid–gas phase transition [45,46] occurs with formation of a concentrated solution of nanocrystals in equilibrium with a diluted one. In the concentrated phase, columns are progressively formed and tend to migrate in order to self-organize in hexagonal patterns. When the size dispersion is low enough, the nanocrystals dispersed in solution tend to self-order in fcc supra-crystals with the formation of straight columns whereas for higher size dispersion values the interactions between particles markedly decrease and the columns are formed with disordered building blocks. This creates defects and the cohesive forces between columns are not large enough to keep them stable and columns tend to fuse to form labyrinths. Hence, by just decreasing the nanocrystal size dispersion, the mesoscopic structure can be tuned from labyrinths to regular dots. The structural property of the column formation controls the final patterns.

SEM patterns of mesostructures of 5.7-nm cobalt nanocrystals having A) 13% and B) 18% size dispersions.
4 Conclusion
Here we show changes in the magnetic, structural and mechanical properties due to the cobalt nanocrystals ordered in 2D and 3D superlattices. The strength of this work comes from the fact that both the ordered and disordered assemblies are made with the same population of cobalt nanocrystals (i.e., same size and same size dispersion). To a certain extent, we also show that nanocrystals in the superlattices can behave as atoms either in the nanocrystals or in the bulk phase. This data adds other examples to the growing list of intrinsic properties arising as a result of long-range mesoscopic ordering in 2D and 3D nanocrystal assemblies.
Acknowledgements
Special thanks are due to our colleagues Drs. A. Courty, D. Ingert, V. Germain, D. Parker, J. Richardi, C. Salzemann, M. Walls, S. Turner, S. Bals and G. Van Tendeloo.


