1 Introduction
During the last decade, due to the emergence of a new generation of high-technology materials, the number of groups involved in nanomaterials has increased exponentially [1,2]. Nanomaterials are implicated in several domains such as chemistry, electronics, high-density magnetic recording media, sensors and biotechnology. This is, in part, due to their novel material properties, that differ from both the isolated atoms and the bulk phase. An ultimate challenge in materials research is now the creation of perfect nanometre-scale crystallites, identically replicated in unlimited quantities, in a state than can be manipulated and that behave as pure macromolecular substances. Thus the ability to systematically manipulate these is an important goal in modern materials chemistry. The electrical, optical and magnetic properties of inorganic nanomaterials vary widely with their sizes and shapes. The major contribution to date has been to produce spherical nanocrystals with a very low size distribution. Deposition processes include using microwave plasma [3], low-energy cluster beam deposition [4], inorganic chemistry [5], ball milling [6], sonochemical reactions [7], gel–sol [8], a flame by vapour phase reaction and condensation [9]. In 1986, we developed a method based on reverse micelles (water-in-oil droplets) to prepare nanocrystals [1,2]. Normal micelles make it possible to produce ferrite magnetic fluids [10].
In 1993 and again in 1995, we were able to regulate the shape of nanocrystals by using colloidal solutions as templates [11,12]. We demonstrated that the template is not the major parameter in controlling nanocrystal shapes. Adsorptions of ions and molecules on various faces enable producing anisotropic nanomaterials [13,14], but all the various parameters that are able to control the shape of nanocrystals have yet to be identified [15].
Self-assembled nanocrystals have attracted increasing interest over the last five years [16–24]. As with other nanomaterials, the level of research activity is growing exponentially, fuelled in part by the observation of physical properties that are unique to the nanoscale domain. Interestingly, it has been recently demonstrated that the physical (optical, magnetic, transport) properties [25–40] of nanocrystals organized in 2D and/or 3D superlattices differ from those of isolated nanoparticles. These changes in the physical properties are due to the close vicinity and to the ordering of nanocrystals at a given distance between each other. Such collective properties are attributed to dipole–dipole interactions. Furthermore, the electron-transport properties drastically change with the nanocrystal organization.
In this review, we discuss the control of size and shape of nanocrystals using colloidal solutions as templates. Then we demonstrate that organizations of nanocrystals in 2D and 3D are produced. These organizations on a mesoscopic scale show collective properties.
2 Production of nanocrystals by using colloidal solutions as templates and their limitations
Fifteen years ago [41], we discovered that water-in-oil droplets, stabilized by a surfactant, called reverse micelles [42] are good candidates for templates. To obtain such assemblies, we need to have a surfactant with a shape like a champagne cork (small polar head and branched hydrocarbon chains). These droplets are displaced randomly and subjected to Brownian motion, they exchange their water contents and reform two distinct micelles. In contrast to direct micelles, their size increases linearly with the amount of water added to the system [43]. These two properties enable their use as variable size nanoreactors. Let us consider A and B solubilized in two micellar solutions. On mixing them, and because of the exchange process, A and B are in contact and react. It is thus possible to fabricate a very wide range of spherical nanomaterials [1] such as semiconductors, metals, oxides and alloys (in this case some of them cannot be produced at the nanoscale whereas they are formed in the bulk phase [15]). The control of the template size, by changing the water content, enables controlling the spherical nanocrystal size (Fig. 1A) [1]. It is of interest to note that this nanoreactor makes it possible to produce metal nanoparticles without any detectable oxide. There is a rather large consensus that reverse micelles are good nanoreactors for obtaining spherical nanomaterials. In most cases, a spherical template produces nanospheres. The particle sizes can be controlled by hydration of the water pool. However, production of various species during the chemical reaction and/or presence of impurities play an important role in the nanocrystal growth, inducing formation of particles having various shapes [15].
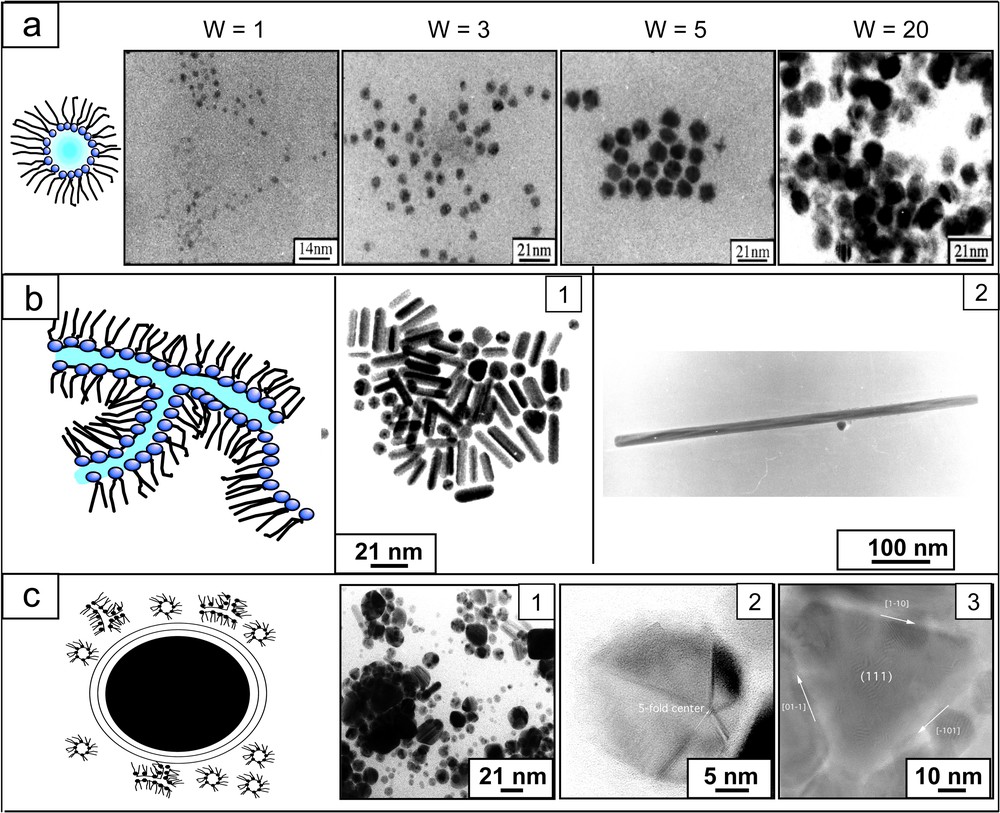
Copper nanocrystals produced in colloidal self-assemblies differing by their shapes and obtained from Cu(AOT)2–H2O–isooctane solution where CU(aot)2 is copper(II)bis (2-ethylhexil)sulphoccinate. (a) Reverse micelles: control of nanocrystal size with the water content, w, i.e., the size of water-in-oil droplets. (b) Sketch of interconnected cylinders: (1) formation of spherical and cylindrical nanocrystals, (2) cylindrical particle composed of a set of deformed fcc tetrahedra bounded by (111) faces parallel to the five-fold axis with an additional plane. (c) Supra-aggregates: (1) Various nanocrystals, (2) particle composed of five deformed fcc tetrahedra bounded by (111) planes, (3) large [111]–oriented flat nanocrystals limited by (111) faces at the top, bottom and edges.
The control of the nanocrystal shape is a real challenge and more data are now needed to ascertain the general principles that determine this shape. This is probably due to the fact that anisotropic materials are not in their thermodynamically stable state. Because the results obtained with reverse micelles are quite convincing and because the same three-component system produces self-assemblies of surfactants having various shapes [44], a number of groups tried to demonstrate that they could be used as templates. The first results obtained are rather persuasive. Our work demonstrates that the shapes of colloidal solutions made of functionalized surfactants partially control those of the nanocrystals [45]. Fig. 1B shows that an interconnected-cylinder template makes it possible to form cylindrical and spherical copper nanocrystals. The crystallinity of these nanomaterials is very high and the cylinder structure is characterized by a five-fold symmetry [46]. In the region of the phase diagram made up of an onion phase containing both internal and external interconnected cylinders, a large variety of shapes is observed (Fig. 1C). This control in the nanocrystal shape by that of the template has been recently confirmed by Simmons et al. [47]. However, the role of the template is not as obvious as described above. Adsorptions of ions and molecules have to be taken into account [15].
In the region of interconnected cylinders, small cylinders of copper metal nanocrystals are obtained (Fig. 1B1). Addition of less than 2 × 10–3 M chloride ions induces formation of copper nanorods [12] (Fig. 1B2), with an aspect ratio controlled by the amount of chloride ions in the microphase. The crystalline structures of these nanorods are similar to those of small cylinders (5-fold symmetry). On replacing NaCl by NaBr, nanorods smaller than those obtained with NaCl and a rather large amount of cubes are produced [13,14]. However, the aspect ratio does not change with bromide concentration. Furthermore, the shape of copper metal nanocrystals drastically changes with the type of salt added to the template [14] (Fig. 2). This cannot be due to changes in the colloidal structure by salt addition. In fact, the structure of the template remains the same in the presence of various salts (at fixed concentration) [13]. Hence, the template is not the key parameter in controlling the nanocrystal morphology. This is explained in terms of selective ion adsorption on facets during the crystal growth. Other examples clearly indicate that selective adsorption of molecules during the crystal growth is also a key parameter in controlling the nanocrystal shape. Nanodisks [48] are produced in the presence of surfactants that no longer form well-defined templates, whereas nanospheres are produced in reverse micelles. The nanodisk size depends on the amount of hydrazine present in solution [49]. Note that this is the first example where it is possible to control the silver nanodisks size and then their optical properties with changes in their colour from red to grey (Fig. 3). To explain the disk formation, we have to take into account the adsorption of hydrazine or/and hydrogen, hydroxyl ions on the faces. Associations of a large variety of molecules [50–55] are used as additives to be selectively adsorbed on the facets to control the particle shapes.
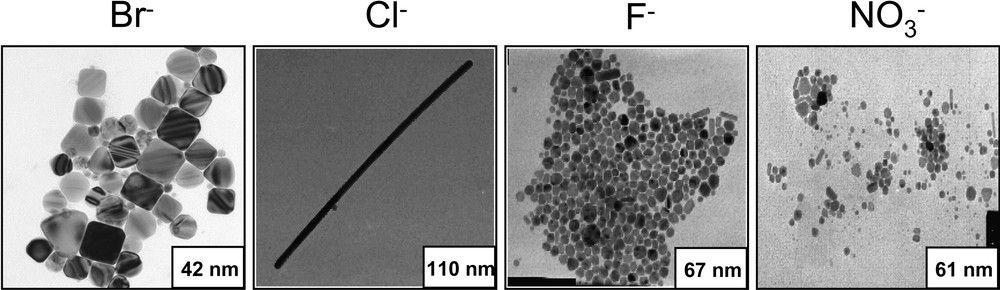
Various shapes of copper nanocrystals produced in interconnected cylinders in presence of various anions and same cation (Na+) having the same concentration. [NaCl] = [NaBr] = [NaF] = [NaNO3] = 10–3 M.
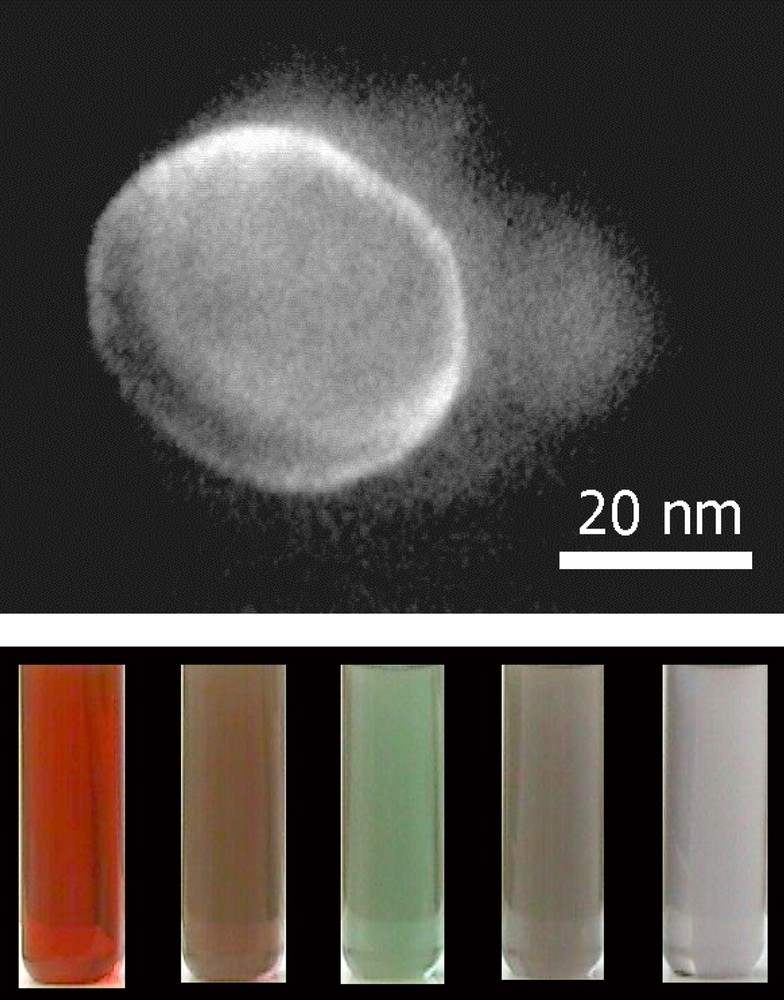
Nanodisks: TEM picture of faceted particle with a flat single crystal, two (111) faces at the top and the bottom, limited at the edges by three other (111) faces and at the corners by more or less extended (100) faces. Optical properties of nanodisks differing by their sizes over the range BIB20 to 100 nm.
3 Organization of nanocrystals
At the end of the synthesis, the powder made of coated nanocrystals is dispersed in a non-polar solvent and the nanocrystal concentration is controlled.
3.1 Nanocrystal self-organization
In 1995, we first demonstrated with M. Bawendi et al. [18] self-organization of nanocrystals with formation, on a mesoscopic scale, of a monolayer in a compact hexagonal network [17]. When a drop of the solution containing nanocrystals is deposited on a transmission electron microscopy (TEM) grid with a filter paper underneath, the solution migrates from the substrate to the filter paper and after a few seconds the solvent is totally evaporated. The TEM pattern obtained for cobalt nanocrystals deposited on the highly oriented pyrolitic graphite (HOPG) shows formation of a compact monolayer arranged in a hexagonal network (Fig. 4, 4A) [24]. If the same nanocrystals are deposited on amorphous carbon instead of HOPG, local disorders are observed (see arrow in Fig. 4, 4B). This clearly indicates that the self-organization of nanocrystals depends on the substrate used. In fact, it depends on the interaction energies between nanocrystals and nanocrystal-substrate. To obtain a well-defined self-organization on a mesoscopic scale, attractive interactions between particles and repulsive ones between nanocrystals and the substrate are needed. This has been well demonstrated with silver sulphide nanocrystals deposited on HOPG and on molybdenum disulfide MoS2 [56]. On increasing the nanocrystal concentration, aggregates of nanocrystals are formed instead of a monolayer (Fig. 5A). At higher resolution (Fig. 5B), nanocrystals organized in four-fold symmetry are observed, indicating an ordering of nanocrystals in an fcc structure. By controlling the evaporation rate and substrate temperature, large ‘supra’ crystals of silver nanoparticles, on a mesoscopic scale with a long distance order, are produced [22,23] (Fig. 5C) with a very sharp edge (Fig. 5D). Similarly, it is possible to make ‘supra’ crystals with an fcc structure of cobalt nanoparticles [24] (Figs. 5E and 5F). In the latter case, all the reflection characteristic of an fcc structure is observed (Fig. 6). This result was not expected because of the dipolar interactions between nanocrystals. In fact, they are weak enough to permit formation of ‘supra’ crystals in an fcc structure.

Deposition of a drop of solution containing cobalt nanocrystals on amorphous carbon (A) and HOPG (B). Deposition of a drop of solution of silver nanocrystals (C) and cigar-like ferrite nanocrystals (D) by using an anticapillary tweezer.

‘Supra’ crystals of nanoparticles at various enhancements: (A) and (B), ‘supra’ crystals of silver sulphide nanocrystals obtained by deposition of a concentrated solution of particles on amorphous graphite; (C) and (D), ‘supra’ crystals of silver nanocrystals obtained by controlling evaporation rate and substrate temperature, (E) and (F) ‘supra’ crystals of silver nanocrystals obtained by controlling evaporation rate and substrate temperature.
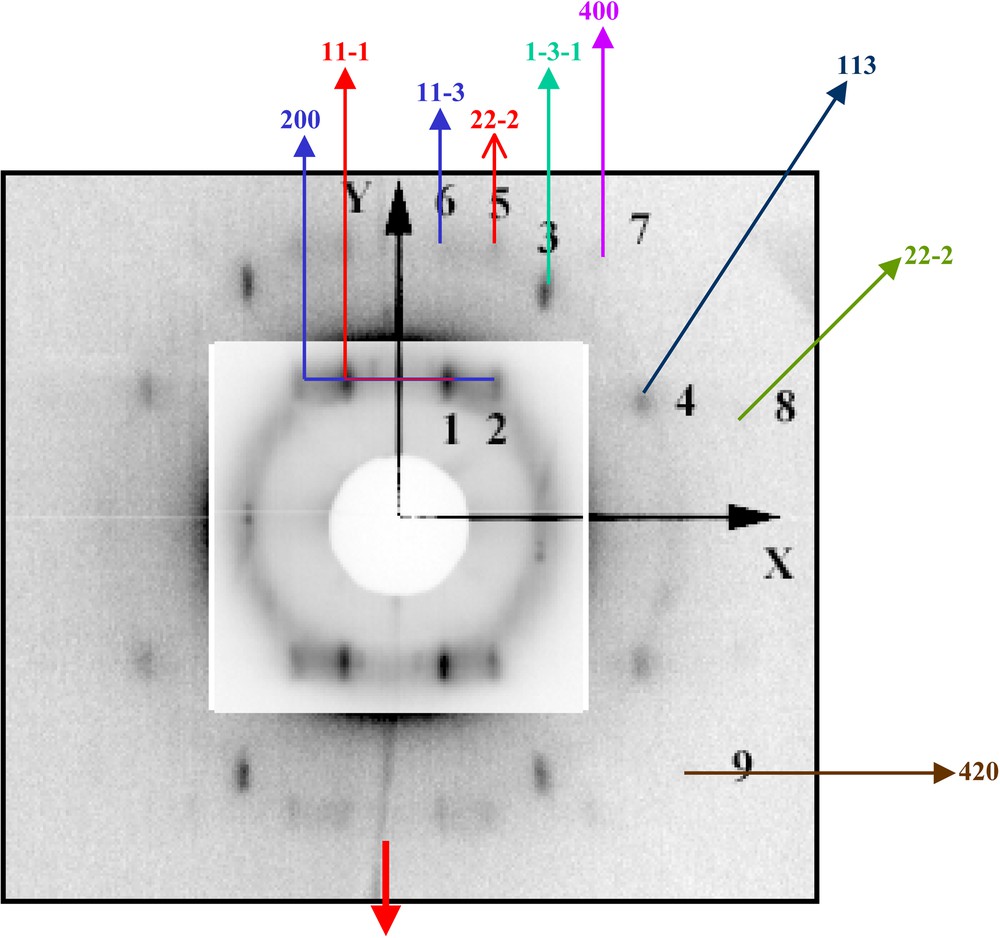
X-ray diffraction pattern obtained in a nearly grazing incidence geometry (tilt angle of substrate surface with respect to the incoming beam: 10°); the intensity is reduced by 20 in the central insert.
Instead of using the procedure described above, let us deposit a drop of solution with an anticapillary tweezer on a TEM grid. It remains on its support until the solvent is totally evaporated (solvent cannot escape from the grid). Fig. 4C shows the formation of rings of nanocrystals [57,58]. This is obtained with a large variety of nanomaterials and depends neither on the substrate used nor on the shape of the nanomaterial (Fig. 4D). It is attributed to Marangoni instabilities [59], induced by a fast evaporation process. With increasing particle concentration, more complex organizations made of close-packed structures are produced. These are similar in shape to those observed in Bénard’s experiment with liquid films and are attributed to a Marangoni effect.
3.2 Mesoscopic structure produced in a magnetic field
During the evaporation, a solution containing magnetic nanocrystals dispersed in a solvent is subjected (or not) to an applied field.
With ferrite nanocrystals [32,36] dispersed in aqueous solution, in the absence of a field, the scanning electron microscopy (SEM) patterns obtained at various magnifications show a large coverage of the substrate (Fig. 7A). The few-μm, cracked film is made of spherical, highly compact agglomerates (Fig. 7B and C). In an applied field parallel to the substrate, the nanocrystals are organized in ribbons. At low applied fields, the roughness of the sample is rather large (Fig. 7D and E). On tilting the sample (Fig. 7F), the ribbons are porous and poorly aligned. A progressive increase in the applied field favours the large coverage characterized by a linear orientation of the nanocrystals along the applied field direction. A needle-like structure, stretched in the magnetic field direction, is observed with a very regular structure. On increasing the strength of the applied field, the nanocrystal organization is highly homogeneous (Fig. 7G and H). On tilting the sample, this organization presents superimposed tubes made of nanocrystals (Fig. 7I).

SEM patterns at various enhancements obtained by evaporation of a solution containing maghemite nanocrystals and subjected to various applied magnetic fields, H, parallel to the substrate. (A), (B) and (C), H = 0; (D)–(F), H = 0.01 T; (G)–(I), H = 1.8 T.
With cobalt nanocrystals solubilized in hexane and subjected to an external magnetic field perpendicular to the substrate, a large variety of mesoscopic structures characterized by various shapes and depending on the strength of the field is observed [60] (Fig. 8). At very low applied fields, there are large dots with a rather wide size distribution (Fig. 8B). On increasing the applied magnetic field, well-dispersed dots are observed with formation of well-defined columns with a very sharp interface (Fig. 8C). A further increase in the applied field induces a decrease in the dot height and the dot interdistance. At higher applied fields, the patterns show worm-like and labyrinth structures. Hence, well-defined 3D superlattices of cobalt spherical nanocrystals on a very large scale are produced. Such structures were previously observed for a ferrofluid confined with an immiscible non-magnetic fluid between closely-spaced parallel plates and subjected to a normal magnetic field normal [61,62]. The major difference is due to the fact that in our case the structures are maintained after total evaporation of the solvent. A simple model [63], assuming that the demagnetising field within the ferrofluid is uniform, was proposed and compared to the experiments. Rosenweig [63] claimed good agreement between the model and experiments. However, very recently, Richardi et al. [64] demonstrated that the model needs to be revised as this agreement is no longer obtained. A new model [65] has been developed, from which the free energy functionals of hexagonal and labyrinthine structures are derived.

SEM patterns obtained by evaporation of a solution containing cobalt nanocrystals and subjected to various applied magnetic fields, H, perpendicular to the substrate. (A), H = 0; (B), H = 0.10 T; (C), H = 0.27 T; (D), H = 0.45 T; (E) H = 0.57T; (F) H = 0.85 T.
4 Collective properties of organized nanocrystals in a mesoscopic structure
4.1 Optical properties
In the UV–visible spectral range, the broad absorption bands of silver nanocrystals are due to plasmon resonance excitations or interband transitions. The absorption spectrum of dilute solutions of silver nanocrystals is modelled with Mie Theory [66–71]. When silver nanocrystals are organized in 2D superlattices on an HOPG substrate, the plasmon resonance peak is shifted to energies lower than that obtained for dilute solutions of isolated particles [72]. In s-polarization, the electric field vector is oriented parallel to the plane of the substrate at all incidence angles, θ. Plasmon resonance modes with components polarized perpendicular to the plane of the substrate are not seen when the incident light is s-polarized. On the other hand, p-polarized light, whose electric field is parallel to the plane of incidence, can probe plasmon resonance excitations whose components are either parallel or perpendicular to the substrate. For 2D assemblies of metal nanocrystals on planar substrates, p-polarized light is thus ideal for probing interparticle interactions. The UV–Vis polarization reflectivity spectrum of a hexagonal 2D assembly of 5-nm silver nanocrystals on an HOPG substrate is independent of the incidence angle, θ, with a plasmon resonance band centred at 2.9 eV, which is similar to that seen in isolated silver nanocrystals. Under p-polarization, a second band appears at higher energy as the incidence angle increases. The peak at high energy is attributed to the fact that each nanocrystal is subjected to the electric field of the incident light plus the dipolar fields of the particles in its vicinity [73]. Experimental and calculated reflectivity spectra of silver nanocrystals, self-assembled in compact hexagonal networks on various substrates (HOPG, gold, silicon and Al0.7Ga0.3As), are compared [74]. The calculated spectra are deduced from a model based on a mean field theory and taking into account the electromagnetic resonances for p (parallel) and s (perpendicular) polarizations. From experimental and calculated spectra, collective optical properties due to the formation of a film made of 5–nm silver nanocrystals are observed. In all cases, the experimental data show an additional resonance at a higher energy than the plasmon resonance of isolated nanocrystals whereas this is not obtained by calculation. However, the major change in the responses is due to the reflective index of the substrate. Because of this, it is impossible to find any substrate effect on the collective optical properties. That is to say, no specific interactions between nanocrystals and substrate can be observed by reflectivity. However, by using absorption [75] and photoemission [76] spectroscopies, the influence of the substrate can be determined with appearance of multipolar interactions.
4.2 Magnetic properties
We asked the following question: is there any change in the magnetic properties of nanocrystals with the film morphology? In other words, we want to know if the physical properties of a monolayer made of nanocrystals are related to their organization.
The magnetic properties described below are recorded at 3 K with a commercial superconducting quantum interference device (SQUID) magnetometer.
As shown in Fig. 7, various morphologies of γ-Fe2O3 nanocrystals are obtained when a magnetic field is applied during the deposition process. The hysteresis curves of γ-Fe2O3 nanocrystals shown in Fig. 7 are recorded with the applied field parallel to the alignment of the nanocrystals (x direction). For all the samples, saturation magnetization is reached at 3 T. Fig. 9A shows that as the strength of the magnetic field during the deposition process increases, the magnetization curves are straightened with an increase in the reduced remanence [36]. This is due to either a progressive partial orientation of the easy magnetization axes or structural changes.
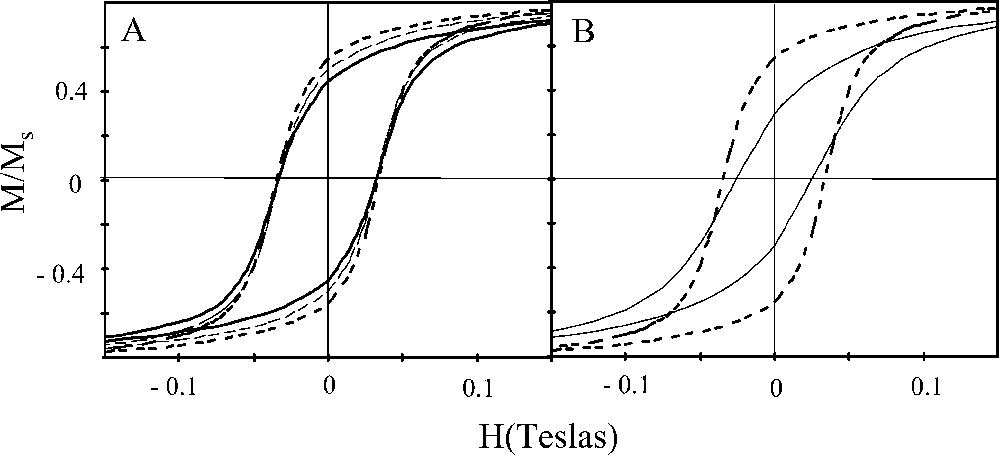
Hysteresis loop recorded at 3 K. (A) Change in the hysteresis loop with the strength of the applied field during the deposition process. (B) Change in the hysteresis loop of sample obtained when the applied field during deposition process is 1.8 T in a measured applied field either parallel (//) or normal (+) to the substrate.
If the easy axes are oriented along a given direction, two behaviours are expected.
- (i) The hysteresis loop measured, when the field is parallel to the easy axes (x direction), is expected to be rectangular [77], whereas, under a perpendicular (y) direction, it is a straight-line with no coercive field.
- (ii) The intensities of the six lines of the magnetic hyperfine spectrum, recorded in the Mössbauer spectra, are expected to drastically change when the easy axes of nanocrystals are oriented compared to those obtained when they are totally disordered.
Fig. 9B shows that when the applied field is normal to the substrate (z direction), the hysteresis loop is smoother compared to that observed when the applied field is parallel. However, the lines of magnetic hyperfine structure do not change with oriented and non-oriented nanocrystals. From these data it can be concluded that the change in the magnetization curve is due to the change in the mesostructure shape and to the orientation of nanocrystals along a given direction [78]. The compactness of the ribbons seems to be the key factor.
This is confirmed with cobalt nanocrystals having average sizes of 5.8 nm [79,80] and 8 nm [81], respectively.
For a monolayer of nanocrystals characterized by an isotropic disorder, the hysteresis loop is squarer than that obtained when nanocrystals are isolated. Two different structures are considered:
- • (i) a well-ordered, square-lattice monolayer, which is chosen as a reference system (Fig. 10A);
- • (ii) a monolayer of particles characterized by an isotropic disorder (hard-sphere-like distribution on the surface, Fig. 10B).

Various structures of nanocrystals deposited on a substrate (simulated and observed by TEM). (A) Square-lattice monolayer. (B) A monolayer of particles characterized by an isotropic disorder (hard-sphere-like distribution on the surface). (C) Nanoparticles aligned along a given direction.
Simulation of the hysteresis loop, for a given coupling constant and considering cobalt nanocrystals as Stoner–Wolfarth particles [82,83], shows no difference between the hysteresis loop of the square lattices and that of the real disordered system when the applied field is either parallel (x direction) or normal (z direction) to the substrate [28]. A ratio of the reduced remanences recorded when the applied field is normal (z direction) and parallel (x direction) to the substrate is defined, γ = (Mr/Ms)⊥ /(Mr/Ms)–. The γ values (0.70 and 0.65) calculated for two nanocrystal sizes (5.8 and 8 nm) are in good agreement with those measured (0.75 and 0.66) [84]. Hence, because of the long-range scale of dipolar interactions, the collective magnetic properties do not depend on the level of order inside the monolayer.
Fig. 11 shows the comparison of the hysteresis loops recorded (for an applied field parallel to the x direction) when the nanocrystals are deposited on a substrate with formation of a disordered monolayer and aligned along an axis. In the latter case, the hysteresis loop is much squarer than the others.
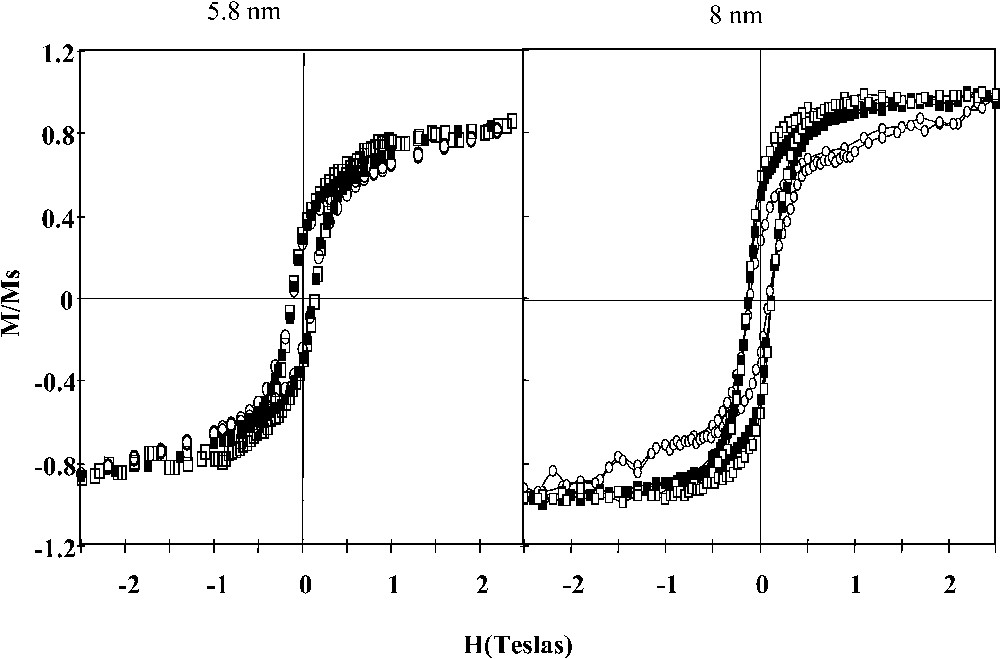
Hysteresis loop of nanocrystals having two different sizes (5.8 and 8 nm) either randomly dispersed on a substrate or aligned along a given direction.
Let us compare the magnetization properties of nanocrystals aligned in chains and 2D superlattices:
- • (i) the reduced remanence increases;
- • (ii) The saturation magnetization does not change although it is reached at 1 T instead of 1.5 T;
- • (iii) the coercivity slightly increases.
In chain superlattices, with an applied field parallel to the substrate, the magnetic response evolves with the orientation of the applied field to the chain direction. The magnetic properties when the applied field is perpendicular (y direction) and parallel (x direction) to the chain direction, keeping the substrate parallel, are:
- • (i) the magnetization is smoother than that obtained when it is parallel;
- • (ii) saturation magnetization is not reached, even at 2.5 T when it is perpendicular;
- • (iii) drops in the reduced remanence and coercivity are observed.
To explain such drastic changes in magnetic properties with the nanocrystal organization, a model is proposed [85] with a chain-like structure of particles (Fig. 10C), parallel to a given direction. The magnetization of this structure is compared to a well-ordered (square lattice) one (Fig. 10A). The simulation of a hysteresis loop for a given coupling constant shows a marked difference between the hysteresis loop of the square lattices and that of the linear chain system when the field is applied parallel to the chains (Fig. 12). A large increase in the reduced remanence is obtained compared to the reference system and the coercivity slightly increases. Applying the field perpendicular to the substrate (z direction) leads to a smoother hysteresis loop, with a large decrease in the reduced remanence. In this case, the coercivity slightly decreases (Fig. 12). Due to the dipolar coupling, the linear chains behave roughly as homogeneous wires with an effective easy axis in the direction of the chains although individual nanocrystals have randomly distributed easy axes.
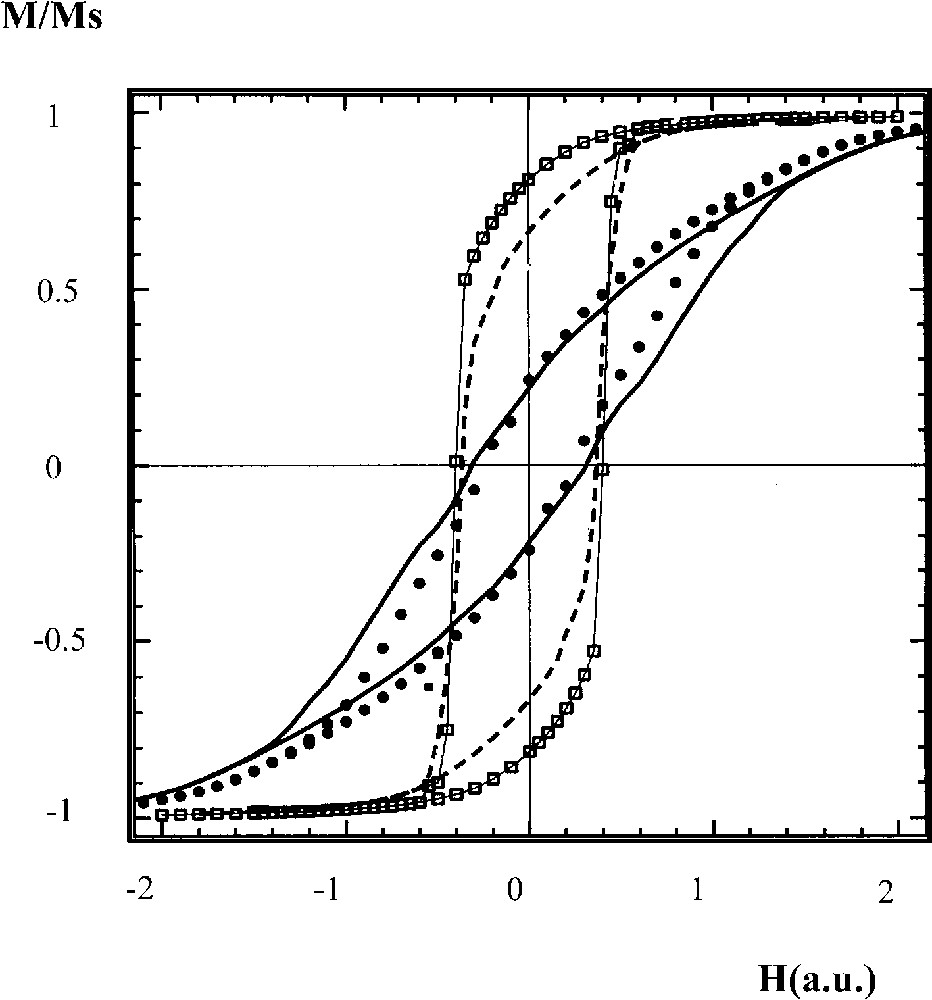
Calculated hysteresis loop of nanocrystals forming either a square-lattice monolayer or aligned along a given direction.
The hysteresis loops recorded either parallel (x direction) or perpendicular (y direction) to the chains enable estimating the strength of the structural effect defined as γ′ = (Mr/Ms)⊥ /(Mr/Ms)||. This value is compared to the experimental value in order to check the magnitude of this structural effect on the collective magnetic properties of the cobalt nanocrystals chains. The γ′ values obtained from experiments [84] (0.77 and 0.42) and from theory (0.83 and 0.61) for the two nanocrystal sizes (5.8 and 8 nm), respectively, have the same order of magnitude. The collective magnetic properties depend on the structure of the organization and these nanocrystals are found to behave roughly as nanowires. These data make it possible to understand the magnetic behaviour of many magnetic bacteria having aligned ferrite nanocrystals [85]. Contrary to what has been claimed, their magnetic behaviour could not be related to the orientation of the easy axis of each particle but to the collective properties due to their organizations along a given direction.
5 Conclusion
In this review we demonstrate that reverse micelles constitute an efficient nanoreactor for controlling the size of spherical nanocrystals whereas only a partial control in the shape is obtained. The major parameters in the shape control of nanocrystals seem to be the selective adsorptions on various faces during the particle growth. This question is still open. Normal micelles are used to produce well-defined ferrite nanocrystals. Nanocrystals are self- organized in 2D either in a compact hexagonal network or in rings. By controlling temperature and evaporation time, ‘supra’ crystals in fcc structures are produced even for magnetic nanocrystals. By applying a magnetic field, various mesoscopic structures of nanocrystals are obtained. Collective properties due to these organizations are pointed out.


