1 Introduction
Because of its ability to selectively observe and characterize the local environments of most constituting atoms of ordered or disordered solids, high-resolution solid-state nuclear magnetic resonance (NMR) spectroscopy has become a tool of choice for materials science. The rapid development of new methods now not only provides means for spectrally resolving and quantifying different chemical environment characterized by their chemical shifts but also allows one to explore the structure of the surrounding of the observed atoms at different length scales using interactions characteristic of distances (dipolar interaction) [1,2] or chemical bonds (J indirect coupling) [3]. These methods can take different forms ranging from spectral edition to measurement and use the through-space or through-bond interactions in multidimensional experiments. The aim of this contribution is to focus on the measurement and use of indirect J couplings, even when involving quadrupolar nuclei, and to emphasize new developments and perspectives.
Silica-based materials can be used as a starting point to illustrate the general problems of materials science that can be assessed using solid-state NMR, including by the exploitation of molecular interactions such as J couplings. These materials are of paramount importance in many different fields of materials sciences in the form of inorganic glasses, sol–gel derived materials, biocompatible or bioinspired materials, porous or mesoporous materials, zeolites, or organic–inorganic hybrids. The structures of silica-based materials are characterized in particular by various extents of order and disorder at length scales that range from molecular to micrometric dimensions, as illustrated with a few typical examples on Fig. 1. Amorphous structures, such as silicate glasses or commercial SiO2, which may be used as a silicon source for silicate materials synthesis, have highly disordered molecular structures that are associated with a wide range of local silicon environments giving rise to broad (ca. 10 ppm, full width at half maximum [fwhm]) 29Si NMR lineshapes (Fig. 1e) that barely allow resolution of chemically different Q3 (i.e., (SiO)3Si–OH or (SiO)3Si–O–) and fully condensed Q4 (Si(SiO)4) 29Si moieties. Similar molecularly-disordered SiO2 structures are also generally found in the walls of self-assembled mesoporous silica despite potentially high degrees of long-range order in their pore architectures, as illustrated on Fig. 1f by the broad lineshapes associated with Q2, Q3, and Q4 environments in the 29Si{1H} cross-polarization (CP) magic angle spinning (MAS) spectrum of the block-copolymer-silica composite whose representative transmission electron microscopy (TEM) image is shown on Fig. 1b [4]. Increasing extents of molecular order, on the other hand, may be clearly evidenced by narrow 29Si NMR resonances that allow distinguishing between chemically similar environments on the basis of subtle differences in their bonding geometries. This is for example the case for non-crystalline surfactant-templated layered silicates with short-range molecular order [5] (Fig. 1c and g) and even more so for high-zeolites such as ZSM-12 [6] (Fig. 1h), where high degrees of long-range three-dimensional (3D) molecular order yield extremely narrow (ca. 0.4 ppm) 29Si MAS NMR lineshapes (Fig. 1h).
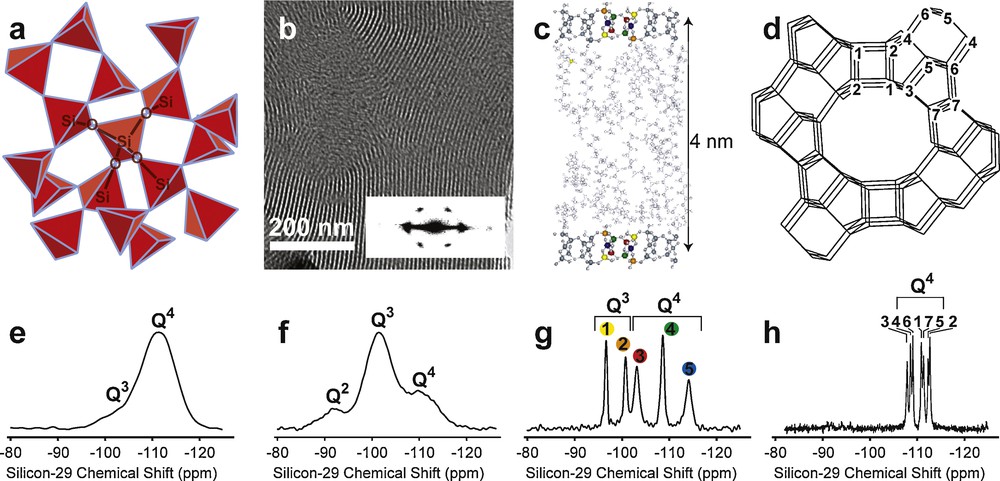
a: schematic representation of an amorphous SiO2 structure, with SiO4 tetrahedra shown in red, and (e) 29Si spin-echo MAS NMR spectrum of commercial silica with 99% enrichment in 29Si; b: transmission-electron microscopy (TEM) image and electron diffraction pattern (inset) and (f) 29Si{1H} CPMAS NMR spectrum of an hexagonal mesoporous silica composite [4]; c: in-plane view of a layered silicate–surfactant mesophase consisting of thin (0.8 nm) molecularly-ordered silicate sheets with five distinct (colored) Si atom sites giving rise to five narrow 29Si resonances in the corresponding 29Si{1H} CPMAS NMR spectrum (g), and separated by alkylammonium surfactant species [5]; d: schematic representation of the highly ordered silicate framework structure and (h) 29Si MAS NMR spectrum with extremely narrow resonances of zeolite ZSM-12 (courtesy D.H. Brouwer).
However, even if the simple 1D 29Si MAS spectra (direct observation or CP from 1H) obviously already provide valuable information on the nature and composition of complex materials at the molecular level, the exact attribution of the different resonances in highly ordered compounds or the understanding of the underlying order or disorder requires a more precise description of the coordination sphere of the observed nuclei. Such information, along with the existence of chemical bonds may be obtained by exploiting or measuring the indirect J coupling between (for example) the different silicon sites (homonuclear coupling) or between silicon and chemically-bound spin-bearing heteronuclei (heteronuclear coupling).
2 J couplings between I = 1/2 nuclear spins
The indirect J coupling splitting was first observed by Proctor and Yu [7] for 121Sb in a NaSbF6 solution and identified by Gutowsky and MacCall in 1951 [8] in liquid phosphorus halides (31P/19F), immediately after the first descriptions of the chemical shift effect [9–11]. The famous Karplus relation [12], established in 1959, showed that the exact measurement of the 3J(H,H) scalar coupling constants between vicinal hydrogen atoms could provide detailed information on the conformation of soluble molecules, pointing to the strong influence of the dihedral angle on these J coupling values. The use of this interaction in multidimensional experiments [13] opened the way to many spectral edition or correlation liquid state NMR methods. The recent development of higher speed MAS, efficient heteronuclear decoupling, and higher fields leading to improved spectral resolution and sensitivity, have triggered a renewed interest in J coupling-based NMR experiments in rigid solids, for which the small J couplings are often masked by inhomogeneous broadenings [3]. These developments offer new ways for separating the through-space (dipolar) and through-bond (J coupling) contributions in various applications, measuring previously unknown couplings with high precision, and exploiting them in multidimensional or spectral editing experiments. Because J couplings are characteristic of the existence of a chemical bond between like or unlike nuclei, they allow a more accurate description of the coordination sphere of the observed nuclei extending to “molecular motifs” up to the nanometer scale [14–17].
High-resolution solid-state NMR uses fast MAS to mimic the Brownian motion of the liquid state and simplify the broad, orientation dependent, static line-shape of solids into isotropic resolved spectra. The coherent mechanical motion of the rotor around the magic angle allows averaging of all first-order perturbations to their traces. Thus, under these conditions, the chemical shift anisotropy tensor (CSA) is averaged to its isotropic part, the indirect J coupling is averaged to its isotropic (scalar) part, and both the dipolar and first-order quadrupolar interactions are averaged to zero. Solid-state NMR experiments never (or seldom) succeed in achieving spectral resolution comparable to that of liquid-state experiments because there exist small but significant higher order terms including shifts and broadening (second-order quadrupolar effects, second-order cross-terms between interactions), residual dipolar coupling terms at limited spinning rates, and distribution of the isotropic contributions due to non-ideal ordering or disorder. Nevertheless, a combination of high-frequency spinning, very accurate magic angle setting (±0.01°) [19] and efficient heteronuclear decoupling allows observation of scalar J couplings in perfectly ordered crystalline phases, as illustrated on Fig. 2 with the 13C CP-MAS spectrum of the (ZnO3P C2H4 CO2H – 0.5 C6H5NH2) layered phosphonate crystalline compound [18,2]. In this spectrum we observe directly two of the above-mentioned effects. These features are easily masked in routine experiments, due to imperfect shiming, magic angle setting or heteronuclear decoupling, and superimpose to the chemical shift information and possible distribution. Here, the two different α13CH2 directly linked to the two non-equivalent 31P sites of the inorganic layer are split into doublets by one-bond 31P–13C scalar (1J) coupling of ca. 40 Hz (top-right inset) and the 13C of the benzyl ring linked to the 14N of the amine reveals a broadening due to a dipolar/quadrupolar cross-term [19,20] (top-left inset).

13C CP-MAS spectrum (300 MHz, 14 kHz) of the crystalline layered phosphonate (ZnO3P C2H4 CO2H – 0.5 C6H5NH2) [18] acquired with an accurate setting (±0.01°) of the MAS angle and optimized proton decoupling, which allows evidencing the 31P–13C 1J splitting on the first carbon of the aliphatic chain and the splitting of the 13C–14NH2 resonance by the dipolar/quadrupolar cross-term (R{14N}13C).
Even when not visible in a regular 1D MAS spectrum due to inhomogeneous broadenings, the J couplings can be indirectly characterized using a J-resolved experiment, as early described in liquid-state experiments [13], and further used in homo- or heteronuclear correlation experiments allowing identification of chemically bound sites. This experiment relies on the accumulation of dephasing coming from J couplings evolution while refocusing all other inhomogeneous interactions and inhomogeneities using a Hahn-Echo. The adaptation of liquid-state NMR experiments to solids in isotropic conditions (i.e., high speed MAS) usually only requires synchronization of the evolution periods with MAS spinning rates, the only limitation remaining the T2’ coherence lifetime of the echo signal [21] which limits the ability to express J couplings smaller than typically 1/T2’. The two-dimensional (2D) J-resolved experiment correlates the usual 1D spectrum to the individual J coupling multiplets allowing a site by site measurement of the coupling constants.
Fig. 3 shows an ultimate example of resolution for J couplings in inorganic materials with the measurement of coupling constants down to a few hertz in the case of CaSiO3 calcium silicate polymorphs consisting in chains of cross-linked Si-based Q2 units [22]. J coupling-based methods are now established as valuable approaches for examining the molecular topologies and structures of a variety of organic and inorganic ordered or disordered solids with examples of homo- and heteronuclear couplings. These include one-bond 13C–13C [23–25,3] and 31P–31P [26,27] 1J couplings, hydrogen-bond-mediated 15N–15N 2hJ couplings [28]; and two-bond 2J couplings such as 31P–O–31P [29–37], 31P–N–31P [38] or 29Si–O–29Si [39–42,22] 2J couplings in crystalline or disordered compounds or glasses, and also heteronuclear couplings such as one-bond 19F–207Pb [43], 31P–113Cd, and 31P–77Se [44–46] 1J couplings, and two-bond 2J(29Si–O–31P) couplings [47–49], among others.
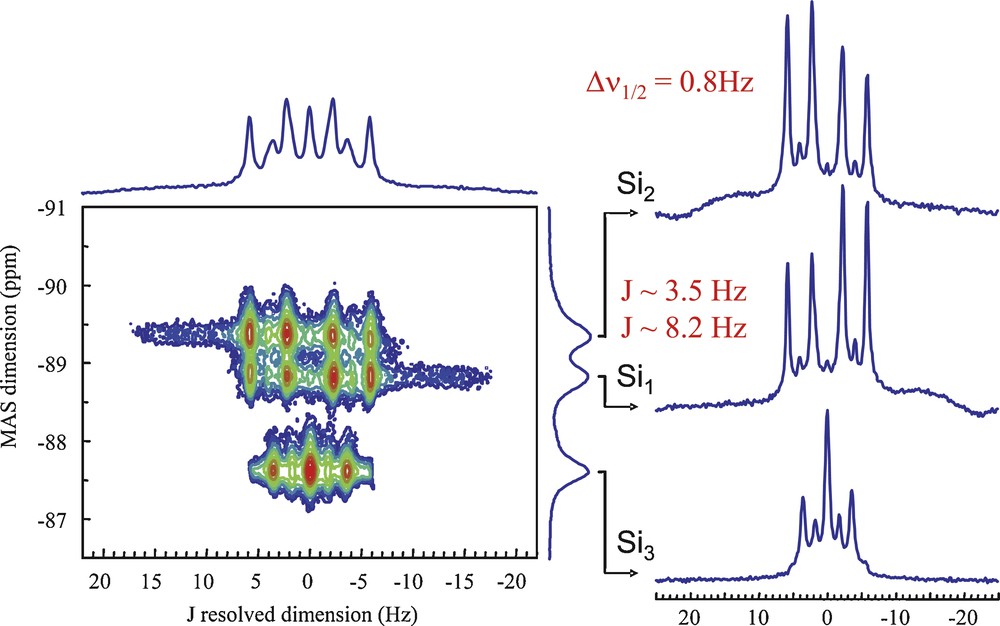
J-resolved experiment on the crystalline wollastonite Ca29SiO3 revealing 2J(29Si–O–29Si) couplings of a few hertz. The full J-resolved spectra can be perfectly modeled by considering 29Si isotopic enrichment and strong coupling effects due to small chemical shift differences (adapted from reference [22]).
3 J couplings involving quadrupolar nuclei
Up to this point we considered J-coupled systems only involving I = 1/2 nuclear spins which are the most commonly observed in liquid-state experiments involving mostly 1H, 13C, 15N, or 31P nuclei. The presence of a fluctuating quadrupolar interaction (molecular reorientation) introduces a significant relaxation broadening which often precludes observation of resolved spectra for quadrupolar nuclei in the liquid phase but there nevertheless exist a few significant reports of J couplings involving one or even two quadrupolar nuclei in the liquid state (17O–35Cl [50], 17O–55Mn [51], 17O–95Mo [52], 17O–51V [53]). The case of solid-state NMR, on the other hand, is significantly different in that the quadrupolar interaction, even when strong, does not fluctuate and thus does not induce relaxation effects. As a result, in solids, it is possible to obtain long enough coherence lifetimes [21,54] for the observation of even small scalar couplings of the order of a few hertz which could not be observed in the liquid state. In that sense, solid-state NMR surpasses liquid state NMR in terms of resolution and of the size of the couplings that can consequently be assessed. Many examples showing scalar couplings between spin-1/2 and quadrupolar nuclei have indeed been reported, including couplings between 13C and 35-37Cl nuclei [56], and between 31P and 27Al [57–62,54,15,16], 63,65Cu [26,27,63–65], 31P–113,115In [66,67], 31P–55Mo [68], 31P–101,99Ru [69], 31P–17O [70], and 19F–93Nb [71]. These examples show a variety of situations with often strong dipolar/quadrupolar cross-terms leading to complex spectra even in rather simple compounds. Finally, there exist very few reports of quadrupolar/quadrupolar J coupling interactions until recently: 11B–75As [72], 17O–17O [73], or 27Al–17O [74,75,14] with applications to the analyses of the details of glass structures and evidence of the presence of μ3 oxygen bridges in calcium aluminate glasses [74] for example.
The general case of scalar J coupling measurements in a solid under fast MAS (fast enough to average out spinning sidebands of central transitions) is depicted on Fig. 4 considering a pair of nuclei I–Q consisting of a nucleus I (nuclear spin I = 1/2) coupled to a quadrupolar nucleus Q (nuclear spin I = 5/2) by a J coupling interaction. The central transition (as well as the satellite) of the quadrupolar nucleus Q (Fig. 4, top, in blue) is significantly shifted and broadened by the second-order quadrupolar interaction, and its coupling to the neighboring nucleus I generates a splitting of the resonance (Fig. 4, top, in green) which usually remains small as compared to the second-order quadrupolar effects. However a high-resolution multiple-quantum (MQ) MAS experiment yielded separation of the two components by removing the second-order quadrupolar broadening allowing direct measurement of the J coupling [76]. Under the same conditions, the J coupling of the observed I to Q yields a splitting in 6(2Q+1) resonances (Fig. 4, bottom, in blue) corresponding to the different spin states of the quadrupolar nucleus. When significant dipolar couplings coexist with a large quadrupolar coupling (Fig. 4, bottom, in green), the complexity of the spectrum increases since the dipolar/quadrupolar cross-terms induce shifts and broadenings of the different components of the J-multiplet, as already seen in the case of 13C/14N for the phosphonate compound on Fig. 2. An experimental illustration of the complex interplay between quadrupolar and J coupling interactions is given on Fig. 5 with the example of the CsNbF6 crystalline phase which features niobium in sixfold coordination to crystallographically equivalent fluorine atoms. 93Nb has a nuclear spin I = 9/2 and its MAS spectrum (Fig. 5a) consists in the superposition of nine different transitions (central transition plus satellite or outer transitions) affected by second-order broadening (with different scaling factors) and J couplings (sevenfold multiplet for the six equivalent bound 19F nuclei). Because the satellite transitions are also affected by first-order quadrupolar broadening at finite spinning rates, they break into spinning sideband manifolds that remain separated under our observation conditions (17.6 T spectrometer, 35 kHz MAS frequency). The processing of the 93Nb CsNbF6 MAS spectrum (Fig. 5a) according to the 2D one pulse (TOP) procedure [55] allows reconstruction of the 2D TOP spectrum separating the different spinning sidebands by order (Fig. 5b) and then the reconstruction of the sum spectrum corresponding to an “ideal infinite spinning rate” spectrum (Fig. 5c) which can be modeled using the dmfit program [77]. In the particular case of a spin I = 9/2, the <±5/2> transitions undergo the smallest second-order quadrupolar effects and clearly exhibit the expected sevenfold multiplet characteristic of its bounding to six equivalent fluorine atoms.
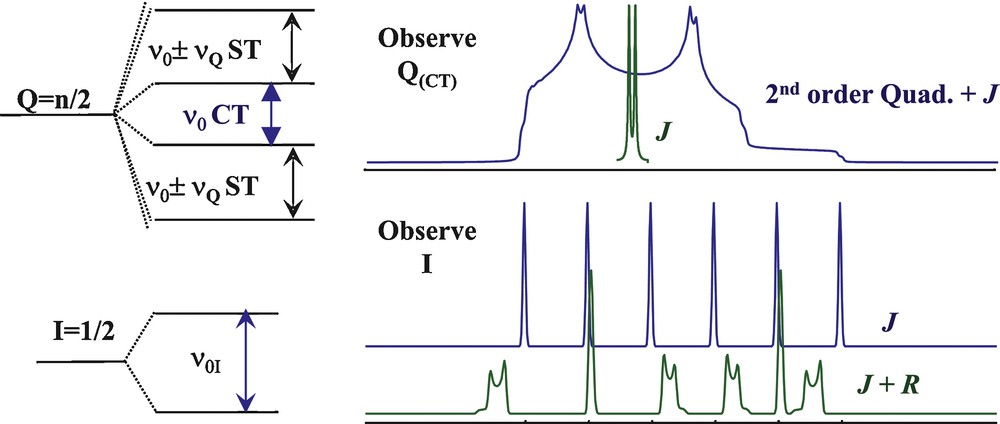
Schematic representation of the effect of the J coupling between a quadrupolar nucleus Q (I = 5/2) and a dipolar nucleus I (I = 1/2). The central transition of the quadrupolar nucleus Q (top, in blue) is broadened to second order by the quadrupolar interraction and split in two by the J coupling to I (in green). The second-order quadrupolar broadening can be removed in an MQMAS experiment allowing to only observe the J coupling multiplet [76]. The signal of the I nucleus is split in a 2 Q + 1 (e.g., 6 for I = 5/2) multiplet. Additional second-order broadenings and shifts arise when R (the dipolar quadrupolar cross-term) becomes significant.
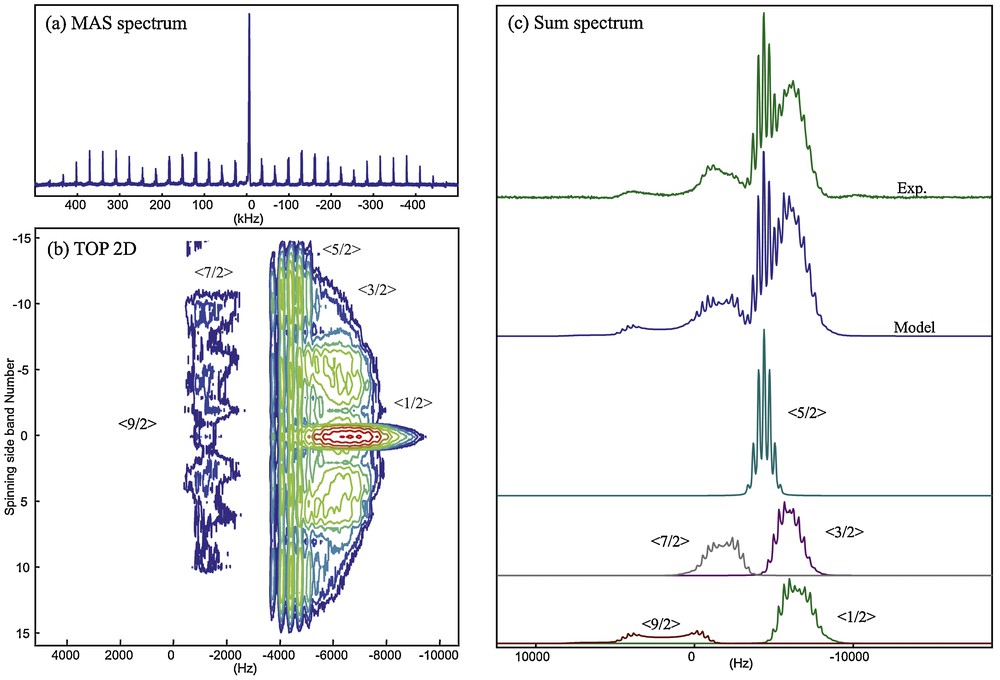
TOP processing of the 93Nb MAS spectrum of CsNbF6, δNb = –1580 ppm, CQ = 10.2 MHz, ηQ = 0.45 (a) allowing 2D reconstruction of the TOP spectrum (b) and the computation of the “infinite spinning rate” TOP spectrum. The TOP spectrum can be modeled (c) considering a 1J coupling of 344 Hz to six chemically bound cristallographically equivalent fluorine, which is reflected by the splitting of each observed transition of the 93Nb resonance in a septuplet.
Because tailoring excitation conditions allows one to selectively excite the central transition as a fictitious I = 1/2 spin using an echo [78,79] the J multiplet of the 93Nb central transition can be indirectly revealed in a heteronuclear {19F}93Nb J-resolved experiment as used to observe 2J(27Al–O–31P) couplings in aluminum phosphates [54,61]. Fig. 6 (left) shows the indirectly-acquired (using a {19F}93Nb J-resolved experiment with a selective refocusing of the 93Nb central transition) sevenfold J multiplet of the 93Nb resonance characteristic of the sixfold coordination to 19F nuclei. The 1D MAS NMR 19F spectrum (Fig. 6, right) similarly exhibits a single contribution for all equivalent fluorine sites but split in a 10-line multiplet corresponding to the 10 different 93Nb spin states (from –9/2 to +9/2). As previously remarked [71] the decuplet is not perfectly symmetric due to spin-state dependent relaxation times and small but nevertheless significant dipolar/quadrupolar cross-terms. A {93Nb}19F J-resolved experiment (Fig. 6, top-right) clearly shows that the 93Nb π pulse only results in a modulation of the two center lines of the multiplet corresponding to the <±1/2> spin states. These results not only demonstrate that it is possible to excite selectively the central transition of a half-integer quadrupolar nucleus and measure dipolar/quadrupolar and J couplings, but also underline the fact that our current experimental protocols completely discard most of the signal by ignoring the satellite transitions. Nevertheless, new perspective offered by efficient excitation of sideband-modulated satellite transitions using adiabatic pulses [80,81] may change this situation and offer novel possibilities to enhance sensitivity and efficiency of experiments involving quadrupolar nuclei.
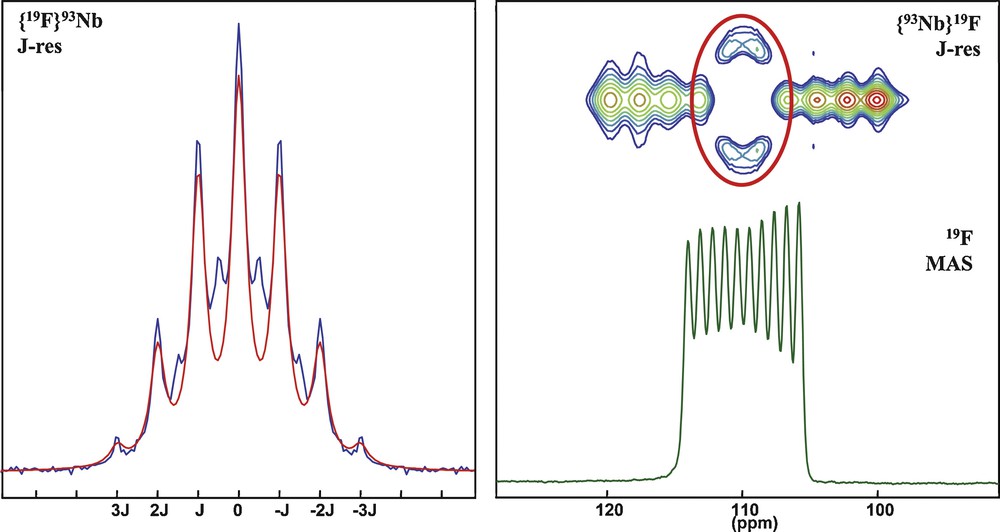
Central transition selective {19F}93Nb J-resolved experiment and its model with a sevenfold multiplet—1D MAS spectrum, δF = 110.1 ppm, 1J = 344 Hz showing coupling to the 10 spin states of a single 93Nb nucleus and {93Nb}19F J-resolved experiment showing that only the two center bands corresponding to <±1/2> central transition of 93Nb is manipulated during the 93Nb excitation.
4 Towards more accurate measurements at high MAS spinning rates
As already mentioned the visibility of indirect J couplings, and thus the ability to measure or use them, relies on the proper averaging of all residual terms by efficient MAS at a precisely fixed angle. This is illustrated on Fig. 7 with the 31P MAS spectrum of α-CaP2O7. While the 2J (P–O–P) coupling remains masked by residual broadenings in a conventional 1D MAS experiment when spinning at 15 kHz and can only be measured indirectly using a 2D J-resolved experiment (Fig. 7, top), an increase of the MAS rate up to 30 kHz leads to the observation of a noticeable splitting of the 1D lines and a clearly improved resolution in the indirect experiment. This is due to the improved coherent lifetime (longer T2′) (Fig. 7, bottom) and is to be related to the improved averaging of residual homonuclear dipolar interaction, dipolar/CSA cross-terms (n = 0 rotational resonance effects) [82]. These effects are known to give rise to unexpected cross-peaks at moderate spinning rates and high fields in correlation experiments [37]. The recent commercial availability of very high speed MAS probes capable of spinning rates up to 70 kHz is very likely to allow new observations in the coming years, especially in protonated materials, as already demonstrated for organic solids [83], and for hybrid organic–inorganic materials with the measurements of 2J (29Si–O–29Si) couplings in mesoporous silica “at natural 29Si abundance (i.e., 4.7%)” [84].
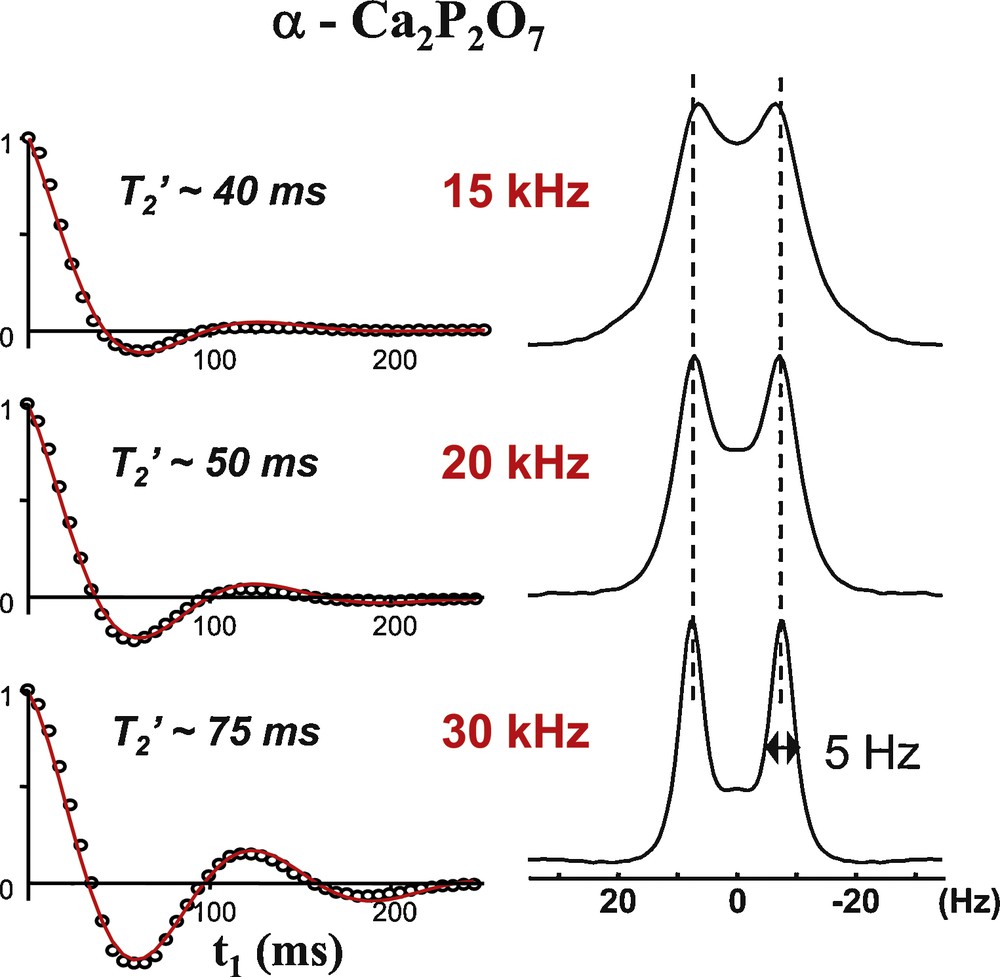
31P J resolved MAS spectra (7.0 T) of α-Ca2P2O7 acquired at exact magic angle (≈ ±0.01°) showing the increased resolution of the 2J(31P–O–31P) coupling with increasing MAS rate, allowing improved removal of residual contributions to transverse dephasing.
5 Preliminary results on cordierite (Mg2Al4Si5O18)
Since the small homo- or heteronuclear 2J couplings across bridging oxygens can be evidenced in aluminosilicate or phosphate materials, they can be further exploited in a variety of experiments that allow characterization of the coordination sphere or structural network with increased details. It then becomes possible to build relayed transfer experiments that allow transferring repeatedly the magnetization from a starting nucleus to its first and second neighbors [15,16], as if “walking” across the covalent 3D network structure. It is also possible to describe experiments dedicated to counting the different NMR-active neighboring nuclei (or to editing the spectrum according to this count) with examples on pairs of nuclei such as {31P}31P, {29Si}29Si, {27Al}31P, {27Al}29Si [36,43,14,17]. These new possibilities can be applied to the study of crystalline α-cordierite magnesium aluminosilicate (Mg2Al4Si5O18) [85]. This compound has a well defined structure featuring some chemical Al/Si disorders (Fig. 8a). The unit cell is made of three equivalent T1 sites, mostly occupied by Al atoms, and six equivalent T2 sites mostly occupied by Si atoms, both with tetrahedral geometry. The T1 sites are connected to four T2 sites with a T1–O–T2 angle of 129° while T2 sites are connected to two T1 and two T2 sites with a T2–O–T2 angle of 172° [85]. The 1D 29Si MAS spectrum of our cordierite sample unequivocally pictures a much more complex situation with several overlapping lines that are likely to translate the variety of possible local environment of 29Si nuclei, and clearly evidences the silicon occupancy of T1 sites based on chemical shifts values [86–90] (around ≈ 80 ppm, see Fig. 8c). From this simple measurement we can already characterize the T1/T2 occupancy ratio. At that stage we can remark that our limited knowledge on 29Si–O29Si 2J couplings seems to indicate that there exist a relation between the T–O–T angle and the scalar coupling with the strongest coupling observed for T–O–T angles close to 180°, as also reported for 29Si–O–29Si 2J in CaSiO3 and justified by cluster ab initio computations (i.e. Gaussian) [22,42]. The J resolved spectrum of cordierite presented on Fig. 8b shows very contrasted J splittings (vertical dimension) for T1 and T2 sites showing the strongest 2J couplings for the sites featuring the largest T–O–T bond angle (Fig. 8d). From this observation it becomes possible to show that the Q4(3Al) site (main resonance of the T2 group) is mostly coupled to a neighboring 29Si T2 for which larger bond angles are expected. Obtaining complementary structural information from 27Al NMR experiments is more complicated, since the simple MAS 1D spectrum does not allow separation of different lines, even at high magnetic field [91,92]. In such a case the spin counting experiment [17] allows characterizing the connectivity of 27Al atoms with neighboring 29Si by generating various multiple quantum coherence order through the evolution under the 27Al–O–29Si 2J scalar couplings. Interestingly, in α-cordierite, counting the neighboring 29Si sites around 27Al nuclei reveals on average three neighboring Si for Al in T2 sites, whereas only two Si are counted for Al in T1 sites, even though T1 sites are surrounded by four T2 sites which are occupied predominantly by Si atoms. This unexpected smaller number of neighboring Si atoms for T1 sites could be explained by a weaker J coupling in T1–O–T2 bonds leading to less efficient excitation of higher coherence orders. A through-space dipolar-mediated spin counting experiment could infirm or confirm this interesting result. We note that such analyzes may be of considerable interest for solving the long-standing problem of Al distributions and repartitions in molecular sieves.

a: α-cordierite XRD structure [85]; b: connectivity of T1 and T2 sites; c: 29Si MAS NMR and (d) 29Si J-resolved spectra of 99% 29Si-enriched cordierite featuring the 2J(29Si–O–29Si) multiplets in the indirect dimension; e: spectral editing of 27Al NMR spectra in 99% 29Si-enriched α-cordierite, corresponding to the 1D spectrum (in red), and the contributions of Al(OSi)≥ 1 (red), Al(OSi)≥ 2 (purple), Al(OSi)≥ 3 (yellow) and Al(OSi)≥ 4 (blue) motives.
6 Disordered materials
Since inorganic and organic–inorganic materials may have various extents of order and disorder at different length scales, as discussed above (Fig. 1), it is particularly interesting that scalar couplings can be measured in amorphous materials as well. The “as purchased” 99% 29Si-enriched silica material (Cortecnet), which may be used as a silicon source for silicate materials synthesis, is a good example of a disordered system of complicated and unknown structure (Fig. 9a and b). Its 1D spectrum can be acquired either by direct polarization (Fig. 9a, in black) of 29Si (leaving time for long relaxation times) or by a CP experiment that transfers magnetization from the silanol OH protons to the associated Q3 sites, and to a lesser extent to nearby Q4 sites. The first experiment is close to quantitative (providing long enough recycle delays, i.e. typically of the order of tens to hundreds of seconds in disordered silica materials) and is dominated by a Q4 broad line that represents 85% of the total intensity. In contrast, the Q3 contribution can be selectively enhanced and turned to dominate the 1D 29Si spectrum when carried out using a polarization transfer. The 29Si J-resolved experiments carried out using these two types of excitation thus allow one to probe separately the 29Si–O–29Si 2J couplings for these two types of environments (Fig. 9). Despite a large broadening of both Q3 and Q4 lines (typically 8.5 ppm, i.e. 500 Hz at 7 T), and as observed in the case of phosphate glasses [33,35,36,14], it is possible to reveal J coupling spectra showing multiplet structures: a quadruplet for Q3 linked to three other 29Si nuclei (2J couplings ≈ 14.5 Hz) and a quintuplet for the Q4 linked to four 29Si nuclei (2J couplings ≈ 16.5 Hz). What is also remarkable is that the 2D plot of the J-resolved experiment is clearly structured and features well identified ridges with a clear correlation between 2J(29Si–O–29Si) couplings and isotropic 29Si chemical shifts values across the Q3 and Q4 lines and a non-random distribution of the individual J couplings values [35,22]. It is of particular interest to interpret such remarkable features of the NMR spectra of disordered silicate and phosphate materials and to understand their implications for the local structure.
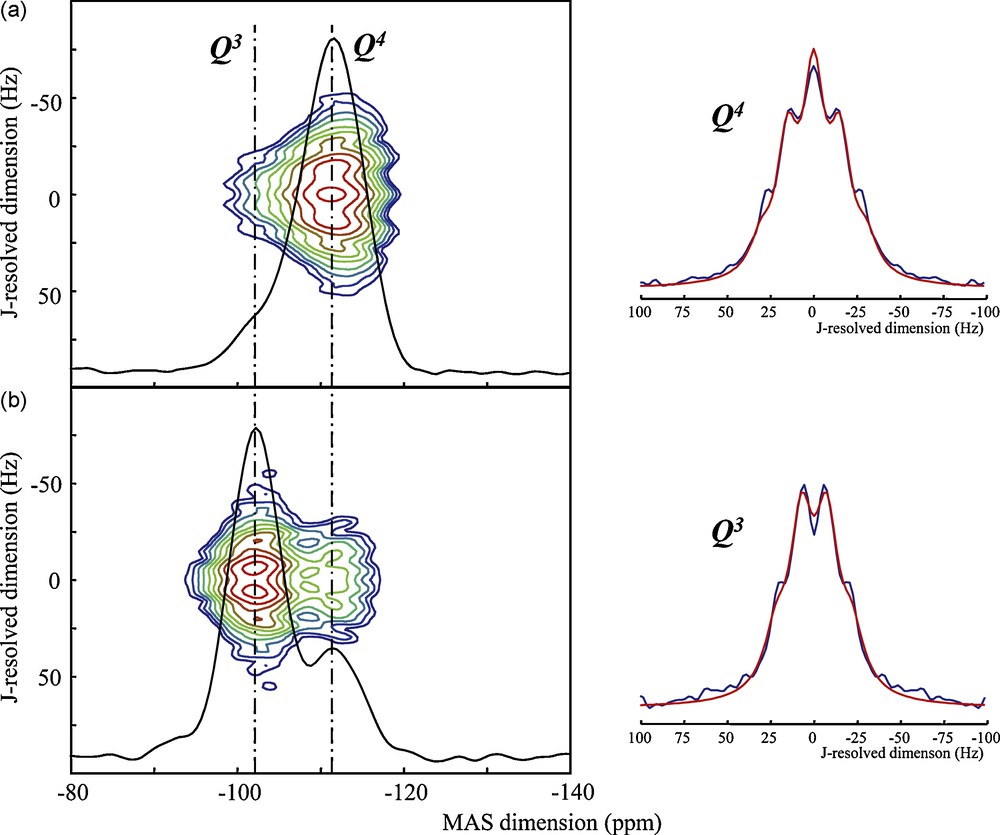
J-resolved experiments performed on a 29Si-enriched SiO2 sample « from the bottle » with (a) direct detection and (b) cross-polarization from 1H. One-dimensional spectra superimposed to the 2D-lineshapes are projections onto the MAS dimension. The slices taken at along the J-resolved dimension at the peak maxima show a quadruplet for Q3 and a quintuplet for Q4 tentatively modeled with J couplings of J(Q3) ≈ 14.0 Hz and J(Q4) ≈ 16.5 Hz.
7 Understanding J couplings
In addition to attesting directly of the existence of chemical bonds (covalent or even hydrogen bonds [28,88]), scalar couplings may provide important local structural information in inorganic and hybrid organic–inorganic materials through the exploitation of their magnitude, which is highly related to the local geometries of the coupled nuclei. By comparison to dipolar couplings for example, deriving structural information from J coupling magnitudes is not straightforward, since these interactions are affected by many local structural parameters that include (among others) bond lengths, bond angles and dihedral angles [93], but also the electronegativity of surrounding nuclei [94]. The relative extents to which these parameters influence the J coupling value notably depend on the coupling type (1J, 2J, or 3J), and on the surrounding bond orders. Because of this complexity, computational approaches are required to extract reliable structural information from J couplings. Semiempirical calculation approaches have been proposed [95], but recent studies have demonstrated that methods based on density functional theory (DFT) are generally more robust and applicable to a broader range of systems.
For solid materials, DFT calculations of J couplings can be conducted using cluster approaches, where a small molecular system is extracted from the solid and considered in isolation. Such approaches are particularly useful for studying local structural disorder, since angular dependences of scalar couplings [93,42,22] (and of other NMR parameters [96,97]) can be easily explored. This was very recently exploited to demonstrate unambiguously that the strong correlation between 29Si chemical shifts and 2J(29Si–O–29Si) couplings observed for glassy wollastonite CaSiO3 (and very similar to that observed on Fig. 9 for amorphous 29SiO2) can be attributed to distributions of 29Si–O–29Si angles that can further be characterized [22]. However, while reliable trends may be established, reproducing quantitatively experimental coupling constants is generally more challenging.
Recent investigations on model Sigma-2 and ZSM-12 zeolite systems [42] have nevertheless demonstrated that, at least in the particular case of zeolites, 2J(29Si–O–29Si) couplings, computed with good accuracy from cluster approaches using appropriate locally-dense basis sets and cluster definitions, agree well with that measured experimentally at natural 29Si abundance. These 2J(29Si–O–29Si) couplings proved to be highly sensitive to the fine details of the local structures of crystalline silicates, which, in contrast to amorphous silica, may consist of more distorted SiO4 tetrahedra (for example), such that 2J(29Si–O–29Si) couplings do not reflect the Si–O–Si angles as directly. In the case of zeolite ZSM-12 (Fig. 10), these studies suggest in particular that the description of local framework geometries might be dramatically improved by integrating scalar couplings into structure-refinement protocols. We anticipate that such “NMR crystallography” methods may become one of the major applications of J couplings in materials in the future. For example, J couplings could readily be integrated, along with other NMR interactions (chemical shift or quadrupolar interaction), in least-square structure-minimization algorithms based on the comparisons between experimental and calculated NMR parameters, as proposed by Brouwer for siliceous zeolites using 29Si CSA interactions [98,99]. The combination of diverse interactions with different physics and thus different sensitivities to the local structures may considerably improve the reliability and robustness of NMR-based structure determination methods for diverse classes of materials with atomic ordering for which diffraction techniques alone are generally inconclusive or yield poorly resolved structures (e.g., layered materials).

a: schematic representation of the structure of ZSM-12; b: solid-state 2D refocused-inadequate 29Si{29Si} NMR spectrum of siliceous zeolite ZSM-12 at natural abundance (black contour plots) and 2D spectral deconvolution (colored map) from which 2J(29Si–O–29Si) values were extracted; c: 1D 29Si NMR slices extracted from the experimental spectrum (in black) and from the 2D deconvolution (in red), along with the measured J couplings (adapted from reference [42]).
Furthermore, in the future, solid-state NMR studies of periodic systems and the protocols for solving or refining their structures will greatly benefit from the new developments in plane-wave-based approaches for the calculation of J couplings [100]. Encouraging agreements between experimental and calculated couplings have already been reported for couplings involving different combinations of nuclei [100], including 2J(31P–O–29Si) couplings in silicophosphates and hydrogen-bond-mediated 2hJNN in ribbon structures [88]. Furthermore, DFT calculations of J couplings with periodic boundary conditions can, in principle, also potentially be used to investigate small amplitude disorder in otherwise crystalline solids, following an approach very recently proposed by some of us [101] on the basis of correlated chemical shifts distributions [41], which could readily integrate J coupling distributions. The strong potential of such distributions of J couplings for the structural interpretation of local disorder, such as the characterization of bond angle distributions for silicate glasses for example [22], is further increased by novel possibilities to examine even highly disordered solids using DFT in periodic boundary conditions, in combination with molecular dynamics and solid-state NMR [102,103].
8 Conclusion
From selected examples of new or recently published data we have shown that it now becomes possible to evidence, measure and use small scalar homo- or heteronuclear J couplings in solid-state inorganic or hybrid materials. This allows direct examination of the chemical bonds around the selectively observed nucleus and opens ways to characterize extended structural motifs at the subnanometer scale in ordered or disordered materials, even when broadening of the resonances due to disorder becomes significantly greater than the J couplings themselves. It is especially remarkable that it is possible to measure couplings involving quadrupolar nuclei in rigid solids while they remain unobservable in liquid state experiments because of quadrupolar relaxation. From a selection of examples, we emphasized on several important and promising points:
- • the increasing possibilities opened by new hardware availability (very high speed MAS spinning);
- • the development of new methods allowing “walking” through a 3D network (from one nucleus to its successive like or unlike neighbors), or selecting resonances of groups of bound nuclei in “spin counting” experiments;
- • the chemical relevance of the measured couplings in terms of local structure as jointly viewed with ab initio computations using cluster or newly developed periodic approaches.
This approach should apply to large classes of inorganic or hybrid materials with possible application to structural refinement, sorting between spatial proximity and chemical bonding, or evidencing local ordering in globally disordered structures.
Acknowledgements
We acknowledge financial support from CNRS, région Centre CNRS, ANR RMNSOLIDE-HR-HC ANR-05-BLAN-0317 and we thank Bruno Bujoli, Florence Babonneau and Christian Bonhomme for numerous and fruitful scientific discussions.


