Simple versus composite nature of the magnetic coupling in copper and nickel-based metallic chains. Over- and underestimation of <i>J</i>

Nuno A.G. Bandeira; Zahra Tabookht; Coen de Graaf; Xavier López

doi:10.1016/j.crci.2011.10.002

Simple versus composite nature of the magnetic coupling in copper and nickel-based metallic chains. Over- and underestimation of J

Nuno A.G. Bandeira ¹ ; Zahra Tabookht ¹ ; Coen de Graaf ^1,² ; Xavier López ¹

¹ Departament de Química Física i Inorgànica, Universitat Rovira i Virgili, Marcel·lí Domingo s/n, 43007 Tarragona, Spain
² Institució Catalana de Recerca i Estudis Avançats (ICREA), Passeig Lluís Companys 23, 08010 Barcelona, Spain

Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 163-169.

Résumés

Anglais
Français

Extended metal atom chains (EMACs) are molecular linear arrangements of metal atoms featuring magnetic properties. By means of the density functional theory (DFT), we have studied the magnetic coupling constants for [Cu₃(dpa)₄Cl₂]⁺, Ni₃(dpa)₄Cl₂ and Ni₅(tpda)₄Cl₂ to understand which is the origin of the previously reported theoretical underestimation of J for nickel complexes. We have decomposed J = J_σ + J_δ, finding that the former contribution is underestimated and the latter part is overestimated at the DFT/B3LYP level of computation. Varying the amount of Hartree-Fock exchange, we show that the B3LYP functional fails to describe the σ interaction properly, whereas the δ coupling is exaggerated.

Les chaînes étendues d’atomes métalliques (EMACs en anglais) sont des composés moléculaires linéaires avec des propriétés magnétiques. En utilisant la théorie de la fonctionnelle de la densité (DFT), nous avons étudié les constantes de couplage magnétique pour [Cu₃(dpa)₄Cl₂]⁺, Ni₃(dpa)₄Cl₂ et Ni₅(tpda)₄Cl₂ pour comprendre l’origine de la sous-estimation théorique de J pour des complexes de nickel décris précédemment. Nous avons décomposé J = J_σ + J_δ et nous avons trouvé que la première contribution est sous-estimée, tandis que la seconde est surestimée au niveau de calcul DFT/B3LYP. Des variations de la fonctionnelle B3LYP montrent que cette fonctionnelle habituelle ne parvient pas à reproduire l’interaction σ de façon adéquate, alors que le couplage δ est exagéré.

Métadonnées

Reçu le : 2011-06-10
Accepté le : 2011-10-04
Publié le : 2011-11-16

DOI : 10.1016/j.crci.2011.10.002

Mots clés : Electronic structure, Transition metals, Ligand effects, Metal–metal interactions, Density functional calculations, Computer chemistry, Molecular modeling

Affiliations des auteurs :

Nuno A.G. Bandeira ¹ ; Zahra Tabookht ¹ ; Coen de Graaf ^{1, 2} ; Xavier López ¹

@article{CRCHIM_2012__15_2-3_163_0,
     author = {Nuno A.G. Bandeira and Zahra Tabookht and Coen de Graaf and Xavier L\'opez},
     title = {Simple versus composite nature of the magnetic coupling in copper and nickel-based metallic chains. {Over-} and underestimation of {\protect\emph{J}}},
     journal = {Comptes Rendus. Chimie},
     pages = {163--169},
     publisher = {Elsevier},
     volume = {15},
     number = {2-3},
     year = {2012},
     doi = {10.1016/j.crci.2011.10.002},
     language = {en},
}

TY  - JOUR
AU  - Nuno A.G. Bandeira
AU  - Zahra Tabookht
AU  - Coen de Graaf
AU  - Xavier López
TI  - Simple versus composite nature of the magnetic coupling in copper and nickel-based metallic chains. Over- and underestimation of J
JO  - Comptes Rendus. Chimie
PY  - 2012
SP  - 163
EP  - 169
VL  - 15
IS  - 2-3
PB  - Elsevier
DO  - 10.1016/j.crci.2011.10.002
LA  - en
ID  - CRCHIM_2012__15_2-3_163_0
ER  -

%0 Journal Article
%A Nuno A.G. Bandeira
%A Zahra Tabookht
%A Coen de Graaf
%A Xavier López
%T Simple versus composite nature of the magnetic coupling in copper and nickel-based metallic chains. Over- and underestimation of J
%J Comptes Rendus. Chimie
%D 2012
%P 163-169
%V 15
%N 2-3
%I Elsevier
%R 10.1016/j.crci.2011.10.002
%G en
%F CRCHIM_2012__15_2-3_163_0

Nuno A.G. Bandeira; Zahra Tabookht; Coen de Graaf; Xavier López. Simple versus composite nature of the magnetic coupling in copper and nickel-based metallic chains. Over- and underestimation of J. Comptes Rendus. Chimie, Volume 15 (2012) no. 2-3, pp. 163-169. doi : 10.1016/j.crci.2011.10.002. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2011.10.002/

Version originale du texte intégral

1 Introduction

Calculation of magnetic coupling constants in molecules and materials from a purely theoretical basis is a common practice among computational chemists and physicists. There exist a few phenomenological spin Hamiltonians (Ising, Heisenberg, etc.) that relate the energies of different spin states with the J parameter, which quantifies the strength of the magnetic interaction. Several methodologies based on quantum mechanics have been applied to compute J, all with their strengths and weaknesses. For small to medium sized systems (either molecules or model fragments of crystals), highly correlated ab initio (wavefunction based) methods can be applied, notably the difference dedicated configuration interaction (DDCI) method [1,2], developed to accurately calculate energy differences. In general, and especially for large systems, a balance between computational time and accuracy is a must.

In this article, we apply the density functional theory (DFT) to the calculation of the J parameter in systems containing 90 to 130 atoms. Apart from one study in which ab initio correlated methods were applied [3], DFT based approaches are commonly used to calculate J in extended metal atom chains (EMACs) [4], our target systems in the present work. Such molecules contain a set of metal atoms disposed in a linear arrangement thanks to the coordination to polydentate organic ligands of the polypyridylamide family [5], of general formula [C₅H₄N-(N-C₅H₃N)_n-N-C₅H₄N]⁽ⁿ⁺¹⁾⁻ and number of binding sites p = 2n + 3, cylindrically wrapped around the chain. The number of binding sites of the purposely-designed organic ligands determines the nuclearity of the metal chain. The homonuclear trimetallic chains, M₃(dpa)₄Cl₂, are the most common examples of EMACs [6–17]. A recurring challenge related to metal string complexes is the synthesis of increasingly longer chains [18–26]. Peng's group achieved an 11-nickel molecular string, the longest metal chain known in 2011 [27,28].

Very recently, we calculated the magnetic coupling constant for Ni₃(dpa)₄Cl₂ and some hypothetical derivatives [29] using the method reported by Labèguerie et al. [30]. The previously proposed decomposition of the J parameter in this compound, J = J_σ + J_δ, was carried out, where each component arises from a different coupling pathway within the molecule. The motivation of the present work arose a few years ago, when Rohmer and Bénard obtained an unexpected DFT underestimation of the J parameter for Ni₃(dpa)₄Cl₂ [4a], a well-known system whose magnetic properties have been characterized [26,31,32]. The smaller value computed contrasts with the typical overestimation of J for the other members of the EMAC family, notably [Cu₃(dpa)₄Cl₂]⁺, and most magnetic systems theoretically studied at the same level of calculation. We herein present calculations on [Cu₃(dpa)₄Cl₂]⁺, Ni₃(dpa)₄Cl₂ and Ni₅(tpda)₄Cl₂ (dpa: dipyridylamido; tpda: tripyridyldiamido), shown in Fig. 1, and discuss why DFT/B3LYP results on Ni derivatives tend to underestimate J in contrast to other compounds of this class.

Fig. 1
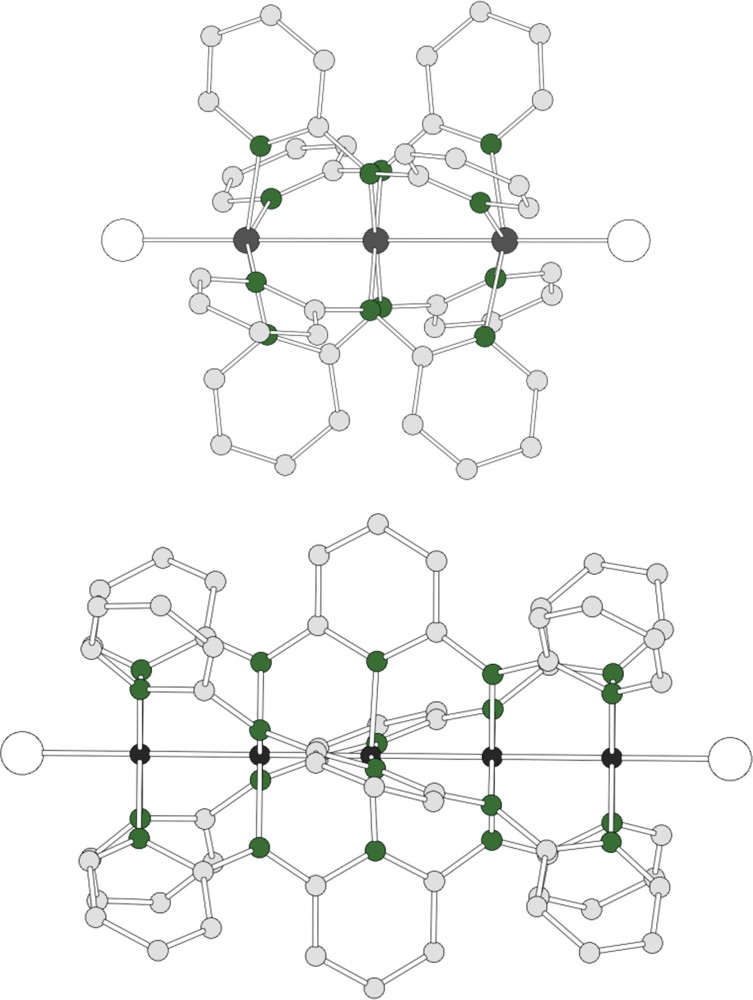
Structure of M₃(dpa)₄Cl₂ (M = Cu, Ni) (top) and Ni₅(tpda)₄Cl₂. The central backbone contains the metal atoms, in grey. Green spheres represent nitrogens. Hydrogen atoms have been omitted for clarity.

2 Computational details

The Gaussian03 [33] suite of programs was used to calculate all the spin state energies using the broken symmetry technique of Noodleman et al. [34,35]. We used Becke's gradient corrected three-parameter B3LYP functional [36], of the form

E_{B 3 L Y P} = E_{S l a t e r, x} + c_{0} (E_{H F x} - E_{S l a t e r, x}) + 0.72 E_{B e c k e 88, x} + E_{V W N 3, c} + 0.81 (E_{L Y P, c} - E_{V W N 3, c})

(1)

built up from Slater's local exchange [37] with Becke's gradient corrections [38], and the Vosko et al.’s [39] local correlation functional with Lee et al.’s [40] gradient corrections. Conventionally, c₀ regulates the amount of Hartree-Fock exchange (HFX) and is set to 0.2. In this study, it was varied between 0.0 and 0.3. For Ni and Cu, LANL2DZ basis sets were used with the addition of an extra polarization f function [41]. The geometries were optimised at the B3LYP level with constraints on the metal-metal and metal-ligand bond lengths to fix them to their experimental values, taking advantage of the D₄ point group symmetry whenever possible. The SCF energy error threshold was set to 10⁻⁸ a.u. for an adequate convergence of every solution.

There has been a great deal of controversy [42–44], in the literature, regarding the use of spin projection with density functionals since the self-interaction error (SIE) [45] tends to mimic static correlation, therefore, making the Kohn-Sham broken symmetry determinant artificially represent more than just half of an open shell singlet. While most hybrid density functionals should carry less SIE with respect to their “pure” counterparts most additions of exact exchange in hybrids are usually modest and do not generally exclude enough SIE to guarantee a sufficient accuracy with spin projection [46]. It should be noted that the formalism devised by Labèguerie et al. [30] does in fact presuppose spin projection in all the broken symmetry solutions.

3 Results

The systems we deal with present two magnetic centres located at both ends of the chain. The central metal atoms (one for M₃ chains, three for M₅ chains) are diamagnetic due to the ligand field of their neighbouring atoms. In the case of [Cu₃(dpa)₄Cl₂]⁺, the terminal d⁹ copper atoms posses a local S = 1/2, whereas for Ni₃(dpa)₄Cl₂ and Ni₅(tpda)₄Cl₂, terminal d⁸ nickel centres have local S = 1. The coupling mechanism in copper complexes is rather familiar, whereas the interaction of two 3d⁸ Ni(II) centres may be viewed as an interference phenomenon between two half-filled fragment molecular orbitals of e_g* symmetry that are composed mainly of the 3d_z2 (σ) and 3d_x2_–y2 (δ) atomic orbitals, yielding linear combinations of gerade and ungerade symmetries. This magnetic interaction can be phenomenologically described by a general form of the magnetic spin Hamiltonian [47–49] that has been successfully applied to single determinant methods such as DFT, more specifically to S = 1 magnetic dimers [29,30].

This Hamiltonian takes the form:

\begin{array}{r} \hat{H} = \sum_{i, j} J_{i j, e f f} ({\hat{S}}_{i} \cdot {\hat{S}}_{j}) + λ_{i j} {({\hat{S}}_{i} \cdot {\hat{S}}_{j})}^{2} + \sum_{i, j, k} \frac{B_{j i} B_{i k}}{2 K_{σ δ}} [({\hat{S}}_{i} \cdot {\hat{S}}_{j}) . ({\hat{S}}_{i} \cdot {\hat{S}}_{k}) + ({\hat{S}}_{i} \cdot {\hat{S}}_{k}) . ({\hat{S}}_{i} \cdot {\hat{S}}_{j}) \\ - ({\hat{S}}_{i} \cdot {\hat{S}}_{i}) . ({\hat{S}}_{j} \cdot {\hat{S}}_{k})] \end{array}

(2)

where J_ij,eff, B_ij and λ_ij are defined as

J_{i j, e f f} \equiv \frac{t_{σ, i j}^{2}}{U} + \frac{t_{δ, i j}^{2}}{U} + \frac{B_{i j}^{2}}{K_{σ δ}} = J_{i j} + \frac{B_{i j}^{2}}{K_{σ δ}}

(3)

B_{i j} \equiv \frac{t_{σ, i j}^{2}}{U} - \frac{t_{δ, i j}^{2}}{U}

(4)

λ_{i j} = \frac{B_{i j}^{2}}{K_{σ δ}} - \frac{J_{i j}^{2}}{4 K_{σ δ}}

(5)

In this formalism, t_σ stands for the hopping integral related to the energy splitting of the in- and out-of-phase σ orbital pair as described, for instance, in the Hay-Thibeault-Hoffmann [50] formalism. Analogously, t_δ is the hopping integral for the δ symmetry pair. U is the promotion energy to attain the ionic configuration with respect to the neutral form, and K_σδ is the direct exchange integral between the σ and δ-type orbitals on the same site. λ_ij is the biquadratic exchange constant and B_ij the three-body interaction constant. In the case of simple bilinear exchange, only (B_ij = λ_ij = 0) Eq. (2) reduces to the more familiar Heisenberg-Dirac-van Vleck Hamiltonian [43] in which J_ij,ef > 0 for ferromagnetic compounds and J_ij,ef < 0 for anti-ferromagnetic interactions.

For the three complexes Ni₅(tpda)₄Cl₂, Ni₃(dpa)₄Cl₂ and [Cu₃(dpa)₄Cl₂]⁺, the nature of the frontier orbitals involved in the magnetic coupling is depicted in Fig. 2. The magnetic centres are the outermost metal atoms in all the cases. The first two constitute a four-electron/four-orbital problem whereas the latter is a simpler two-electron/two orbital-problem. The orbitals classified as δ in Fig. 2 are responsible for the J_δ magnetic coupling, and those classified as σ participate in J_σ. The two pathways are theoretically well known from previous studies [4b,29].

Fig. 2
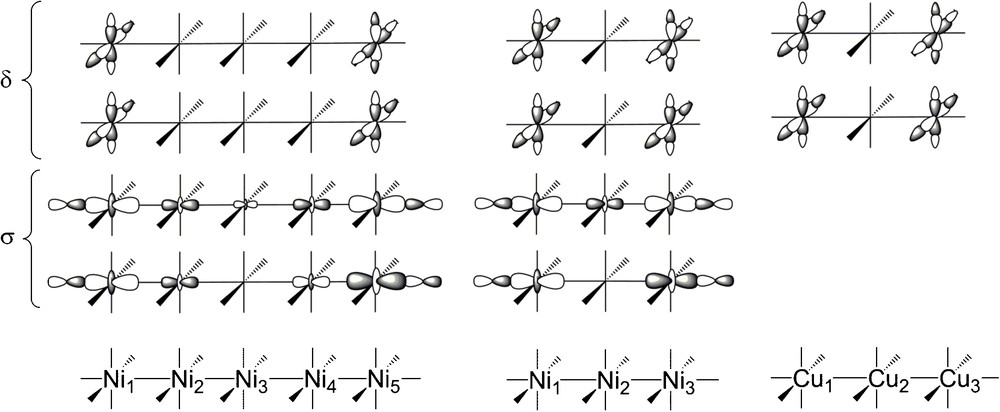
Sketch of the magnetic orbitals for the three complexes Ni₅(tpda)₄Cl₂, Ni₃(dpa)₄Cl₂ and [Cu₃(dpa)₄Cl₂]⁺. The orbital overlap is much smaller in the σ channel than in the δ one.

A second-order perturbative treatment of the energy allows extracting electronic structure parameters related to the magnetic properties of molecules. Let us take the S = 1 systems (Ni₃ and Ni₅) and vary the occupation of the magnetic orbitals of σ and δ nature with ↑ and ↓ spins. We obtain the set of open-shell configurations listed in Table 1, whose single determinant representations can be classified as follows: one M_s = 2 solution (Q) two M_s = 1 solutions (T1 and T2) and two M_s = 0 solutions (S1 and S2). The perturbative treatment of their energies leads to Eqs. (6)–(10), which contain the electron structure parameters t, U and K. These values can be extracted if the energies of the states listed are known. In the present article, energies are obtained from DFT calculations. Our main goal is to calculate separately the two contributions to the total J parameter, which for an antiferromagnetic system with two S = 1 centres are, at the second order of perturbation:

\begin{array}{l} J = J (AF) - J (F) \\ = E (↑ ↑ \dots ↓ ↓) - E (↑ ↑ \dots ↑ ↑) = E (S 1) - E (Q) \\ = - 2 \frac{t_{σ}^{2}}{U} - 2 \frac{t_{δ}^{2}}{U} \\ = J_{σ} + J_{δ} \end{array}

		Ni₁	Ni₃/Ni₅
M_s	Electronic configuration	σ	δ	σ	δ	E⁽²⁾
0	“Singlet” 1: S1	↑	↑	↓	↓	−2t_σ²/U − 2t_δ²/U	(6)

0	“Singlet” 2: S2	↓	↑	↑	↓	−2t_σ²/U − 2t_δ²/U + 2K_σδ	(7)

1	“Triplet” 1: T1	↑	↓	↑	↑	−2t_δ²/U + K_σδ	(8)

1	“Triplet” 2: T2	↓	↑	↑	↑	−2t_σ²/U + K_σδ	(9)

2	Quintet: Q	↑	↑	↑	↑	0	(10)

^a Ni₁ and Ni₃/Ni₅ are the terminal atoms in nickel chains.

where AF and F stand for antiferromagnetic and ferromagnetic, respectively. This is the common way to obtain the total J from broken symmetry DFT calculations. To decompose the final expression J = J_σ + J_δ into the two components, we can make use of Eqs. (6)–(8) from Table 1:

(1) and (2) : K_{σ δ} = \frac{E (S 2) - E (S 1)}{2}

(11)

(11) and (3) : \frac{t_{δ}^{2}}{U} = \frac{- E (T 1) + K_{σ δ}}{2}

(12)

(12) and (2) : \frac{t_{σ}^{2}}{U} = K_{σ δ} - \frac{E (S 2)}{2} - \frac{t_{δ}^{2}}{U}

(13)

The values extracted from Eqs. (12) and (13) provide the individual antiferromagnetic contributions to the total J_eff, namely J_δ and J_σ, respectively. The value of U could not be presently computed using the closed-shell solution and its second-order perturbative energy expression since the occupations of the magnetic orbitals are different from those shown in Table 1. In the present nickel derivatives, the stable closed-shell configuration corresponds to (σ^nb)²(σ*)², with empty magnetic δ orbitals. Thus, an undetermined ΔE(δ − σ) parameter appears, whose extraction is not straightforward by single determinant techniques and requires the use of effective Hamiltonian approaches and ab initio calculations. Consequently, t_σ and t_δ cannot either be extracted from the present analysis since they require the knowledge of U. Summarizing, from Table 1, only three equations are needed to obtain the parameters we are looking for in each system, the other two being redundant¹.

3.1 [Cu₃(dpa)₄Cl₂]⁺

We will now turn to the three complexes to see how the B3LYP functional fares in describing all the magnetic coupling parameters heretofore described. The analysis of the copper complex is straightforward since it consists of two S = ½ magnetic centres and the coupling pathway involving the δ orbitals depicted in Fig. 2 and J can be simply derived from the energies of the ferromagnetic determinant (↑···↑) and the antiferromagnetic (↑···↓) broken symmetry solution. The experimental value of J = –34 cm⁻¹ in [Cu₃(dpa)₄Cl₂]⁺, whereas the B3LYP value is approximately double (–63.9 cm⁻¹). This is the typical trend observed in DFT/B3LYP calculations of J applying spin projection. In the copper system, the values of J vary dramatically (by over 200 cm⁻¹) across the range 0–30% HFX in the expected way (see Fig. 3a) that is, the coupling constant decreases when more HFX is added to the functional. The chart shows that less %HFX favour the stabilisation of the singlet broken symmetry solution. The variation of J features a smooth exponential decrease reaching a value close (–39.0 cm⁻¹) to the experimental one (–34 cm⁻¹) at 25% HFX. The previously reported overestimation of J by DFT/B3LYP (–64 cm⁻¹) is herein reproduced [4b].

Fig. 3
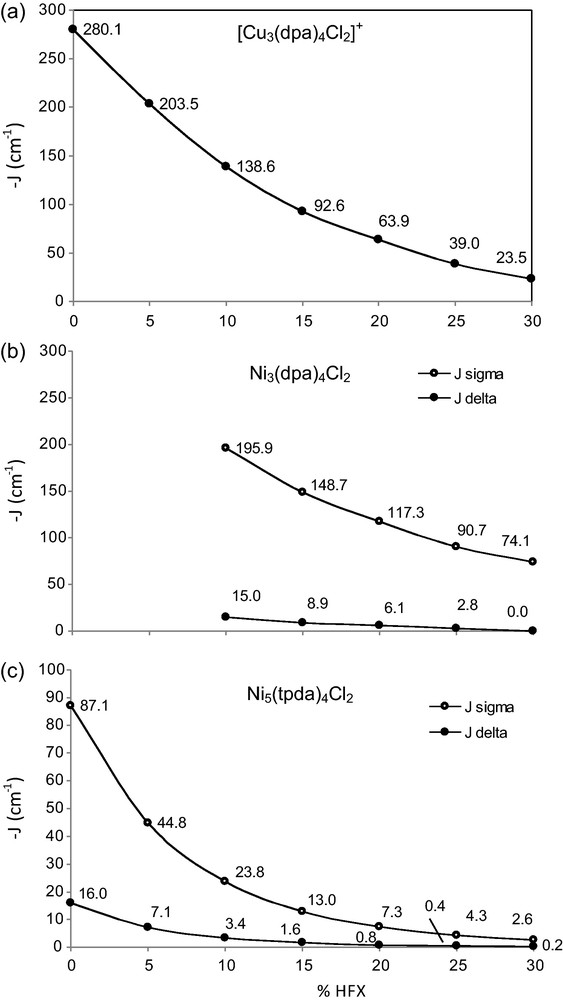
Dependency of –J (cm⁻¹) versus the percentage of exact exchange (%HFX) for (a) [Cu₃(dpa)₄Cl₂]⁺, (b) Ni₃(dpa)₄Cl₂ and (c) Ni₅(tpda)₄Cl₂. The vertical scale in (c) is different.

3.2 [Ni₃(dpa)₄Cl₂] and [Ni₅(tpda)₄Cl₂]

Fig. 3b-c contains the values of J_σ and J_δ computed for the nickel derivatives with different %HFX in the density functional. The x-axis origin corresponds to BLYP. In the case of the Ni₃(dpa)₄Cl₂ complex, it has been shown before that the σ pathway largely dominates whereas the contribution from the δ path is tiny in comparison [29]. Supposedly, the latter is overestimated by generalization² of the tricopper case and many other DFT studies featuring the same type of covalent metal-ligand interaction. However, it is worth noting that the sum of both contributions at 20% HFX (B3LYP) is J^calc = –123.4 cm⁻¹, clearly below the experimental value (–218 cm⁻¹). Given the fact that the variation in J_σ is much larger than for J_δ, it is interesting to pinpoint the origin of such apparently incoherent behaviour of the computed J values for different compounds. If we analyze the variation of J_σ and J_δ in Ni₃(dpa)₄Cl₂ upon changes in the amount of HFX (Fig. 3b-c), we see that the rates at which J_σ and J_δ grow are very different. The absolute change of both contributions is –6 to–15 cm⁻¹ and –117 to–196 cm⁻¹ for the δ and σ pathways, respectively. At smaller amounts than 20% of HFX, the dominating σ pathway resembles the experimental value. It may be deduced that the B3LYP functional overestimates the tiny J_δ but underestimates the largely dominant J_σ, overall underestimating J.

The discrepancy between the calculated and experimental J found in the Ni₃(dpa)₄Cl₂ complex with B3LYP is also observed in Ni₅(tpda)₄Cl₂. The pentanickel compound has an experimental J = –33.5 cm⁻¹, well beyond the spin projected value of –8.1 cm⁻¹ obtained with the B3LYP functional, with J_σ = –7.3 cm⁻¹ and J_δ = –0.8 cm⁻¹, in line with the trend observed for Ni₃(dpa)₄Cl₂. The amount of HFX has to be reduced to ∼10% also in the computation of the Ni₅ coupling constant to reproduce the experimental data (see Table 2 and Fig. 3). This establishes a rational trend in the calculation of J values in compounds featuring the J_σ – and J_δ – coupling parameters, such as the nickel derivatives herein discussed. The spin densities as a function of the exact exchange introduced vary as expected, that is, more delocalisation from metal to ligands in BLYP than at 30% HFX, following the variation of J.

	%HFX	K_σδ^b	J_σ = t_σ²/U	J_δ = t_δ²/U	B_ij	λ_ij	J_eff
Ni₃(dpa)₄Cl₂	10	523.8	–195.9	–15.00	–180.9	5.11	–218.6
15	576.7	–148.8	–8.94	–139.8	2.86	–161.9
20	613.6	–117.4	–6.13	–111.2	1.73	–126.0
25	670.4	–90.70	–2.83	–87.91	1.02	–95.0
30	712.7	–74.1	–0.00	–74.12	0.718	–75.0
					Exp.^c	–218

Ni₅(tpda)₄Cl₂	0	421.3	–87.12	–16.01	–71.1	0.705	–104.6
5	474.7	–44.78	–7.12	–37.66	0.194	–52.27
10	525.6	–23.80	–3.36	–20.40	0.055	–27.26
15	574.8	–13.00	–1.62	–11.37	0.016	–14.65
20	622.1	–7.34	–0.76	–6.61	0.0056	–8.11
25	667.2	–4.32	–0.42	–3.87	0.0016	–4.74
30	709.7	–2.63	–0.24	–2.42	0.0008	–2.87
					Exp.^d	–33.5

^a Values in cm⁻¹.

^b Values in meV.

^c Taken from [31].

^d Taken from [32].

The present analysis allows obtaining other electronic structure parameters such as the intrasite exchange integral, K_σδ, the biquadratic exchange constant, λ_ij, and the three-body interaction constant, B_ij, presented in Eqs. (2)–(5). K_σδ is an atomic parameter defined positive related to the energy difference between two parallel and antiparallel local spins. It amounts the same for both nickel compounds (at the same %HFX) as shown in Table 2. Its value decreases in parallel with the %HFX, that is, with more diffuse orbitals. As K_σδ decreases, the local triplet gradually becomes closer in energy to the open-shell singlet. In a previous report [29], we computed the rather small K_σδ = 243 meV with the B3LYP functional for the magnetic Pd(II) atoms in the hypothetical Pd₃(dpa)₄Cl₂ compound. In that case, the smaller intrasite exchange constant associated to the diffuse 4d valence orbitals of palladium allows low-energy local singlet states.

In the case of a largely dominant t_σ over t_δ, the λ_ij parameter is governed by the term (t_σ)⁴/KU². From Table 2, λ_ij decreases from 5.11 to 0.718 cm⁻¹ (10–30%HFX) in Ni₃, and from 0.705 to 0.0008 (0–30%HFX) in Ni₅. Thus, comparing Ni₃ and Ni₅ with the same functional, λ_ij is smaller by one order of magnitude for the pentanickel compound due to its smaller t_σ²/U contribution to the magnetic coupling. If we consider this parameter as the deviation from the Heisenberg model, it arises that such deviation goes to zero as the %HFX is increased, and it is much smaller in the pentanickel system. The three-body term, B_ij, although being numerically larger, behaves similarly to the λ_ij parameter. Expectedly, it increases as %HFX decreases since it is governed by the difference between J_σ and J_δ. Finally, it can be observed from the three rightmost columns of Table 2 that J_eff approaches the sum of J_σ and J_δ as B_ij decreases at large amounts of HFX. Although the difference between J_eff and the two magnetic contributions is not very large in any case, it can become notable for systems with more diffuse valence orbitals, like palladate systems [29].

We have observed that the amount of HFX that comes close to reproducing the experimental values is ∼10% for the nickel complexes analyzed. In a private communication, Prof. Bénard pointed out that the recently calculated J for longer nickel chains is also smaller than expected. Thus, this behaviour for Ni_n string complexes could be general to systems with any n. The present data show that the B3LYP functional not always overestimates J, as generally accepted. Indeed, we report a general underestimation when a dominating J_σ coupling based on weak metal-metal interactions is present. It arises that this issue can be related to the range at which electron-electron interactions responsible for antiferromagnetism take place. In the present nickel compounds, the two coupling pathways, the δ one occurring via covalent Ni-dpa bonds and the weak, non-covalent one via Ni···Ni interactions (d_Ni-Ni = 2.43 Å) might be very differently treated with a functional like B3LYP. We tentatively propose that range-separated functionals can help understanding this problem and reproducing the experimental magnetic coupling constants, if they get to increase the presently underestimated J_σ and decrease the overestimated J_δ for the same molecule, Ni₃(dpa)₄Cl₂, a fact not reported before. Results obtained with the range-separated LC-ωPBE [51] functional on the trinickel compound using the procedure herein discussed give J_σ + J_δ = –155.9 cm⁻¹, with J_σ = –152.6 cm⁻¹ and J_δ = –3.3 cm⁻¹. Although the total J is still underestimated, this result follows the desired trend and confirms that the main source of error in the calculation of magnetic coupling constants in S = 1 systems comes from the poor description of the σ pathway.

4 Conclusion

The theoretical analysis of [Cu₃(dpa)₄Cl₂]⁺, Ni₃(dpa)₄Cl₂ and Ni₅(tpda)₄Cl₂ using a general spin Hamiltonian reveals that decreasing the amount of Hartree-Fock exchange in a hybrid functional produces a generalized increment of |J|. A theoretical decomposition of the total J = J_σ + J_δ has been carried out to analyze the total J in tri- and pentanickel complexes. The previously reported DFT/B3LYP underestimation of J originates in the dominant J_σ component since it is poorly described with this functional. On the other hand, we assume that J_δ is overestimated in both nickel complexes by generalization of the findings made for [Cu₃(dpa)₄Cl₂]⁺ in the present and previous reports. For the Ni₅(tpda)₄Cl₂ complex, B3LYP also underestimates the total J with respect to the experimental value, thus exhibiting the same trend as its trinuclear congener. We suggest that B3LYP fails to reproduce the weak overlap between the neighbouring d_z²-like atomic orbitals responsible for the σ interaction. From this study, we learnt (i) the uniqueness of nickel complexes of the EMAC family from the magnetic point of view due to the presence of a dominating J_σ coupling based on weak metal-metal interactions, and (ii) that the B3LYP functional not always overestimates J, as generally accepted, but it can actually underestimate it when the range at which electron-electron interactions responsible for antiferromagnetism does not take place via metal-ligand covalent bonds. In line with the last possibility, we observed that J_σ grows and J_δ decreases if a range-separated LC-ωPBE functional is used.

Acknowledgements

This work was supported by the Spanish MICINN (CTQ2008 – 06644-C02-01/BQU) and by the Generalitat de Catalunya (2009SGR-00462). X.L. thanks the Ramón y Cajal program (RYC-2008-02493).

¹ For Ni₅(tpda)₄Cl₂, the exchange and hopping integrals (K and t_δ) were computed with the T2 energy rather than S2. This is because S2 is much higher in energy for this system, and the error associated with the Q–S2 gap is unacceptably large yielding an imaginary t_δ. The use of T2 to calculate t_δ is more reliable since the Q–T2 gap is about half of Q–S2.

² This fact cannot be tested because there is no way to decompose both magnetic contributions experimentally.

Bibliographie

[1] J. Miralles; J.P. Daudey; R. Caballol Chem. Phys. Lett., 198 (1992), p. 555

[2] J. Miralles; O. Castell; R. Caballol; J.P. Malrieu Chem. Phys, 172 (1993), p. 33

[3] Z. Tabookht; X. López; C. de Graaf J. Phys. Chem. A, 114 (2010), p. 2028

[4] P. Kiehl; M.M. Rohmer; M. Bénard; M. Bénard; J.F. Berry; F.A. Cotton; C. Gaudin; X. López; C.A. Murillo; M.M. Rohmer; X. López; M.Y. Huang; G.C. Huang; S.M. Peng; F.Y. Li; M. Bénard; M.M. Rohmer; X. López; M. Bénard; M.M. Rohmer; X. López; M. Bénard; M.M. Rohmer; M.M. Rohmer; I.P.C. Liu; J.C. Lin; M.J. Chiu; C.H. Lee; G.S. Lee; M. Bénard; X. López; S.M. Peng; X. López; M.M. Rohmer; M. Bénard J. Mol. Struct, 43 (2004), p. 3151

[5] S. Wagaw; S.L. Buchwald J. Org. Chem., 61 (1996), p. 7240

[6] L.P. Wu; P. Field; T. Morrissey; C. Murphy; P. Nagle; B.J. Hathaway; C. Simmons; P.J. Thornton Chem. Soc. Dalton Trans. (1990), p. 3835

[7] G.J. Pyrka; M. El-Mekki; A.A. Pinkerton J. Chem. Soc. Chem. Commun. (1991), p. 84

[8] S. Aduldecha; B.J. Hathaway Chem. Soc. Dalton Trans. (1991), p. 993

[9] J.T. Sheu; C.C. Lin; I. Chao; C.C. Wang; S.M. Peng Chem. Commun. (1996), p. 315

[10] E.C. Yang; M.C. Cheng; M.S. Tsai; S.M. Peng J. Chem. Soc. Chem. Commun. (1994), p. 2377

[11] F.A. Cotton; L.M. Daniels; G.T. Jordan Chem. Commun. (1997), p. 421

[12] F.A. Cotton; L.M. Daniels; G.T. Jordan; C.A. Murillo J. Am. Chem. Soc., 119 (1997), p. 10377

[13] F.A. Cotton; L.M. Daniels; C.A. Murillo; I. Pascual J. Am. Chem. Soc., 119 (1997), p. 10233

[14] F.A. Cotton; L.M. Daniels; C.A. Murillo; I. Pascual Inorg. Chem. Commun., 1 (1998), p. 1

[15] C.J. Hsiao; S.H. Lai; I.C. Chen; W.Z. Wang; S.M. Peng J. Phys. Chem. A., 112 (2008), p. 13528

[16] S.H. Lai; C.J. Hsiao; J.W. Ling; W.Z. Wang; S.M. Peng; I.C. Chen Chem. Phys. Lett., 456 (2008), p. 181

[17] G.C. Huang, I.P.C. Liu, J.H. Kuo, Y.L. Huang, C.Y. Yeh, G.H. Lee, S.M. Peng, Dalton Trans. (2009) 2623.

[18] S.A. Hua; G.C. Huang; I.P.C. Liu; J.H. Kuo; C.H. Jiang; C.L. Chiu; C.Y. Yeh; G.H. Lee; S.M. Peng Chem. Commun., 46 (2010), p. 5018

[19] C. Yin; G.C. Huang; C.K. Kuo; M.D. Fu; H.C. Lu; J.H. Ke; K.N. Shih; Y.L. Huang; G.H. Lee; C.Y. Yeh; C.H. Chen; S.M. Peng J. Am. Chem. Soc., 130 (2008), p. 10090

[20] J.F. Berry, F.A. Cotton, C.S. Fewox, T. Lu, C.A. Murillo, X. Wang, Dalton Trans. (2004) 2297.

[21] I.P.C. Liu; M. Bénard; H. Hasanov; I.W.P. Chen; W.H. Tseng; M.D. Fu; M.M. Rohmer; C.H. Chen; G.H. Lee; S.M. Peng Chem. Eur. J., 13 (2007), p. 8667

[22] I.P.C. Liu, W.Z. Wang, S.M. Peng, Chem. Commun. (2009) 4323.

[23] C.Y. Yeh, C.H. Chou, K.C. Pan, C.C. Wang, G.H. Lee, Y.O. Su, S.M. Peng, J. Chem. Soc. Dalton Trans. (2002) 2670.

[24] C.Y. Yeh; Y.L. Chiang; G.H. Lee; S.M. Peng Inorg. Chem., 41 (2002), p. 4096

[25] C.C. Wang; W.C. Lo; C.C. Chou; G.H. Lee; J.M. Chen; S.M. Peng Inorg. Chem., 37 (1998), p. 4059

[26] S.M. Peng; C.C. Wang; Y.L. Jang; Y.H. Chen; F.Y. Li; C.Y. Mou; M.K. Leung; J. Magn Magn. Mater, 209 (2000), p. 80

[27] J.H. Kuo, T.B. Tsao, G.H. Lee, H.W. Lee, C.Y. Yeh, S.M. Peng, Eur. J. Inorg. Chem. (2011) 2025.

[28] R.H. Ismayilov; W.Z. Wang; G.H. Lee; C.Y. Yeh; S.A. Hua; Y. Song; M.M. Rohmer; M. Bénard; S.M. Peng; Angew Chem. Int. Ed., 50 (2011), p. 2045

[29] Z. Tabookht; X. López; M. Bénard; C. de Graaf J. Phys. Chem. A., 114 (2010), p. 12291

[30] P. Labèguerie; C. Boilleau; R. Bastardis; N. Suaud; N. Guihéry; J.P. Malrieu J. Chem. Phys., 129 (2008), p. 154110

[31] R. Clérac; F.A. Cotton; K.R. Dunbar; C.A. Murillo; I. Pascual; X. Wang Inorg. Chem., 38 (1999), p. 2655

[32] J.F. Berry; F.A. Cotton; T. Lu; C.A. Murillo; X. Wang Inorg. Chem., 42 (2003), p. 3595

[33] M.J. Frisch, G.W. Trucks, S. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, J.A. Montgomery Jr., T. Vreven, K.N. Kudin, J.C. Burant, J.M. Millam, S.S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G.A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M.M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. Klene, X. Li, J.E. Knox, H.P. Hratchian, J.B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R.E. Stratmann, O. Yazyev, A.J. Austin, R. Cammi, C. Pomelli, J.W. Ochterski, P.Y. Ayala, K. Morokuma, G.A. Voth, P. Salvador, J.J. Dannenberg, V.G. Zakrzewski, S. Dapprich, A.D. Daniels, M.C. Strain, O. Farkas, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J.V. Ortiz, Q. Cui, A.G. Baboul, S. Clifford, J. Cioslowski, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, M. Challacombe, P.M.W. Gill, B. Johnson, W. Chen, M.W. Wong, C. Gonzalez, J.A. Pople, Gaussian03, in 2006.

[34] L. Noodleman; J. Joe; G. Norman J. Chem. Phys, 70 (1979), p. 4903

[35] L. Noodleman J. Chem. Phys, 74 (1981), p. 5737

[36] A.D. Becke J. Chem. Phys., 98 (1993), p. 5648

[37] J.C. Slater Phys. Rev., 81 (1951), p. 385

[38] A.D. Becke Phys. Rev. A., 38 (1988), p. 3098

[39] S.H. Vosko; L. Wilk; M. Nusair Can. J. Phys., 58 (1980), p. 1200

[40] C. Lee; W. Yang; R.G. Parr Phys. Rev. B, 37 (1988), p. 785

[41] A.W. Ehlers; M. Böhme; S. Dapprich; A. Gobbi; A. Höllwarth; V. Jonas; K.F. Köhler; R. Stegmann; A. Veldkamp; G. Frenking Chem. Phys. Lett., 208 (1993), p. 111

[42] O. Kahn Molecular magnetism, Wiley-VCH, New York, 1993

[43] F. Illas; I. de; P.R. Moreira; J.M. Bofill; M. Filatov Phys. Rev. B, 70 (2004), p. 132414

[44] C. Adamo; V. Barone; A. Bencini; R. Broer; M. Filatov; N.M. Harrison; F. Illas; J.P. Malrieu; I. de P.R. Moreira J. Chem. Phys, 124 (2006), p. 107101

[45] E. Ruiz; J. Cano; S. Alvarez; V. Polo J. Chem. Phys, 124 (2006), p. 107102

[46] E. Ruiz; S. Alvarez; J. Cano; V. Polo J. Chem. Phys, 123 (2005), p. 164110

[47] I. de; P.R. Moreira; N. Suaud; N. Guihéry; J.P. Malrieu; R. Caballol; J.M. Bofill; F. Illas Phys. Rev. B, 66 (2002), p. 134430

[48] R. Bastardis; N. Guihéry; C. de Graaf Phys. Rev. B, 76 (2007), p. 132412

[49] R. Bastardis; N. Guihéry; C. de Graaf J. Chem. Phys, 129 (2008), p. 104102

[50] P.J. Hay; J.C. Thibeault; R. Hoffmann J. Am. Chem. Soc, 97 (1975), p. 4884

[51] O.A. Vydrov; G.E. Scuseria J. Chem. Phys, 125 (2006), p. 234109

Commentaires - Politique

Ces articles pourraient vous intéresser

Ferromagnetic coupling induced by spin-orbit coupling in dipyridylamide linear trinuclear Cu-Pd-Cu and Cu-Pt-Cu complexes

Daniel Maynau; Hélène Bolvin; Willem Van den Heuvel; ...

C. R. Chim (2012)

Insight in the mechanism of deactivation of a Pt/mordenite (MOR) catalyst during the isomerization of n-pentane

Christophe Lenoir; Friedemann Rohr; Michael Stöcker; ...

C. R. Chim (2005)

On the protonation of ruthenium-PTA complexes in water. X-ray crystal structure of RuCl₄(PTAH)₂·4 H₂O (PTA = 1,3,5-triaza-7-phosphaadamantane)

Dina N. Akbayeva; Simonetta Moneti; Maurizio Peruzzini; ...