Thiol-functionalized hierarchical zeolite nanocomposite for adsorption of Hg<sup>2+</sup> from aqueous solutions

Oranous Fardmousavi; Hossein Faghihian

doi:10.1016/j.crci.2014.05.001

Thiol-functionalized hierarchical zeolite nanocomposite for adsorption of Hg²⁺ from aqueous solutions

Oranous Fardmousavi ¹ ; Hossein Faghihian ¹

¹ Department of Chemistry, Islamic Azad University, Shahreza branch, Shahreza, Iran

Comptes Rendus. Chimie, Volume 17 (2014) no. 12, pp. 1203-1211.

Résumé

A thiol-functionalized hierarchical zeolite nanocomposite was synthesized and investigated with a view to remove mercury from aqueous solutions. The hierarchical zeolite was prepared by the use of a beta zeolite and of cetyltrimethylammoniumbromide (CTAB). The ligand, 3-mercaptopropyltrimethoxysilane containing thiol (–SH) groups, was then immobilized on the surface of the hierarchical zeolite through grafting with surface silanol groups. FTIR, XRD, SEM, TG-DTG, and N₂ adsorption–desorption techniques were used to characterize the nanocomposite before and after functionalization. Adsorption experiments showed that this adsorbent was an excellent one to bind mercury with high selectivity; an adsorption capacity of 8.2 mequiv·g⁻¹ of adsorbent was obtained. Furthermore, the adsorbent retained most of its capacity after regeneration with nitric acid and thiourea solutions. The adsorption data was fitted to the Freundlich isotherm.

Métadonnées

Reçu le : 2014-01-07
Accepté le : 2014-05-05
Publié le : 2014-07-01

DOI : 10.1016/j.crci.2014.05.001

Mots clés : Hierarchical zeolite, Thiol-functionalized, Hg removal, Adsorption, Selectivity

Affiliations des auteurs :

Oranous Fardmousavi ¹ ; Hossein Faghihian ¹

¹ Department of Chemistry, Islamic Azad University, Shahreza branch, Shahreza, Iran

@article{CRCHIM_2014__17_12_1203_0,
     author = {Oranous Fardmousavi and Hossein Faghihian},
     title = {Thiol-functionalized hierarchical zeolite nanocomposite for adsorption of {Hg\protect\textsuperscript{2+}} from aqueous solutions},
     journal = {Comptes Rendus. Chimie},
     pages = {1203--1211},
     publisher = {Elsevier},
     volume = {17},
     number = {12},
     year = {2014},
     doi = {10.1016/j.crci.2014.05.001},
     language = {en},
}

TY  - JOUR
AU  - Oranous Fardmousavi
AU  - Hossein Faghihian
TI  - Thiol-functionalized hierarchical zeolite nanocomposite for adsorption of Hg2+ from aqueous solutions
JO  - Comptes Rendus. Chimie
PY  - 2014
SP  - 1203
EP  - 1211
VL  - 17
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crci.2014.05.001
LA  - en
ID  - CRCHIM_2014__17_12_1203_0
ER  -

%0 Journal Article
%A Oranous Fardmousavi
%A Hossein Faghihian
%T Thiol-functionalized hierarchical zeolite nanocomposite for adsorption of Hg2+ from aqueous solutions
%J Comptes Rendus. Chimie
%D 2014
%P 1203-1211
%V 17
%N 12
%I Elsevier
%R 10.1016/j.crci.2014.05.001
%G en
%F CRCHIM_2014__17_12_1203_0

Oranous Fardmousavi; Hossein Faghihian. Thiol-functionalized hierarchical zeolite nanocomposite for adsorption of Hg²⁺ from aqueous solutions. Comptes Rendus. Chimie, Volume 17 (2014) no. 12, pp. 1203-1211. doi : 10.1016/j.crci.2014.05.001. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2014.05.001/

Version originale du texte intégral

1 Introduction

The pollution of water resources with heavy metals has been causing worldwide concern in the last few decades. Wastewater from many industries contains one or more toxic heavy metals [1]. Mercury is one of the most toxic heavy metals commonly found in the global environment and its toxic nature has been known for centuries. It is primarily used in battery, gauges, and monometer manufacturing. It has a very high tendency to bind to proteins and due to that it mainly affects the renal and nervous systems [2]. Consequently, the selective separation of Hg²⁺ from natural samples needs much more attention.

In recent years, many studies have been focused on the adsorption of mercury [3–6]. Walcarius and Delacote [7] and Aguado et al. [8] used ordered mesoporous silica materials for the adsorption of mercury and reported that the adsorbent had higher adsorption capacity than other silica materials. The ordered mesoporous silica materials, due to their regular pore array with uniform and tunable mesopore diameter, high surface area and pore volume, have proved to be of considerable interest compared to other silica materials [9].

On the other side, zeolites have received much attention because of their regular porous structure with excellent stability [10], but they have poor adsorption capacity because of diffusion limitation in the microporous network [11], while mesoporous silica possesses poor stability compared to zeolites [12]. The hierarchical zeolites may be considered as desirable candidates for adsorption because they show a dramatically improved performance over the mesoporous materials. The reason is that hierarchical zeolites combine the strongly hydrothermal stability characteristic of zeolites with the excellent mass transport properties of mesoporous materials [13]. Extensive researches have been performed regarding the preparation and application of these types of zeolites in various reactions [14–18]. Nevertheless, limited researches have been accomplished on the adsorption of heavy metals using hierarchical zeolites.

In this study, thiol-functionalized beta zeolite-MCM-41 nanocomposite (SH-Beta/MCM-41) was prepared by hydrothermal procedure and post-synthesis grafting of 3-mercaptopropyltrimethoxysilane (MPTMS). The synthesized adsorbent was employed for the extraction of Hg²⁺ from aqueous solutions. The effect of different parameters, including pH, initial concentration, contact time and temperature on Hg²⁺ adsorption was investigated and optimized. Adsorption isotherms, thermodynamic parameters and kinetics of the process were studied by application of different models. The selectivity and reusability of the adsorbent was also examined.

2 Experimental

2.1 Materials and methods

Tetraethylammoniumhydroxide (20%, Merck), cetyltrimethylammoniumbromide (CTAB, Merck), aerosol-200 (Fluka) as silica source, 3-mercaptopropyltrimethoxysilane (MPTMS, ≥ 95%, Merck), toluene (≥ 99%, Merck), ethanol (≥ 99.9%, Merck) and mercury nitrate [Hg(NO₃)₂, ≥ 98.0%, Merck] were used without further purification. All aqueous solutions were prepared with double-distilled water ≤ 1.8 μS.cm⁻¹. FTIR spectra of the samples were obtained using a PerkinElmer spectrum 65 FTIR spectrophotometer (wavenumber: 400–4000 cm⁻¹, USA) with the KBr pressed-disk technique. Thermogravimetric analysis was performed using a Mettler TG-50 thermal analyzer from ambient temperature to 800 °C. The atmosphere was pure nitrogen and the heating rate was 15 °C·min⁻¹. X-ray diffraction patterns were recorded using a Bruker (Germany), D8 ADVANCE X-ray diffractometer using Cu Kα radiation (wavelength: 1.5406 Ǻ and filter: Ni) up to 2θ = 45° at ambient temperature. Nitrogen adsorption–desorption isotherms were determined at 77 K and the specific surface area was measured by applying the BET equation to the isotherm. The pore size distribution was calculated using the adsorption branch of the isotherm and the Barrett–Joyner–Halenda (BJH) formula. For measurement on mercury, a PerkinElmer A Analyst 300 atomic absorption spectrophotometer was used.

2.2 Preparation of materials

Beta/MCM-41 composite was synthesized by the procedure suggested by Ooi et al. [19]. To prepare SH-Beta/MCM-41, 5.0 g of Beta/MCM-41 composite was refluxed in 250 mL of toluene containing 5.0 g of MPTMS at 110 °C for 24 h. The solid phase was then recovered by filtration and washed with toluene followed by ethanol. The residual organosilane was removed by the Soxhlet extraction method over ethanol for 24 h [20].

2.3 Characterization methods

FTIR spectra of the samples were obtained using a PerkinElmer (USA) spectrum 65 FTIR spectrophotometer (wavenumber: 400–4000 cm⁻¹) by using the KBr pressed-disk technique. Thermogravimetric analysis was performed using a Mettler TG-50 thermal analyzer from ambient temperature to 800 °C. The atmosphere was pure nitrogen and the heating rate was 15 °C·min⁻¹. X-ray diffraction patterns were taken using a Bruker (Germany), D8ADVANCE X-ray diffractometer using Cu Kα radiation (wavelength: 1.5406 Å and Ni filter) up to 2θ = 45° at ambient temperature. Nitrogen adsorption–desorption isotherms were determined at 77 K and the specific surface area was measured by applying the BET equation to the isotherm. The pore size distribution was calculated using the adsorption branch of the isotherm and the Barrett–Joyner–Halenda (BJH) formula. A PerkinElmer AAnalyst 300 cold-vapor atomic absorption spectrophotometer was used to measure mercury concentration.

2.4 Adsorption experiments

The batch technique was used to study the kinetics and equilibrium of the adsorption process. In order to evaluate the kinetic data, a known amount of the adsorbent was added in polyethylene bottles containing 25 mL of Hg²⁺ solution. A separate bottle was prepared for each time interval. The adsorption isotherms were constructed at four different temperatures of 25, 35, 45 and 55 °C by putting 0.050 g of the adsorbent in contact with 25 mL of the mercury solution (50 to 1500 mg·L⁻¹). The effect of the pH was studied in the range from 1 to 4 (adjusted with HNO₃). After the required time, the adsorbent was separated by filtering and the concentration of mercury in the filtrate was measured by cold-vapor atomic absorption spectrophotometry. The equilibrium uptake was calculated by the following equation [9]:

q_{e} = (C_{0} - C_{e}) V / w

(1)

where q_e is the equilibrium uptake (mg·g⁻¹), C₀ and C_e are the initial and equilibrium concentrations (mg·L⁻¹) respectively, V is the volume of the solution (L) and w is the mass of the adsorbent (g).

3 Results and discussion

3.1 Adsorbent characterization

The FTIR spectra of Beta/MCM-41 and SH-Beta/MCM-41 obtained by the KBr pellet method are shown on Fig. 1. The broad band that appeared around 3422 and 3452 cm⁻¹ was mainly attributed to the Si–OH stretching vibration of water adsorbed on the surface of the silica material. The peak at about 1630 cm⁻¹ was also attributed to adsorbed water [21]. In both samples, the Si–OH–Al band appeared at ∼ 3630 cm⁻¹, indicating that the zeolite structure was not changed during functionalization with mercaptosilane groups [22]. The wide bands around 1080 and the smaller band at 800 cm⁻¹ were attributed to Si–O–Si asymmetric and symmetric stretching vibrations, respectively [23]. The weak band around 2550 cm⁻¹ in Fig. 1b, which is typically very weak due to the aggregation of mercapto groups within the monolayer and to hydrogen binding effects [24,25], and the peak at 2933 cm⁻¹ belonged to the stretching vibrations of CH bonds, indicating the presence of organic groups adsorbed on the surface of the adsorbent [25].

Fig. 1
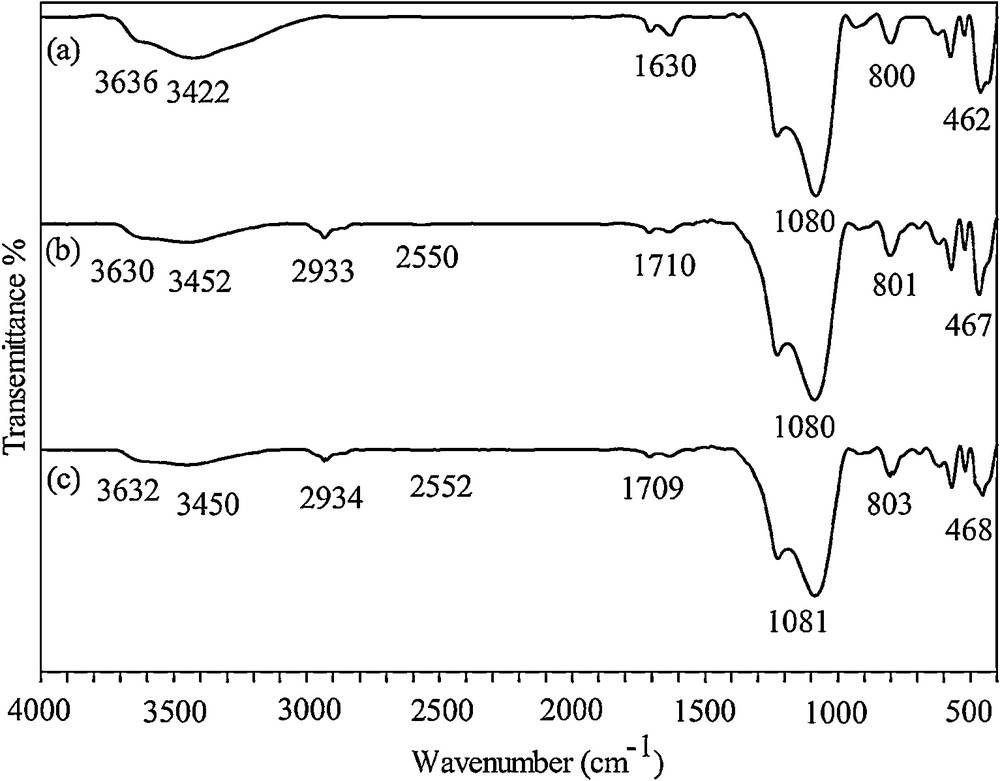
FTIR spectra of Beta/MCM-41 (a), SH-Beta/MCM-41 (b) SH-Beta/MCM-41 treated with the thiourea solution and HNO₃ (c).

The TG and DTG curves of Beta/MCM-41 and SH-Beta/MCM-41 are shown in Fig. 2. In the thermal curves of Beta/MCM-41, a characteristic dehydration peak between 25 and 200 °C was observed (Fig. 2a) [26], while in the thermal curve of SH-Beta/MCM-41, two distinct weight loss events were observed. The first weight loss that appeared around 100 °C was attributed to the dehydration of the water molecules adsorbed on the surface of the sample, whereas the second weight loss around 330 °C was assigned to the decomposition of mercaptosilane groups (Fig. 2b) [8,27].

Fig. 2
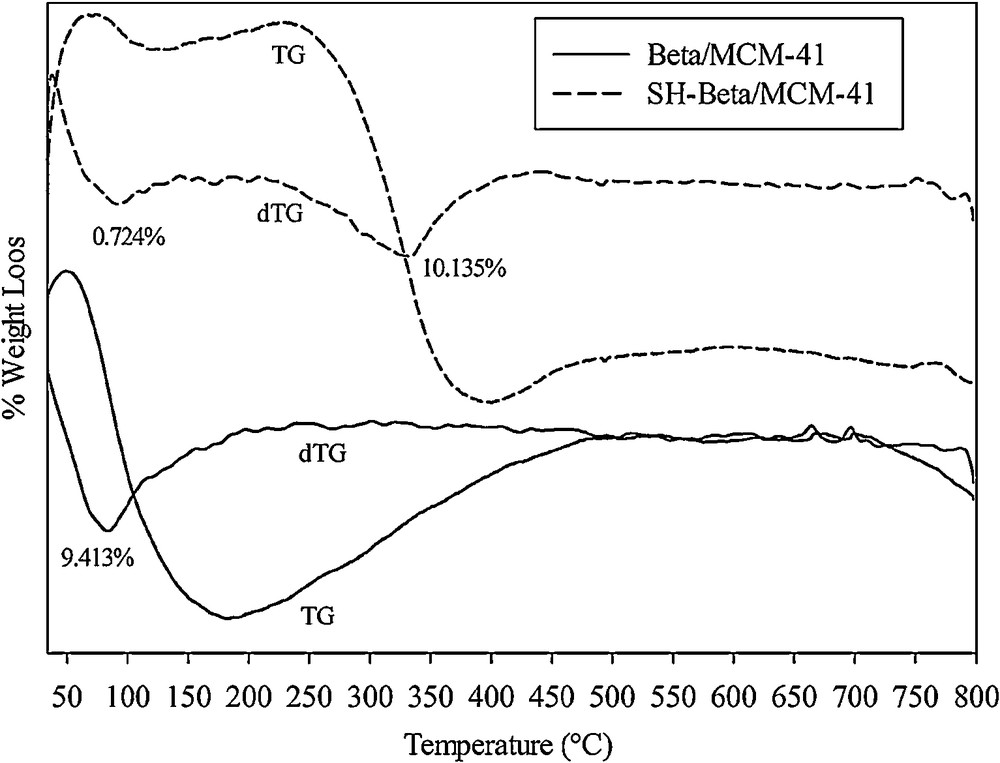
TG-DTG curves of Beta/MCM-41 and SH-Beta/MCM-41.

In the XRD pattern of the calcined Beta/MCM-41 composite, the characteristic diffraction lines of beta zeolite at 7.9° and 22.5° were clearly observed (Fig. 3a). For the functionalized sample, SH-Beta/MCM-41, similar diffraction lines were observed, with a slightly lower intensity (Fig. 3b) [28]. The diffraction lines of MCM-41 were not observed in low-angle diffraction patterns (Fig. 3c). This was in agreement with the results reported by Ooi et al. [19].

Fig. 3
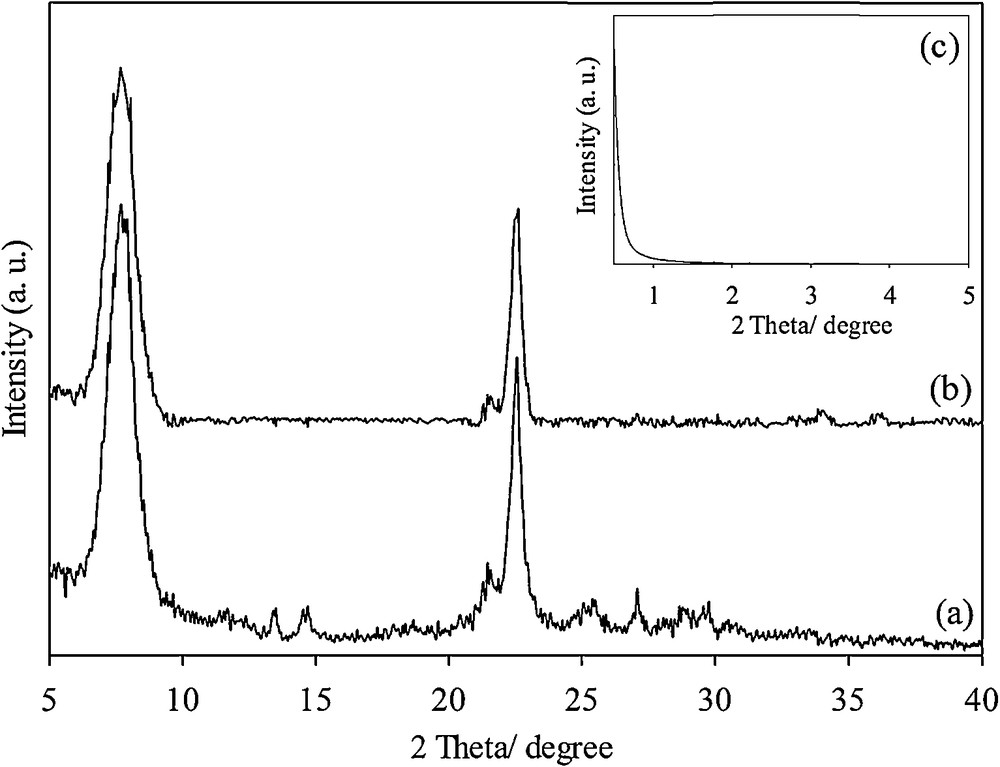
Wide-angle XRD pattern of Beta/MCM-41 (a), SH-Beta/MCM-41 (b), and low-angle XRD pattern of for both (c).

In the SEM images of Beta/MCM-41 and SH-Beta/MCM-41, massive and spherical beads were observed. The beads of Beta/MCM-41 composite had a relatively smooth surface, indicating that the composite was homogeneously formed (Fig. 4a) [19,29]. The SH-Beta/MCM-41 image revealed that the particles are more agglomerated. This was attributed to the presence of mercaptosilane groups on the surface of the composite (Fig. 4b) [9].

Fig. 4
SEM images of Beta/MCM-41 (a), SH-Beta/MCM-41 (b).

Fig. 5 shows the adsorption–desorption isotherms and the pore size distribution. The isotherm of Beta/MCM-41 has a typical hysteresis loop in the range P/P₀ = 0.75–0.95, indicating the presence of framework-confined mesopores [30]. In addition, in the isotherm of SH-Beta/MCM-41, the gap of adsorption and desorption is low because the mercaptosilane groups are located within the mesopores and the occupied pores volume [31]. The BET surface area and the average pore size of the samples are shown in Table 1. The Beta/MCM-41 composite sample synthesized via two-step crystallization had a less pronounced mesopore size than mesoporous materials [19]. By grafting mercaptosilane groups on the sample, the BET surface area of the new composite (SH-Beta/MCM-41) decreased from 604 to 82 m²·g⁻¹. This was attributed to the occupancy of mercaptosilane groups into the mesoporous structure of the host sample by occupation of the pores [27]. Also, due to the presence of the propyl chains of mercaptosilane groups in the pores of Beta/MCM-41, the pore volumes were reduced from 0.617 to 0.295 cm³·g⁻¹ and 0.42 to 0.005 cm³·g⁻¹ for the mesopores and the micropores, respectively. The presence of this group also significantly expanded the pore diameters of meso- and micropores [32] (Table 1).

Fig. 5
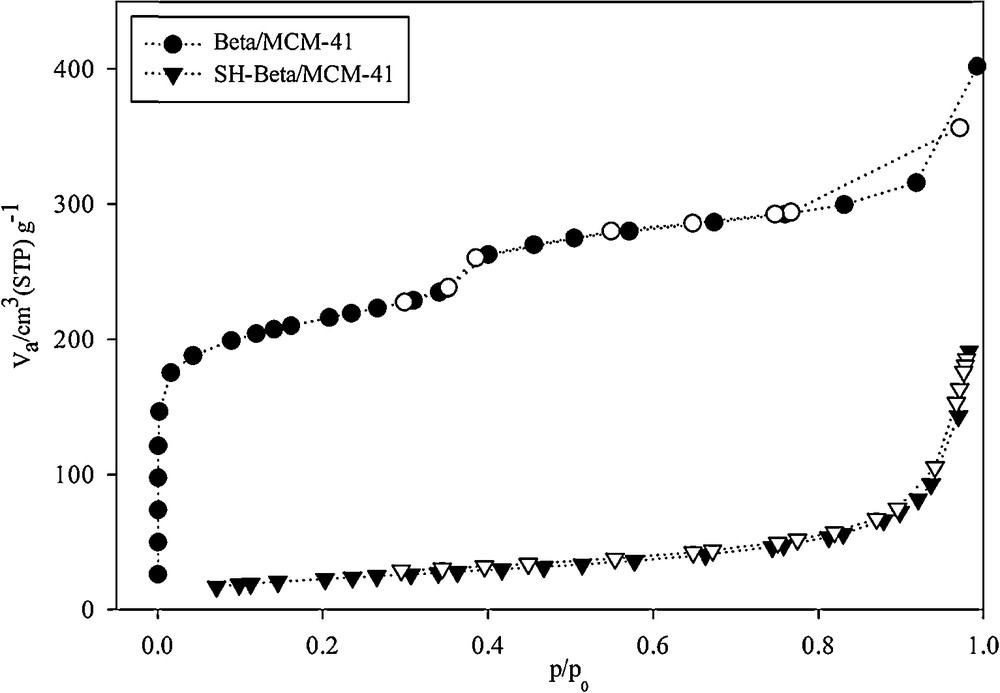
N₂ adsorption–desorption isotherm of Beta/MCM-41 and SH-Beta/MCM-41.

Samples	S_BET (m²·g⁻¹)	V_p(meso) (cm³·g⁻¹)	V_p(micro) (cm³·g⁻¹)^a	d_p(meso) (nm)	d_p(micro) (nm)^a
Beta/MCM-41	604	0.617	0.42	4.08	1.20

SH-Beta/MCM-41	82	0.295	0.005	14.25	1.90

^a Calculated by MP-Plot method.

The micropore sizes of Beta/MCM-41 and SH-Beta/MCM-41 samples were calculated using MP-Plot in Table 1. Further MP-Plot analyses also confirm the existence of microporosity within the samples (Fig. 6).

Fig. 6
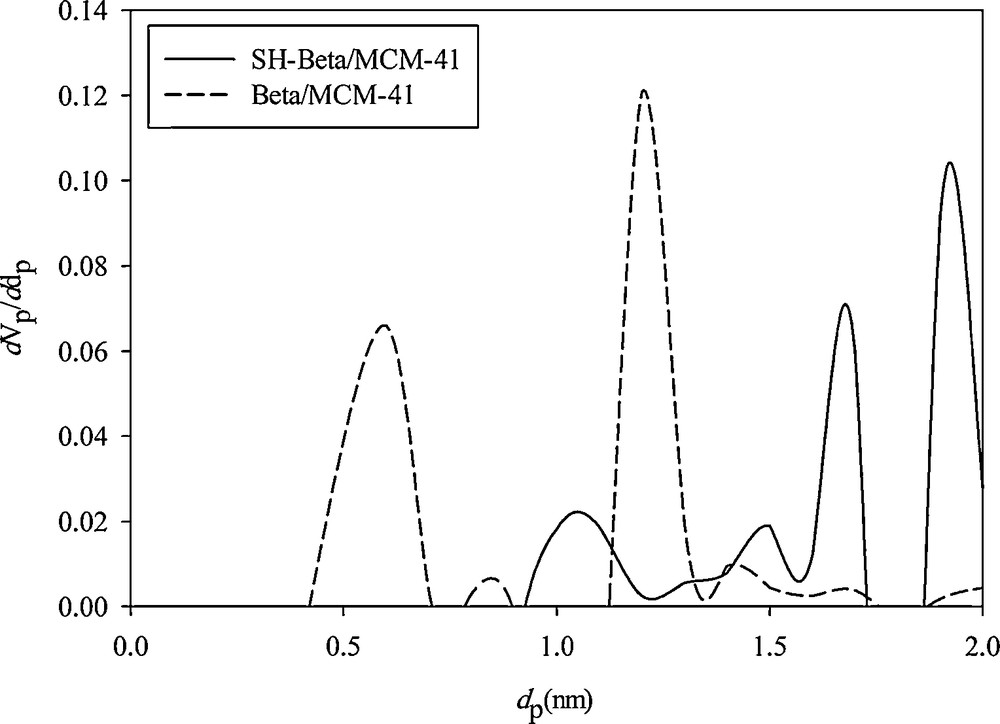
Micropore size distribution curve of Beta/MCM-41 and SH-Beta/MCM-41 (MP-plot).

3.2 Adsorption optimizing

The effect of initial concentration on the adsorption capacity was studied in the 50–1500 mg·L⁻¹concentration range. As shown on Fig. 7, with increasing cation concentrations, the adsorption rate increased and then leveled off. The optimized uptake was obtained at a concentration of 1000 mg·L⁻¹. At pH = 2, an extremely high adsorption capacity of 6.6 mequiv·g⁻¹ was obtained, which was much higher than the one previously reported. Kao et al. [4] reported that the adsorption capacities of their adsorbent for Hg²⁺ binding increased in proportion to the amount of thiol groups incorporated and the maximum adsorption capacity reached 415 mg·g⁻¹. The maximum adsorption capacity of a thiol-SNHS nano-adsorbent prepared by Rafati et al. in 330 mg·L⁻¹ of Hg²⁺ solution was 160 mg·g⁻¹ [9]. The high adsorption capacity was attributed to the presence of thiol groups on the surface of the adsorbent. The thiol group, as soft bases, has highly polarizable donor centers capable to strongly interact with low-lying orbitals of soft acids [33].

Fig. 7
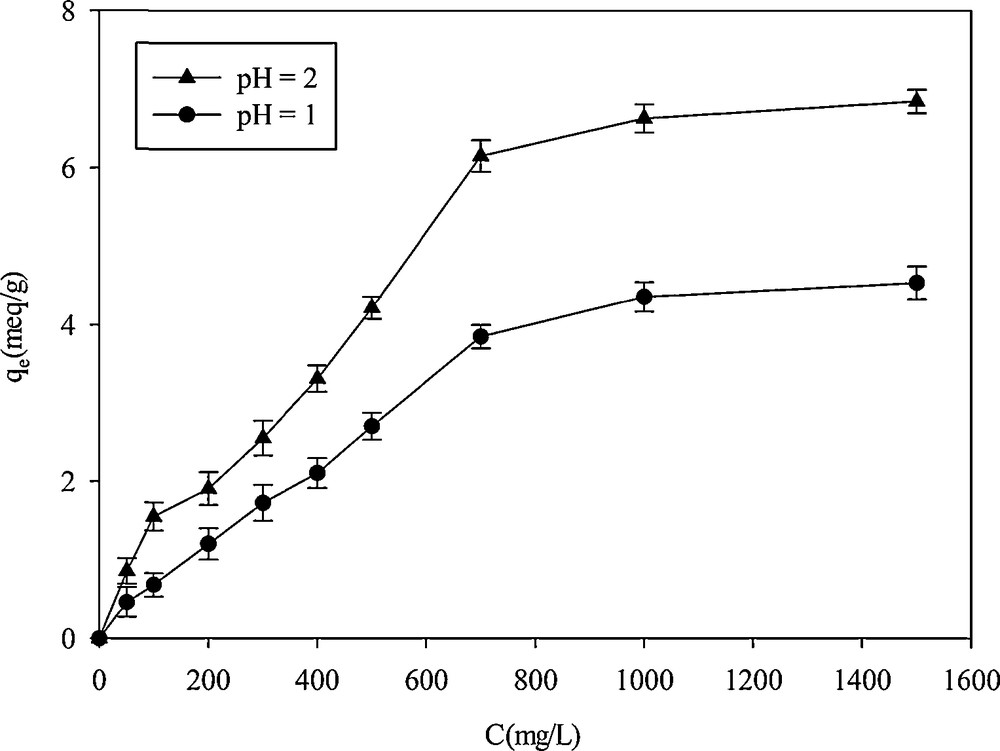
Effect of the initial concentration on Hg²⁺ adsorption on SH-Beta/MCM-41.

Adsorption isotherm models were used to describe experimental adsorption data. The model parameters and the underlying thermodynamic assumptions of these adsorption models can provide some insight into the sorption mechanism, the surface properties, and the affinity of the adsorbent. Therefore, obtaining the ‘best-fit’ isotherm is very important. Langmuir and Freundlich isotherms were examined. In the Langmuir isotherm model, the assumption is that the adsorption process is mono-layered [34]:

C_{e} / q_{e} = 1 / q_{m} K_{L} + C_{e} (1 / q_{m})

(2)

where q_e is the equilibrium adsorption uptake of the heavy metal ion, in mg·g⁻¹, C_e is the equilibrium concentration of the adsorbed ion, in mg·L⁻¹, q_m is the maximum adsorption capacity corresponding to the complete monolayer coverage, in mg·g⁻¹; and K_L is the Langmuir constant which is related to the energy of adsorption. An essential characteristic of Langmuir isotherm can be expressed by a dimensionless constant called equilibrium parameter:

R_{L} = 1 / (1 + K_{L} C_{0})

(3)

where C₀ is the highest concentration of initial ions (in mg·L⁻¹). The value of R_L indicates that the type of the isotherm is either unfavorable (R_L > 1), linear (R_L = 1), favorable (0 < R_L < 1) or irreversible (R_L = 0) [35]. The slope of the linearized Langmuir plot was used to calculate the adsorption constants (Fig. 8 and Table 2).

Fig. 8
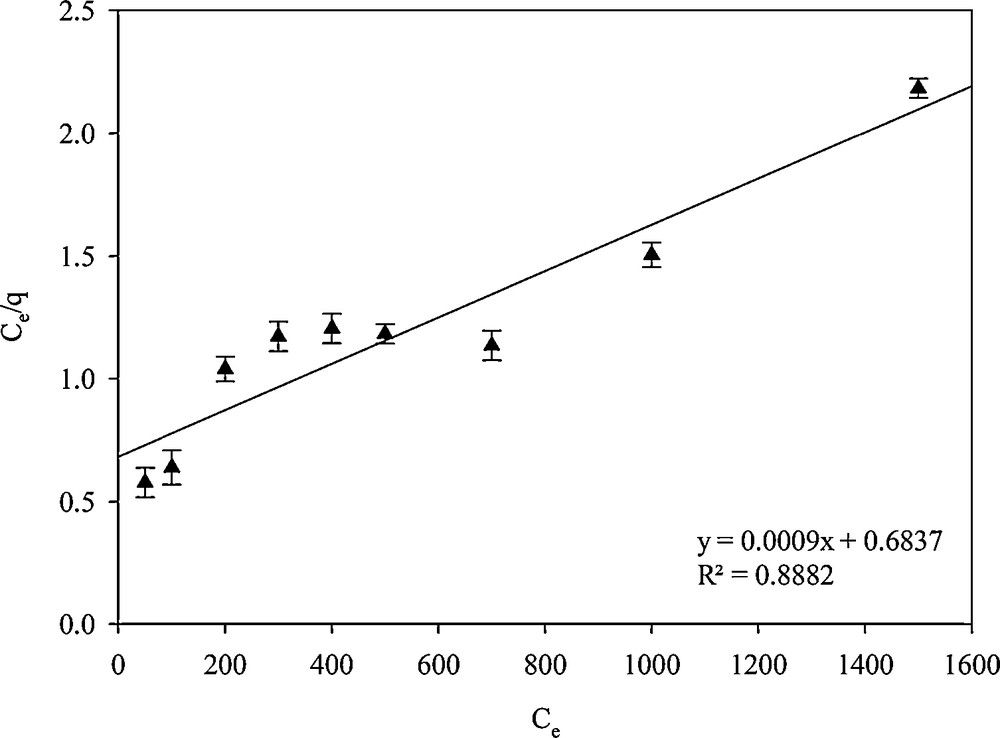
Linear plots for calculating the parameters of the Langmuir isotherm.

Adsorbent	Langmuir isotherm	Freundlich isotherm
	R²	K_L	q_m	R²	K_F	n
SH-Beta/MCM-41	0.8882	1.316 × 10⁻³	111.11	0.9692	6.996	1.539

In the Freundlich isotherm model, the assumption is that the adsorption process is multi-layered [34]:

\log q_{e} = n \log C_{e} + \log K_{F}

(4)

where q_e is the equilibrium adsorption uptake of the heavy metal ion, in mg·g⁻¹, C_e is the equilibrium concentration of the adsorbed ions, in mg·L⁻¹, K_F and n are the Freundlich parameters related to adsorption capacity and adsorption intensity, respectively. For n = 1, the partition between the two phases is independent of the concentration. The situation n < 1 is the most common and corresponds to a normal Langmuir isotherm, while n > 1 is indicative of a cooperative sorption, which involves strong interactions between the adsorbent and the adsorbate [34]. The slope and the intercept of the linear plot on Fig. 9 are used to calculate Freundlich parameters. The calculated adsorption isotherms parameters are listed in Table 2. The higher correlation coefficients indicated that the Freundlich model fitted the adsorption data better than the Langmuir model. This means that the mercury adsorption process does not absolutely follow this model, because the absorption process is complicated and several models will be going ahead at the same time. The n values are greater than 1, which indicates strong interactions between the SH-Beta/MCM-41 with Hg²⁺ species.

Fig. 9
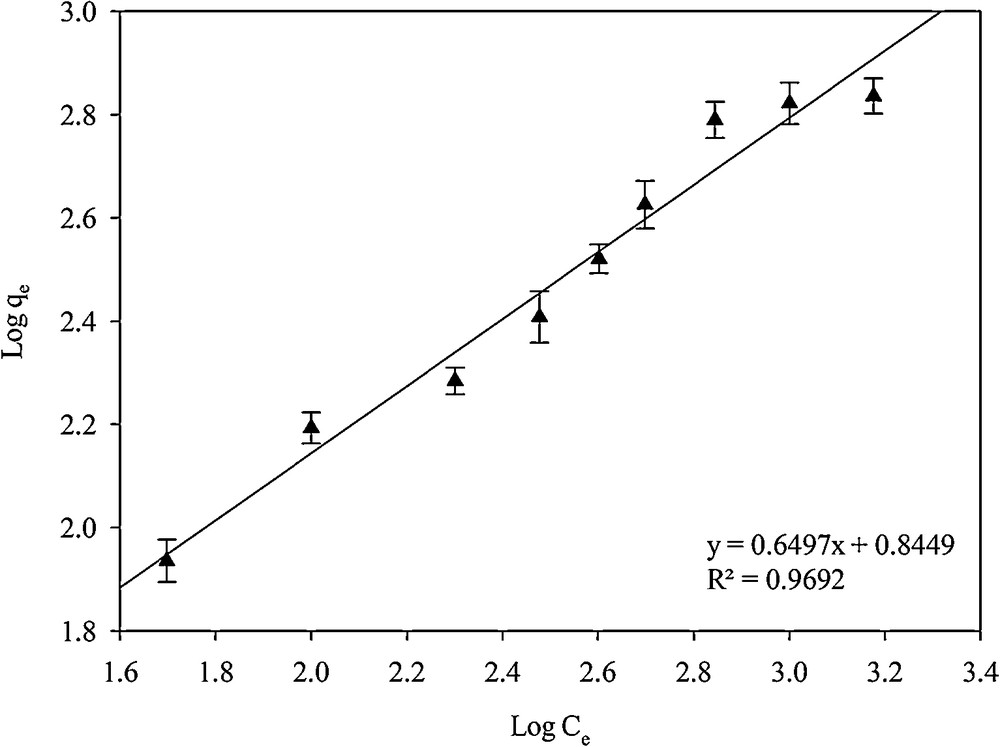
Linear plots for calculating the parameters of the Freundlich isotherm.

Measurement of the adsorption capacity at different pH values indicated that Hg²⁺ binding to SH-Beta/MCM-41 strongly depended on the pH of the solution (Fig. 10). At higher pH, the formation of metal hydroxides coincides with the absorption process. At a concentration of 1000 mg·L⁻¹ of Hg²⁺, the pH of precipitation was 2.4. Therefore, the adsorption capacity obtained beyond this pH was not valid [36]. At lower pH, because of the competition for adsorption between H₃O⁺ and Hg²⁺ ions on the surface of the adsorbent, the adsorption capacity toward Hg²⁺ was lowered. Moreover, in aqueous solutions, divalent metal ions may exist in different forms—M(OH)¹⁺, M(OH)₂⁰, and M(OH)₃¹⁻—and their abundance is dependent on the pH of the solution. The most favorite species for adsorption on the adsorbent surface is the M²⁺ species, which would be the dominant species at a particular pH for each individual cation [7,36]. Walcarius and Delacote investigated the effect of pH on the adsorption of mercury by thiol-functionalized mesoporous silica. By plotting the species distribution curves of Hg²⁺, Hg(OH)⁺ and Hg(OH)₂ against the pH of the solution, they concluded that the maximal adsorption capacity was observed at pH = 2 because Hg²⁺ was the most abundant species at this pH [7].

Fig. 10
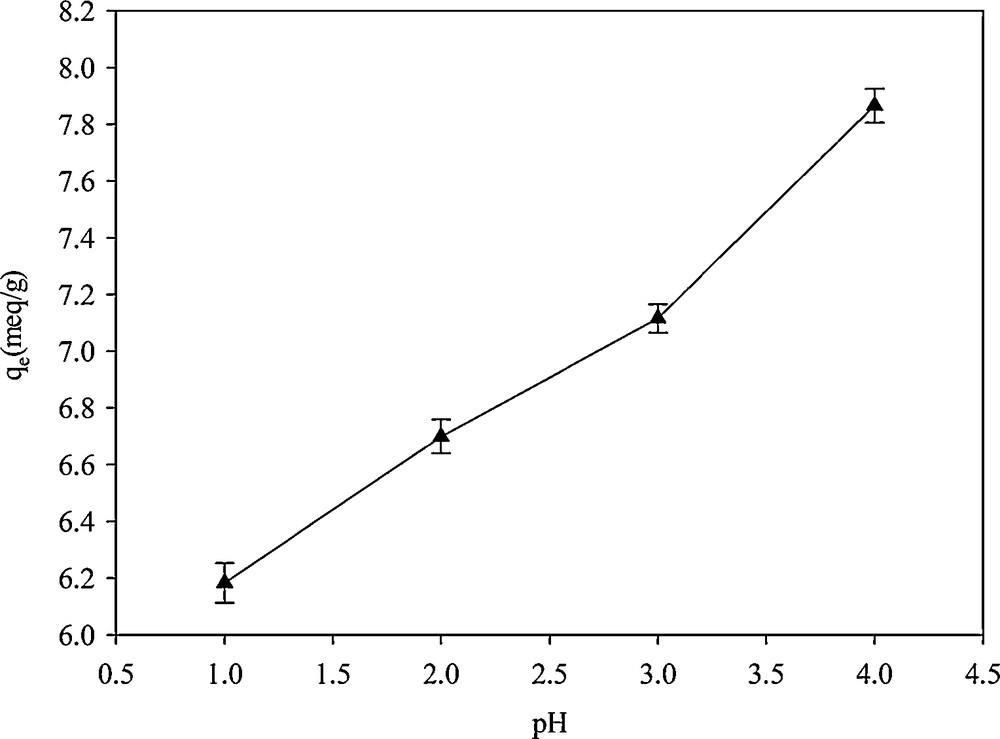
Effect of pH on Hg²⁺adsorption in SH-Beta/MCM-41.

The effect of contact time on Hg²⁺ adsorption was studied in 1000 mg·L⁻¹ mercury solutions with an initial pH of 2.0 (Fig. 11). Adsorption was kinetically fast and the equilibration was attained after 5 min. At the beginning of the experiment, Hg²⁺ concentration was high and therefore the number of effective interactions between the adsorbates and the adsorbents was fast. Then the adsorbent surface was saturated by the cations and the rate of adsorption remained constant [37].

Fig. 11
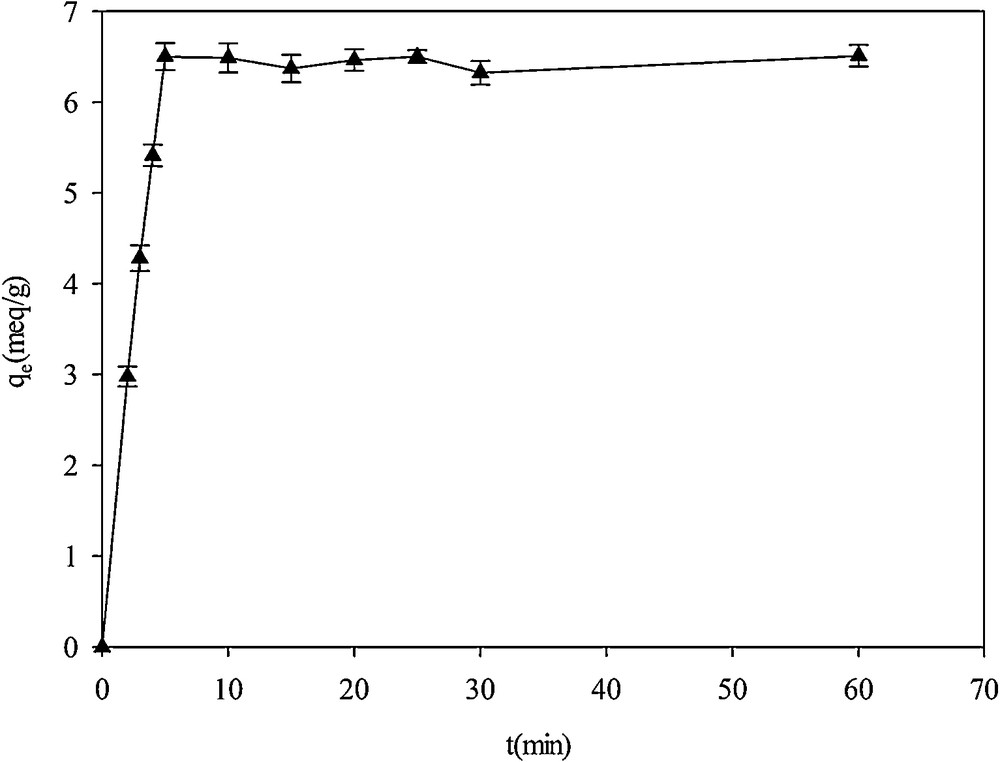
Effect of contact time on Hg²⁺adsorption on SH-Beta/MCM-41.

In order to analyze the adsorption kinetic parameters, two kinetic models, namely, pseudo-ﬁrst-order and pseudo-second-order models, were applied.

The pseudo-ﬁrst-order kinetic model can be expressed in linear form [9]:

\log (q_{e} - q_{t}) = \log q_{e} - (k_{1} / 2.303) t

(5)

where k_l is the adsorption rate constant of the ﬁrst-order kinetic model, in min⁻¹; q_e and q_t, in mg·g⁻¹, are the equilibrium adsorption uptake (at time t = ∞) and adsorption uptake (at time t), respectively. The slope and the intercept of the linear plot (Fig. 12) are used to calculate the adsorption rate constants (k₁); the results are summarized in Table 3.

Fig. 12
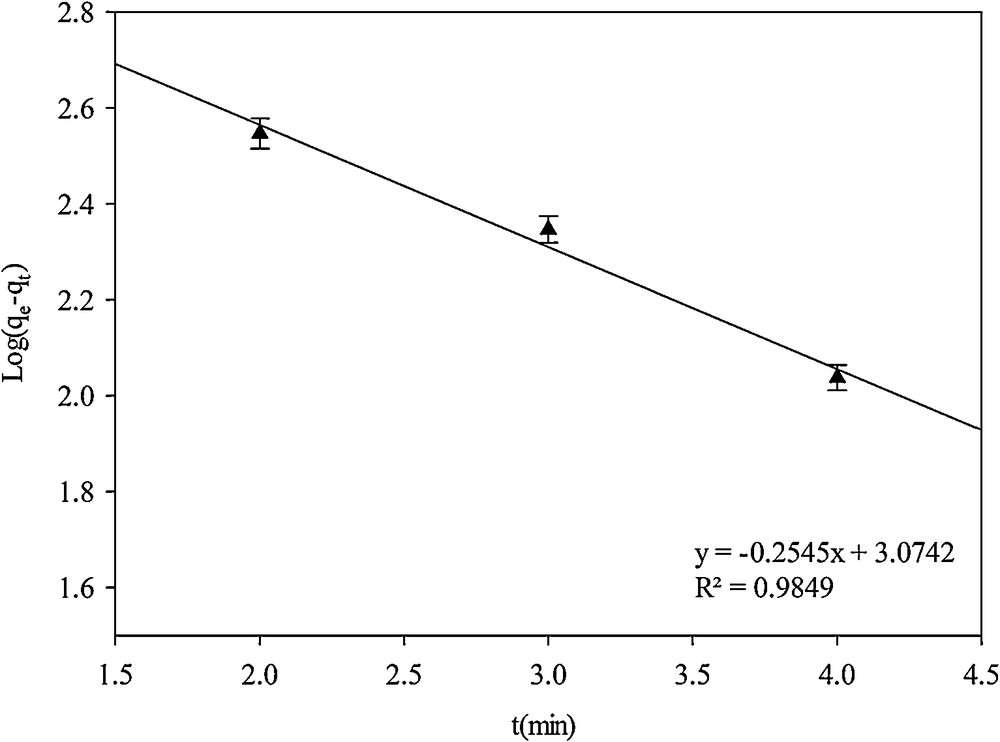
Pseudo-first-order kinetic model.

Kinetic models	K	R²
Pseudo-first-order	0.5861	0.9849

Pseudo-second-order	8.141 × 10⁻⁴	0.9989

The pseudo-second-order kinetic model can be expressed in linear form [9]:

t / q_{t} = 1 / k_{2} {q_{e}}^{2} + (1 / q_{e}) t

(6)

where k₂ is the adsorption rate constant of the second-order kinetic model, in mg⁻¹·min⁻¹; q_e and q_t, in mg·g⁻¹, are the equilibrium adsorption uptake (at time t = ∞) and adsorption uptake (at time t), respectively. The slope and the intercept of the linear plot in Fig. 13 are used to calculate the adsorption rate constants (k₂); the results are summarized in Table 3. The correlation coefficient values of the pseudo-second-order kinetics model are higher than those of the pseudo-first-order kinetics model. The agreement of the experimental data with the pseudo-second-order kinetics model indicated that the adsorption of Hg²⁺ onto the adsorbents was controlled by chemical adsorption. In chemical adsorption, it is assumed that the adsorption capacity is proportional to the number of active sites occupied on the adsorbent surface. The pseudo-second-order kinetic equation was developed for the sorption process and there are three consecutive steps taking place in the sorption of an adsorbate by a porous adsorbent:

• migration of the metal ions from the solution to the surface of the adsorbent;
• migration of the metal ions into the pores of the adsorbent;
• adsorption of the metal ions on the interior surface of the adsorbent [9].

Fig. 13
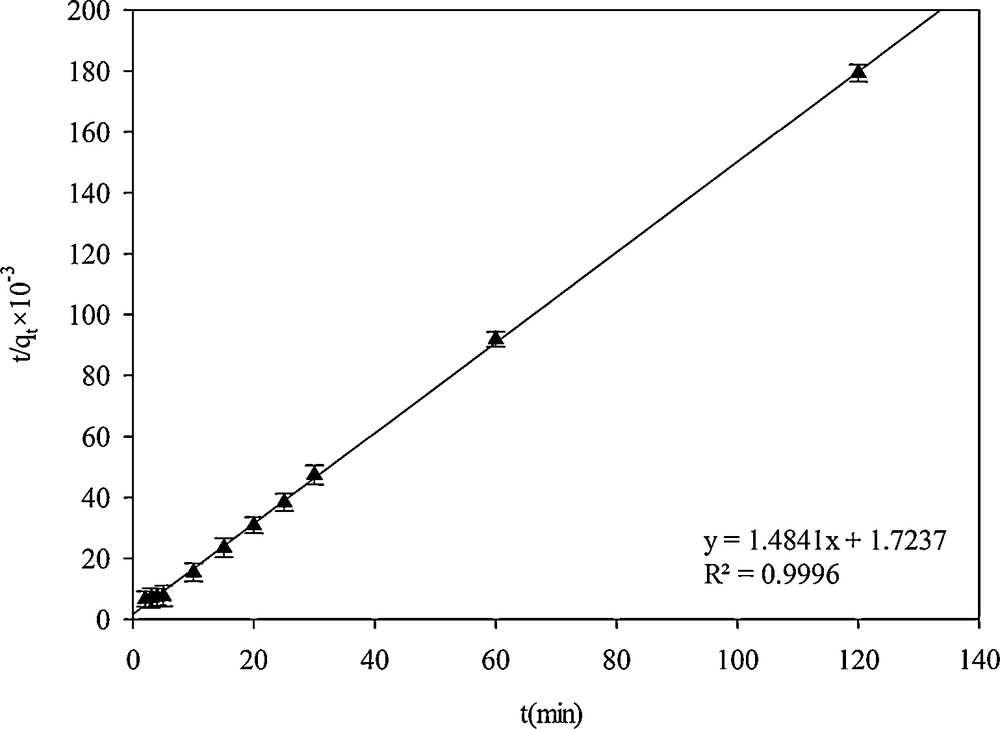
Pseudo-second-order kinetic model.

The rate of the reaction is mainly controlled by the first two steps.

Removal of mercury ions from the aqueous solution occurs mainly either by electrostatic interaction (ionic interaction between positively charged metal ions and negatively charged matrices) or by chelation (donation of the lone-pair electrons of the matrices to metal ions to form coordinate bonds) (Scheme 1) [38].

Scheme 1
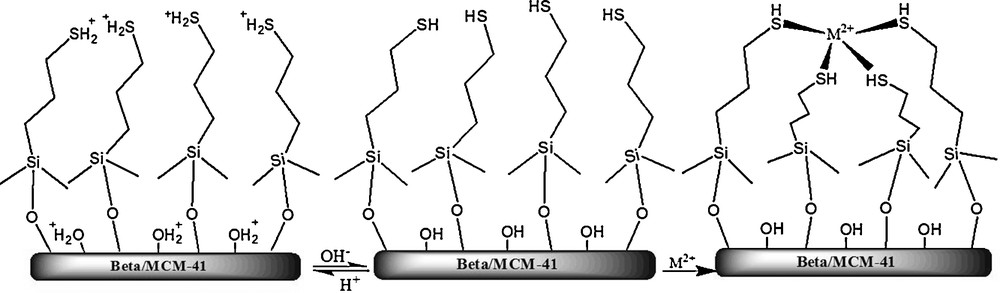
The mechanism of the adsorption of M²⁺ on the Beta/MCM-41.

The adsorption capacity of the adsorbent was measured at a constant Hg²⁺ concentration solution and at four different temperatures (Fig. 14). Adsorption capacity decreased from 8.2 mequiv·g⁻¹ at 25 °C to 6.1 mequiv·g⁻¹ at 55 °C. This is in agreement with the results reported by Arencibia et al. [39]: the mercury loading changes from 1.22 mmol·Hg·g⁻¹ at 20 °C to 1.16 mmol·Hg·g⁻¹ at 60 °C, which was attributed to the weakening of the bond between the cation and the sorption sites. Absorption capacity decreased with increasing temperature due to the weakening of the bond between the cation and the sorption sites. This was in agreement with the results reported by Arencibia et al. [39]. The change in Gibbs free energy, enthalpy and entropy of adsorption were calculated using the following equations [40]:

K_{d} = q_{e} / C_{e}

(7)

Δ G^{0} = Δ H^{0} - T Δ S^{0}

(8)

Fig. 14
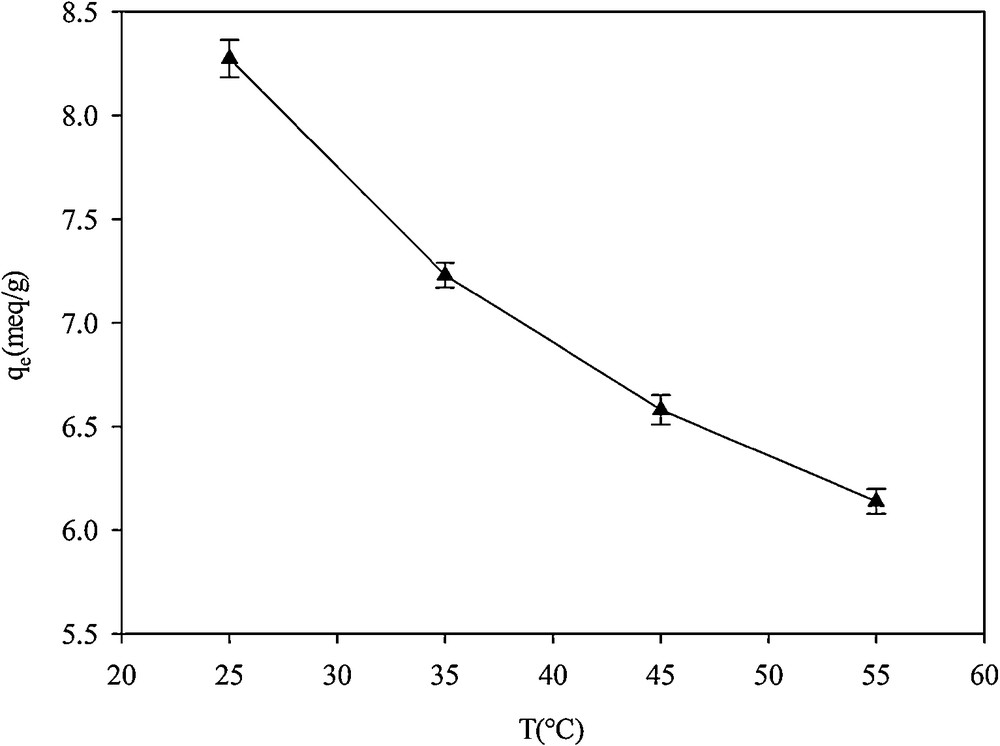
Effect of temperature on the adsorption of Hg²⁺ in SH-Beta/MCM-41.

According to Van’t Hoff equation:

ln K_{d} = Δ S^{0} / R - Δ H^{0} / R T

(9)

where R is the gas constant (8.314 J·mol⁻¹·K⁻¹), K_d is the equilibrium constant and T is the temperature in Kelvin.

The plot of lnK_d versus 1/T was linear. The negative values of ΔH⁰ evidenced the exothermic nature of adsorption (Fig. 15). The negative values of ΔG⁰ indicated that the adsorption process led to a decrease in Gibbs free energy and that the adsorption process was feasible and spontaneous for Hg²⁺ at each temperature. The positive values of ΔS⁰ represented the increase of irregularity during the absorption process; this issue was predicted to increase the mobility of the molecules due to the temperature rise. The thermodynamic parameters for the removal of Hg²⁺ were given in Table 4.

Fig. 15
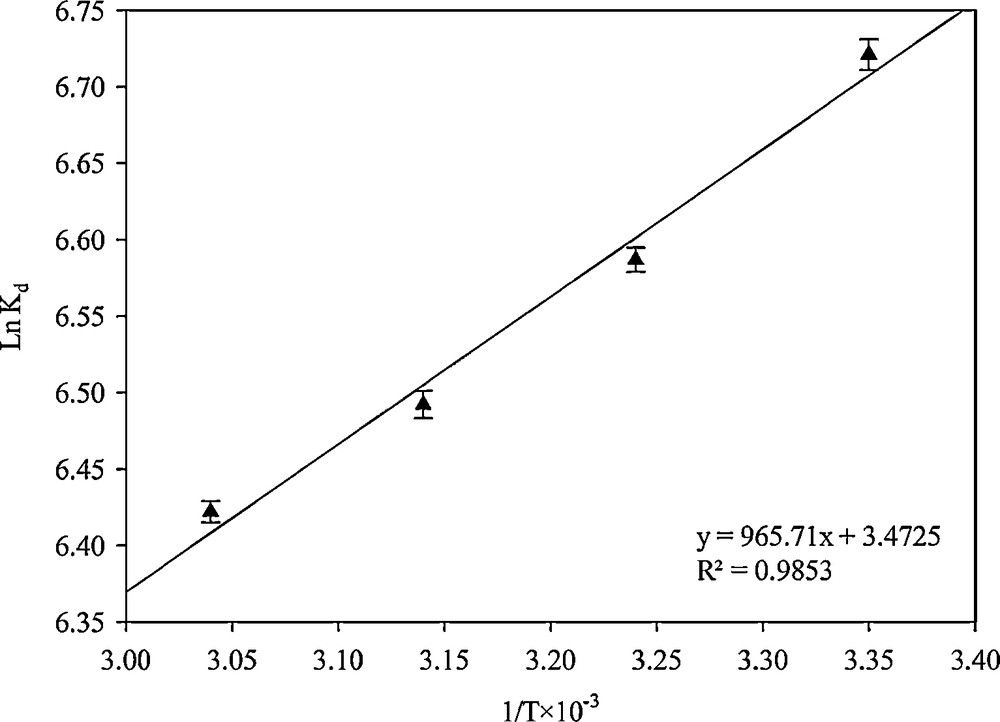
Linear plots for calculating the thermodynamic parameters.

ΔH⁰ (J·mol⁻¹)	ΔS⁰·(J·mol⁻¹·K⁻¹)	ΔG⁰ (J·mol⁻¹)
−8028.91	28.87	298 K	308 K	318 K	328 K
		−16632.17	−16920.87	−17209.57	−17498.27

3.3 Reusability of the adsorbent

Reusability feature of the functionalized composite was examined for five regeneration cycles by washing the used adsorbent with a thiourea solution (5% w/v) and HNO₃ 3 M [6]. The optimized regeneration value was obtained with the 1:1 thiourea–HNO₃ solution. The FTIR spectra taken from the sample treated with 1:1 thiourea–HNO₃ showed no significant changes (Fig. 1c).

Arencibia et al. [39] compared a variety of complexing agents, such as KBr, KSCN and thiourea, and reported that thiourea had the highest complexing ability with mercury and was able to remove the higher amount of mercury from the aqueous solution. This effect can be attributed to the presence of sulfur and to the multidentate character of thiourea as a ligand, which leads to a larger mercury complexing capacity. The multidental character of thiourea and the presence of sulfur created larger mercury complexing capacity. It was a stronger nucleophile than the sulfur atom of the thiol group; therefore mercury was readily washed out into the solution [39] (Scheme 2).

Scheme 2
The mechanism of desorption of Hg²⁺ with thiourea.

The adsorption capacity of the adsorbent declined with the number of reuse cycles (Fig. 16). This was attributed to the blockage of adsorptive centers or the decomposition of some active sites during the regeneration process.

Fig. 16
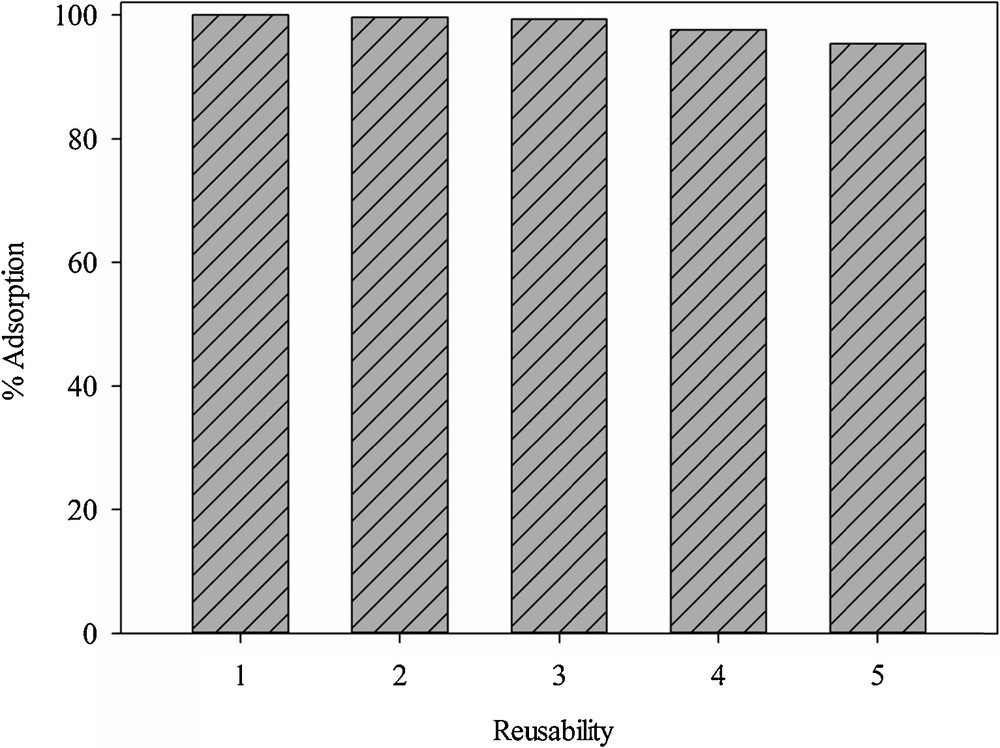
Reusability of SH-Beta/MCM-41 for Hg²⁺ removal.

According to the hard–soft acid–base theory, Hg²⁺ is classified as a soft ion. Soft ions form very strong bonds with groups containing nitrogen and sulfur atoms [41]. Soft cations are tending to establish a covalent interaction and have an affinity toward the soft sulfur. Therefore, the sulfur atom in the mercaptosilane group acts as a soft base that has a favorable interaction with Hg²⁺ as a soft acid, and forms a hard bond (covalent bond) with Hg²⁺.

3.4 Selectivity of the adsorbent for mercury

The tolerance limit is defined as the interfering ion concentration causing a relative error ≥ 5% on the adsorption of the measured cation by the adsorbent [6]. To measure the tolerance limit of the interfering cations, Pb²⁺ and Ni²⁺ solutions containing 1000 mg/L of Hg²⁺ (optimized concentration) and of interfering cations (50–3000 mg·L⁻¹) were prepared. Twenty-five milliliters of each solution were equilibrated with 0.010 g of the adsorbent. After equilibration, the mixture was filtered out and the amount of Hg²⁺ was determined. The results demonstrated that the adsorbent retained its selectivity for Hg up to a Pb²⁺ concentration of 1500 mg/L and a Ni²⁺ concentration of 2500 mg/L (Table 5).

Competitive cations	Tolerance limit for adsorbent (mg·L⁻¹)
Pb(II)	1500

Ni(II)	2500

The selectivity of the adsorbent was also examined by measurement of competitive adsorption distribution coefficients K_d (mL/g), the selectivity coefficient (k) of Hg²⁺/M (M: Pb²⁺, Ni²⁺) by the following equations:

K_{d} = (C_{i} - C_{f}) / C_{f} W

(10)

k = K_{d Hg} / K_{d M}

(11)

C_i and C_f represent respectively the initial and equilibrated concentrations of the given metal ion in the solution. K_d (Hg) and K_d (M) represent respectively the distribution coefficient of Hg²⁺ and M ions; k represents the selectivity coefficient of Hg²⁺ in the presence of the interfering cation. The results indicated that the selectivity coefficient of Hg²⁺/Pb²⁺ and Hg²⁺/Ni²⁺ were, respectively, 142.6 and 382.

4 Conclusion

The functionalized hierarchical zeolite nanocomposite prepared in the frame of this research possessed the structural advantages of a zeolite and of a mesoporous material. It showed excellent capacity for the adsorption of mercury from aqueous solutions. The adsorption process was kinetically fast and the equilibrium state was established within 5 min. The adsorption data have been fitted to the Freundlich isotherm. The selectivity of the binding process, in particular with respect to the accessibility to the active centers in the presence of other metal ions interferences was studied. SH-Beta/MCM-41 was an excellent adsorbent to bind the mercury with high selectivity because the –SH group is highly sensitive to Hg²⁺ ion. Furthermore, a maximum adsorption capacity of 8.2 mequiv·g⁻¹ was obtained, which was much higher than the earlier-reported values.

Acknowledgment

The support by the Islamic Azad University, Shahreza Branch (IAUSH) Research Council and Center of Excellence in Chemistry is gratefully acknowledged.

Bibliographie

[1] S. Štandeker; A. Veronovski; Z. Novak; Ž. Knez Desalination, 269 (2011), pp. 223-230

[2] N. Kabay; Y. Baygu; H.K. Alpoguz; A. Kaya; Y. Gök Dyes Pigments, 96 (2013), pp. 372-376

[3] H.-Y. Wu; C.-H. Liao; Y.-C. Pan; C.-L. Yeh; H.-M. Kao Micropor. Mesopor. Mater., 119 (2009), pp. 109-116

[4] H.-M. Kao; T.-Y. Shen; J.-D. Wu; L.-P. Lee Micropor. Mesopor. Mater., 110 (2008), pp. 461-471

[5] L. Mercier; T.J. Pinnavaia Environ. Sci. Technol., 32 (1998), pp. 2749-2754

[6] D. Kara Anal. Lett., 38 (2005), pp. 2217-2230

[7] A. Walcarius; C. Delacote Anal. Chim. Acta, 547 (2005), pp. 3-13

[8] J. Aguado; J.M. Arsuaga; A. Arencibia Micropor. Mesopor. Mater., 109 (2008), pp. 513-524

[9] R. Rostamian; M. Najafi; A.A. Rafati Chem. Eng. J., 171 (2011), pp. 1004-1011

[10] J. Weitkamp Solid State Ionics, 131 (2000), pp. 175-188

[11] F. Na Gu; F. Wei; J. Yuan Yang; N. Lin; W. Gang Lin; Y. Wang; J. Hua Zhu Chem. Mater., 22 (2010), pp. 2442-2450

[12] T.-O. Do; A. Nossov; M.-A. Springuel-Huet; C. Schneider; J.L. Bretherton; C.A. Fyfe; S. Kaliaguine J. Am. Chem. Soc., 126 (2004), pp. 14324-14325

[13] C.H. Christensen; K. Johannsen; E. Tornqvist; I. Schmidt; H. Topsøe; C.H. Christensen Catal. Today, 128 (2007), pp. 117-122

[14] J. Perez-Ramırez; C.H. Christensen; K. Egeblad; C.H. Christensen; J.C. Groen Chem. Soc. Rev., 37 (2008), pp. 2530-2542

[15] K. Egeblad; C.H. Christensen; M. Kustova; C.H. Christensen Chem. Mater., 20 (2008), pp. 946-960

[16] J. Zheng; X. Zhang; Y. Zhang; J. Ma; R. Li Micropor. Mesopor. Mater., 122 (2009), pp. 264-269

[17] M.S. Holm; E. Taarning; K. Egeblad; C.H. Christensen Catal. Today, 168 (2011), pp. 3-16

[18] D.P. Serrano; R.A. Garcia; G. Vicente; M. Linares; D. Prochazkova; J. Cejka J. Catal., 279 (2011), pp. 366-380

[19] Y.-S. Ooi; R. Zakaria; A.R. Mohamed; S. Bhatia Appl. Catal., A-Gen., 274 (2004), pp. 15-23

[20] X.-Y. Zhang; Q.-C. Wang; S.-Q. Zhang; X.-J. Sun; Z.-S. Zhang J. Hazard. Mater., 168 (2009), pp. 1575-1580

[21] C.F. Song; M.K. Lu; F. Gu; S.W. Liu; S.F. Wang; D. Xu; D.R. Yuan Inorga. Chem., 6 (2003), pp. 523-526

[22] N.-Y. Topsoe; K. Pedersen; E.G. Derouane J. Catal., 70 (1981), pp. 41-52

[23] H. Sepehrian; S.J. Ahmadi; S. Waqif-Husain; H. Faghihian; H. Alighanbari J. Hazard. Mater., 176 (2010), pp. 252-256

[24] G. Li; Z. Zhao; J. Liu; G. Jiang J. Hazard. Mater., 192 (2011), pp. 277-283

[25] P. Tran Thi Thu; T. Truong Thanh; H. Nguyen Phi; S. Jin Kim; V. Vo J. Mater. Sci., 45 (2010), pp. 2952-2957

[26] H. Faghihian; M.H. Mohammadi Appl. Surf. Sci., 264 (2013), pp. 492-499

[27] A.M.F. Guimarães; V.S.T. Ciminelli; W.L. Vasconcelos Appl. Clay Sci., 42 (2009), pp. 410-414

[28] H. Xu; J. Guan; S. Wu; Q. Kan J. Colloid Interf. Sci., 329 (2009), pp. 346-350

[29] W. Guo; L. Huang; P. Deng; Z. Xue; Q. Li Micropor. Mesopor. Mater., 44–45 (2001), pp. 427-434

[30] S. Mintova; J. Čejka, Studies in Surface Science and Catalysis, vol. 168, Elsevier B.V. (2007), pp. 301-326

[31] H. Zhang; Y. Li Powder Technol., 183 (2008), pp. 73-78

[32] R.J. Kalbasi; N. Mosaddegh; A. Abbaspourrad Appl. Catal., A-Gen., 423–424 (2012), pp. 78-90

[33] C. Zhang; J. Sui; J. Li; Y. Tang; W. Cai Chem. Eng. J., 210 (2012), pp. 45-52

[34] J. Hu; S.W. Wang; D.D. Shao; Y.H. Dong; J.X. Li; X.K. Wang Open Environ. Pollut., 1 (2009), pp. 66-73

[35] M.A. Tofighy; T. Mohammadi Chem. Eng. Res. Des., 90 (2012), pp. 1815-1822

[36] C. Delacôte; F.O.M. Gaslain; B. Lebeau; A. Walcarius Talanta, 79 (2009), pp. 877-886

[37] U.F. Alkaram; A.A. Mukhlis; A.H. Al-Dujaili J. Hazard. Mater., 169 (2009), pp. 324-332

[38] S. Wu; F. Li; R. Xu; S. Wei; G. Li Nanopart. Res., 12 (2010), pp. 2111-2124

[39] A. Arencibia; J. Aguado; J.M. Arsuaga Appl. Surf. Sci., 256 (2010), pp. 5453-5457

[40] H. Faghihian; M. Iravani; M. Moayed; M. Ghannadi-Maragheh Chem. Eng. J., 222 (2013), pp. 41-48

[41] R. Qu; C. Sun; F. Ma; Y. Zhang; C. Ji; Q. Xu; C. Wang; H. Chen J. Hazard. Mater., 167 (2009), pp. 717-727

Commentaires - Politique