Étude comparative de deux méthodes de caractérisation de membranes d’ultrafiltration et de nanofiltration : la porométrie bi-liquide et le transport de solutés neutres

Fatma Ellouze; Nihel Ben Amar; André Deratani

doi:10.1016/j.crci.2014.10.009

Étude comparative de deux méthodes de caractérisation de membranes d’ultrafiltration et de nanofiltration : la porométrie bi-liquide et le transport de solutés neutres

Fatma Ellouze ^1,² ; Nihel Ben Amar ^1,² ; André Deratani ³

¹ Laboratoire de modélisation mathématique et numérique dans les sciences de l’ingénieur, ENIT, université Tunis–El-Manar, campus universitaire, BP 37 Le Belvédère, 1002 Tunis, Tunisie
² Institut national des sciences appliquées et de technologie, université de Carthage, BP 676, 1080 Tunis cedex, Tunisie
³ Institut européen des membranes, université Montpellier 2 (ENSCM, UM2, CNRS), cc 47, 2, place Eugène-Bataillon, 34095 Montpellier cedex 5, France

Comptes Rendus. Chimie, Volume 18 (2015) no. 5, pp. 482-491.

Résumés

Français
Anglais

Dans cette étude, nous expérimentons deux méthodes de caractérisation pour déterminer la taille des pores de quatre membranes composites (GE-Osmonics) d’ultra- et de nanofiltration. Ces deux méthodes sont le transport de solutés neutres et la porométrie bi-liquide. La méthode de transport de solutés neutres a été employée en utilisant des solutions contenant des mélanges de polyéthylène glycol (PEG) de différentes masses moléculaires. À partir des rétentions des PEG, les modèles log-normal et celui de l’encombrement stérique ont été appliqués pour déterminer la taille des pores des membranes testées. Nous avons également testé la porométrie pour déterminer directement la distribution de la taille des pores ouverts. Nous avons observé que, pour toutes les membranes, le seuil de coupure indiqué par le fournisseur est inférieur à celui déterminé expérimentalement. Pour les membranes HL et GK, le seuil de coupure dépasse deux fois la valeur annoncée par le fournisseur. Les deux modèles mathématiques prédisent le même diamètre de pore moyen $({\bar{d}}_{p} \approx 1 nm)$ pour la membrane GH. La porométrie bi-liquide montre une distribution de taille des pores et des diamètres de pores plus larges que ceux obtenus par la méthode de transport des PEG. Cette surestimation de la taille des pores par porométrie suggère le gonflement des pores des membranes due à l’utilisation de l’isobutanol.

In this study, four commercial ultra- and nanofiltration membranes (GE-Osmonics) were characterized by determining their mean pore size and their size distribution. To this aim, two characterization methods were used: neutral solutes transport methods and bi-liquid displacement porometry. The neutral solutes transport experiments were conducted using mixtures containing polyethylene glycol PEG with various molecular weights. The log-normal and the Steric Hindrance Pore (SHP) models were applied to the PEG rejection to determine the pore size distribution of the tested membranes. The liquid–liquid displacement porometric technique was used to directly determine the open pore size distribution. The experimental results show that for all membranes, the molecular weight cut off specified by the supplier is lower than that determined experimentally. For HL and GK membranes, the MWCO exceed two times the manufacturer MWCO values. The two mathematical models (SHP and log-normal) predict the same mean pore diameter $({\bar{d}}_{p} \approx 1 nm)$ for the GH membrane. The pore size distribution obtained by transport of PEG is significantly different from that obtained by bi-liquid porometry. A comparative study of both techniques suggests that the overestimation of the pores size by the porometric technique is due to the membrane pores swelling caused by the use of an organic solvent (isobutanol).

Métadonnées

Reçu le : 2014-04-08
Accepté le : 2014-10-21
Publié le : 2015-04-04

DOI : 10.1016/j.crci.2014.10.009

Mot clés : Ultrafiltration, Nanofiltration, Distribution de taille des pores, Porométrie bi-liquide, Transport de solutés neutres
Keywords: Ultrafiltration, Nanofiltration, Pore size distribution, Bi-liquid displacement porometry, Neutral solute transport

Affiliations des auteurs :

Fatma Ellouze ^{1, 2} ; Nihel Ben Amar ^{1, 2} ; André Deratani ³

¹ Laboratoire de modélisation mathématique et numérique dans les sciences de l’ingénieur, ENIT, université Tunis–El-Manar, campus universitaire, BP 37 Le Belvédère, 1002 Tunis, Tunisie
² Institut national des sciences appliquées et de technologie, université de Carthage, BP 676, 1080 Tunis cedex, Tunisie
³ Institut européen des membranes, université Montpellier 2 (ENSCM, UM2, CNRS), cc 47, 2, place Eugène-Bataillon, 34095 Montpellier cedex 5, France

@article{CRCHIM_2015__18_5_482_0,
     author = {Fatma Ellouze and Nihel Ben Amar and Andr\'e Deratani},
     title = {\'Etude comparative de deux m\'ethodes de caract\'erisation de membranes d{\textquoteright}ultrafiltration et de nanofiltration~: la porom\'etrie bi-liquide et le transport de solut\'es neutres},
     journal = {Comptes Rendus. Chimie},
     pages = {482--491},
     publisher = {Elsevier},
     volume = {18},
     number = {5},
     year = {2015},
     doi = {10.1016/j.crci.2014.10.009},
     language = {fr},
}

TY  - JOUR
AU  - Fatma Ellouze
AU  - Nihel Ben Amar
AU  - André Deratani
TI  - Étude comparative de deux méthodes de caractérisation de membranes d’ultrafiltration et de nanofiltration : la porométrie bi-liquide et le transport de solutés neutres
JO  - Comptes Rendus. Chimie
PY  - 2015
SP  - 482
EP  - 491
VL  - 18
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crci.2014.10.009
LA  - fr
ID  - CRCHIM_2015__18_5_482_0
ER  -

%0 Journal Article
%A Fatma Ellouze
%A Nihel Ben Amar
%A André Deratani
%T Étude comparative de deux méthodes de caractérisation de membranes d’ultrafiltration et de nanofiltration : la porométrie bi-liquide et le transport de solutés neutres
%J Comptes Rendus. Chimie
%D 2015
%P 482-491
%V 18
%N 5
%I Elsevier
%R 10.1016/j.crci.2014.10.009
%G fr
%F CRCHIM_2015__18_5_482_0

Fatma Ellouze; Nihel Ben Amar; André Deratani. Étude comparative de deux méthodes de caractérisation de membranes d’ultrafiltration et de nanofiltration : la porométrie bi-liquide et le transport de solutés neutres. Comptes Rendus. Chimie, Volume 18 (2015) no. 5, pp. 482-491. doi : 10.1016/j.crci.2014.10.009. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2014.10.009/

Version originale du texte intégral

NomenclatureC_p

concentration des solutés dans le perméat

C_R

concentration des solutés dans le rétentat

D_∞

coefficient de diffusion des solutés, à dilution infinie

d_p

diamètre de pore

{\bar{d}}_{p}

diamètre de pore moyen

d_s

diamètre des PEG

e

épaisseur géométrique de la couche active de la membrane

J

flux molaire du soluté

J₀

flux volumique de l’eau pure

J_0,t

flux volumique de l’eau pure correspondant à la fraction de pores à travers laquelle passe le soluté

J_v

flux volumique du solvant

J_v,t

flux volumique du solvant correspondant à la fraction de pores à travers laquelle passe le soluté

k_c

coefficient de friction convectif

k_d

coefficient de friction diffusif

L_p

perméabilité à l’eau pure

M

masse moléculaire des PEG

MWCO

seuil de coupure

MWCO_f

seuil de coupure fournisseur

Pe

nombre de Péclet

PEG

polyéthylène glycol

R

rétention observée

R_réelle

rétention réelle

r_p

rayon de pore

SHP

Steric Hindrance Pore model

ΔP

Pression transmembranaire

Symbolsɛ

porosité

η

viscosité du solvant

θ

angle de contact

σ

écart type de la distribution de taille des pores

τ

tortuosité de la membrane

Ф

coefficient de partition

1 Introduction

L’ultra- et la nanofiltration sont des techniques séparatives qui ont prouvé leur efficacité durant ces dernières années dans diverses applications (dessalement de l’eau de mer, fractionnement des protéines laitières, l’épuration bactérienne du lait, etc.). Ces techniques sont souvent appréciées pour leur faible consommation d’énergie et leur bonne sélectivité. De plus, la filtration membranaire offre la possibilité d’un fonctionnement dans des conditions particulièrement douces (sans élévation de température, sans changement d’état et sans utilisation de solvant organique), ce qui la rend compétitive par rapport aux techniques de séparation conventionnelles.

La filtration membranaire permet, en appliquant un gradient de pression, de purifier, concentrer ou encore fractionner des composés dissouts dans un solvant par passage au travers d’une membrane poreuse semi-sélective. La séparation entre solutés repose essentiellement sur leurs différences de tailles, formes et charges. Il est important de bien caractériser les membranes pour mieux les sélectionner pour une application donnée et également pour mieux comprendre l’évolution de leur performance en cours d’utilisation [1,2].

La connaissance de la taille des pores et leur distribution est nécessaire pour prédire les performances de séparation des membranes. Pour évaluer ces deux paramètres, différentes techniques de caractérisation ont été étudiées. Parmi ces techniques, nous citons la microscopie à force atomique [3], la microscopie électronique à balayage [4], la thermoporométrie, la porométrie bi-liquide [5,6] ou encore le transport de solutés neutres [7,8]. Vu les multiples méthodes de caractérisation, Pontié et al. [2] ont proposé une nouvelle approche systématique spécifique à la caractérisation des membranes NF et OI pour le dessalement des eaux saumâtres. D’autres auteurs ont comparé entre les résultats des différentes méthodes de caractérisation. Par exemple, Khayet et al. [9] ont comparé la microscopie à force atomique (AFM) et la méthode de transport des PEG. Ils ont observé que la taille des pores déterminée par AFM est supérieure à celle obtenue par transport des PEG. Récemment, Otero et al. [10] ont comparé trois méthodes de caractérisation : la microscopie à force atomique (AFM), la porométrie bi-liquide et la rétention des PEG, pour déterminer la distribution de taille des pores de deux membranes en polyamides (AFC 40 et AFC 80, PCI Membranes^®). Ils ont observé une concordance des résultats obtenus par les trois méthodes, sauf pour la membrane AFC 40, où une légère différence a été observée entre les résultats de porométrie (rayon de pores moyen de 0,56 ± 0,12 nm) et ceux des PEG (rayon de pores moyen de 0,43 ± 0,06 nm).

À ce niveau, vue la diversification des méthodes de caractérisation et la divergence des résultats obtenus par ces différentes techniques, nous proposons, dans cette étude, de caractériser des membranes commerciales d’ultra- et de nanofiltration (HL, GH, GK, et GM, GE-Osmonics) par deux méthodes différentes : la porométrie bi-liquide et le transport des solutés neutres (les polyéthylènes glycols, PEG). Notre choix s’est porté sur ces deux techniques parce qu’elles n’évaluent que les pores ouverts, contrairement aux méthodes microscopiques, qui estiment la taille des pores (ouverts ou bloqués) à la surface de la membrane.

Pour la méthode de transport des PEG, nous allons confronter les résultats de rétention des PEG filtrés seuls et en mélange. À partir des rétentions obtenues, nous proposons d’appliquer deux modèles (le modèle log-normal et le modèle d’encombrement stérique) pour déterminer la taille des pores des membranes et leur distribution. Nous avons également estimé la distribution de taille des pores des membranes par porométrie bi-liquide, et les résultats obtenus ont été comparés à ceux déterminés par transport des PEG.

2 Théorie

2.1 Évaluation du diamètre de pore moyen et de la distribution de taille des pores par transport des polyéthylène glycol

Cette technique permet d’évaluer le diamètre de pore moyen des membranes et leur distribution par la mesure de la rétention R (Eq. (1)) d’une série de molécules neutres de tailles différentes. En confrontant la courbe de sélectivité (pourcentage de rétention des solutés en fonction de leur taille) à des modèles prédéfinis, les caractéristiques des membranes peuvent être déduites.

R = (1 - \frac{C_{p}}{C_{R}}) \times 100

(1)

Deux modèles ont été étudiés pour modéliser la courbe de rétention des PEG : le modèle log-normal et le modèle d’encombrement stérique [Steric Hindrance Pore Model, (SHP)].

2.1.1 Loi log-normale de distribution

D’après les travaux de Michaelis [11], la fonction log-normale est une méthode précise pour décrire les courbes de sélectivité des membranes UF. La variation de la rétention des solutés en fonction de leur taille d_s suit une relation log-normale représentée par l’équation suivante :

R (d_{s}) = \int_{0}^{d_{s}} \frac{1}{d_{s} σ \sqrt{2 π}} \exp (- \frac{{(\ln d_{s} - \ln {\bar{d}}_{p})}^{2}}{2 σ^{2}}) d d_{s}

(2)

où

{\bar{d}}_{p}

correspond au diamètre de pore moyen et σ à l’écart type de la distribution de taille des pores.

Ces deux paramètres ( ${\bar{d}}_{p} et σ$ ) sont déterminées en traçant sur un papier log-normal l’évolution de la rétention en fonction du diamètre des PEG (d_s). Si nous obtenons une courbe linéaire, cela veut dire que l’évolution de la rétention suit la loi log-normale et que, dans ce cas, le diamètre de pore moyen ${\bar{d}}_{p}$ est déterminé à partir de cette droite pour une rétention de 50 %. L’écart type logarithmique σ est calculé en faisant le rapport du diamètre équivalent à 84,13 % de rétention à celui équivalent à 50 % de rétention.

La masse moléculaire des PEG, M, est convertie en diamètre selon l’expression empirique (Eq. (3)) dérivant de l’équation d’Einstein–Stokes [12] :

d_{s} (PEG) = (16,73 \times 10^{- 10} \times M^{0,557}) \times 2

(3)

2.1.2 Modèle d’encombrement stérique

Pour les solutés neutres, l’expression du flux molaire est donnée par une équation du type solubilisation–diffusion convection [13] :

J = - k_{d} D_{\infty} \frac{d C}{d x} + k_{c} C \frac{J_{v}}{ε}

(4)

où ɛ est la porosité de la membrane, qui est égale au rapport de l’aire des pores sur la surface de la membrane, D_∞ est le coefficient de diffusion du soluté, à dilution infinie, dans le solvant, C est la concentration du soluté dans la membrane et J_v est le flux volumique du solvant. Les coefficients k_d et k_c sont respectivement des coefficients de friction diffusif et convectif, qui peuvent être exprimés en fonction du rapport λ (

λ = \frac{r_{s}}{r_{p}}

étant le rapport entre le rayon du soluté r_s et le rayon du pore r_p). Dans la littérature [14], les expressions de ces coefficients ont été proposées (Eq. (5) et Eq. (6)). Elles reposent sur l’analyse détaillée de la mécanique des fluides de particules sphériques en mouvement dans un tube cylindrique.

k_{c} = (2 - φ) \cdot (A + B λ + C λ^{2} + D λ^{3})

(5)

k_{d} = E + F λ + G λ^{2} + H λ^{3}

(6)

où les constantes (A, B, C…) sont égales à [13,15,16] :

\begin{array}{c} A = 1, B = 0,054, C = - 0,988 et D = 0,441 \\ E = 1, F = - 2,30, G = 1,154 et H = 0,224 \end{array}\} 0 < λ \leq 0,8

et

\begin{array}{c} A = - 6,830, B = 19,348, C = - 12,518 et D = 0 \\ E = - 0,105, F = - 0,318, G = - 0,231 et H = 0 \end{array}\} 0,8 < λ \leq 1

ϕ correspond au coefficient de partition :

ϕ = {(1 - λ)}^{2}

(7)

Étant donné que le flux du soluté J peut être exprimé en fonction de C_p (concentration du soluté dans le perméat) selon $J = \frac{C_{p} J_{v}}{ε}$ [10], l’équation (4) devient :

\frac{d C}{d x} = \frac{1}{ε D_{\infty}} [\frac{k_{c}}{k_{d}} C - \frac{1}{k_{d}} C_{p}] J_{v}

(8)

C, ɛ et D_∞ correspondent respectivement à la concentration du soluté dans la membrane, à la porosité de la membrane et au coefficient de diffusion du soluté, à dilution infinie, dans le solvant.

L’équation (8) peut être intégrée aux conditions limites de concentrations C_m (concentration à l’entrée du pore) et C_p (la concentration à la sortie du pore) et être ainsi utilisée pour évaluer l’expression de rétention réelle donnée par :

R_{réelle} = 1 - \frac{k_{c} φ}{1 - \exp (- P e) (1 - k_{c} φ)}

(9)

où Pe est le nombre de Péclet, dont l’expression est donnée par la relation :

P e = \frac{1}{D_{\infty} L_{p}} (\frac{k_{c} r_{p}^{2}}{k_{d} 8 η})

(10)

L_p correspond à la perméabilité de la membrane, η à la viscosité de la solution d’alimentation, et J_v est le flux volumique total.

À partir des deux équations (9) et (10), nous observons que la rétention R est fonction de J_v, r_s, D_∞, r_p, L_p et η. Ainsi, connaissant la rétention des PEG en fonction de J_v, r_s, D_∞, L_p et η, le rayon r_p de la membrane peut être déterminé. D_∞ est calculé par l’équation de Stokes–Einstein et la viscosité η a été prise équivalente à celle de l’eau.

Sachant que les solutions de PEG utilisées ont une concentration de 1 g/L, le phénomène de polarisation de concentration a été négligé dans cette étude et nous avons supposé que la rétention réelle et la rétention observée sont égales.

Afin d’évaluer la distribution de taille des pores des membranes, on suppose que la rétention des PEG n’est régie que par le phénomène d’exclusion stérique et dans ce cas le bilan de masse peut s’écrire ainsi :

J_{v} C_{p} = J_{v, t} C_{m}

(11)

J_v,t est le flux volumique correspondant à la fraction de pores à travers laquelle passe le soluté.

Sachant que les solutions de PEG utilisées sont diluées (donc J_v,t = J_0,t), l’équation (11) devient :

J_{0, t} = \frac{J_{v} C_{p}}{C_{m}} = J_{v} (1 - R)

(12)

J_0,t est le flux volumique de l’eau pure correspondant à la fraction de pores à travers laquelle passe le soluté.

La distribution de taille des pores est exprimé par $\frac{d \frac{J_{0, t}}{J_{0}}}{d d_{p}}$ . La représentation graphique de $\frac{J_{0, t}}{J_{0}}$ en fonction de la taille des PEG correspond à la fraction du flux passant à travers les pores de diamètres supérieurs à celui du soluté. La courbe obtenue a pour fonction empirique [17] :

\frac{J_{0, t}}{J_{0}} = \frac{1}{1 + {(\frac{d_{p}}{B})}^{α}}

(13)

α et B sont des constantes qui peuvent être déterminées en ajustant, par la méthode des moindres carrés, les résultats expérimentaux au modèle théorique (Eq. (13)). De cette façon, la dérivée du flux J_0,t en fonction du diamètre de pore d_p représentant la distribution de taille des pores peut être obtenue.

\frac{d (\frac{J_{0, t}}{J_{0}})}{d d_{p}} = \frac{- \frac{α}{B} {(d_{p})}^{α - 1}}{1 + {(\frac{d_{p}}{B})}^{α}}

(14)

2.2 Évaluation du diamètre de pore moyen et de la distribution de taille des pores par porométrie bi-liquide

La porométrie bi-liquide permet de caractériser les membranes en déterminant leur distribution de taille des pores. Cette méthode utilise une corrélation entre pression appliquée et rayon de pore donnée par l’équation de Washburn [18] :

Δ P = \frac{4 γ}{d_{p}} \cos θ

(15)

γ étant la tension de surface, θ l’angle de contact entre interface du liquide et la surface du pore et d_p le diamètre des pores.

La procédure consiste à utiliser deux liquides immiscibles avec une faible tension superficielle permettant ainsi des mesures de la taille de pores à des faibles pressions. Le liquide (A) mouillant la membrane est déplacé avec le liquide (B) (non miscible avec le premier) en appliquant une pression ΔP suffisante pour ouvrir le pore le plus large (Fig. 1).

Fig. 1
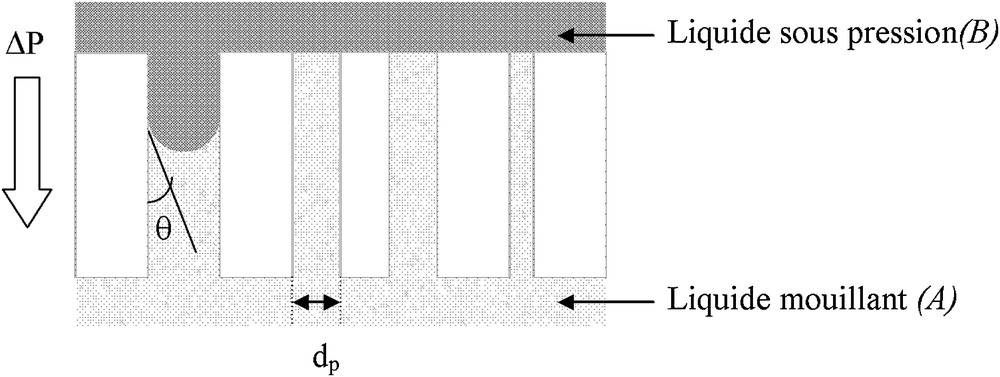
Principe de la porométrie bi-liquide. Représentation des pores cylindriques.

La distribution des rayons de pores, représentée par f(r), peut être déduite de l’équation de Cantor (Eq. (16)), qui suppose que l’angle de contact est égal à 0 pour les liquides ayant une faible tension superficielle [19,20].

Δ P = \frac{4 γ}{d_{p}}

(16)

Le déplacement du liquide mouillant commence par le pore ayant le plus large rayon, suivi par les plus petits. Le flux résultant peut être décrit par l’équation de Hagen–Poiseuille (Eq. (17)). En supposant que les pores sont cylindriques, l’équation peut être utilisée pour corréler le flux, J_v, avec N₀, le nombre de pore ouvert par unité de surface à la pression donnée.

J_{v} = \frac{N_{0} π d_{p}^{4} Δ P}{128 η e τ}

(17)

où e et τ sont respectivement l’épaisseur géométrique de la couche active et la tortuosité de la membrane.

Le nombre de pores N₀ est donné par la relation :

N_{0} = N \int_{d_{\min}}^{d_{\max}} f (d_{p}) d d_{p}

(18)

N est le nombre total de pores (par unité de surface), d_min est le diamètre du plus petit pore ouvert et d_max est le diamètre du plus large pore ouvert.

En combinant les équations (17) et (18), l’expression de J_v devient [21] :

J {}_{v}= \int_{d_{\min}}^{d_{\max}} N \frac{π {d_{p}}^{4} Δ P}{128 η δ} f (d_{p}) d d_{p} = \frac{N π}{128 η δ} Δ P \int_{d_{\min}}^{d_{\max}} {d_{p}}^{4} f (d_{p}) d d_{p}

(19)

La dérivée de J_v par rapport à d_p et le réarrangement de l’équation (19) donne l’expression finale de la fonction représentative de la distribution de taille des pores [21].

f (d_{p}) = (\frac{d J_{v}}{d (Δ P)} - \frac{J_{v}}{Δ P}) \frac{Δ P^{5} 128 η δ}{{(2 γ)}^{5} N π}

(20)

3 Matériels et méthodes

3.1 Membranes et solutés

Le présent travail a été conduit avec quatre membranes commerciales (HL, GH, GK et GM, GE-Osmonics). Ce sont des membranes composites planes constituées de trois couches : une trame non tissée, une couche intermédiaire en polysulphone et une couche active en polyamide aromatique. Les caractéristiques données par les fournisseurs des membranes sont présentées dans le Tableau 1.

Membrane	Classe	Pression max (bar)	MWCO (Da)
HL	NF	40	150–300^a
GH	UF	27	1000^b
GK	UF	27	2000^b
GM	UF	27	4000^b

^a Donné en équivalent glucose–sucrose.

^b Donné en équivalent polyéthylène glycol.

Nous avons étudié, en mélange ou séparément, la filtration de l’éthylène glycol (62 g/mol) et des polyéthylène glycols de différentes masses moléculaires (200 à 35 000 g/mol), à une concentration totale de 1 g/L.

Pour les expériences de porométrie bi-liquide, le méthanol (Fluka, pureté 99,8 %) et l’isobutanol (2 méthylpropan-1-ol) (Aldrich, pureté 99 %) ont été utilisés.

3.2 Procédure de filtration des PEG

Les expériences de filtration des PEG ont été effectuées en filtration frontale dans une cellule (Amicon stirred cell 8400) d’une capacité de 400 mL et de surface active 41,8 cm². Une agitation de 300 rpm a été maintenue à l’intérieur du module afin de limiter le phénomène de polarisation de concentration. La cellule est sous pression d’azote laquelle est régulée avec une vanne et un manomètre montée sur la conduite d’alimentation de l’azote. Les expériences ont été effectuées à des pressions variant de 1 à 4,5 bar et à une température ambiante de 25 ± 3 °C. La masse du perméat (m) est mesurée à l’aide d’une balance Sartorius (précision ± 0,01 g) connectée à un ordinateur qui, par l’intermédiaire d’un logiciel d’acquisition (Winwedge) permet de suivre la masse du perméat collectée en fonction du temps. Toutes les expériences de filtration ont été refaites au minimum trois fois, afin de s’assurer de la reproductibilité des résultats. L’erreur maximale calculée sur la rétention est de 3 %.

Les échantillons de perméat et rétentat prélevés, après chaque expérience de filtration, sont analysés, soit par chromatographie à exclusion stérique couplée à un détecteur réfractométrique (OPTILAB DSP, Wyatt Technology Co) pour déterminer la concentration des PEG en mélange, soit par le détecteur réfractométrique dans le cas des PEG seuls. La colonne analytique utilisée, dans le cas des mélanges de PEG, est la Superose 12HR (GE Healthcare).

3.3 Procédure expérimentale de la porométrie liquide–liquide

Le porométre liquide–liquide utilisé lors de cette étude (PRM-2000-LL-R, GEPS) est entièrement automatisé. Il est composé d’un système de régulation de pression (connecté à la conduite du gaz comprimé), d’un réservoir, d’un débitmètre de précision (Brooks Quantim Coriolis) et d’une cellule de filtration frontale ayant une surface active de 12,5 cm². L’acquisition et le traitement des données sont réalisés par deux logiciels qui permettent de présenter la variation du flux en fonction de la pression appliquée et de traiter les données en les convertissant en distribution de taille des pores.

Au préalable, les membranes étudiées ont été lavées et caractérisées en termes de perméabilité à l’eau pure (Eq. (21)). Par la suite, nous avons imprégné celles-ci de phase organique (liquide mouillant, (A)) en appliquant dessus des pressions élevées (de 7 à 10 bar) pendant 4 minutes.

L_{P}^{0} = \frac{J_{0}}{Δ P}

(21)

$L_{P}^{0}, J_{0}$ , et ΔP correspondent respectivement à la perméabilité et au flux volumique de l’eau pure, ainsi qu’à la pression transmembranaire.

Le liquide mouillant est ensuite déplacé par la phase aqueuse en appliquant une pression suffisante pour ouvrir le pore le plus large. Au fur et à mesure que la pression augmente, le débit correspondant à chaque pression transmembranaire est mesuré jusqu’à ce que tous les pores soient ouverts.

Le mélange utilisé pour les expériences de porométrie est composé de méthanol/isobutanol/eau ultra pure dans les proportions volumiques 15/32/53. Ce mélange est préparé dans une ampoule à décanter. Après une bonne agitation, on laisse reposer le mélange pendant 24 heures pour décanter. Au bout de 24 heures, deux phases sont récupérées. La première, riche en alcool, est utilisée comme phase mouillante (A) et la seconde (la phase aqueuse) sert à déplacer la phase organique (B). La tension superficielle du mélange ternaire est de 0,35 mN/m [22,23].

4 Résultats et discussion

4.1 Transport des polyéthylène glycols

4.1.1 Loi log-normale

La corrélation log-normale entre la rétention des PEG et leur taille permet d’étudier la taille des pores des membranes et leur distribution [24]. Nous avons tout d’abord testé les expériences de filtration des PEG, seuls et en mélange, sur la membrane GH. Les rétentions obtenues en fonction de la masse moléculaire, dans les deux cas, sont présentées dans la Fig. 3. D’après Tam et Trembley [25], l’utilisation d’un mélange de solutés tend à sous-estimer la valeur du seuil de coupure à cause d’interactions entre celles-ci. Dans notre cas, les rétentions des PEG seules et en mélange sont similaires (Fig. 3), ce qui signifie qu’il n’y a pas d’interactions entre les solutés. Ces résultats sont cohérents avec les travaux de Rohani et al. [8], qui proposent une nouvelle approche pour la détermination des seuils de coupure des membranes d’UF et NF en une seule filtration en utilisant des mélanges de PEG. Le seuil de coupure de la membrane GH obtenu à partir des PEG seuls est de 1750 Da contre 1850 Da lors de la filtration des PEG en mélange. Cette concordance des résultats nous a permis de minimiser le nombre d’expériences à effectuer en filtrant sur les membranes HL, GK et GM des PEG en mélange au lieu de filtrer chaque PEG séparément.

Fig. 3
Distributions de taille des pores des membranes HL, GH, GK et GM déterminées par la fonction de densité de probabilité.

Le tracé de la rétention des PEG en fonction de leurs diamètres (calculé à partir de l’Eq. (3)) sur un papier log-normal donne des courbes linéaires (R² ≥ 0,97). Le diamètre de pore moyen ${\bar{d}}_{p}$ et l’écart type σ obtenus sont résumés dans le Tableau 2.

	Membranes
	HL	GH	GK	GM
${\bar{d}}_{p} (nm)$	0,57	1,19	2,07	2,2
σ	1,71	1,72	1,6	1,67
MWCO (Da)	580 ± 50	1850 ± 100	5000 ± 300	6200 ± 500
MWCO_f (Da)	150–300	1000	2000	4000

Le profil log-normal de rétention des PEG établi permet de déterminer le seuil de coupure des membranes utilisées (Fig. 2). Les seuils de coupure des membranes HL, GH, GK et GM déterminés sont largement supérieurs à ceux communiqués par le fournisseur (Tableau 2). Cette différence observée peut être liée aux solutés, aux modes de filtration ou aux conditions opératoires utilisés, qui influent directement sur la valeur des seuils de coupure [26–28].

Fig. 2
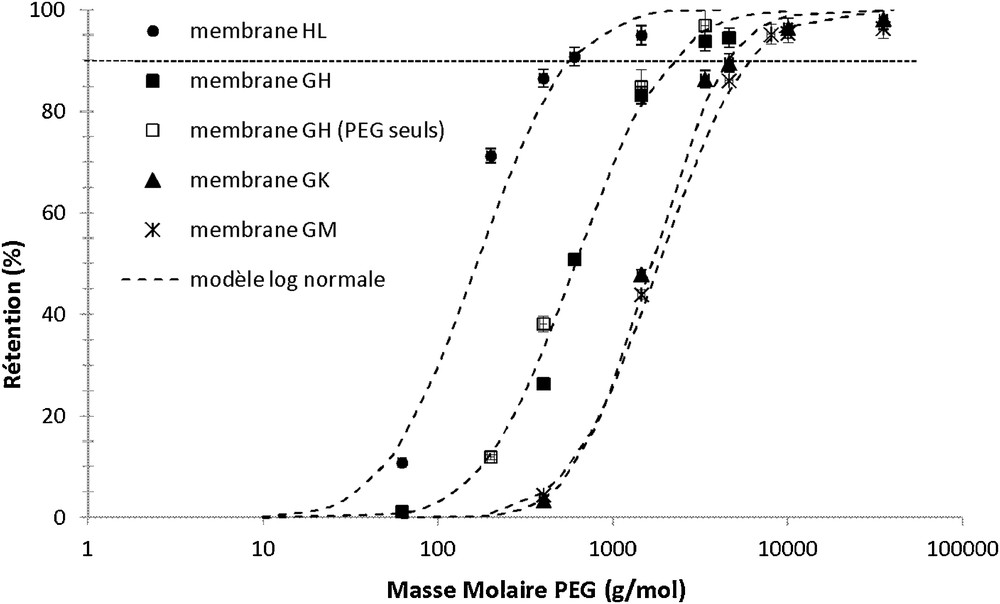
Rétention des PEG en fonction de leurs masses moléculaires pour les membranes HL, GH, GK et GM déterminés par le modèle log-normal à ΔP = 2 bar et C_totale = 1 g/L. Marqueurs pleins : PEG filtrés en mélange, marqueurs vides : PEG filtrés seuls.

Les écarts type des distributions de taille des pores des membranes calculés sont assez similaires et cohérents avec les travaux de Michaels [11]. Nous observons que l’augmentation des seuils de coupure correspond à un élargissement des pores des membranes, excepté pour les membranes GK et GM qui ont des diamètres de pores moyens très proches respectivement égales à 2,1 et 2,2 nm.

À partir des valeurs de ${\bar{d}}_{p}$ et de σ, la distribution de la taille des pores a été générée par la fonction de densité de probabilité [9,24]. Les distributions de la taille des pores des membranes testées sont représentées dans la Fig. 3.

La membrane HL a la distribution la plus étroite, avec une densité de probabilité de l’ordre de 1,5 nm⁻¹ et environ 60 % de pores de diamètre inférieur à 0,64 nm (Fig. 3). La membrane GH a une distribution plus large que la membrane HL. La densité de probabilité maximale avoisine 0,7 nm⁻¹, avec seulement 14 % de pores de diamètre inférieur à 0,64 nm. Les membranes GK et GM ont des distributions des tailles de pores similaires, avec des densités de probabilité maximales respectivement de 0,44 et 0,39 nm⁻¹. Même si nous avons noté une différence de 24 % par rapport aux valeurs de seuil de coupure des membranes GK et GM (Tableau 2), nous observons que cette différence n’est plus significative en comparant les diamètres de pores moyens et les distributions de tailles des pores de ces deux membranes. Les membranes GK et GM ont a priori les mêmes performances de séparation. À ce stade, nous concluons qu’une caractérisation par le seuil de coupure n’est pas suffisante et que d’autres caractérisations sont primordiales afin de bien sélectionner une membrane.

4.1.2 Modèle d’encombrement stérique

Le modèle d’encombrement stérique [Steric Hindrance Pore Model (SHP)] a été appliqué sur la membrane GH pour déterminer la distribution de taille des pores des membranes à partir de la rétention des PEG en mélange à différentes pressions. Par ajustement de la rétention théorique (Eq. (9)), nous déterminons les rayons de pores r_p. Dans cette partie, nous avons simplifié le modèle, en supposant que le phénomène de polarisation de concentration est négligeable et que, de ce fait, R_réelle = R [2]. En effet, toutes les expériences de perméation des solutions de PEG ont été effectuées dans un milieu dilué (C = 1 g/L), avec un taux de conversion inférieur à 6 % et sous agitation continue de 300 rpm pour minimiser la polarisation de concentration. La représentation graphique du flux volumique des solutions de PEG, à travers la membrane GH, en fonction de la pression transmembranaire montre une droite linéaire croissante ayant pour pente $L_{P}^{PEG} = 2,9 {L/m}^{2} /h/bar$ . Cette valeur est similaire à celle de la perméabilité à l’eau pure ( $L_{P}^{0} = 3 {L/m}^{2} /h/bar$ ), ce qui confirme la quasi-absence du phénomène de polarisation de concentration.

La Fig. 4 montre la rétention des PEG par la membrane GH en fonction du flux volumique. La courbe en discontinu représente les résultats d’ajustement de l’équation (9) aux rétentions expérimentales des PEG.

Fig. 4
Rétention des PEG en fonction du flux sur la membrane GH. Le trait discontinu représente l’ajustement de la rétention théorique par le modèle SHP.

Les rayons de pores sont convertis en distribution de taille des pores selon l’équation (14) représentant la variation de $\frac{d (\frac{J_{0, t}}{J_{0}})}{d d_{p}}$ en fonction de d_p (Fig. 5). Les constantes α et B ont été déterminées en ajustant les résultats expérimentaux de J_0,t/J₀ au modèle empirique défini par l’Eq. (13). La qualité de l’ajustement a été évaluée par le calcul d’un pseudo-cœfficient R² [29]. La valeur de R² calculée est supérieure à 0,995, ce qui reflète le fait que le modèle s’adapte très bien aux résultats expérimentaux.

Fig. 5
Distribution des tailles de pores de la membrane GH à partir de la rétention des PEG selon deux modèles ; SHP : trait continu et log-normal : trait discontinu.

La distribution des tailles de pores calculée à partir du modèle d’encombrement stérique est similaire à la distribution obtenue par le modèle log-normal (Fig. 5). L’écart type de la distribution prédite par le modèle SHP a été calculé et la valeur trouvée est de 1,61 [29]. Cette valeur est légèrement inférieure à l’écart type de la distribution du modèle log-normal (σ = 1,71, Tableau 2), ce qui se traduit, pour ce dernier modèle, par une légère traînée vers les larges pores. Selon le modèle log-normal, 75 % des pores ont un diamètre inférieur à 1,2 nm, contre 81 % pour le modèle SHP. Nous observons cependant que les deux modèles prédisent le même diamètre de pore moyen (≈1 nm).

Les résultats obtenus par les deux modèles sont similaires. Le modèle log-normal reste néanmoins plus pratique à appliquer vu que la rétention des PEG à une seule pression est suffisante pour prédire les caractéristiques de la membrane.

4.2 La porométrie bi-liquide

Toutes les expériences porométriques ont été refaites trois fois sur les mêmes échantillons pour les membranes HL, GH, GK et GM. Les essais effectués ont montré une bonne reproductibilité des courbes porométriques (débit en fonction de la pression). Les résultats obtenus pour la membrane GH sont présentés en tant qu’exemple dans la Fig. 6.

Fig. 6
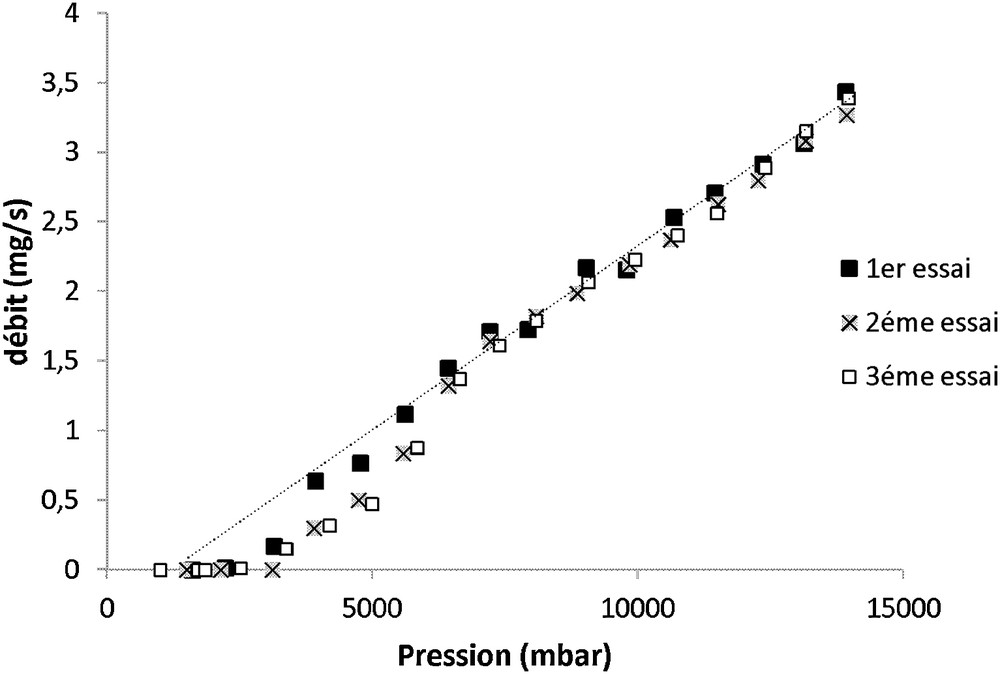
Courbes porométriques (débit en fonction de la pression) de la membrane GH. Le trait discontinu représente la variation du débit de la phase aqueuse après ouverture de tous les pores.

L’allure en « S » de la courbe porométrique est due à trois phases distinctes. Lors de la première phase, la pression n’est pas assez élevée pour entraîner l’ouverture des pores les plus larges, d’où l’obtention d’un flux quasi nul. La deuxième phase, relative à la courbure de la courbe, correspond au début d’ouverture des pores, ce qui entraîne l’apparition du flux. L’augmentation progressive de la pression engendre l’ouverture de pores de plus en plus petits et, par conséquent l’augmentation significative du flux. À la fin de l’ouverture de tous les pores apparaît la troisième phase. Lors de cette phase, l’augmentation du flux n’est due qu’à l’augmentation de la pression (la pente de l’augmentation du flux au niveau de cette phase est moins importante qu’au niveau de la deuxième phase) (Fig. 6).

Les données expérimentales (débit en fonction de la pression) converties en distribution de taille des pores sont présentées dans la Fig. 7.

Fig. 7
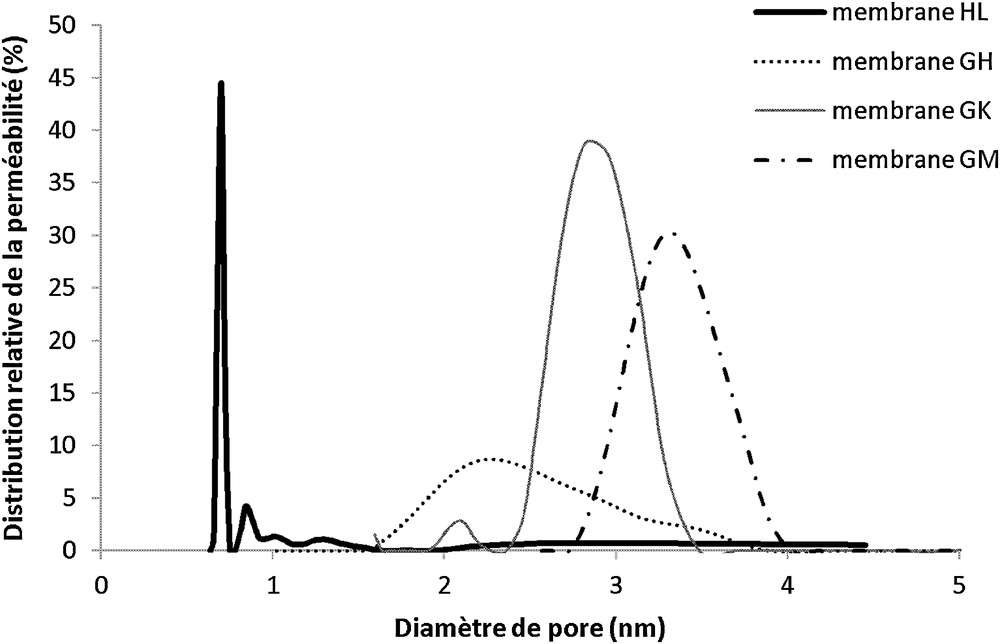
Distribution de tailles des pores des membranes HL, GH, GK et GM obtenue par porométrie bi-liquide. Mouillage des membranes par filtration à haute pression de la phase organique.

Nous observons que la membrane HL a la distribution la plus étroite et un diamètre de pore moyen de 0,7 nm. La membrane GH a la distribution la plus large avec une traînée vers les larges pores et un diamètre de pore moyen de 2,1 nm. Les membranes GK et GM ont respectivement des diamètres de pores moyens de 2,9 et 3,3 nm. Contrairement à la méthode de transport des PEG, les distributions de taille des pores des membranes GK et GM ne sont pas similaires : 80 % des pores de la membrane GM sont supérieurs à 3,1 nm en diamètre contre seulement 20 % pour la membrane GK.

De plus, les diamètres de pores obtenus par porométrie liquide–liquide sont bien supérieurs aux résultats obtenus par rétention des PEG (Tableau 2) avec des distributions plus étroites.

Cette différence observée est peut être liée à l’estimation du rayon hydrodynamique des PEG. De façon générale, le rayon hydrodynamique est défini comme le rayon d’une sphère qui diffuserait à la même vitesse que la particule elle-même. Or, cette définition est quelque peu problématique vu que les PEG en solution n’ont pas une forme sphérique, mais plutôt allongée [30].

Récemment, Otero et al. [10], en comparant la porométrie bi-liquide et la méthode de transport des PEG ont trouvé des résultats équivalents aux nôtres. Ils ont suggéré que la surestimation de la taille des pores par porométrie est probablement due à une faible rétention de l’isobutanol lors du mouillage des membranes [10]. Afin de vérifier cette supposition, nous avons testé la rétention de l’isobutanol en filtrant la phase organique à différentes pressions sur les différentes membranes. Nous n’avons observé aucune rétention de l’isobutanol, ce qui infirme l’hypothèse d’Otero et al.

D’autres auteurs [7,31,32] ont annoncé que l’utilisation de solvant organique (isobutanol) entraîne le gonflement des membranes, ce qui influence la mesure de la taille des pores. Calvo et al. [32] ont observé (par microscopie à balayage) une augmentation du rayon de pore moyen, de la densité des pores et de la porosité d’une membrane d’ultrafiltration après les expériences porométriques. Nous avons mesuré la perméabilité à l’eau des membranes après les expériences de porométrie liquide–liquide (PLL) (Tableau 3).

Membrane	HL	GH	GK	GM
$L_{P}^{0}$ (L/m²/h/bar)	10	3	14	13
$L_{P}^{0}$ après PLL (L/m²/h/bar)	11,7	3,7	20,4	15

Le Tableau 3 montre que la perméabilité à l’eau des membranes n’augmente pas systématiquement avec l’augmentation des seuils de coupure de ces mêmes membranes. La perméabilité de la membrane HL (NF) est supérieure à celle de la membrane GH (UF) et les perméabilités à l’eau des membranes GK et GM sont similaires. Ceci prouve que la perméabilité ne dépend pas que de la taille des pores des membranes, mais que d’autres paramètres comme l’épaisseur, la porosité et l’hydrophobie peuvent influencer la valeur de la perméabilité.

Après les expériences de porométrie, nous observons que la perméabilité à l’eau des membranes augmente d’au moins d’un facteur de 1,2. Cette augmentation suggère une modification des propriétés intrinsèques des membranes, ce qui confirme les travaux de Calvo et al. [32] quant à l’augmentation des rayons de pores et de la porosité des membranes après l’utilisation de solvants organiques.

5 Conclusion

Vu la diversification des techniques de caractérisation des membranes et l’importance de la caractérisation dans le choix des membranes, l’idée de ce travail était de comparer certaines de ces techniques de caractérisation afin, peut-être, d’en privilégier une par rapport à une autre. Nous avons, dans cette étude, caractérisé des membranes commerciales d’ultra et de nanofiltration, par deux méthodes différentes : la méthode de transport des PEG et la porométrie bi-liquide, en déterminant leurs diamètres de pores moyens et leurs distributions de taille.

Les résultats ont montré que les seuils de coupure des membranes HL, GH, GK et GM déterminés à partir de la filtration des PEG sont supérieurs à ceux annoncés par le fournisseur. Une différence de plus que 35 % a été notée. Nous avons également observé une concordance entre les profils log-normaux, de la membrane GH, déterminés par un mélange de PEG et par des PEG seuls. Le seuil de coupure déterminé à partir de filtration de mélange de PEG est de 1850 Da contre 1750 Da lors de la filtration de PEG seuls. Les valeurs de rétention des PEG ont été converties en distribution de taille de pores en utilisant deux modèles : le modèle log-normal et celui de l’encombrement stérique. Les deux modèles ont prédit le même diamètre de pore moyen pour la membrane GH d’une valeur avoisinant 1 nm. Le modèle log-normal reste néanmoins plus pratique à appliquer vu que la rétention des PEG à une seule pression est suffisante pour prédire les caractéristiques de la membrane. La porométrie a également été utilisé pour déterminer le diamètre des pores moyen des membranes utilisées. La porométrie en comparaison avec la méthode de transport des PEG a révélé des diamètres de pores moyens plus larges. La différence maximale a été observée pour la membrane GH, avec un écart de 50 %. Cette différence entre les diamètres de pores peut être liée soit à la sous-estimation de la taille des PEG, soit au gonflement des pores des membranes causé par l’utilisation de l’isobutanol. La mesure de la perméabilité à l’eau des membranes après les analyses porométriques a dévoilé des perméabilités à l’eau plus élevées, ce qui tend à confirmer la deuxième hypothèse, qui suggère que le mouillage des membranes par la phase riche en isobutanol cause l’augmentation de la taille des pores.

Au vu de ces conclusions, toute technique a ses inconvénients, mais la méthode de transport des PEG nous semble, a priori, la plus pratique et la plus fiable. La porométrie bi-liquide est certes une technique intéressante, mais elle nécessite davantage de précautions, et des études plus approfondies quant à l’utilisation de solvant organique sont à considérer.

Remerciements

Les auteurs tiennent à remercier le ministère français des Affaires étrangères (projet CMCU 04PRE01) et le projet européen Co-advise (FP7-IRSES-COADVISE-230833) pour leur participation au financement de ce présent travail.

Bibliographie

[1] C. Causserand Filtration membranaire (OI, NF, UF)–caractérisation des membranes, Techniques de l’ingénieur, référence W4100, 2006

[2] M. Pontié; H. Dacha; J. Leparc; M. Hafsid; A. Lhassani Desalination, 221 (2008), pp. 174-191

[3] A.M. ElHadidy; S. Peldszus; M.I. Van Dyke J. Membr. Sci., 429 (2013), pp. 373-383

[4] Y. Wyart; S. Nitsche; D. Chaudanson; K. Glucina; P. Moulin Membr. Water Treat., 2 (2011), pp. 251-266

[5] P. Carretero; S. Molina; A. Lozano; J. de Abajo; J.I. Calvo; P. Prádanos; L. Palacio; A. Hernández Desalination, 327 (2013), pp. 14-23

[6] J.I. Calvo; R.I. Peinador; P. Prádanos; L. Palacio; A. Bottino; G. Capannelli; A. Hernández Desalination, 268 (2011), pp. 174-181

[7] F.P. Cuperus; C.A. Smolders Adv. Colloid Interf. Sci., 34 (1991), p. 135

[8] R. Rohani; M. Hylanda; D. Patterson J. Membr. Sci., 382 (2011), pp. 278-290

[9] M. Khayet; T. Matsuura Desalination, 158 (2003), p. 57

[10] J.A. Otero; O. Mazarrasa; J. Villasante; V. Silva; P. Prádanos; J.I. Calvo; A. Hernández J. Membr. Sci., 309 (2008), p. 17

[11] A.S. Michaels Sep. Sci. Technol., 15 (1980), pp. 1305-1322

[12] T. Gumi; M. Valiente; K.C. Khulbe; C. Palet; T. Matsuura J. Membr. Sci., 212 (2003), p. 134

[13] W.R. Bowen; A.V. Mohammad; N. Hilal J. Membr. Sci., 126 (1997), p. 91

[14] V. Silva; P. Pradanos; L. Palcio; A. Hernandez Desalination, 245 (2009), pp. 606-613

[15] W.R. Bowen; A.O. Sharif J. Colloid Interf. Sci., 168 (1994), p. 414

[16] S. Bandini; D. Vezzani Chem. Eng. Sci., 58 (2003), p. 3303

[17] N.A. Ochoa; P. Prádanos; L. Palacio; C. Pagliero; J. Marchese; A. Hernández J. Membr. Sci., 187 (2001), p. 227

[18] J.I. Calvo; A. Hernández; P. Prádanos; L. Martinez; W.R. Bowen J. Colloid Interf. Sci., 176 (1995), p. 467

[19] J.A. Fernando; D.D.L. Chung J. Porous Mater., 9 (2002), p. 211

[20] J.G. Minnery; J.G. Jacangelo; G. Joseph; L.I. Boden; D.J. Vorhees; W. Heiger-Bernays Environ. Sci. Technol., 43 (2009), pp. 9419-9424

[21] K.S. McGuire; K.W. Lawson; D.R. Lloyd J. Membr. Sci., 99 (1995), p. 127

[22] G. Capannelli; F. Vigo; S. Munari J. Membr. Sci., 15 (1983), p. 289

[23] K.J. Kim; A.G. Fanen; R. Ben Aim; M.G. Liu; G. Jonsson; I.C. Tessaro; A.P. Broek; D. Bargemand J. Membr. Sci., 81 (1994), pp. 35-46

[24] S. Singh; K.C. Khulbe; T. Matsuura; R. Ramamurthy J. Membr. Sci., 142 (1998), p. 111

[25] C.M. Tam; A.Y. Tremblay J. Membr. Sci., 57 (1991), p. 271

[26] A.-L. Zydney; A. Xenopoulos J. Membr. Sci., 291 (2007), p. 180

[27] N. Ben Amar; N. Kechaou; J. Palmeri; A. Deratani; A. Sghaier J. Hazard. Mater., 170 (2009), p. 111

[28] D. Nabarlatz; C. Torras; R. Garcia-Valls; D. Montan Sep. Purif. Technol., 53 (2007), p. 235

[29] E. Anton; J.I. Calvo; J.R. Álvarez; A. Hernández; S. Luque J. Membr. Sci., 470 (2014), pp. 219-228

[30] H. Lee; R.M. Venable; A.D. MacKerell; R.W. Pastor Biophys. J., 95 (2008), p. 1590

[31] L. Germic; K. Ebert; R.H.B. Bouma; Z. Borneman; M.H.V. Mulder; H. Strathmann J. Membr. Sci., 132 (1997), p. 131

[32] J.I. Calvo; A. Bottino; G. Capannelli; A. Hernández J. Membr. Sci. (2008), p. 531

Commentaires - Politique