1 Introduction
Free radicals are molecular species that contain an unpaired electron. They are well recognised as playing a dual role as both beneficial and deleterious species. Enzyme systems continuously produce free radicals as part of normal cellular function, and at moderate, low levels they are essential for health because of their involvement in various life processes. Body defence mechanisms regulate the balance between the production and the removal of free radicals, which ensures their optimal concentrations. Oxidative stress appears when an imbalance occurs caused either by endogenous overproduction of free radicals (e.g., by infection and inflammation) or by exogenously produced free radicals (e.g., by UV radiation and air pollution). Many free radicals (e.g., hydroxyl •OH and alkyl peroxyl ROO•) are highly reactive and can extract an electron from other molecules, therefore behaving as oxidants. Excess of free radicals may attack cells’ proteins, lipids, and nucleic acids, thus playing a significant role in the aetiology of human diseases, such as cardiovascular and coronary heart diseases, diabetes, neurodegenerative diseases, and some forms of cancer [1,2].
Polyphenols (e.g., phenolic acids, flavonoids, and stilbenes) are ubiquitous phytochemicals in fruit and vegetables and they can act as exogenous antioxidants, protecting human health. Phenolic compounds include thousands of compounds with different chemical structures and they have been extensively studied because of their biological activities and low toxicity [3]. The hydroxybenzoic acids occur mainly in the form of glycosides and are rarely free in edible plants, such as rosaceous fruits (strawberry, blackberry, blackcurrant and raspberry), potatoes, black radishes, grape seeds, onions, wines, and teas. As conjugates, hydroxybenzoics are components of plant complex polyphenolic structures, such as lignins and hydrolysable tannins [4–6].
Like numerous other natural phenolic compounds, hydroxybenzoic acids exhibit antioxidative properties as free radical scavengers and metal ion chelators [7]. The structure of phenolic compounds, especially the number and position of OH groups, seems to play the crucial role in their antioxidant, antiproliferative, cytotoxic and enzyme-inhibition activities [8]. Many of the health-promoting activities of phenolic compounds are ascribed to their antioxidant activities as well as to their ability for modifying cellular signalling pathways. Most ingested flavonoids are extensively degraded to various hydroxybenzoic acids, some of which possess high radical scavenging ability [9,10]. The synthetic antioxidants used in foodstuffs to protect fats against oxidative rancidity are phenols: butylated hydroxyanisole (BHA), butylated hydroxytoluene (BHT), 2-tert-butilhydroquinone (TBHQ), and propyl gallate. Recently, BHA and BHT are suspected to be potentially harmful to human health [11]. Currently, there is considerable interest on natural sources of antioxidants and these generally belong to the phenolic group of compounds.
Quantitative structure–activity relationship (QSAR) modelling is a powerful tool in searching for phenolic structures with high free radical scavenging potency. Numerous attempts have been made to establish the relationship between the structure of hydroxybenzoic acids and their free radical scavenging activity [12–14]. In the development of antiradical QSAR models, many descriptors could be used. Several thousand molecular descriptors accounting for electronic, topological, steric, hydrophobic/polarity and other features of the molecules can be calculated [15]. However, for many of them, it is difficult to ascribe a clear physicochemical meaning and its relation to modelled activity. Searching for molecular descriptors related to mechanisms of free radical scavenging by phenolic compounds is our current effort [16–18].
Antiradical properties of phenolic compounds, here hydroxybenzoic acids and simple phenols, PhOH, are related to their ability to transfer their phenolic H-atom to a free radical, RO•:
| PhOH + RO• → PhO• + ROH |
It has been recognized that this reaction proceeds via at least three different mechanisms: single-step hydrogen atom transfer (HAT), single electron-transfer followed by proton transfer (SET–PT) and sequential proton loss electron-transfer (SPLET) [19,20]. All three mechanisms may take place in parallel, but occur at different rates. The net result of all three mechanisms is the same, that is, the most stable phenoxyl radical PhO• is produced. Because the reactants and products are the same in all three mechanisms, they have equal net thermodynamic balance: ΔHHAT = ΔHSET−PT = ΔHSPLET [21]. The radical scavenging mechanism is influenced by many molecular parameters (that can be calculated at different theoretical levels), such as bond dissociation enthalpy (BDE), ionization potential (IP), proton dissociation enthalpy (PDE), proton affinity (PA), electron-transfer enthalpy (ETE), chemical hardness (HOMO–LUMO gap), spin delocalization, etc. [22–25]. On the other side, the measured activity is influenced by many parameters, like concentration, pH, solvent, temperature, as well as by the nature of a free radical scavenged [26,27]. As a consequence, it is often not possible to correlate experimental results with a single theoretical parameter (descriptor) at the high level of statistical significance.
2 Results and discussion
The data set we used for development of QSAR models, an experimental one containing vitamin C equivalent antioxidant capacity (VCEAC) values of various polyphenolics, was taken from Kim and Lee [12]. From this data pool, we selected 21 phenolic compounds embracing hydroxybenzoic acids, hydroxyphenylacetic acids, phenolic synthetic food additives and simple phenols (Fig. 1, Table 1). VCEAC is defined as the antioxidant capacity equivalent to vitamin C concentration (mg/L). The antioxidant capacity of vitamin C was designated at a value of 100 mg/L. The higher the VCEAC value of the test compound, the more effective the antioxidant. VCEAC value greater than 100 indicates that the corresponding compound is a more effective antioxidant than vitamin C.
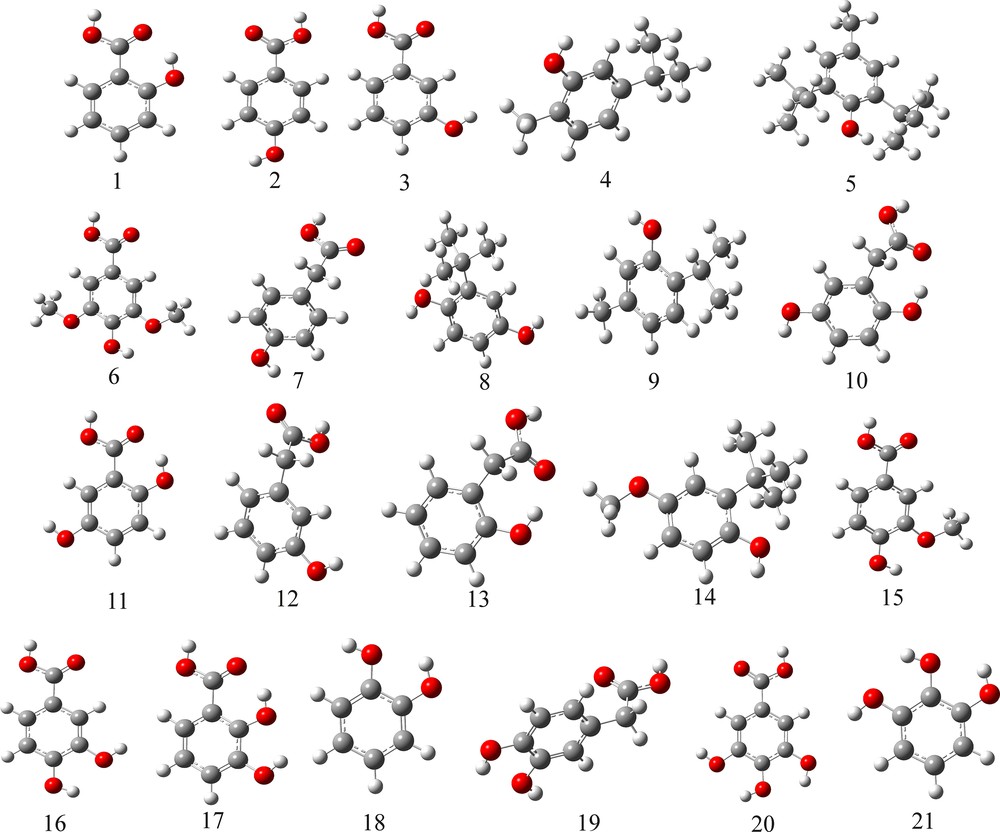
(Color online) Structure of the studied hydroxybenzoic acids and simple phenolics.
DFT SMD reaction enthalpies (kJ/mol) calculated in water for the HAT, SET–PT and SPLET mechanisms for phenolic acids and simple phenolics. Energetics of frontier orbitals, nOH and nOHvic are included. VCEAC (12) and TEAC (13) denote experimental antiradical activity.
| Compound | BDE | IP | PDE | PA | ETE | EHOMO | ELUMO | HOMO–LUMO gap | nOH | nOHvic | VCEAC | TEAC | |
| 1 | Salicylic acid | 400.7 | 550.8 | 31.0 | 148.9 | 432.9 | –785.6 | –74.1 | 711.6 | 1 | 0 | 1.4 | 0.04 |
| 2 | 4-OH benzoic acid | 392.4 | 564.9 | 8.5 | 132.6 | 440.9 | –792.7 | –50.1 | 742.6 | 1 | 0 | 4.8 | 0.08 |
| 3 | 3-OH benzoic acid | 383.2 | 552.1 | 12.2 | 146.5 | 417.8 | –786.5 | –73.6 | 712.8 | 1 | 0 | 53.7 | 0.84 |
| 4 | Carvacrol | 363.1 | 501.7 | 42.5 | 159.0 | 385.2 | –735.0 | 63.8 | 798.8 | 1 | 0 | 58.0 | – |
| 5 | BHT | 333.7 | 482.5 | 32.3 | 165.8 | 349.0 | –709.0 | 69.6 | 778.7 | 1 | 0 | 77.4 | – |
| 6 | Syringic acid | 351.7 | 515.8 | 17.0 | 131.4 | 401.4 | –746.2 | –57.3 | 688.9 | 1 | 0 | 80.4 | 1.36 |
| 7 | 4-OH phenylacetic acid | 371.0 | 523.0 | 29.1 | 153.2 | 398.9 | –754.0 | 34.4 | 788.4 | 1 | 0 | 82.8 | 0.34 |
| 8 | TBHQ | 338.2 | 470.7 | 48.6 | 163.2 | 360.7 | –700.9 | 50.9 | 751.8 | 2 | 0 | 83.9 | – |
| 9 | Thymol | 359.6 | 501.6 | 39.1 | 158.8 | 381.9 | –733.6 | 58.8 | 792.4 | 1 | 0 | 85.3 | – |
| 10 | Homogentisic acid | 340.0 | 482.3 | 38.8 | 151.1 | 370.0 | –722.6 | 21.5 | 744.1 | 2 | 0 | 87.8 | 0.91 |
| 11 | Gentisic acid | 358.5 | 505.2 | 34.4 | 153.1 | 386.4 | –735.9 | –81.1 | 654.7 | 2 | 0 | 90.8 | 1.04 |
| 12 | 3-OH phenylacetic acid | 374.1 | 523.7 | 31.5 | 152.5 | 402.7 | –764.4 | 17.0 | 781.4 | 1 | 0 | 91.6 | 0.90 |
| 13 | 2-OH phenylacetic acid | 364.9 | 521.7 | 24.4 | 86.9 | 459.2 | –768.7 | 31.0 | 799.7 | 1 | 0 | 95.1 | 0.99 |
| 14 | BHA | 337.0 | 466.4 | 51.7 | 164.3 | 353.8 | –697.1 | 52.6 | 749.7 | 1 | 0 | 97.6 | – |
| 15 | Vanillic acid | 371.0 | 526.0 | 26.1 | 132.5 | 419.6 | –755.1 | –53.4 | 701.6 | 1 | 0 | 117.2 | 1.43 |
| 16 | Protocatechuic acid | 361.0 | 532.8 | 9.3 | 119.1 | 425.8 | –763.5 | –54.5 | 709.0 | 2 | 2 | 163.2 | 1.19 |
| 17 | 2,3-diOH benzoic acid | 362.1 | 518.3 | 24.9 | 131.6 | 418.7 | –753.9 | –74.4 | 679.5 | 2 | 2 | 169.6 | 1.46 |
| 18 | Catechol | 346.7 | 503.0 | 24.8 | 139.1 | 388.7 | –736.5 | 60.8 | 797.3 | 2 | 2 | 253.1 | – |
| 19 | Homoprotocatechuic acid | 316.5 | 500.3 | –2.7 | 138.8 | 358.8 | –733.2 | 48.5 | 781.7 | 2 | 2 | 316.7 | 2.19 |
| 20 | Gallic acid | 345.7 | 532.5 | –5.7 | 108.8 | 418.0 | –765.2 | –56.4 | 708.8 | 3 | 3 | 324.3 | 3.01 |
| 21 | Pyrogallol | 332.1 | 503.8 | 9.4 | 129.7 | 383.5 | –740.7 | 84.8 | 825.5 | 3 | 3 | 331.2 | 1.91 |
| VCEAC (r) | –0.641 | –0.170 | –0.578 | –0.393 | –0.184 | 0.147 | 0.229 | 0.206 | 0.809 | 0.915 | 0.903 | ||
| TEAC (r) | –0.761 | –0.403 | –0.615 | –0.417 | –0.337 | 0.426 | 0.153 | –0.005 | 0.744 | 0.776 | 0.903 |
The development of QSAR models is a procedure based on some generally accepted principles related to correct data selection and partition, selection of molecular descriptors, testing of the models’ complexity and robustness, model validation, and model accuracy estimation [28]. To be applicable, the model should be simple and its involved descriptors should possess clear physicochemical interpretation.
As initial descriptors, we selected BDE, IP, PDE, PA and ETE, i.e. descriptors related to the energetics of HAT, SET–PT and SPLET mechanisms of free radical scavenging. The HAT mechanism is characterised by the BDE of the phenolic OH group. A lower BDE value, usually attributed to a greater ability of the hydroxyl group to donate a hydrogen atom, results in an easier free radical scavenging reaction. It has been suggested that BDE is an excellent primary descriptor of the antioxidant activity [29]. The SET–PT mechanism is controlled by the IP of the phenolic molecule and the PDE of the radical cation PhOH•+. The SPLET mechanism is governed by the heterolytic bond dissociation enthalpy of the OH group (the PA of the phenoxide anion PhO−) as well as by the ETE of the phenoxide anion. All those descriptors (BDE, IP, PDE, PA; and ETE) were calculated by DFT method (Table 1) and used in the development of QSAR models. Furthermore, some other descriptors relevant to free radical scavenging have also been computed: the energy of the highest occupied molecular orbital (EHOMO), the energy of the lowest unoccupied molecular orbital (ELUMO), and the HOMO–LUMO gap. The EHOMO characterizes the electron-donating ability, and ELUMO the electron accepting ability of phenolic compounds. Higher EHOMO increases electron donating ability and contributes to effective radical scavenging. A small energy gap between the HOMO and LUMO increases the antiradical activity.
To this pool of descriptors (Table 1), we added the number of phenolic OH groups (nOH) and the number of vicinal phenolic OH groups (nOHvic). The nOH has been widely used in the modelling of phenolic antiradical activity [30]. It is well accepted that the antioxidant activity of phenolics is markedly influenced by the number and position of phenolic OH groups. The increased number of OH groups could be related to the increased ability of H-atom abstraction or electron donating capacity and increased free radical scavenging activity. It should be noted that descriptor nOH has its own limitations, because the assumption of equal contributions of OH groups at different positions to free radical scavenging is questionable. Obviously, an equivalent value of nOH does not necessarily equally contribute to the activity.
Many studies have shown that phenolics with more hydroxyl groups, especially those located ortho to one another (catechol moiety, i.e., vicinal OH groups) are extremely effective antioxidants [3]. Favourable positions of OH groups, like the catechol moiety, is a prerequisite for the stability of phenoxyl radical by hydrogen bonding and odd electron delocalization over the entire molecule. The particular importance of catechol moiety arises from its ability for scavenging two radicals via double radical scavenging mechanisms [18] or scavenging of several free radicals in a cyclic process [31]. Additionally, this moiety enables effective transition metal ion chelation involved in the formation of free radicals [8].
Because the experimental evaluation of the antioxidant capacity of the studied compounds has been performed in water or in water mixtures of polar solvents [12], we performed the DFT calculations of energetics related to antiradical processes also using water as a solvent. While the SPLET mechanism is dominant in a polar environment that promotes the solvation of the intermediate ionic species, the HAT mechanism may occur in a non-polar medium since the charge separation is smaller than in SPLET [32]. The SET–PT mechanism is less feasible because of the first step of this reaction, since the formation of the radical cation is extremely slow [33]. Regardless of the reaction medium, superior correlations between the antiradical activities of polyphenols with O–H BDE were usually found [16].
The best one-descriptor model was obtained by using nOHvic as a molecular descriptor, Eq. (1):
| VCEAC = 73.0 (± 10.4) + 80.86 (± 8.20) nOHvic | (1) |
In the above and in subsequent equations, N represents the number of compounds, r is the correlation coefficient, s the standard error of estimate, and F is Fisher's F-value. Regression coefficients and the corresponding errors of regression coefficients were computed using the least-squares fit procedure. A reliable QSAR model should have high r and F, low s, and the least variables. The stability and validity of the model has been tested by the leave-one-out cross-validation (LOO CV) technique. The LOO CV correlation coefficient (rcv) and standard error of fit (scv) are included.
The best two-descriptor model was obtained by using BDE and nOHvic as molecular descriptors, Eq. (2):
| VCEAC = 601.6 (± 127.8) – 1.46 (± 0.35) BDE + 69.26 (± 6.64) nOHvic | (2) |
The best three-descriptor model was obtained by using PA, ETE and nOHvic as molecular descriptors, Eq. (3):
| VCEAC = 1059 (± 245) – 2.09 (± 0.68) PA – 1.71 (± 0.39) ETE + 65.32 (± 7.80) nOHvic | (3) |
N = 21, r = 0.962, rcv = 0.945, s = 29.1, scv = 35.8, F = 70.3
In Fig. 2, we give the plot of experimental VCEAC values versus VCEAC values calculated using Eq. (3).
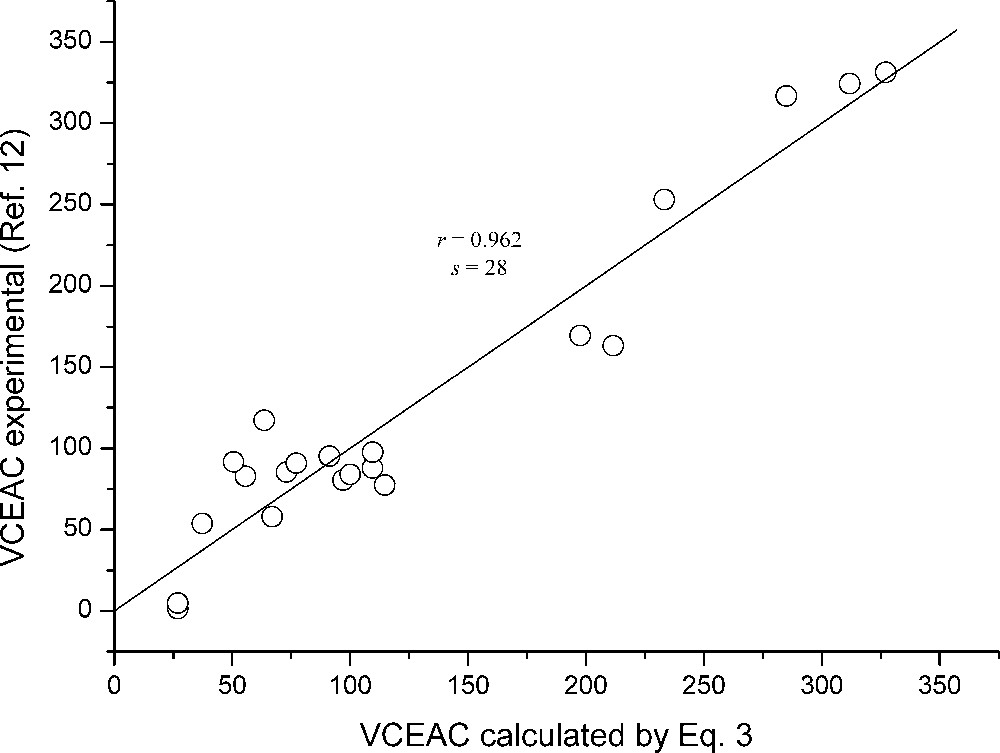
Scatter plot of experimental VCEAC values obtained by ABTS radical versus VCEAC values calculated by Eq. (3).
The descriptors used in the construction of the QSAR models 1–3 (nOHvic, BDE, PA and ETE) possess a clear physicochemical meaning and reflect some driving forces related to antiradical activity. Among reaction enthalpies related to different free radical scavenging mechanisms, the BDE mostly accounts for the observed VCEAC (see r values in the last two rows of Table 1). This is so because the total energy requirements related to the SET–PT [IP + PDE] and the SPLET [PA + ETE] are perfectly correlated with the BDE [16]. This reveals why the BDE descriptor explains most of the variance in measured VCEAC data, even in the case when the underlying mechanism is not HAT. It also explains why statistical characteristics of the two-descriptor model (2) and three-descriptor model (3) are very similar. Because these descriptors are not independent [16,25], to assume which free radical scavenging mechanism will be mostly operative, additional factors, such as the polarity and the acidity of the reaction medium should be taken into consideration [34]. Model (2) is related to the HAT mechanism and model (3) describes the SPLET mechanism. Obviously, in water, the feasible mechanism could be SPLET, not HAT. Experimental VCEAC values [12] were determined in phosphate buffered saline solution at pH 7.4, which indicates that the SPLET mechanism could be the preferred one. Because of the negative sign of the regression coefficients for PA and ETE in model (3), a decrease in the PA and ETE values results in an increase of VCEAC. As expected, the presence of vicinal phenolic OH groups highly increases VCEAC.
To verify the obtained QSAR models, we used another data set (Table 1, the last column), i.e., experimental results obtained by the ABTS free radical (as in the case of VCEAC assay), but expressed as TEAC (Trolox equivalent antioxidant capacity). TEAC is defined as the concentration of Trolox solution with equivalent antioxidant potential to a 1 mM concentration of the compound under investigation. Using identical compounds from two data sets with corresponding antiradical activities determined by the same method but in different laboratories can serve not only to validate QSAR models, but also for the validation of the experimental techniques used for the measurement of activities for a series of molecules [27]. The data set we used for this kind of model validation was taken from Rice-Evans et al. [13]. As can be seen from the last two columns of Table 1, free radical scavenging activity rankings in few cases differ significantly. This illustrates the fact that small changes in methodology can cause large differences in the obtained results [26]. Consequently, a not particularly high correlation (r = 0.903) exists between experimental VCEAC and TEAC data sets containing 15 identical compounds. For both data sets, correlation coefficients presented in the last two rows of Table 1 indicate nOH, nOHvic and BDE as descriptors with high predictive potency. The corresponding models using TEAC data to models (1–3) possess slightly less significant statistical characteristics (data not shown).
In order to obtain better information about the significance of the obtained models (1–3), using the Dragon 5.4 program [15], more than 1400 descriptors were calculated for the same data pool of 21 compounds, starting from their 3D structures. The number of descriptors was reduced to 1114 by removing highly inter-correlated descriptors, and by excluding constant or almost constant descriptors. From this set of descriptors, we selected the best models containing one, two and three-descriptors, using the computer program developed for efficient variable selection [35]. These models obtained for VCEAC are given in equations (4–6):
| VCEAC = –51.1 (± 32.4) + 116.9 (± 19.5) nArOH | (4) |
Here, nArOH is the number of aromatic hydroxyls.
| VCEAC = 22.4 (± 28.1) + 111.6 (± 13.8) nArOH + 344.9 (± 76.6) MATS3m | (5) |
N = 21, r = 0.915, rcv = 0.890, s = 41.7, scv = 48.7, F = 46.4
MATS3m is the Moran autocorrelation-lag 3 weighted by atomic masses (MATS3 m) belonging to the 2D autocorrelation class of descriptors (calculated from the molecular graph by summing the products of masses of the terminal atoms of all the paths of path length 3) [36].
| VCEAC = 154.8 (± 13.6) + 90.5 (± 8.8) Hy + 526.0 (± 57.4) MATS3m + 309.0 (± 71.9) Mor22m | (6) |
Hy is a molecular descriptor named hydrophilic factor. In the calculation of this descriptor, the number of hydrophilic groups (–OH, –SH, –NH), the number of carbon atoms, and the number of all atoms (hydrogen excluded) are taken into account. The lowest value of the Hy index is –1 for alkanes, with an infinite number of carbon atoms [36].
Mor22m is the molecular descriptor from the class of 3D-MoRSE descriptors (3D-MOlecule Representation of Structures based on Electron diffraction, or simply MoRSE descriptors). These molecular descriptors are calculated by summing up the atom weights viewed by a different angular scattering function within different ranges (for example, signal 22 corresponds to a summation within the distance of 2.2 Å from the atom centre) [36].
Dragon's descriptor nArOH matches the number of phenolic OH groups, nOH. An increased number of hydrophilic phenolic OH groups increases the Hy value and this descriptor has been used in the modelling of the antiradical activity of coumarins [37]. When compared with descriptor nArOH or enthalpy parameters from Table 1, it is evident that descriptors MATS3m and Mor22m are more complex for calculations and also more difficult for the physicochemical interpretation of models. They do not possess unequivocal physicochemical meaning related to free radical scavenging mechanisms. The inferior statistical characteristics of models (4–6) and the lack of clear physicochemical meaning of molecular descriptors MATS3m and Mor22m indicate that models (1–3) are superior to models (4–6).
The lack of standardized antioxidant assays and consequently of reliable experimental datasets [27,38] makes the successful use of the QSAR procedure doubtful. However, by taking into account some driving forces of the radical scavenging processes and related descriptors with clear physicochemical meaning, it is possible to generate fair antiradical QSAR models.
3 Conclusion
The quantitative structure–activity relationship (QSAR) of the free radical scavenging potency of 21 selected hydroxybenzoic acids and simple phenolics were examined. We found that the descriptors related to the energetics and structural aspects of free radical scavenging processes enable the development of reliable QSAR models that possess better statistical characteristics than the best models developed using more than thousand molecular descriptors from the large Dragon set. The lack of standardized antioxidant assays makes the successful use of the QSAR procedure doubtful. However, we showed that by taking into account some driving forces of the free radical scavenging and associated descriptors (BDE, PA, ETE and nOHvic), it is possible to generate fair antiradical QSAR models. It may help in searching for phenolic structure with increased antiradical potency.
4 Computational details
4.1 DFT calculations
Density functional theory (DFT) represents a powerful tool for studying the free radical scavenging mechanisms of polyphenolic compounds [23,39]. Geometry optimizations of all studied compounds and their corresponding radicals, radical cations, and anions have been carried out using the M05-2X functional [40] in conjunction with the 6-311++G(d,p) basis set as implemented in the Gaussian 09 package [41]. The M05-2X functional has been recommended for kinetic calculations and for calculating reaction energies involving free radicals [42]. It has been successfully used by independent authors for these purposes [31,43–46]. The influence of water as a solvent was approximated by the SMD solvation model, the continuum solvation model based on the quantum mechanical charge density of a solute molecule interacting with a continuum description of the solvent [47]. Unrestricted calculations were used for open-shell systems. The optimized structures were confirmed to be real minima by frequency analysis (no imaginary frequency). Relative enthalpies were calculated at 298 K.
The O–H BDE is calculated using the following equation: BDE = H(PhO•) + H(H)–H(PhOH), where H(PhO•) is the enthalpy of the phenoxyl radical generated after H-atom abstraction, H(H) is the enthalpy of the hydrogen atom, and H(PhOH) is the enthalpy of the phenolic compound (hydroxybenzoic acid or simple phenol). The IP is calculated as follows: IP = H(PhOH•+) + H(e−)–H(PhOH), where H(PhOH•+) is the enthalpy of the radical cation generated after electron abstraction and H(e−) is the enthalpy of the electron. The PDE is calculated by the equation: PDE = H(PhO•) + H(H+)–H(PhOH•+), where H(H+) is the enthalpy of the proton. PA is defined by the equation: PA = H(PhO−) + H(H+)–H(PhOH), where H(PhO−) is the enthalpy of the phenoxide anion generated after proton abstraction. ETE is calculated by the equation: ETE = H(PhO•) + H(e−)–H(PhO−) [22]. The solvation enthalpies of the proton (H+) and electron (e−) were taken from the literature [48].
4.2 CROMRsel calculations
The CROMRsel procedure [35] is a multivariate procedure that has been designed to select the best possible model among the set of models obtained for a given number of descriptors, the criterion being the standard error of estimate. By using the CROMRsel procedure, we considered all possible models that can be generated with the descriptors presented in Table 1. The number of compounds (N = 21) indicates that up to three-descriptor models are reliable.
4.3 DRAGON calculations
A large set of molecular descriptors was calculated by the Dragon 5.4 program [15]. All 20 classes of descriptors included in the Dragon 5.4 program (containing more than 1500 descriptors), from the constitutional class to the molecular property class, were computed. The meaning of these molecular descriptors and the calculation procedures are summarized elsewhere [36]. About 400 descriptors were omitted because of constant or almost constant values, and statistical analysis (calculation of correlation coefficients and analysis of their distribution) was performed on the remaining 1114 molecular descriptors.
Acknowledgements
The Ministry of Science of the Republic of Serbia (Projects No. 172015 and 174028), and the Ministry of Science, Education and Sports of the Republic of Croatia are gratefully acknowledged for financial support. We also gratefully acknowledge the anonymous reviewers for their constructive comments.


