1 Introduction
Light-responsive molecular switches, machines that can be controlled by light, usually exist in two stable forms that can be isomerized when irradiated with light. This property makes them interesting because no direct contact is needed, but the remote control is possible. Various classes of molecules have been investigated for this purpose [1–5]. Aroyl hydrazones present a promising group of molecules that can be used for photoswitchable devices [6–10]. N′-[1-(2-Hydroxyphenyl)ethyliden]isonicotinoyl hydrazone (HAPI) is taken as a representative of this class and its photoswitching behavior was investigated with the addition of different cations [11,12], although its biological activity and complexation of iron were known from before [13–17]. The enolimine form was taken to be the dominant one in the previous contributions [12].
When it is assumed that the investigated system is affected by the solvent (analysis of vibrations, electronic transitions, reaction mechanisms), three possible approaches can be used [18]: the continuum model, the discrete model, and the semicontinuum model. When the bulk effect of the solvent is treated, then the continuum model, a low-cost method, is the first choice. In this method, a cavity of solvent molecules is formed, described by the macroscopic dielectric constant [19]. The main disadvantage of this approach is that specific interactions between the solvent and solute are not included (e.g., hydrogen bonds) [20]. One of the most common continuum models is the polarizable continuum model (PCM) [21,22]. Discrete (explicit solvent) model is formed when solvent molecules are positioned around the molecule of interest. This way the short-range interactions are described properly. Because the computational cost rises with size, the bulk effect cannot be studied this way. The third model includes both of the aforementioned models.
Implementation of the explicit solvent effect by the introduction of one or more solvent molecules has been used in various research fields [23–25]. The optical properties of molecules, dyes, for example, were better reproduced when explicit solvent molecules were added and treated by molecular dynamics simulations [26]. Besley and Hirst [18] commented that if a molecule of formamide is surrounded with 13 molecules of the solvent and placed in a continuum model, then important local and bulk effects are encountered in the calculation. The investigated solvent effect on two lowest-lying singlet excited states of 5-fluorouracil proved that density functional theory (DFT) methods give good results for energy transitions, but the energy shifts were not described appropriately [27]. Various contributions showed that addition of one water molecule to anion improves the values of calculated dissociation constants of organic acids [23,28]. Addition of solvent molecules influences the possible mechanism of chemical reactions, as proven for the antioxidant activity [29–31]. For the description of the various properties of molecular switches in solution DFT along with PCMs is used [32–36].
In this contribution, we present results of the implementation of the explicit solvent model (by the introduction of one and five molecules of water) and its effect on the electronic spectra of a potential molecular switch ((E)-HAPI). The optimized structures were analyzed by DFT, with special emphasis on specific solvent–solute interactions investigated additionally with natural bond orbital (NBO) analysis and quantum theory of atoms in molecules (QTAIM). The novelty of this approach includes the discussion of the right positioning of the solvent molecule with respect to the groups responsible for the electronic transitions.
2 Theoretical methods
The Gaussian program package [37] was used for all of the calculations discussed throughout the article. The geometries of deprotonated HAPI were fist optimized at different levels of theory to find the functional that gives the excitation energies close to the experimental ones. The functionals used were B3LYP [38], CAM-B3LYP [39], PBE1PBE [40], and M06-2X [41] all with Dunning's triple zeta, cc-pVTZ [42], and double zeta, cc-pVDZ, basis sets. Stationary points were verified by the absence of imaginary frequencies. PCM was used for the preliminary explanation of the solvent effect [43]. The electronic spectrum was calculated by the time-dependent DFT (TDDFT) approach [44,45]. The explicit solvent effect was encountered first by the addition of five water molecules to the sites that were assumed to have the highest possibility of influencing the electronic spectrum. These spectra were compared with the experimental spectrum obtained by Franks et al. [12]. The NBO [46] analysis was carried out for all of the structures with one and five solvent molecules. QTAIM [47–49] was used for the analysis of specific interactions of water molecules with protonated and deprotonated forms of HAPI, as well as for hydrogen bonds formed within each of the molecules. QTAIM analysis was done in the AIMAII [50] package.
3 Results and discussion
The first part of the article investigates the effect of basis set and functional on the theoretical electronic spectra of HAPI. The experimental UV–vis spectrum of HAPI at pH 7.4 by Franks et al. [12] is taken as the reference for the comparison. This spectrum has three characteristic peaks at 288, 325, and 400 nm, solely attributed to E-isomer. When this solution is irradiated with UVA light (400–315 nm), the metastable specie is formed, and it was concluded that this reflects E/Z isomerization, with a notable change in the spectrum—the shift of 13 nm in transition at 288 nm and attenuation of two other peaks. Both of isomers are assumed to be fully deprotonated at the experimental pH.
The selected functionals (B3LYP, CAM-B3LYP, PB1PBE, and M06-2X with the same basis set cc-pVDZ) were used to find the most stable conformer of both deprotonated E and Z isomers. No major differences in the structures optimized with different functionals were observed, and only structures obtained with CAM-B3LYP/cc-pVDZ are shown in Fig. 1. The more stable isomer is deZ, but the energy difference is dependent on the chosen functional. Table S1 gives the difference in enthalpy and Gibbs free energy between these two compounds. The most prominent difference between deprotonated E and Z is the value of dihedral angle N2-N1-C-C(O), which has value of 178.7° and 2.5°, respectively. This proves that deE-isomer is almost planar.
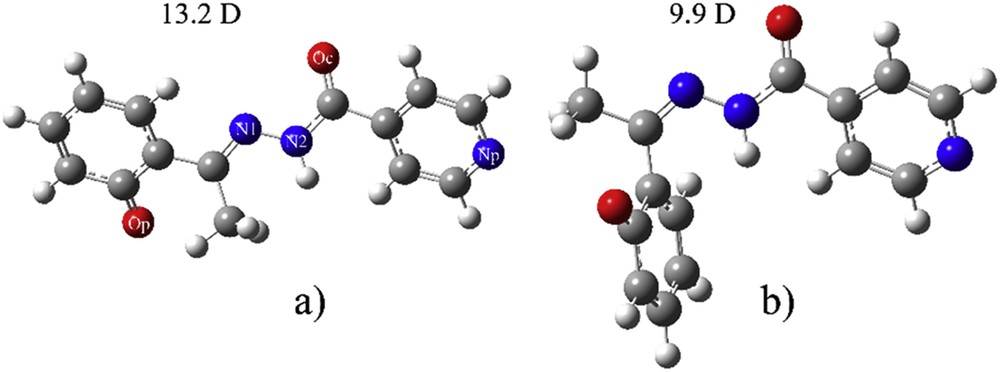
The optimized structure at CAM-B3LYP/cc-pVDZ of (a) deE-isomer and (b) deZ-isomer.
The electronic spectra of two isomers are predicted for structures optimized with the polarizable continuum solvent model, as these can be compared with the experimental spectrum to determine the appropriate functional/basis set combination. The graphical representation of experimental and theoretical spectra is given in Fig. 2. The theoretical spectra are obtained from the excitation energies and for the further discussion, only their position is important because the bandwidth can be changed due to different internal and external factors.
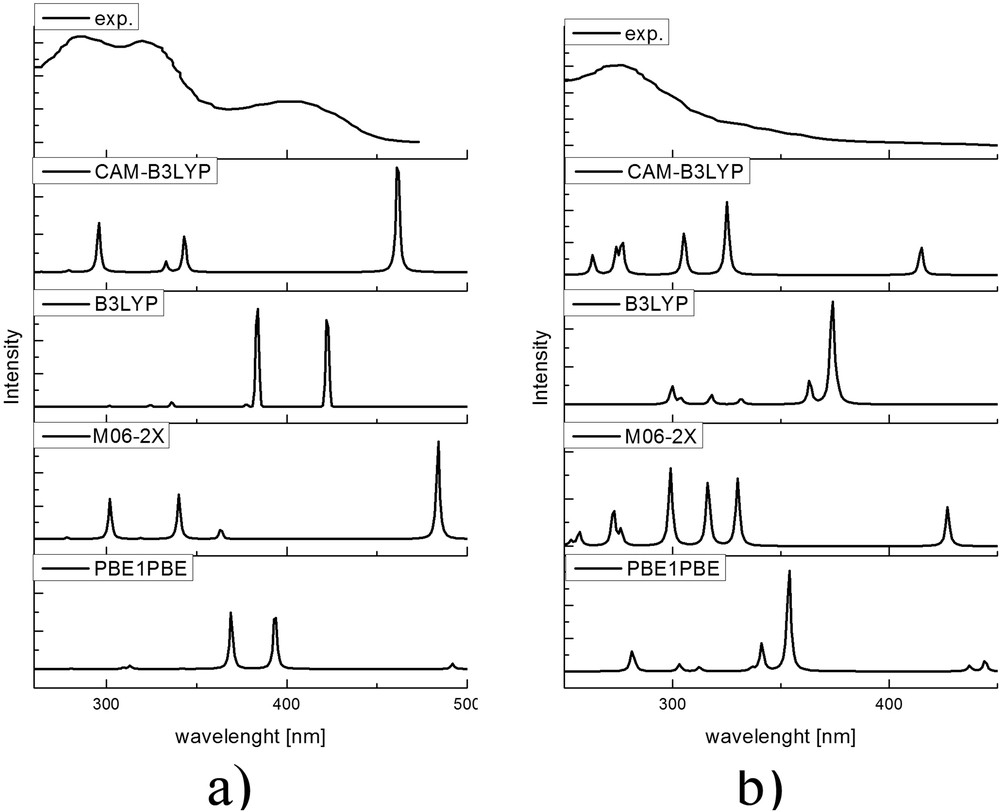
Digitalized spectra of HAPI at pH = 7.4 (from Fig. 2 of Franks et al. [12]) before and after the irradiation and theoretical spectra of (a) deE and (b) deZ isomers.
Within the investigated set of functionals, there were notable differences in theoretical spectra. In the case of deprotonated E-isomer in the range of experimentally available wavelengths, there were three major peaks predicted by CAM-B3LYP and M06-2X, with two peaks positioned close to the experimental values. The peak with the longest wavelength is poorly reproduced by both functionals, with the difference of ≈50 nm for CAM-B3LYP and ≈100 nm for M06-2X. The other two functionals predicted only two peaks in the range of interest that can be attributed to the first two transitions but even then the difference is very large. The relative intensities differ from experimental, as seen for the transition at the longest wavelength for spectra with CAM-B3LYP and M06-2X. The experimental spectrum of deprotonated Z-isomer shows one wide peak at 275 nm, which could contain the transitions predicted by CAM-B3LYP and M06-2X. The experimental spectrum probably presents the mixture of protonated and deprotonated form as well to some extent. But it should be noted that there is a better agreement between experimental and theoretical spectra for deZ. It was concluded that, based on the preliminary research, CAM-B3LYP gives the best reproduction of experimental values. The effect of the basis set was investigated with the following sets: cc-pVDZ and cc-pVTZ to encounter for the change in values when the basis set increases, as shown in Table S2. The transitions with cc-pVTZ are closer to the experimental values for 3–4 nm. The notable change is in the transition at 440 nm where the difference is around 10 nm but still very far from the experimental value. This result is in accord with literature data, which suggest hybrid functionals with cc-pVTZ basis set for calculation of electric properties [51]. The electronic transitions include the following orbitals: HOMO − 2, HOMO, LUMO, LUMO + 1, LUMO + 2. More of the effect of atomic groups is discussed in the following section.
3.1 Optimization of other relevant structures and NBO analysis
To understand the solvent effect on the process of isomerization, the geometries of both protonated E and Z isomers were optimized at CAM-B3LYP/cc-pVTZ with PCM solvent used (Fig. 3) as well.
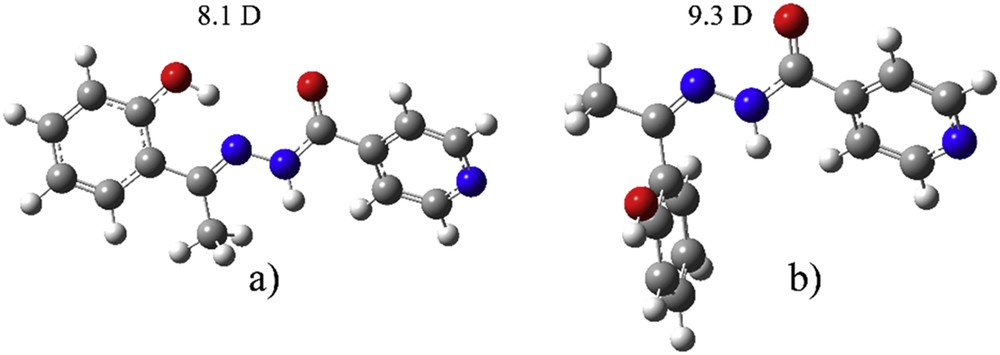
Optimized geometries of (a) E-isomer and (b) Z-isomer.
When E-isomer is deprotonated, there is a change in the position of oxygen atom on the phenolate ring. The dihedral angle N1-C-C-C(O) changes from 6.4° to 160.9°. The rotation goes in the direction of the formation of weak hydrogen bonds with a methyl group. In E-isomer the distance between O-H and N is 1.72 Å, which allows formation of a strong hydrogen bond. This type of change was not observed in the case of Z-isomer. The most stable species is protonated E-isomer that is 26.8 kJ/mol more stable than protonated Z-isomer. When deprotonation occurs in solution at experimental pH, the deE is less stable than deZ for 3.8 kJ/mol. As expected, deprotonated structures were more stabilized due to charge distribution over the structure and positions of electronegative groups. Dipole moments are reported in Figs. 1 and 2, to predict the strength of interactions with water molecules. This is given for the predictive purpose, although dipole moments are not gauge-invariant. From the data for dipole moments, it can be concluded that the polar solvent effect is strongest in the case of deprotonated E-isomer, whereas it is the weakest for protonated E-isomer, and will, therefore, affect the electronic spectrum. This change in dipole moment is attributed to the rotation of the phenolate ring and partial stabilization due to the weak hydrogen bond between phenolate O and a methyl group.
In the structure of both isomers of HAPI there are several possible places for the hydrogen bond formation with the solvent molecules—carboxylate O (Oc), phenolate O (Op), pyridine group nitrogen (Np), and two nitrogen atoms in the immino group—but these effects cannot be explored with a given solvent model that does not take into the account the specific solvent–solute interactions. To approach this more quantitatively, the NBO charges on the atoms of interest are given in Table 1.
Electronic charges on potential atoms for hydrogen bond formation with PCM and with five molecules of water added.
| Atom | Water | Explicit solvent—5 molecules of water | ||||||
| E-isomer | Z-isomer | dE-isomer | dZ-isomer | E-isomer | Z-isomer | deE-isomer | deZ-isomer | |
| Ophen | −0.704 | −0.685 | −0.833 | −0.835 | −0.720 | −0.717 | −0.786 | −0.850 |
| N1 | −0.329 | −0.274 | −0.327 | −0.315 | −0.314 | −0.261 | −0.385 | −0.301 |
| N2 | −0.421 | −0.433 | −0.429 | −0.432 | −0.430 | −0.463 | −0.416 | −0.485 |
| Ocarb | −0.635 | −0.640 | −0.656 | −0.659 | −0.625 | −0.656 | −0.666 | −0.633 |
| Npyr | −0.444 | −0.446 | −0.450 | −0.450 | −0.461 | −0.458 | −0.480 | −0.483 |
Data presented in Table 1 show that the most significant difference between E and Z is the charge on Op and N1 (as given in the numbering scheme in Fig. 1). In E-isomer there is a hydrogen bond formed between these two atoms, which makes them more electronegative. In Z-isomer these two atoms are further from each other, and this is well reflected in the value of dipole moment due to the separation of charges. When deprotonation occurs there is an increase in negative charge on Op and, in the case of Z, increase in charge on N1. The other atoms are not influenced by the loss of a proton. The change in charge on two mentioned atoms leads to the increase of dipole moment, with the fact that this effect is more prominent on E-isomer due to the planarity of the molecule. This result suggests the possible groups for the specific solvent–solute interactions.
To gain better insight into the reasons for the discrepancy in spectra, the molecular orbitals included in transitions of deE and deZ are visualized in Figs. 4 and S3.

Molecular orbitals included in the electronic transition of deE-isomer (isovalue 0.05): (a) HOMO − 2, (b) HOMO − 1, (c) HOMO, (d) LUMO, (e) LUMO + 1, and (f) LUMO + 2.
The molecular orbitals are localized on the phenolate group in HOMO − 2, HOMO, and LUMO + 2 of deE isomer. For LUMO and LUMO + 1, orbitals are localized on isonicotine moiety. The most distinct orbital is HOMO − 1 localized mostly on phenolate oxygen. In case of deZ isomer, the spatial distribution is similar, with smaller delocalization due to the broken planarity of the molecule. On the basis of the visualization of orbitals included in transitions, it was concluded that solvent molecules should be placed close to phenolate oxygen (localized electron density in HOMO − 1 and HOMO), carbonyl oxygen (HOMO − 1, HOMO, and LUMO + 2), immino group (HOMO − 2 and LUMO + 1), and pyridine nitrogen (LUMO, LUMO + 1, and LUMO + 2). It is interesting to notice that the first transition is charge transfer from HOMO to LUMO [52], as this is the transition with the highest discrepancy between experimental and theoretical values.
3.2 Structures with five molecules of water and electronic spectra of deE-isomer
To investigate the explicit solvent effects on the theoretical electronic spectra, five molecules of water were added based on the previous conclusions. The optimizations were done without any geometrical constraints, just by placing five molecules of water next to the mentioned groups. The absence of imaginary frequencies was a proof of the energy minimum for the final structures. The optimized structures are shown in Fig. 5.
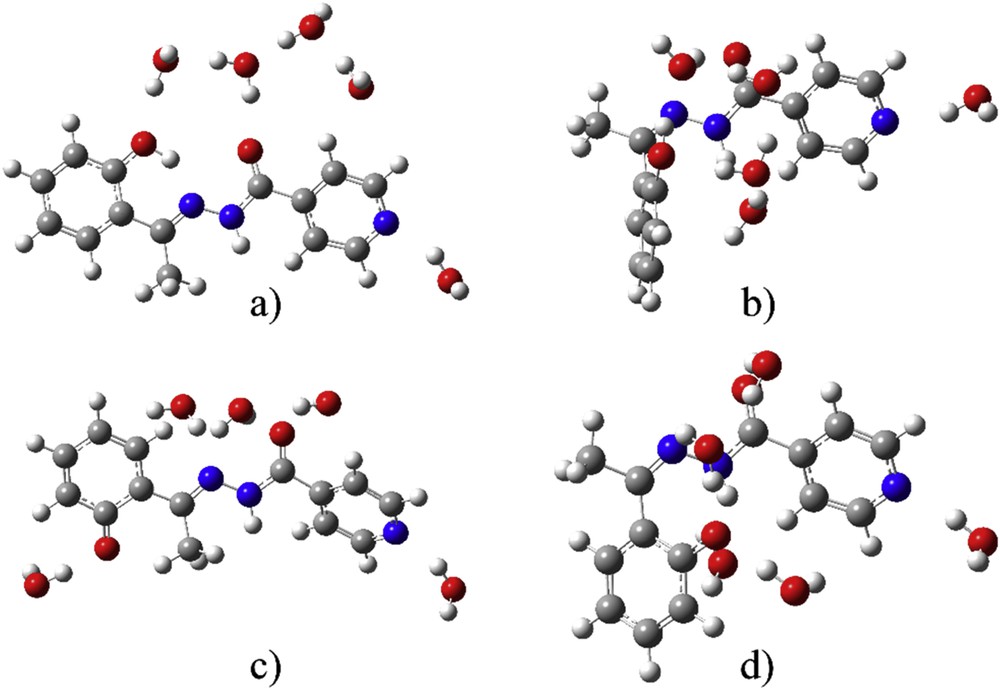
Optimized geometries with five molecules of water of (a) protonated E-isomer, (b) protonated Z-isomer, (c) deprotonated E-isomer, and (d) deprotonated Z-isomer.
The relative stability of these structures was calculated by the following formula:
| (1) |
Change in enthalpy due to the formation of hydrogen bonds.
| Molecule | Enthalpy (kJ/mol) |
| E-isomer | −124 |
| Z-isomer | −162 |
| deE-isomer | −166 |
| deZ-isomer | −202 |
As it can be seen in Table 2, structures with five molecules of water are more stable than separate structures of solvent and solutes, which proves that the effects of specific interactions are not negligible (reaction enthalpy). The relative position of electronegative atoms is the reason for the water molecules to spread across the structures of investigated molecules. The strongest interactions are with deZ-isomer, because of the geometry, which allows the formation of multiple bonds. As it can be seen in Fig. 5 the OH group of the first part of the molecule is still directed toward nitrogen atom, therefore strong interactions with water molecules are not possible, which leads to the lowest change in enthalpy. The other two structures have a similar value of the thermodynamic parameters. The better insight in the strength of hydrogen bonds is obtained when QTAIM analysis is applied in Section 3.4.
From Table 1, the electronic charges on atoms are heavily influenced by the presence of the solvent molecule. This change is dependent on the position of atom and protonation/deprotonation. When these charges are compared with charges of atoms in a PCM solvent, it is obvious that charge on phenolate oxygen in protonated species and deprotonated Z-isomer increases, whereas it lowers on carbonyl oxygen and pyridine nitrogen because of hydrogen bonds of different strength (QTAIM). On the contrary, the charge on Op in deprotonated E-isomer is lowered with the same effect on the other two atoms. This can be explained by observing the optimized structures with five molecules of water—only in the case of deE-isomer, there is an isolated water molecule next to the phenolate oxygen. In other cases, water molecules are surrounded by other water molecules, thus decreasing the interaction energy with this atom. Electronic spectrum of deE was used again as models for comparison with experimental spectra (Fig. 6). The wavelengths, orbitals included in transitions and oscillatory strengths of the most intense transitions are given in Table S4.
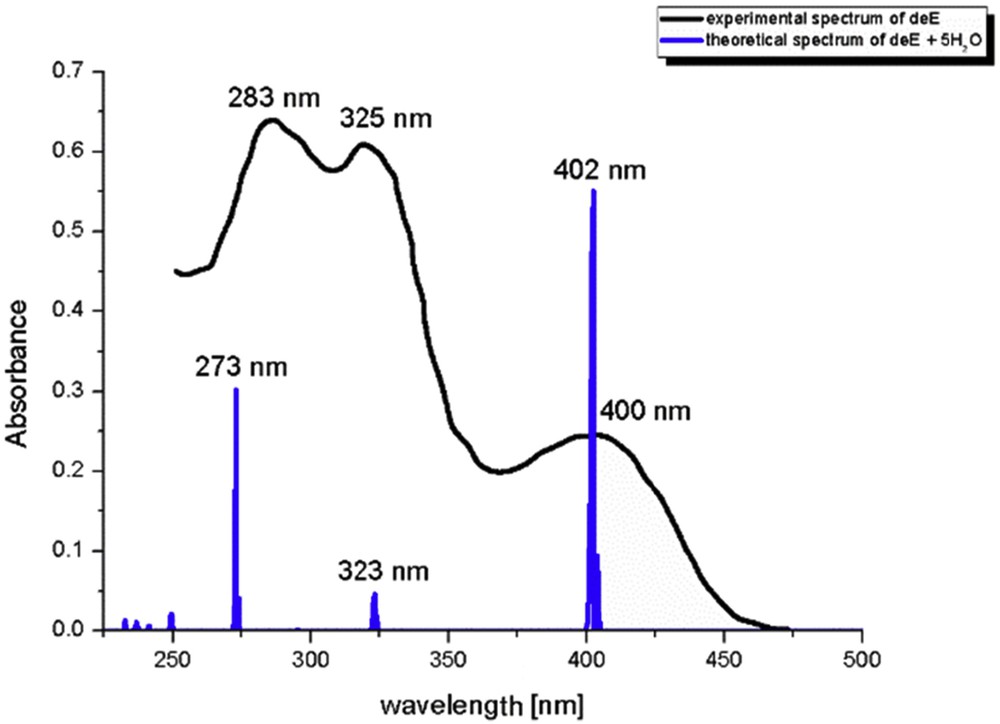
The experimental and theoretical spectrum of HAPI as a mixture of the protonated and deprotonated form.
When wavelengths of the calculated transitions were compared (Table S4) to the experimental value, it was concluded that the inclusion of five molecules of water notably improves the calculated spectra. The HOMO → LUMO transition for deE-isomer has a hypochromic shift of 50 nm, proving that solvent effect stabilizes HOMO orbital. The other two transitions are reproduced with the difference of 2 and 10 nm. The experimental peak at 283 nm is very wide, so it could be possibly attributed to several transitions within protonated and deprotonated species, therefore the difference is negligible. Also, long-range interactions with molecules of water play an important role here, because it can be seen in optimized structures that some of the water molecules are surrounded by other solvent molecules, which decreases the strength of interaction with HAPI.
The spectrum of Z is characterized by a wide peak in the experimentally available range. Both of the predicted transitions are very close to the experimentally determined wavelength of maximum absorption. HOMO → LUMO transition is not observed as well, because of relative positions of two parts of molecules and low overlap of orbitals. The spectrum of deZ is also well reproduced, with HOMO → LUMO transition now having the increased value of relative oscillatory strength as compared with the case when no water molecules were introduced. This is explained when the two structures of deprotonated Z-isomer were compared with and without solvent molecules (Figs. 1 and 5). In a structure without solvent molecules the phenolate ring is pointing in the opposite direction with respect to the pyridine ring, whereas when a molecule of solvent is added, this group points toward the pyridine ring and makes the distance between these two groups lower and probably allows better overlap between HOMO and LUMO. The highest discrepancy between experimental and theoretical energies is observed for protonated E. The first transition has offset of 30 nm, whereas for the other two the difference is 3 and 2 nm. Here it should be noted that probably the results would be better if several starting structures with five molecules of water were investigated, because in case of E-isomer most of the molecules are grouped together, thus limiting their interaction with HAPI.
3.3 Structures with one molecule of water and electronic spectra
After the optimization of structures with five molecules of water, the question was whether one molecule of the solvent is enough for the good reproduction of the experimental spectrum. With this in mind, the optimization process was carried out for deprotonated E-isomer as a representative example with distinctive transitions. Five structures with one molecule of water were prepared to investigate the specific sites for interaction. The starting structures were made by removing four molecules of water from the optimized structure of deE with five solvent molecules, and after the optimization, there were in total four different structures with one water molecule, as shown in Fig. 7.
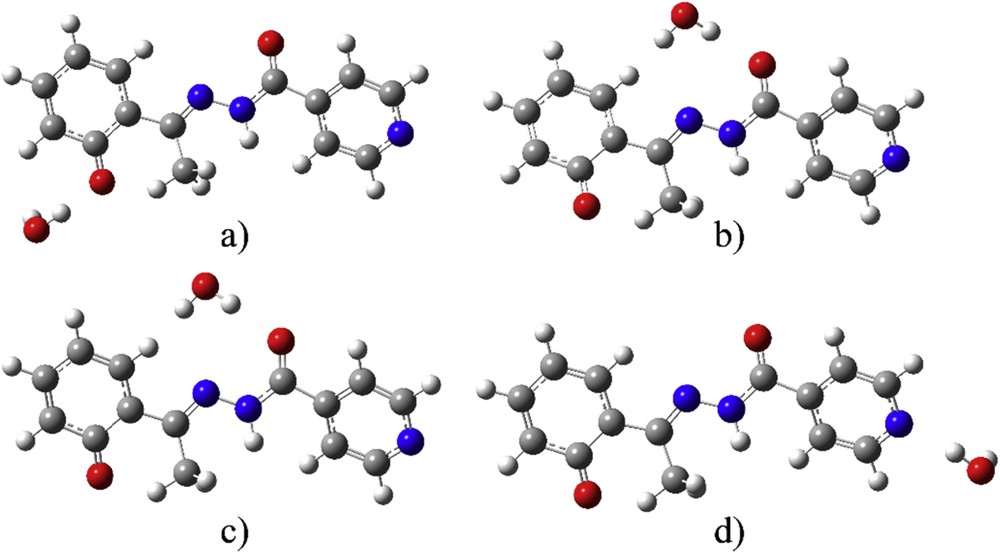
Optimized structures with one molecule of water at positions (a) 1, (b) 2, (c) 3, and (d) 4.
Structure 1 shows a water molecule close to the Op. Structures 2 and 3 differ in the relative position of a water molecule—in structure 2 the water molecule is above the plane of the molecule, and in structure 3 it is below it. In structure 4 water molecule is close to the pyridine group. The relative stability of these structures differs depending on the position of a water molecule. The values for the difference in enthalpy between the optimized structure and separate structures of the solvent molecule are given in Table S5. These values are again corrected for zero point energies. From these values it can be concluded that the most stable structure is structure 1 (change in enthalpy −52 kJ/mol), then almost the same stability for structures 2 and 3 is calculated (−37 kJ/mol). The lowest stability, with the value of (−24 kJ/mol) is predicted for structure 4. From the calculation, it was proved that all of these water molecules influence the stability of HAPI structure in water, but the specific place determines the change in energy of transition, because of different orbital localization in the molecule. The proximity of the water molecule changes the charge on specific atoms.
Table S6 shows NBO charges on atoms of interest. There is a change in charges throughout molecule even if one molecule of water is present (Tables S6 and 1). The change is most pronounced for atoms closest to a water molecule (as in the case of Op in structure 1). As water molecule moves away from a specific atom, the charge becomes more similar to that of the isolated molecule. Dipole moments for structures 1–4 are 10.4841, 10.0289, 10.0910, 9.6972 D, respectively, whereas this value is 9.5729 for isolated deE-isomer. This proves that separation of charges influences the dipole moment, and relative position of the solvent is important for a realistic representation of experimental conditions. The change in dipole moment is well correlated with the increase in positive charge on the rest of the phenolate group due to the formation of a hydrogen bond between oxygen atoms and a water molecule. Also, the negative charge on nitrogen increases with the decrease in distance from the water molecule. On the basis of this discussion it is obvious that the electronic spectrum of deprotonated E-isomer is influenced by the presence of solvent molecules.
The predicted spectra for structures with one molecule of water are given in Fig. S7. As water molecules are further from Op and therefore localized orbitals on this atom, the peak is moving toward the higher wavelengths. This proves that the HOMO is additionally stabilized by the presence of solvent molecules and higher energy is required for the HOMO → LUMO transition. It is interesting that as solvent molecule moves away from Op, there is a new peak appearing at 320 nm (corresponding to HOMO → LUMO + 2), which in structures 2 and 3 moves to 343 nm and finally to 352 nm for the last structure. There is a peak appearing for structure 4 at 343 nm corresponding to HOMO → LUMO + 1. From this analysis, it is clear that one molecule of water positioned at right position can lower the discrepancy between experimental and theoretical spectra for over 40 nm.
3.4 QTAIM analysis of the explicit solvent effect – the role of hydrogen bonds
QTAIM was used in this article to discuss the strength and other properties of chemical bonds through topological parameters: electron density and Laplacian. On the basis of the analysis in bond critical point (BCP), interactions can be divided into two groups. If electron density is on the order of 0.1 eA and large negative Laplacian, then it is considered to be a shared interaction (covalent bond) [47]. The other common combination is for closed-shell interactions (ionic bonds, hydrogen bonds, and van der Waals interactions) where the electron density has a value between 0.001 and 0.040 eA and small and positive Laplacian. To properly describe all of the interactions, the optimized structures were used. With increasing bond length the electron density lowers, proving that lower value of electron density usually represents a weaker bond [53]. The places of interest were hydrogen bonds between phenolate oxygen, carbonyl oxygen, and pyridine nitrogen with molecules of solvent, possible intramolecular hydrogen bonds, and polar bonds with highest electron density based on the NBO analysis (Table 1—C-O, CO, C-N-C). Table S8 gives values for electron density, Laplacian, and bond length for the mentioned bonds.
In the structure of deE-isomer, there is an intramolecular hydrogen bond present between phenolate oxygen and hydrogen atoms of a methyl group (with all of the mentioned characteristics of the hydrogen bond, ρ=0.028 au, and ). This proves that when deprotonation occurs this species is stabilized by this hydrogen bond and rotation of the phenolate ring additionally stabilizes this structure. This hydrogen bond is present even in a structure with five molecules of water, although it is weaker due to the formation of hydrogen bonds with solvent molecules. The changes in the electronic spectrum can be discussed when parameters of BCPs for deE with and without five molecules of water are compared. When five molecules of water are added, C-O group in the phenolate ring is stabilized more (difference in electronic density 0.01 eA), whereas the difference in electronic density in the C-N group in pyridine moiety is only 0.002 eA. There are also hydrogen bonds present between electronegative atoms and water molecules—the hydrogen bond with oxygen is stronger because of the negative charge concentrated on it (−0.786 eA vs. −0.480 eA, Table S8), which additionally stabilizes HOMO as compared with LUMO. The hydrogen bond is also formed with two nitrogen atoms of the immino group, next to the phenolate ring. This hydrogen bond is weaker than the previous one, because of the charge on immino atoms (Table 1). For the transition with shortest wavelength the theoretical value is 10 nm lower than experimental, proving that five molecules of water in the optimized structure overestimate the stabilization of HOMO − 2 probably because of stronger interaction with atoms with localized electron density of this orbital (including all atoms able to form hydrogen bond except pyridine nitrogen), whereas in LUMO only pyridine nitrogen and carbonyl oxygen are included. Probably more water molecules are needed around this part to stabilize it more and lower energy.
The effects of water molecules in a specific position can be discussed for structures with one solvent molecule. As mentioned in the previous section, as water molecules move away from phenolate oxygen the HOMO is less stabilized resulting in the bathochromic shift in the electronic spectrum. Electron density in BCP between C and O in the phenolate group approaches the value of molecule without water as water molecules move away and hydrogen bond gets stronger with increasing electron density. The strongest hydrogen bond formed in a structure with one water molecule is between phenolate oxygen and a water molecule, because of the same reason mentioned in the previous paragraph (ρ = 0.051 au and ). For the peak with the lowest wavelength, the consideration is similar because HOMO − 2 is less and less stabilized as water molecule moves away from the phenolate group. Fig. 8 gives comparative graphs for the dependence of electron density on the bond lengths for bonds within molecule and hydrogen bonds for all of the structures discussed throughout the article (presented in Table S8).
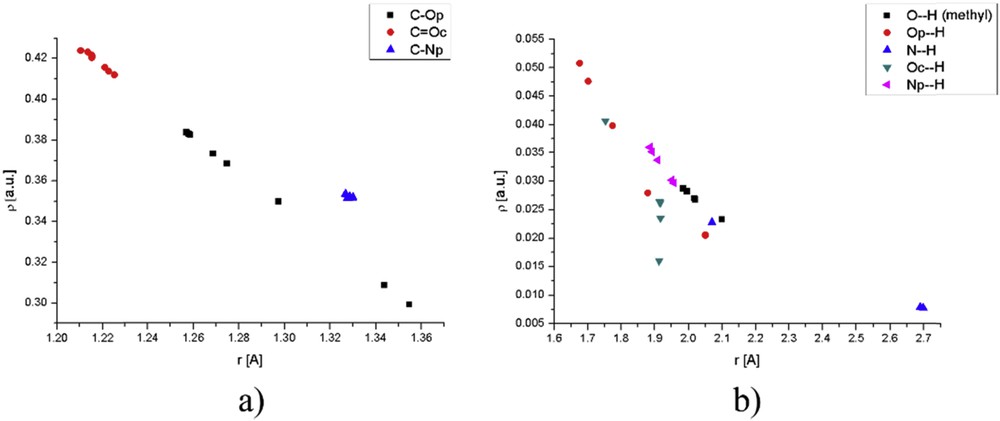
Comparative graphs for (a) bonds and (b) hydrogen bonds in the investigated molecules.
The graphs shown previously are reported, so the effects of distance between molecules on hydrogen bonds can be investigated. The densities of hydrogen bonds are the order of magnitude lower than densities in BCPs of the molecule, although the bond lengths are doubled. The first part of the graph shows the bonds inside of the molecule for all of the investigated species, namely COp, COc, and CNp. From the range of possible distances the most prominent effect in on the first bond, with distances ranging from 1.3 to 1.4 with a large difference in electron density. The bond in carbonyl group is less influenced by the surrounding molecules because of its partial double character and also the charge on this oxygen atom is lower than that on the phenolate one, so the interactions are weaker. The pyridine nitrogen has almost constant bond length with carbon because of the rigid ring structure, and molecules of water do not induce any significant change. Hydrogen bonds are much more interesting because they have different slopes depending on the charge in an atom and its position. For the case of phenolate, oxygen electron density decreases rapidly with distance, with a different slope than for hydrogen bond formed with methyl group of the molecule, probably because the distance between oxygen and methyl group cannot change that much because of rotation barrier. The change in electron density of pyridine nitrogen is less prominent with distance because of the lower partial charge on nitrogen as compared with oxygen (NBO analysis). Carbonyl oxygen has a specific position and from Fig. 8 can be concluded that whenever molecule of water interacts with this group, there are usually several other groups included, or in the most cases this oxygen atom is surrounded by several molecules of water (Fig. 5), and the investigated bond may be weaker, which is not true for two previously mentioned atoms. The same applies to nitrogen in the immino group.
4 Conclusions
The explicit solvent effect investigated by addition of several solvent molecules around the species of interest is widely used to encounter for short-range interactions between solute and solvent. This technique was used for the investigation of water effect on structure, charges, and electronic transitions of the novel molecular switch, HAPI, to reproduce the experimental electronic spectrum. In the first part of the article the suitable functional and basis set were chosen from the set of functionals: CAM-B3LYP, B3LYP, PBE1PBE, and M06-2X and basis sets: cc-pVDZ and cc-pVTZ, based on the experimental spectra, with the main criterion being the resemblance between theoretical and experimental wavelengths. CAM-B3LYP/cc-pVTZ was used for the optimization of protonated and deprotonated isomers of HAPI, and comparison of structure, dipole moment, and NBO charges in water (PCM). It was concluded that PCM distorts charges in molecule thus increasing the dipole moment. On the basis of the NBO analysis of orbitals that are included in transition, it was concluded that positions with the highest possibility for formation of hydrogen bonds are phenolate oxygen, carbonyl oxygen, and pyridine nitrogen and immino group. Structures of protonated and deprotonated isomers with 5 molecules of water are also included. The relative positions of water molecules in the optimized structure are highly dependent on the dipole moment of the molecule. The calculated values for transitions of deprotonated E-isomer were 402, 323, and 273 nm as compared with 400, 325, and 283 nm that are present in the experimental spectrum. Calculated wavelengths for protonated E-isomer were 292 and 253 nm. The influences of water molecules at different positions were also investigated by optimization of structures with one solvent molecule in previously discussed positions. From the electronic spectrum, it was understood that placing one water molecule next to phenolate oxygen significantly improves the theoretical spectrum. The position of the long-wavelength peak improves as the solvent molecule is closer to this oxygen atom. QTAIM analysis was used to discuss the influences of water molecules on strength and topological parameters. In the investigated structures the highest influence is on COp, whereas immino nitrogens and pyridine nitrogen are not affected by the presence of water molecules because of the rigid double bonds and ring structure. There is an evident change in the decrease of electron density with distance for hydrogen bonds formed with electronegative atoms in the molecule, and it is well correlated with the partial charges.
Acknowledgments
The author would like to thank the Ministry of Education, Science and Technological Development of the Republic of Serbia for the financial support through grant no. 174020.


