1 Introduction
Spin crossover (SCO) compounds are switchable molecules capable of reversible switching from a low-spin (LS) electronic state to a high-spin (HS) electronic state [1–11]. This spin state change can be induced by various external stimuli such as temperature [11], pressure [12], light irradiation [13–17], magnetic [18] and electric field [19], guest molecules [20–22], and so forth. From a thermodynamic point of view, the switching from the low-spin (LS) to the high-spin (HS) vibronic state originates from a competition between enthalpy, which tends to favor the lower energy fundamental state at low temperatures, and the entropy, which favors the most disordered thermodynamic phase at high temperatures. In the solid state, SCO materials can exhibit a first-order transition involving the existence of a latent heat and hysteretic behaviors can also be observed [23,24]. Abrupt spin transition and bistability phenomenon occurs when intermolecular interactions between SCO compounds are strong enough. Intermolecular interactions have an elastic origin, mainly because of the difference in volume, shape, and elasticity between the HS and LS phases [25–27]. Indeed, a HS molecule surrounded by LS molecules generates a local elastic strain field, and an elastic stress builds up in the whole crystal [28–31]. The elastic collective behaviors can be viewed as a combination of both short- and long-range interactions, usually called cooperativity [25]. The strong complexity of interaction mechanisms coupled with molecular properties very sensitive to controllable small energetic inputs gives rise to a large diversity of experimentally observed phenomena, which is perfectly illustrated by the different possible thermoinduced SCO curves recorded in these materials (Fig. 1).
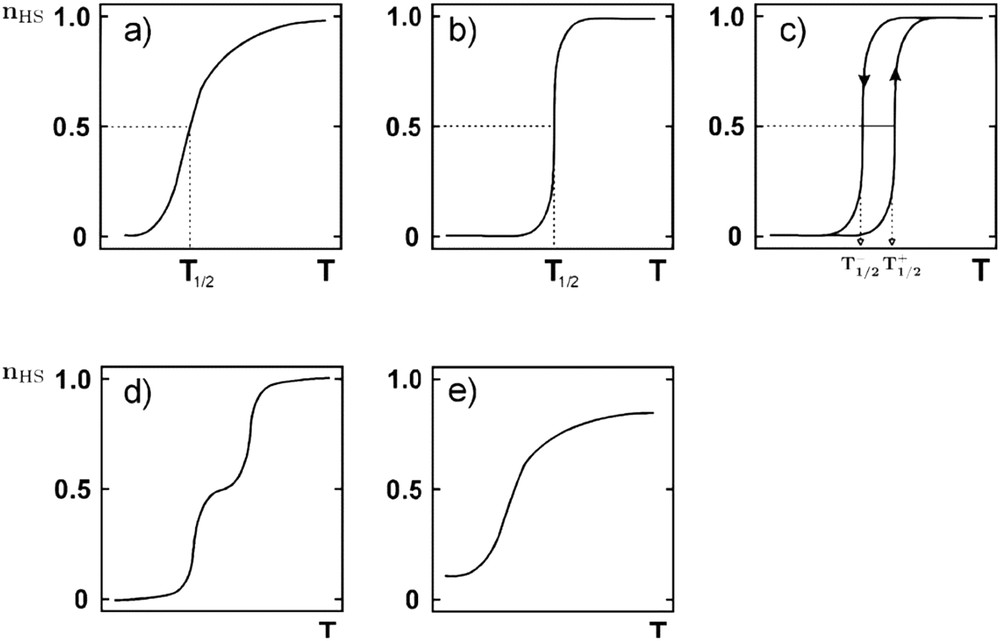
Schematic representation of the main thermoinduced SCO curves. The spin state change is followed by the thermal evolution of the fraction of molecules in the HS state, the so-called HS fraction (nHS). (a) Gradual spin conversion, (b) abrupt spin transition, (c) abrupt spin transition with hysteresis loop, (d) two-step transition, and (e) incomplete spin conversion (from Ref. [11]).
To these behaviors are added the different nonequilibrium processes as photoexcitation [16], kinetic relaxations from metastable states [32–36], dynamical equilibrium [37,38], ultrafast experiments [39–43], and so forth.
Because of the drastic modifications in physical properties of the SCO materials upon an SCO (magnetic, optical, electric, structural, vibrational, elastic, etc.), static, quasi-static, and nonequilibrium spin state changes can be monitored by various experimental techniques (magnetic, optical measurements, vibrational spectroscopies, Mössbauer techniques, etc.) [8,11]. In parallel to these intense experimental investigations, the modeling of SCO phenomena has been developed early. Initially, theoretical studies have mainly focused on the reproduction of spin conversion curves and the understanding of the different accessible experimental data. To this aim, macroscopic thermodynamic models have been introduced, in which the available physical quantities from calorimetric, crystallographic and spectroscopic measurements are injected, in addition to more phenomenological model parameters. At the same time, models based on statistical physics' considerations (Hamiltonian approaches), usually called microscopic models, have been proposed with the aim to give a description of SCO phenomenon at the chemical bonds and at molecular level (for an overview of microscopic models see also Refs. [44,45]). This class of model allows analyzing the spin conversions beyond the mean field or Bragg–Williams approximation, considering spatial fluctuations and correlations [46–50].
Historically, the first simple use of microscopic approaches for SCO systems has been initiated on the basis of discrete multilevel fictitious spin models [51]. Starting from a four-level fictitious spin model [52], a degenerated two-level Ising model has been developed in the 1990s, in which intermolecular interactions between Ising spins are described by phenomenological exchange-like coupling [53]. The so-called Ising-like model allows retrieving one-step/two-step thermal conversions and the main different results obtained from macroscopic models [53,54]. This later approach gave a microscopic origin to SCO phenomena, by specifying the possible ordering processes originated from the observed macroscopic curves (modulated structures, quenching, etc.).
The prediction of the SCO curves of a particular material from only a simple consideration of the molecular structure remains nowadays impossible. Indeed, the SCO phenomenon is still a complex problem: a small chemical modification of the SCO compound leads usually to strong modifications of the thermal switching behavior and structural properties affecting cooperative mechanisms and so on. The polymorphism of SCO materials, shown in Fig. 2, highlights this limited power of prediction of both macroscopic and microscopic models.

An example of experimental thermal evolution of magnetic susceptibility measured in three polymorphs of the same complex [FeLBr (dca)2], where LBr is N,N′-bis [(5-bromo-2-pyridyl)methyl] ethane-1,2-diamine and dca is dicyanamide [55]. α form exhibits abrupt spin transition with hysteresis, β form a two-step spin transition, and γ form does not present an SCO.
During the past few decades, a particular interest fell on the detailed analysis of the different spatial and temporal steps of the spin state change [56]. The different observations, in the case of abrupt SCO, show that the first-order character of the spin transition in highly cooperative materials gives rise to heterogeneous phase transformation, whereas homogeneous phase transformations are observed in weakly cooperative or diluted systems (Fig. 3).

Schematic representation of the transition mechanisms and associated thermal spin transition curves in three characteristic SCO systems having different degrees of cooperativity: (a) in solution (no cooperativity, gradual conversion); (b) in a solid exhibiting a weakly cooperative spin conversion (intermediate cooperativity, more abrupt transition); and (c) in a solid exhibiting a first-order spin transition (high cooperativity, abrupt transition with thermal hysteresis loop). LS and HS molecules are depicted by blue and red circles, respectively [56].
Microscopic models seem to be more suitable to grasp nucleation and domain growth mechanism. Therefore, the Ising exchange-like coupling has been substituted by a more realistic description of elastic interactions and by a better modeling of electron–phonon coupling, including lattice distortions [57]. Strongly inspired by the study of Bari and Sivardière [58] and a mesoscopic approach of Spiering and Willenbacher [26,27], atom–phonon [59] and spin–phonon (mechanoelastic [60] electroelastic [61], anharmonic [62] spin–phonon) models have emerged in the beginning of the 21st century (see also Ref. [45] and references therein). Different aspects and mechanisms of spatiotemporal dynamics have been successfully explained by such class of models (for an overview see also Ref. [56] and references therein).
However, quantitative analysis and predictions of the spatiotemporal behaviors of particular SCO compound are nowadays not achieved. The knowledge of elastic, mechanical (bulk, Young and shear moduli, Poisson ratio, etc.), and thermal transport properties (thermal conductivity, convection transfer coefficient, etc.) remains scarce [63–68], and it is still difficult to relate such macroscopic quantities to parameters of microscopic models [69].
A similar limitation is encountered in another hot topic of the SCO phenomenon: size reduction effects [70–77]. An important question concerns the becoming of phase stability, bistability and the major macroscopic observed properties after size reduction, at the nanoscale, and the consequence of the predominance of surface physical properties on the spin transition.
In this review, different thermodynamic aspects of the SCO phenomenon are reviewed. First, basic considerations of crystal field theory and thermodynamics are recalled. Then, the different thermodynamic models including cooperativity through phenomenological terms, simulation of electron–phonon coupling, or continuum mechanics approach are reported, and their respective results concerning the simulation of spin transition curves are discussed. Finally, recent developments of thermodynamic models coupled with ab initio calculations for the simulation of two-step transitions are presented. Finally, recent nonextensive thermodynamic approaches, taking surface/interface contributions in SCO nanoparticles into account, are evoked.
2 Thermodynamic aspects
2.1 Crystal field theory
The understanding of the SCO phenomenon starts with the study of the required electronic properties for a molecule to be switchable. In a first step, the molecular energy spectrum has to be determined. However, the complicated electronic structure of a SCO molecule prevents to obtain analytical solutions from Schrödinger's equation. In the past few decades, first principle and quantum chemical calculations adapted for SCO molecules have been intensively developed and success in the simulation of molecular vibrational properties has been realized [78]. However, the systematic prediction of the ground state and the precise estimation of the ground energy level remain a challenge. Therefore, it becomes essential to use more simplified approaches. In this sense, crystal field theory is very convenient to qualitatively describe the SCO electronic structure and spin conversion phenomenon [79]. In this context, ligands are considered as punctual electric charges interacting with the metallic cation. The octahedral symmetry leads to a partial degeneracy splitting of the 3d energy level of the metallic cation. For example, for the Fe(II) cation, the five 3d orbitals are degenerated in the absence of the ligands. When this cation is placed in an octahedral field formed by six ligands, electrons of the cations are submitted to repulsive forces and the occupation of d orbitals is governed by electrostatic energy minimization. The 3d energy level splits into two levels: a lower energy level t2g, containing the three degenerated orbitals dxy, dxz, dyz, and a higher energy level eg formed by the two orbitals dz2 and dx2-y2. The energy difference between these two levels can be expressed in terms of ligand field force or crystal field splitting being 10 Dq, where Dq corresponds to a semiempirical parameter related to the crystal force field. The energies of the t2g and eg levels can be divided into two contributions: a spherical part whose only effect is to shift the electronic levels of the free ion and another contribution related to the lowering of the symmetry leading to the degeneracy partial splitting (Fig. 4).
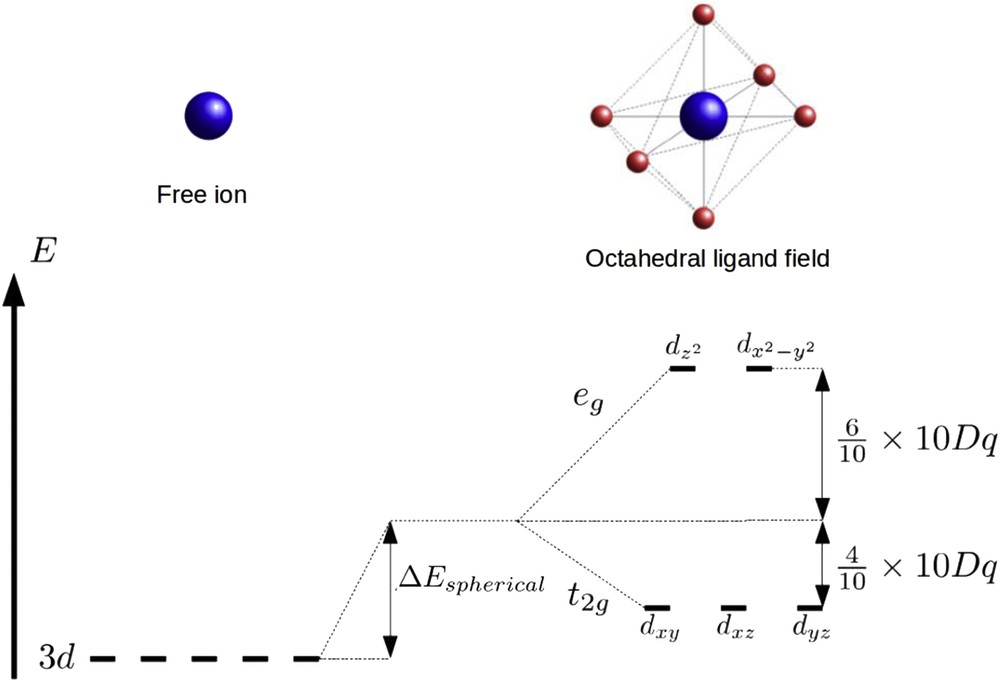
Schematic representation of the partial degeneracy splitting of 3d orbitals due the presence of the octahedral ligand field.
At the molecular scale, two main effects compete: on one hand, electrons tend to occupy d orbitals according to Hund's rule due to the exchange coupling. On the other hand, electrons tend to fill the t2g level, which is the lowest energy level. The consequence of these antagonist effects is the existence of two possible ground states according to the strength of the ligand field that is strongly spin state dependent in comparison with the electron pairing energy Π, which is almost insensitive to the spin state. In the case of a weak ligand field, electrons mainly occupy t2g orbitals and the total spin momentum takes a minimal value (S = 0 for Fe(II)), corresponding to the LS state (1A1g term symbol). On the contrary, when the ligand field is strong in comparison with the electron pairing energy, electrons occupy a maximum number of orbitals, in agreement with Hund's rule, and the spin momentum value is maximal (S = 2 for Fe(II)) corresponding to the HS state (5T2g term symbol). When the ligand field force is of the same order of magnitude of electron pairing energy, any small external perturbation is able to switch the molecule from one to the other spin state in a reversible manner.
This phenomenon is called spin crossover, spin equilibrium, or spin conversion and commonly spin transition. The range of ligand field values for which an SCO can be observed is narrow as it can deduced from the Tanabe Sugano's diagram (Fig. 5). A first direct “consequence” of this electronic configuration change upon LS to HS conversion is an increase in metal–ligand distances, around 10%, corresponding to an increase in the octahedron volume of about 25%. This variation suggests important differences in terms of vibration modes as inferred from IR and Raman spectroscopy measurements (Fig. 6). For example, in a FeN6 octahedron, stretching vibrational modes ν(FeN) are greater in the LS state than in the HS state with typical ratio νLSFeN/νΗSFeN ranging from 1.1 to 1.9 [81].
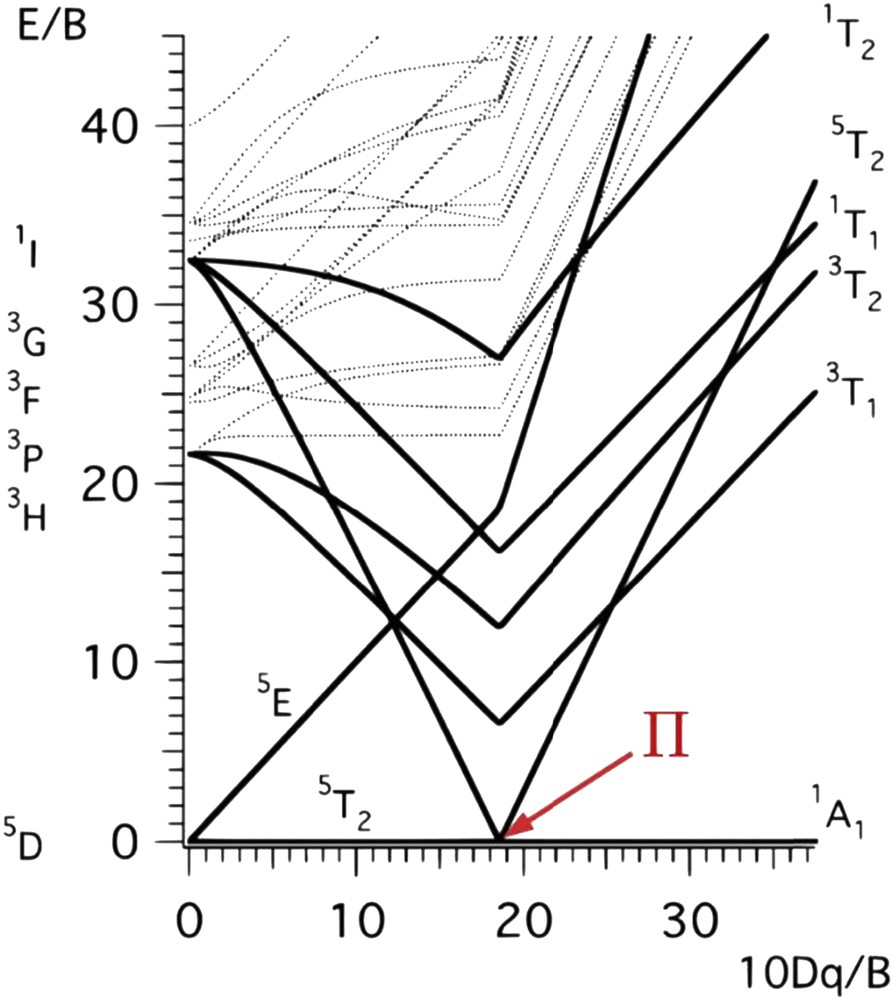
Tanabe Sugano's diagram giving the energy levels of the electronic state as a function of the ligand field energy for a metallic ion of electronic configuration d6 embedded in a octahedral ligand field (Racah parameter B: electronic repulsion [80].
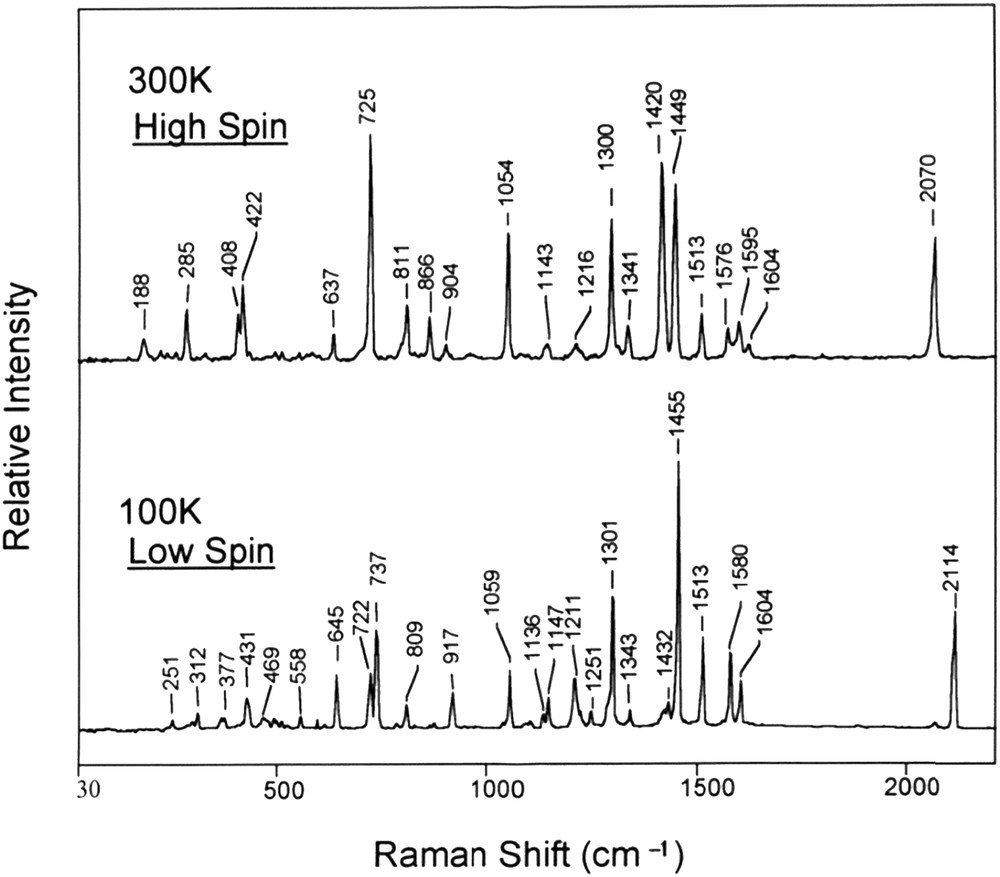
Raman spectra of Fe (phen)2(NCS)2 in the HS state (300 K) and LS state (100 K) [81]. In the range <600 cm−1 where the entropy values are maximized, the average of vibrational modes are νav,HS = 298 cm−1 and νav,LS = 393 cm−1 in the HS and LS states, respectively, leading to a ratio νav,HS/νav,LS ∼1.3.
A thermoinduced spin conversion is possible when the difference between the zero-point energies of the two spin states has the same order of magnitude as the thermal energy, that ΔE = EHS0 − ELS0 ≈ kBT. In SCO compounds, the zero-point energy corresponds to the sum of electronic and vibrational contributions. Except for few rare SCO compounds [82–86], the lowest zero-point energy is the LS state and thus the ground state is the LS state at zero temperature (Fig. 7). However, at high temperature, the HS state becomes the thermodynamic stable state. This change is due to the entropic contributions, which are more important in the HS state than in the LS state. Indeed, the entropy difference has two origins: electronic origins due to a higher spin multiplicity (and to a lesser extent to the orbital momentum, vide infra) in the HS state and especially a vibrational origin due to weaker vibrational frequencies [80]. It is commonly accepted that the SCO can be seen as an entropy-driven phase conversion.

Schematic representation of a configurational diagram in the case of an Iron(II) complex. The two spin states are represented by a harmonic potential double well in the adiabatic approximation (T = 0).
2.2 Thermodynamic aspects of the spin conversion
When SCO molecules interact with an external environment, the spin conversion phenomenon can be understood by axiomatic thermodynamic aspects. In a first step, a set of N noninteracting (isolated) SCO molecules in contact with a thermal bath T is considered with a possible control of the external pressure P, the so-called isothermal and isobaric ensemble (N,P,T). At constant pressure, the spin conversion can be viewed as a thermal equilibrium between two phases. The relevant state function for such experimental conditions corresponds to Gibbs energy G = H − TS, where H and S stand for the enthalpy and the entropy of the system, respectively. Thermodynamic properties of the system are described by the Gibbs energy difference between the HS and LS phases:
| (1) |
| (2) |
From Eq. 2, when T < T1/2 the enthalpic term is dominant and the LS state is favored, whereas for T > T1/2, the entropic term becomes dominant and the HS state is favored, justifying hence the terminology “entropy-driven phase conversion”.
Let us consider the different contributions to enthalpy and entropy variations. ΔH can be subdivided into two parts: a temperature-independent electronic part ΔHel and a vibrational part ΔHvib. In a similar manner, ΔS can be arbitrarily divided into different contributions to the statistical disorder:
| (3) |
The two last terms ΔStrans and ΔSrot correspond, respectively, to the entropy variation due to translation and rotation, respectively, and are neglected most of the time in the solid state. The first term ΔSel = ΔSorb + ΔSspin is the electronic entropy variation and originates from the difference in terms of degeneracy (orbital and spin momenta) between the HS and the LS electronic states:
| (4.1) |
and
| (4.2) |
Electronic entropy favors the HS state and is temperature independent. The second term ΔSvib is the vibrational entropy variation. In the case of isolated molecules, ΔSvib is only dependent on the variation of intramolecular modes between the HS and LS states. In the solid states, the contribution related to intermolecular vibrations has to be added, even if this contribution is often considered as less important than the intramolecular part (in fact intramolecular and intermolecular vibrations are coupled and it is difficult to distinguish their respective contributions). Vibrational entropy can be expressed as follows (a more detailed analysis is described in Ref. [82]):
| (5) |
| (6) |
| (7) |
Considering a perfect octahedron (λ = 15 molecular vibrational modes) and taking 〈νLS〉/〈νHS〉 = 1.3 (Fig. 6), we obtain ΔSvib ≈ 32.7 J mol−1 K−1 in agreement with the experimental measurements [81].
This result allows us to draw two important conclusions. First, vibrational entropy is higher in the HS state and then this latter is favored at high temperatures. Then, the variation in vibrational entropy shows the important role of vibrations in the SCO phenomena. More generally the entropy variation ΔS ranges from 40 to 80 J mol−1 K−1 in comparison with ΔSel = 13.38 J mol−1 K−1. It is important to note that all of these thermodynamic quantities can be extracted from calorimetric measurements [88–90] (Fig. 8), whereas vibrational properties can be assessed with Raman and infrared spectroscopies [81,91,92].
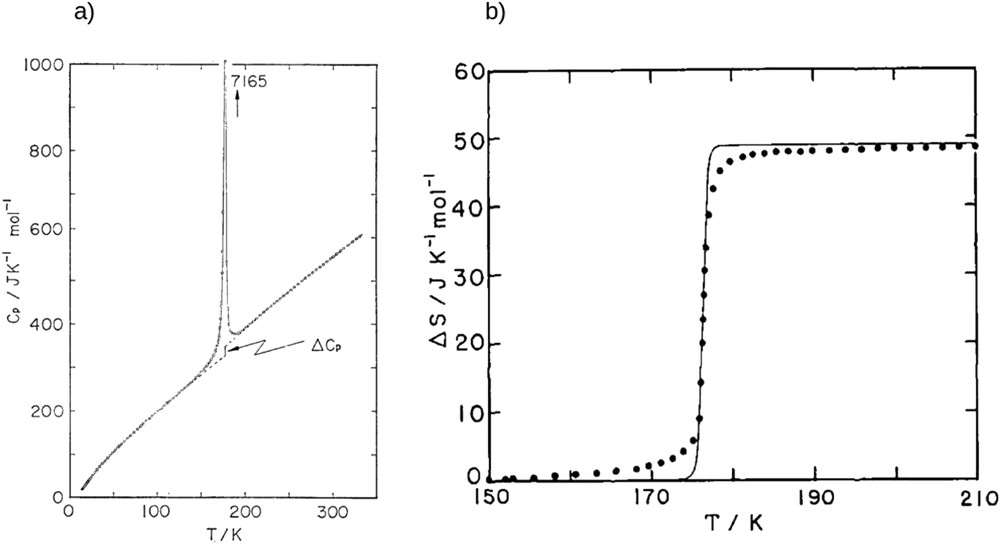
(a) Temperature dependence of the heat capacity of Fe(Phen)2(NCS)2 crystal. ΔCp corresponds to the discontinuity associated with the spin transition. (b) Temperature dependence of entropy variation of the same compound (full black circles). Straight line corresponds to a fit using the so-called domain model [88] (vide infra).
The mixing entropy Smix has not been discussed yet. Considering N noninteracting molecules, among them NHS are in the HS state, and we can define the HS fraction nHS = NHS/N, which is abusively called the order parameter of the spin transition. We can express the Gibbs energy of an SCO system as
| (8) |
The mixing entropy corresponds to a loss of statistical information for the system related to the large number of possibilities to distribute NHS molecules in the HS state among N molecules. In the thermodynamic limit, mixing entropy can be written as
| (9) |
The equilibrium condition corresponds to
| (10) |
It is then possible to follow the thermal evolution of the HS fraction (Fig. 9):
| (11) |

Thermal evolution of the HS fraction nHS (blue line) in the case of noninteracting SCO molecules. The equilibrium temperature T1/2, where nHS = 0.5 is indicated with a red dashed line.
In the case of noninteracting SCO molecules, a gradual spin conversion can only be observed from the LS to the HS state by increasing the temperature. The occurrence of abrupt first-order transition with bistability phenomena is directly related to the emission or absorption of a latent heat whose existence is completely governed by interactions between SCO compounds. In contrast to the basic thermodynamic approaches describing the SCO phenomenon of isolated molecules, taking into account the complex interaction mechanism between SCO molecules needs most of the time the introduction of phenomenological parameters whose links with measurable experimentally quantities are not trivial at all. These parameters imply drastic simplifications of collective behavior mechanisms in the solid state. In the next section, a brief summary of several macroscopic/thermodynamic models simulating interacting SCO compounds is presented.
3 Macroscopic/thermodynamic models
3.1 Collective behaviors or cooperativity
The thermodynamic approach introduced in the previous section is only valid for diluted systems as solutions (solid or liquid). Interactions between molecules can no more be neglected in bulk solid materials. The increase in the octahedron volume upon LS to HS switching is around 25%. In parallel, vibrational modes are higher in frequency in the LS state. It means a higher bonding energy (and also a higher stiffness) in the LS state than in the HS state. In the crystal packing, the change in structural properties of a molecule upon a spin state change has an important impact not only on its immediate environment but also affects the whole lattice (long-range interactions). The switching from LS (respectively HS) molecule to HS (respectively LS) state implies important local strains because of the expansion (respectively the contraction) of the molecular volume. The HS (respectively LS) molecule is submitted to a compressive (respectively tensile) stress exerted by the neighboring molecules, which tend to switch back the molecule to its initial state. These elastic mechanisms induce collective effects, which lead, if they are strong enough, to first-order transition, that is, discontinuities of first derivatives of Gibbs energy (entropy, volume, and also HS fraction). Spin state change induces modifications in volume of the whole material (VHS–VLS/VLS ≈ 13%) [93] and of the bulk modulus B (BLS − BHS/BHS ≈ 30%) [94]. From the first basic point of view, these two ingredients play an important role in the magnitude and range of the interactions. In the SCO field, all of these intermolecular interaction mechanisms are usually called cooperativity. It is important to understand that the response of the lattice to the switching of a molecule is not local. The spin state change of one or several molecules generates elastic distortions, which spread in the whole crystal and give rise to a global response of the lattice, sometimes called image pressure. This image pressure is a complicated and inseparable combination of short- and long-range interactions. The complexity degree in the modeling of cooperative aspects in SCO materials is obviously dependent on the kind of experimental observations to simulate (spin transition curves, nonequilibrium process, nucleation and domain growth processes, mechanical properties, etc.). Macroscopic/thermodynamical models are an excellent first step in the simulation of SCO curves and nonequilibrium kinetic curves (macroscopic master equations). In this review, we limit the description of macroscopic models to equilibrium spin transition curves. The microscopic models are addressed in other dedicated articles within this special issue [44,45].
3.2 Slichter and Drickamer models and “domain” model
In 1972, Slichter and Drickamer [95] have introduced a first thermodynamic model based on regular solid solution theory. Starting from Gibbs energy given by Eq. 8, they added a nonlinear phenomenological term ΓnHS (1 − nHS), which takes into account intermolecular interactions. By analogy with magnetism, it can be seen as a second-order Taylor's expansion as a function of the HS fraction nHS:
| (12.1) |
| (12.2) |
| (12.3) |
| (12.4) |
The interaction parameter Γ is directly related to the force of intermolecular interactions in the crystal (cooperativity). In the initial model, Slichter and Drickamer have proposed that Γ parameter should be temperature and pressure dependent because of the importance of vibration and mechanical properties in SCO systems. However, the knowledge of temperature and pressure dependence of this phenomenological term is difficult, and despite some links with microscopic spin–phonon models have been established [69], Γ is most of the time kept constant. As previously, the extrema of Gibbs energy (which are no more unique) are given by Eq. 10 [95].
| (13) |
It is important to note that in some cases, three values of HS fraction can give the same temperature. This is the signature of the existence of stable, metastable, and unstable states. To verify the stability of the extrema, it is interesting to inspect the sign of the second derivative of Gibbs energy around the equilibrium temperature (i.e., nHS = 1/2):
| (14) |
From Eq. 14, three situations can occur (see Fig. 10). If Γ < 2RT1/2 (weak interactions), then the second derivative is positive and the state nHS = 1/2 is a minimum point of Gibbs energy. The spin state change is gradual (spin conversion). If Γ > 2RT1/2 (strong interactions), the second derivative is negative and nHS = 1/2 is a maximum of Gibbs energy. The transition is abrupt (first-order phase transition) with the presence of a hysteresis loop. There are also two transition temperatures corresponding to minima of Gibbs energy: T1/2+ (warming process) and T1/2− (cooling process) corresponding to the limit of the metastability and whose average is approximately the equilibrium temperature. For example, during a warming process, when T < T1/2− the material is in the stable LS phase. By increasing the temperature until T1/2− < T < T1/2, a metastable HS phase appears, separated from the stable LS phase by an unstable state. For T = T1/2, the HS and LS phases are both stable. In the range T1/2 <T <T1/2+, the LS phase becomes metastable and the more stable phase is the HS one. However, the system remains in the metastable LS phase due to the presence of the energy barrier generated by the unstable state. For T > T1/2+, the energy barrier disappears and the system switches from the LS to the HS phase. The behavior of the SCO materials is similar in the cooling mode. If Γ = 2RT1/2 the second derivative is null, which corresponds to an inflexion point. The SCO is abrupt without hysteresis. This situation corresponds to the critical point of the phase diagram related to the critical temperature TC = T1/2 = Γ/2R, which gives the limit conditions of the two previous cases.
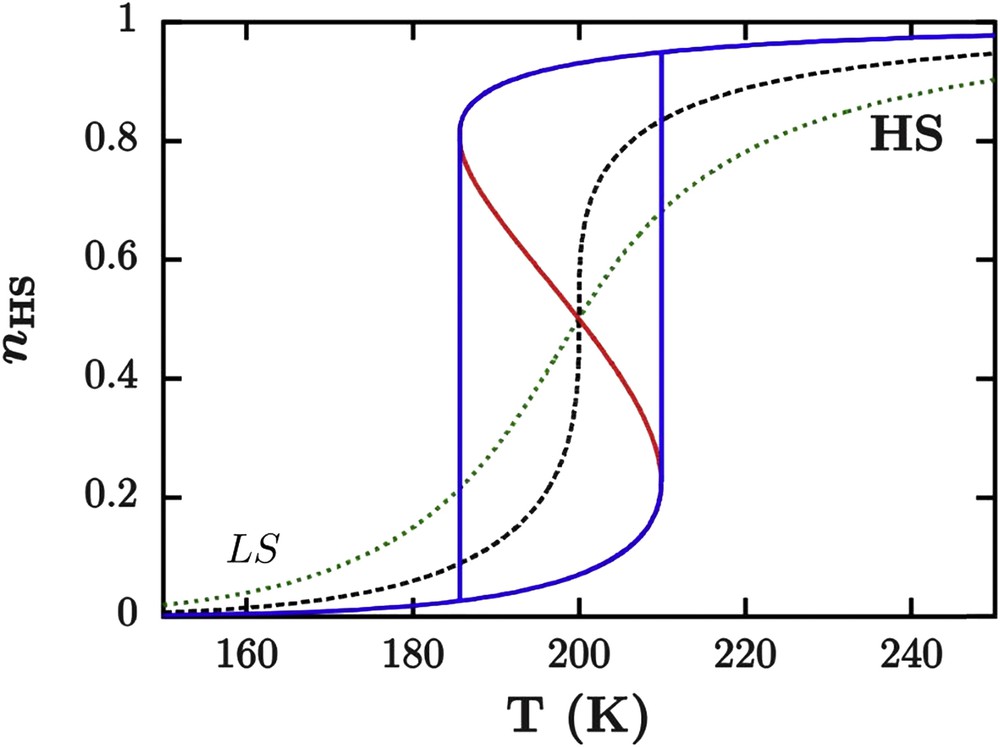
Simulation of thermoinduced spin transition with the Slichter and Drickamer model for different interaction strengths. Variations in enthalpy and entropy are, respectively, ΔH = 12,000 J mol−1 and ΔS = 60 J mol−1 K−1. Three different values of Γ have been chosen to illustrate three different situations: the spin conversion (gradual, green dotted line) 2RT1/2 > Γ = 2000 J mol−1, the abrupt transition (black dashed line) 2RT1/2 = Γ = 3324 J mol−1, and the first-order transition with hysteresis phenomenon (blue full line) 2RT1/2 < Γ = 5000 J mol−1. The red curve represents the instable states of the transition (local maxima of Gibbs energy).
The increase in Γ tends to amplify the abrupt character of SCO until the occurrence of a first-order transition. In classical terms, the transition is called first-order phase transition because the first derivative of the free energy F is discontinuous (the discontinuity corresponds to the generated entropy term: S = −(δF/δT)v). The Slichter and Drickamer model does not take into account the interface energy between the HS and LS phases. This supposes a homogeneous spin conversion without domain formation. Indeed, the expression of the mixing entropy assumes that a molecule can be equivalently distributed at any part of the lattice: this is the mean field approximation. First-order phase transitions are usually accompanied by heterogeneous phase transformation related to the spatiotemporal dynamics governed by a nucleation and domain growth mechanism [30]. Spin transition phenomenon belongs to this class of phase transformations. Indeed heterogeneous phase separation has been indirectly observed by X-ray diffraction measurements [96,97] due to the structural differences between the HS and LS phases and has been directly highlighted using optical microscopy techniques for a decade [56].
Early in the 1970s, the existence of spin like-domains, that is, adjacent molecules in the same spin state, has been speculated by Sorai and Seki [88]. To take into account this finding, they considered that the system is divided in ND clusters of similar shape in which molecules have the same spin state. There is no interaction between domains. Thus, the mixing entropy does not describe the distribution of molecules in the material any more, but rather the arrangement of domains. The Gibbs energy of the so-called “domain model” can be expressed as
| (15) |
This model is able to reproduce spin conversions and abrupt spin transitions in the limit of large clusters (highly cooperative materials) without the possibility to simulate hysteretic behaviors (Fig. 11). Next, Purcell and Edwards [98] have modified the interaction parameter Γ of the Slichter and Drickamer model to make it dependent on the number and the spin state of pairs of molecules:
| (16) |
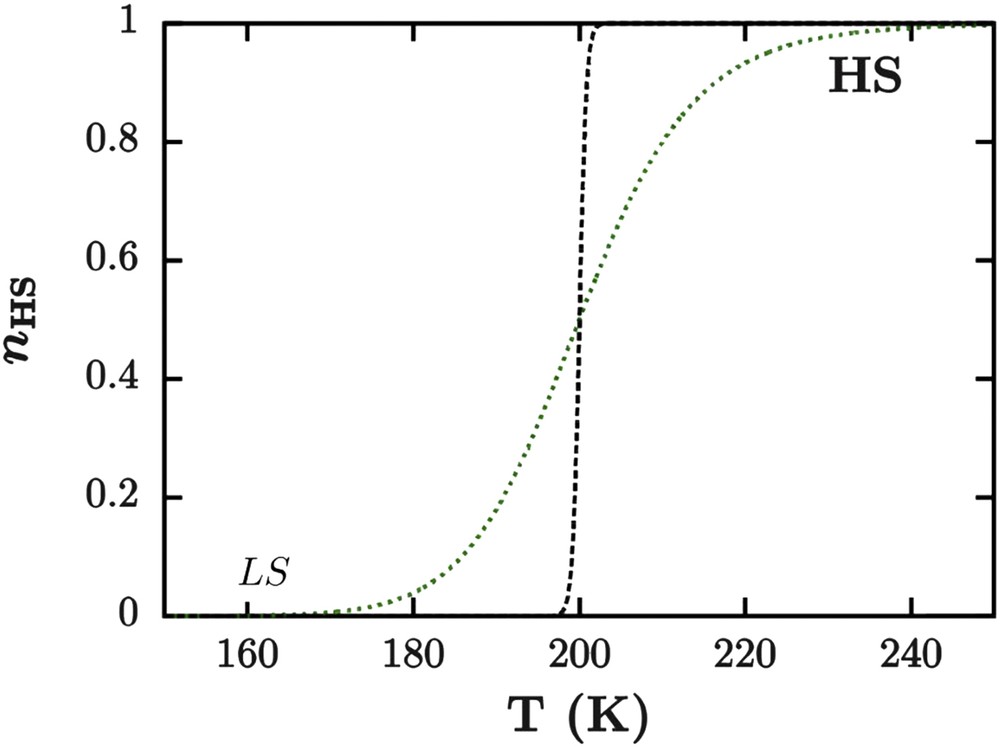
Spin transition curves simulated with domain model for nD = 0.015 mol−1 (green dotted line) and nD = 0.25 mol−1 (black dashed line). Other values of model parameters (entropy and enthalpy variations) are the same as Fig. 10.
3.3 Incomplete, multistep transitions, and macroscopic spin–phonon models
In SCO materials, other spin transition curves, different from simple spin conversions or abrupt transitions can be experimentally observed. Indeed, the elastic origin of intermolecular interactions and the strong electron–lattice interplay are able to give rise to richer phase diagrams. Incomplete transitions have been observed with the occurrence of residual HS fractions at low temperature and/or residual LS fractions at high temperature. Incomplete transitions have various origins like quenched effects (kinetic), a HS ground state at zero temperature [82–86], presence of microstructures, size reduction effects (surface effects) [99,100], or nonequivalent metallic sites in the crystal packing, and so forth. For this latter case, two-step transitions have also been observed: each metallic site having different transition temperatures [101,102]. The existence of multistep spin transitions has other possible origins. This phenomenon has been first detected in polynuclear SCO systems [66,103]. The switching of one of the two metallic centers generates elastic distortions within the molecule, preventing the switching of the other metallic centers. In mononuclear SCO compounds, the presence of multistep transitions has been interpreted as a competition between short- and long-range interactions, which favor modulated ("chessboard") structures such as a regular alternance of HS–LS molecules in the crystal. To account for these experimental observations, the description of the interaction parameter contained in the domain and the Slichter and Drickamer models has been refined. For example, Cantin et al. [104] consider new ingredients as intra- and interdomain interactions and domain size effects. This thermodynamic model predicts the occurrence of HS thermally metastable and stable states at low temperature, and thus the possible existence of incomplete (Fig. 12a)) and irreversible LS to HS (Fig. 12b) transitions.
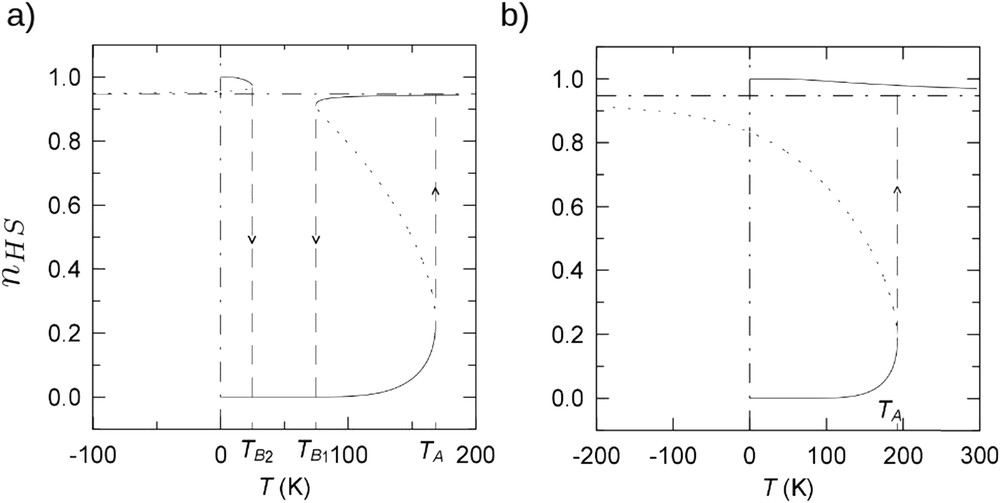
Thermal evolution of the HS fraction modeled with a thermodynamic model taking into account intra- and interdomain interactions and domain size distribution [104]. (a) Simulation of metastable HS state at low temperature. (b) Modeling of irreversible LS to HS transition.
The previously introduced thermodynamic model is able to reproduce the main features of the experimentally observed spin transition. However, the main drawback of this model is the absence of a more realistic description of the elastic intermolecular interactions and electron–lattice coupling. In this context, Zimmermann and König [105] developed an elastic model solved in the framework of the Bragg–Williams approximation—equivalent to a mean field treatment of the Slichter and Drickamer model—in which lattice vibrations have been taken into account through the Debye temperatures of the HS and LS phases. This approach allows us to establish strong relations with thermodynamic models and gives an elastic origin to the cooperativity. It is important to note that in parallel to the thermodynamic models, microscopic models based on statistical physics approaches have been developed, which are out of the scope of this present review. Although the Slichter and Drickamer model and the mean field Ising-like model are completely equivalent, as shown by Bousseksou and co-workers [53,54], the Zimmerman and König model is isomorph to spin–phonon, mechanoelastic, or electroelastic microscopic models (discussed within the present special issue [45]) in the framework of Debye's model and Bragg–Williams approximation. The addition of phonon contribution improves the fitting of experimental data (Fig. 13a)) [105]. Then, Koudriavtsev [106] has developed a similar approach to the Zimmermann and König model for the description of electron–phonon coupling. The spin state dependence of vibration modes between neighboring molecule pairs coupled with specific spatial correlation conditions (called occupational conditional probability) is able to fit two-step transition curves (Fig. 13b).
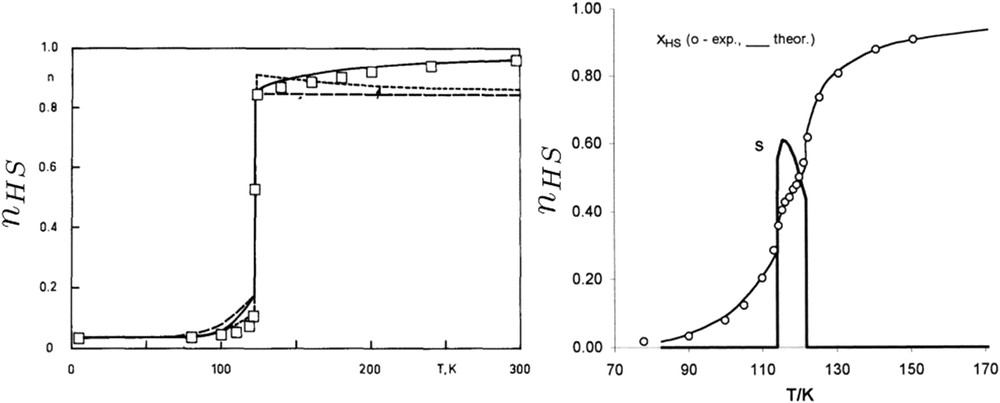
(a) Temperature dependence of the HS fraction for the compound [Fe (4,7-(CH3)2-phen)2(NCS)2)] (open squares). The dashed curves represent results of a calculation within the electronic SCO model including the electrostatic interaction between HS ions. The solid curve gives results obtained by the model including the contribution by phonons [105]. (b) Two-step spin transition fitted by the Koudriavtsev approach [106]. The quantity s is directly related to the fraction of HS–LS molecule pairs.
It is worth mentioning at this stage that two-step crossover has also been grasped using the Landau–Devonshire theory in which spin transitions can be viewed as an isostructural transition with a totally symmetric order parameter [107]. To reproduce the long-range ordering of different spin states, a model is developed in which the spin transition is coupled with a structural transformation through an order parameter, which “measures” the symmetry breaking. However, this latter approach is very similar to the well-known mean field Ising-like model for two-step SCO [53] with two interacting sublattices and the elastic nature of interactions is not explicitly taken into account. Of course, the symmetry breaking (from magnetism point of view) has also been predicted by the Ising-like model for a binuclear system in the symmetrical case (identical ferro-like interaction with neighbors of both binuclear centers) [54].
3.4 “Mesoscopic” elastic model
In the Zimmermann and König model and the Koudriatsev approach, intermolecular interactions are considered through lattice vibrations and vibronic coupling. An alternative description of the cooperative mechanism in SCO solids is a mesoscopic model based on continuum mechanics. Starting from the theory of Eshelby [108], Ohnishi and Sugano [109] have developed an elastic model taking into account overall lattice deformations and local deformations attributed to the change in metal–ligand distances during the spin state change. Thereafter, Spiering and co-workers explicitly considered the interaction term by expressing the Gibbs energy of a set of SCO molecules distributed in a host matrix with the aim to identify the different terms. Gibbs energy is given by Refs. [26,110]:
| (17) |
| (18) |
| (19a) |
| (19b) |
| (20a) |
| (20b) |
4 Recent extensions and prospects
As mentioned previously, the main drawback of most thermodynamic models lies in the need to introduce phenomenological interaction parameters. Describing the collective behavior between SCO compounds by means of elastic approaches already corresponds to a modeling of electronic reorganizations within the solids induced by the spin state change. In the past decade, macroscopic models based on numerical predictions using ab initio calculations have been developed and can be seen as another vision of cooperative aspects, which complements the common description of interaction mechanisms by elastic-driven cooperativity [111–113]. This method assumes that the Γ parameter of the Slichter and Drickamer model can be divided into two contributions: weak bond contacts (van der Walls interactions) and polarization effects due to charge redistributions upon ligand fields, geometry reorganizations, and lattice expansion. parameter corresponds to a modulation of the electrostatic contributions generated by the crystal environment (Madelung fields). The authors show that interactions through weak bond contacts are not sufficient to explain the existence of hysteretic behaviors in some SCO materials. In this study, the growth of hysteresis loop is controlled by electrostatic contributions (fluctuations of Madelung fields).
In another context, thermodynamic models have evolved with the aim to investigate the very important question concerning the SCO phenomena at the nanoscale. Switchable properties are generally strongly affected by size reduction effects resulting in a change in both phase stability (transition temperatures, completeness of the transition, etc.) and cooperativity mechanisms (first-order character of the spin transition and bistability properties) [99,100,114–121]. In SCO systems, reducing the size usually leads to a downshift in the transition temperature, the occurrence of residual HS or/and LS fraction, respectively, at low and high temperatures. Hysteretic behavior and also bistability can disappear or survive by approaching the nanometer scale according to the SCO nanomaterials. Intriguingly, a nonmonotonic size evolution of the hysteresis loop has been observed: a shrinking of the hysteresis loop with the size reduction followed by a reappearance of bistability phenomenon in ultrasmall nanoparticles (ca. 2 nm) [100].
It is well known that size reduction does not only imply a decrease in the quantity of matter but also an increase in the surface-to-volume ratio. Similar thermodynamic behaviors and physical properties are observed in nano-objects with the same surface-to-volume ratio, whatever their respective volumes. At the nanometric scale, surface/interface chemical and physical properties can no more be ignored. From a thermodynamic point of view, taking into account surface properties can be achieved by introducing the concept of surface energy density as it has been proposed by Gibbs in the end of the 19th century [122]. Then, in the 1970s, Hill [123] has extended the idea of surface energy to “small systems”, developing a new thermodynamic formalism called “nanothermodynamics”. In the SCO field, a spin state–dependent energy density has been included in a Slichter and Drickamer approach adapted for the modeling of core–shell nanoparticles [124]. The phase stability in SCO nanoparticles has been demonstrated to be completely governed by the difference in terms of surface energies between the HS and LS phases, which constitute the driving force of the spin transition at the nanoscale. First, estimations of the difference between a HS and LS surface leads to [124]. According to this result, a HS surface usually has an energy cost lower than a LS surface. This may explain the important downshift in the transition temperature and the spin state of surface molecules, which seems to be fixed in the HS state. To go further, an interfacial elastic energy density and an interfacial stress of a core–shell SCO nanoparticle have been expressed as a function of the Young moduli and Poisson's ratios of the hybrid system in the framework of a continuum mechanics approach [125]. According to the structural misfit and differences in the mechanical properties between an inactive core and a SCO shell, this interfacial elastic energy density favors either the HS (tensile stress) or the LS (compressive stress) state. It results, respectively, in a downshift or an upshift of the transition temperature, giving the perspective of the control of phase stability in SCO nano-objects. The main advantage of such approaches is the possibility to inject experimentally accessible mechanical properties of core–shell systems. However, the total surface energy can be divided into many contributions: chemical, elastic, disorder... so forth, whose effects are strongly intricated. Nevertheless, the experimental measure of the total surface energy in both spin states is still lacking and its knowledge seems to be of paramount importance for deeper theoretical investigations of size effects and especially surface effects on phase transition in SCO nano-objects.
The preservation of bistability phenomena through the presence of hysteretic behavior in SCO nanoparticles seems to be counterintuitive if analogies are established with the size evolution of other phase transitions, like melting process or ferromagnetism [73,126]. However, the elastic origin of collective behaviors in SCO systems constitutes an important difference with the other examples: elastic properties may be size dependent. Mössbauer spectroscopy measurements have shown a drastic increase in the Debye temperature with the size reduction in Prussian-Blue analogue [124] and SCO coordination nanoparticles [100]. This increase in the Debye temperature means stiffening—at least in appearance—of the nanoparticle by approaching the nanoscale, which may be explained by the existence of a compressive stress exerted by the external environment. This experimental finding has been injected in the nanothermodynamic version of the Slichter and Drickamer model, considering the linear dependence of the phenomenological interaction parameters Γ with the bulk modulus () [110] established in the framework of the mesoscopic elastic model (Section 3.4). This combination experiments–thermodynamic model allows us to give a possible explanation of the existence of bistability phenomena in ultrasmall SCO nanoparticles.
Most of these thermodynamic approaches emphasize the primary role of structural and elastic properties for the understanding of cooperative mechanisms in SCO materials. If investigations of crystallographic properties are routine and X-ray diffraction experiments are common characterization techniques to probe of mechanical/elastic properties remains scarce and experimental techniques, which allow a systematic determination of such properties, are still lacking. It would be important to further probe elastic and vibrational properties of SCO materials and nanomaterials to constitute a database of elastic moduli of molecular materials and coordination networks. Various techniques have been proposed to this aim: Brillouin spectroscopy [64], X-ray diffraction under pressure [71], near-field microscopy techniques (atomic force microscopy) [72,127], Mössbauer spectroscopy [66], and so forth. In particular, nuclear inelastic scattering measurements [128] have been performed to probe lattice dynamics of SCO powder [68] and nanoparticles [129,130] in both spin states. Nuclear inelastic scattering techniques permit accessing to the density of vibrational states from which the Debye sound velocity and different thermodynamical quantities can be extracted. More recently, the integration of SCO materials into microelectromechanical systems (MEMS) devices [131,132], for the conception of microactuator able to convert heat, into motion constitutes an original possibility to measure mechanical properties of SCO thin films [133,134]. All of these new techniques combined with the old ones will undoubtedly make it possible to complete the lack of characterization of the mechanical properties of SCO materials. The access to a database listing the thermal and mechanical properties of SCO materials may succeed in the prediction of the effects of the different physical ingredients on the observed equilibrium properties [135]. However, the thermodynamic aspects of nonequilibrium kinetic processes or spatiotemporal dynamics (nucleation and domain growth mechanisms) need the knowledge of thermomechanical properties of SCO solids of which we currently have only orders of magnitude. In particular, the spatiotemporal evolution of the spin transition seems to be very sensitive to heat exchange with the external environment [136] and the experimental determinations of the thermal conductivity, the heat and the radiative transfer coefficients become unavoidable for the building of a thermomechanical model in the framework of the local equilibrium approximations.
5 Conclusions
SCO is a phenomenon that involves two electronic states (HS and LS) close in energy and in a thermodynamical equilibrium. The thermodynamic approach for the phenomenological description of the measured properties is therefore crucial and has accompanied all of the experimental observations made since the discovery of the phenomenon. Many models called microscopic models going beyond the phenomenological descriptions made on the molecular or supramolecular SCO compounds including the kinetics and spatiotemporal aspects have been proposed. A point of convergence between the thermodynamical and microscopic approaches certainly lies in the analysis of objects of reduced size (nano-objects) going even to the single molecule or an assembly of molecules. This analysis can be called nanothermodynamics where the notion of surface energy, the ratio of the core to the shell in core–shell nano-objects, the stiffness of the chemical bonds, the matrix surrounding the molecule, and so forth, become crucial parameters to consider to go deeper into the understanding and the control of the SCO phenomenon.
Acknowledgments
This work was supported by the European Commission through the SPINSWITCH project (H2020-MSCA-RISE-2016, Grant Agreement No. 734322).


