1. Introduction
Separation and recycling of critical metals is important for the success of present and future carbon-free technologies. Hydrometallurgical separation based on nanoscience is one of the first technologies allowing the take-off of circular economy. Liquid–liquid (L/L) extraction is the core technology for the recycling of metals of interest. The optimization of this technology for industrial developments is done through experimental designs by varying many parameters [1, 2, 3]. These experimental designs are long and expensive, in particular because of the lack of knowledge on the fundamental mechanisms involved [4]. Therefore, the design of a cost-effective, adaptive and predictive formulation is still out of reach. Emulsification and demulsification processes in extraction devices are only efficient when the coexisting phases in dynamic equilibrium are located between binodal tie-lines in the Winsor II regime.
Most extraction processes are based on the combination of an extractant with a diluent. The main drawback of these processes is the formation of viscous emulsions known as a third phase. This occurs when the processes are intensified by increasing the concentration of solute and/or extractant. In this case, the organic phase splits into two phases of different compositions and densities: one, which is heavy, viscous and concentrated in ions and/or extracted acid [5], the other lighter, containing mainly the diluent and only minor amounts of extractant and solutes.
This third phase phenomenon causes increases in density and viscosity which complicate aqueous–organic mixing in L/L extraction devices and can also lead to a deviation in process performance. The consequences of an accident involving this third phase on an industrial scale would cost millions of euros and months of downtime for the extraction devices. An even more important problem is the nuclear criticality that can occur when dealing with fissile materials, especially in the reprocessing of nuclear fuel. For these reasons, the formation of the third phase is proscribed and must be avoided at all costs in industrial-scale L/L extraction operations.
To avoid this phenomenon, the mechanisms responsible for its occurrence must therefore be understood and predictable in all nuclear or non-nuclear recycling plants. Considerable work has therefore been devoted to the study of the third phase formation in several L/L extraction systems. Multiple exploratory studies have been made by identifying the experimental factors controlling and leading to the formation of the third phase [6, 7, 8]. The goal of these investigations is to find appropriate parameters for upscaling to the industrial scale. It has been emphasized that the lipophilicity of the extractant as well as its concentration, the nature of the diluent and the quantity of extracted acids and ions influence the formation of the third phase [9]. Although the study of the parameters makes it possible to find an optimal formulation without third phase formation, it is still necessary to have a model that can predict the formation of the third phase.
In the direction of the pioneering work of Osseo-Asare [10], the third phase can be understood not by considering the organic phase as a molecular solution, but as a complex fluid consisting of reverse micellar solutions. The understanding of the third phase formation was then advanced by using small-angle X-ray and neutron scattering to determine the molecular aggregation [11, 12]. Erlinger et al. established for the first time by SAXS analysis that the origin of the third phase formation arises from the short-range attractive interactions between the polar cores of reverse aggregates. This approach was then used to explain the formation of the third phase in several other organic extractant phases [6, 8, 13, 14, 15, 16].
In order to prevent the appearance of this third phase, phase modifiers are often added to the organic phase, such as fatty alcohols known as “lipotropes” (e.g. n-octanol, isodecanol, tridecanol) [17]. Since the electrolytes present in the organic phase have a well-identified Born energy that varies with the permittivity of the medium considered, it is advantageous to increase the relative permittivity of the diluent. Further increasing the polarity of the solvent by adding a phase modifier delays the appearance of the third phase, thus allowing a large increase in charge. However, these additives complicate the process due to their volatile nature. Moreover, their effect on the extraction efficiency as well as their mechanism of action remain poorly understood.
Indeed, several works have been devoted to clarifying the mechanisms responsible for the appearance of the third phase [6, 7, 14, 15, 16, 18, 19, 20]. In contrast, the effect of phase modifiers on aggregation and extraction has been poorly studied. For example, Kertes et al. suggested that the effect of the phase modifier is to increase the solubility of the complexes due to secondary solvation of the complex. The alkyl chain of modifiers around the complex tends to increase its solubility [21]. This is the main explanation given for the effectiveness of the modifier in preventing third phase, but a clear understanding of the effect of the modifier is still needed. Several experimental results are described in the literature. The main studies involve the use of alcohols with different chain lengths for the systematic determination of the LOC (Limiting Organic Concentration) values above which the third phase appears, as described in the review by Rao et al. for TBP systems [22]. However, it was observed that the addition of phase modifiers leads to a modification of the physicochemical properties of the organic phase influencing the extraction efficiency. Indeed, the advantage of phase modifiers in quenching third phase formation comes with a cost of an increase in the free energy of transfer. However, the effect of the modifiers on the structural organization of the organic phase is poorly discussed, even less in the presence of metal cations.
Despite the essential role and extensive application of phase modifiers, few studies have been dedicated to the effect of these molecules on aggregation properties of extraction systems, and to the best of our knowledge, none concern its structural effect on the origin of the third phase in the presence of metallic cations, or on the extraction efficiency of metals. Abécassis et al. studied the effect of n-octanol on the supramolecular organization of the extractant DMDOHEMA in dodecane after contact with aqueous nitric acid phases [23]. They demonstrated that n-octanol behaves differently depending on its concentration in the organic phase, acting as a co-surfactant at low concentrations and a co-solvent for higher concentrations. At low concentrations, n-octanol interacts with the extractant molecules by penetrating the amphiphilic film of the aggregate. At higher concentration, a new microstructure appears instead of the reverse aggregates. Thus, the micellar structure formed by the extractants before addition of n-octanol is destroyed. Indeed, n-octanol is known to form oligomers by intermolecular hydrogen bonds constituting regions of high electron density compared to the aliphatic parts [24, 25]. The properties of the extractant film are expected to be modified with possible consequences on the extraction properties. Nevertheless, this interesting study was performed in the absence of metal cations, and does not provide information on the impact of the phase modifier on the extraction efficiency.
In addition, Bauduin et al. compared the efficiency of different phase modifiers, called lipotropes, in suppressing the third phase. They tested different lengths of the alkyl chain of n-alcohols and showed that the longer the chain, the more effective the n-alcohol at repelling the third phase [17]. This study confirms the results reported by Dhamodaran and Srinivasan and summarized in the review by Rao et al. [7]. Dhamodaran et al. showed that increasing the carbon chain length of the alcohol from C4 to C9 leads to an increase in the LOC in the Th(IV)/TBP system [26]. Srinivasan et al. showed a similar effect of alcohol between butanol and heptanol on the LOC of a Pu(IV)/TBP system [7]. However, no metal cation was involved in the study by Bauduin et al. and the structural mechanisms by which the phase modifier inhibits the third phase were not investigated.
Lu et al. carried out a phenomenological and mechanistic study of the role of n-octanol as a phase modifier on the appearance of the third phase in the AMEX process for the extraction of uranium in sulfuric medium [27]. They first showed that n-octanol does not affect the extraction properties of the Trioctylamines (TOA) ligand, but it plays an important role in its aggregation. Indeed, the critical concentration for TOA aggregation and third phase formation are shifted to higher concentrations by the presence of n-octanol in the organic phase. They then characterized the structure of these aggregates by small-angle neutron scattering (SANS). Density profile fitting (i.e., SLD) of the aggregates, performed on samples containing deuterated and non-deuterated n-octanol, allowed the localization of the n-octanol molecules in the structure of the organic phases to be determined. Contrary to what was proposed by Abécassis in the case of the DMDOHEMA extractant [23], the surface tension results demonstrate that n-octanol is not a co-surfactant because its addition increases the surface tension of the organic phase as well as the cac (Critical Aggregation Concentration) value. n-Octanol does not decrease the curved area per molar head of the extractant, meaning that n-octanol does not penetrate into the core of the aggregates. Using a fit of the SANS data, with a form factor and a structure factor, of systems containing deuterated or non-deuterated n-octanol molecules, they showed that the effect of n-octanol on preventing third phase formation would be due to a decrease in attractive interactions between the aggregates, and a steric barrier effect by preferential adsorption. By penetrating the alkyl chains of the extractants and forming an outer shell around the aggregates, n-octanol creates a protective barrier that prevents the aggregates from swelling and coalescing with each other.
In all these studies, the phase modifiers considered are “reverse hydrotropes” or “lipotropes”. This term is used to define amphiphilic molecules with a hydrophilic/lipophilic ratio lower than that of surfactants forming reverse micelles. The objective of this paper is to explore another class of molecules, the “hydrotropic” molecules, in the study of the formation of the third phase. These two classes of molecules have common properties [17], which leads us to believe that hydrotropes can be effective in inhibiting third phase formation since these molecules are both water- and oil-soluble. These common properties are as follows: (i) The ability to solubilize hydrophilic or hydrophobic compounds in apolar or polar solvent, respectively; (ii) The low aggregation capacity; (iii) The ability to break up ordered structures such as hexagonal or lamellar structures.
For this purpose, a model hydrotrope (PnP) is considered as a replacement for commonly used phase modifiers. Our aim in this work is to determine the modifications induced when the most industrially used hydrotrope (PnP) is added to one of the most common extractants HDEHP or DMDOHEMA, in order to get a first clue about the relationship between modification in solvent-phase self-assembled nanostructures and the modified distribution coefficients. Chemical names and structures of the investigated molecules are presented in Figure 1 and Table 1. Therefore, the effect of PnP on the appearance of the third phase is first studied for two extraction systems. Then, its role as a phase modifier is identified and quantified by coupling surface tension and neutron scattering experiments. Furthermore, a comparison of the mechanisms at the origin of the suppression of the third phase between “lipotropes” and “hydrotropes” at the structural scale is performed. The analogy between phase modifiers and co-solvents/co-surfactants is systematically taken into account in our approach. The objective is to provide a clear and general interpretation on the role of phase modifiers in the disappearance of the third phase. Finally, the consequences of these mechanisms on the extraction efficiency are discussed.
Structure of the molecules used in this work: (a) HDEHP, (b) DMDOHEMA, (c) TOA, (d) PnP and (e) n-octanol.
Abbreviations and chemical names of compounds employed
| Species | Abbreviation | Chemical name |
|---|---|---|
| Extractant | DMDOHEMA | N,N′-dimethyl-N,N′-dioctylhexyl-ethoxy-malonamide |
| HDEHP | bis(2-ethylhexyl)phosphoric acid | |
| TOA | Trioctylamine | |
| Hydrotrope | PnP | 1-Propoxy-2-propanol or Propylene Glycol Monopropyl Ether |
| Lipotrope | n-octanol | - |
2. Experimental
2.1. Chemicals
The solvating extractant N,N′-dimethyl-N,N′-dioctylhexyl-ethoxy-malonamide—C29H58N2O3 (DMDOHEMA)—was purchased from Technocomm Ltd with a purity higher than 99%, determined by gas chromatography coupled to mass spectrometry (GC-MS). The cation exchanger bis(2-ethylhexyl)phosphoric acid (HDEHP) was purchased from Sigma Aldrich with a purity higher than 97%. Dodecane and PnP (1-propoxy-2-propanol) were purchased from Sigma Aldrich with purity higher than 99%. The chemical products used for SANS experiments (deuterated dodecane, deuterated n-octanol, D2O and 70% DNO3) were purchased from Eurisotope. Water was deionized using a Millipore Milli-Q purification system (Merck Millipore, Billerica, MA). All other chemicals were purchased from commercial sources: 70% nitric acid HNO3 (Sigma Aldrich), europium (III) nitrate hexahydrate Eu(NO3)3⋅6H2O (Sigma Aldrich; purity >99.9%) and iron (III) nitrate nonahydrate Fe(NO3)3⋅9H2O (Sigma Aldrich; purity >99.999%). All chemical products were used without further purification.
2.2. Solution preparation and extraction systems
A range of concentration of 0.02−2 mol/L of extractant molecules (HDEHP or DMDOHEMA) was first diluted in n-dodecane together with 1 to 10% vol of PnP as a phase modifier. The organic solutions obtained were further contacted with equal volumes of an aqueous phase containing nitric acid and metals. The compositions of the aqueous phase used in this work are summarized in Table 2. After being mixed at 500 rpm, 25 °C for 1 h, organic and aqueous phases were centrifuged at 12,000 rpm, 25 °C for 20 min.
Compositions of the extraction systems considered in this study
| System | Ions | Acid |
|---|---|---|
| HDEHP/n-dodecane | [Eu] = 100 mM and [Fe] = 30 mM | [HNO3] = 0.03 M |
| DMDOHEMA/n-dodecane | [Eu] = 100 mM and [Fe] = 30 mM | [HNO3] = 4 M |
2.3. XRF
The commercial XRF spectrometer used to analyse both aqueous and organic phases after extraction is a SPECTRO XEPOS (AMETEK) model. It is commercially equipped with an energy dispersive X-ray analyser (ED-XRF) that uses the energy loss of the X photons in a silicon material to determine the spectrum by a suitable signal processing. Secondary targets reduce background noise compared to the output signal from the tube and improve fluorescence detection. Liquid samples were placed in 6 mm diameter cups, the bases of which consisted of a 4 mm thick prolene film. The XRF spectrometer was used to analyse a series of 11 cups in sequence, using a rotating carousel that positions the sample to be measured above the inverted optical part. A volume of 200 μL of each of the samples was placed in the micro-cups for analysis for a duration of 40 min. The X-ray tube generator was set at 40 kV and an intensity of 0.160 mA. The Zirconium secondary target was monitored between 15 and 17 keV to visualize the fluorescence of all lanthanides while for iron it was monitored between 4 keV and 10 keV.
The free energy of transfer of any cation present in a mixture and in acidic conditions can be written as:
| (1) |
| (2) |
2.4. Inductively Coupled Plasma Optical Emission Spectroscopy (ICP-OES)
Rare-earth elements extraction was also analysed by ICP-OES: aqueous solution ion concentrations were measured before and after extraction. The equipment used for this study is a SPECTRO ARCOS ICP-OES, which is equipped with a circular detector consisting of 32 linearly aligned CCDs, each having a resolution of 3648 pixels covering wavelengths ranging from 130 to 770 nm. The resolution of the detector is 8.5 pm from 130–340 nm and 15 pm from 340–770 nm with an intensity dynamic range of eight orders of magnitude. CCDs were read out simultaneously and a complete spectrum was generated under two seconds. The circular polychromator (Paschen-Runge design, optical components: MgF2, Zerodur structure) has a focal distance of 750 mm. The radio frequency generator works at a frequency of 27.12 MHz and has a power output of 0.7 to 1.7 kW with an efficiency of 70% and a stability of 0.1%.
A typical sample analysis was carried out as follows: the sample was diluted to an appropriate concentration ranging between 5 and 15 mg⋅L−1 using 2% HNO3 in water. Before each run, a calibration was performed with metal standards made from a calibrated solution (1000 mg⋅L−1) which was diluted to obtain standards at 0, 1, 5, 7.5, 10 and 15 mg⋅L−1. Each sample was measured three times for statistical reproducibility and after each measurement the system was purged with 2% HNO3.
2.5. Interfacial tension measurements
Interfacial tensions γ between aqueous and organic phases are measured at 25 ± 0.1 °C using a Krüss rotating drop tensiometer (SDT) coupled to a high-resolution USB3 camera. The measurement is based on the deformation of a drop under centrifugal force. For this purpose, the aqueous phase was used as the external phase in the capillary as well as to completely rinse the capillary before the measurement. The organic phase droplet, composed of extractant diluted in an organic solvent of varying concentrations as well as phase modifier, is injected into the capillary held horizontally at 2000–3000 rpm. The capillary is then rotated and the droplet elongates under the effect of centrifugal forces as the rotation speed increases. The speed of rotation is chosen so that the length of the drop at equilibrium is greater than four times its radius. Therefore, measurements are made in the range between 5000 and 8000 rpm. Using only the data obtained in the rotational speed range described above, where the interfacial tension values are nearly constant, two different oil droplets were measured at different rotational speeds. The standard calculation of the interfacial tension from the rotating droplet size requires density data of the two phases, which was obtained using an Anton-Paar DSA 5000 densitometer.
The tensiometer is combined with ADVANCE software. This software performs image analysis by applying either Vonnegut approximation functions or by using an evaluation algorithm based on a Young–Laplace fit. For the measurements presented here, the experiments are performed by applying the Young–Laplace approach for curved surfaces under the influence of a centrifugal field, where the curvature of the drop shape is used instead of the diameter, to extend the measurement range to higher interfacial tension values. The diameter and curvature of the drop is determined from the video image of the drop. Calibration of the tensiometer is performed before each measurement to obtain the scale of the image.
2.6. Small-angle neutron scattering
Small-angle neutron scattering measurements were performed at the Institut Laue-Langevin (ILL, The European Neutron Source, Grenoble, France) on the instrument D11 (lowest momentum transfer small-angle diffractometer) operated with a monochromatic beam (relative FWHM 10%) and with 3He detectors. Within the framework of two beam times, different configurations were used to cover a large range of q. These configurations that are detailed in Table 3, allowed to cover a total q-range from 0.005 to 0.7 Å−1 or from 0.025 to 0.5 Å−1, where q is the magnitude of the wavevector (q = (4π/𝜆) sin(𝜃/2), 𝜃 being the scattering angle). All measurements were performed under atmospheric pressure and at room temperature. Samples prepared with deuterated solvents to increase contrast and reduce incoherent background were contained in quartz cuvettes type 120-QS of 1 mm pathway (Hellma, Müllheim, Germany). Standard corrections for sample volume, neutron beam transmission, empty cell signal subtraction, and detector efficiency were applied to obtain the scattered intensities. The absolute scale (cm−1) was calculated by normalization with the incident neutron beam. Data reduction was performed with Grasp 9.25b [29], accounting for detector background (measured with 10B4C), transmission, sample pathway, parallax, scattering by D2O, and dividing by the scattering of 1 mm H2O as a flat field correction. The intensity of 1 mm H2O was used as a secondary standard to obtain absolute scale. A constant was further subtracted to account for incoherent background due to hydrogen. Data are available on demand (DOI: 10.5291/ILL-DATA.EASY-877 and 10.5291/ILL-DATA.EASY-1040).
Configurations used for SANS measurements (doi: 10.5291/ILL-DATA.EASY-877; doi: 10.5291/ILL-DATA.EASY-1040)
| Beamtime | Wavelength (Å) | Sample-to-detector-distance (m) | q-range (Å−1) |
|---|---|---|---|
| 1 | 4.6 | 1.7 | 0.005–0.7 |
| 16.5 | |||
| 2 (only for dodecane/n-octanol samples) | 4.6 | 2.5 | 0.025–0.5 |
2.7. SANS modelling
SANS data modeling was performed using the SASET or SASWIEV programs. Two models were used:
- An Ornstein–Zernike (OZ) model: I(q) = I0∕(1 +𝜉 2 q2) accounting for clusters, with 𝜉 being the correlation length of the OZ domains. In order to determine the correlation length and radii of the aggregates, the OZ formalism is used for fitting the data in the small q range (0.2–4 nm−1). The OZ function can always formally be converted to an effective radius of gyration RG of compact aggregates—if they are present—by:
where 𝜉 is the correlation length and I0 is the intensity for q = 0. I0 takes into account the density of the scattering lengths of the different species and the volume fraction of each phase. The spherical radius RS of all identical compact spherical aggregates is equal to:(3) (4)
In this case, the relation between the correlation length and the spherical radius of the aggregate is valid:
| (5) |
- A core–shell spherical form factor model and details of equations are given in the supporting information. The form factor, p(q), depends on the core and aggregate radii and on their scattering length densities.
3. Results and discussion
In order to determine the role of the phase modifier, different extraction systems are considered and are summarized in Table 2. The effect of PnP as a phase modifier on the appearance of the third phase as well as on the supramolecular structuring of the organic phase is studied. For this purpose, surface tension combined with neutron and small angle X-ray scattering is used. Then, the influence of the PnP content on the extraction properties is evaluated. Finally, a comparison between a hydrotropic (i.e., PnP) and a lipotropic (i.e., n-octanol) phase modifier is performed and the mechanisms involved in each case are discussed.
3.1. The action of the hydrotrope PnP as a phase modifier: phase diagrams
In order to highlight the action of PnP as a phase modifier, the phase diagrams of the systems studied are explored. The appropriate way to represent the phase behavior, according to the Gibbs phase rule, in systems containing more than three components would be a multidimensional phase diagram, transforming the two-dimensional triangle representation into a three-dimensional prism [23, 24]. However, the visualization is complex, therefore, cuts through the phase prisms are necessary. The location of the cut in phase prism used in this study is represented by a thick red line in the insert of Figure 2. We vary the extractant concentration in the diluent used as well as the concentration of the added phase modifier (i.e., PnP on the Z-axis). In this study, we focus on the solvent-rich side of the phase prism (i.e., the organic phase). The resulting cuts projected on an XY plane are shown in Figure 2. Two extraction systems are examined: Figure 2(a) in the case of an ionic extractant (HDEHP) and Figure 2(b) in the case of a solvating extractant (DMDOHEMA).
Evolution of phase stability with different amounts of phase modifier as a function of extractant concentration in dodecane containing different quantities of PnP after contact with an aqueous phase containing rare-earth elements (see Table 2 for the compositions of the aqueous phase considered in this study).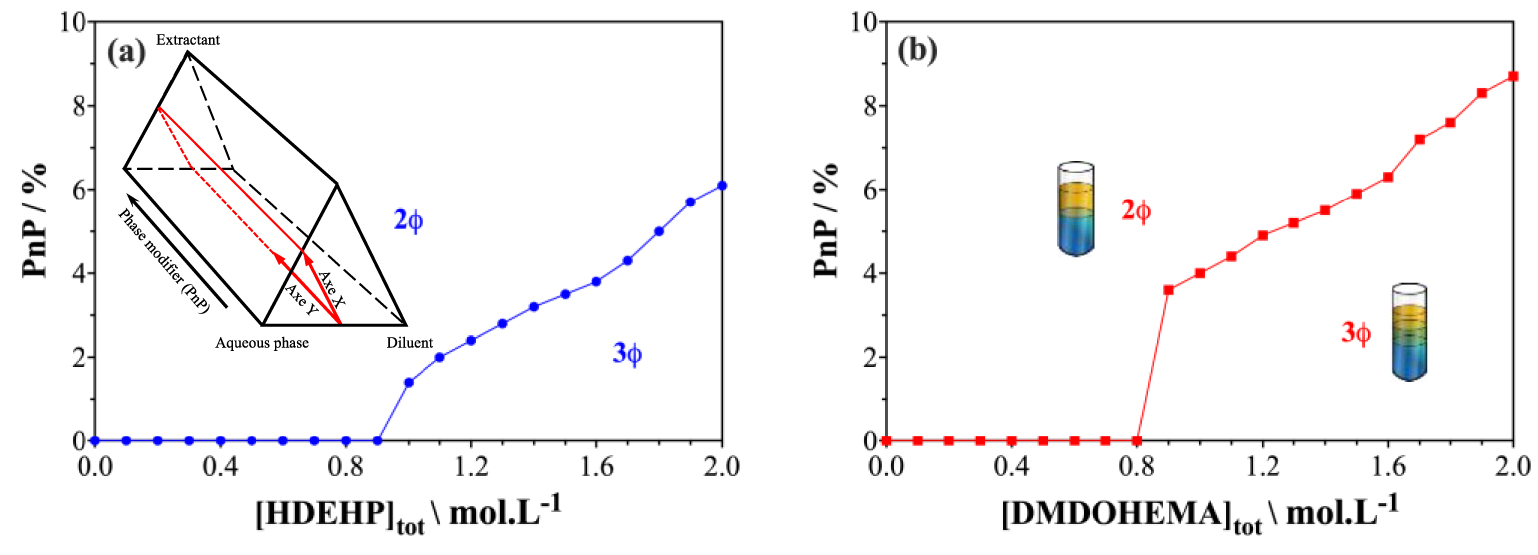
The aim is to study the influence of PnP addition to the organic phase on the third phase formation for two different extraction systems (i.e., HDEHP/dodecane/nitric acid and DMDOHEMA/dodecane/nitric acid) as well as to compare its effect as a function of the nature of the extractant molecule used. The concentration of PnP was varied from 1 to 10 vol% (0 to 0.75 mol/L) and the concentration of extractant molecules from 0 to 2 mol⋅L−1. The compositions of the aqueous phases were kept constant for the two systems. The compositions of the aqueous phases used for each extraction system are chosen so that the distribution coefficients after contact of the two phases are greater than 1. The compositions of the different aqueous phases used in this study are summarized in Table 2. For a given extraction system, the aqueous phase composed of acid and ions of interest is contacted with an organic phase containing the extractant diluted in dodecane with 0 to 10% PnP as phase modifier. The contacting is performed at a volume ratio of organic to aqueous phase (O/A) equal to 1, for 1 h at a temperature of 25 ± 1 °C. It should be noted that the tie-lines for the considered extraction systems were determined in the presence of PnP. In the concentration range of PnP used in this study, the tie-lines are directed to the pure aqueous phase. Therefore, no pre-equilibration step is necessary.
The stability of the organic phase is examined as a function of the extractant concentration. For each concentration of PnP, the third phase limits were determined by a step-wise increase of extractant concentration until a visible phase instability appears. Conversely, for each extractant concentration at which the third phase appears, PnP is added until the third phase disappears. Figure 2 shows the results obtained for the two extraction systems.
The large domain for which two phases are observed in Figure 2 corresponds to a Winsor-II type, where a water-swollen solvent-rich phase is in equilibrium with an aqueous phase [30, 31]. This situation is suitable for L/L extraction. Still, it should be noted that in this representation of the phase diagram, the tie-lines cannot be drawn, as they are out of the plane of the figure. The three phase regions, denoted (3Ø), correspond to the domain where a third-phase appears. Approaching the biphasic–triphasic transition usually increases extraction yields, since the extractant concentration is increased. However, the formation of a multiphase viscous fluid is encountered, resulting in blockage of the mixer-settlers or pulsed column used.
Figure 2 shows that PnP reduces or even completely suppresses the third phase domain for the two extractants studied. Therefore, PnP acts as a phase modifier and quenches efficiently the spontaneous emulsification as a three-phase fluid. In the absence of PnP, a third phase is formed from an extractant concentration of 0.9 mol⋅L−1 for HDEHP and 0.8 mol⋅L−1 for DMDOHEMA. Moreover, the more the extractant is added, the larger the volume of the third phase becomes. Adding 5% of PnP is sufficient to push the third phase boundary by 50% in extractant content to the left. For higher PnP concentrations, no third phase formation was observed in the range of extractant concentration investigated (0.1 to 2 mol⋅L−1 for both extractants). It should be noted that the third phases obtained for the DMDOHEMA system are more viscous than those of the HDEHP system. This quenching of the third concentrated phase allows the extraction process to be intensified, i.e., increasing the loading capacity of the extraction system.
We have highlighted that PnP as a hydrotrope also acts as a phase modifier. We have shown that PnP inhibits the formation of the third phase for the two extraction systems considered. However, the effectiveness of the phase modifier depends on the nature of the extraction system chosen. In the following, the effect of PnP as a phase modifier is examined at the nanoscale. The objective is to understand how PnP reduces this triphasic domain and what changes are induced by the addition of PnP on the structuring of the organic phase.
3.2. The structural effect of the phase modifier on the formation of the third phase and the induced molecular forces
In order to identify the molecular forces involved in this suppression of the third phase using a hydrotrope (PnP), surface tension and neutron scattering are used. The aim is to elucidate the role of PnP on the structuring of the aggregates in the organic phase for the two extraction systems considered.
3.2.1. Surface tension
First, we consider the surface tension of the aqueous–organic interface. Any significant decrease in surface tension is indicative of the emergence of a micrometric layer at the aqueous–organic interface, forming an interphase [32] that stiffens the macroscopic water–solvent interface [33] and also considerably slows down the kinetics of ion transfer [34].
Figure 3 shows the interfacial tension results, between the aqueous and organic phase, as a function of the extractant concentration. The surface tension is measured with organic phases containing different amounts of PnP. Although PnP has similar effects on the phase diagrams of the two extraction systems considered (HDEHP and DMDOHEMA), the effect of adding a hydrotrope to organic phase on the surface tension are surprisingly different. The presence of PnP in the case of an ion-exchanger extractant (HDEHP) induces an increase in surface tension (cf. Figure 3(a)), whereas it shows a decrease in the case of a neutral solvating extractant (DMDOHEMA cf. Figure 3(b)). The decrease of the surface tension curves as a function of the extractant concentration indicates that the extractant molecules adsorb at the interface, which reflects the amphiphilic and surface-active behavior of the molecule.
Interfacial tension of different extraction systems with different quantities of 1-propoxy-2-propanol (PnP) as a function of extractant concentration in dodecane (a) HDEHP (b) DMDOHEMA.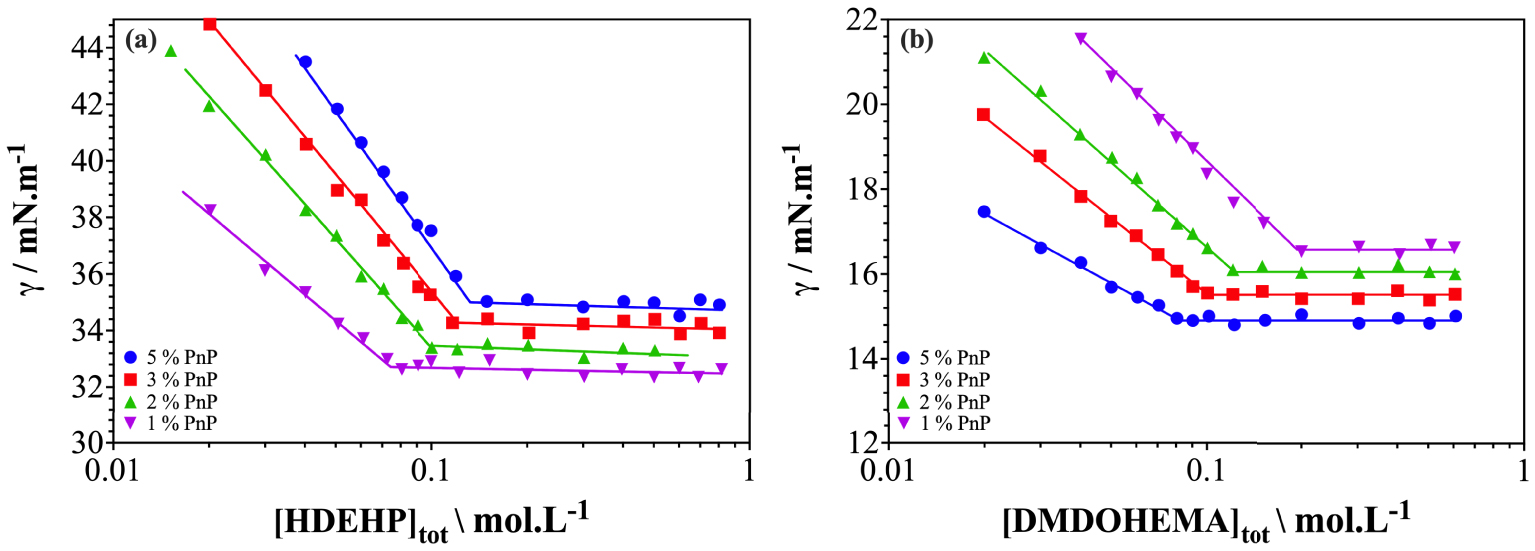
Furthermore, the point where the break of the γ-slope is observed, shifts to a higher extractant concentration with the amount of added PnP, when the acidic extractant (HDEHP) is considered. Conversely, this breakpoint shifts to lower extractant concentrations when a neutral extractant is used (DMDOHEMA). The break of the γ-slope observed on each curve indicates the critical aggregation concentrations (cac) when the extractant starts to form aggregates in the organic phase. The cac of each series corresponds to the concentration above which the surface excess of extractant remains constant and gives the chemical potential of the free extractant in the organic solution. The cac values for the different extraction systems are plotted in Figure S1 in the SI.
In the case of HDEHP, cac values of 0.07, 0.1, 0.11 and 0.12 mol⋅L−1, are obtained with 1, 2, 3 and 5% of PnP, respectively. This means that the presence of PnP as a phase modifier inhibits the formation of aggregates. Furthermore, the addition of a higher concentration of PnP to the organic phase induces an overall increase in surface tension values for the same concentration of HDEHP. As a consequence, PnP in this case does not play the role of a co-surfactant.
In the case of DMDOHEMA, the cac value decreases from 0.2 mol⋅L−1 for 1% of added PnP to 0.08 mol⋅L−1 for 5% of added PnP. Moreover, the surface tension for the same concentration of DMDOHEMA decreases with increasing amounts of added PnP (cf. Figure 3(b)). The decrease in surface tension is due to the propensity to form more or larger reverse aggregates that shift the chemical potential of the free extractant into the organic phase. This means that PnP plays the role of co-surfactant in this case, since aggregates are easily formed by adding PnP. A co-surfactant is a molecule that cannot form micelles by itself in a given solvent, but once a micelle is formed by an extractant molecule (here DMDOHEMA), a cosurfactant molecule participates in the micellar structure. In other words, a co-surfactant facilitates the formation of mixed films in micelles as well as in microemulsions, without forming micelles by themselves.
In order to confirm the co-solvent and co-surfactant effects of PnP in the formation of aggregates in the organic phase, the surface tension measurements are converted to surface area per polar head of extractant in the aggregate, using the Gibbs equation (see Equations (S1) and (S2) in the SI). If PnP plays the role of a co-surfactant, its addition to the organic phase would result in an increase in the surface area per polar head, since PnP in this case is intercalated into the interfacial film. If PnP has a co-solvent behavior, the surface area per polar head will decrease with the amount of PnP added, since PnP does not promote aggregate formation. Figure S1 shows the results obtained for the two extraction systems considered. In agreement with expectations, the surface area per polar head decreases with increasing PnP content for HDEHP, while it increases with increasing PnP concentration for DMDOHEMA. This confirms that PnP molecules do not play the role of co-surfactant in the case of HDEHP extractants. However, for DMDOHEMA, PnP acts as a co-surfactant and penetrates into the polar core of the aggregate.
The first major conclusion is that the interfacial film formation at the water–oil interface is facilitated by the presence of PnP in the case of a neutral extractant (DMDOHEMA). This effect is a “co-surfactant” effect, since the formation of amphiphilic film, either curved as water–oil in the bulk or flat at the macroscopic water–oil interface, is more easily formed in presence of the hydrotrope. Moreover, surface tension measurements showed that the surface area per polar head of extractant increases with the addition of PnP.
In the case of the acidic extractant (HDEHP), the effect is opposite to that observed with DMDOHEMA. More extractant is required to form water in oil curved interface or flat macroscopic interfacial films. This means that the monomer–micelle equilibrium is disturbed and a molecular dispersion state is favored. This effect corresponds to a “co-solvent” effect.
Both effects, co-solvent and co-surfactant, prevent the third phase formation, but for completely different reasons: on the one hand due to a higher molecular dispersion in the case of ion exchanger extractant, and on the other hand due to an easier formation of curved mixed films (or mixed aggregates) in the case of solvating extractant.
Two important differences occur in the molecular mechanisms: hydrotropes as co-surfactants increase the active interface made from adjacent molecular films on which an adsorption isotherm must be considered [35]. In contrast, hydrotropes as co-solvents reduce the total active interface made from adjacent extractant molecules forming an active film [36]. On the other hand, co-surfactant as well as co-solvent effects increase the local density of the extractant and hydrotropes, thus, modifying the configurational entropy term, crucial in extraction, as initially shown by Rey [32, 33] and confirmed by Špadina et al. [37].
3.2.2. SANS
In order to clarify at the nanoscale the difference between co-solvent and co-surfactant effects and their impact on the appearance of the third phase, the supramolecular structure of the organic phase is investigated by neutron scattering, using deuterated dodecane, as well as the combination of deuterated and non-deuterated polar core of the aggregates [12].
Since X-ray scattering is dominated by heavy atoms and the scattering contrast between the alkyl chain of the extractant and the organic diluent is not sufficient in SWAXS, the signals are more complex to interpret and the scattering length density is a less smooth function in SAXS than in SANS when a deuterated solvent is used. In addition, the polar cores produce strong scattering, making direct interpretations of the X-ray spectra more ambiguous. For these reasons, SANS is used to better understand the colloidal structure that leads to the suppression of the third phase. The SANS intensities are primarily sensitive to the contrast between the deuterated and non-deuterated parts of the organic phase. Therefore, the experiments were performed in a deuterated diluent (n-dodecane-d26) and a hydrogenated extractant in order to obtain a sufficiently high contrast between the extractant chains and the diluent.
For a first semi-quantitative analysis of the spectra, a fitting model was chosen to obtain qualitative trends. Due to the high volume fraction of the scatterers, the results give only an approximate overview and show trends, as the structure factor is crucial, but is difficult to fit correctly. Indeed, an average aggregation number cannot be unambiguously determined by a decomposition of the form factor and the structure factor, especially when the scattering is best represented by an OZ function without detectable asymptotic Porod or Kirste-Porod correction [38].
The model chosen is a simple OZ fit that indicates the correlation between two correlation centers. The interpretation of the correlation length obtained must be done on a case-by-case basis. It can represent the average size of the fluctuating particles or the average entanglement length in the case of semi-diluted polymers. In our case, the cube of the correlation length or the volume of a sphere of equivalent radius of gyration divided by extractant molecular volume of the extractant can be used as a first estimation of the effective aggregation number, if aggregation as a distinct “preferred” aggregate exists. Without aggregation, the Debye model of random ideal mixing close to the theta point of the binary system used is the best approximation.
In order to confirm the co-surfactant/co-solvent dichotomy, SANS experiments on absolute scale were performed for the two cases studied (HDEHP and DMDOHEMA). The absolute intensity expressed in cm−1 is presented in linear as well as in logarithmic scale as a function of the wave vector q (cf. Figures 4 and 5), with and without added hydrotrope. In Figures S2 and S3, the slight difference in SANS using D2O and H2O shows that the polar core volume does not vary significantly with the low amount of co-extracted water present. Data is shown in logarithmic scale to illustrate that core–shell micelle modelisation using a Baxter model for the structure factor is difficult in the absence of Porod asymptotic q−4 decay at high q.
SANS spectra of organic phases containing 0.6 M HDEHP in deuterated dodecane charged 10 mM La. Grey dashed lines represent fits obtained with a simple OZ fit.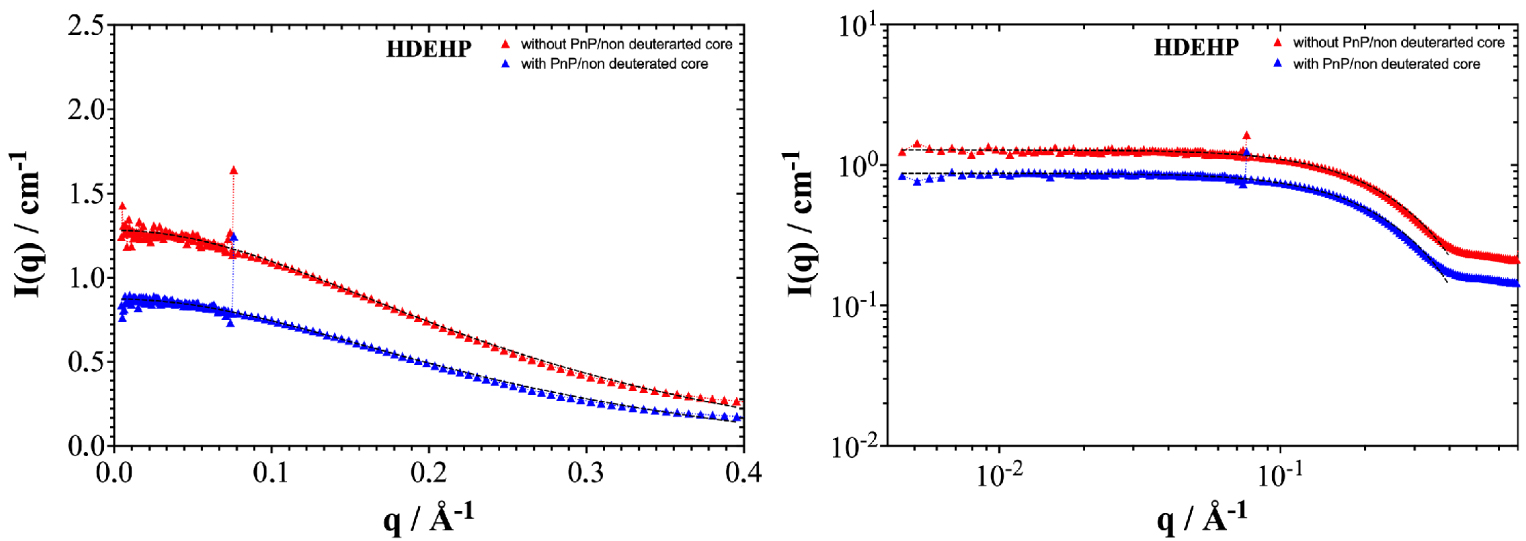
SANS spectra of organic phases containing 0.6 M DMDOHEMA in deuterated dodecane charged 10 mM La. Grey dashed lines represent fits obtained with a simple OZ fit.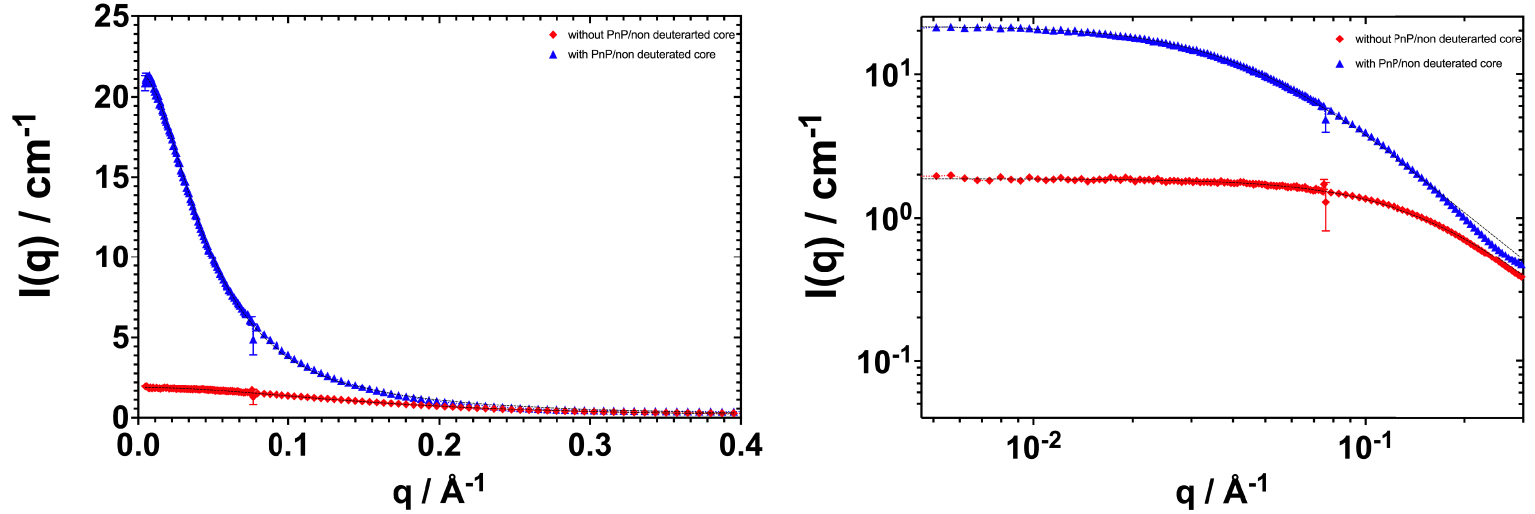
Figure 4 shows SANS spectra for organic phases containing 0.6 mol⋅L−1 of HDEHP diluted in deuterated dodecane without added hydrotrope (red spectrum) and with 5% vol of added PnP (blue spectrum). The data were collected for organic phases after being contacted with the aqueous phase (cf. Table 2). The addition of PnP causes a decrease in the diffusion intensity at low q which could be due either to fewer or smaller aggregates, or to a less efficient interaction between aggregates considered as hard spheres. The same behavior is observed with or without deuteration of the polar core (cf. Figure S2). The addition of 5% PnP induces a decrease in diffusion to the asymptotic small q value of 35% for HDEHP. The curves with and without hydrotrope are still homothetic i.e., vertically shifted only on log-scale. There is hardly any induced variation in the correlation length as can be seen by examining Table 4.
Microstructural determination obtained by fitting the scattering by an OZ behavior
| Forward scattering I0 (cm−1) | Correlation length (Å) | RG | RS | |
|---|---|---|---|---|
| HDEHP system without adding PnP | 1.54 | 3.86 | 6.69 | 8.65 |
| HDEHP system with PnP | 1.07 | 4.23 | 7.33 | 9.47 |
| DMDOHEMA system with PnP | 21.49 | 21.90 | 37.93 | 49.06 |
| DMDOHEMA system without PnP | 1.92 | 6.15 | 10.65 | 13.78 |
For the HDEHP extractant, the OZ fit indicates a slight decrease in correlation length in the presence of PnP (see Table 4). This means that the number of aggregates decreases with the presence of PnP as a phase modifier. As a consequence, the cac decreases. This is in agreement with the surface tension measurements. The co-solvent molecules solubilize the extractant molecules as monomers and reduce the average aggregation number, quantified in Table 4 by the equivalent gyration radius. The data obtained with and without deuteration of the aqueous phase are very similar. This is due to the low co-extraction of water and acid in the case of the HDEHP extractant, which are water-poor w/o reverse aggregates (less than one water molecule per extractant molecule).
In summary, PnP acts as a co-solvent for the ion-exchanger extractant (HDEHP). The cac increases and the diffusion intensity at small q decreases with the addition of PnP to the organic phase. This means that PnP solubilizes the extractant aggregates in the organic phase. The structure of the organic phase changes and the average aggregation number decreases when PnP is added.
Figure 5 shows the spectra collected in the case of a solvating extractant (DMDOHEMA) with and without the addition of phase modifier. In contrast to the ion-exchanger extractant, the diffusion intensity increases when PnP is added to the organic phase, by a factor of 10. Since the intensity is proportional to the number of scattering objects, we can infer that the presence of PnP in the solution increases the number of aggregates and/or their size. This is in agreement with the surface tension results, where the presence of PnP decreases the cac of the solvating extractant. In order to quantitatively evaluate the effect of PnP addition, OZ fits are performed and listed in Table 4.
The correlation length increases in the presence of PnP, with or without deuteration of the polar core. The number of aggregation increases from 12 to 40 for DMDOHEMA. This confirms that PnP participates in the aggregation of the extractant molecules and penetrates into the polar core of the aggregate. Upon addition of PnP, the w/o aggregates become larger by an average factor of 4.
In summary, PnP acts as a co-surfactant for the solvating extractant DMDOHEMA and its addition to the organic phase decreases the cac. PnP molecules participate in the aggregation of the extractants in the organic phase by increasing the size of the aggregates formed.
3.3. Hydrotropes/lipotropes comparison
As pointed out in the introduction, the phase modifiers used in hydrometallurgy are often fatty alcohols such as n-octanol. The addition of n-octanol to the diluent effectively prevents the presence of third phase for many extraction systems [24, 27]. However, the molecular mechanisms involved cannot be unambiguously determined when only small-angle X-ray scattering is used experimentally [23]. The analogies of behavior in phase diagrams, between these molecules and hydrotropes, have been highlighted by Bauduin et al. by coining the term “lipotropic” [17]. The aim of this section is to compare the mechanisms of action of two categories of phase modifiers, “hydrotrope” and “lipotrope”, at the structural scale. For this purpose, we consider the structural study performed by Lu et al. on the effect of n-octanol on the TOA/n-dodecane extraction system [27].
Figure 6 shows the results obtained in the work of Lu et al. [27]. In this study, the n-octanol phase modifier is considered and its effect on the structural organization of the TOA/n-dodecane extraction system is studied. The organic phases were analyzed after contact with an aqueous phase containing 0.1 mol⋅L−1 H2SO4, 0.1 mol⋅L−1 Li2SO4, 1.05 mmol⋅L−1 U(VI) and 2.28 mmol⋅L−1 Fe(III).
(a,b) Water/surface tension and SANS on logarithmic scale comparing the scattering in the case of the TOA extractant/deuterated dodecane/n-octanol system, adapted from the work of Zijun et al. [27].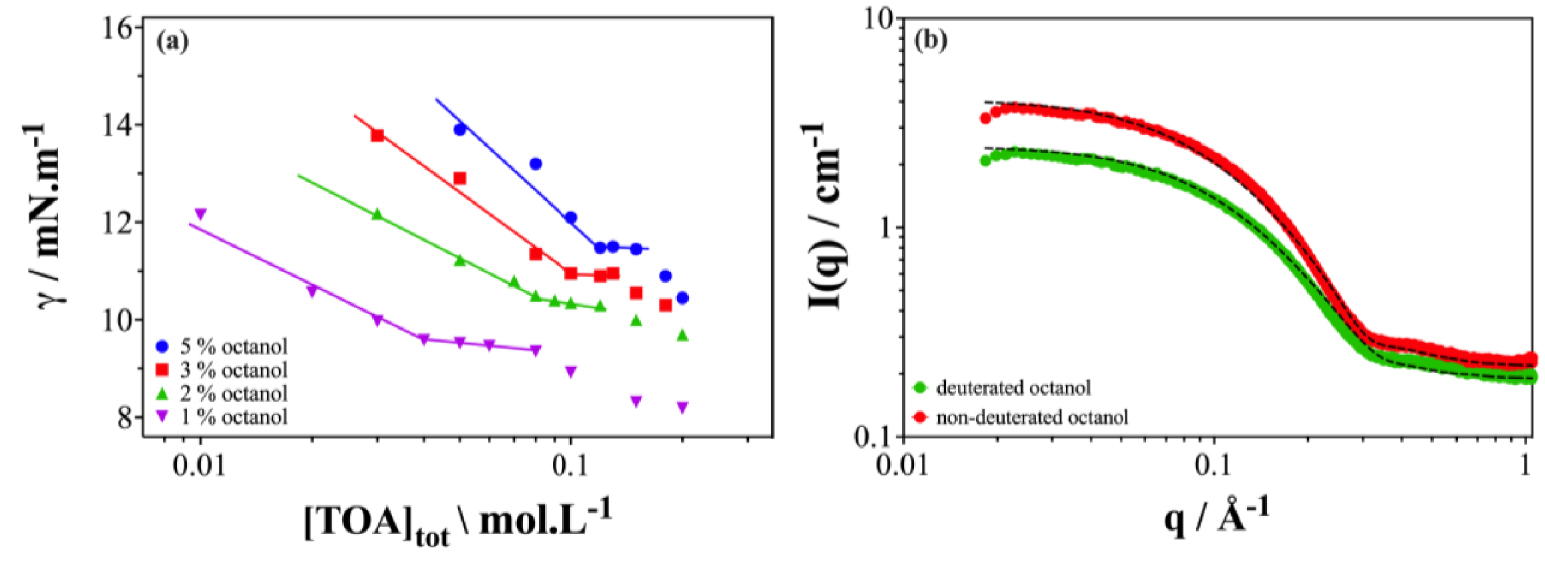
As can be seen in Figure 6(a), the surface tension in the case of the extractant TOA with the addition of n-octanol resembles the case of the co-solvent. The cac increases with the addition of n-octanol, as well as the overall surface tension values for a given concentration. This means that there are less extracting molecules at the oil–water interface when adding n-octanol.
Figure 6(b) shows the neutron scattering spectra of organic solutions containing 0.3 mol⋅L−1 of TOA, with 3% in volume fraction of non-deuterated and deuterated n-octanol. The scattering intensity decreases significantly when n-octanol is deuterated which means that the aggregate appears as a smaller volume when deuterated n-octanol is used. This decrease reveals that n-octanol molecules are located in the aggregate structure. This apparent swelling in the presence of n-octanol keeps the average number of TOAs per aggregate constant. It appears that the n-octanol molecule in the study of Lu et al. adsorbs on the outer surface of the aggregate [27]. This seems counterintuitive, as there is no possible weak adsorption due to (enthalpic) attraction. So what is the origin of this swelling?
In order to clarify this point and to detect possible local structuring, as was found in the case of the n-octanol/ethanol binary mixture [39], SANS experiments of n-octanol/deuterated n-dodecane binary mixtures are carried out over a wide range of q and at three different concentrations of n-octanol: 3%, 9% and 27% in volume fraction with or without prior contact with H2O or D2O. Figure 7 shows the obtained spectra.
SANS spectra for 3, 9, and 27% n-octanol in deuterated dodecane shown in logarithmic scale: (a) uncontacted, (b) contacted with D2O and (c) contacted with H2O, (d) Small q intensity (I0) and Porod constant as a function of n-octanol volume fraction with or without H2O or D2O pre-contact.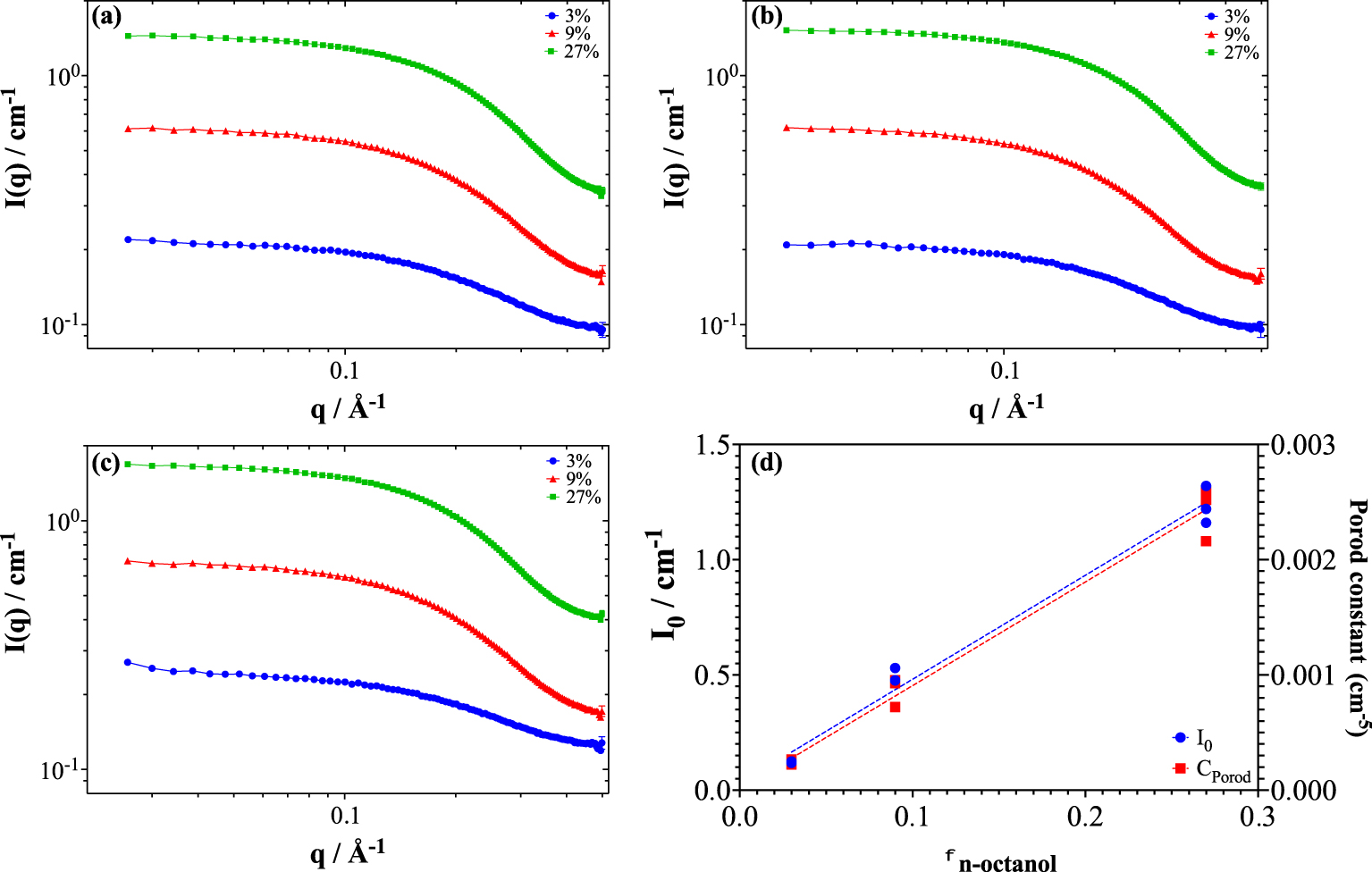
These data are then exploited and Figure 7(d) shows that the diffusion intensity at small q (i.e., I0) as well as the Porod constant are proportional to the volume fraction of added n-octanol.
The same values are obtained when the solution is contacted with H2O or D2O. The spectra with or without contact of H2O or D2O are similar (see Figure S4). This means that the n-octanol/n-dodecane binary system does not form aggregates of preferential size, unlike hydrotropes [40]. Indeed, when we plot the intensity at zero angle (I0) versus n-octanol volume fraction, one can see that there is no critical micellar concentration (cmc) below 27% (i.e., 1.7 M). This means that there is no micelle–monomer dynamic equilibrium.
If we plot the intensity and the corresponding core–shell fits, an apparent aggregation number of around four n-octanol molecules is obtained (cf. Figure 8). This either means progressive aggregation [41], or no correlation between aggregates at all, or a solubility parameter around 1∕2 close to a theta solvent [42]. Progressive aggregation means that transient aggregates of all sizes coexist, with an exponential decay of probability of occurrence [40]. In ternary systems, apparent aggregation numbers occur without any presence of micelles of well-defined preferential number. In our case, apparent aggregation number is close to four at any concentration. This means probably weak linking between adjacent octanols, maybe sometimes as pairs of dimers linked to a water molecule, and in no case micelles with a well-defined aggregation number.
SANS spectra of the n-octanol/dodecane non-pre-contacted binary mixture for n-octanol volume fractions of: 3%, 9% and 27%. Experimental data are shown as symbols and fit data as solid black lines. The data are the same as in Figure 7(a) but after subtracting a linear interpolation of the experimental data for the two pure solvents.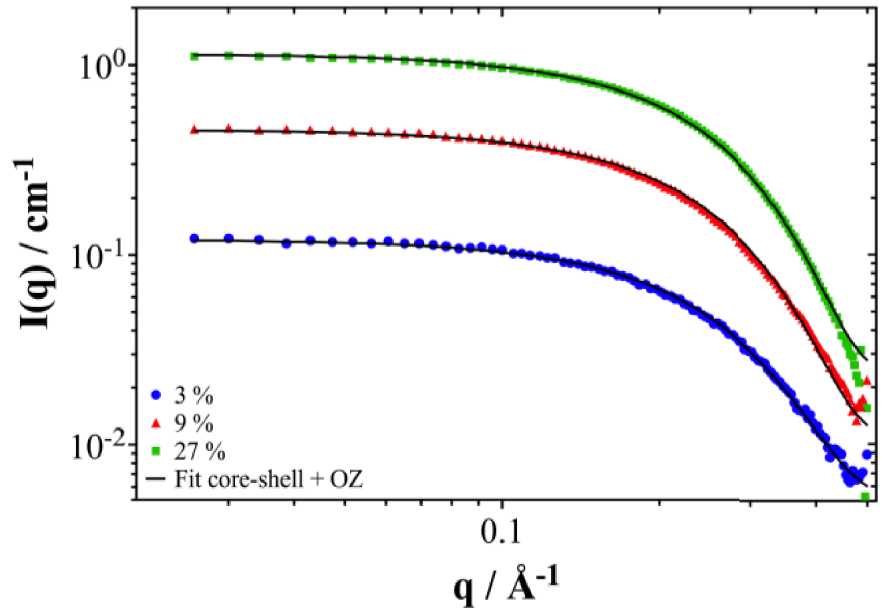
This means that n-octanol forms tetrameric aggregates of completely uncorrelated “holes” in dodecane and the core–shell model applies well here. The local attraction is very weak, therefore, the presence of reverse aggregates containing a polar core with four to six extractant molecules forms a favorable interface on which preferential adsorption is provoked by a small adsorption energy, i.e., an interaction of the order of kT [43, 44]. Preferential adsorption means that a significant amount of n-octanol is concentrated in the first layer around the aggregate compared to the “bulk”. In our case, we find seven octanol molecules adsorbed on the aggregate. Those are quenching the third phase transition by a steric effect.
If we now turn back to the TOA/n-dodecane system with n-octanol as a phase modifier, we can conclude that n-octanol exhibits a preferential adsorption mechanism towards the outer layer of the reverse aggregate. According to Lu et al., the inverse aggregate has a radius of 8.9 Å and an aggregation number of 4.9 [27]. This outer shell of the oil-in-water (o/w) aggregate contains on average 7.5 molecules of n-octanol, or 1.5 molecules of n-octanol per TOA extractant. Therefore, there is no more space for n-dodecane in this layer. We are in the case of a strong preferential solvation on the aggregate [43, 45]. In the TOA/n-dodecane system, n-octanol does not belong to the class of co-surfactants involving a decrease in cac, nor to the class of co-solvents involving a partial dissolution of the aggregates, but to the preferential solvation of n-octanol over n-dodecane with a penetration of n-octanol into the apolar volume. The lower sketch in Figure 9 schematizes this situation that clearly differs from co-solvent and co-surfactant effects.
Summary of the effect of the phase modifier on the organization of organic phases.
In this section, we have highlighted a third mechanism linked to the presence of lipotropic phase modifier (i.e., n-octanol), thanks to the study of Lu et al. [27]. It is a preferential solubilization of the phase modifier on the external layer of the aggregate compared to the diluent and thus the phase modifier forms a protective barrier preventing the formation of the third phase. For the same system, TOA/n-dodecane, changing the nature of the modifier from a “hydrotrope” to a “lipotrope” completely changes the organization of the organic phase. In the first case (hydrotrope), the third phase is avoided due to the solubilization of the aggregates in the solvent or due to a co-surfactant effect, while in the second case (lipotrope), the size of the aggregates does not change and the third phase is avoided by the formation of a protective barrier around the aggregate via a preferential solvation of the lipotrope.
3.4. Consequences on the extraction efficiency
The role of PnP in preventing the third phase was studied at the macro- and nanoscale. Now, we will explore the effect of the addition of this phase modifier (PnP) on the extraction properties for the two extraction systems considered. For this purpose, the organic phases are contacted to their corresponding aqueous phases in equal volumes (O/A = 1) for 2 h under constant stirring of 500 rpm at 25 °C. The phases are then separated by centrifugation and the pre- and post-extraction concentrations are measured for europium and for iron. The extraction properties are evaluated for organic phases containing 0 and 5%, by volume fraction, of PnP. The results are presented in Table 5. A negative value of 𝛥G allows efficient extraction. The ideal value to allow a compact efficient process is 𝛥G = −4 to −8 kJ/mol, corresponding to 97% of extraction. Obtaining this value requires tuning of the acidity as well as design of the spontaneous packing parameter of the hydrocarbon chains [46].
Comparison of free energies of transfer of the three extraction systems
| 𝛥G without PnP (kT⋅mol−1) | 𝛥G with PnP (kT⋅mol−1) | 𝛥𝛥G (kT⋅mol−1) | |
|---|---|---|---|
| HDEHP system | −7.18 | −7.57 | −0.39 |
| DMDOHEMA system | −1.74 | −2.99 | −1.25 |
Examining Table 5, we can see that adding 5% of PnP as a hydrotropic modifier allows in any case to gain 0.5 to 1 kT in extraction efficiency. i.e., a factor of three to seven on the extraction efficiency and the corresponding improvement of total volume of solvent, thus reducing cost and effluents by a similar factor. This improvement in yield by addition of hydrotropes cannot be obtained twice if synergic mixtures of extractants are considered, since the gain is of configurational entropy nature [37]. This gain in yield in a process is not linked to any excess of complexation enthalpy energy as is often assumed: these are clearly entropic terms that are not taken into account with self-consistency. In the case of co-surfactant effect, this improvement in efficiency is due to the swelling of the polar cores of aggregates allowing the solubilization of higher quantities of ions. In the case of co-solvent effect, the increase in free energy is due to Born energy of the electrolyte in the solvent. Indeed, the addition of PnP leads to an increase in the dielectric constant of the organic phase. Consequently, the Born energy is decreased and the charged species (solutes) are stabilized in apolar medium.
However, this strategy of using a co-surfactant or co-solvent to improve yield and costs towards more economically and environmentally acceptable metal recycling process when the benefit of using configurational entropy of mixing has already been obtained by using a synergetic extractant. We hope that the identification of the different molecular mechanisms associated to modifiers and its consequence on the entropic part associated to solvent reorganization that are so important in L/L extraction will allow much more efficient and knowledge-based process design in the near future.
3.5. Influence on the selectivity of the extraction systems
Previously, we demonstrated that when PnP is added, the extraction of europium is significantly improved. An additional question is: how does the Eu/Fe selectivity of these systems (HDEHP and DMDOHEMA) change with the addition of the phase modifier? Is it increased?
To answer this question, we will investigate the effect of the phase modifier on the selectivity for two extraction systems. Table 6 shows the separation coefficients of the europium solute with respect to iron, SEu∕Fe. The separation factor is defined as the following:
| (6) |
Separation factors between the solutes Eu and Fe, obtained with the two extractants studied
| SEu∕Fe | Dodecane | PnP |
|---|---|---|
| HDEHP | 1.20 | 1.42 |
| DMDOHEMA | 123 | 63 |
The compositions of the aqueous and organic phases are summarized in Table 2.
As shown in Table 6, the selectivity of HDEHP extractant between europium and iron is very low. This does not change by adding PnP to the organic phase. Therefore, PnP does not impact the selectivity of this system.
Contrary to the previous cases, the selectivity of the extraction systems with DMDOHEMA decreases with the amount of added PnP. Indeed, for a concentration of DMDOHEMA of 0.6 mol⋅L−1, the Eu/Fe selectivity decreases from 123 to 63 after the addition of 5% PnP. This is due to the increase in the volume of the polar core with the addition of PnP to these extractants, allowing the solubilization of other metals even if they are not directly chelated by the extractants.
4. Conclusion
Although the origin of third phase formation has been extensively studied, the understanding of the effect of phase modifiers on its appearance on a structural scale remains limited. In previous works, only phase modifiers belonging to a class of “lipotropic” molecules have been studied. Their effect on the appearance of the third phase was studied in most cases in the absence of metal cations. As a result, these studies are not representative of actual L/L extraction processes and have not clarified the mechanism by which phase modifiers inhibit the third phase. To the best of our knowledge, the only study reported in literature on the effect of the phase modifier with an extraction system containing the ions to be extracted is that by Lu et al. [27].
In this work, another class of molecules has been considered: hydrotropic molecules. The effect of a model hydrotrope (PnP) on the appearance of the third phase is studied using a multi-scale approach (macro- and nanoscale). In order to generalize our findings, two types of extractant molecules are studied: HDEHP, and DMDOHEMA. We have shown that PnP avoids the formation of the third phase for the two considered extraction systems. Moreover, by combining surface tension measurements with neutron scattering, we were able to elucidate by which structural mechanisms PnP prevents the formation of the third phase. Two mechanisms were highlighted depending on the nature of the extractant studied:
- A co-solvent effect is underlined when HDEHP extractant is considered. The surface tension of the organic phase containing these extractants increases with the addition of PnP. Moreover, the addition of PnP does not promote the formation of aggregates (the cac increases) and increases the surface area per polar head. These results prove that PnP in this case does not penetrate into the cores of aggregates. In parallel, using neutron scattering and unconstrained OZ fitting, we confirmed the co-solvent role of PnP and demonstrated that in the case of HDEHP, the aggregation number remains constant but the number of aggregates in the bulk decreases.
- A co-surfactant effect is shown for the extractant DMDOHEMA. In this case, the surface tension decreases with the addition of the modifier and the aggregation is favored (the cac decreases). Using neutron scattering, we confirmed the co-surfactant effect of PnP and showed that the aggregation number increases when PnP is added to the organic phase. The scattering intensity with a deuterated polar core proves that the aggregates become larger.
The consequences of the addition of PnP on the extraction properties were also evaluated. We showed that when PnP is added to both extractants, an improvement in europium extraction is observed. This is in agreement with the increase in size of the polar core of the aggregates in the case of a co-surfactant effect. In other words, there is more polar volume accessible in the organic solvent.
Although the extraction properties are improved with the addition of PnP, the increase in size of the polar cores decreases the selectivity of the extraction systems and the impurities can be extracted by solubilization effect in the larger aggregates, although they are not directly chelated by the extractants.
The comparison between lipotropic and hydrotropic phase modifier revealed a third mechanism by which the third phase is avoided. This is a preferential solvation mechanism. Indeed, the lipotrope, n-octanol in our case, is neither co-solvent nor co-surfactant but adsorbs on the external layer of the aggregate in order to form a protective barrier around it, thus decreasing the attractive interactions between aggregates.
Another way to explore is the addition of a second extractant to the organic phase to avoid the third phase. This addition can have two effects. Firstly, the addition of an extractant with a higher curvature modifies the average curvature (co-surfactant effect). Secondly, the addition of a second extractant can lead to a “positive” configurational entropy contribution. The mixing of two extractants can also have two positive effects that could help to develop new formulation techniques.
Finally, the three possible microstructural changes that can be induced by modifiers in water-poor reverse micelles formed by extractants are of similar nature, but somehow different from the three microstructures obtained when adding amino-acids or peptides to classical flexible w/o microemulsions formulated via AOT [47]. In the latter case, one encounters the three cases of co-surfactant, co-solvent, or co-solute in the liquid water pool, the solute is not located in the polar core. Contrary to the case of HDEHP, in the case of AOT, the preferential absorption as well as the co-surfactant regimes are more favored in the case of the heavily used efficient formulations applied for extraction of solutes from water [48].
Conflicts of interest
The authors declare no competing financial interest.
Acknowledgments
TZ acknowledges support from ERC grant agreement no. [320915] “REE-CYCLE”: Rare Earth Element reCYCling with Low harmful Emissions. The authors would like to thank Stephane Pellet-Rostaing for useful discussions.




 CC-BY 4.0
CC-BY 4.0