1 Introduction
The interest in the properties of water confined in the nanometer-scale channels and pores of zeolites and other inorganic open framework materials dates back to the pioneer work of Barrer and Bratt [1]. From a practical point of view, water plays a key role in many applications such as ion-exchange and separation. It has been observed for some time that the (often unwanted) presence of pre-adsorbed water in the nano-porous solid affects the adsorption selectivity with respect to the hydrocarbon mixture that one wants to separate [2]. The mechanism producing these effects is poorly understood. Being able to understand and predict the effect of water on fluid (such as hydrocarbons) adsorption is considered as a key challenge in the adsorption community today [3]. From the fundamental point of view, water in zeolite represents a model system for a wide range of experimental as well as theoretical investigations, aimed at understanding the effect of confinement on the structure [4], dynamics [5,6] and thermodynamics [7,8] of molecular fluids.
Adsorption properties in zeolites are closely related to the location of nonframework cations and to their accessibility to adsorbed molecules. The partition of these cations among the different sites does not usually change during the course of the (non polar) hydrocarbon adsorption process. On the other hand, cation redistribution is suspected to occur upon adsorption of polar molecules. Mellot-Draznieks and Cheetham et al. [9] have carried out a neutron scattering study of CFCl3 adsorption in NaY and observed cation redistribution together with a new and previously unknown cation location. Recently, a change in the cation location upon water adsorption has also been predicted in zeolite sodium-mordenite by molecular dynamics simulation [10].
We report here a molecular simulation study of water adsorption in zeolite sodium-faujasite NaY and NaX. These two zeolites only differ by their Si/Al ratio, i.e. by the number of nonframework cations. We use a recently developed Monte Carlo simulation method that enables the nonframework cation distribution to change upon water adsorption [11]. Until now, most of the theoretical adsorption studies were using fixed cation distributions [12,13].
2 Models and methods
Faujasite is known to be a very stable zeolite, and hydration has very little impact on its overall structure, unlike some other open framework solids (clinoptilolite, aluminophosphates) [14,15]. We thus used a simple rigid framework system, as in our previous studies [11,16,17]. Molecular simulations were performed in the classical limit (no bond breaking take place, for instance). This justified by the fact that no hydrolysis is observed upon water adsorption [7], due to the weak bonding of water with the faujasite framework. We used the simple TIP4P effective potential model for water [18]. The polarization effects are not explicitly taken into account in this forcefield. The cation force field has been adapted from the work of Jaramillo and Auerbach [19] in the way described in Ref. [11]. The cation-framework potential consists of an exp-6 repulsion-dispersion term that acts between the cation and the oxygen atoms of the faujasite and a coulombic term that acts between the cation and both the oxygen and T atoms of the framework (the Al and Si atoms were not differentiated in this work). Sodium cations interact with each other through a single coulombic term. The water-framework interaction is calculated using Lennard–Jones type potential with faujasite oxygen atoms (σwater–O = 3.31 Å and ɛwater–O = 70.05 K) and sodium cations (σwater–Na = 2.87 Å and ɛwater–Na = 78.32 K). Ewald sums were used to calculate the long-range coulombic terms.
The cation distribution in faujasite is usually described as follows (see Fig. 1). Na+ can occupy sites I, located in the hexagonal prisms which connect the so-called sodalite cages. Sites I′ are inside the sodalite cages facing sites I. Sites II are in front of the six-rings inside the supercages. Sites III are also in the supercages, near the four-rings of the sodalite cages. Site I has a multiplicity of 16 per unit cell, sites I′ and II have a multiplicity of 32, and site III has a multiplicity of 48 per unit cell. Site III is believed to be of higher potential energy than sites I, I′, and II. At low occupancy (Si/Al > 2), cations are known to occupy sites I, I′, and II only [21].

Schematic view of a faujasite supercage with the site I, I′, II, and III locations.
Adsorption simulations have been performed in two test cases. The first one is NaY faujasite (Si/Al = 3; 48 cations per unit cell, a unit cell being made of eight supercages), and the second one is NaX (Si/Al = 1.53; 76 cations per unit cell). As shown in Fig. 2, the cation distribution in a dry Na48Y sample corresponds to a full occupancy of site I (16 cations) and site II (32 cations), while all sites I′ and III are empty. The cation distribution in dry Na76X corresponds to a partial occupancy of site I (six cations), I′ (24), and III (14) and a full occupancy of site II (32).
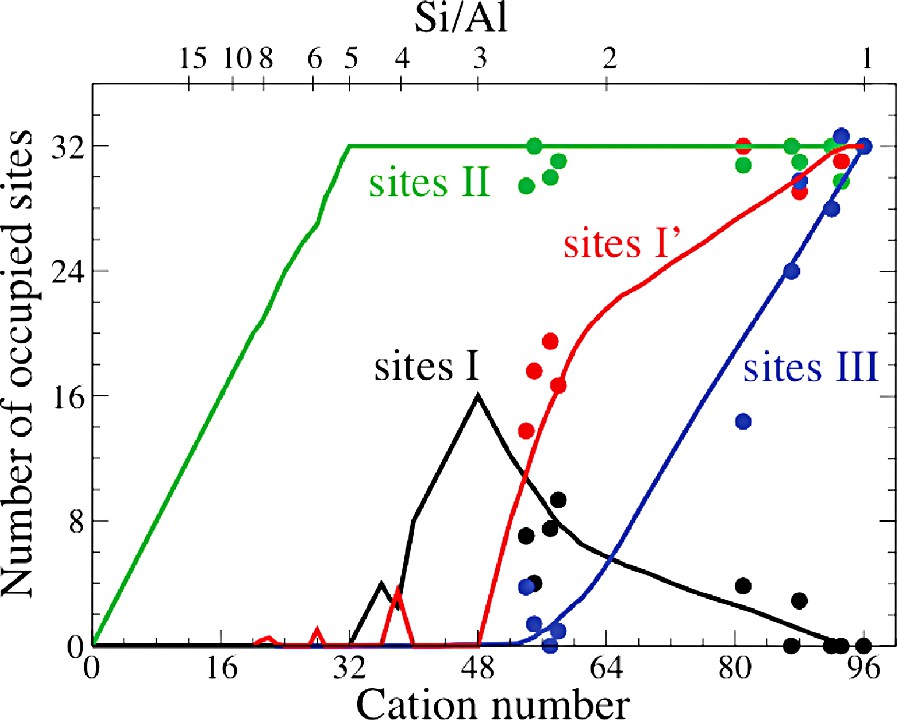
Sodium cation occupancy in dry faujasite, as a function of the cation number (CN) or silicon to aluminum ratio (Si/Al). Full lines: computed occupancies from replica-exchange Monte Carlo simulations [11]. Filled circles: experiments [20–25].
We performed Grand Canonical Monte Carlo (GCMC) simulations to compute the average number of adsorbed water molecules for several values of the chemical potential of the (fictitious) vapor reservoir at 298 K. To relate the chemical potential to the water vapor pressure we used tabulated fugacity data. During the course of the adsorption process, at each value of the water vapor pressure, canonical Monte Carlo moves were performed for the nonframework cations, enabling a spontaneous change in their partition among the available sites. In the case of Na48Y, which is known to display several metastable cation distributions [26], we complemented the computations with replica-exchange canonical simulations recently developed in our group in order to improve the sampling of the configuration space and thus the convergence of the Monte Carlo algorithm [11].
3 Results
The computed adsorption isotherm of water in Na48Y at 298 K is shown in Fig. 3 (blue curve). The starting cation distribution for the empty zeolite is the following: 16 cations in site I, none in site I′, 32 in site II and none in site III. This we call a (16,0,32,0) distribution. It corresponds to the dry Na48Y faujasite case described in the preceding section. Upon water adsorption, a spontaneous cation redistribution takes place. For low water content, we observed a solvation of the site II cations in the supercages. Above ~50 molecules per unit cell (i.e. roughly 1.5 water molecules per site II cation), a redistribution of site I and I′ cations takes place (Fig. 4). Sodium cations progressively move from site I to neighboring sites I′ in the sodalite cage. This is accompanied by a progressive occupancy of the sodalite cages by water molecules. The cation distribution observed at full loading, i.e. 208 water molecules per unit cell, is (4,12,32,0). Also shown in Fig. 3 are the two isotherms computed with fixed cation distributions (16,0,32,0) and (4,12,32,0), corresponding to the red and black curves respectively. It is clear from the Fig. 3 that cation redistribution upon water adsorption, whenever it occurs, can have a large effect on the computed thermodynamic quantities. More details on the Na48Y simulations can be found elsewhere [27].
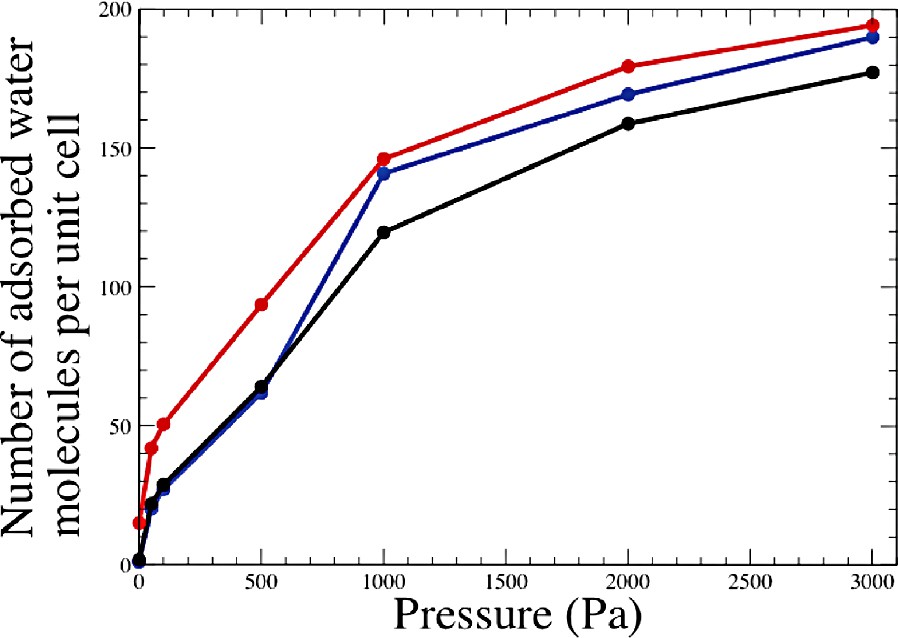
Computed adsorption isotherms of water in Na48Y faujasite. Red curve: fixed cations in the (16,0,32,0) distribution. Black curve: fixed cations in the (4,12,32,0) distribution. Blue curve: free cations.
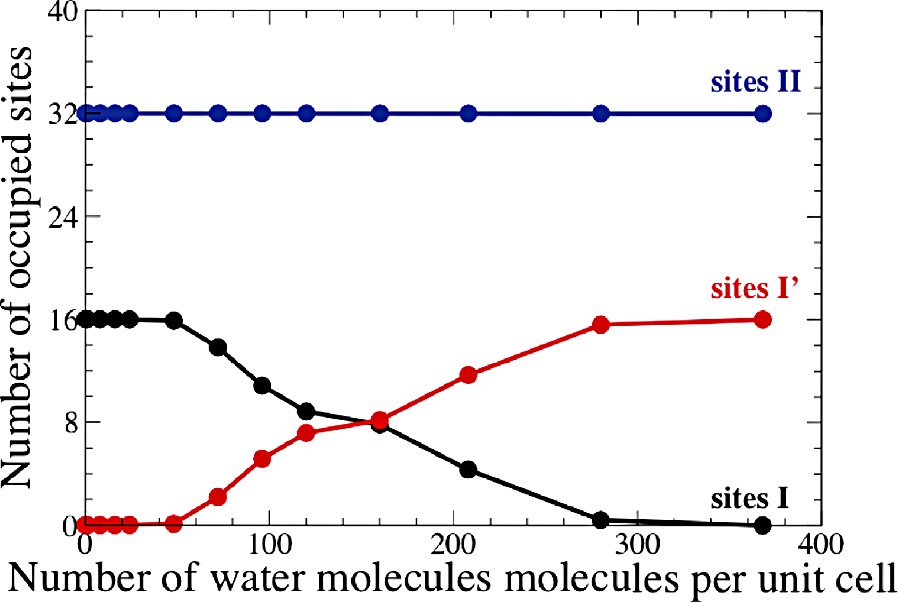
Computed sodium cation distributions in Na48Y for different water content.
The second part of the work deals with a faujasite model that contains a larger amount of cations, namely Na76X. In this case, the initial equilibrium cation distribution for the dry zeolite (6,24,32,14) is such that water can start adsorbing in the sodalite cages at very low pressure, because of the large amount of sodium cations in site I′. In contrast with the former Na48Y we found no I–I′ cation redistribution here. This is presumably due to the fact that a full occupancy of a sodalite cage corresponds to roughly three water molecules. Since each cation in site I′ solvates ~1.5 water molecules, there is no need to displace more cations from site I to site I′ to completely fill the sodalite cages. We have found essentially the same result for a Na56Y system. The initial (8,16,32,0) configuration displays the minimum number (16) of cations in site I′ necessary to solvate 24–25 water molecules per unit cell at full loading. Indeed, no cation redistribution took place in the Na56Y case either, thus confirming our hypothesis. It should be stressed that previous NMR [28] and calorimetric experiments [7] have found value of four molecules per sodalite cage, which is somewhat larger than the three molecules found here. However, our interpretation holds if we consider a solvation of each cation by two water molecules instead of 1.5 in the present simulations. This difference may well be due to the oversimplification of the water model used here.
Na76X is also of great interest to this work because thermodynamic data are available for this system, enabling us to test the validity of the model. In Fig. 5, we report the computed and experimental isosteric heat of adsorption. The agreement between simulation and experimental values is surprisingly good, given the simplicity of our model. The GCMC method enables to compute separately the water-framework and water–water contribution to the heat of adsorption. These are shown in Fig. 5. It is interesting to note an almost constant total heat of adsorption in the range 30–200 water molecules. This does not mean that the water molecules ‘feel’ a uniform external field during the course of adsorption, but it simply results from a simultaneous decrease of the water–zeolite and increase of the water–water contributions.

Isosteric heat of adsorption as a function of the number of adsorbed water molecules for Na76X. Black line: computed total heat. Blue line: experiments [8]. Green line: computed water-framework contribution. Red line: computed water–water contribution.
The adsorption isotherm (not shown here), is also rather well reproduced in the low pressure regime, but the simulations underestimate the water content at full loading by some 17%. The maximum loading obtained by simulation is 215 water molecules per unit cell. Work is in progress to develop more sophisticated models for the water-framework interaction potential, by incorporating explicit polarization term, in order to reach a better agreement with experiments.
Boddenberg et al. [7], as well as Moïse et al. [8] have suggested that, at full loading, water forms a liquid with “dissolved cations”. We have found no evidence of this in our simulations. Only does, from time-to-time, one or another site III cation move from one site to another. Whether or not this discrepancy can be attributed to the oversimplification of the model used in this work remains an open question.
4 Conclusion
We have performed Monte Carlo simulations of water adsorption in model NaY and NaX faujasite, using a rather simple model (this is especially true for the effective TIP4P model used for water), and found a fair agreement with the available experimental data. In the method used in this work the nonframework cations are allowed to move from place to place in the sample, and are not fixed anymore in their crystallographic sites, as in most of the previous adsorption simulations reported in the literature. This is the most original part of the method used in this work. One of the interest of this method lies in the fact that it can, in principle, be extended to any type of adsorbent–adsorbate system.
We have indeed observed a cation redistribution upon water adsorption in a low cation content faujasite (Na48Y). Although these data were obtained using equilibrium Monte Carlo simulations (i.e. we have no direct information on the cation and water dynamics), it seems clear that we are faced with a concerted cation–water motion. To begin with, water molecules are preferentially adsorbed in sites II. By the time each site II cation is solvated by roughly 1.5 water molecules, it becomes energetically interesting for water molecules to solvate site I cations. As the hexagonal prism connecting two sodalite cages is too small to accommodate a water molecule, cations in site I will progressively move to sites I′, enabling water molecules to adsorb in sodalite cages.
No such cation redistribution was observed in the higher cation content Na76X faujasite. This we explain by the fact that the site I′ occupation is large enough in this case to enable a full water solvation in the sodalite cages (three molecules per cage in this work, four in the experiments). It turns out, from the above findings, that the water adsorption process can be very different, depending on the Si/Al ratio of the aluminosilicate faujasite.
Work is now in progress to develop more reliable models for the water-framework interaction, which is presumably the weakest part of the reported simulations.


