1 Introduction
The nature of the metal–metal bond in transition metal complexes continues to be a topic of actual interest. On this regard numerous experimental and theoretical investigations have been undertaken in the past decades [1–4]. Metal compounds containing two or more atoms hold together by a direct and substantial metal–metal bonding are known as cluster complexes. Unfortunately this definition is sometimes ambiguous because the metal–metal bond distances, associated to a particular bond order, show a much greater variation than those observed between light main group elements or for metal–ligand bonds. In addition, the identification of a ‘direct’ metal–metal bonding gets more problematical when the metal atoms are connected by bridging ligands. In this last case, the symmetry of the orbitals associated to the metal–metal bond match some of the linear combinations of orbitals of the bridging ligand atoms difficulting the metal–metal bond analysis in these cluster complexes.
Lately topological approaches, such as the atoms in molecules (AIM) theory or the electron localization function (ELF) analysis, have emerged aimed to investigate the nature of chemical bonding as an alternative to the widely used molecular orbital interpretation [5,6]. These approaches, based on the theory of dynamical systems, offer an orbital independent framework enabling a partition of the molecular space into basins of attractors bearing a chemical meaning. The simplest dynamical systems are the gradient field of a scalar function called the potential function. The AIM theory uses the electron density as the potential function. However, the criteria based on the electron density are too restrictive to account for the large variety of covalent and dative bonds found in transition metal compounds. Fradera et al. [7] have shown that the delocalization index δ(A, B), which provide the number of electrons shared or exchanged between atoms A and B, is more sensitive for analyzing bonding effects. Large values for δ(A, B) are indicative of electron shared interactions while low δ(A, B) values characterize closed-shell interactions (i.e. ionic or hydrogen bond). The application of the virial theorem for the energy density evaluation at the bond critical point (bcp) has also shown its utility in bond analysis where negative values of the energy are assigned to the bonding [8]. The topological analysis of the ELF gradient field constitutes an alternative to the AIM use of the electron density as potential function. Such analysis allows to recover chemical objects such as atoms, bonds and lone pairs and therefore provides a reliable mathematical model for Lewis' valence theory as well as for the valence shell electron pair repulsion (VSEPR) model of Gillespie [9–11].
In this account, we examine topologically the metal–metal and metal–ligand bonds interactions in some di-, tri- and tetranuclear metal compounds combining the AIM theory with the analysis of the ELF. Topological results are basically independent of the level of calculation; therefore, this allows us to compare atomic populations between systems computed with different methodologies and different basis sets. The paper is organized as follows; the first section provides a conceptual survey of the topological analysis of ELF. In the subsequent sections the topological bond principles are applied to various transition metal cluster complexes of conceptual relevance within Inorganic Chemistry, namely, a series of M2L4 dimers (L = formamidinate) with different nominal bond orders, electron rich carbonyl trimers of formula Fe3(CO)12 and electron poor trinuclear clusters with incomplete cubane-type Mo3(μ3-S)(μ-S)3 structures. Finally, the topological changes associated to the insertion of a second metal M′ into the Mo3(μ3-S)(μ-S)3 core to produce Mo3M′S4 (M′ = Cu or Ni) heterodimetallic complexes are also analyzed.
2 Topological analysis of the ELF
The intuitive picture of the microscopic structure of the matter implicitly adopted in Chemistry is that of an assembly of atoms interacting through their valence electrons. Except for hydrogen, the electrons assigned to each atom are distributed into a kernel gathering the chemically inactive electrons of the atomic inner shells and into a valence shell. Each kernel surrounds a nucleus and belongs to one and only one atom whereas the valence shell can be partitioned into bonding and non bonding regions. The non bonding region belongs to one atom whereas the bonding region may be shared by several atoms and therefore be a part of their valence shells. The numbers of electrons assigned to each of these latter regions constitutes the chemical electronic structure which is expected to obey the simple rules prescribed by Lewis [9]. The link with rigorous quantum mechanics can be achieved in the following way. Consider first a partition of the geometrical molecular space into a set of adjacent non overlapping volumes (the loges in the sense of R. Daudel) and expected to have a chemical meaning so as the numbers of electrons within them can be considered as defining the chemical electronic structure [12,13]. In our approach these volumes are the basins of the gradient dynamical system of the ELF introduced by Becke and Edgecombe [14]. The partition scheme by itself is not important at this stage and will be considered later. In order to carry out the electron count we introduce population operators which are defined in Eq. (1):(1)
In the case of chemical bonding, the information carried by the local values of the function should be closely related to the pairing of electrons, a cornerstone in all bonding theories. As electrons are half integer spin particles (fermions), two electrons with identical spins tend to avoid each other more strongly than two antiparallel spin electrons. The recently introduced spin pair composition function happens to be a valuable indicator of the pairing within a molecule [16]. It represents the ratio of the numbers of parallel and anti parallel spin pairs of electrons within a sampling volume around a reference point. It has been shown that the previously introduced Becke and Edgecombe's ELF is an excellent approximation of the spin pair composition. Its closed analytical expression enables the efficient calculation of its derivatives and therefore its use in the dynamical system analysis. It is confined within the [0, 1] interval [6,14]. It tends to 1 where parallel spins are highly improbable (for example, inside a lone pair or a bond region), and is close to 0 near the boundaries of the electronic domains where parallel spin electrons are compelled to come close one another.
The ELF topological analysis provides a partition of the molecular space in basins, which is consistent with the assumptions of Lewis theory. There are accordingly core and valence basins labeled C (A) and V (A, B, …), respectively, with A and B being the atoms concerned. The valence basins are characterized by the number of core basins with which they share a boundary. This number is called the synaptic order. This notion of synaptic number introduces a homogeneous nomenclature for the valence basin (monosynaptic, non bonding part of the valence shell; disynaptic, bonding region share by two valence shells; trisynaptic, by three valence shell…) that accounts for multicenter bonds in a natural fashion [17]. The ELF basins provide a complementary view to the standard valence one. Instead of counting the atoms coordinated to a given nucleus, one is immersed in the basin of interest and counts the bordering cores. In this context, a valence shell of an atom, say A, corresponds to the union of all the valence basins which share a boundary with the core basin C (A).
3 Dimetallic complexes M2(formamidinate)4
The tetrabridged metal dimers of formula M2(HNCHNH)4, represented in Fig. 1, with M = Nb, Mo, Tc, Ru, Rh or Pd provides a series of isostructural complexes with paddlewheel structures differing only in the nature of the metal and consequently in the number of metal electrons available for metal–metal bond. The nominal bond order estimated on the basis of the quadruple bonded molecular orbital scheme is four for Mo, three for Nb and Tc, two for Ru, one for Rh and zero for Pd. Based on that scheme, interactions between transition metal atoms are due to overlap of the metal “d” orbitals giving rise to σ, π and δ bonding and antibonding molecular orbitals [18]. Whenever the number of electrons occupying the bonding orbitals exceeds those in the antibonding orbitals, metal–metal bonds will be formed.
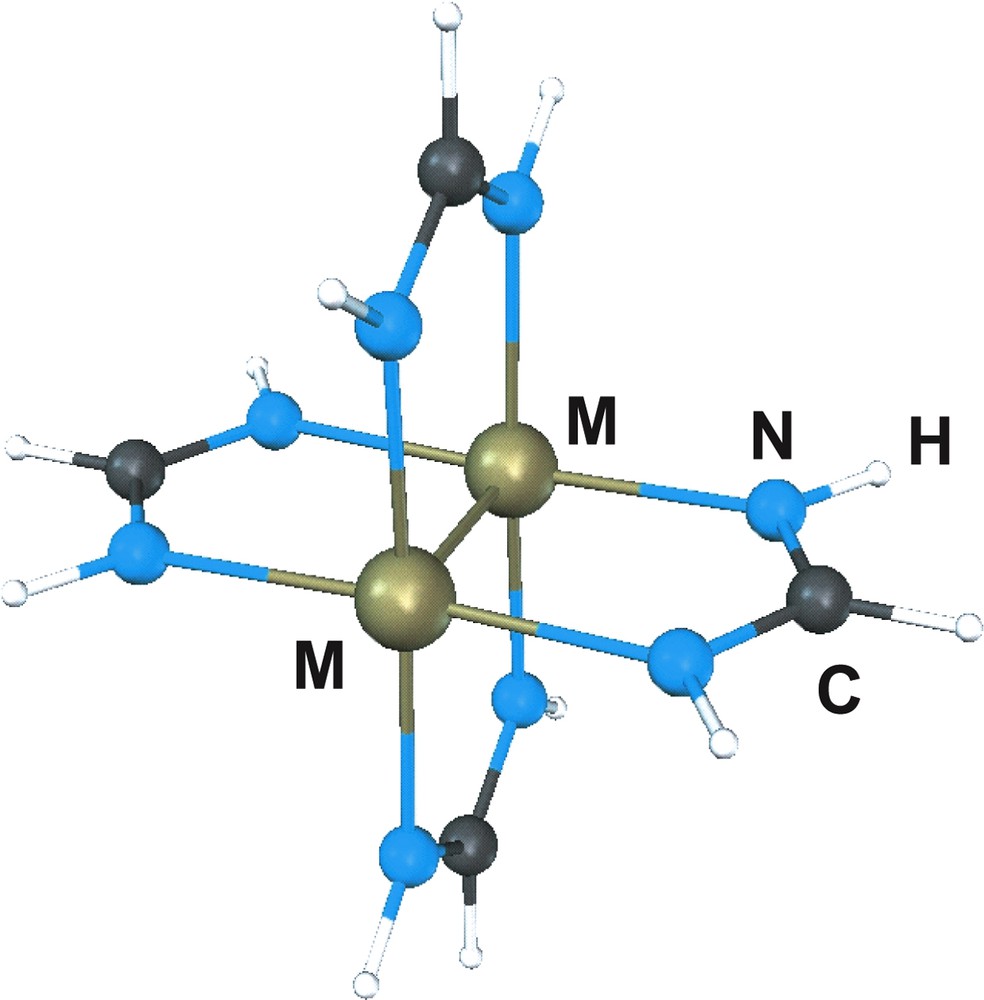
Ball and sticks representation of M2(HNCHNH)4.
According to the AIM theory, a chemical structure is represented by a network of bond paths or unique lines of maximum electron density that link the nuclei of neighboring atoms in an equilibrium geometry. The presence of a bond path provides an universal indicator of bonding between atoms. The molecular graph for M2(HNCHNH)4 reproduces the bond path corresponding to the M–M, M–N and N–C bonds. Table 1 lists the metal atom net charges together with the bcp characteristics of the metal–metal bond and the intermetallic experimental and optimized bond distances. Geometry optimization is successfully achieved by combining the B3LYP density functional with all electron basis sets [19,20]. The net charge of the metal atoms, formally considered as M2+, is always higher than the AIM charge. There is a charge transfer from the formamidinate (HNCHNH)– ligand towards the metals that increases from Nb to Pd. Such increase with the atomic number has also been observed for the MX2 halides and attributed to the σ-donation from the ligand [21]. On the other hand, the metal–metal delocalization indexes, also listed in Table 1, follow the tendency of the formal bond order. For the quadruply bonded molybdenum dimer the Mo–Mo delocalization index has a rather large value, 2.994, in comparison with the δ(Mo–N) of 0.296. On the other hand, the low values calculated for the charge density ρ(rbcp) at the M–M bcp as well as for the energy density E (rbcp) makes ambiguous any classification of the metal–metal bond using only AIM criteria. This circumstance has been already pointed out for other bonds in transition metal complexes [22–25]. On this regard, a similar situation is found in the F2 molecule where the topological analysis of the Becke and Edgecombe localization function (ELF) enables an unambigous characterization of the F–F bond as covalent [26].
Geometrical and topological data for M2(formamidinate)4 complexes (B3LYP/3-21G**)a,b
| d (M–M)exp (Å) | d (M–M)calc (Å) | Q(M) | BO | δ(M, M) | ρ (rc) (e bohr–3) | ∇2ρ (rc) (e bohr–5) | E (rc) (hartree bohr–3) | |
| Nb | – | 2.224 | +1.26 | 3 | 2.514 | 0.147 | 0.392 | –0.079 |
| Mo | 2.085 | 2.092 | +1.11 | 4 | 2.994 | 0.185 | 0.550 | –0.113 |
| Tc | – | 2.082 | +1.04 | 3 | 2.712 | 0.179 | 0.609 | –0.092 |
| Ru | 2.475 | 2.493 | +1.03 | 2 | 1.321 | 0.079 | 0.168 | –0.013 |
| Rh | 2.434 | 2.459 | +1.05 | 1 | 1.008 | 0.072 | 0.158 | –0.013 |
| Pd | 2.622 | 2.691 | +0.85 | 0 | 0.260 | 0.042 | 0.115 | –0.011 |
a Atomic populations are given in electrons.
b Experimental M–M bond distances are taken from crystal structure data of M2(RNCHNR)4 (R = p-CH3C6H4). See [19] and references therein
The topology of the ELF isosurface for M2(HNCHNH)4 with M = Mo and Nb identifies seven reducible domains: four correspond to the ligand valence shell that include the V (Mo–N), V (C–N), V (C–H) and V (N–H) attractors, two to the molybdenum cores and the other to the V (M, M) attactors. This latter domain contains four equivalent attractors lying in the σh plane. No disynaptic V (M, M) basins are found for the dimers with the shortest (Tc) and the longest (Pd) intermetallic distances and there is a single V (M, M) basin for the Ru and Rh complexes. Table 2 lists the atomic basin populations for these complexes. The V (M, M) basins are not the dominant feature of metal–metal interaction due to their low population values that vary between 0.6 e– for Mo and 0.25 e– for Ru. The different character of the interaction can be quantified by calculating the atomic basin contribution to the various disynaptic basins. The V (C, H), V (N, H) and V (C, N) correspond to covalent interactions because the atomic basin of the two linked atoms noticeable contribute to their population, the different contributions being due to electronegativity differences. The V (M, N) basin is essentially populated thanks to the nitrogen atomic basin density being clearly of the ‘donor–acceptor’ type. However, the classification of the M–M interaction is less straightforward partly due to the low V (M, M) populations and because there is a huge electronic delocalization between the two metallic cores, testified by the C (M) covariance contribution to the C (M) variance. The B (M, M) covariance factor accounts for about 80% of the delocalization index δ(M, M).
Atomic basin populations and covariances (e–) for M2(formamidinate)4 complexes (B3LYP/3-21G**)
| Nb | Mo | Tc | Ru | Rh | Pd | |
| BO | 3 | 4 | 3 | 2 | 1 | 0 |
| V (M, M) | 0.17 × 4 | 0.15 × 4 | – | 0.25 | 0.32 | – |
| V (C, H) | 2.18 | 2.18 | 2.24 | 2.19 | 2.16 | 2.20 |
| V (N, H) | 1.88 | 1.86 | 1.84 | 1.88 | 1.84 | 1.86 |
| V (M, N) | 3.68 | 3.72 | 3.78 | 3.70 | 3.69 | 3.79 |
| V (C, N) | 2.03 | 2.01 | 1.94 | 2.00 | 1.99 | 1.92 |
| V (M, N)| M | 0.10 | 0.12 | 0.12 | 0.10 | 0.10 | 0.04 |
| V (C, N)| N | 0.89 | 0.88 | 1.05 | 1.12 | 1.04 | 1.01 |
| C (M) | 39.05 | 40.12 | 41.50 | 42.47 | 43.42 | 44.42 |
| C (N) | 2.12 | 2.12 | 2.11 | 2.09 | 2.15 | 2.12 |
| C (C) | 2.13 | 2.14 | 2.12 | 2.13 | 2.13 | 2.12 |
| B (M, M) | 1.025 | 1.255 | 1.371 | 0.551 | 0.373 | 0.124 |
The origin of the low values for the V (M, M) population, compared to the expected one based on the ‘nominal bond order’ value of four (8 e–), is certainly the ambivalent character of the ‘d’ orbitals that can be considered as core orbitals and as valence orbitals depending on the nature of the chemistry under study. In the case of solid metals, it has been found that the transition metal ‘d’ orbitals almost do not contribute to the interstitial density [27]. In the present case the orbital contributions to the C (M) and V (M, M) basin provide the pertinent information: the molecular orbitals involving the ‘4d’ function of the metal (denoted Eu, A1g and B2g in the dimer D4h symmetry) essentially contribute to the C (M) populations. The variance analysis of the C (M) basins provide a clue for understanding the singularities of these metal core basins. The large electron fluctuation which occurs between the two metallic cores can be interpreted in terms of simple resonance arguments. The proposed resonant structures for each metal dimer, together with their weight factors and the estimated variances, are compared in Table 3 with the calculated populations of the core metal basins, C (M), and their covariance values, B (M, M).
Resonant structures, variances, estimated and calculated core populations, C (M), and covariances, B (M, M), for the metal–metal bond in M2(formamidinate)4 dimers
| M | Resonant structures (weight) | Variance (σ2 (e–)2) | Cest (M) (e–) | Best (M, M) (e–) | Ccalc (M) (e–) | Bcal (M, M) (e–) |
| Nb | M([Kr]π4)−M([Kr]σ2) ↔ M([Kr]σ2)− M([Kr]π4) (1) | 1 | 39 | 1 | 39.05 | 1.025 |
| Tc | M([Kr]π4 δ2)−M([Kr]σ2δ2) ↔ M([Kr]σ2δ2)−M([Kr]π4 δ2) (1) | 1 | 41 | 1 | 41.50 | 1.371 |
| Mo |
|
| 40 | 1 | 40.12 | 1.255 |
| Ru |
|
| 42 | 0.5 | 42.47 | 0.551 |
| Rh |
|
| 43.75 | 0.25 | 43.42 | 0.373 |
| Pd | M([Kr] π4σ2δ2)−M([Kr] π4σ2δ2) | 0 | 44 | 0 | 44.52 | 0.116 |
Because the metal dimer is in a closed-shell singlet state, there is no spin polarization and each metallic core should be considered as a local closed-shell subsystem whose orbitals fulfill the C4v point group symmetry requirements. Let us exemplify the resonance arguments with the molybdenum dimmer: the Mo core population is close to 40 e– with a covariance of 1.255 e– and, as a consequence, an average of four out of the six electrons formally considered as valence according to the MO theory should now be incorporated into the core. Following the traditional greek characters usually used to described the quadruple metal–metal bonding MOs (σ2π4δ2), the following core configurations are compatible with the molecular symmetry: [Kr]π4, [Kr]σ2δ2, [Kr]π4δ2 and [Kr]σ2, [Kr] π4σ2 and [Kr]δ2. A resonance structure between the first two configurations: Mo([Kr]π4)−Mo([Kr]σ2δ2) ↔ Mo([Kr]σ2δ2)−Mo([Kr]π4), corresponds to an average core population of 40 e– with a variance of zero. To recover the calculated covariance between the Mo atoms of 1.255 e–, the resonant structures listed in Table 3 that involve the remaining configurations must be considered. The orbital ordering energies (Eπ ≈ Eσ < Eδ) supports the higher weight assigned to the resonance structure with the low lying metal ‘d’ orbitals (π) incorporated into the core. In addition, the ‘d’ orbitals are the main contributors to the populations of the four V (Mo, Mo) basins (53% π, 27% σ and 7% δ). Similar arguments are used to propose the resonant structures for the Nb, Tc, Ru, Rh and Pd dimers.
The picture of the bond that emerges from the topological analysis is that of a strong resonance interaction due to the fluctuation of the metal ‘d’ electrons within the cores. In contrast, the MO picture treats the metal ‘4d’ orbitals as valence orbitals which combine under the dimer symmetry to produce the σ, π and δ canonical orbitals with their antibonding counterparts. This scheme yields bond orders ranging from zero to four which correlate well, except for the Rh dimer, with the M–M distances and with the B (M, M) core covariances.
4 Trinuclear complexes
Trinuclear transition metal clusters can be classified depending on the number of metal electrons available for the metal–metal bond formation in electronically-rich and electronically-poor complexes. Electronically-rich trimers are usually formed by metals to the right side of the d-block of the periodic table, in which the metal atoms in low oxidation states are combined with π-acceptor ligands, e.g., Fe3(CO)12. On the other hand, electronically-poor complexes are formed by metals in high oxidation states bonded to σ donor ligands, e.g. [Mo3S4(PH3)6Cl3]4+.
4.1 Electron-rich complexes with carbonyl ligands: Fe3(CO)12
The structure of the trinuclear Fe3(CO)12 complex was first characterized in 1969 by Wei and Dahl and later confirmed by Cotton and Troup [28,29]. Two isomers, represented in Fig. 2, have been structurally characterized, one with four terminal carbonyl groups per iron atoms and a D3h symmetry structure and the other hand with a C2v symmetry where two of the iron atoms are bridged by two carbonyl ligands. This latter C2v isomer is the most stable. The geometries of the two isomers have been optimized at the B3LYP level with the 6-311G(d) basis set yielding both structural parameters and relative stability (the C2v isomer is calculated to be more stable than the D3h one by 9.4 kcal mol–1) in fair agreement with the experimental results [30].
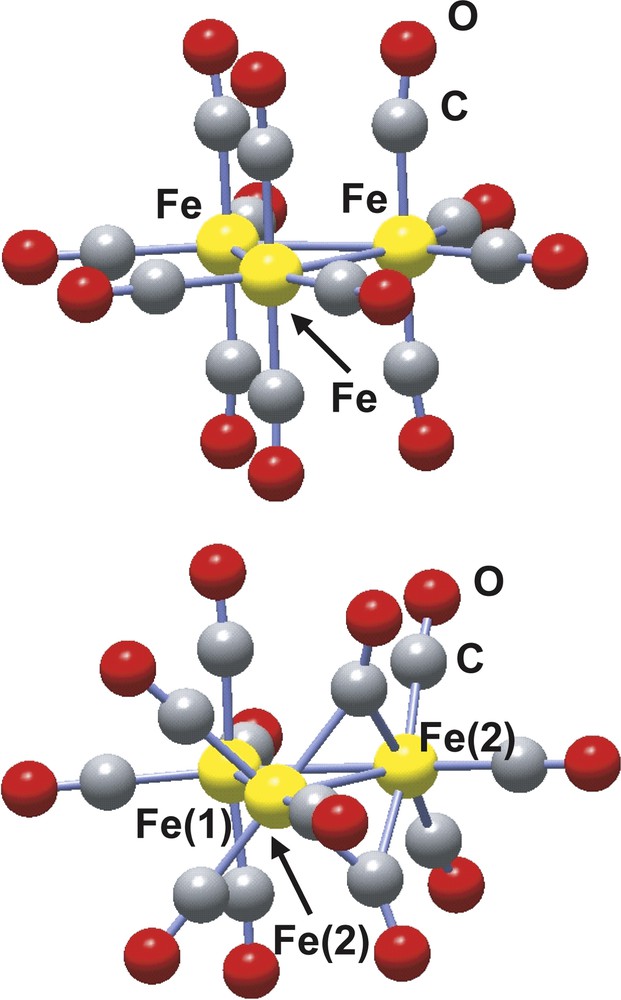
Ball and stick representation of the D3h (left) and C2v (right) Fe3(CO)12 isomers.
Several theoretical studies dealing with the bonding pattern in these complexes have been published. Recently, Hunstock et al. [31] have shown that the HOMO and HOMO-1 orbitals in the most stable Fe3(CO)12 isomer are responsible of the two Fe–(μ-CO–Fe bonding interactions and that these orbitals have at the same time an Fe–Fe antibonding character.
The AIM analysis shows a total of three Fe–Fe, 12 Fe–C plus 12 C–O bond paths for the D3h isomer [30]. In constrast, no Fe–Fe bond path is found for the bridged Fe–(μ-CO)2–Fe interaction in good agreement with the antibonding character predicted by the orbital analysis. As already pointed out for the M2(formamidinate)4 complexes, the charge density at the Fe–Fe bcp ρ(rbcp) is close to zero and its laplacian is small and positive. The charge density at the Fe–C bcp is also small, although larger than that calculated for Fe–Fe, and its laplacian is positive and large, which are the AIM signatures of the metal–carbonyl dative bonds [32]. A deeper insight into the nature of the bond within the Fe3 (CO)12 trinuclear cluster can be obtained from the delocalization indexes. The δ(Fe, Fe) delocalization indexes are ca. 0.4 for the Fe–Fe bonds except for the Fe–(μ-CO)2–Fe interaction in the C2v isomer, for which the delocalization index is lower, δ(Fe, Fe) = 0.26. This last value is equal to the δ(Pd, Pd) calculated for the Pd2(formamidinate)4 dimer for which a metal–metal bond order of zero is assumed based on molecular orbital analysis.
The bonding in the D3h and C2v Fe3 (CO)12 isomers has been also investigated by topological analysis of the ELF function by Chevreau et al. [30]. The irreducible localization domains of the Fe3 (CO)12 isomers are displayed in Fig. 3. In the ELF picture, the complex appears as 12 CO ligands linked to a Fe3 cluster. The electron density associated to each ligand is partitioned into five basins, namely the carbon C (C) and oxygen C (O) core basins, the disynaptic V (Fe, C) and V (C, O) ones associated to the Fe–C dative bond and to the C–O bond, respectively, and the oxygen lone pairs V (O) monosynaptic basin. The trimetallic unit of the D3h cluster has three core basins C (Fe) and three disynaptic valence basins V (Fe, Fe) as shown in Fig. 4. In the C2v isomer, the valence basin corresponding to the metal–metal interaction along the bridged Fe–(μ-CO)2–Fe triangle edge is missing.
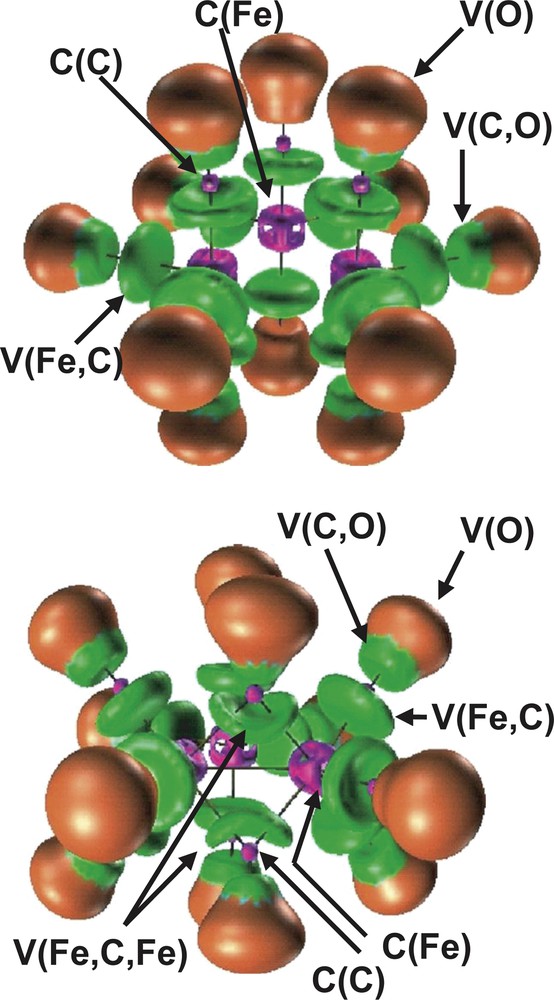
Localization domains of the Fe3(CO)12 isomers. Left: D3h, right: C2v. The ELF value defining the bounding isosurface is 0.75. Color code: magenta = core, red = monosynaptic, blue = protonated disynaptic, green = disynaptic.
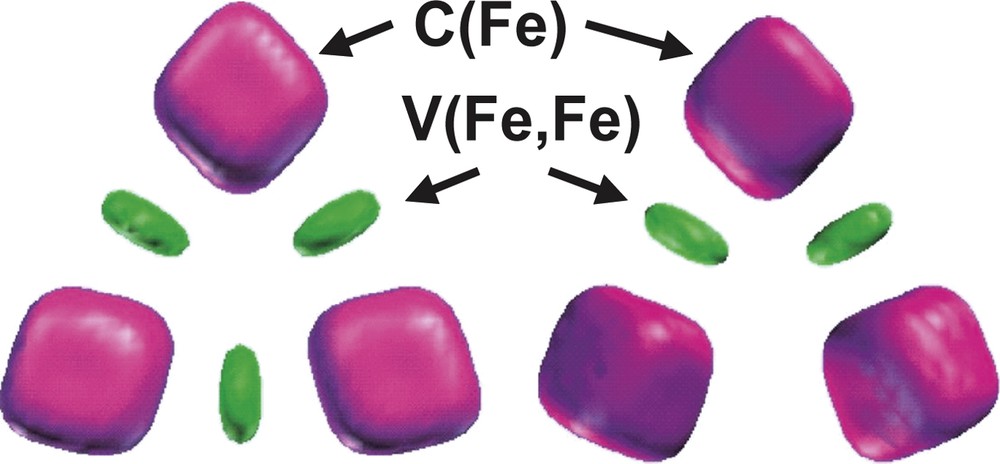
Localization domains of the Fe3 moiety of the Fe3(CO)12 isomers. Left: D3h, right: C2v. The ELF value defining the bounding isosurface is 0.30. Color code: magenta = core, green = disynaptic.
The populations of the iron core basins are very similar for both isomers, 23.50 e– for the D3h structure and 23.47 e– for the C2v, which corresponds to a local [Ar]d6 configuration where the remaining density of 1.5 e– is located in the V (Fe, Fe) valence basins. The population of these latter basins, 0.65 e– for D3h and 0.55 e– for C2v, is not consistent with a picture where the iron atoms form covalent bonds between them. The superposition of resonance structures seems more satisfactory and is supported by the large values of the variance of the V (Fe, Fe) populations compared to the populations themselves. For the D3h isomer the variance of V (Fe, Fe) is 0.64 (e–)2, while the variance of the Fe core population is also very large, typically of the order of 2.75 (e–)2. The covariance analysis of the iron core shows that the delocalization mostly involves the V (Fe, C) basins and to a lesser extend the V (Fe, Fe) and the other C (Fe) basins. On the other hand and in constrast with the formamidinato dimers, the Fe–Fe core covariance is small 0.09 e– so the value of the delocalization index δ(Fe, Fe) = 0.4–0.26 can not be associated to the electron fluctuation between core areas.
Table 4 lists the valence basin populations of the ligands in both isomers together with the free CO population and the net electron transfer from the Fe3 cluster. The analysis of the differences in population between the free and coordinated CO ligand is made in an attempt to compare the topological results with the σ-donation and π-backdonation provided by the Deward–Chatt–Duncanson [33,34] scheme.
CO moieties basin populations N, transfers with respect to free CO ΔN, and net electron transfer δQ (e–)
| V (Fe, C) | V (C, O) | V (O) | |||||
| N | ΔN | N | ΔN | N | ΔN | δQ | |
| Free CO | |||||||
| 2.64 | 3.25 | 4.14 | |||||
| D3h | |||||||
| Apical (ap) | 3.04 | 0.40 | 3.02 | –0.23 | 4.31 | 0.17 | 0.34 |
| Equatorial (eq) | 3.16 | 0.52 | 3.07 | –0.18 | 4.35 | 0.21 | 0.55 |
| C2v | |||||||
| Fe(1) ap | 2.95 | 0.31 | 3.13 | –0.12 | 4.33 | 0.19 | 0.38 |
| Fe(1) eq | 3.16 | 0.52 | 3.12 | –0.13 | 4.33 | 0.19 | 0.58 |
| Fe(2) ap | 3.06 | 0.42 | 3.05 | –0.20 | 4.35 | 0.21 | 0.43 |
| Fe(2) eq | 3.12 | 0.48 | 3.13 | –0.12 | 4.36 | 0.22 | 0.58 |
| Fe(2) br | 3.43 | 0.79 | 2.79 | –0.46 | 4.71 | 0.57 | 0.90 |
In both isomers the net electron density transfer towards CO is larger for the equatorial position than for the apical one. This is consistent with the shorter Fe–C bond distances found for the equatorial positions. In the case of the bridging position, the electron transfer is twice that in the apical position. This charge transfer process corresponds to a gain of electron density in the V (Fe, C) and V (O) basins and to a loss in the V (C, O) one. This latter loss is larger in magnitude for the ligands in apical position which explains why the CO bond length increases more than in equatorial ligands. For bridging ligands the V (C, O) loss amounts to 0.55 e–, about twice the equatorial value.
In conclusion, the topological analysis shows that the Fe3 cluster is not linked by three single bonds, but rather by a delocalized electron pair and that the stabilization of the C2v isomer with respect to the D3h one is mostly due to the replacement of two two-center dative bonds by two three-center ones. This is accompanied by a larger charge transfer towards these bridging ligands. It is not possible to establish a direct correspondence between the valence population analysis and the Deward–Chatt–Duncanson scheme.
4.2 Electron-poor complexes with Mo3S4 cluster cores
Molybdenum and tungsten have proved to have a great tendency to form trinuclear clusters under a variety of reaction conditions [35]. Among the different structural types encountered for these trinuclear clusters, our interest will be focused on the incomplete cubane-type model cluster with formula [Mo3(μ3-S)(μ-S)3(PH3)6Cl3]+ and represented in Fig. 5, similar to the one reported by Cotton and Llusar [36] in the late 80s, where the diphosphine outer ligands have been replaced by PH3. In this model cluster, the three metal atoms define an equilateral triangle with one capping atom (μ3-S) above and three bridging atoms (μ-S) bellow the plane described by the metals. Three more ligands, two phosphine molecules and one chlorine anion, on each metal are distributed so as to complete the local metal octahedra. Geometry optimization is successfully achieved at the B3LYP level using all electron basis sets as well as a combination of effective core pseudopotential for the metal atoms combined with all electron basis sets for the rest [37].
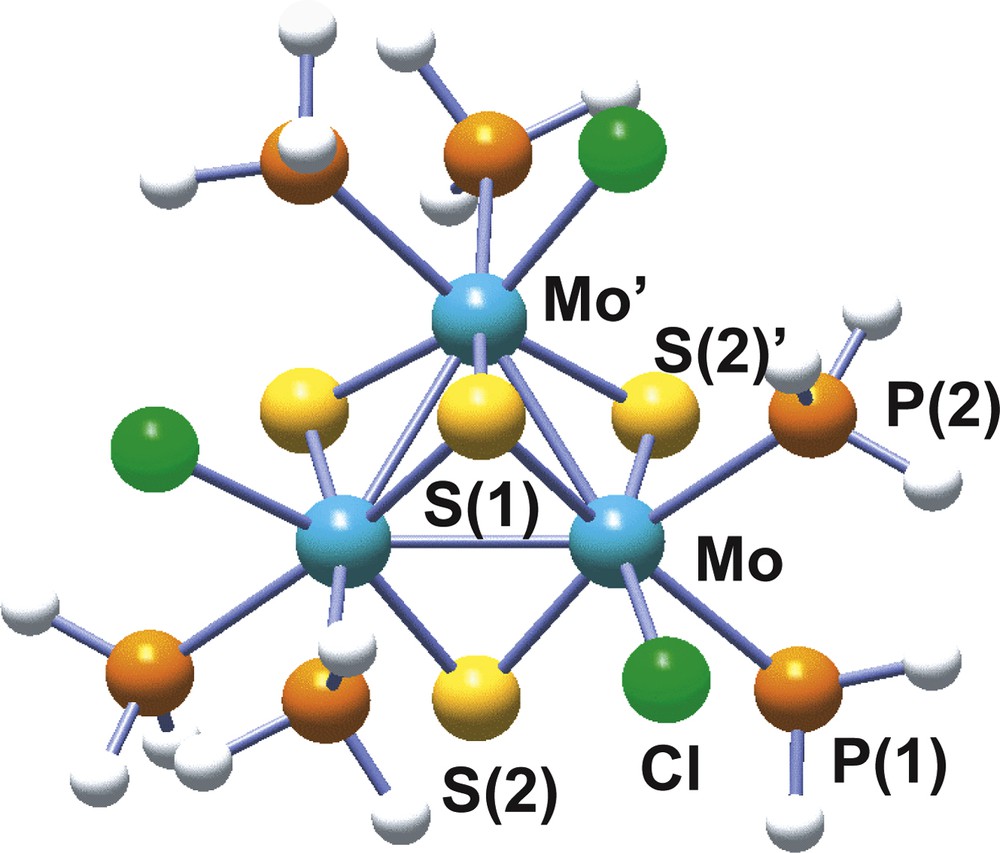
Structure of the model trimer [Mo3S4(PH3)6Cl3]+ with atom numbering scheme.
A simple but widely used scheme of the metal–metal bonding in this M3X13 system is the one based on the empirical method formulated by Cotton and Haas (CH) [38,39] for the Mo3O13 unit in the early sixties. This simplified scheme was also supported by the Dahl's qualitative orbital analysis model that predicted the existence of nine cluster orbitals involving metal–metal interactions among which three are strongly bonding (1a1 and 1e) and one is weakly bonding (2a1) [40]. Most Mo3S4 complexes are electron precise with a 1a12 1e4 electronic configuration which result according to the MO interpretation in the formation of tree metal–metal bonds. Although qualitative symmetry arguments seem to be valid in most cases, it is clear that extensive mixing between the metals and the core and outer ligands complicate the bonding situation and in consequence, a detailed analysis of the interactions must be carried out for a particular system [41,42].
The topological AIM analysis shows that the molecular graph obtained for [Mo3S4(PH3)6Cl3]+ unit reproduces the bond paths associated to the Mo–Mo, Mo–S, Mo–P and Mo–Cl interactions [37]. As already pointed out for the M2(formamidinate)4 and Fe3(CO)12 complexes, the bcp properties are characterized by its small and positive ρ(rbcp) values and the small and negative E (rbcp) quantities, which represent a mixture of closed-shell and shared parameters. As for the other cluster complexes considered in this account, the laplacian of the electron density shows that there is no bonded charge concentration within its outer shell of charge, in contrast with the bonding characteristics found for main group atoms. The AIM atomic populations of the metals are also higher than its conventional values.
The nature of the different bonds within the Mo3S4 unit can be better understood by considering the delocalization index [7]. The δ(Mo, Mo) has been calculated to be 0.56, this value is approximately one half the one calculated for the Rh2(formamidinate)4 dimer, with a Rh–Rh topological bond order of 1.008 in spite that a formal metal–metal bond order of one is assigned to both complexes. It is worth nothing that the Mo–S delocalization indexes are noticeably larger.
The ELF analysis defines domains as units with a chemical significance. A reducible domain splits into several domains containing an atractor upon increasing the value of ELF. The successive reductions result are represented in the so called bifurcation diagram shown in Fig. 6 for the cluster complex [Mo3S4(PH3)6Cl3]+.
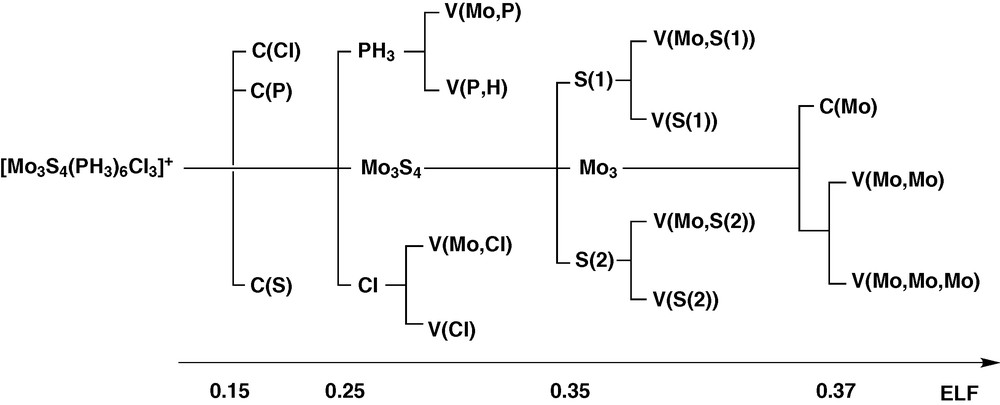
Bifurcation diagram of the [Mo3S4(PH3)6Cl3]+ complex.
According to the ELF topology, the Mo3S4 and Mo3 cluster units behaves as specific entities. The bonding within the Mo3 core arises from the presence of a three-center bond associated to a group of three disynaptic V (Mo, Mo) and one trisynaptic V (Mo, Mo, Mo) basins, showed in Fig. 7. Because the reduction of the Mo3 domain takes place in a very narrow ELF range, the chemically meaningful entity is the superbasin that includes the four metallic valence basins as a whole rather than the individual domains.
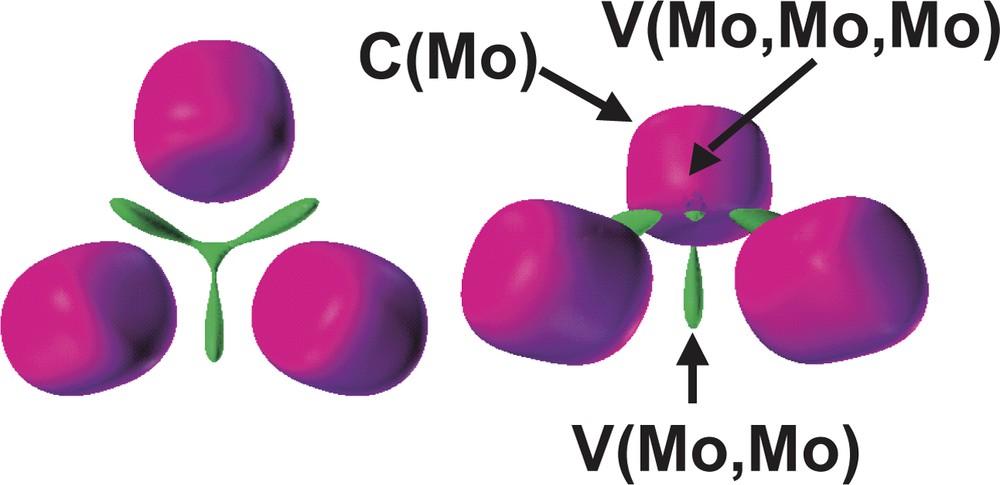
Detail of the [Mo3] subsistem in [Mo3S4(PH3)6Cl3]+ containing the Mo cores and the valence Mo–Mo basins. The ELF values defining the bounding isosurface are 0.36 (left) and 0.37 (right). Color code: magenta = core, green = disynaptic.
Within the Mo3(μ3-S)(μ-S)3 valence domain the trihapto coordinated sulfur atom, S(1), is surrounded by three V (Mo, S(1)) disynaptic basins assigned the three covalent Mo–S(1) bonds with a population of 1.43 e– each and a monosynaptic basin populated by 2.92 e–. On the other hand, the basins involving the metal bond to the three bridging sulfur ligands, Mo–S(2) and Mo–S(2)′, have populations of 1.05 and 1.27 e–, respectively, due to the asymmetry in the sulfur coordination: trans to the P or to the Cl atom. In this particular case differences in basin population have not chemical meaning due to the difficulties in reducing the V (S(2)) valence domains, that possesses a global population of 7.15 e–, into two Mo–S basins and one monosynaptic containing the two sulfur lone pairs. Most of the atomic contributions to the Mo–S basins, 80% for the Mo–S(1) and approximately 78% for Mo–S(2), comes from sulfur supporting the partial ionic character of the bond. The most important contribution to the variance of the lone pairs of the V (S(2)) basins comes from the C (Mo), with a 24% of the contribution, and from the V (Mo, S(2)) and V (Mo, S(2)′) basins, with a 37% for each one. This is in agreement with a delocalized Mo–(μ-S(2))–Mo bonding suggested by Li et al. [43]. These authors relate this delocalization with the existence of a 3c–2e– bond and name this situation as “pseudo-aromaticity”.
The Mo3 cluster unit behaves as a specific entity where the bonding arises from the presence of a three-center bond associated to a group of basins involving three disynaptic V (Mo, Mo) and one trisynaptic V (Mo, Mo, Mo) basins. The fact that the valence Mo3 superbasin separates into the previously mentioned four domains in a very narrow range of ELF, justifies that the four basins group are a whole chemically meaningful entity. The total population of this Mo3 valence superbasin is 1.42 e–, a large value as compared to the value of 0.68 e– calculated for the disynaptic intermetallic basin in the Mo2(formamidinate)4 quadruply bonded dimer. The metal–metal bond in the M2(formamidinate)4 dimers, where M = second row transition metal, is considered to be due to the high fluctuation of electrons within core areas [20]. However, this is not the case for the Mo3 unit under consideration where the Mo–Mo core covariance is small, B (Mo, Mo) = 0.12 e–, in spite of the rather large value of the Mo core population variance, σ2 = 2.50 (e–)2. On the other hand, the basins V (S(2)) and V (Mo, S(2)) contributes to this value of variance in 0.25 and 2 × 0.17 e–, respectively, in agreement with the Mo–(μ-S(2))–Mo delocalization phenomena. The molybdenum core population, 38.87 e–, which corresponds with an assignment of the oxidation state Mo (+3) instead of Mo (+4), is the molybdenum formal oxidation state in these Mo3S4 units.
5 Tetranuclear complexes
The incorporation of copper(I) or nickel(0) into the [Mo3S4(PH3)6Cl3]+ complex affords the 16 metal electron clusters [Mo3CuS4(PH3)6Cl4]+ and Mo3NiS4(PH3)6Cl4, represented in Fig. 8 [44,45]. These two heterodimetallic complexes differ in their redox properties, while the copper cluster is 0.31 V easier to reduce than its trinuclear precursor, the nickel compound is 0.58 V more difficult to reduce.
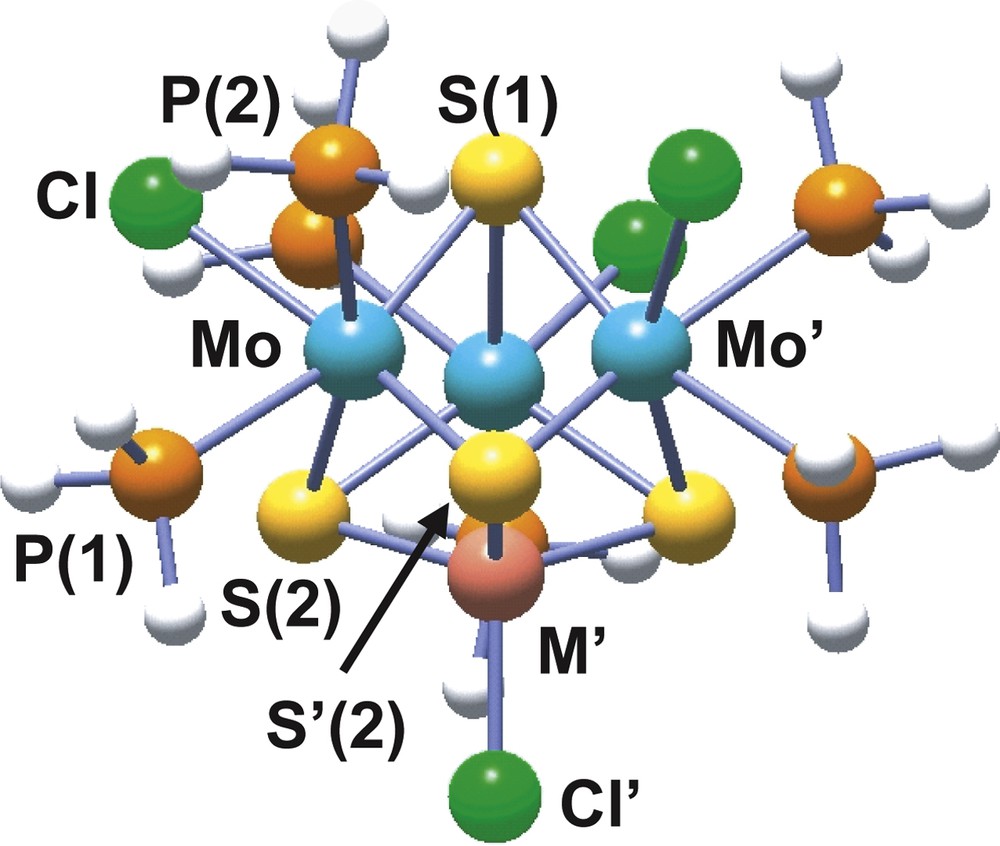
Structure of the model cubane [Mo3M′S4(PH3)6Cl4]n (M′ = Cu, n = +1; M′ = Ni, n = 0) cluster.
Although some authors suggest that such differences are due to changes in the Mo oxidation states, Mo(IV)3Cu(I) versus Mo(IV) Mo2(III) Ni(II), theoretical studies by Bahn et al. [46] indicate that the oxidation states of the molybdenum atoms do not change upon insertion of Cu(I) or Ni(0). Fenske-Hall calculations on M3M′S4 complexes show the presence of a group of three strongly bonding molecular orbitals (1e and 1a1), doubly degenerate M′-based bonding orbital (2e), a group of three weakly antibonding cluster molecular orbitals (2a1 and 3e) and three strongly antibonding MOs. Metal electrons in excess of 16 will occupy strongly antibonding orbital making these population the most common for these Mo3M′S4 cubane-type clusters.
According to the AIM theory, the molecular graph for the [Mo3CuS4]5+ and [Mo3NiS4]4+ compounds obtained from a B3P86 calculation reproduces the bond paths corresponding to the Mo–Mo, Mo–Ni and Mo–S interactions [45]. However, no bond path associated to the Mo–Cu and M′–S interactions within the Mo3CuS4 unit is detected. Table 5 lists the most relevant topological data concerning the Mo3M′S4 cluster compounds together with the equivalent values in the Mo3S4 trinuclear precursor. Geometry optimization is successfully achieved with the B3P86 functional using the ECP-SBKJC combination, where the Stevens' effective core potential replaces the inner electrons of the transition metals and the {4211/4211/411} basis set represents the external metallic electrons. All electron 6-31G (d, p) basis set are employed for the remaining atoms.
Topological data for [Mo3S4(PH3)6Cl3]+, [Mo3M′S4(PH3)6Cl4]n (M′ = Cu, n = +1; M′ = Ni, n = 0) clustersa,b
| Mo3S4 | Mo3CuS4 | Mo3NiS4 | |
| QAIM(Mo) | +1.08 | +1.05 | +0.99 |
| QAIM(M′) | – | +0.53 | +0.43 |
| δ(Mo, Mo) | 0.56 | 0.58 | 0.58 |
| δ(Mo, M′) | – | 0.20 | 0.46 |
| δ(Mo, S(2))av | 1.12 | 1.03 | 0.93 |
| δ(M′, S(2)) | – | 0.54 | 0.72 |
| N(C(Mo)) | 38.87 | 38.88 | 38.96 |
| N(C(M′)) | – | 27.10 | 25.99 |
| N(V(Mo, Mo)) | 0.42 | 0.45 | 0.46 |
| N(V(Mo, M′)) | – | – | 0.21 |
| N(V(Mo, Mo, Mo)) | 0.16 | – | – |
| N(V(Mo, Mo, Mo, M′)) | – | 0.36 | 0.25 |
a Averaged basin populations are given in electrons.
b The topological studies were performed using the B3P86 functional and the Ahlrichs TZV basis set for the metals and the 6-311G(d, p) basis set for the remaining atoms [45].
As pointed out for the trinuclear complex, the values of the charge density, its lapacian and the energy at the bcp makes ambiguous the bond classification. On the other hand, the atomic AIM charges for the molybdenum atoms in these tetranuclear clusters are approximately one, equal to the values calculated for the metal atoms in the trinuclear complex.
The incorporation of the heterometal into the trinuclear Mo3S4 unit does not produce significant changes in the δ(Mo, Mo) values. However, there is decrease in the δ(Mo, S(2)) and δ (Mo, S(2)′) indexes between 0.1 and 0.2 upon metal insertion. On the other hand, the δ(Cu, S) index is lower than the δ(Ni, S) value, this observation is consistent with the higher covalent character of the Ni–S bond versus the Cu–S interaction.
An analysis of the topology of the ELF isosurface for the Mo3M′S4 unit identifies the four following irreducible domains assigned to the S(1) and S(2) sulfur valence shell, V (Mo–S) and V (S), as found for the Mo3S4 cluster unit plus a reducible metallic Mo3M″ superbasin. No disynaptic V (M′, S) basin is observed. In the ELF topology the Mo3Cu cluster unit behaves as an entity in a similar way to the Mo3 core in their trinuclear precursor, where the bonding arises from the presence of a tetrasynaptic V (M′, Mo, Mo, Mo) plus three disynaptic V (Mo, Mo) basins. In the case of the nickel complex, one tetrasynaptic V (Ni, Mo, Mo, Mo) and three disynaptic V (Mo, Ni) basins are also identified. The total population of the Mo3M′ superbasin is 1.71 e– for the copper complex and 2.26 e– for the nickel compound in front of the value of 1.42 e– calculated for the Mo3 trinuclear precursor. Higher Mo3M′ basin populations are associated to higher values of the δ (Mo, M′) delocalization index. As already found for the other trinuclear complexes considered in this account, the presence of a metal–metal bond is not associated to the fluctuation of electrons within the core areas seen in the Mo2(formamidinate)4 dimer. The Mo–Mo core covariance in both tetrametallic complexes is similar to that calculated for the trinuclear precursor where the major contributions to the Mo core covariance are also the S(2) sulfur lone pair and the V (Mo, S(2)) disynaptic basins. This fact supports the existence of a Mo–(μ-S(2))–Mo delocalization effect as found in the molybdenum trinuclear complex. On the other hand, the highest contribution to the C (M′) covariance comes from the V (S(2)) lone pair indicating the presence of a M′–S(2) delocalization. This population analysis shows that the Mo3M′S4 core behaves as a unique chemical entity, an observation supported by its reactivity where the tetrametallic unit can be easily modified by substitution reactions of the outer ligands [47].
The molybdenum core populations of these tetranuclear clusters (see Table 5) does not show significant changes in going from the trinuclear to the tetranuclear compounds; as a consequence changes in the redox behavior can not be attributed to variations on the oxidation states of the molybdenum atoms as suggested by other authors based on XPS experiments [48]. On the other hand, the calculated populations for the copper and nickel cores are 27.10 and 25.99 e–, respectively, supporting a M′(II) oxidation state for these metals. This oxidation state assignment agrees with the high vibrational CO stretching frequency measured for the Mo3NiS4 clusters, but enters in contradiction with the theoretical investigations of Harris et al. which support a zero oxidation state for the nickel atom in these cluster complexes. These authors claimed that the Mo3 framework may be view as a tridentate π-acceptor metalloligand to the Ni(0) atom. Other investigations on the topic are in progress in our group.
Acknowledgements
Financial support from Ministerio de Ciencia y Tecnología (research project BQU2002-00313) is gratefully acknowledged. S.B. thanks the European Comission for a Marie Curie postdoctoral fellowship and F.S. thanks ‘Fundació Caixa Castelló–Universitat Jaume I’ for financing a research stay at this University.


