1 Introduction
Antiferromagnets with competing interactions are said to be geometrically frustrated. As a result, they exhibit a variety of fascinating phenomena [1]. In this context, the term frustration describes a situation where, in the ground state of the corresponding classical spin system, not all interactions can be saturated simultaneously. A typical picture for such a situation is a triangle of antiferromagnetically coupled spins, where classically the spins are not in the typical up–down–up configuration, but assume a ground state that is characterized by a relative angle of 120° between neighboring spins. This special type of classical ground state characterizes several frustrated spin systems, among them are giant Keplerate molecules [2–4], the triangular lattice antiferromagnet, and the kagome lattice antiferromagnet.
Among the phenomena caused by frustration are magnetization plateaus and jumps as well as unusual susceptibility minima, as observed for example for the kagome lattice antiferromagnet [5,6]. Some of these effects can also occur in certain strongly frustrated magnetic molecules such as the Keplerate {Mo72Fe30} [7] and in a cuboctahedral molecule [8] which has been already synthesized as {Cu12La8}, but has not yet been magnetically characterized [9]. It has also soon be noticed that the high degeneracy of magnetic levels at the saturation field, where the unusual jumps occur, should also have an enormous impact on the magnetocaloric effect. An adiabatic process should yield a massively enhanced cooling rate in the vicinity of large magnetization jumps. Such a behavior was first anticipated for the classical version of the kagome lattice antiferromagnet [10] and subsequently demonstrated for certain low-dimensional quantum spin systems [11]. In addition it could be shown that this effect is rather stable against perturbations [12]. In the following sections, some of these effects will be reviewed in more detail.
Interlinking the zero-dimensional molecular units to cluster-based networks is a highly interesting new route in molecular magnetism, especially if the degree of magnetic exchange between the cluster entities can be varied over a wide range. Examples for such cluster-based networks are given by chains [13] and square lattices [14,15] of the magnetic Keplerate molecule {Mo72Fe30}. These systems show new combinations of physical properties that stem from both molecular and bulk effects. As an example for a quasi one-dimensional molecule-based frustrated spin system, the recently synthesized three-leg ladder compound [(CuCl2tachH)3Cl]Cl2 will be discussed [16,17].
Throughout the article the spin systems are modeled by an isotropic Heisenberg Hamiltonian augmented with a Zeeman term, i.e.:
| (1) |
2 Frustration effects in magnetic molecules
For not too strong frustration, i.e. not too large deviation from bipartiteness [18,19], many spin systems possess properties that are similar to or in accord with their unfrustrated, i.e. bipartite counterparts. This is for instance the case for antiferromagnetically coupled Heisenberg spin rings, which – if even-membered – are covered by such famous rigorous results as the sign rule of Marshall and Peierls [20] and the theorems of Lieb, Schultz, and Mattis [18,19]. A key quantity of interest is the shift quantum number associated with the cyclic shift symmetry of the rings. The corresponding crystal momentum is then 2πk/N. For the aforementioned rings with even N (bipartite) one can explain the shift quantum numbers for the relative ground states in subspaces of total magnetic quantum number M [18–20]. In recent investigations we could numerically verify and prove in some cases that even for frustrated rings with odd N astonishing regularities hold, and thus a generalized sign rule can be established, which holds for chains of arbitrary sizes [21].
An antiferromagnet that can be decomposed into two sublattices has as its lowest excitations the rotation of the Néel vector as well as spin wave excitations [22]. In finite size systems, these excitations are arranged in rotational (parabolic) bands of energy eigenvalues as a function of total spin. Such a behavior is most pronounced for bipartite, i.e. unfrustrated systems [23–25]. It turns out that the idea of rotational bands can be used to approximate the low-lying energy spectrum of the Keplerate molecule {Mo72Fe30} which, due to the huge size of the Hilbert space, practically, cannot be dealt with by other quantum methods [26]. Such an approximation can explain the field dependence of the magnetization at low temperatures [26]. It also predicts a strong resonance in the inelastic neutron scattering cross-section at the separation between the two lowest bands, which was indeed discovered in a recent experiment using inelastic neutron scattering [27].
Nevertheless, the agreement of some properties with those of the corresponding non-frustrated counterparts is only approximate. Frustrated antiferromagnets exhibit their very own characteristic features. One of them is given by independent magnons which occur in certain spin arrays. It has been found that the minimal energies Emin(S) of antiferromagnetic molecules of cuboctahedral and icosidodecahedral structures depend linearly on total spin S above a certain total spin [28]. Such a dependence, which is depicted in Fig. 1 (top) for an icosidodecahedron with intrinsic spin s = 1/2, results in an unusually big jump to saturation, as can be seen in Fig. 1 (bottom). Although first noticed for the Keplerate molecule {Mo72Fe30}, such a behavior is quite common for a whole class of frustrated spin systems, including for instance the kagome or the pyrochlore lattice antiferromagnet [6,29], as well as for other frustrated magnetic molecules [8]. The underlying reason is that, due to the special geometric frustration in such systems – even polygons are surrounded by triangles –, the relative ground states in subspaces are for big enough M given by product states of independent localized magnons. This is one of the rare examples where eigenstates of an interacting many-body Hamiltonian can be constructed analytically.
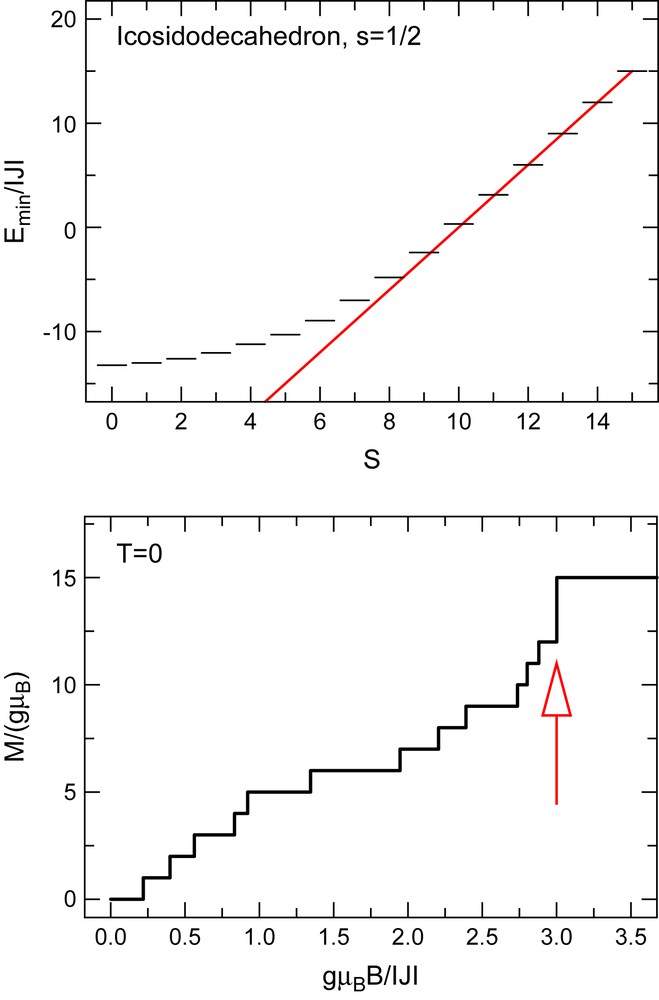
Top: minimal energies of the icosidodecahedron for s = 1/2. The highest four levels fall on a straight line. Bottom: resulting (T = 0) − magnetization curve. The magnetization jump of ΔM = 3 is marked by an arrow.
From a condensed matter point of view, the occurrence of independent and localized magnons can be understood by looking at the band structure in one-magnon space. Fig. 2 shows as an example the energy levels of the sawtooth chain, a structure that can exhibit a truly giant magnetization jump of half of the saturation magnetization [29]. In one-magnon space, the energy levels form two bands: an N/2-times degenerate (flat) ground state band and a cosine shaped excited band. It is clear that the degenerate states of the flat band can be superimposed in order to form localized objects which are independent if well-enough separated. The occurrence of flat bands seems to be rather common [30]: they exist for instance in the magnetic molecules of icosidodecahedral and cuboctahedral structures discussed previously as well as in the kagome and the pyrochlore antiferromagnet [29].
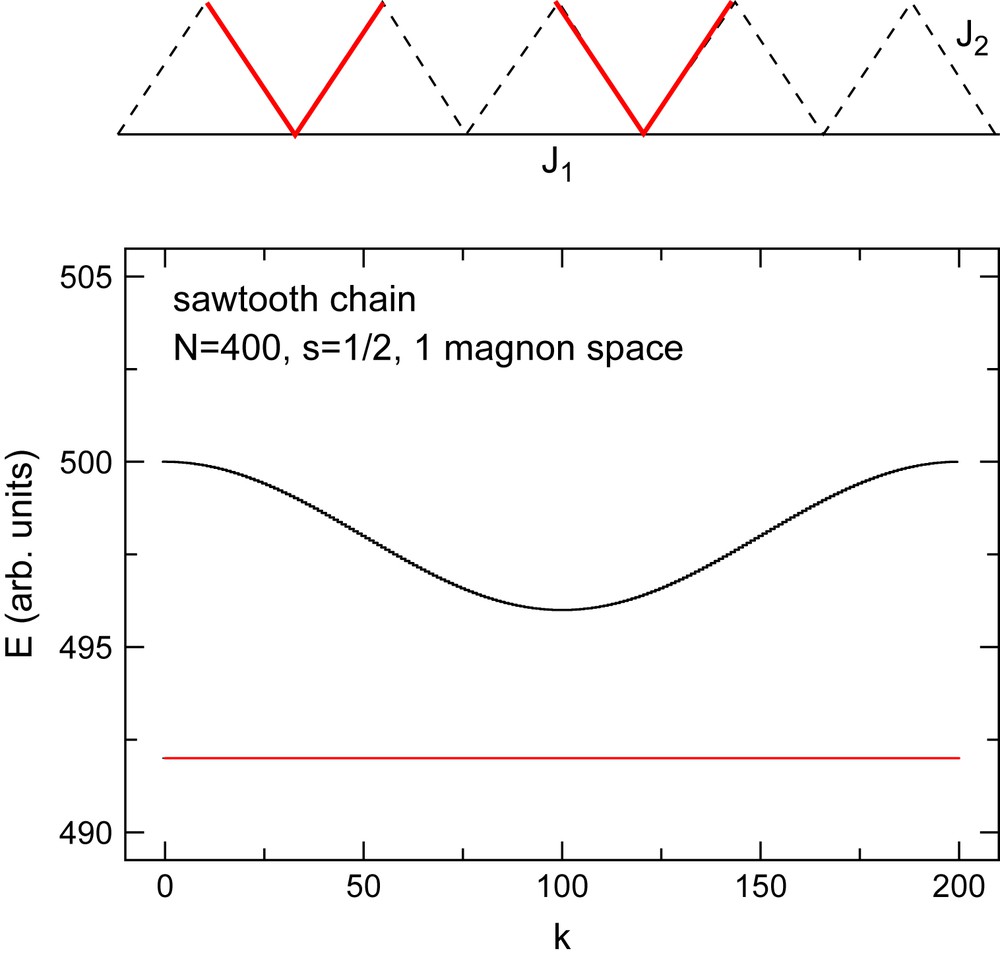
Top: structure of the sawtooth chain, which hosts independent magnons (V) for J2 = 2J1. Bottom: energy bands in one-magnon space; the flat band consists of N/2 degenerate levels.
As the last point of this section, I want to discuss the observation that hysteresis can occur without anisotropy. Usually the observation of hysteresis effects in magnetic materials is an outcome of their magnetic anisotropy. In a recent article, we could report that magnetic hysteresis (Fig. 3) occurs in a spin system without any anisotropy [31]. Specifically, we investigated an icosahedron where classical spins mounted on the vertices are coupled by antiferromagnetic isotropic nearest-neighbor Heisenberg interaction, giving rise to geometric frustration. At T = 0 this system undergoes a first-order metamagnetic phase transition at a critical field between two distinct families of ground-state configurations. The metastable phases of the system are characterized by temperature and field-dependent survival probability distributions. Our exact classical treatment shows that the abrupt transition at T = 0 originates in the intersection of two energy curves belonging to different families of spin configurations that are ground states below and above the critical field. The minimum of the two energy functions constitutes a non-convex minimal energy function of the spin system and this gives rise to a metamagnetic phase transition [32]. We could also show that the corresponding quantum spin system for sufficiently large spin quantum number s ≥ 4 possesses a non-convex set of lowest energy levels when plotted versus total spin [31], which again leads to a nontrivial magnetization jump. Nevertheless, the investigation of the hysteretic behavior of the quantum systems remains an open problem so far, since the magnetization dynamics should involve the modeling of the relaxation of the quantum spin system in a time-dependent field and coupled to a thermostat. This future investigation will either be performed by solving the complete Schrödinger dynamics of the coupled spin and bath systems or by following effective Master equations (compare Ref. [33]).

Hysteresis behavior of the classical icosahedron in an applied magnetic field obtained by classical spin dynamics simulations (thick lines) as well as by analytical stability analysis (grey lines). The curves match perfectly [31].
3 Frustration effects of the three-leg ladder compound [(CuCl2tachH)3Cl]Cl2
Recently we reported the magnetic features of a new one-dimensional stack of antiferromagnetically coupled equilateral copper(II) triangles, see top of Fig. 4 [16,17]. High-field magnetization measurements (bottom of Fig. 4) showed that the interaction between the copper triangles is of the same order of magnitude as the intra-triangle exchange, although only coupled via hydrogen bonds. Thus, this molecule-based infinite chain turns out to be an interesting example of a frustrated cylindrical three-leg ladder with competing intra- and inter-triangle interaction.
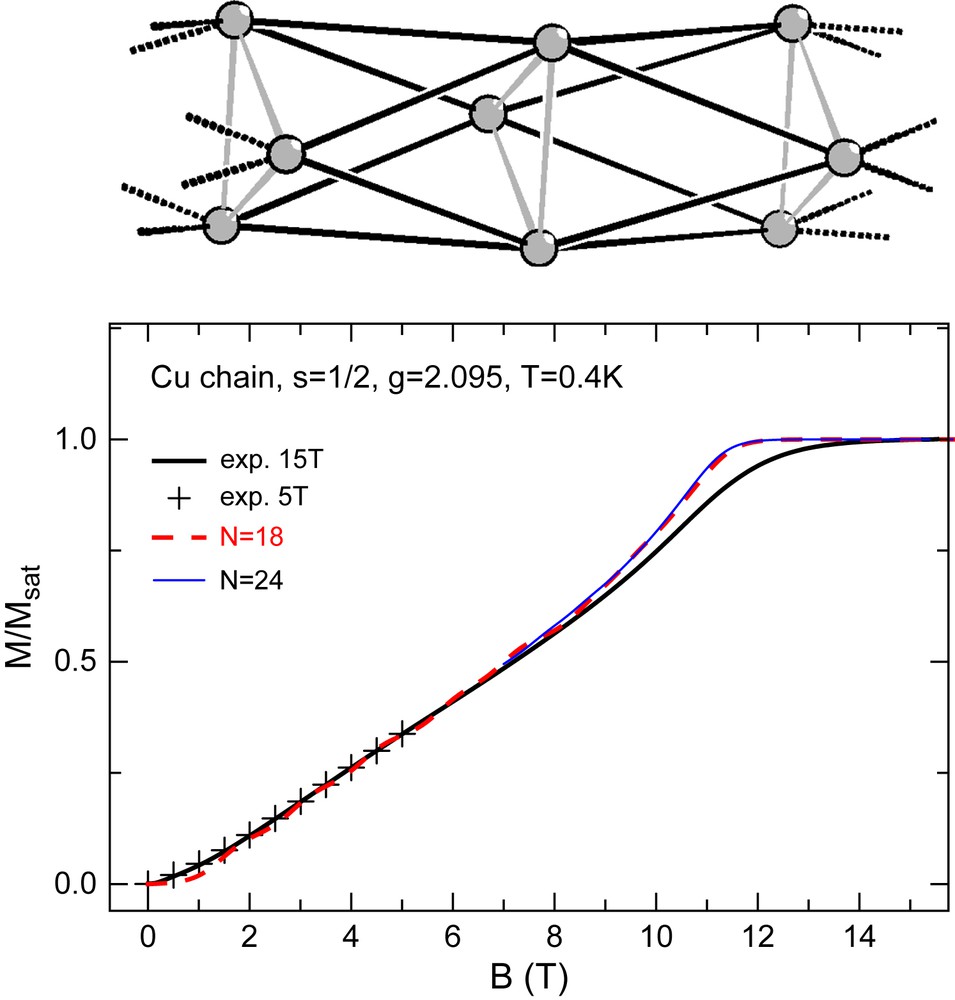
Top: schematic structure of the triangular copper chain. The copper ions are placed at the vertices, intra-triangle exchange pathways are drawn by grey lines (J1 = −0.9 K), inter-triangle couplings are given by black lines (J2 = −1.95 K). Bottom: magnetization per copper triangle. Experimental data taken at a cryostat temperature of 0.4 K are given by thick solid lines, the two datasets are practically identical. The theoretical estimates are given for 18 and 24 spins, i.e. 6 or 8 triangles. The saturation field is Bsat = 11 T [17].
A key question concerns the structure of the low-lying levels, and especially the existence of a singlet–triplet and a singlet–singlet gap. Finite-size extrapolations of Lanczos diagonalization results seemed to suggest that the singlet ground state is gapped from the triplet excitation (compare top panel of Fig. 5). For all finite size systems, it turned out that also the first excited singlet is gapped from the ground-state singlet (see bottom panel of Fig. 5). It is amazing that the singlet–singlet gap seems to be nearly independent of the system's size.
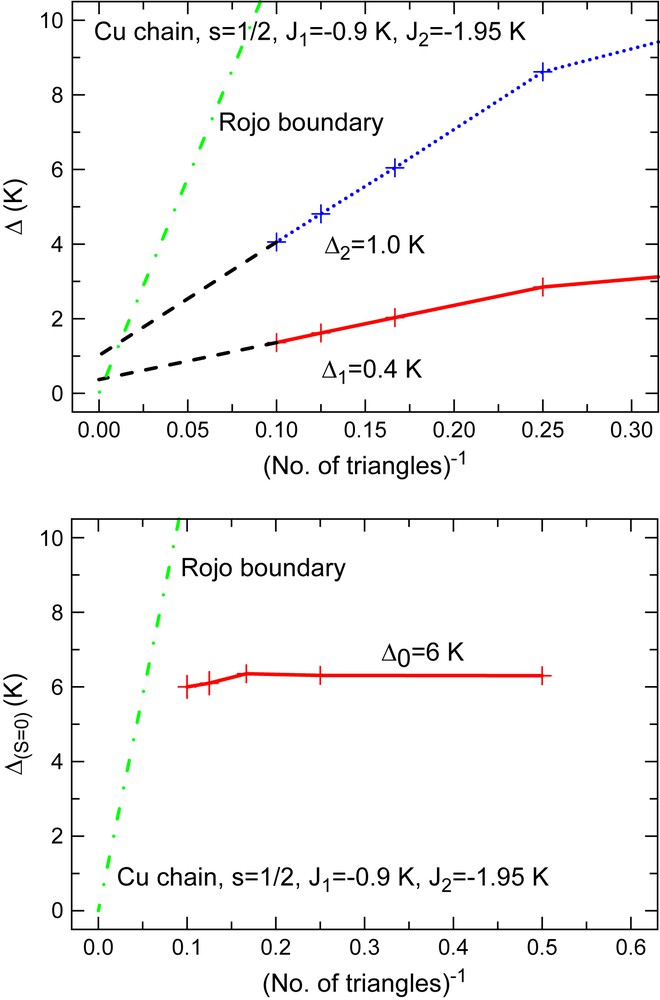
Top: finite-size extrapolation of the singlet–triplet gap Δ1 = Emin(S = 1) − Emin(S = 0) and the pentuplet–single gap Δ2 = Emin(S = 2) − Emin(S = 0) for [(CuCl2tachH)3Cl]Cl2. Both gaps for the infinite chain are estimated to be non-zero. Bottom: finite-size behavior of the singlet–singlet gap for [(CuCl2tachH)3Cl]Cl2. The two leftmost data points for 8 and 10 triangles have an uncertainty of about ± 0.2 K due to the restricted accuracy of the Lanczos procedure for excited states [17]. The dashed line in both figures shows the upper boundary of the gap size according to Ref. [41].
Our findings provoked theoretical investigations of related models [34–40], which yield that this frustrated spin system should not have a gap. The arguments are as follows:
- (i) It is shown in Ref. [34] that the Hamiltonian of a ladder compound such as [(CuCl2tachH)3Cl]Cl2 can be mapped onto a simpler Hamiltonian of a linear chain of effective spins. For weak inter-triangle couplings J2 each triangle basically remains in the triangular ground state with Striangle = 1/2, and thus the ladder should be an effective s = 1/2 chain, which is augmented by additional chiral degrees of freedom [34]. Such a chain should have a twofold degenerate ground state. In the opposite case where the inter-triangle coupling dominates, the triangular ground state should have Striangle = 3/2, and then the ladder should be an effective s = 3/2 chain, which, since being a half-integer chain, is gapless.
- (ii) Ref. [35] also provides a numerical argument. The Hamiltonian of [(CuCl2tachH)3Cl]Cl2 is diagonalized for the relevant exchange parameters J1 = −0.9 K, J2 = −1.95 K with the help of Density Matrix Renormalization Group Techniques (DMRG). Using DMRG one can determine the ground state energies in subspaces of total magnetic quantum number M for much larger chains. Nevertheless, due to technical problems with the boundary conditions which are intrinsic to the method only the gap to the pentuplet Emin(S = 2) − Emin(S = 0) could be determined, which indeed tends to zero.
- (iii) The most general argument of Ref. [35] states that the three-leg ladder should either have a degenerate ground state or be gapless according to a proof given in Ref. [41]. This proof is applicable for arbitrary ladder compounds with an odd number of sites on the rungs and half-integer intrinsic spin quantum number as long as the system possesses translational symmetry along the ladder. To the best of our knowledge this proof should be correct.
The above arguments suggest that the finite size extrapolation of Ref. [17] might be biased by too short sample systems (up to 10 triangles). In addition the role of the boundary conditions might be crucial for the actual numerical convergence. In order to estimate, to which system size a precise gap estimation must be performed in order to definitely decide about low-lying gaps, the upper bound according to Ref. [41] is displayed as a dashed line in Fig. 5. It seems realistic to reach conclusion about the singlet–singlet gap, whereas the two other gaps Δ1 = Emin(S = 1) − Emin(S = 0) and Δ2 = Emin(S = 2) − Emin(S = 0) approach the theoretical bound for rather large system sizes only.
Summarizing, the existence of low-lying gaps in the new frustrated three-lag ladder appears to be ruled out for the perfect model system. Investigations on the real spin system, both theoretically and experimentally, will continue.
Acknowledgement
It is my pleasure to thank K. Bärwinkel, A. Honecker, P. Kögerler, M. Luban, H. Nojiri, J. Richter, H.-J. Schmidt, and C. Schröder for the fruitful collaboration that produced so many exciting results. I am especially thankful to H.-J. Schmidt for valuable discussions about the three-lag ladder compound. This work was supported by the Ph.D. program of the University of Osnabrück as well as by the Deutsche Forschungsgemeinschaft (grant nos. SCHN 615/5-1, SCHN 615/5-2, and SCHN 615/8-1).


