1 Introduction
The energy difference between an uncharged species and its negative ion, referred to as its electron affinity (EA), is an important property of atoms and molecules which was discussed in detail by Schaefer's group [1]. Organic molecules and ligands with high EA are interesting for the design of systems exhibiting flexible reduced states. In this context, actinide complexes with the cyclopentadienyl Cp or Cp* ligands (Cp = C5H5; Cp* = C5Me5) deserve a special attention. For about 30 years the organometallic chemistry of actinides (uranium in particular) has witnessed a spectacular development, with the synthesis of new molecular compounds exhibiting interesting structural, physical and chemical properties [2–6]. Cyclopentadienyl complexes play a major role in catalytic reactions, as well as in multi-electron reductants chemistry combining the traditional U(III)/U(IV) couple and formal ligand based reductions involving the Cp−/Cp system [7].
Very few experimental or theoretical studies of the EA of actinide compounds have been published up to now. Among them, a study of Kiplinger and co-workers [8] concerns the fluoroketimide complexes (Cp*)2U(-N = CMeR)2 (R = 4-F-C6H4 or C6F5), while a relatively few voltammetry experiments exist for tris- and biscyclopentadienyl compounds in relation with the U(IV)/U(III), U(V)/U(IV) and U(VI)/U(V) redox systems [9–16].
Recently, our group, using relativistic DFT calculations, showed that the EAs of the tris- and biscyclopentadienyl uranium complexes Cp3UX (X = Cl, BH4, SPh, SiPr and OiPr) and [X2 = (BH4)2, (NEt2) Cl, Me2 and (OEt)2] correlate very nicely with the electron donating capacity of the ligand X following the order: Cl < BH4 < SPh < SiPr < OiPr for the first series [17] and (BH4)2 < (NEt2)Cl < Me2 < (OEt)2 for the second one [18]. These studies showed that the quantum method selected, namely the ZORA/DFT technique coupled with the COSMO approach for taking into account solvent effects, is very reliable to study the redox process of organo-uranium complexes. Therefore, we found interesting to estimate the electron affinity of several biscyclopentadienyl uranium(IV) bisborohydride complexes, related to the U(IV)/U(III) redox system, using current relativistic ZORA/DFT techniques (see computational details). Our aim is to investigate the influence of the aromatic L ligand on the electron affinity of the following series of uranium complexes L2U(BH4)2 [L2 = Cp2 [19], (tmp)2 [20,21], (tBuCp)2 [22], (Cp*)(tmp) [23] and [23] where tmp = tetramethylphospholyl (C4Me4P) and tBuCp = tBuC5H4] for which half-reduction potentials are available. Comparison of compounds with aromatic ligands which are isosteric but have distinct electron donating capacities like Cp* and tmp [23], highlighted the importance of the electronic effects of the ligands to explain and predict the structure and the stability of uranium complexes.
The main goals of the work are: (i) to correlate the calculated EA values and the measured half-wave potentials; (ii) to study the role of involved orbitals (singly occupied molecular orbital –SOMO– of anionic U(III) species or lowest unoccupied molecular orbital –LUMO– of neutral U(IV) species) in the redox process; (iii) to investigate the influence of the nature of the L ligand.
2 Computational details
The calculations were performed using Density Functional Theory (DFT) [24]. Relativistic corrections were introduced via the Zero Order Regular Approximation (ZORA) [25]. Solvents effects have been taken into account using the Conductor-like Screening Model (COSMO) [26]. The ZORA/DFT calculations were performed using the Amsterdam Density Functional (ADF2008.01) program package [27c]. The Vosko-Wilk-Nusair functional (WVN) [28] for the local density approximation (LDA) and the gradient corrections for exchange and correlation of Becke and Perdew [29], respectively, i.e. the BP86 functional, have been used.
Triple-ζ Slater-type valence orbitals (STO) augmented by one set of polarization functions (TZP) were used for all atoms. For all elements, the basis sets were taken from the ZORA/DFT/TZP database. The frozen-core approximation where the core density is obtained from four-component Dirac-Slater calculations has been applied for all atoms. 1s core electrons were frozen respectively for boron B.1s and carbon C.1s. For phosphorus P.2p, the 1s/2s/2p cores were frozen. The U.5d valence space of the heavy element includes the 5f/6s/6p/6d/7s/7p shells (14 valence electrons). Several studies have shown that the ZORA/DFT approach reproduces the experimental geometries and ground states properties of f-block element compounds with a satisfying accuracy [30–34].
The theoretical determination of electron affinities has been so far a difficult task [1]. EA computations generally involve odd-electron systems where spin contamination and SCF convergence problems add to the difficulty of producing reliable results.
Since available experimental molecular EAs are largely adiabatic, the most direct theoretical method comes from the calculation of the difference of the energies of both the neutral and anionic forms of the complexes at their respective optimized geometries, i.e. the “ΔE method”.
In terms of the energies E at optimized geometries, the theoretical definition of EA is:
The ADF program that we use produces Total Bonding Energies (TBE) rather than total energies, so that EA is computed in our case as the TBE(neutral) − TBE(anion) difference.
3 Results and discussion
3.1 Molecular geometry optimizations
We have considered the highest spin states of all species, i.e. a triplet state (5f2) for the U(IV) neutral complexes and a quartet state (5f3) for the anionic U(III) ones. All compounds have been taken in the C1 symmetry.
First, the complete geometry optimizations of the neutral complexes Cp2U(BH4)2, (tBuCp)2U(BH4)2, (tmp)2U(BH4)2, (Cp*)(tmp)U(BH4)2 and U(BH4)2 and their anionic forms were carried out in the gas phase, at the spin unrestricted level of the theory.
Geometries were then further reoptimized in the tetrahydrofuran (THF) solvent using the COSMO approach. The non-default Delley type of cavity was used, the solvent being considered with its dielectric constant of 7.58 and a radius of 3.18 Å. Then, in a third step, we carried out single-point calculations in order to estimate spin-orbit corrections, using the previously optimized geometries, for both the gas phase and solution.
As will be seen later in the text, we also carried out calculations using the more extended ZORA TZ2P basis set which contains two sets of polarization functions (Supporting Information (SI) for more details). Molecular geometry and molecular orbital plots were generated, respectively, by using the MOLEKEL 4.3 [35] and the ADFVIEW [27c] programs.
In Table 1, we give the most relevant computed geometric parameters, i.e. metal–ligand distances and bond angles for the two U(IV) and U(III) species in the gas phase, as well as in solution (for more details, see the SI where one can find all the optimized structures and coordinates).
Computed distances (Angstrom) and angles (deg.) for the L2U (BH4)2 complexes at ZORA/BP86/TZP level in the gas phase and in solution (in parentheses); in square brackets, the experimental X-ray values given for the U(IV) species, Cp2U(BH4)2 [19], (tmp)2U(BH4)2 [20] and Cp*2U(BH4)2 [23].
| Complex U(IV)/U(III) values | (tmp)2U(BH4)2 | Cp2U(BH4)2 | (tBuCp)2U(BH4)2 | (Cp*)(tmp) | |
| U–Cp1 | 2.458/2.575 | 2.442/2.499 | 2.505 / 2.581 | 2.592/2.583 | 2.522/2.536 |
| (2.513/2.523) | (2.456/2.471) | (2.519/2.558) | (2.559/2.582) | (2.507/2.542) | |
| [2.519] | - | - | - | [2.46] | |
| U–Cp2 | 2.461/2.592 | 2.476/2.488 | 2.468 /2.517 | 2.523/2.551 | 2.522/2.593 |
| (2.518/2.523) | (2.456/2.471) | (2.483/2.500) | (2.502/2.535) | (2.508/2.554) | |
| [2.503] | - | - | - | [2.48] | |
| U–B1 | 2.508/2.570 | 2.525/2.619 | 2.526 /2.585 | 2.510/2.594 | 2.529/2.597 |
| (2.517/2.618) | (2.530/2.631) | (2.513/2.602) | (2.524/2.617) | (2.541/2.617) | |
| [2.553 + 0.001] | [2.58–2.63] | - | - | [2.58] | |
| U–B2 | 2.508/2.563 | 2.525/2.619 | 2.529/2.589 | 2.511/2.597 | 2.528/2.598 |
| (2.521/2.618) | (2.532/2.629) | (2.516/2.606) | (2.520/2.617) | (2.540/2.611) | |
| [2.553 + 0.001] | [2.61–2.63] | - | - | [2.58] | |
| <U–C>cp1 | 2.742/2.886 | 2.755/2.767 | 2.745/2.793 | 2.896/2.911 | 2.799/2.812 |
| (2.822/2.828) | (2.754/2.752) | (2.762/2.778) | (2.873/2.900) | (2.786/2.818) | |
| [2.811 + 0.004] | [2.4–2.8] | - | - | [2.723] | |
| <U–C>cp2 | 2.737/2.895 | 2.724/2.766 | 2.781/ 2.813 | 2.761/2.835 | 2.799/2.863 |
| (2.821/2.828) | (2.737/2.752) | (2.794/2.829) | (2.782/2.812) | (2.787/2.829) | |
| [2.811 +0.004] | [2.4–2.8] | - | - | [2.757] | |
| <U–H>BH41 | 2.314/2.384 | 2.323/2.434 | 2.334 /2.403 | 2.305/2.407 | 2.326/2.415 |
| (2.323/2.433) | (2.333/2.449) | (2.323/2.431) | (2.326/2.435) | (2.346/2.424) | |
| [2.29 + 0.20] | - | - | - | - | |
| <U–H>BH42 | 2.314/2.377 | 2.323/2.434 | 2.325/2.407 | 2.306/2.405 | 2.326/2.414 |
| (2.327/2.433) | (2.333/2.447) | (2.319/2.344) | (2.322/2.434) | (2.345/2.432) | |
| [2.29 + 0.20] | - | - | - | - | |
| <C–C> | 1.416/1.420 | 1.421/1.423 | 1.425/1.424 | 1.429/1.429 | 1.429/1.428 |
| (1.421/1.422) | (1.422/1.425) | (1.424/1.425) | (1.430/1.428) | (1.430/1.430) | |
| [1.401 + 0.002] | - | - | - | - | |
| Cp1–U–Cp2 | 119.1/126.6 | 120.5/115.7 | 120.0/118.4 | 129.5/128.3 | 131.8/130.0 |
| (126.7/126.9) | (121.5/119.9) | (119.1/117.1) | (129.1/127.6) | (131.6/129.6) | |
| [123.5] | - | - | - | [133.0] | |
| B1–U–B2 | 89.9/101.3 | 100.0/99.8 | 101.2/105.4 | 99.0/99.7 | 99.1/103.0 |
| (100.9/97.9) | (100.0/99.4) | (103.0/104.0) | (97.5/97.7) | (98.2/99.8) | |
| [100.4] | [99.6–102.5] | - | - | [101.0] | |
| <Cp–U–B> | 111.0/108.2 | 108.6/110.7 | 108.8/107.6 | 106.2/106.5 | 105.2/105.1 |
| (106.6/107.1) | (108.3/108.9) | (108.4/108.7) | (106.4/106.9) | (105.6/105.9) | |
| [108.4] | - | - | - | [104.5] |
First of all, the analysis of Table 1 shows a good agreement between the computed geometrical parameters and the available crystallographic data, namely for (tmp)2U(BH4)2, Cp2U(BH4)2 and We note that, for all complexes, the computed U–B distances (of 2.508 to 2.529 Å) of the (BH4)2 ligands which exhibit a tridentate ligation mode with the central metal are slightly smaller than those determined by X-ray diffraction (2.553 to 2.630 Å) [19–23]. The same observation can be made for the U–Cp distances (Cp = centroid of the five-membered ring) where the variation does not exceed 0.04 Å.
The angles Cp1–U–Cp2, B1–U–B2 and <Cp–U–B> are also well reproduced. For example, the theoretical values of B1–U–B2, 101.3°C for (tmp)2U(BH4)2, 99.8° for Cp2U(BH4)2 and 105.1° for reproduce correctly the experimental values of 100.4°, 99.6–102.5° and 101.0°, respectively. The computed U–P1 (2.903 Å) and U–P2 (2.295 Å) distances of (tmp)2U(BH4)2 complex agree well with the experimental values (2.897 and 2.913 Å respectively). The theoretical value (89.9°) of the <C–P–C> bond angle is very close to X-ray data (90.1°).
Moreover, the reduction process of the neutral U(IV) species involves an appreciable increase of some internuclear distances, particularly U–X and <U–C> by an amount of 0.06–0.10 Å and 0.04–0.14 Å respectively, correlating with the increase of 0.160 Å in the radii of the U4+ and U3+ ions [36]. This increase is particularly important in the case of the U–Cp distances of the (tmp)2U(BH4)2 complex (approximately 0.13 Å); this is probably due to the dominating role of the tmp ligand which increases the antibonding character of the highest occupied molecular orbital of the U(III) anionic species (see further the frontier MO diagram of the U(III) complexes in Fig. 5). By contrast, the variation of the C–C bond lengths of the Cp ring when passing from the neutral to the anionic form is very slight (the variation does not exceed 0.02 Å); this indicates that the reduction process does not affect the Cp ring.
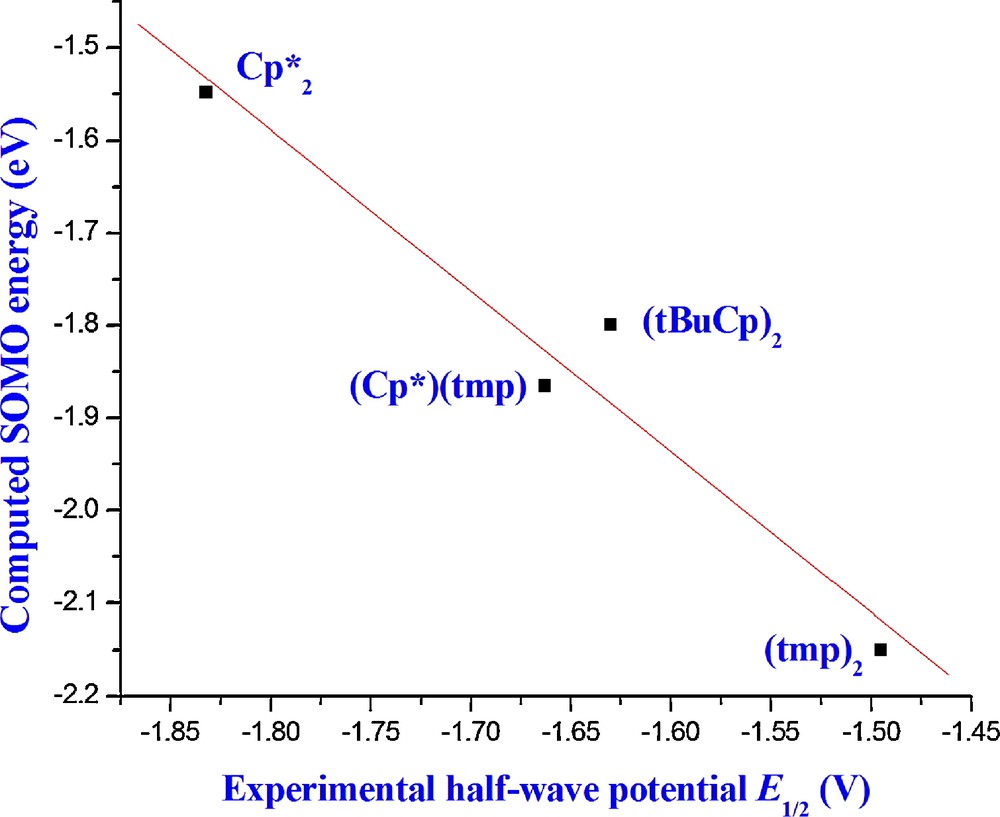
Correlation U(III) SOMO energies- Experimental E1/2.
We note also, in the results of Table 1, that the geometrical parameters computed in solution (tetrahydrofuran) are similar to those evaluated in the gas phase. However, when U(IV) passes to U(III), the difference of distances observed in solution is less large than that observed in the gas phase. For example, the <U–Cp> distances of the (tmp)2U(BH4)2 complex computed in the gas phase are 2.459 and 2.583 Å for U(IV) and U(III) respectively, with an increase in distance of 0.124 Å, whereas in solution they pass to 2.515 and 2.523 Å, with an increase of only 0.008 Å. It is interesting to note that for the X-ray characterized neutral U(IV) species, the agreement between the optimized metal-to-ligand distances and the experimental data is slightly better considering the THF values than the gas phase ones. Thus, for , the average U–B and U–Cp distances of 2.541 and 2.507 Å calculated in solution are closer to the experimental values (2.58 and 2.46 Å respectively) than those of 2.529 and 2.522 Å evaluated in the gas phase. Interestingly, the U–P2 bond length decreases in the solvent whereas the other U–P1 one increases.
Finally, the use of a larger basis set, i.e. TZ2P, as expected gives optimized geometries which are practically identical to those obtained with the TZP ones (see SI).
The optimized molecular geometries of the neutral U(IV) and anionic U(III) species are depicted on Fig. 1.

Optimized geometries of L2U(BH4)2 at the BP86/TZP level in solution.
3.2 Electron affinities
In all cases, the electron affinities were computed (Table 2), at the ZORA/BP86/TZP (and TZ2P) level of theory in the gas phase as well as in solution, as differences of the TBEs of the neutral U(IV) and anionic U(III) species at their optimized geometries. The TBE values are given in the SI section.
Electron affinities (eV) of the U(IV)/U(III) complexes at ZORA/BP86/TZP (and TZ2P) level in the gas phase and in THF (in parentheses) and experimental half-wave potentials E1/2 (V).
| Complex | (tmp)2 | Cp2 | (tBuCp)2U(BH4)2 | (Cp*)(tmp) | |
| TZP | 1.620 (3.060) | 1.592 (3.051) | 1.955 (3.184) | 1.449 (2.854) | 1.537 (3.111) |
| TZP-SO | 1.976 (3.404) | 1.905 (3.479) | 1.918 (3.278) | 1.774 (3.204) | 1.578 (3.066) |
| TZ2P | 1.632 (3.121) | 1.589 (3.101) | 1.961 (3.166) | 1.458 (2.850) | 1.543 (3.105) |
| TZ2P-SO | 1.987 (3.405) | 1.905 (3.425) | 1.922 (3.237) | 1.785 (3.198) | 1.587 (3.061) |
| E1/2 exp (V) | −1.495 | −1.620 | −1.630 | −1.663 | −1.832 |
The values of the electron affinities consigned in Table 2 are all positive (U(III) species more stable than U(IV) ones). In the last line of this table are displayed the measured half-wave reduction potentials (E1/2 vs. [Cp2Fe]+/0) of the neutral uranium(IV) complexes (see the Experimental Section).
The effect of a polar solvent, which is more important for an anionic species than for a neutral one, leads consequently to an important variation of EAs. However, it is worth noting that the ordering of the reduction ability of the U(IV) complexes under consideration is the same considering EAs in the gas phase or in THF.
Considering the Cp2, (tBuCp)2 and (Cp*)(tmp) species, it is worth noting that the correct ranking of their EAs relatively to half-wave potentials is reached when taking into account the spin-orbit correction and solvent effects. Substitution of the cyclopentadienyl ring by one or more donor groups lowers the electron affinity of (tBuCp)2U(BH4)2 and with respect to Cp2U(BH4)2. Indeed, the substitution of only one hydrogen decreases by 0.21 eV the EA of (tBuCp)2U(BH4)2 whereas the substitution of five hydrogen makes it possible to decrease the EA of by 0.40 eV. Thus, , which has the lowest half-wave potential (−1.832 V) and is the most difficult to reduce, has the lowest EA whereas (tmp)2U(BH4)2, which exhibits the highest potential presents the largest EA. We notice that only Cp2U(BH4)2 deviates from the other complexes since its EA of 3.425 eV exceeds that of (tmp)2U(BH4)2 (3.405 eV), whereas its measured half-wave potential (−1.620 V) is lower than that of (tmp)2U(BH4)2 (−1.495 V). However it must be pointed out that the experimental E1/2 value is questionable. Indeed, it is observed experimentally, on the one hand, an instability of the complex (exchange of ligands between the complex and solvent) and, on the other hand, a progressive degradation of the compound in solution in the presence of the used electrolyte salt, Bu4NPF6 [14].
It is interesting to note that the EA of (Cp*)(tmp)U(BH4)2 which bears one Cp* and one tmp ligand (1.774 eV in the gas phase, 3.204 eV in solution) is exactly the mean value of the EAs of U(BH4)2 and (tmp)2U(BH4)2 (1.578 and 1.976 eV in the gas phase, 3.066 and 3.404 eV in solution, respectively). The same behaviour is observed considering the measured half-wave reduction potentials (i.e. −1.663 V for (Cp*)(tmp) vs. −1.495 and −1.832 V for (tmp)2 and ). Therefore, in this case the influence of ligands on EAs or E1/2 seems to be additive.
The use of a larger basis set (TZ2P) leads to slight readjustments of EAs, in particular for the Cp2U(BH4)2 and (tBuCp)2U(BH4)2 complexes which exhibit EAs of 3.479 and 3.278 eV, respectively, at the TZP level, and which undergo a lowering of 0.03 and 0.04 eV, respectively, whereas EAs of the other complexes practically remain without changes.
The comparison between the computed EAs and measured half-wave reduction potentials E1/2 (excluding Cp2U(BH4)2) shows a very good linear correlation (r2 = 0.99) and the use of the TZ2P basis set gives the same result (Fig. 2). Including the questionable E1/2 value of Cp2U(BH4)2 in the regression leads to a r2 value equal to 0.86. The slope of the line is equal to −1.01 eV/V. This agreement between theory and experiment shows the relevance of the choice of the method used (relativistic DFT coupled to the COSMO approach) for the study of the reduction process in solution.
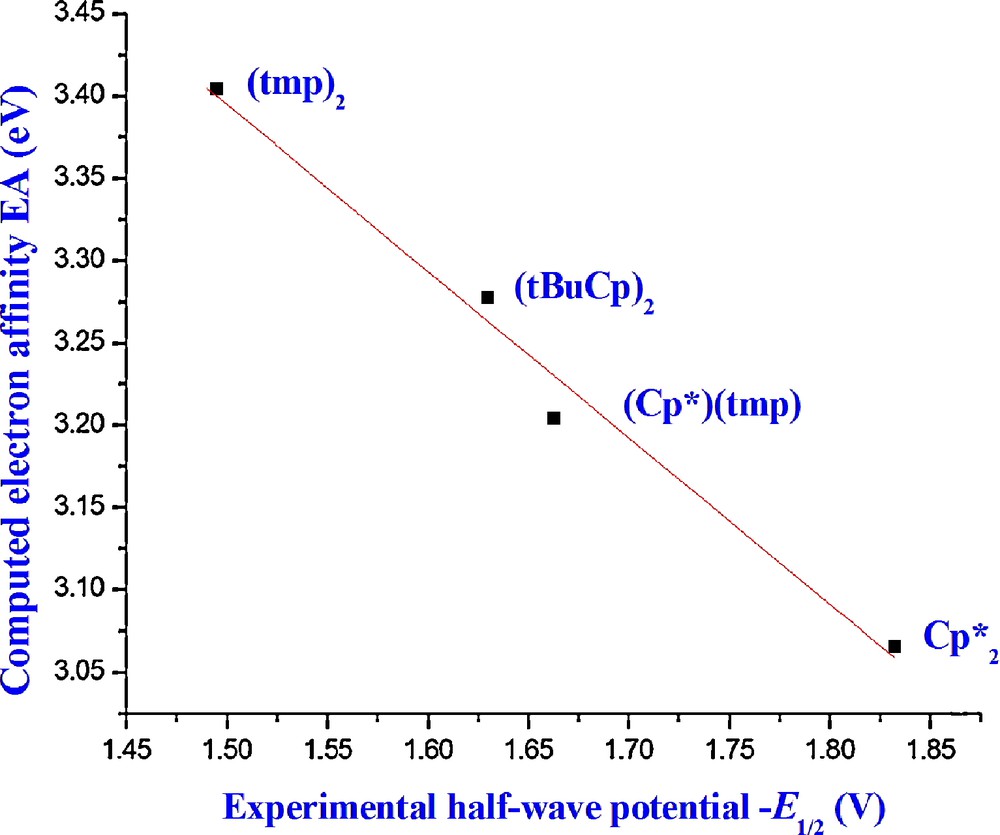
Correlation between the computed electron affinity EA and the measured half-wave potential for the L2U(BH4)2 complexes at the TZP-SO level (in solution).
We notice that neglecting spin-orbit coupling greatly affects the TBE; under such conditions the correlation EA-E1/2 worsens dramatically (r2 lower than 0.9). This shows the importance of spin-orbit corrections to reach a good agreement between computed EAs and half-wave reduction potentials measured in solution. This result agrees with a recent DFT study taking into account solvation effects (COSMO) which shows that spin-orbit corrections to the An(VI)/An(V) reduction potential of [AnO2(H2O)5]n+ (An = U, Np, Pu) complexes are essential [31b].
The variation of the EAs clearly reflects the electron donating capacity of the L2 (or LL′) ligands. As given by the Hammet constants [37], the electron donating (or accepting) ability of the L2 ligand should follow the order: (tmp)2 < (tBuCp)2 < (Cp*)(tmp) < Cp*2, which correlates well with the variation of the electronic affinity (Table 3).
Computed frontier MO energies (eV) of the U(IV)/U(III) complexes at ZORA/BP86/TZP (TZ2P) level in the gas phase and in THF solution (in brackets).
| Complex | (tmp)2 | Cp2 | (tBuCp)2 | (Cp*)(tmp) | |
| TZP_LUMO U(IV) | −3.795 (−3.914) | −3.983 (−4.009) | −3.794 (−3.854) | −3.472 (−3.656) | −3.305 (−3.474) |
| TZP_SOMO U(III) | 0.570 (−2.150) | 1.155 (−1.891) | 1.003 (−1.791) | 0.849 (−1.865) | 1.112 (−1.548) |
| SO_LUMO U(IV) | −3.921 (−3.963) | −4.051 (−4.156) | −3.895 (−3.952) | −3.583 (−3.760) | −3.422 (−3.596) |
| SO_SOMO U(III) | 0.368 (−2.353) | 0.822 (−2.202) | 0.695 (−1.991) | 0.605 (−2.095) | 0.837 (−1.781) |
| TZ2P_LUMO U(IV) | −3.810 (−3.912) | −4.056 (−4.099) | −3.852 (−3.880) | −3.506 (−3.672) | −3.346 (−3.496) |
| TZ2P_SOMO U(III) | 0.541 (−2.163) | 1.079 (−1.925) | 0.941 (−1.816) | 0.809 (−1.880) | 1.069 (−1.572) |
| SO_LUMO U(IV) | −3.937 (−3.992) | −4.129 (−4.208) | −3.956 (−3.967) | −3.618 (−3.792) | −3.466 (−3.618) |
| SO_SOMO U(III) | 0.340 (−2.380) | 0.748 (−2.237) | 0.635 (−1.979) | 0.564 (−2.103) | 0.793 (−1.802) |
The computed energies of frontier MOs, the SOMOs of the U(III) complexes and the LUMOs of the U(IV) ones are given in Table 3, in the gas phase and in solution, including or not spin-orbit corrections and solvent effects.
The LUMO energies of the neutral U(IV) complexes are all negative, indicating the capacity of these species to undergo a process of reduction; in contrast, the energies of the SOMO of the anionic U(III) compounds are positive. However, these SOMOs are drastically stabilized in the THF solvent, their energies becoming negative.
The effect of spin-orbit corrections on these energies is more important on the U(III) species in their quartet state (an average reduction of approximately 0.3 eV) than on the neutral U(IV) complexes in their triplet state.
One notes that the energy of the LUMO of Cp2U(BH4)2 is lower than that of (tmp)2U(BH4)2, which is somewhat unexpected, in view of their relative half-wave reduction potentials. Here again we see that the experimental E1/2 of Cp2U(BH4)2 is likely to be not reliable. The larger electronic affinity which is related to the electron withdrawing properties of the ligands in Cp2U(BH4)2 compared with (tmp)2U(BH4)2 is probably in relation to the fact that the energy of the accepting orbital is the lowest of the series, −3.983 eV in the gas phase (−4.208 eV in solution) against −3.795 eV (−3.992 eV) found for (tmp)2.
Fig. 3 shows three frontier MOs of the U(IV) complex, i.e. the two SOMOs bearing each a single electron and the empty LUMO. The percentages 6d/5f/U/L2 indicate the weights of the 6d and 5f metal orbitals as well as those of uranium and L2 ligand in the MOs (full frontier MO diagrams of the U(IV) and U(III) complexes are given in the ESI).
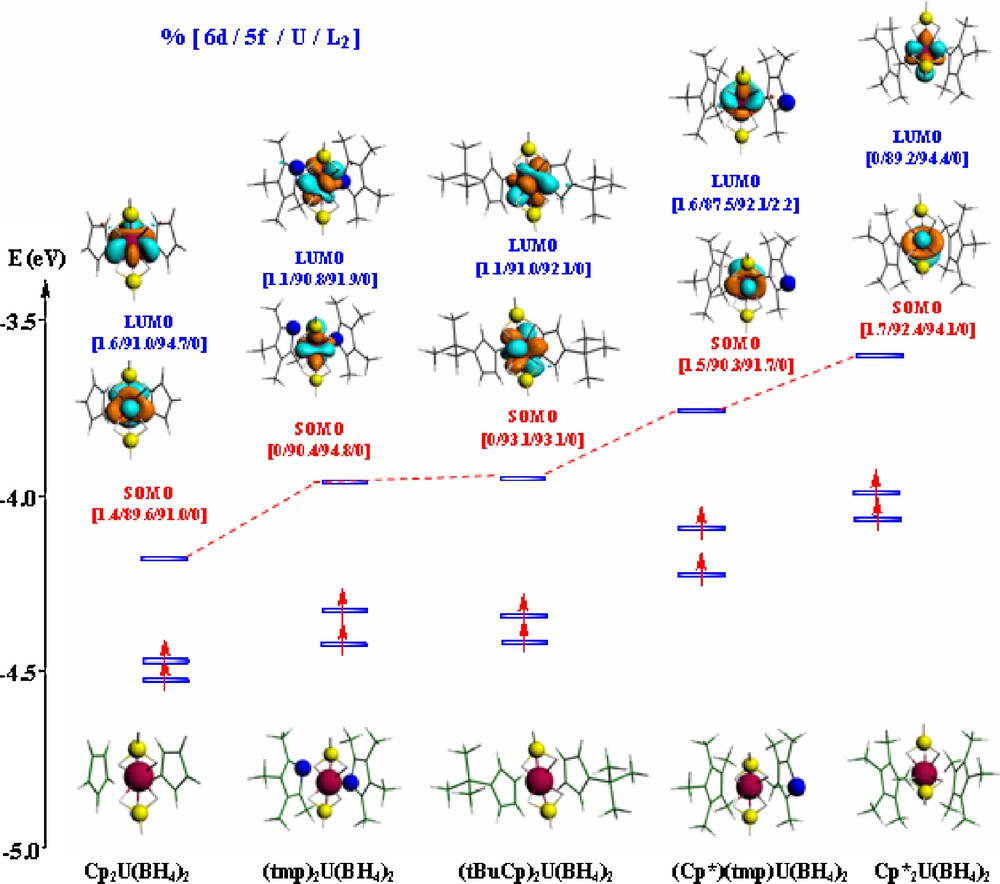
Frontier MO diagrams of the U(IV) L2U(BH4)2 complexes (solvated molecule at the TZP level).
These orbitals are localized on the U metal center and are mainly of 5f character. The L2 contribution to the LUMO is 0, except (Cp*)(tmp) with 2.2%. The (BH4)2 contribution, computed as the difference 100% – %U – %L2, is slightly higher for Cp2U(BH4)2 (9%) than for the other species (5.6% for , for example).
This MO diagram for complexes in solution confirms that the energies of the LUMO follow the same order as the EAs, the lowest LUMO (THF + SO) corresponding to the highest EA (THF + SO): Cp2 < (tmp)2 < (tBuCp)2 < (Cp*)(tmp) < Cp*2. The complex, being the weakest electron acceptor and then the most difficult to reduce, exhibits the highest LUMO energy (−3.618 eV).
The frontier MO diagram of the anionic U(III) species, displaying their three SOMOs, is given in Fig. 4. As for the U(IV) congeners, these MOs are mainly of 5f metal character.
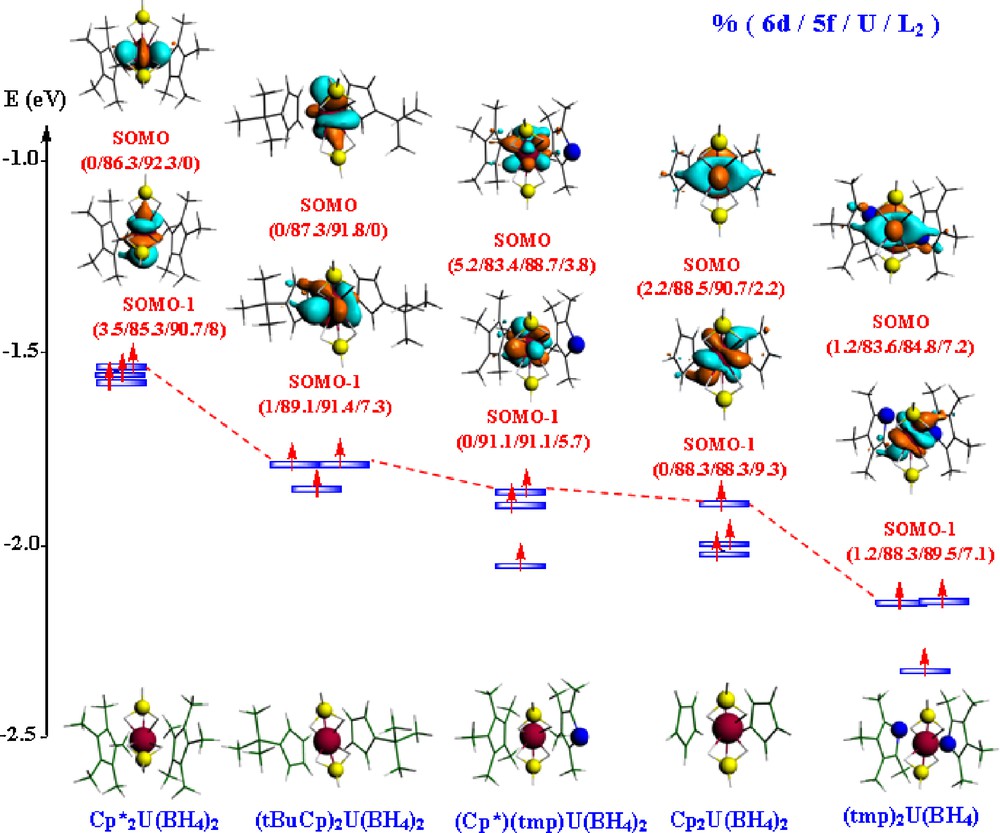
Frontier MO diagrams of the U(III) [L2U(BH4)2]− complexes (solvated molecule at the TZP level).
One notices that the contribution of the L2 ligand to this MO is rather marked in the case of the (tmp)2 species (7.2%) relatively to Cp2 (2.2%), (Cp*)(tmp) (3.8%) and 0% for the other species.
Expectedly, the correlation between the SOMO energies of the anionic U(III) species calculated at the TZP-SO or TZ2P-SO levels, and the measured half-wave potentials E1/2 (Fig. 5, r2 = 0.95) is not so satisfying as the correlation between EAs and E1/2. Indeed, the computed EAs take into account the electronic and nuclear relaxation following the redox process, and thus can be correlated to the adiabatic measured half-wave potentials, whereas the SOMO energies do not.
The metal spin density, the atomic net charges of the Mulliken Population Analysis (MPA) and the Nalewajski and Mrozek (N-M) bond indices multiplicity [38] of the L2U(BH4)2 series are summarized in Table 4. MPA, which is rather qualitative, accounts for some aspects of the U–L2 interaction, like the major charge transfers and the bonding interactions occurring in molecules.
MPA and N-M bond orders of the L2UX2 complexes at the TZP level in the gas phase and in solution (in parentheses).
| Complex | Spin State | Mulliken population analysis (MPA) | N-M bond ordersa | ||||
| Metal spin density | Net charges | U–L | U–L′ | ||||
| Uq | L2 | (BH4)2 | |||||
| (tmp)2U(BH4)2 | Q | 2.90 (2.90) | +0.242 (+0.359) | −0.733 (−0.690) | −0.509 (−0.669) | 1.561 (1.566) | 1.509 (1.626) |
| T | 2.25 (2.25) | +0.038 (+0.084) | +0.057 (+0.088) | −0.096 (−0.172) | 1.537 (1.566) | 1.599 (1.493) | |
| Cp2U(BH4)2 | Q | 2.97 (2.97) | +0.505 (+0.570) | −0.882 (−0.811) | −0.624 (−0.759) | 1.219 (1.428) | 1.481 (1.451) |
| T | 2.21 (2.26) | +0.338 (+0.336) | −0.157 (−0.093) | −0.181 (−0.243) | 1.196 (1.432) | 1.481 (1.495) | |
| (tBuCp)2U(BH4)2 | Q | 3.05 (3.05) | +0.477 (+0.519) | −0.956 (−0.815) | −0.521 (−0.704) | 1.196 (1.383) | 1.464 (1.411) |
| T | 2.20 (2.27) | +0.425 (+0.372) | −0.280 (−0.144) | −0.145 (−0.228) | 1.366 (1.232) | 1.544 (1.486) | |
| (Cp*)(tmp)U(BH4)2 | Q | 2.93 (2.94) | +0.251 (+0.420) | −0.741 (−0.716) | −0.440 (−0.704) | 1.547 (1.513) | 1.554 (1.564) |
| T | 2.24 (2.24) | +0.103 (+0.178) | −0.060 (+0.016) | −0.043 (−0.194) | 1.290 (1.276) | 1.437 (1.490) | |
| U(BH4)2 | Q | 3.06 (3.08) | +0.320 (+0.492) | −0.831 (−0.725) | −0.489 (−0.767) | 1.318 (1.252) | 1.430 (1.461) |
| T | 2.25 (2.27) | +0.309 (+0.364) | −0.165 (−0.079) | −0.144 (−0.286) | 1.172 (1.270) | 1.430 (1.459) |
a The two L aromatic ligands are labelled L and L′.
In this table, Q (for quartet) and T (for triplet) indicate, respectively, the anionic U(III) and the neutral U(IV) species. Metal spin density is calculated as the difference between the total α and β electronic populations of the metal. By net charges of L2, one understands the global charge of the two L aromatic entities and not only that of the atom connected to uranium; moreover, the charge of (BH4)2 is the sum of the two BH4 ligands.
A weak delocalization of the unpaired electrons is noticed insofar as the density of spin is not equal to 2 in the case of the 5f2 U(IV) complex or to 3 for the 5f3 U(III) derivative. Indeed, the DFT results indicate for example 2.90 unpaired electrons on U metal for [(tmp)2U(BH4)2]− with minor spin density on the L2 ligand while the metal spin density is 2.25 for the corresponding U(IV) species in the gas phase (negligible effects of solvent). On the contrary, for (tBuCp)2U(BH4)2 and , this MPA spin density appears larger than the number of 5f electrons in the case of the U(III) species (3.05 and 3.06 respectively). This means that a small negative spin density is spread over the ligands.
The ligand-to-metal donation is shown well by the net charge of the metal being much lower than its oxidation state (+4 and +3 for the neutral and anionic species respectively) on the one hand, and on the other hand, by the weak negative charges borne by the L2 and (BH4)2 ligands. Let us note that unlike the other complexes, the net charge of the ligand L2 is positive for the U(IV) compounds having one or two atoms of phosphorus [+0.088 in solution for (tmp)2U(BH4)2 and +0.016 for (Cp*)(tmp)]. We note finally that solvation generally leads to a small variation of MPA net charges, whereas metal spin densities remain practically unchanged.
The spin density distribution changes after the electron capture are related to the SOMO in the anionic species (Fig. 4). One notes that the values of the metal spin densities of the anionic U(III) species follow the same order as those of EAs, i.e. except for the (Cp*)(tmp) complex which deviates slightly from this correlation. The MPA evaluated with the use of a larger basis set, i.e. TZ2P, shows that the values of the spin densities remain practically constant, except that of the Cp2U(BH4)2 complex which passes from 2.21 (in TZP basis) to 2.26 (in TZ2P basis), whereas the net charges carried by uranium and the L2 and ligands undergo an increase of 0.05–0.07 for U and a lowering of 0.02–0.04 for L2 and .
It is interesting to follow the electronic charge redistribution following the reduction process, i.e. when passing from the U(IV) to the U(III) species; the values of the charge variation Δq of the aromatic ligand L2, computed as the difference between its charge in the U(III) and U(IV) complexes, are the following:
| Ligand | (tmp)2 | Cp2 | (tBuCp)2 | (Cp*)(tmp) | |
| Δq | −0.790 | −0.725 | −0.676 | −0.681 | −0.666 |
It is noteworthy that the tetramethylphospholyl tmp group recovers a net charge of −0.790 for only −0.666 for the pentamethylcyclopentadienyl Cp* ligand, the latter being less electron withdrawing than the tmp ligand. The negative charges gained by (tBuCp)2 and (Cp*)(tmp) are practically equal. This charge variation is related to the electron withdrawing ability of the ligands.
The Nalewajski and Mrozek bond orders [38] have been successfully used as a supplementary analysis tool of the electronic structure of organometallic complexes. Generally, the calculated bond multiplicity indices correlate very well with experimental predictions based on bond lengths and vibrational frequencies. In Table 4, for the (Cp*)(tmp)U(BH4)2 complex, the two tmp and Cp* ligands are labelled L and L′ respectively; for the L aromatic ligand the N-M bond indices is the sum of the contributions of the five U–C bonds of the two Cp (or tmp) rings.
The N-M method predicts a decrease in all U–X bond multiplicity in the anionic species with respect to the neutral congeners, this lowering being more significant for the compounds (0.199 in average in solution). It is interesting to note that the Nalewajski-Mrozek method accounts well for the changes of the geometrical parameters after electron capture. Indeed, the diminution of the N-M bond indices multiplicity (for the tmp2 ligand by 0.013 and for by 0.199) corresponds well to the variation of the U–Cp centroid distances during the reduction process (from tmp with Δ(U–Cp) = 0.008 Å to Cp* with 0.041 Å).
4 Conclusions
The relativistic ZORA/DFT method including spin-orbit coupling was used to estimate the electron affinities of a series of biscyclopentadienyl and phospholyl uranium(IV) borohydride complexes L2U(BH4)2 [L2 = Cp2, (tmp)2, (tBuCp)2, (Cp*)(tmp) and ]. Solvent effects have been taken into account using the COSMO approach. E1/2 half-wave potentials have been measured in solution (THF) under the same rigorous conditions for all the species under consideration.
A very good linear correlation (r2 = 0.99) has been obtained between the computed EAs and the measured electrochemical half-wave potentials E1/2. Our study brings to light the importance of spin-orbit coupling and solvent effect and the use of a large atomic basis set in order to achieve this good agreement between theory and experiment.
Considering the frontier MO diagrams, the SOMO of the reduced U(III) species, the Mulliken population analysis and the Nalewajski-Mrozek bond orders, we could study the influence of the electron capture on the structural properties of the complexes and explain the evolution of the EA with the nature of the substituted aromatic ligand L2, particularly with their electron donating power. EAs decrease according to: for the L2U(BH4)2 series, in agreement with the electron donating strength of the L ligands. This study demonstrates that one can connect and predict the evolution of the EA of these uranium complexes according to the substituents of the cyclopentadienyl ligands. We could also, by comparison with the theoretical EA, bring to light the fact that the measured E1/2 of Cp2U(BH4)2 should be considered with caution. Finally, this study on biscyclopentadienyl uranium complexes and the previous one on triscyclopentadienyl complexes confirm the reliability of the theoretical method used, namely ZORA/DFT including spin-orbit corrections computations coupled with the COSMO solvation approach, for the evaluation to the electron affinity of actinide complexes.
5 Experimental section
5.1 Reagents
Air-sensitive complexes were handled with the rigorous exclusion of oxygen and moisture in Schlenk-type glassware. The complexes Cp2U(BH4)2 [19], (tmp)2U(BH4)2 [20,21], (tBuCp)2U(BH4)2 [22], [23] and (Cp*)(tmp)U(BH4)2 [23] were prepared according to the published methods. Tetrahydrofuran (Aldrich) was stored under vacuum over sodium and benzophenone and transferred directly into the electrochemical cell by simple condensation (static vacuum method). Tetrabutylammonium hexafluorophosphate (Fluka-electrochemical grade), used without further purification, was dried under vacuum.
5.2 Electrochemical measurements
Electrochemical experiments were performed in a single-compartment three-electrode cell designed for highly air-sensitive compounds and connected to an argon/vacuum line. The working electrodes were a platinum conventional disc electrode Radiometer Analytical Pt30 (0.5 mm radius) and a platinum disc microelectrode Radiometer Analytical MEPT (7.5 μm radius). The auxiliary electrode was a platinum wire Radiometer Analytical Pt 11. The reference electrode was a wire Ag/AgCl in THF + Bu4NPF6 (Radiometer Analytical RDJ 10). The ferricinium/ferrocene ([Cp2Fe]+/0) system was used as internal standard reference. All potentials are referenced to this couple. Electrochemical measurements were carried out with EG&G Princeton Applied Research Potentiostat/Galvanostat Model 273 A controlled by a computer. In cyclic voltammetry, iR drop was compensated by feedback method. Electrochemical behaviour of the L2U(BH4)2 complexes was investigated in THF/0.1 M NBu4PF6 electrolyte by cyclic voltammetry. The complexes were reduced according to a reversible one-electron transfer process. Half-wave potentials (E1/2) of reduction processes were determined from voltammograms obtained at conventional microelectrode under pure diffusion condition from (Epc + Epa)/2 and at ultramicroelectrode under steady state diffusion condition (with low potential scan rate: 50 mV s−1) from the potential at ilim/2. The E1/2 values of U(IV)/U(III) redox system given in the text are corresponding to the mean values of E1/2 determinations (at least three experiments). Among the L2U(BH4)2 complexes, only electrochemical studies of Cp2U(BH4)2 have been already published [14]. If we can notice during electrochemical experiments a relative good stability of , (Cp*)(tmp)U(BH4)2, (tBuCp)2U(BH4)2, and (tmp)2U(BH4)2 complexes in the electrolytic solution [39], Cp2U(BH4)2 was found to be not stable in the presence of the used electrolyte salt, Bu4NPF6 [14].
Acknowledgements
We thank Dr Philippe Gradoz (CEA/Saclay) for the synthesis of the studied complexes. We also thank the French and Algerian governments for the research grant CMEP 07 MDU 700. Computing facilities were provided by IDRIS Computing Centre of CNRS.


