1 Introduction
The field of molecular magnetism has grown considerably since the 1980s, with the search for single-molecule magnets (SMM) [1] and multifunctional materials [2]. During the past two decades, much achievement has been made, both experimentally [3–5] and theoretically [6–11] in the studies of magnetic properties of transition metal and lanthanide species. An important issue is the measurement and the quantum mechanical calculation [11] of magnetic exchange coupling constants J between magnetic centres. In the framework of Density Functional Theory (DFT), the J constant is generally extracted from high spin (HS) and broken symmetry (BS) state energy computations [7–9a]. This technique introduced initially by Noodlemann et al. [12] was successfully used in combination with the hybrid B3LYP functional, in the case of di-, polynuclear d-transition and mixed 4f-d complexes [6–11].
Since the characterization of the first diuranium(V) phenylenediimido-bridged [(MeC5H4)3U]2(μ-1,4-N2C6H4) complex, exhibiting antiferromagnetic coupling [13a] a number of fascinating diuranium systems has been synthesized and their magnetic properties brought to light by variable-temperature magnetic susceptibility experiments [14–18]. Thus, a number of di-, tri- and tetranuclear uranium species were synthesized, including the binuclear amide complex [U(η8-C8H8)]2[μ-η4:η4-HN(CH2)3N(CH2)2N(CH2)3NH] which contains the shortest U···U separation observed up to now in a molecule [19]. Arene bridging diuranium complexes, such as [(Mes(tBu)N)2U]2(μ-η6:η6-C7H8) and [(Cp*)2U]2(μ-η6:η6-C6H6) systems [20] and pyrazolate-bridged [U(Me2Pz)4]2 (Me2Pz = 3,5-dimethylpyrazolate) complex [16a], are also likely to exhibit interesting magnetic properties. Recently, a new bis(imido) diuranium(V) complex [U(NtBu)2(I)(tBu2bpy)]2 has been synthesized and X-ray characterized by Spencer et al. [17d] which exhibits an antiferromagnetic coupling between the two metallic 5f1-5f1 ions. B3LYP calculations combined with the BS approach, which have been performed on the model system [U(NtBu)2(I)2(bpy)]2, predict correctly that the singlet BS state is lower in energy than the triplet HS state [17d]. An interesting class of trinuclear molecules exhibiting magneto-structural correlations with variable exchange interactions is the mixed uranium-transition metal one [17c–e]. It is noteworthy that, despite a growing number of various synthesized actinide-containing molecules, the study of their magnetic behavior remains a challenge for quantum chemistry methods [16d].
For our part, we are particularly interested in two isomers of the U2imido system i.e., the para- and meta-U2imido binuclear (5f1-5f1) complexes [(C5H5)3U]2(μ-1,4-N2C6H4) and [(C5H5)3U]2(μ-1,3-N2C6H4) containing one active electron per centre and for which no systematic theoretical study has been undertaken, to our knowledge. These systems are of particular interest, because they demonstrate antiferromagnetic behavior for the former (para) and ferromagnetic character for the latter (meta) as confirmed by recent experimental measurements [13b]. Thus, they offer opportunity to investigate theoretically the origin of this difference and the role of the bis(imido) bridging ligand and of the metal 5f orbitals in the determination of the magnetic character of these U(V) isomers. Finally, and to our knowledge, the present study is the first one using the ZORA Hamiltonian combined with the BS approach aiming for the investigation of magnetic exchange properties of binuclear uranium complexes.
2 Theoretical background and computational details
The magnetic interaction between two atomic spins is usually described by the phenomenological Hamiltonian of Heisenberg, Dirac and Van Vleck (HDvV) [21] given by Ĥ = −2JŜ1·Ŝ2, where Ŝ1 and Ŝ2 are the respective spin angular momentum operators. A positive sign of the coupling constant J indicates a ferromagnetic interaction (parallel alignment of spins) whereas the negative sign indicates an antiferromagnetic interaction (antiparallel alignment of spins). It must be noted that to estimate the coupling constant J, one has to calculate energy differences that are often smaller than ∼0.5 kcal/mol or even smaller (few tens cm−1) [7b,8b]. Accurate quantum mechanical evaluation of the coupling constant requires the use of multideterminantal post-Hartree-Fock calculations [7b,22]. However such ab initio methodology is computationally challenging for great size systems and its use is reduced to small molecules or simplified models [22a]. An alternative is provided by Density Functional Theory and making use of the broken symmetry (BS) approach as originally proposed by Noodleman et al. [12]. The DFT/BS approach has been widely proved to be one of the most efficient tools to investigate the magnetic properties of transition metal complexes [6–11,23]. In numerous cases, good agreement has been achieved with the experimental data using the BS recipe in conjunction with the B3LYP functional [24]. In some cases a mixing of Hartree-Fock exchange between 33% and 50% was found to lead to better results than the 20% used in B3LYP ([8b] and ref. therein).
All computational results reported in this work were performed using the Amsterdam Density Functional program (ADF2010.02 release) [25]. Relativistic corrections have being introduced via the Zero Order Regular Approximation (ZORA) [26] accounting for scalar relativistic effects. The GGA Becke-Perdew (BP86) [27] and B3LYP hybrid [24] functionals have been used. For all elements, Triple-ζ Slater-type valence orbitals (STO) augmented by one set of polarization functions were used taken from the ADF/ZORA/TZP database. The B3LYP computations are all electron ones. The frozen-core approximation where the core density is obtained from four-component Dirac-Slater calculations has been applied for all atoms in the case of BP86 calculations. A 1s core electrons were frozen respectively for carbon C[1s] and nitrogen N[1s]. The actinide U [5d] valence space of the heavy elements includes the 5f/6 s/6p/6d/7 s/7p shells (14 valence electrons). Our previous work [28,29] and several recent studies [15c,20b,30,31] have shown that such ZORA/BP86/TZP computations reproduce the experimental geometries and ground state properties of f–element compounds with a satisfying accuracy. Therefore, the geometries of the two considered complexes respectively noted henceforward para-U2imido (Cs symmetry) and meta-U2imido (C1) have been optimized at this ZORA/BP86/TZP level. The so obtained optimized geometries have been used for the B3LYP computations. A lot of computational time was needed to obtain converged results observing an aufbau electron configuration with the electronic structure 5f1-5f1 for the para- and the meta-U2imido binuclear complexes under consideration. This has been achieved in several steps. The HS state was studied first; the smearing procedure implemented in ADF, permitting a fractional occupation of the 5f orbitals by the two unpaired electrons, was turned on. Then the electron smearing was progressively reduced until reaching the required 5f electrons distribution. Several keywords of ADF2010 have been used for that, among them “smearq”, “occupations” and “modify start potential”. Finally it must be pointed out that the SCF processes converge usually very slowly (often several hundreds of cycles) especially when using the B3LYP functional.
Spin-orbit corrections to the energy difference between the HS and BS states have not been considered, although it has been shown that their effect is noticeable when computing properties like electron affinities of actinide complexes. In the latter case, we found [28b] that the energy of the U(III)/U(IV) redox system undergoes a change of the order of 0.3 eV when taking into account these corrections; this is mainly due to the fact that the electron configuration of metal ion is not the same in the reduced and neutral forms of the complexes (respectively 5f3 and 5f2). These corrections are of atomic nature [15f,26d,28b] i.e. not very sensitive to the environment of the metal ion for a given oxidation state. In the present study, the metal electron configuration is 5f1 for each U(V) ion, whatever the HS or BS state, so that neglecting spin-orbit corrections seems to be a valid assumption. The obtained results corroborate this assumption. Recent DFT calculations of magnetic exchange coupling for biuranium(IV) and (V) species [17d,18] did not also include spin-orbit corrections.
On Fig. 1, we show the ferromagnetic (two α spins) and antiferromagnetic (one α and one β spins) electronic structures in the case of the para-U2imido complex.

Ferro- and antiferro-magnetic couplings.
The singlet BS state energy (EBS) has been obtained performing a single point calculation using the MOs of the HS structure as starting guess and changing the spin on the second uranium atom (using the spinflip keyword of ADF2010). Molecular geometries and molecular orbital plots were generated using ADFview program [25].
3 Results and discussion
The molecular structures obtained from the geometry optimization of two models are depicted on Fig. 2.
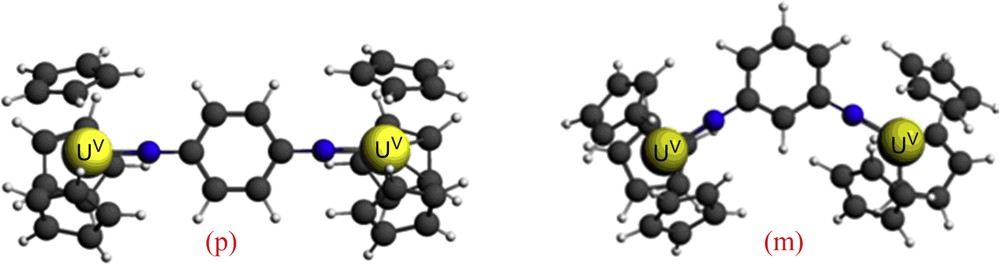
(p): para- and (m): meta-U2 imido ZORA/BP86 optimized geometries.
In Table 1 are given relevant optimized bond distances and angles values for the HS triplet state of the two complexes computed at the ZORA/BP86/TZP level. In Table 1 are also given for comparison, X-ray structural parameters for the mono-imido U(V) namely the bis- and triscyclopentadienyl (C5Me5)2UV(=N-Ar)F (where Ar = 2,4,6-tBu3C6H2) [30a] and (C5H4Me)3UV(=Nph) [32] respectively. No structural experimental data are available for the complexes under consideration.
Relevant average optimized bonds distances (Å) and angles (°) for para-U2imido (Cs) and meta-U2imido (C1) complexes in their triplet HS state and available experimental geometrical parameters.
| Geometrical parameter | Para-U2imido | Meta-U2imido | X-raya |
| U–N | 2.084 | 1.972 | 1.965(8)*, 2.019(6)** |
| N–C | 1.442 | 1.377 | 1.415(11)*, 1.36(1)** |
| U–U | 10.103 | 8.146 | – |
| U–Cpcentroid | 2.591 | 2.527 | 2.505*, 2.48** |
| U–N–C | 176.5 | 177.1 | 171.0(7)*, 167.4(6)** |
As it can be seen in Table 1, there is good overall agreement between optimized and X-ray data. The U–N bond distances are in range of multiple short bond in agreement with experimental structural data of imido uranium(V) complexes found in the literature [28a,30a,32]. Furthermore, as it can be seen in Table 1, linear U–N–C coordination is indicative of multiple bonding, and such coordination in the diuranium(V) complex, throughout the para-phenylenediimido bridging ligand, is likely to maximize the possibility of electronic and magnetic communication. We expect that the 5f uranium orbitals are not only responsible for this peculiar geometry, but could play a key role in magnetic exchange interaction cooperatively with the π-conjugated bis(imido) bridging ligand. This point will be discussed and supported by the MO analysis, which follows.
In Table 2, are reported the energy difference (ΔE = EBS – EHS) between the HS and BS states and the <S2> mean values of the squared spin operator through which spin contamination can be estimated. As expected the latter is much more important in the BS state (this value should be zero for a pure singlet state) than in the HS one (exact value equal to 2). Also, it is worth noting that <S2> values are higher using B3LYP than BP86, for both the HS and BS states. To our knowledge, no <S2> values have been published up to now for actinide complexes, so that a comparison is not possible. However, it must be noted that in the case of transition metal complexes, the deviation of <S2> from the value of a pure spin state is generally larger for the BS of an antiferro species than for a ferromagnetic one [9a,10b].
ΔE(BS−HS) (eV and cm−1) energy differences and <S2> values.
| U2imido | ΔE(BS−HS) eV | ΔE(BS−HS) cm−1 | <S2> HS | <S2>BS |
| Para/BP86 | 0.0010 | 8.0 | 2.062 | 1.079 |
| Para/B3LYP | −0.0113 | −91.1 | 2.315 | 1.419 |
| Meta/BP86 | 0.0007 | 5.6 | 2.069 | 1.065 |
| Meta/B3LYP | 0.0088 | 71.3 | 2.135 | 1.111 |
First of all, it can be seen that the ferromagnetic character of meta-U2imido, i.e. that the HS energy is lower than the BS one, is correctly given by the two functionals. More interestingly, from the results of Table 2, it appears that BP86 gives a BS state of higher energy than the HS one for the para-U2imido complex predicting so a ferromagnetic character contrarily to B3LYP which predicts the actual antiferromagnetic character (measured coupling constant equal to –19 cm−1 [13a]). It is very gratifying that the used procedure i.e. ZORA/B3LYP in conjunction with the BS approach successfully predicts the actual magnetic character of such diuranium species. However, it must be noted that the value of the antiferromagnetic constant of para-U2imido which can be estimated from Table 2 is largely overestimated. Finally, the failure of BP86 is not surprising if not expected ([33] and ref. therein).
In Table 3, are reported for comparison, available magnetic data for diuranium systems exhibiting the 5f1-5f1 or 5f2-5f2 electron configuration and different aromatic bridging ligands.
Magnetic character of different diuranium complexes.
| U2 complex | Bridging ligand | Di-atomic configuration | Magnetic behavior | Ref. |
| [(MeC5H4)3U]2(μ-1,4-N2C6H4) | Para-imido | 5f1-5f1 | AF | [13a,b] |
| [(MeC5H4)3U]2(μ-1,3-N2C6H4) | Meta-imido | 5f1-5f1 | F | [13a,b] |
| [U(NtBu)2(I)2(bpy)]2 | Imido | 5f1-5f1 | AF | [17d] |
| [(NN’3)2U2(p-DEB)] | Para-DEB | 5f2-5f2 | AF | [18] |
| [(NN’3)2U2(m-DEB)] | Meta-DEB | 5f2-5f2 | F | [18] |
As it can be seen in Table 3, the para and meta isomers exhibit respectively an antiferro- or a ferromagnetic character. Our theoretical results (Table 2) for the bis(imido) system are in agreement with these findings.
We shall consider first the para-U2imido complex in order to understand its antiferromagnetic character. The study of the ferromagnetic meta-U2imido isomer will come after.
Spin densities in HS and BS states, play a key role for the qualitative understanding of ferromagnetic and antiferromagnetic exchange coupling [10,16b]. Some mechanisms have been proposed to explain the exchange coupling between the magnetic centres by the spin polarization and spin delocalization phenomena in d-transition metals complexes [8b,10,22,23c]. The obtained spin density distributions (difference between the α and β electron densities) for the para-U2imido complex are displayed on Fig. 3.
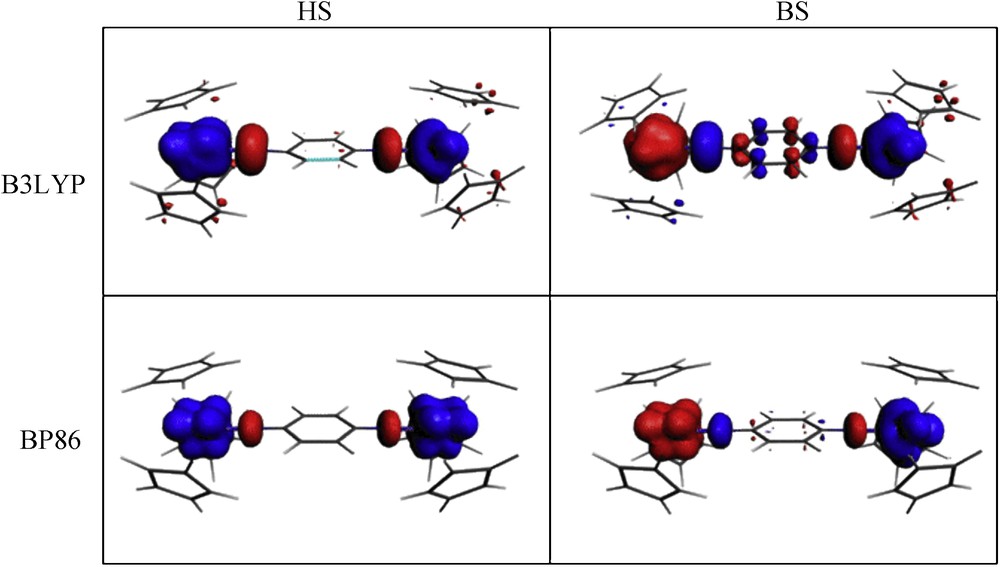
Spin density plots for the HS triplet and BS states of para-U2imido (blue color: positive and red color: negative spin density).
We note that the HS state spin density distributions obtained by both B3LYP and BP86 methods exhibit completely localized spin densities on the two magnetic uranium centres with no contribution on the bridging ligand. The BS spin density in the B3LYP case, shows that the two magnetic centres are antiferromagnetically coupled, with significant spin density contributions from bis(imido) ligand atoms. The fact that spin polarization and spin delocalization are involved in the mechanism driving antiferromagnetic coupling, appears clearly through the latter spin density distribution. We also note that the Cp ligands are practically not involved in this coupling. On the contrary, the BP86 functional appears to be inadequate to give the spin distribution required to predict the antiferromagnetic character of the para-U2imido complex.
The antiferromagnetic coupling correctly predicted by the B3LYP functional is also clarified by the alternating signs of the Mulliken atomic net spin populations (difference of the α and β atomic charges) found in the BS state along the path linking the two magnetic metal centres as given in Table 4 and depicted on Fig. 4 by up and down arrows for dominant α and β spins respectively. Despite its known drawbacks, the Mulliken population analysis remains a useful tool to compare the variation of electronic populations in homologous series of compounds computed at the same level of theory.
Mulliken atomic spin populations and atomic net charges (between parentheses) for HS and BS states of para-U2imido.
| Atoms | BP86 | B3LYP | ||
| HS (S = 1) | BS | HS (S = 1) | BS | |
| U1 | 1.240 (0.827) | 1.272 (0.826) | 1.535 (0.864) | 1.607 (0.865) |
| N2 | −0.126 (–0.387) | −0.105 (−0.389) | −0.245 (−0.646) | −0.273 (−0.646) |
| C3 | −0.002 | 0.032 | 0.005 | 0.068 |
| C4 | −0.011 | −0.027 | −0.021 | −0.059 |
| C5 | −0.011 | 0.026 | −0.018 | 0.059 |
| C6 | −0.002 | −0.031 | 0.011 | −0.088 |
| C7 | −0.011 | 0.026 | −0.018 | 0.058 |
| C8 | −0.011 | −0.027 | −0.021 | −0.059 |
| N9 | −0.126 (−0.388) | 0.131 (−0.388) | −0.464 (−0.588) | 0.503 (−0.585) |
| U10 | 1.240 (+0.828) | −1.280 (0.827) | 1.658 (0.872) | −1.779 (0.876) |

Para-U2imido net spin populations.
In Table 4, atoms are numbered as indicated on Fig. 4. Atomic net charges for the uranium and nitrogen atoms are given in parentheses.
As expected, it can be noted from Table 4 that the two uranium(V) ions exhibit a net charge (+0.86 in average with B3LYP) much lower than their oxidation state (+5) due to ligands to metal electron transfer. Besides, it is worth noting that all atomic spin populations increase significantly in absolute value when passing from the BP86 to the B3LYP functional. B3LYP atomic spin populations on the two uranium atoms, for HS (respectively 1.535 and 1.658) and BS (1.607, −1.779) states are different from the values of the free ions (i.e. 1 in the HS case). Moreover, the larger absolute values of atomic spin populations in BS state in comparison with HS state is responsible for the stabilization of this state relatively to the HS one. The alternating signs of the spin populations along the path linking the two magnetic metal centres in the BS state due to spin polarization and spin delocalization indicate the communication between magnetic centres through the bridging ligand (superexchange mechanism [1]).
The MO diagram depicted on Fig. 5, displays the singly occupied molecular orbitals (SOMOs) of the HS state at the left side, with the corresponding BS SOMOs at the right side. In this diagram %(6d/5f/U/ligand) represents the weight of respectively the 6d, 5f orbitals, the uranium atoms and the bridging ligand within the displayed MOs.
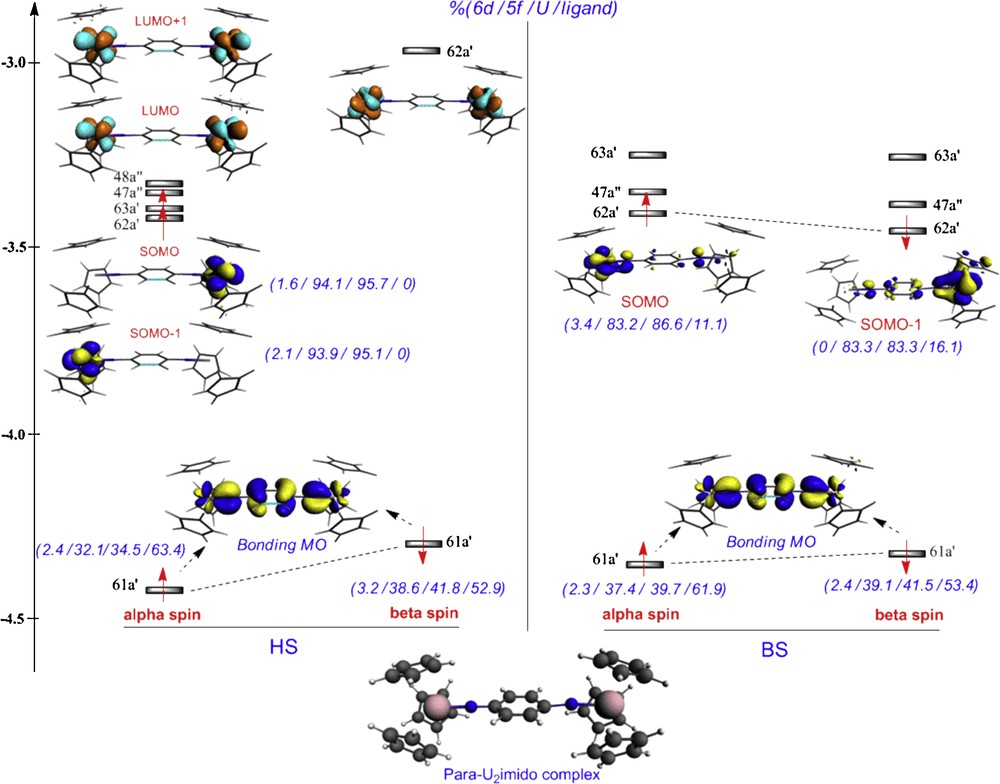
B3LYP HS and BS states MO diagrams for the para-U2imido complex (Cs).
In the HS (Triplet) state, the SOMO and SOMO–1 (i.e. 63a’ and 62a’ MOs) are essentially 5f orbitals of the two uranium(V) atoms with no contribution from the bridging ligand. On the contrary, in the BS state, the corresponding SOMOs i.e. α-62a’ and β-62a’, are significantly different and appear to be more delocalized with non negligible contribution of the bis(imido) ligand as attested by the orbital percentages. Immediately below, MOs #61 with a’ symmetry, are entirely delocalized over the metals and the linking bridge in both the HS and BS states. These MOs exhibit large π-bonding interactions, involving uranium 5f orbitals and π-orbitals of the bridging ligand. More details are given in Table 5 where are reported the nature and the percentage contribution of the different 6d and 5f uranium orbitals to SOMO and SOMO-1, i.e. to α and β spin MOs #61a’ and 62a’ in the BS state. Two values are given between parentheses, respectively, for the two uranium atoms.
Uranium (6d, 5f) AO percentage composition of the α- and β-spin SOMOs of the para-U2imido complex (BS state).
| SOMO | (U1/U2) |
| Alpha spin | |
| 62a’ | 6dz2 (1.4/0.0), 6dx2-y2(4.6/0.0), 5fxz2(2.9/0.0), 5fyz2(9.2/0.0), 5fx(z2–y2)(59.3/0.0), 5fy(z2–x2)(14.5/0.0) |
| 61a’ | 6dxy (1.1/0.0), 6dx2-y2(2.5/2.1), 5fxz2(19.2/12.1), 5fx(z2–y2)(1.2/0.0) |
| Beta spin | |
| 62a’ | 6dz2 (0.0/1.5), 6dx2-y2(0.0/4.6), 5fxz2(0.0/4.4), 5fyz2(0.0/10.9), 5fx(z2–y2)(0.0/57.6), 5fy(z2–x2)(0.0/13.2) |
| 61a’ | 6dxy (0.0/1.1), 6dx2-y2(2.5/2.1), 5fxz2(11.7/19.5), 5fx(z2–y2)(0.0/1.2) |
It appears from Table 5 that the 5f orbitals which dominate the SOMO 62a’ are the 5fx(z2–y2) and to a lesser extent, the 5fy(z2–x2) and 5fyz2 ones. Furthermore, for SOMO-1 #61a’ which exhibits a metal-ligand bonding character, the 5fxz2 is well oriented toward the imido ligand to maximize π-orbital overlap U(5fxz2)-N(2pz). The splitting of the 5f orbitals block (Fig. 5) gives evidence for the participation of the 5f orbitals in metal-ligand bonding. It is interesting to note that this splitting (i.e. energy differences between the 62a’, 63a’, 47a’…MOs) is more important in the BS state than in the HS one, indicating the greater involvement of the 5f orbitals in bonding in the former case.
We consider now the case of the ferromagnetic isomer, i.e. the meta-U2imido complex. In Fig. 6 we show the spin density distribution of the HS and BS states computed using the B3LYP functional.
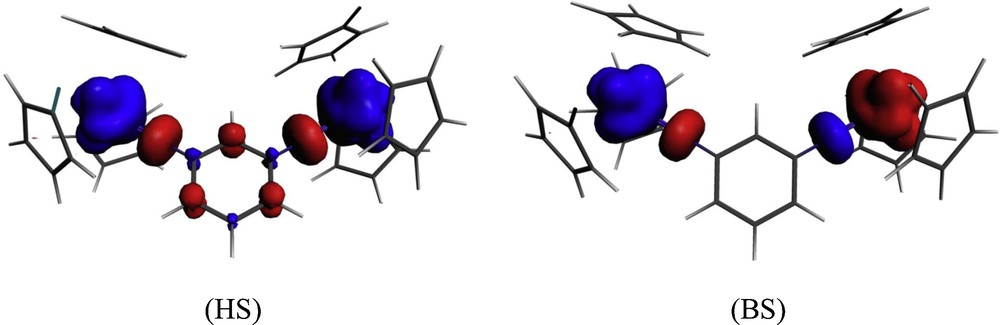
B3LYP spin density plots for the HS triplet and BS states of meta-U2imido (blue color: positive and red color: negative spin density).
As it can be seen the spin density plot of the BS state of the meta-U2imido complex is radically different from the para-U2imido one; the bridging ring is not involved in the spin delocalization and polarization. On the contrary the bridging ligand is involved in spin delocalization for the HS state of the meta-U2imido isomer, and this was not the case for the para-U2imido one. We have reported in Table 6 the values of the atomic spin polarizations and the net charges for HS and BS states of the meta isomer.
Mulliken atomic spin polarizations and atomic net charges (between parentheses) for HS and BS states of Meta-U2imido.
| Atoms | BP86 | B3LYP | ||
| HS (S = 1) | BS | HS (S = 1) | BS | |
| U1 | 1.255 (0.805) | 1.248 (0.805) | 1.402 (0.919) | 1.375 (0.918) |
| N2 | −0.110 (−0.396) | −0.107 (−0.395) | −0.192 (−0.579) | −0.179 (−0.579) |
| C3 | 0.021 | −0.008 | 0.043 | −0.014 |
| C4 | −0.042 | 0.000 | −0.076 | −0.001 |
| C5 | 0.021 | 0.008 | 0.044 | 0.015 |
| C6 | −0.041 | −0.002 | −0.072 | −0.004 |
| C7 | 0.015 | 0.000 | 0.032 | 0.000 |
| C8 | −0.041 | 0.001 | −0.072 | 0.003 |
| N9 | −0.107 (−0.390) | 0.104 (−0.390) | −0.196 (−0.576) | −0.183 (−0.576) |
| U10 | 1.247 (0.796) | −1.239 (−0.796) | 1.393 (0.908) | −1.365 (−0.907) |
It appears that comparatively to the BS state of the para-isomer (Table 4), the values of the atomic spin populations over the imido bridging cycle are very small or equal to zero. This explains why the meta linking pathway does not favor an antiferromagnetic coupling. On the contrary the HS state of the meta isomer exhibits exactly the needed alternating signs of the net spin populations ensuring the ferromagnetic coupling of the magnetic centres.
4 Conclusions
The magnetic exchange coupling interactions in bis(imido) para-[(C5H5)3U]2(μ-1,4-N2C6H4) and meta-[(C5H5)3U]2(μ-1,3-N2C6H4) diuranium(V) complexes, have been investigated for a first time using relativistic ZORA/DFT computations combined with the broken symmetry (BS) approach. The used theoretical approach, based on the B3LYP functional was successful to predict the ferromagnetic character of the meta-U2imido complex and the antiferromagnetic one of its para-U2imido isomer. The failure of the BP86 functional to predict the actual antiferromagnetic character of the para-U2imido complex is not surprising. The magnetic exchange coupling has been rationalized considering spin density distributions and Mulliken atomic spin populations. The analysis of the spin density distribution of para-U2imido complex in the BS state, as obtained with B3LYP, reveals the role of spin polarization principally and of spin delocalization leading to the antiferromagnetic interaction. Furthermore, from the MO point of view, the antiferromagnetic interaction between the two uranium(V) ions in the para-U2imido complex, mediated by aromatic imido bridges, is mainly due to the effective π-overlap between 5f orbitals and nitrogen atoms on bis(imido) bridging ligand groups along the path linking the two magnetic uranium(V) centres. In the same way, the consideration of the spin density and atomic spins populations of the meta-U2imido congener shows that an antiferromagnetic coupling between the two spin U(V) centres is not possible and that a ferromagnetic coupling is favored. For both isomers the spin polarization mechanism explains well their observed magnetic behaviour.
Acknowledgements
Computing facilities were provided by IDRIS, Computing Centre of CNRS.


