1 Introduction
Pyrochlore-type oxides have attracted great attention for a long time due to their remarkable physical and chemical properties as high thermal stability, high resistance to radiation damage and low thermal conductivity. These properties entitle them to extensive applications, for instance as catalysts [1,2], ionic/electric conductors [3], lithium ion batteries [4], radiation-damage-resistant materials [5], nuclear waste disposal [6,7], thermal barrier coatings [8] or solid electrolytes in high temperature fuel cells [9]. Pyrochlore oxides have the general formula A2B2O6O′ with z = 8; A, B are cations and O, O′ are anions. Most pyrochlore oxides crystallize in space group
2 Experimental
The solid solutions were prepared by solid-state reaction of stoichiometric amounts of reagent-grade Bi2O3 (99.9%), Sb2O3 (99%), Nb2O5 (99%) and CuO (99%) (Aldrich Chemical Company Ltd). The mixtures were ground for 1 h with an agate mortar and pestle. The resulting powders were calcined at 500 °C for 24 h in an alumina crucible. Then, the powders were again ground and calcined two more times successively at 700 °C and 900 °C for 48 h each. The resulting powders were re-milled for 1/2 h and uniaxially pressed into pellets about 13 mm in diameter and 2 mm in thickness. Then, they were sintered at 1000 °C for 48 h in the air. The samples’ color was brown. The specimens were initially characterized by X-ray powder diffraction using a PANalytical X’Pert Pro X-ray diffraction system. Data were collected using Cu Kα radiation. Rietveld refinement [15] of the X-ray powder diffraction data was carried out using the FULLPROF program [16]. Polished specimens were examined using a conventional Philips SEM XL30 scanning electron microscope. The magnetic susceptibility of powder samples was measured from 4 to 400 K with SQUID. Electrical conductivity measurements were carried out using an impedance lock-in EG&G 7220-type with a 10-mV AC signal amplitude at frequencies between 30 Hz and 120 kHz.
3 Results and discussion
3.1 Structural characterization
3.1.1 Study of Bi1.5Sb1.5–xNbxCuO7 solid solution
Previous studies [17] showed that the substitution of copper by manganese in compound Bi1.5Sb1.5CuO7 [18] forms a continuous solid solution with a pyrochlore structure. Here, we substitute antimony by niobium according to this system: Bi1.5Sb1.5–xNbxCuO7. Fig. 1 shows X-ray diffraction patterns of as-synthesized Bi1.5Sb1.5–xNbxCuO7. All the diffraction lines in each pattern can be well indexed in the pyrochlore pattern (ICSD 01-077-8429). The results indicated that all compounds had a single cubic pyrochlore structure of Bi1.5Sb1.5–xNbxCuO7 belonging to space group
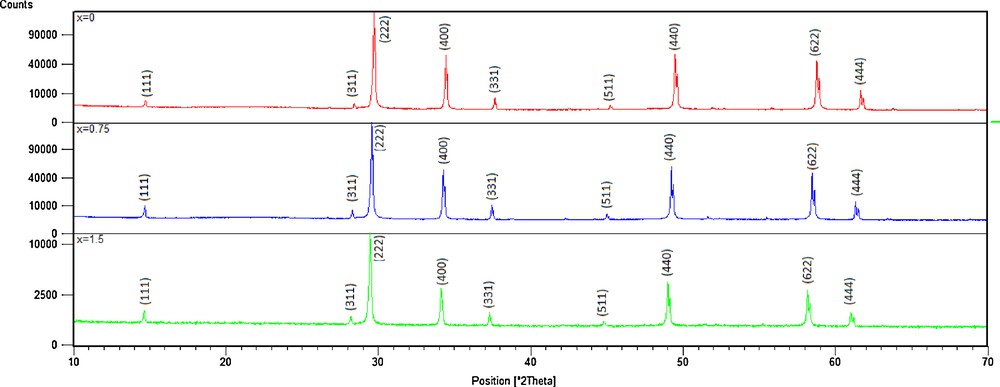
(Color online.) XRD patterns of Bi1.5Sb1.5–xNbxCuO7 solid solutions.

SEM micrograph of Bi1.5Sb1.5–xNbxCuO7 compounds (x = 0; x = 0.5; x = 1; x = 1.5).
3.1.2 Structural refinement
The highly symmetrical ideal pyrochlore structure A2B2O7 crystallizes in space group
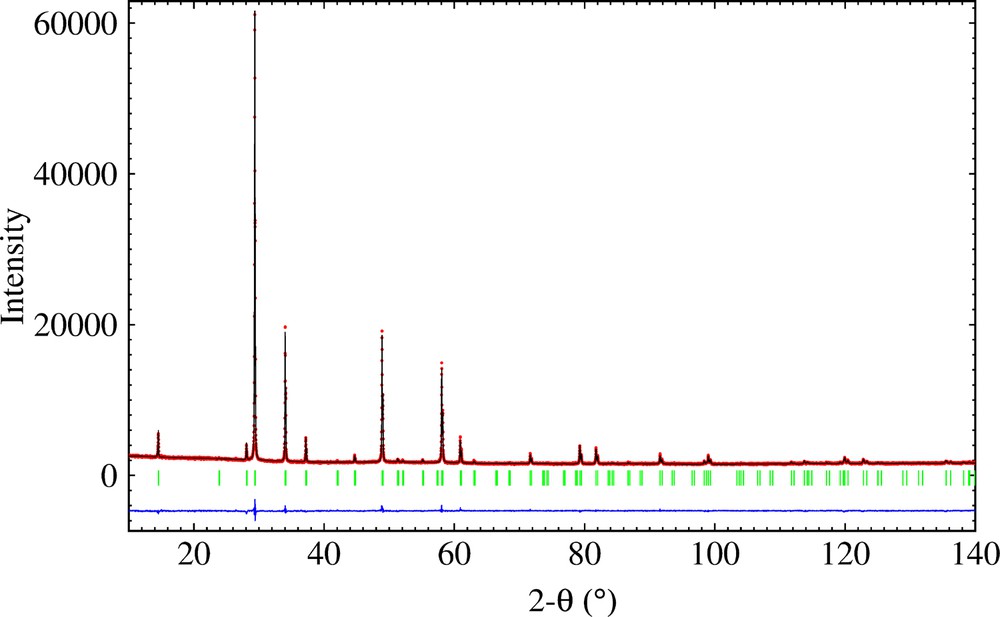
(Color online.) Observed, calculated and difference X-ray powder diffraction patterns of Bi1.5Nb1.5CuO7.
Rietveld refinement results of Bi1.5Sb1.5–xNbxCuO7 solid solutions.
| Sample | x = 0 | x = 0.75 | x = 1.5 |
| Global formula | Bi12Cu8Sb12O56 | Bi12Cu8Sb6Nb6O56 | Bi12Cu8Nb12O56 |
| Formula mass | 5373.6 g | 5200.2 g | 5026.88 g |
| Crystalline system | Cubic | Cubic | Cubic |
| Space group | |||
| Cell parameter | 10.42009(3) Å | 10.47193(3) Å | 10.52679(4) Å |
| Cell volume | 1131.393(6) Å3 | 1148.366(6) Å3 | 1166.510(8) Å3 |
| Wyckoff sequence | fdcb | fdcb | fdcb |
| Number of reflexion | 74 | 74 | 73 |
| Number of refined parameters | 14 | 17 | 14 |
| Function profile | Pseudo-Voigt | Pseudo-Voigt | Pseudo-Voigt |
| Rwp | 3.67 | 3.35 | 2.97 |
| Rp | 2.59 | 2.41 | 2.36 |
| Rexp | 2.03 | 1.86 | 2.32 |
| RBragg | 6.51 | 5.72 | 6.54 |
Atomic positions and site occupancies from Rietveld refinement results of Bi1.5Sb1.5–xNbxCuO7 solid solutions.
| Atom | Position | Site occupancy | x | y | z | Biso [Å2] | |
| x = 0 | Bi(1)/Cu(1) | 96g | 0.125/0.041 | 0.5076(7) | 0.5076(7) | 0.4709(9) | 0.10(9) |
| Sb(2)/Cu(2) | 16c | 0.75/0.25 | 0 | 0 | 0 | 0.10(5) | |
| O1 | 48f | 1 | 0.3243(9) | 1/8 | 1/8 | 1.7(3) | |
| O2 | 32e | 1/4 | 0.346(3) | 0.346(3) | 0.346(3) | 1.7(3) | |
| x = 0.75 | Bi(1)/Cu(1) | 96g | 0.125/0.041 | 0.5101(7) | 0.5101(7) | 0.4705(9) | 0.10(9) |
| Sb(2)/Nb(2)/Cu(2) | 16c | 0.375/0.375/0.25 | 0 | 0 | 0 | 0.60(9) | |
| O1 | 48f | 1 | 0.3239(8) | 1/8 | 1/8 | 1.4(3) | |
| O2 | 32e | 1/4 | 0.342(1) | 0.342(1) | 0.342(1) | 1.4(3) | |
| x = 1.5 | Bi(1)/Cu(1) | 96g | 0.125/0.041 | 0.5140(9) | 0.5140(9) | 0.4697(9) | 0.90(9) |
| Nb(2)/Cu(2) | 16c | 0.75/0.25 | 0 | 0 | 0 | 0.10(4) | |
| O1 | 48f | 1 | 0.3154(6) | 1/8 | 1/8 | 1.4(3) | |
| O2 | 32e | 1/4 | 0.354(3) | 0.354(3) | 0.354(3) | 1.4(3) |
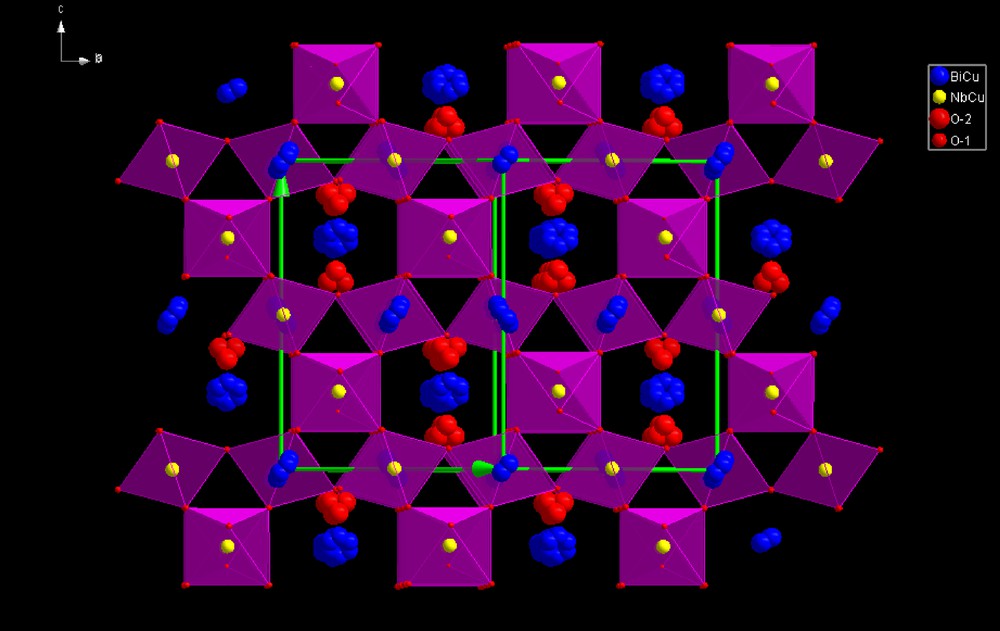
(Color online.) (Bi1.5Cu0.5)(Nb1.5Cu0.5)O7 cubic pyrochlore structure.
3.2 Magnetic susceptibility
Magnetic data obtained for the compounds indicate that the samples were overall paramagnetic in nature, with an effective moment of 1.74(5) and 1.70(3) μB for the copper in compounds Bi1.5Sb1.5CuO7 and Bi1.5Nb1.5CuO7. The inverse susceptibility versus temperature data for the Bi1.5Nb1.5CuO7 show upward curvature at the lowest temperatures and at high temperatures deviate somewhat from a linear Curie–Weiss behavior (regions between 200 and 300 K). The observed effective magnetic moments (μeff/mol Cu), calculated from the slopes of the Curie–Weiss fits indicates the “2 + ” oxidation state of the copper. The temperature dependence of the magnetic susceptibility and its inverse are shown in Fig. 5. The copper oxidation state confirm the pyrochlore formula (1.5–1.5–1-7 compound), since bismuth has a “3 + ” and niobium and antimony [29] have a “5 + ” oxidation state.
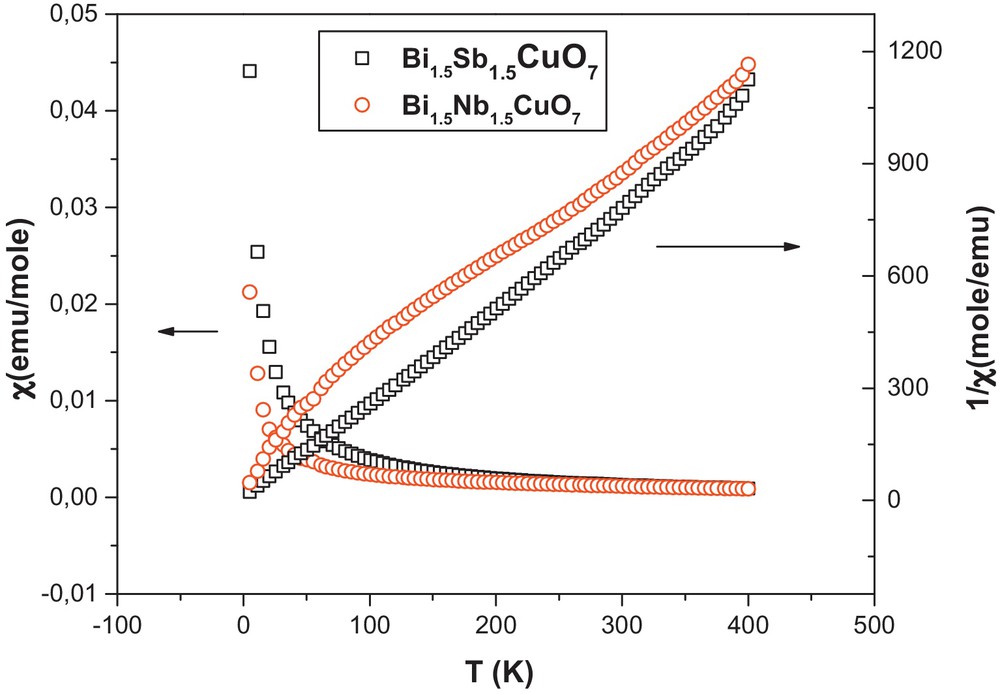
(Color online.) Susceptibility and inverse susceptibility versus temperature of Bi1.5Sb1.5CuO7 and Bi1.5Nb1.5CuO7.
3.3 Electrical characterization
Fig. 6 shows the temperature dependence of the total conductivity of Bi1.5Sb1.5–xNbxCuO7 ceramics, obtained from AC electrical measurements and impedance plots over the temperature range between 300 and 800 K in the air. Clearly, the total conductivity of Bi1.5Sb1.5–xNbxCuO7 ceramics gradually increases with increasing temperature from 300 to 800 K. The temperature dependence of the total conductivity of Bi1.5Sb1.5–xNbxCuO7 ceramics can be described by the Arrhenius equation, σ T = σ0 exp (–E/kB T) where σ, T, σ0, E, and kB are the total conductivity, absolute temperature, pre-exponential factor, activation energy and Boltzmann constant, respectively. The total conductivity data follow a linear behavior, which confirms that the electrical conductivity process is thermally activated. The activation energy for the total conductivity of Bi1.5Sb1.5–xNbxCuO7 ceramics slightly decrease with increasing the niobium content. The activation energies were determined as 0.45, 0.42 and 0.41 eV for the samples doped with x = 0, 0.5 and 1, respectively. The decrease in the activation energy is the result of an increasing in the conductivity with increasing the Nb content, and reflects the impurity level shift toward the conduction or valence band by increasing the number of sharing electrons or holes. All compounds are considered as semi-conductors.
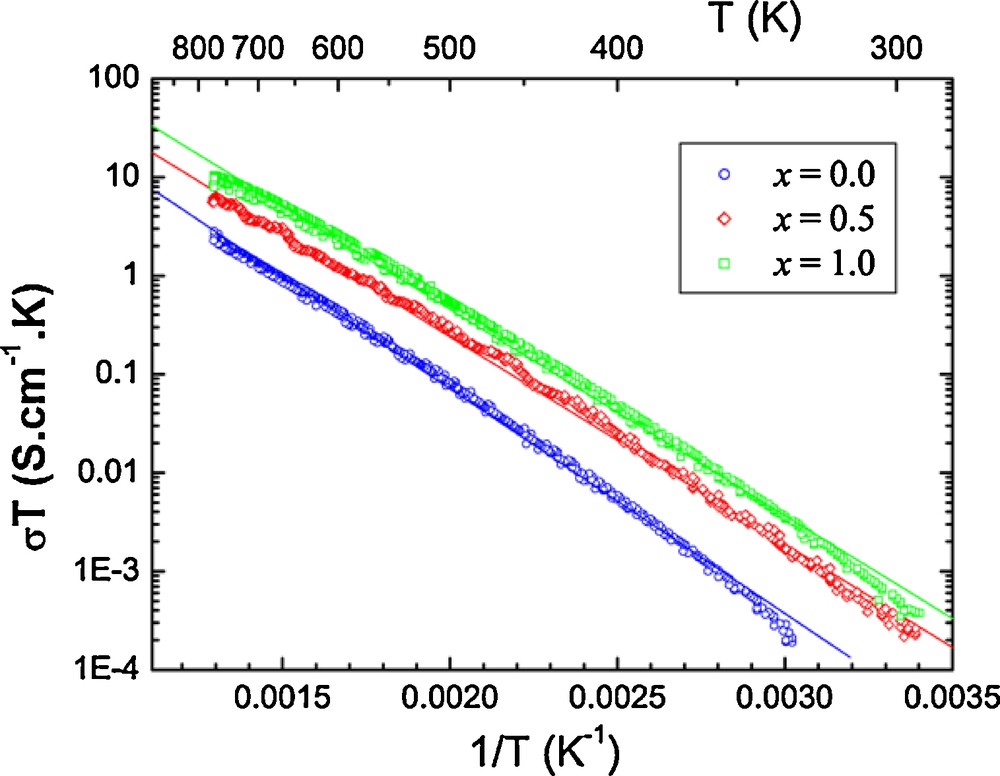
(Color online.) Conductivity variation versus inverse temperature (1/T) of Bi1.5Sb1.5–xNbxCuO7 compound.
4 Conclusion
A new pyrochlore solid solution with formula Bi1.5Sb1.5–xNbxCuO7 was synthesized by solid-state reaction at 1000 °C. All samples had a single cubic pyrochlore structure of Bi1.5Sb1.5–xNbxCuO7 with space group
Acknowledgment
This work was supported by PNR 2011 (Projet national de recherche) of MESRS-Algeria with the collaboration of CRISMAT Laboratory.


