1 Introduction
Titania, i.e. titanium dioxide (TiO2), is a commonly applied material and has received frequent attention as a catalyst and catalyst support, especially in the case of photo-catalytic applications [1–3]. In essence, titania can form three main crystal structures: a) brookite with an orthorhombic structure, b) rutile and c) anatase both with tetragonal structures containing unit cells consisting of 6 and 12 atoms, respectively. Since each of these crystal structures gives rise to different physico-chemical properties, the use of mixed phases or polymorphs as a catalyst support should give rise to different behavior from morphological and catalytic points of view.
It is well known that TiO2 manifests a strong metal–support interaction (SMSI, [3–8]) with platinum group metals under reduction with H2, at high temperatures (usually more than 523 K). This phenomenon is largely dependent on the phase of titanium oxide. As a result of SMSI, the catalytic properties are improved, especially in the case of hydrogenation reactions [6–8]. As an example, Li et al. [6] showed that a Pd catalyst supported on anatase exhibited a better selectivity upon hydrogenation of alkadienes compared to rutile-based materials and that the reduction temperature of the impregnated materials should be higher than 473 K. The improved catalytic performance was explained by the beneficial effect of SMSI, especially in the case of anatase based materials that acted as an electronic modifier on the metal catalyst. The strong interaction between the support and the nanostructured phase of the metal emerged as a result of the genesis of reductive Ti3+ centers on the surface, very close to Pd nanoparticles. Indeed, H2 reduction generates oxygen vacancies in the form of coordinatively unsaturated cations in the vicinity of the active metal, thus leading to altered catalytic properties and stability [8].
This phenomenon has been reported for different hydrogenation reactions like hydrogenation of acetylene [3], of long chain alkadienes [6], of maleic anhydride [7] and of nitrate in water [8]. Despite a large body of literature concerning titania-based catalysis in the catalytic direct synthesis of H2O2 (CDS) [9–13], the influence of the titania phase structure has not been systematically studied for this reaction.
Our objective in this study was to investigate whether the SMSI phenomenon has any influence on the selective hydrogenation of molecular oxygen to hydrogen peroxide. Hereupon, 1 wt. % Pd/TiO2 catalysts were studied in the absence of any added selectivity enhancers. The materials were prepared by the impregnation method according to ref. [14] and their catalytic performance was evaluated at 275 K in a batch reactor. The materials were characterized by means of X-ray Röntgen Diffraction (XRD), nitrogen physisorption (BET) analysis, CO2- and NH3-temperature-programmed desorption (TPD) as well as CO chemisorption and H2-TPR. The goal was to relate the structural features of the materials to their catalytic activity. Further, EPR (Electron paramagnetic resonance) spectroscopy was used to quantify the Ti(III) centers generated during the reduction stage.
2 Experimental section
2.1 Materials
Unless otherwise stated, all the reagents and materials were used as received from the suppliers. All titania materials were commercially available: Aerolyst 7708 (A82), Aerolyst 7709 (A05), Aeroxide P25 (P25) from Degussa, Anatase (A98) and Rutile (A3) from Sigma-Aldrich. Hydranal composite 2 and ammonium molybdate tetrahydrate (Fluka); sodium thiosulfate pentahydrate (99.5%), potassium iodide, starch, concentrated sulfuric acid, tetrahydrofuran (THF, 99.99%, used freshly distilled) were purchased from Sigma-Aldrich. HPLC grade methanol (99.99%) from J.T. Baker; H2, O2 and CO2 (99.999% mol/mol purity) from AGA gas.
2.2 Characterization techniques
The Inductively Coupled Plasma (ICP-OES) measurements were carried out with a PerkinElmer, Optima 5300 DV device according to the quantitative standard mode whereas the Karl Fisher titrations were carried out with a Titrino GP 736 from Metrohm. The determination of the metal dispersion (D) was carried out by using a Autochem 2910 apparatus (Micrometrics). Also, the accessibility for the metals was determined by CO chemisorption using a pulsed technique. The catalyst (ca. 0.1 g) was heated in He (50 cm3/min) at 383 or 573 K (10 K/min) for 30 min, followed by a reduction in H2 (50 cm3/min) for 1 h, flushing by He flow (50 cm3/min) at the same temperature for 1 h and, finally cooling to 298 K before CO pulsing. The stoichiometric ratio between Pd and CO was assumed to be unity. The mean metal particle size, ds, was calculated from the metal surface area (MSA, m2/g metal) according to the method described in Hugues et al. [15] where the nanoparticles were assimilated with cubes with one face in contact with the support. The equation is the following one: ds (nm) = 5·105/(MSA·ρ), where ρ is the metal density (g cm−3).
Still, the surface area measurements (Sorptometer 1900, Carlo Erba Instruments) by nitrogen adsorption were performed as follows: the solids were outgassed at 423 K for 3 h prior to the measurement of the surface area. Upon calculation of the surface area and pore volume, the Brunauer-Emmett-Teller (BET) equation was used, whereas for pore size distribution, the Horváth–Kawazoe method was applied.
The temperature-programmed desorption (TPD) of CO2 and NH3 were carried out using Autochem 2910 apparatus (Micrometrics). Accordingly, 0.1 g of support was placed in a quartz U-shaped tube and dried under helium flow (573 K for 1 h), followed by adsorption of CO2 at room temperature (or NH3 at 373 K). The flushing of physisorbed species was carried out under temperature-programmed desorption (heating rate 10 Kmin−1) until 973. Temperature-programmed reduction (TPR) was performed on calcined materials under a 5.0 vol. % H2/Ar mixture in the temperature range from 298 to 973 K with a heating rate of 10 Kmin−1. The H2 consumption measurements were performed in Autochem 2910 apparatus (Micrometrics).
The EPR experiments were performed using a Bruker ER200D spectrometer operating at X-band (∼9.53 GHz). The device was equipped with a rectangular cavity, ER4102ST, fitted with a cryostat and a variable-temperature controller, Bruker ER4111VT; the microwave frequency was measured by a frequency counter, HP5342A. All spectra were obtained using the following parameters: microwave power 2.1 mW; modulation amplitude 0.3 mT; modulation frequency 100 kHz; time constant 41 ms; conversion time 82 ms; scan width 100 mT; 1024 points; temperature 130 K; all spectra were obtained as the average of nine scans. For each sample, a weighed quantity of the material (approx. 60–100 mg) was placed in a quartz EPR tube (i.d. 4 mm). The overall amount of Ti(III) in the samples was determined by double integration of the EPR spectra; before integration, all spectra were corrected for the background signal of the cavity and their intensity was normalized by sample weight.
Powder X-ray diffraction (XRD) patterns of the catalysts were measured with a HZG4 diffractometer (Freiberger Präzisionsmechanik, former DDR) with a scintillation detector. Diffraction patterns were registered in the range of 5–65°2-theta. Also, semi-quantitative XRD analysis was done using a Bruker d8 Advance instrument in θ–θ mode. The device was equipped with an optical configuration consisting of a primary Göbel mirror and a Våntec-1 detector. Continuous scans were applied to the sample.
2.3 Preparation of 1 wt. % Pd/TiO2
Monometallic 1 wt. % Pd/TiO2 catalysts were prepared by impregnation method according to ref. [14], using palladium acetate and THF as the metal precursor and solvent, respectively. After the impregnation step, the solvent was evaporated and the solids were further dried overnight in an oven at 383 K. The materials were then calcined at 573 K for 4 h (5 K/min). Finally, the materials were heated with an Argon flow (60 cm3/min) at 573 K and reduced for 4 h in a H2 flow (60 cm3/min) at the same temperature.
2.4 Batch experiments
Catalytic tests were carried out in a 600 cm3 stainless steel, tailor made batch reactor with a maximum working pressure of 200 bar, equipped with a Heidolph RZR 2021 rotor (200–1000 rpm) and a K-type thermocouple suitable for continuous temperature detection. A more detailed description of the reactor is reported in our previous work [16].
According to ref. [17], the experimental conditions were chosen as follows: in a typical experiment, 0.15 g of the catalyst was loaded in the reactor. The reactor was then closed, CO2 (18.4 bar) and O2 (6 bar) were fed directly from the cylinders at 298 K. When the pressure of the gas mixture had stabilized, 420 cm3 (VL) of methanol was fed with a HP pump at a feed-rate of 20 cm3/min. Consequently, the reactor was cooled down to 275 K. The equilibrium between the liquid and the gas phase was reached by means of switching on the stirrer and adjusting the agitation speed to 1000 rpm. After the stabilization of the pressure and temperature (275 K), the stirrer was switched off and H2 was fed until the desired amount was reached. Hydrogen was always the limiting reagent. The number of moles of hydrogen introduced into the reactor (nH2,0) was calculated from the Delta P of hydrogen pressure in the pre-batch chamber. Thus, the composition of the gas mixture was 2.5% H2, 25.5% O2 and 72% CO2, respectively. When the delivery of the desired amount of H2 was completed, the stirrer and the pump (in recirculation mode) were switched on again. This was considered as the time zero of the reaction. During the course of the reaction, portions of the liquid phase were periodically withdrawn from a six-way valve placed in the recirculation line of the reactor for hydrogen peroxide and water analysis; their volume (Vsample) was small enough (>0.4%) to ensure that the amount of the catalyst per unit volume of the liquid phase was practically constant during the whole test. The concentration of the products in the samples ([H2O2], [H2O]′; mM) was determined by iodometric and Karl Fischer titrations, respectively. The initial concentration of water, [H2O]0 was also determined by the Karl Fischer titration of the solvent and used to calculate the concentration of water actually produced by the reaction, [H2O]:
These data were used to monitor the progress of the reaction and selectivity towards H2O2, whereas the conversion was calculated using the following formula:
The selectivity towards hydrogen peroxide at time t (SH2O2,t) was calculated as:
The initial rates (Table 4) were estimated by fitting the initial data (trend) of H2O2 and H2O concentrations for the first 15 min. These values were then used to calculate the initial H2O2 productivity and the cumulative productivity (H2O2+H2O2) to estimate the specific and overall activity of the catalysts in the CDS. The initial selectivity was then defined as the ratio between H2O2 productivity and cumulative productivity. Table 4 also reports the instant values obtained from H2O2 and H2O production at 50% of H2 conversion, including the time required to reach 50% hydrogen conversion.
Catalytic results in CDS in batch conditions.
| Samples | Pd amounta | Initial cumul. productivityb | Initial H2O2 productivityc | Initial selectivityd | t½e | Selectivity at t½d |
| Pd-A98 | 1.41 | 4817 | 1080 | 22.4 | 14 | 20 |
| Pd-A3 | 1.40 | 2434 | 504 | 20.7 | 38 | 16 |
| Pd-A82 | 1.41 | 3651 | 949 | 26 | 23 | 24 |
| Pd-A05 | 1.42 | 4749 | 683 | 14.4 | 14 | 15 |
| Pd-P25 | 1.41 | 5571 | 917 | 16.5 | 11 | 14 |
a mol·105.
b mol(H2O2+H2O)·mol−1(Pd)·h−1.
c mol(H2O2)·mol−1(Pd)·h−1.
d %.
e Time (min) for 50% H2 conversion.
3 Results and discussion
3.1 Characterization of the supports
The properties of the materials (titania) used as supports for the palladium based catalysts are reported in Table 1. The commercial anatase and rutile were not ultra-pure but contained 2 or 3 wt. % of the other phase as well. These samples are from now on called as A98 and A3, respectively. In general, the name coding of the supports indicates the percentage of anatase amount (except in the case of sample P25, a common benchmark catalyst support). Also Aerolyst 7708 (A82) and Aerolyst 7709 (A05) are common materials often used in chemical and photocatalysis. The surface areas for rutile (A3), anatase (A98) and A05 were very low, whereas the samples A82 and P25 exhibited higher values (Table 1). The P25 material, used as a reference, was in the form of nano-powder. XRD investigation revealed that the mean crystallite sizes of anatase and rutile phases were greater for the materials A98, A3 and A05 than those of A82 and P25 samples, respectively.
Characteristics of TiO2 supports.
| TiO2 samples | Spa (m2 g−1) | Vpa (cm3 g−1) | Average crystallite sizeb (nm) | Anataseb (wt. %) | |
| Anatase | (A98) | 10 | 0.10 | 65 (anatase), 65 (rutile) | 98 |
| Rutile | (A3) | 11 | 0.01 | 51 (anatase), 60 (rutile) | 3 |
| Aerolyst 7708 | (A82) | 34 | 0.22 | 19 (anatase), 31 (rutile) | 82 |
| Aerolyst 7709 | (A05) | 12 | 0.12 | 41 (anatase), 59 (rutile) | 0.5 |
| Aeroxide P25 | (P25) | 35 | 0.28 | 17 (anatase), 26 (rutile) | 84 |
a Specific surface area (Sp) and pore volume (Vp) determined by N2-sorption.
b Average crystallite size of two phases and anatase amount determined by XRD.
The acid–base properties of the materials were evaluated by ammonia and carbon dioxide temperature-programmed desorption (NH3- and CO2-TPD), respectively (Figs. 1 and 2). This type of analysis was performed to estimate the differences in terms of surface properties for all the materials. The underlying motivation was to quantify the interactions that could potentially occur between the support and the metal precursor (e.g., control of metal distribution during the impregnation) and between the support and the nanostructured metal phase. These interactions could lead to important consequences like change in catalytic properties or resistance to active metal leaching [18]. As reported in the literature [19–22], the nature of acid sites on titania-based materials has been identified as unsaturated Ti4+ ions (i.e. Lewis acid type), whereas Brønsted acid sites were absent. The nature of basic sites in titania materials is of Lewis type too, according to Weitz et al. [23].
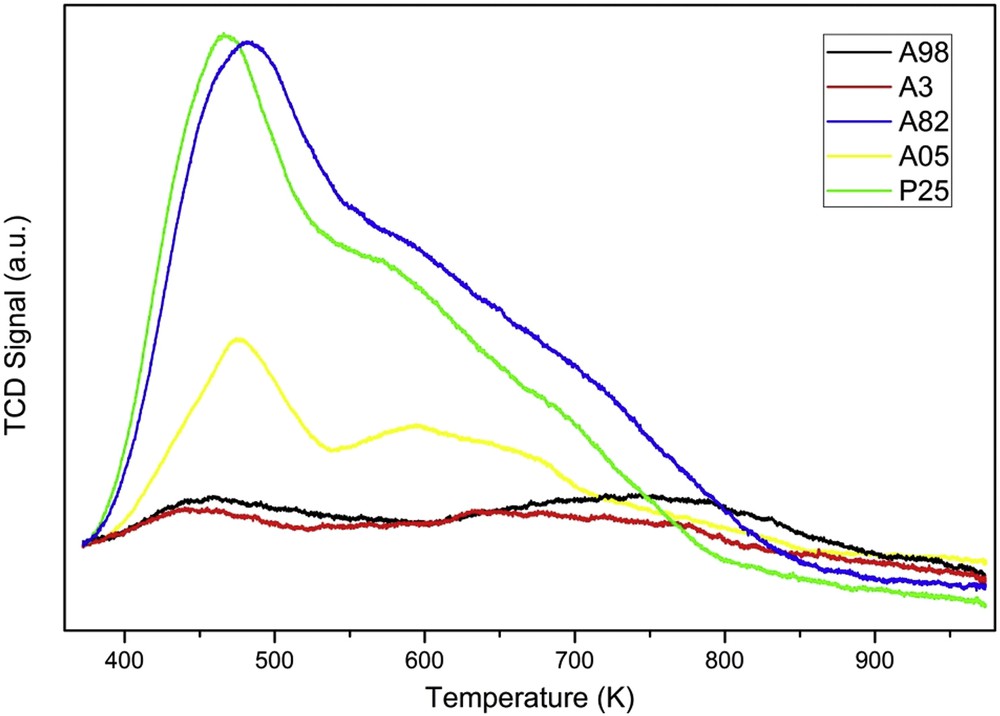
Ammonia temperature-programmed desorption of all the titania samples used as supports.
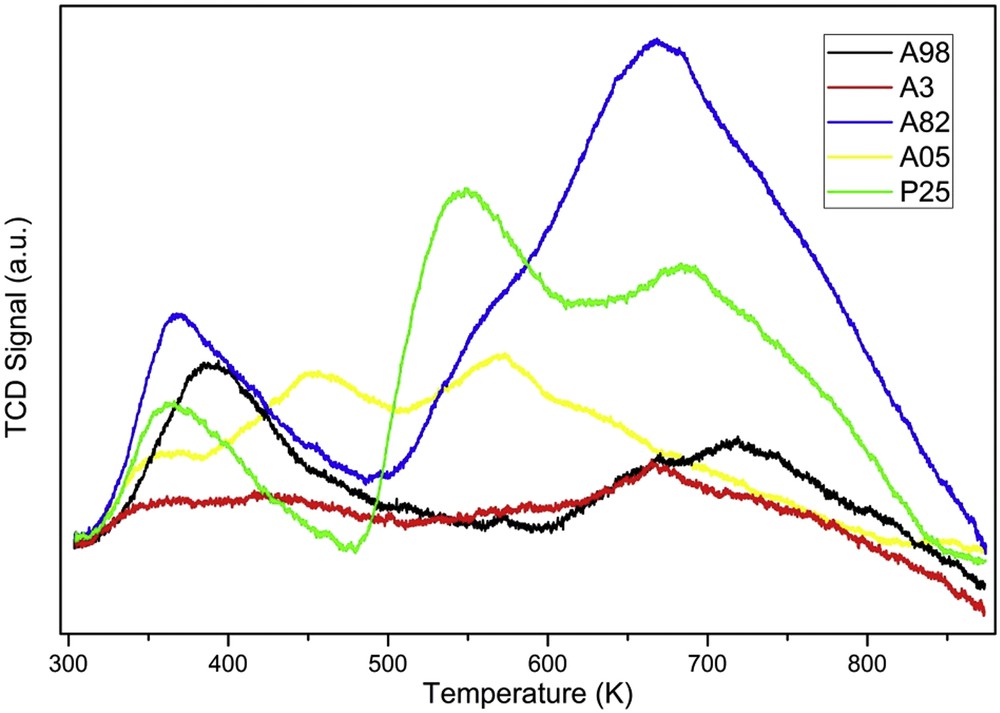
Carbon dioxide temperature-programmed desorption of all the TiO2 samples used as supports.
The acid site distribution patterns could be classified into weak (373–473 K), medium (473–673 K) and strong (673–873 K), depending on the desorption temperature of ammonia [24]. Likewise, the distribution patterns of basic sites could be classified into weak (desorption up to 673 K), medium (673–873 K), and strong (over to 873 K) ones, respectively [23]. Herein, the total acidity and basicity are also shown as sums of the number of NH3 and CO2 molecules desorbed throughout the entire temperature range (Table 2). The amount of NH3 desorbed close to 373 K might have contained some minor amounts of physisorbed ammonia too. When studying Table 2, it is evident that the pure phase materials, A98 and A3, contained the lowest number of basic and acidic sites. The A05 sample shows a gradual increase in the basicity and acidity features, even though the crystallite sizes described earlier were similar to those present in A98 and A3 samples. The highest number of basic as well as acidic sites was found in the samples A82 and P25 (Table 2), both of which contained very similar number of sites. Interestingly, the nature of basic sites in the samples A82, A05 and P25, respectively, appeared to be different whereas the nature of acid sites was similar. Anyway the following conclusions could be drawn: (1) the nature of the active surface sites in the supports was essentially of Lewis type, as also reported elsewhere [19–22,24,25]; (2) A82 and P25 materials were the ones richest in Lewis sites.
Quantitative analysis of acid–base surface properties of the supports.
| Sample | Probe | Temperature (K) | Amount of acid/basic sites (0.10−5 mol/g) | |||
| Weak | Medium | Strong | Total | |||
| A98 | CO2 | 394 | 2.3 | – | – | 3.8 |
| 723 | – | 1.5 | – | |||
| NH3 | 440 | 0.4 | – | – | 2.3 | |
| 723 | – | 1.9 | – | |||
| A3 | CO2 | 408 | 0.8 | – | – | 2.1 |
| 665 | 1.3 | – | – | |||
| NH3 | 440 | 0.23 | – | – | 0.48 | |
| 700 | – | 0.25 | – | |||
| A82 | CO2 | 368 | 2.9 | – | – | 16.5 |
| 593 | 2.6 | – | – | |||
| 668 | – | 11.0 | – | |||
| NH3 | 481 | – | 23.8 | – | 31.1 | |
| 605 | 7.4 | |||||
| A05 | CO2 | 393 | 0.8 | – | – | 7.1 |
| 456 | 2.3 | – | – | |||
| 573 | 4.0 | – | – | |||
| NH3 | 474 | 7.5 | – | – | 9.5 | |
| 597 | – | 2.0 | – | |||
| P25 | CO2 | 366 | 1.8 | – | – | 12.1 |
| 548 | 4.4 | – | – | |||
| 683 | – | 5.9 | – | |||
| NH3 | 465 | 22.0 | – | – | 25.6 | |
| 600 | – | 3.6 | – |
3.2 Preparation and characterization of the catalysts
The set of the Pd catalysts was prepared by wet impregnation of palladium acetate in THF, drying in oven at 383 K overnight, calcined in static air at 573 K for 4 h and reduced with H2, at same temperature and time.
Successively, the materials were investigated by CO chemisorption to evaluate the mean size of the as obtained metal nanoparticles (Table 3). Interestingly, Pd nanoparticles supported on anatase (A98) and rutile (A3) were showing higher dispersion with a small mean diameter in the range of 2–5 nm, despite the lower surface area and the lowest number of surface sites compared to A05, A82 and P25. Supports with the highest number of Lewis sites gave rise to a lower metallic surface area, except in the case of the P25 based material. Keeping in mind these results, it seems that no features like the composition of the TiO2 phase, its surface properties or the size control of nanostructured metal is obviously correlated. From this point of view, nucleation and growth kinetics of the metal nanoparticles most probably drive each process of metal nanostructured formation towards different pathways, depending on the combination of support features in general. Indeed, the P25 based material exhibited a high metal dispersion for nanoparticles despite the surface properties that were similar to those of A82.
Characterization of the catalysts. Data from CO chemisorption analysis and EPR spectroscopy.
| Sample | Pd amounta (wt. %) | Db (%) | MSAc (m2/g metal) | dd (nm) | H2/Pd molar ratioe | Ti(III) amountf |
| Pd-A98 | 1.02 | 36.8 | 164.2 | 2.5 | 1.15 | 1.0 |
| Pd-A3 | 1.01 | 21.0 | 93.8 | 4.4 | 1.00 | 1.4 |
| Pd-A82 | 1.01 | 9.9 | 44.0 | 9.5 | 1.59 | 1.5 |
| Pd-A05 | 1.00 | 7.3 | 32.4 | 12.8 | 1.24 | 2.6 |
| Pd-P25 | 1.02 | 23.6 | 105.2 | 4.0 | 1.42 | 1.5 |
a Pd amount by ICP analysis.
b Dispersion.
c Metal surface area.
d Diameter estimated from the CO/Pd molar ratio equal to 1 and according to ds (nm) = 5.105/(MSA.ρ), where ρ is the metal density (g cm−3) [15].
e Molar ratio between Pd amount and H2 moles consumed in TPR experiments.
f The relative amount of Ti(III) as estimated from the double integration of the EPR spectra.
Another key point is the relation between the phase composition of the support and the as-produced metal nanoparticles. The metallic surface area of Pd nanoparticles (as well as dispersion) diminished the following order: Pd-A98 > Pd-P25 > Pd-A3 >> Pd-A82 > Pd-A05. The mean size of nanostructured metal aggregates seemed to be independent of the anatase phase composition, suggesting that it did not drive the growth kinetics of Pd nanoparticles. This phenomenon has also been reported earlier [3].
The TPR analysis applied to all sets of materials was performed as reported in Fig. 3. As a conclusion from this analysis, the amount of consumed H2 reported as the H2/Pd molar ratio could be estimated (Table 3).
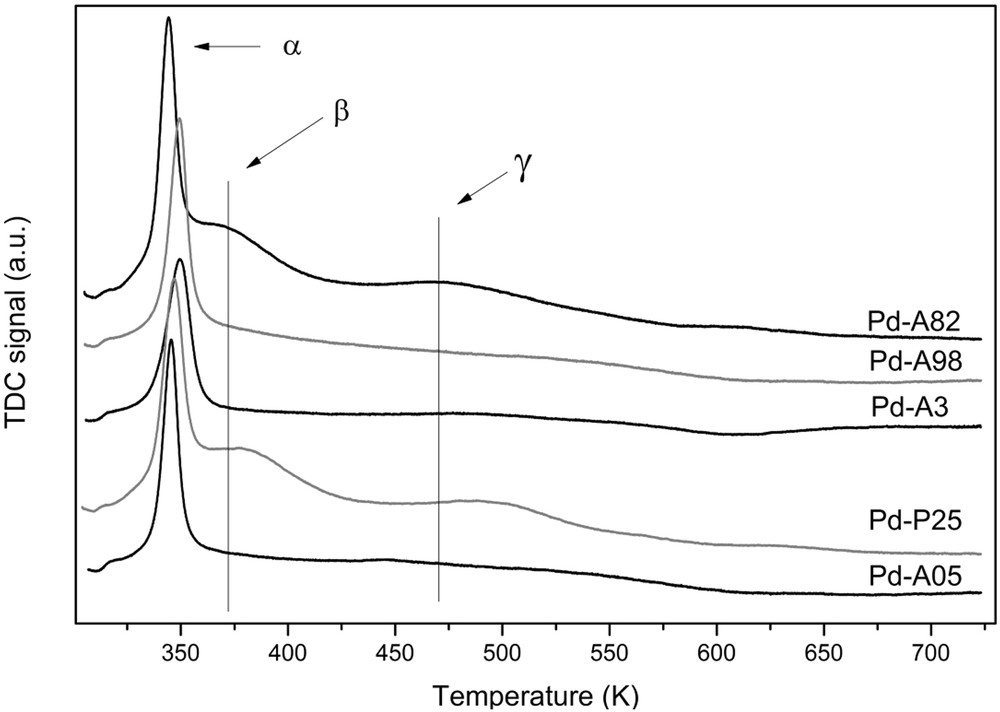
H2-TPR profiles of the set of Pd/TiO2 catalysts.
Fig. 3 represents the H2-TPR profiles of the five materials investigated. Each one gave rise to a strong peak (peak α) in the range of 320–365 K due to the reduction of the palladium. Pd-A82 and Pd-P25 samples also gave rise to another weak band centered at 380 K (peak β) and a broad band (peak γ) in the range of 410–573 K (also the Pd-A05 sample has a similar band, but weaker and broader). The H2 TPR profiles of blank materials (not reported) indicated no H2 consumption in the range 300–600 K. Over this range, all materials experienced a change in their color from white to pale grey without significant H2 consumption. For similar materials, the literature is commonly reporting a broad peak in the range of 630–770 K attributed to the non-mediated reduction of surface from Ti(IV) to Ti(III) [3,7,8,26]. Nevertheless, the peak γ in Fig. 3 was probably due, at least in part, to the H2-spillover effect from the Pd surface to the support surface. It is well known that the spillover of dissociatively chemisorbed hydrogen on a noble metal promotes the partial reduction of TiO2 [6,8,26], leading to the so-called strong metal–support interactions (SMSI). Furthermore, the estimation of the H2 consumption during the H2 TPR, in particular for the Pd-A82 and Pd-P25 samples, exhibited a H2-to-Pd molar ratio larger than unity. This excess H2 was most probably consumed during the hydrogen spillover. The hydrogen spillover has been reported to be responsible for interesting catalytic effects, especially upon hydrogenations occurring under mild conditions and at high temperatures, i.e. hydrogenation of long chain alkadienes [6], of maleic anhydride [7], of nitrate ions in water [8], or of succinic acid in water [12].
The EPR analysis, as reported in refs. [6,12], can be used to investigate the formation of Ti(III) centers in more detail. Consequently, the catalysts were analyzed by EPR spectroscopy to evaluate the amount and the nature of the Ti(III) centers formed during the reduction process [27–31]. The EPR spectra of the catalysts are reported in Fig. 4, respectively. Indeed, the g<2 region of the spectra of reduced titania contains superimposed signals that arise from different defective sites. Since all Ti(III) centers resonate within the same region, it is impossible to properly estimate the relative amount of each site. Consequently, only the overall quantity of Ti(III) centers are reported in Table 3, expressed as the amount of Ti(III) relative to the Pd-A98 catalyst. The data suggest that all catalysts contained almost identical amounts of Ti(III) sites, with only one sample, Pd-A05, showing a greater degree of reduction.
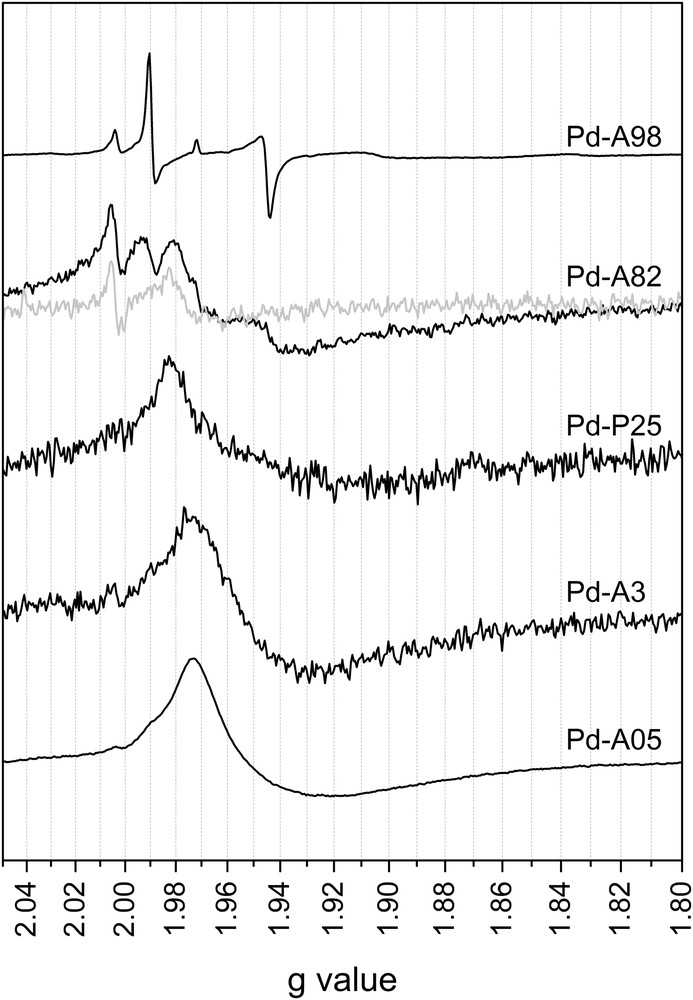
EPR results of the set of Pd/TiO2 catalysts, T=130 K, microwave frequency 9.5300 GHz. In grey, the EPR spectrum of the Pd-A82 catalyst reduced at 473 K. All spectra have been normalized to unit intensity for the reader's convenience, except for the grey spectrum (see text).
In addition, to verify the effect of the reduction temperature on the amount of Ti(III) sites, we prepared the Pd-A82 catalyst reducing it at 473 K, 100 K less than the other catalysts: the spectrum is reported in grey in Fig. 4 (appropriately scaled relative to the same catalyst reduced at 573 K). As can be seen, the number of Ti(III) centers greatly increased when higher reduction temperature was applied: when integrating the EPR spectra, one observes an increase almost by a factor of 170. This result confirms that a significant reduction of the support occurs only after the reduction of palladium.
The low-intensity peak(s) in the g>2 region of the EPR spectra are characteristic of oxygen-centered radicals interacting with titania [28]. The peaks in g<2 region are attributed to the Ti(III) centers in titania: this region is different for the different catalysts. In our samples, the presence of oxygen causes a broadening of the signals of the surface defects beyond detection and of the defects in direct contact with the metal nanoparticle. Therefore, a detailed analysis of the centers directly involved in the SMSI is excluded [27]. As reported in the literature [30], Ti(III) centers residing in reduced anatase and rutile have different EPR spectra, with species in anatase giving rise to larger g values than in the case of rutile. Indeed, the gradual shift from high to low g values observed in our samples was compatible with the increase in the rutile fraction in the support. The spectra of the Pd-A98 and Pd-A82 catalysts show well-defined resonances, whereas much broader peaks were found for Pd-A82, in the g 2.01–1.94 region. These peaks are likely originating from the isolated lattice electron trapping sites in anatase with minor contributions from rutile sites [29]. The spectrum of Pd-P25 is similar to that of Pd-A82, but lacks the resolved structure of the latter. The spectra of Pd-A3 and Pd-A05 show only two broad resonances, with a prominent peak at g ≈ 1.97 and a broad shallow peak at g ≈ 1.92 that can be attributed to Ti(III) centers in the bulk [27].
3.3 Catalytic tests
The catalysts were tested in the direct synthesis of H2O2 in a batch reactor at 275 K similarly as reported in Ref. [17] and the results are illustrated in Figs. 5 and 6, respectively. The concentrations of the desired product (H2O2) and the by-product (water) as well as H2 conversion and H2O2 selectivity are reported.
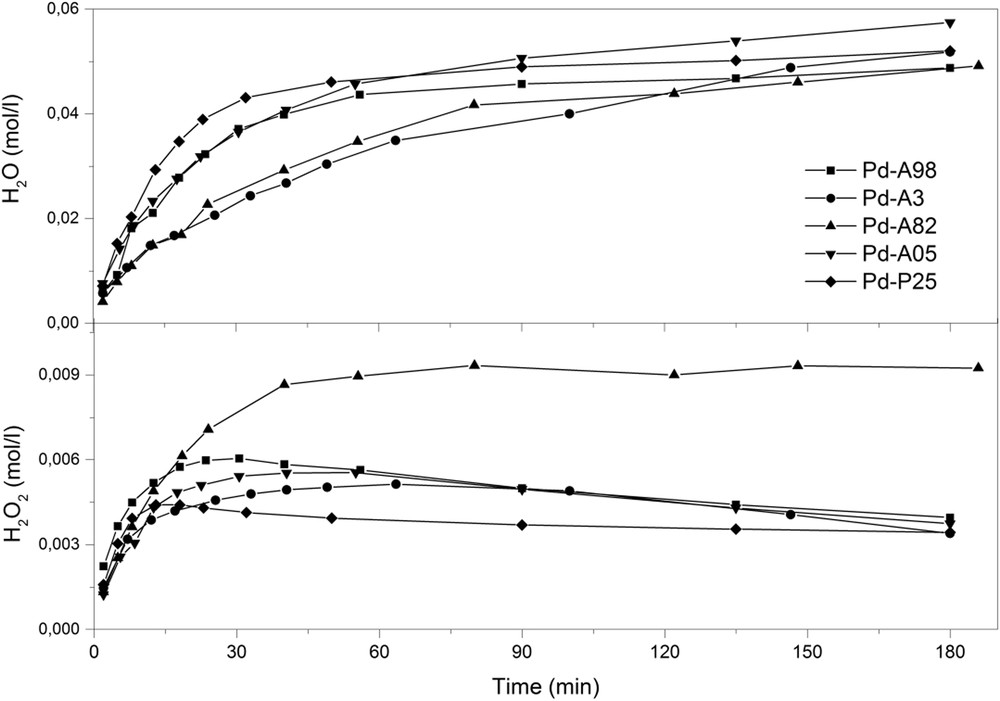
Molar concentrations of water and H2O2 as functions of time over TiO2 supported Pd catalysts.
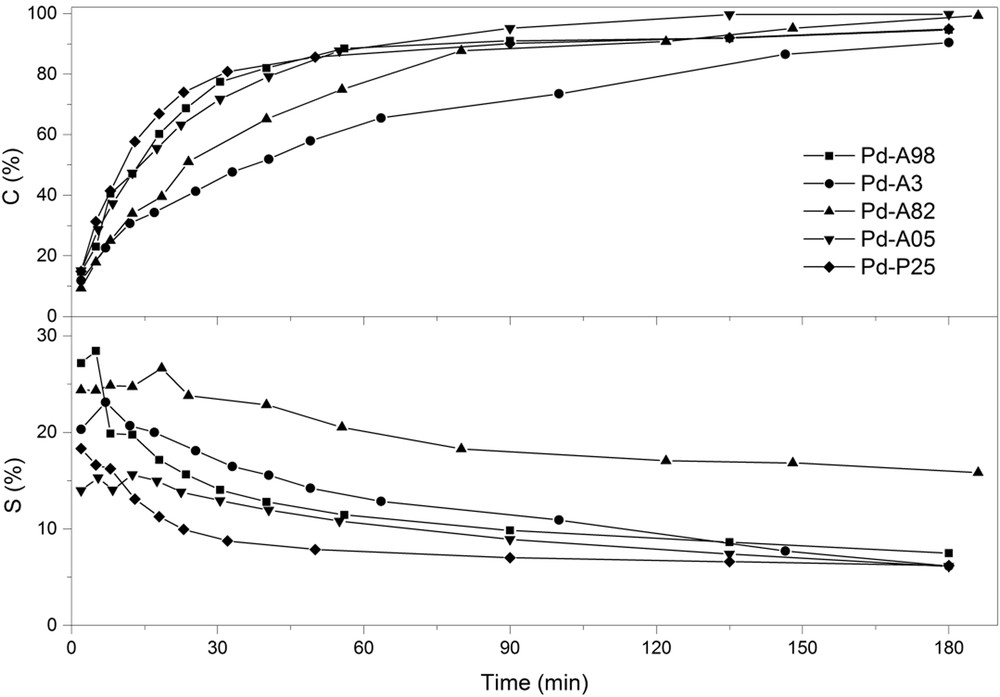
H2 conversion and H2O2 selectivity as functions of time over TiO2 supported Pd catalysts.
Table 4 shows the experimental results obtained upon analysis of the profiles of the two products (H2O2 and water). In general, the catalysts gave rise to high activity with a sudden consumption of H2. Except in the case of catalyst Pd-A3, the H2 conversion was more than 50% during the first 30 min with high initial cumulative productivities (Table 4, 3th and 6th column). This was especially true in the case of the Pd-P25, Pd-A98 and Pd-A05 samples. The initial cumulative productivity trend can be summarized as follows: Pd-P25 > Pd-A98 ≈ Pd-A05 > Pd-A82 > Pd-A3. Conversely, the initial H2O2 productivities were dropping in the following order: Pd-A98 > Pd-A82 > Pd-P25 > Pd-A05 > Pd-A3. Consequently, low initial selectivity for H2O2 could be observed, which also remained pretty constant after 50% of hydrogen consumption. The Pd-A3 material gave rise to the lowest productivities, both cumulative and in terms of H2O2, however exhibiting a H2O2 selectivity similar as in the case of other samples.
In general, no clear relationship between the phase composition of TiO2 support and the catalytic activity could be determined. Indeed, the most active materials (Pd-P25, Pd-A98 and Pd-A05 samples) had a widely variable anatase abundance. Even the selectivity seems not to be influenced by the phase composition of the support. Most probably, the complicated nature of CDS does not allow an easy connection between material features and catalytic behavior (Fig. 7). The lack of any obvious correlations is also true in terms of the Pd nanoparticle size. Indeed, the most active materials in the CDS were Pd-P25 (4.0 nm), Pd-A98 (2.5 nm) and Pd-A05 (12.8 nm), whereas the Pd-A3 was the least productive (overall), even though the mean nanoparticle size was 4.4 nm. It is well known in the literature that the a direct synthesis of hydrogen peroxide seems to be a structure-sensitive reaction, but that the correlations between the size distribution of metal nanoparticles and the catalytic performance are often unclear in spite of numerous trials and can be reviewed from recent reviews [31,32]. Furthermore, some authors explained that the selectivity enhancers (e.g., halide and acids) in the reaction mainly work as electronic modifiers [31]. In this case, the electronic modification due to the SMSI effect seems to produce no evident change (Fig. 8), unlike in the case of other hydrogenation reactions. This aspect was carefully evaluated and the results led to consider that possible strong interactions obtained between the support and active metal phase did not produce any clear effects in terms of the catalytic reaction or, if anything, this effect is negligible. Nevertheless, this result gave new insights into this challenging reaction and useful information considering development of future catalyst materials.
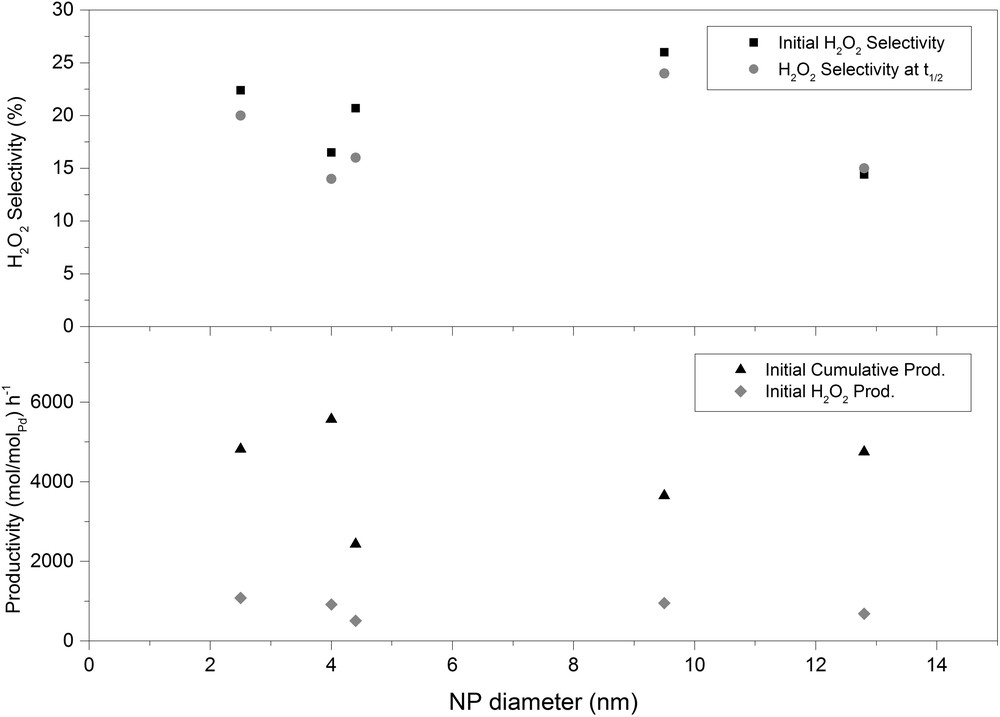
Correlation between catalytic properties (productivity and selectivity) and nanoparticle size.
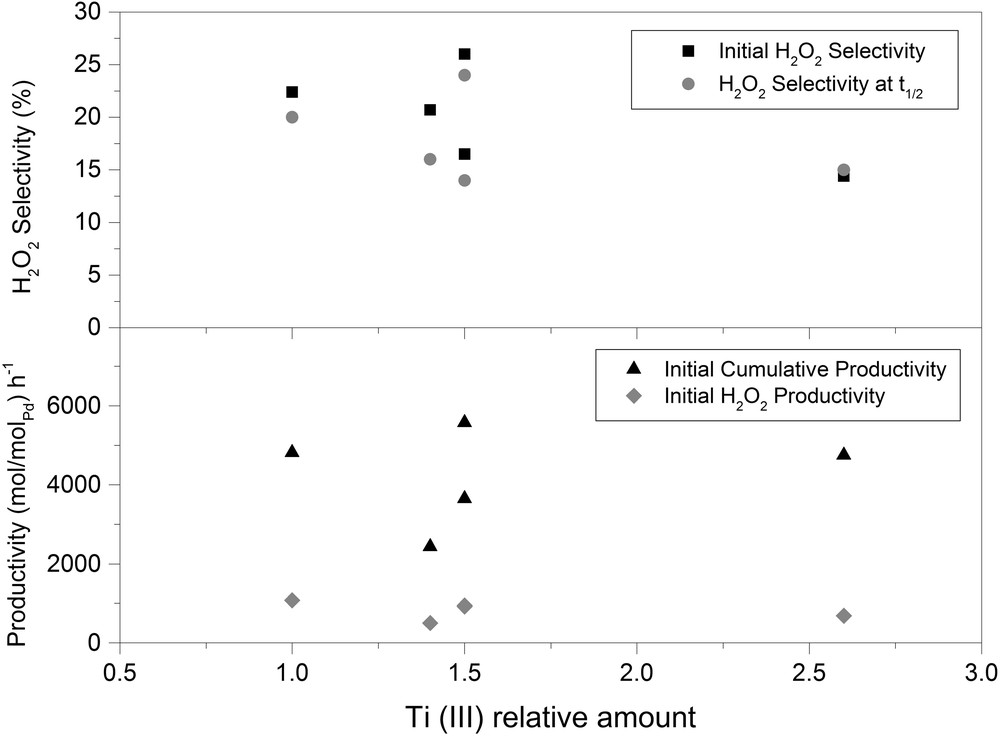
Correlation between catalytic properties (productivity and selectivity) and the relative amount of Ti(III).
4 Conclusions
In this paper, a set of palladium catalysts supported on different titanium oxides were prepared and their performance was evaluated in the direct synthesis of hydrogen peroxide. All materials were titania-based with different morphologies and composition, containing both anatase and rutile phases. The characterization results of the oxides verified the differences in the surface properties, e.g., surface area, number of Lewis acid and basic sites, etc. as well as the existence of different phase compositions, e.g., amount of anatase phase and crystallite size. The palladium catalysts prepared by wet impregnation, calcination and reduction at 573 K gave rise to size distributions not clearly related to the surface properties or the phase composition. Two of the materials, Pd-A05 and Pd-A98, seem to hint the existence of the so-called SMSI, strong metal–support interaction showing 1080 and 683 molH2O2·molPd−1·h−1 of H2O2 productivity and 22 and 14% of H2O2 selectivity, respectively. However the best material, Pd-A82, showed 949 molH2O2·molPd−1·h−1 of H2O2 productivity and 26% of H2O2 selectivity. The SMSI phenomenon has been shown to modify the catalytic performance of many hydrogenation reactions, e.g., reduction of nitrate ions in water or hydrogenation of long chain alkadienes, but in this case, we could not identify any evident effects. The selective hydrogenation of molecular oxygen is a complex process with a partial unclear mechanism, in spite of many efforts by several groups. The complex reaction mechanism could have partially eclipsed the SMSI effect. Another possibility is that the catalytic activity was influenced by more than a single feature and the results represent a sum of different effects. Most importantly, it was seen that the palladium nanocluster size strongly depended on the features of the TiO2 used as the support. Moreover, it was seen that the H2O2 direct synthesis was strongly affected by the palladium nanocluster size.
Since a catalyst is influenced by the (electronic) action of any selectivity enhancers, the possible absence of any SMSI effect supplies new information on the catalysts for the H2O2 direct synthesis, giving rise to new ideas to develop selective catalysts.
Acknowledgements
This work is a part of the activities of Process Chemistry Centre (PCC) financed by the Åbo Akademi University (ÅA). Dr. Stefano Sterchele is grateful to the Johan Gadolin scholarship 2013-14 (ÅA). Financial support from the Academy of Finland is gratefully acknowledged. Dr. Pierdomenico Biasi gratefully acknowledges the Kempe Foundations (Kempe Stiftelserna) for financial support. In Sweden, also the Bio4Energy program is acknowledged.


