1. Introduction
The field of Theoretical and Computational Chemistry applies the laws of physics and chemistry coupled with computer programs to calculate the structures and chemical and physical properties of molecules in different states of matter, such as thermodynamic properties, spectroscopic signals, chemical reaction pathways, phase diagrams, etc. The arsenal of theoretical tools in computational chemistry has evolved in recent years, nowadays also including theoretical methods from Operation Research (OR), which uses algorithms to build solutions on well-formulated problems, or Artificial Intelligence (AI), which uses various Machine Learning methods, based in particular on neural networks, not only to predict new physical and chemical states, events and properties, but also to develop, for example, force fields or DFT functionals for simulations. This new era has triggered a revival in the field of theoretical and computational chemistry for research teams to develop new theoretical methods that include OR and/or AI to go beyond the simple use of “classical numerical methods”.
Over the past decade, our group has approached this new era through the prism of algorithmic graph theory, in the context of OR and AI, based on the representation of matter in topological graphs [1, 2, 3, 4, 5].
A graph encodes topological properties of matter (in the same way for molecules, assemblies of molecules, liquids, solid materials, also interfaced with liquids) by means of vertices and edges that reflect the specific interactions (in pairs) between vertices. At the molecular level of representation, the vertices are usually associated to atoms while the edges report on interactions between atoms, e.g., chemical bonds and intermolecular interactions. Most graphs are defined in two dimensions (2D-graphs), any information related to, e.g., distances, angles, is usually not encoded into topological 2D-graphs unless vertices/nodes are specifically labeled with such information. Graphs can however be also three-dimensional, with an indication of coordinates in space that would thus encode intra- and inter-molecular interactions between atoms. Easier to obtain or to predict than 3D-graphs, 2D-graphs already carry information on the structure, the functional properties, and even the 3D shape of the materials they model. Examples include the classification of similar molecules according to their topology [6, 7], the prediction of patterns in biological molecules [8], the prediction of the 3D structure of small molecules [9], etc. Molecular graphs are also commonly used in supervised machine learning algorithms, the framework of graph-based models for molecules is indeed naturally suited to carry out predictions in message-passing neural network schemes.
In bio-/chemo-/materials informatics, the challenge is to identify or design algorithms capable of obtaining molecular properties from input graphs and to follow these properties in time. We have developed a series of 2D-graphs, at various levels of granularity of representation, and associated algorithms in order to analyze physical and chemical structures and properties from atomistic molecular dynamics (MD) simulations (DFT-based MD and classical force field FF-MD). In these developments, our aim was to ensure that 2D-graphs and algorithms could be applied without any modification to “simple” isolated molecules, as well as to assemblies of molecules and to more complex liquid and solid states of matter, including inhomogeneous solid/liquid interfaces [1, 2, 3, 4, 5, 10, 11].
This paper reviews some of our developments and achievements, which are also included in the GaTewAY software [12, 3, 2]. Other research groups, also experts in MD simulations, have worked on 2D-graphs. In the last decade, there have been developments of algorithmic graph theory devoted to the analysis of various types of molecular dynamics simulations, from, e.g., the conformational analysis of gas phase molecules and clusters, to their chemical reactivity, to the dynamics of H-bonds in liquids, to the dynamics of the solvation shells of ions in liquids, to the structural and dynamical analysis of complex aqueous interfaces in condensed matter [13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 1, 10].
Section 2 of this paper reviews the definitions used in the atomistic 2D-MolGraphs developed by our group [1, 10], and the associated algorithms, including the key isomorphism algorithm ensuring that a whole trajectory can be analyzed in terms of the relationships between the conformations explored over time. The topological analyses hence provide a statistical view over the whole timescale of the trajectory and over the whole set of conformations explored. Statistics is crucial for the detailed knowledge of the dynamics of isolated molecules as well as for the dynamics of molecules in the liquid state, as applications in Section 3 will show.
We also review our recent developments of 2D-graphs consisting of H-bonded cycles and the key polymorphism algorithm [4], which have been built to go beyond the atomistic representation in 2D-MolGraphs and to be able to represent (bio-)molecules whose 3D structures and dynamics are solely based on hydrogen bonds. The algorithms we have developed enable us to track the complex conformational dynamics of flexible H-bonded molecules in real time. Section 3 will show that, while the interpretation of the complex conformational dynamics of a highly flexible hexapeptide in the gas phase would remain elusive at the atomistic level of representation (2D-MolGraphs), it is well understood by means of coarse-grained graphs of H-bonded cycles (polygraphs) and by means of polymorphic “metastructures”. Only the coarse-grained representation in the graphs allows such comprehension.
Section 3 will further show how atomistic 2D-MolGraphs can easily be included in automated high-throughput in silico reactivity workflows and how essential they are in some of the decisive steps to be taken in these workflows. We implemented the 2D-MolGraphs in the computational catalytic reaction space exploration method ReNeGate [5] and the high-throughput reactivity screening HiREX workflow [11], specifically designed to explore realistic catalytic systems and identify thermodynamically feasible chemical transformations, corresponding to secondary catalyst deactivation and inhibition paths.
Prospects and new developments in progress are discussed in Section 4, which, with this review of methods and applications, we hope will spark further requests for additional algorithms and new applications in our physical chemistry and chemistry communities.
2. Methods
2.1. 2D-MolGraph for modeling a conformation
Our developments have been aimed at defining topological 2D molecular graphs (labeled 2D-MolGraph) and associated algorithms in order to automatically analyze MD trajectories from the knowledge of the time evolution of the conformations and hence automatically detect conformational changes through topological changes. Our 2D-MolGraphs share a similar degree of granularity in representing the topology of molecular systems to the one used by previous implementations in the literature in chemistry [14, 13, 17], i.e., a vertex in the 2D-MolGraph represents an atom or a molecule and an edge between two vertices represents the interactions/bonds (covalent bond, hydrogen bond …) between two atoms/molecules. Most of the literature on graphs in the chemical community does not consider the chemical nature of the atoms in the vertices, which is not efficient for recognizing identical structures where chemically identical atoms have been swapped. Moreover, they lack specific chemical information (e.g., covalent bonds, hydrogen bonds, exchange of atoms in homogeneous clusters, etc.) that might be relevant for a more detailed characterization of the structures.
One crucial step in our method has been to define a model that represents any molecular conformation with the right level of granularity and be transferable without any modification from gas phase molecules and clusters to the condensed phase (solids, liquids, interfaces between solids and liquids). To that end, we have chosen to define any molecular conformation by a colored mixed graph G = (V,EC,AH,EI,EO), with both (directed) arcs and (undirected) edges. Such a graph is denoted 2D-MolGraph, in which each vertex represents an atom while the edges represent covalent bonds (EC), hydrogen bonds (AH), ionic (or electrostatic) interactions (EI) typically between a cation/anion atom and other atoms, organometallic interactions (EO) between metallic atoms and their surrounding. Only the hydrogen bonds are associated to directed edges (from the donor to the acceptor atom). The hydrogen atoms in a molecular system are not included in vertices of the 2D-MolGraph. Instead, their presence is solely known by directed edges. Hence, any hydrogen that is not involved in a hydrogen bond is not represented in the 2D-MolGraph.
The definition of bonds and interactions is mainly based on Euclidian distances. The Euclidian distance between a pair of atoms [a,b] with respective Cartesian coordinates (xa,ya,za) and (xb,yb,zb) is: . There is a covalent bond or an interaction between two atoms if the Euclidean distance is less than a cutoff distance Dr. For covalent bonds, the algorithm defines the Dr distance by the sum of covalent radii of atoms a and b with an additional 2% margin (that typically includes the effect on distances from vibrational motions). For hydrogen bonds, the algorithm sets up the default Dr value between the hydrogen atom (donor) and the acceptor atom (heavy atom) to 2.3 Å, which can be changed by the user. For the organometallic and ionic interactions, the user is free to set case-specific Dr distances. For example, the distance between manganese and oxygen atoms used in one of the applications in Section 3 was set to 2.44 Å. This choice was made because the developers assume that the covalent bonds are stronger than the other types of interactions between atoms. More details are found in [1, 12, 5].
One can easily define and implement new relevant interactions that are needed to describe a given molecular system, and hence augment the number of definitions for the edges in the 2D-MolGraphs.
In order to take into account the chemical type of the atoms in a 2D-MolGraph, we apply a special case of graph coloring, such that the vertices of a given 2D-MolGraph display the same color if and only if the corresponding atoms have the same chemical type (see Figure 1). Figure 2 illustrates an adjacency matrix built prior to the construction of a 2D-MolGraph. The matrix shown here is associated to a selected part of the Z-Ala6–COOH peptide from Figure 1a (3D structure) and Figure 1b (2D-MolGraph). As the peptide contains 80 atoms, only a selected part of the peptide has been extracted here for this illustration. The figure shows that covalent bonds and hydrogen bonds of interest in the conformation of this peptide are encoded in the adjacency matrix (with crosses and circles, respectively) and that the matrix has the colored information of the actual chemical nature of the atoms. The graph on the right side of the figure is the subgraph of the 2D-MolGraph associated to the selected part of the molecule encoded in the matrix.
Illustration of the passage from a 3D conformation (a) to a 2D-MolGraph (b). (a) One snapshot in the 3D representation of the gas phase Z-Ala6–COOH peptide (C26H39N7O8) extracted from a MD trajectory. Carbon atoms are colored turquoise, nitrogen atoms blue, oxygen atoms red, and hydrogen atoms light gray. (b) Associated topological 2D-MolGraph. Vertices are colored dark gray, blue, and red, corresponding to carbon, nitrogen and oxygen atoms, respectively. Hydrogen atoms are not included in vertices, their knowledge is included only through directed edges that represent hydrogen bonds. Edges are black lines for a covalent bond and red dashed lines (arcs) for hydrogen bonds, the latter directed from the donor to the acceptor of the H-bond.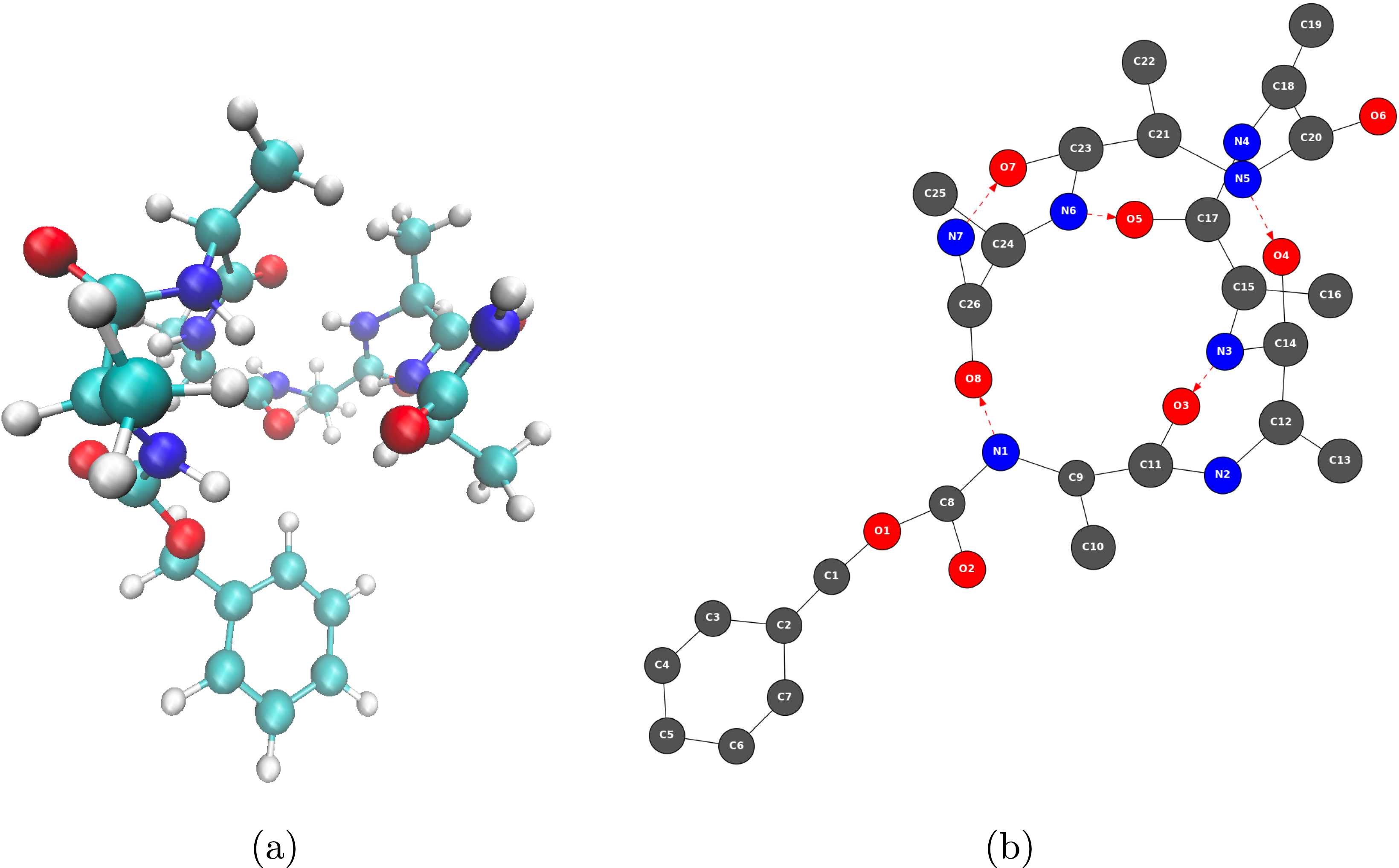
Illustration of an adjacency matrix for a selected portion of the Z-Ala6–COOH peptide shown in Figure 1a (3D-structure) and Figure 1b (2D-MolGraph).
With 2D-MolGraphs in our hands, the exploration with time of molecular conformations along MD simulations can easily be seen as the exploration of graph topologies, that can be tracked using graph theory-based methods, such as isomorphism. Graph isomorphism as defined in [23] allows representation of each conformer with a fingerprint graph and comparisons between graphs. In our applications, isomorphism consists in comparing the distribution of edges between two 2D-MolGraphs: if the graphs compared have the same set of bonds/interactions connected to the same set of atoms (in terms of chemical types/colors for the graphs), these graphs are then isomorphic, i.e., the two graphs are identical. More formally, an isomorphism is a bijection between the vertex sets of the two graphs if and only if it induces a corresponding bijection between their edge sets (if such an isomorphism exists, the two graphs are said to be isomorphic). A (non-polynomial) algorithm to check if such an isomorphism exists is proposed in [24, 23, 25, 26].
Isomorphism checks, together with keeping the chemical nature of the atoms, are the key components of the conformational search over MD trajectories. The changes in conformations are hence followed over time by scanning trajectories for changes in bonding patterns of choice (among hydrogen bonds, proton transfers, coordination numbers, covalent bonds, and organometallic interactions). Once the different conformations of the molecular system have been found by graph analysis, a graph of transitions can be generated, similar to the ones considered in different analysis or generation of temporal graph sequences [27, 28, 29]. This graph has its vertices composed of the conformations that have been identified and its edges are composed by the transitions found between conformations. Both vertices and edges in the graph of transitions contain information on the percentage of existence of a conformation over the duration of the trajectory (for the vertices) and the percentage of times a transition between two vertices/conformations has been seen (for the edges). In one glance, one can hence see the relationships between the conformations and associated statistics.
Figure 3 shows an example of a graph of transitions. This graph is composed of four vertices, each vertex represents one molecular conformation that has been identified by isomorphism along the trajectory. Each vertex has a number and a label that represents the conformation. For instance, one vertex in this picture is labeled with “1” and “N1-O1”, meaning this is the first conformation identified over the trajectory, and the associated conformation has one hydrogen bond between atoms “N1” and “O1”. The “68.97%” number in the vertex is the percentage of time this conformation has been seen over the whole trajectory. Hence, in this graph of transition, conformation 1 is the most frequent conformation that has been observed over the trajectory, with a total percentage of appearance of ∼69% over the trajectory. The edges between the vertices are labeled with two kinds of information: (1) the total frequency rate for going from one conformation to the other one, (2) the bond(s)/interactions(s) that have changed when going from one conformation to the other. For instance, one can observe a large conformational dynamics between conformations 1 and 2 in the graph of transitions in Figure 3; such an event occurs around 130 times, back and forth. Also of note, the hydrogen bond N1⋯ O1 disappears when going from conformation 1 to conformation 2 (and appears on the reverse way). Conformation 2 in the graph of transitions is labeled with “2” and “.”, the latter meaning that this conformation contains no hydrogen bond. Conformation 2 has been seen ∼30% over the whole trajectory.
Graph of transitions. See text for nomenclature and colors.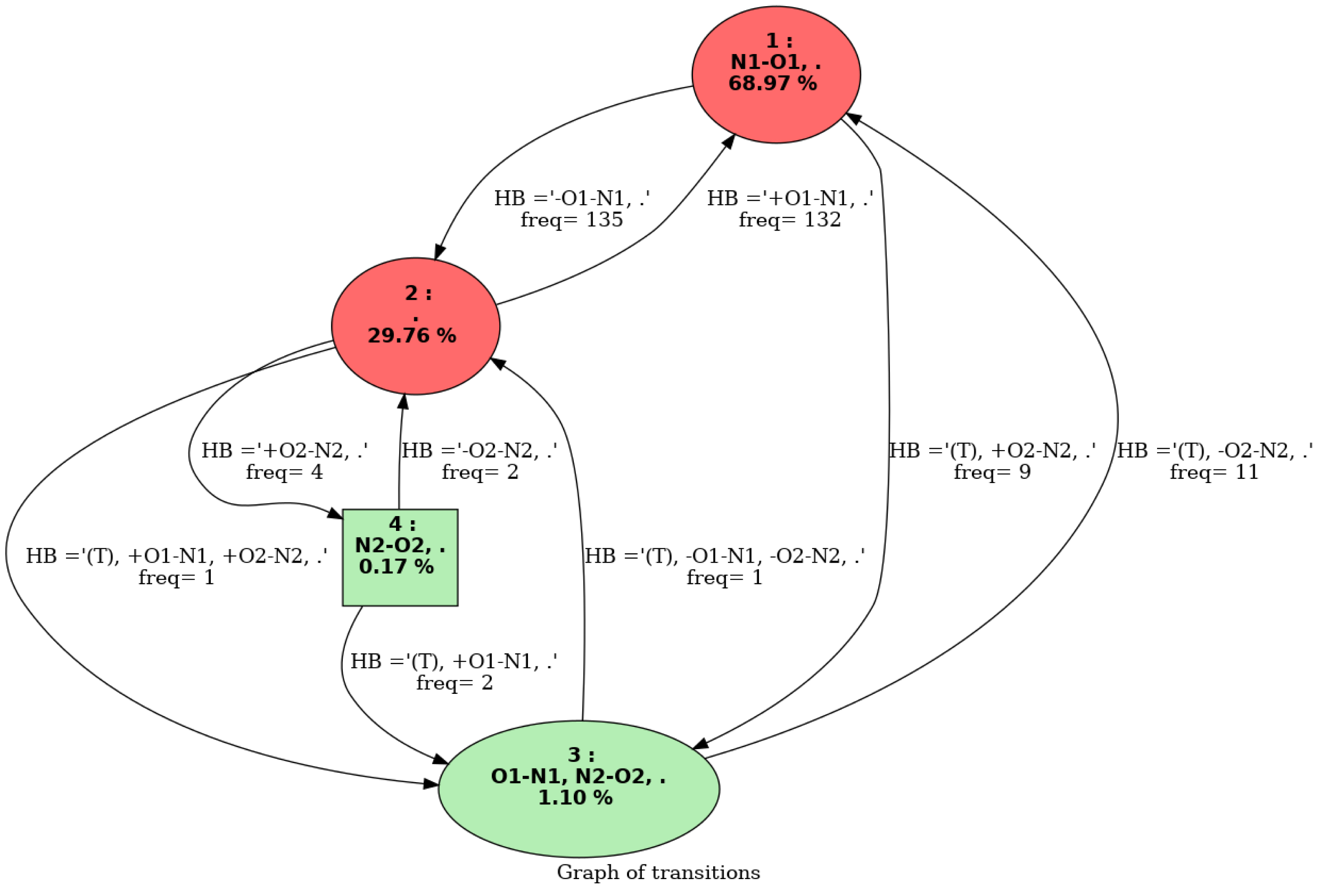
The colors of the vertices in the graph of transitions directly give the most relevant conformations in terms of appearance periods. We hence colored red the conformations that appear at least Pmin% (an input parameter that the user can change the default value of 4% has been used here) and the ones in green occur below this threshold. All the conformations explored along the MD simulations can be kept in the graph of transitions. Such information might indeed be useful for some analyses, typically when rare events (rare conformations) are investigated. The user can modify this at will.
2.2. From a topological 2D-MolGraph to a coarse-grained graph of H-bonded cycles
In [3, 2] we have shown that the rationalization of the conformational dynamics becomes complex and almost impossible to achieve for flexible H-bonded molecules that isomerize frequently over time through the dynamics of breaking and forming of their H-bonds. As shown in these references, a simple short peptide such as Z-Ala6–COOH (illustrated by one 2D-MolGraph in Figure 1) already shows a high flexibility of its network of N–H⋯ O H-bonds at relatively low temperatures (gas phase MD trajectories). Numerous breaking/forming of H-bonds were observed over the trajectories, which signaled the appearance and disappearance of several conformers of the gas phase peptide numerous times along the trajectory. This high dynamical flexibility of the H-bond network, however well represented by the 2D-MolGraphs and their graph of transitions [3, 2], prevents a clear rationalization of the actual conformational dynamics of the peptide. In particular, some of the H-bonds in the network, though formed between different atoms, seem to play a similar role into the final 3D structure of the peptide molecule, i.e., into the final folded/semi-folded/unfolded skeleton. This is not captured by the 2D-MolGraphs at the atomic level of representation, but this similarity of H-bonded cycles can be captured by graphs defined at a higher/coarser granularity of representation. We therefore defined graphs in which the vertices are directly associated to the H-bonded cycles formed, whose polymorphism is furthermore taken into account. These concepts are now explained.
Cycles in molecular graphs have been shown to be good representations of the structure of molecular systems [30, 31, 32]. We hence proposed a representation of each conformation identified by a 2D-MolGraph over a trajectory based on a well chosen set of cycles. The cycles of interest to us are the ones formed by at least one H-bond. With these, we will be able to quantify and follow in time the changes in the H-bonded network of molecular structures. Our current developments have been done for gas phase molecules only [4]. Note that the number of cycles in a graph can be exponential with respect to the number of vertices. Therefore in our approach, we only consider a subset of cycles in the 2D-MolGraph, called “minimum cycle basis”, restricted to the H-bonded cycles for each 2D-MolGraph of the trajectory. Given a graph, finding a minimum cycle basis, which is not necessarily unique, can be done in polynomial time with an evolution of the algorithm of Horton [33]. More details can be found in [4].
Given a 2D-MolGraph, we compute its minimum basis set of H-bonded cycles. The associated graph of cycles is defined as a graph in which the set of vertices is the cycle basis, and there is an edge between two vertices (cycles) if and only if these two cycles interact, i.e., they share at least one covalent bond or one hydrogen bond in the 2D-MolGraph. Hence each 3D-conformer in the trajectory of a molecule is represented by a graph of cycles. The evolution in time of the conformations in a MD trajectory can be represented by the sequence of their graphs of cycles.
Figure 4 illustrates the transformation from a topological graph (Figure 4a) to a graph of cycles (Figure 4c). Considering the 2D-MolGraph in Figure 4a and the minimum cycle basis in Figure 4b, there are four H-bonded cycles, each of them of various size, composed of one or several hydrogen bonds. Hence, the pink vertex in Figure 4c is built on one H-bonded cycle composed of six vertices/atoms in the 2D-MolGraph (this is a six-membered H-bonded cycle), while the larger orange vertex/cycle is built upon two hydrogen bonds (see the two directed dashed red edges in Figure 4a). Figure 4c shows the graph of cycles obtained from the minimum cycle basis shown in Figure 4b. In this graph, the vertices are the H-bonded cycles, labeled by the heavy atoms involved in the hydrogen bond(s) producing them. Taking once again the examples of the pink and orange cycles/vertices depicted in Figures 4b–4c, the pink vertex is labeled N3O3 as it is built on the N3–H⋯ O3 hydrogen bond, while the orange vertex is labeled with its two constitutive H-bonds N1–H⋯ O8 and N5–H⋯ O4. The orange, pink and blue vertices/cycles interact with each other as seen through the edges connecting these three vertices (i.e., sharing at least one covalent bond or one hydrogen bond). On the other hand, the green vertex (related to the H-bonded cycle N7O7) interacts only with the orange one.
Example for the coarse-grained representation of a 2D-MolGraph for one conformation of the gas phase peptide Z-Ala6–COOH. See text for details.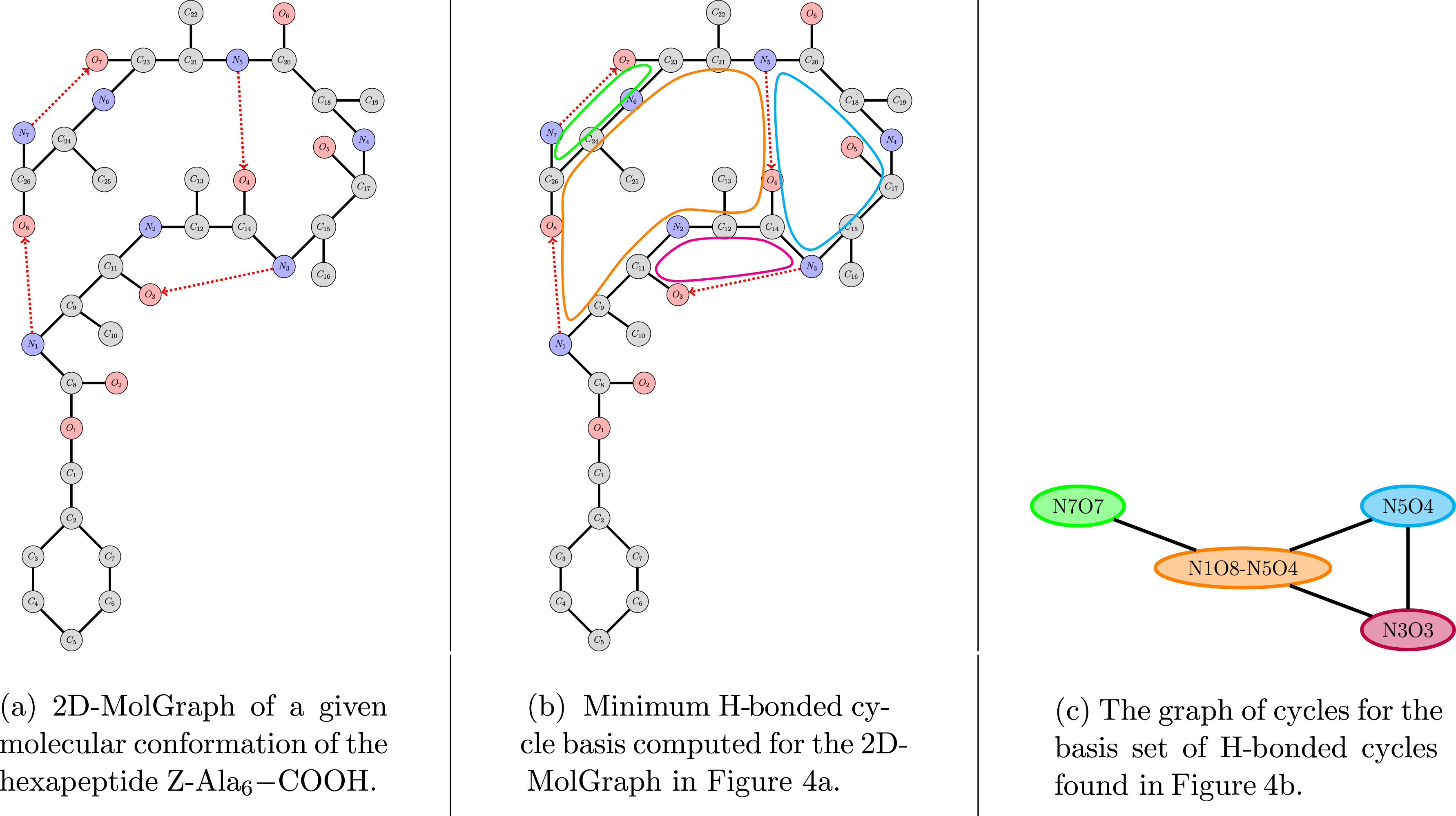
Given a MD trajectory, each 2D-MolGraph is now associated to a minimum cycle basis and to the corresponding graph of cycles. In other words, there is one graph of cycles per 2D-MolGraph (i.e., per identified molecular conformation).
The set of conformational isomers explored over the MD trajectory can furthermore be summarized by one single graph of cycles uniting those of all the identified conformers. This union takes into account all the possible H-bonded cycles as well as all the possible interactions between these cycles which were observed in all the identified conformers. Some of these H-bonded cycles can be identical in different conformers. Some of these H-bonded cycles can be similar to each others in the sense that they are built upon different donor/acceptor atoms but they are playing the same role in the final structure of the molecule. One therefore has to recognize the similarity between the H-bonded cycles of the different miminum cycle bases (i.e., similarity between the H-bonded cycles in the different identified conformations).
To that end, the next stage was to develop an algorithm that can group together the cycles of different minimum cycle bases which are similar, i.e., the ones playing the same role in the structure of different conformers. The similarity constraint that we introduced is the basis to cluster the union of cycles in all the minimum cycle bases of all the conformers of the trajectory that we finally want to obtain. Each part in such a clustering is called a polymorphic cycle, in which all cycles are considered as different forms of a same cycle in the structures of the conformers it appears in. The hypothesis that we made is that a cycle can evolve over time, that is to say that its set of links can evolve while retaining its same role in the molecular structure. The trajectory can therefore be seen as the interaction of the H-bonded cycles evolving over time in their atomic structure (polymorphism) and still interacting in the same way, but with some of these cycles appearing or disappearing over time. The final graph thus obtained is called a polygraph, a contraction of “polymorphic cycle graph”; note that this definition is different from the one of a polygraph as a generalization of the directed graph [34], or that used in chemoinformatics related to polymers [35]. The whole algorithms have been detailed in [4].
We now show an application of this methodology for the gas phase chondroitin disulfate CS2S4S molecule, for which a 3D snapshot is reported in Figure 5. Figure 6 reports the polygraph obtained for a 600 K trajectory of this gas phase molecule. Each vertex of the polygraph is labeled by “P-XX” where P stands for polycycle and XX is the set of oxygen and/or nitrogen atoms (with their associated label number in the list of the molecule’s atoms) involved in the H-bond of the polycycle (i.e., one of the two partners which close the H-bonded cycle). Each polycycle has been assigned a given color. Note that a polycycle can be built over one or over several H-bonds (two to three for this molecule). In that case, the atoms involved in the series of H-bonds are written on a line with a “,” between them. See some examples in the vertex colored in violet for several instances of multiple H-bonds forming a polycycle.
A 3D representation of chondroitin disulfate CS2S4S (C14H20NO18S2). Colors for the atoms: carbon in turquoise, nitrogen in blue, oxygen in red, hydrogen in light gray, and sulfur in yellow.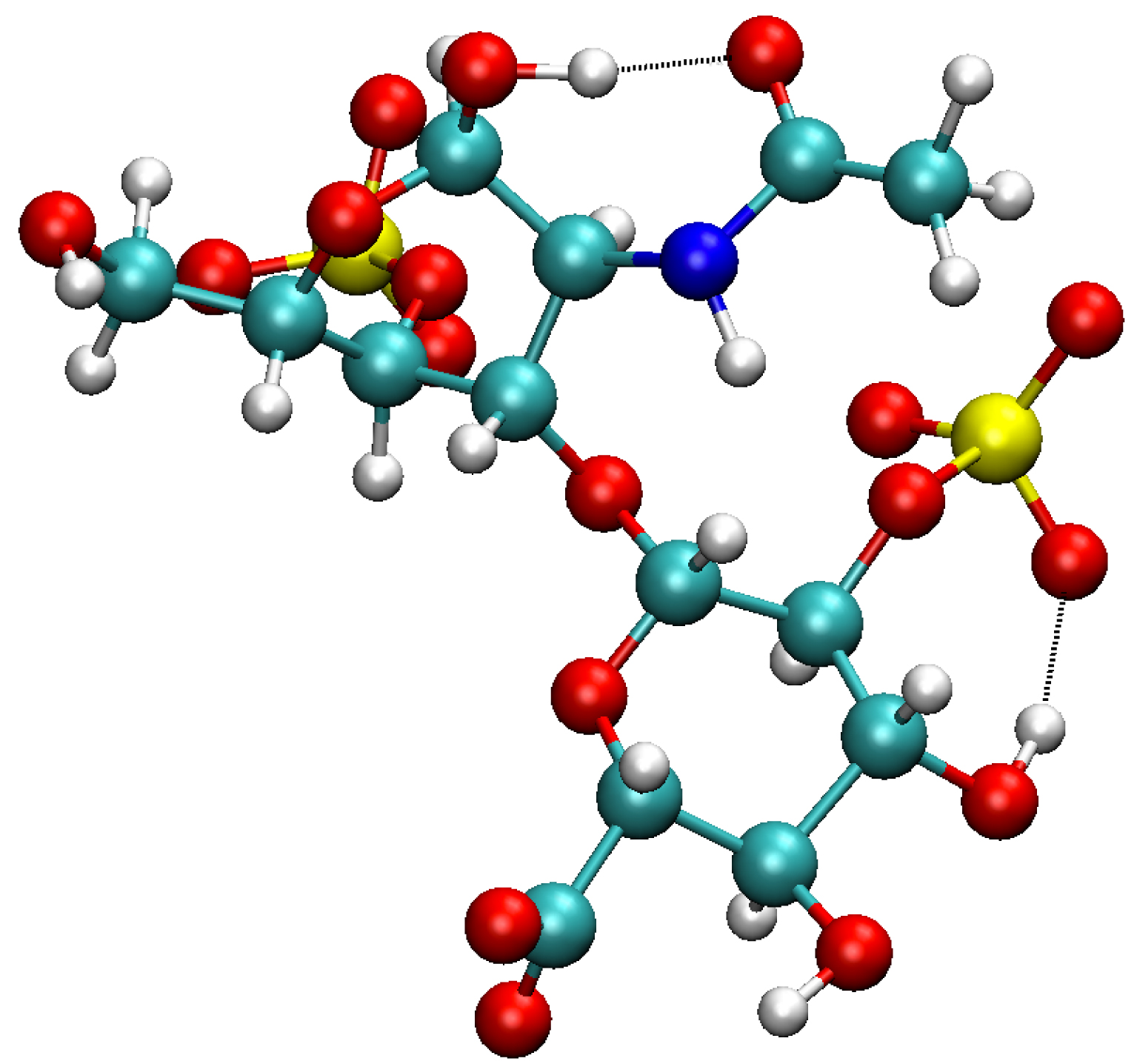
The polygraph obtained for a MD trajectory of the gas phase chondroitin disulfate CS2S4S molecule.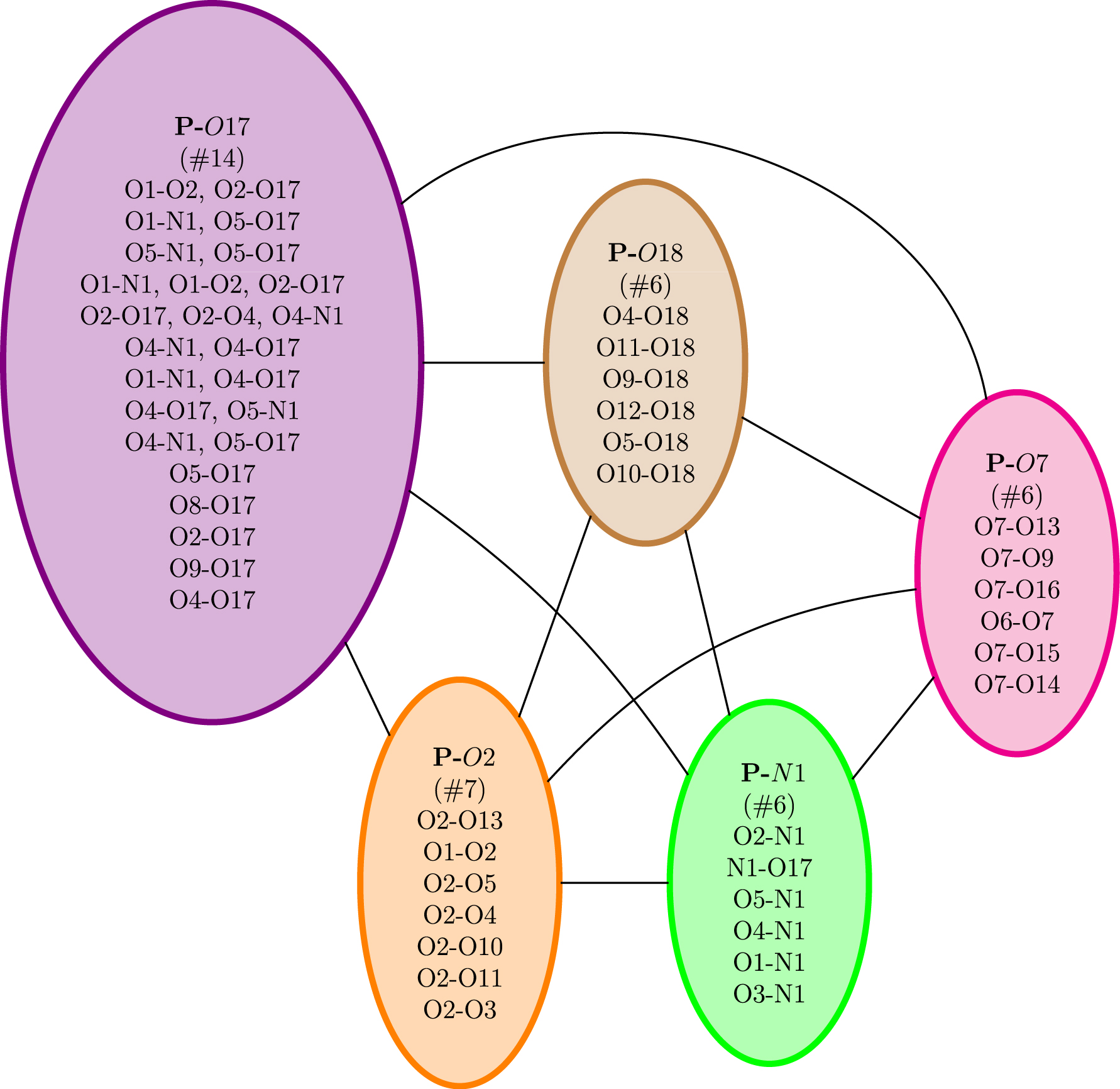
Figure 6 shows that this polygraph is a complete graph made of five vertices. It is complete because there is an edge between each pair of vertices. As a reminder, there is an edge between two polycycles whenever these two cycles have atoms that share at least one covalent bond or one H-bond in the initial 2D-MolGraph (i.e., these polycycles are interacting with each other within the molecular structure). Because the polygraph is complete, the number of polycycles cannot be reduced. All vertices involve different polymorphic identities. Four of the five vertices have six or seven different actual identities for the H-bonded cycle that forms the polycycle (dark green, pink, green, and orange), while there is an even larger diversity of 14 different identities for polycycle P-O17 (purple). For instance, vertex P-O7 is associated to a polycycle that can have six different identities of the H-bond that closes the cycle/polygon with the O7 atom. As can be seen, this O7 can either H-bond to the H atom carried by the O13, or to O9, O16, O7, O15 and O14. In the vertex in the violet color, some of the lines report other identities than the P-O17 identity. For instance, one line reports O1-O2 and O2-O17, which means that the P-O17 polycycle is built over two simultaneous hydrogen bonds, i.e. the O2-O17 H-bond but also the O1-O2.
3. Review of selected applications
3.1. H-bond dynamics of a flexible gas phase peptide and the relevance of the coarse-grained graphs of H-bonded cycles
The conformational dynamics of the gas phase hexapeptide Z-Ala6–COOH (C26H39N7O8, 80 atoms, 3D illustration in Figure 7) is analyzed hereby both in terms of the 2D-MolGraphs (atomistic level of topology representation) and in terms of the coarse-grained polymorphic cycles (coarse-grained level of topology representation) in order to present the strengths and limitations of each level. An ab initio MD (AIMD) trajectory of ∼6.0 ps (12,294 snapshots, δt of 0.5 fs) at ∼450 K serves as the basis for the conformational dynamics to analyze. This temperature has been chosen as a good example for the analysis of trajectories where several medium and large conformational changes are expected to occur, which are always rather hard to characterize without the help of topological graphs.
A 3D representation of the hexapeptide Z-Ala6–COOH. Colors for the atoms: dark gray for carbon, dark blue for nitrogen, red for oxygen, white for hydrogen.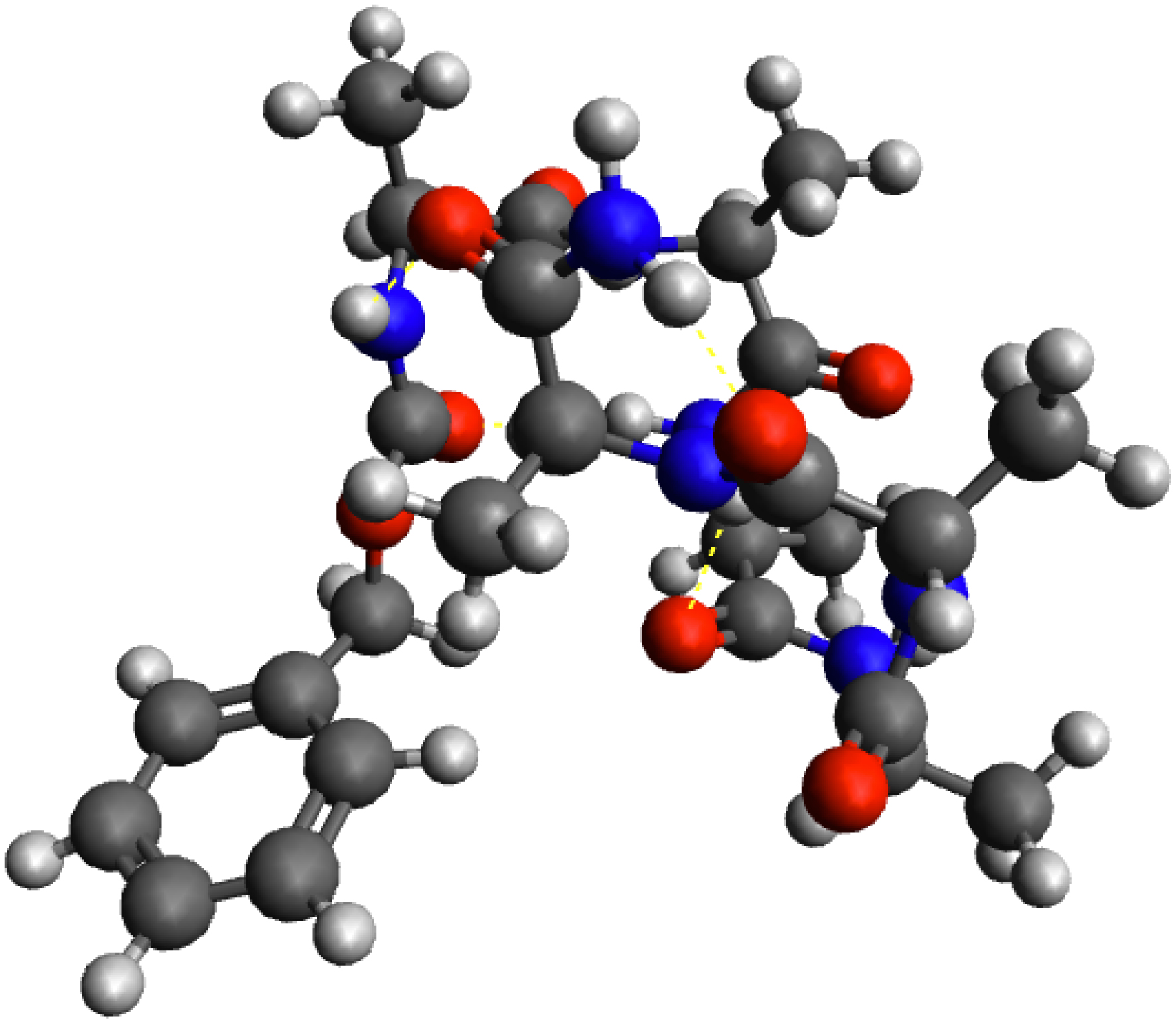
3.1.1. A high conformational dynamics of Z-Ala6–COOH provided by the 2D-MolGraphs
The analysis of the trajectory in terms of topological molecular 2D-MolGraphs [1, 3] indicates that 93 different conformations are sampled over ∼6 ps (which hence shows a rather highly dynamical peptide), built over nine different H-bonds. The structure of each identified conformer is composed of one to six H-bonds that are formed simultaneously. The peptide is found in either opened structures where a low number of simultaneous H-bonds are present or in H-bonded folded structures.
As illustrations, Figure 8 presents two 2D-MolGraphs corresponding to two identified conformers of Z-Ala6–COOH, respectively produced by five (Figure 8c) and three H-bonds (Figure 8d). Two of these H-bonds (N7⋯ O7 and N6⋯ O5) are present in both conformations.
Two 2D-MolGraphs (c and d) of the gas phase peptide Z-Ala6–COOH and their associated 3D structures (a and b) extracted from the MD trajectory analysis. Colors of the vertices: dark gray for C atoms, dark blue for N, red for O. No vertices for hydrogens, their knowledge is in the directed edges (arcs). Solid black edges in the graphs are for covalent bonds, the red arcs are the hydrogen bonds directed from the donor to the acceptor (heavy) atoms.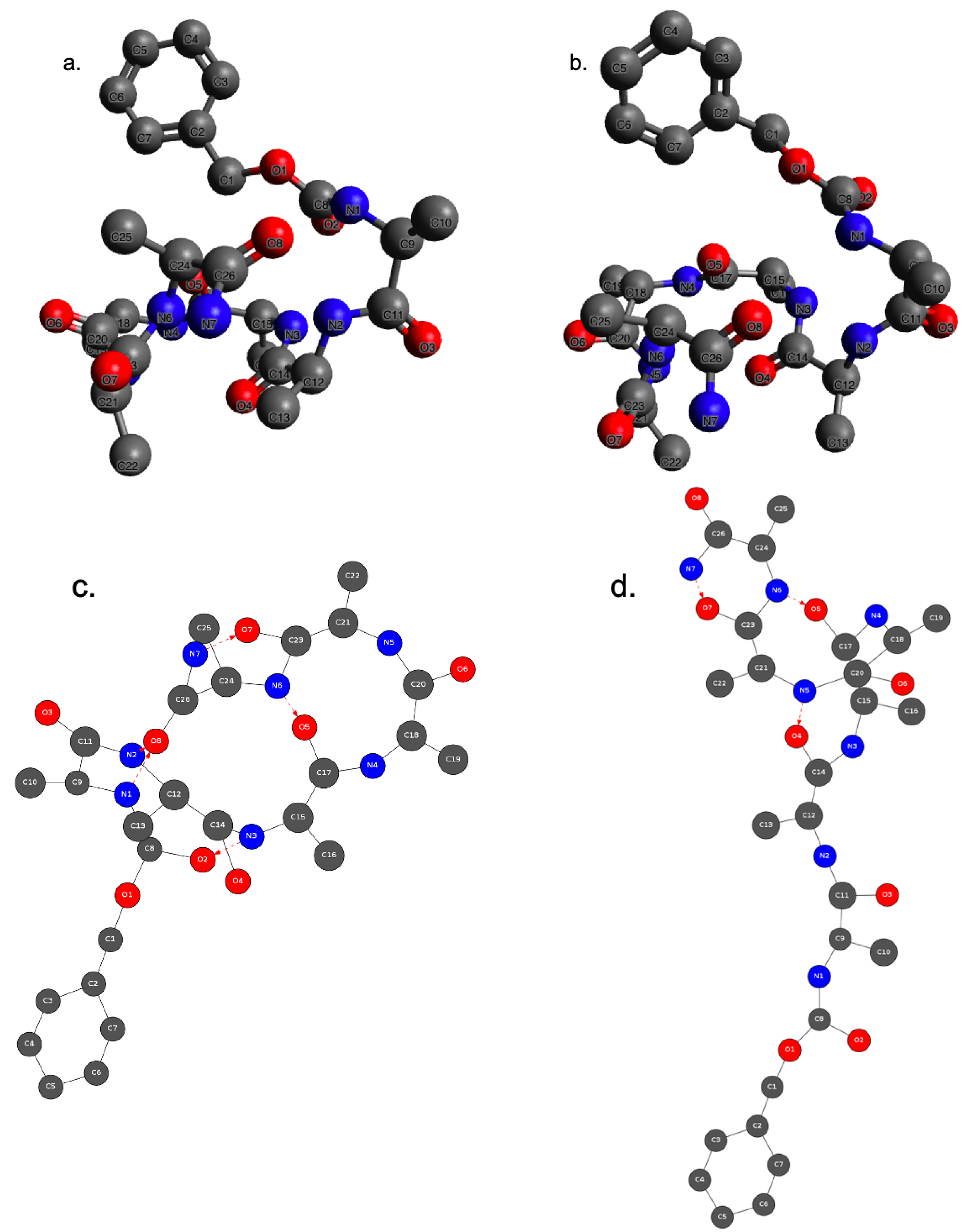
Figure 9 is the graph of transitions that summarizes the whole 6 ps of conformational dynamics of Z-Ala6–COOH at 450 K. As can be immediately seen, this graph of transitions is composed of an extremely high number of vertices and edges connecting these vertices, which is the signature of the high dynamicity and high flexibility of the peptide. There are 93 vertices in the graph for the 93 different conformers of Z-Ala6–COOH found. In the graph of transitions reported in Figure 9, most of the identified conformers (in the green vertices) appear over very short periods of time (less than 0.24 ps) while two conformers (red vertices) appear over larger durations of time.
Graph of transitions for the 450 K dynamics of the gas phase Z-Ala6–COOH peptide. The vertices indicate the explored conformers. Vertices in red are for conformers with a total percentage of appearance Pmin% greater than 4% of the dynamics time (parameter Pmin% can be modulated at will), vertices in green are for conformers with Pmin % < 4 %. Directed edges between vertices indicate transitions between two conformers as observed over time. The labels on each edge provide the total percentage of occurrence of the transition and the associated chemical change(s) that occur. A zoom over a small portion of the graph of transitions is provided on the left-hand side.
While the high number of vertices and edges in the graph of transitions in Figure 9 illustrates the high flexibility of the peptide at 450 K that is nicely captured by our 2D-MolGraph topological graphs, it also illustrates the limit of the atomic level of granularity used in the 2D-MolGraphs for highly flexible molecular systems where presumably too much information is provided in the graph of transitions and is hard to process. Furthermore, some of the periods of times that the 2D-MolGraphs analyze as breaking/forming covalent bonds and/or H-bonds correspond in practice to the dynamics of these bonds around the threshold values employed in the method for conformational recognition. Some of the transitions observed between conformers are thus in practice the actual signature of the existence of one single “meta-conformation” around which dynamicity and flexibility occur.
This information can however not be extracted from the atomistic topological 2D-MolGraphs. To get that information, one has to analyze the trajectory with a coarse-grained topology representation, whose results are described in the following section.
3.1.2. Polygraphs are the good coarse-grained representation to analyze the conformational dynamics of Z-Ala6–COOH
To go beyond the limitations of the atomistic representation in the topology highlighted above in the case of the highly flexible Z-Ala6–COOH, we now apply the coarse-grained topology representation described in Section 2.2 to analyze the conformational dynamics of this peptide: it now consists in representing a molecule through the ensemble of its H-bonded cycles and to apply an algorithm of polymorphism in order to recognize the cycles that are isomorphic to each others. Figures 10 and 11 illustrate the two immediate outputs of this analysis, respectively showing the global polygraph generated over the whole 450 K trajectory in Figure 10 and the chronogram (time evolution) of the nine identified polymorphic cycles in Figure 11.
The global polygraph obtained over the 6 ps AIMD trajectory of the Z-Ala6–COOH peptide at 450 K. The color coding of the vertices is identical to the color coding of the lines in the chronogram in Figure 11. Each vertex of the polygraph is labeled by “P-XX” where P stands for polycycle and XX is the set of the oxygen atom and/or the nitrogen atom (with their associated label number in the list of the atoms of the molecule) involved in the H-bond of the polycycle. Each vertex contains the list of the polymorphic cycles, each one being labeled by the atoms’ names and labels in the H-bond(s) building the H-bonded cycle.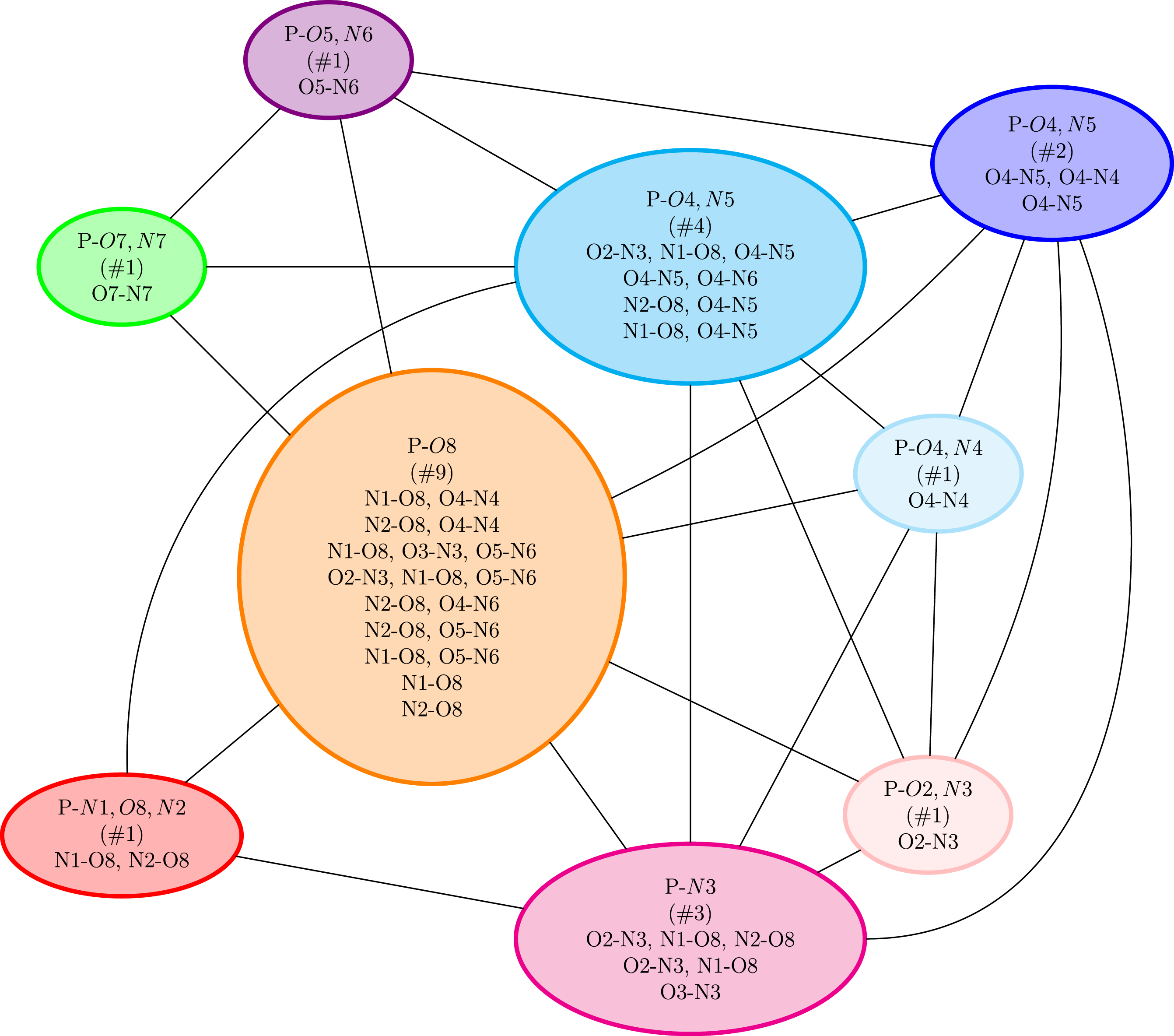
There is a total of 23 H-bonded cycles over the 93 2D-MolGraphs extracted from the ∼6 ps trajectory of Z-Ala6–COOH at 450 K. Once polymorphism has been applied over these 23 H-bonded cycles, some of the cycles could be merged, thus resulting into nine polymorphic cycles. Each polycycle contains between one and nine possible identities. The obtained global polygraph that represents the whole 6 ps trajectory is shown in Figure 10, built over the nine vertices that represent the nine identified polymorphic H-bonded cycles. One can therefore see that five of the vertices/polycyles have only one possible identity in terms of the H-bonded cycle (note that the H-bonded cycle for the polycyle P-N1,O8,N2 is built upon two hydrogen bonds, i.e., N1⋯ O8 and N2⋯ O8), two other vertices have a limited number of isomorphic identities (two identities for the dark blue vertex P-O4,N5, three identities for the magenta vertex P-N3). Two vertices are much more polymorphic as they adopt four (cyan vertex P-O4,N5) and up to nine (orange vertex P-O8) different polymorphic identities. Furthermore, one can remark that several of these polycycles are built upon two or three H-bonds. For instance, in the orange P-O8 polycycle, the first identity “N1-O8,O4-N4” is built upon two H-bonds (N1⋯ O8 and O4⋯ N4), the first identity of the cyan polycycle P-O4,N5 is built upon three H-bonds (O2⋯ N3, N1⋯ O8, and O4⋯ N5).
The low/high number of identities within each polymorphic H-bonded cycle informs on the sections of the peptide with a low/high structure flexibility. The higher polymorphic nature of two of the polycycles in Z-Ala6–COOH corresponds to high structure flexibility in these two zones, while maintaining the same general role of the H-bonded cycle into the final 3D structure. This high flexibility was already observed in the previous section with the atomistic topological analysis of the 2D-MolGraphs. The analysis with the polymorphic H-bonded cycles immediately identifies the underlying “meta-structures” that are of interest for the comprehension of the conformational dynamics of the peptide.
In the polygraph, there is an edge between two vertices whenever two polycycles interact together, i.e., the conformations belonging to each vertex share at least one covalent bond or one H-bond. The polygraph in Figure 10 is not complete, i.e., not all the polycycles are directly connected in pairs by an edge. This incompleteness can be explained by the following two reasons that are related to the rules applied for building a polygraph: (i) either there is a conformation for which the identities of the two polycycles appear simultaneously, without interaction (the criterion for interaction/edge is the sharing of at least one covalent bond or one H-bond); or (ii) there is no conformation for which the two identities appear simultaneously, however their merging does not respect the polycycle rules. For example, we found that the blue P-O4,N5 polycycle/vertex and the orange P-O8 polycycle/vertex do not interact because there is at least one identity from P-O4,N5 and one identity from P-O8 that appear simultaneously in one conformation of Z-Ala6–COOH. As these two polycycles do not share one covalent bond/H-bond, there is thus no interaction/edge in the polygraph.
The chronogram of the Z-Ala6–COOH polycycles, presented in Figure 11, shows the evolution in time of the nine polycycles at the temperature of 450 K. The reader has to keep in mind that each polycycle can have several identities in terms of the atoms that form the H-bonded cycle (see discussion above). Five distinct periods of time can be extracted, labeled as period 1 to period 5 in the figure. Each time period is associated to a different structural organisation of the nine polycycles in Z-Ala6–COOH. During period 1, six polycyles coexist. Period 2 starts as the polycycle P-N3 disappears and polycycle P-O2,N3 appears. There is then the simultaneous disappearance of this polycycle at time ∼2.2 ps and appearance of polycycle P-N1,O8,N2 at the slightly earlier time ∼1.9 ps, which marks a clear change in the 3D structure of the peptide, and thus the end of period 2 and start of period 3. Interestingly, polycycles P-O7,N7 (green line), P-O4,N5 (dark blue) and P-O4,N5 (cyan) are formed over the whole 6 ps trajectory (or almost always, with smallish periods of time of interruption). These H-bonded polycycles thus form strong pillars for the global 3D structure. See more details in [4]. One has to remark that one of these three polycycles (P-O4,N5, darker blue) can adopt up to four different identities. This is an important pillar of the 3D structure with high flexibility.
Chronogram obtained over the 450 K AIMD trajectory of the Z-Ala6–COOH peptide. Five time periods have been identified (see text for details). The color coding of the lines is identical to the color coding of the vertices in the polygraph in Figure 10.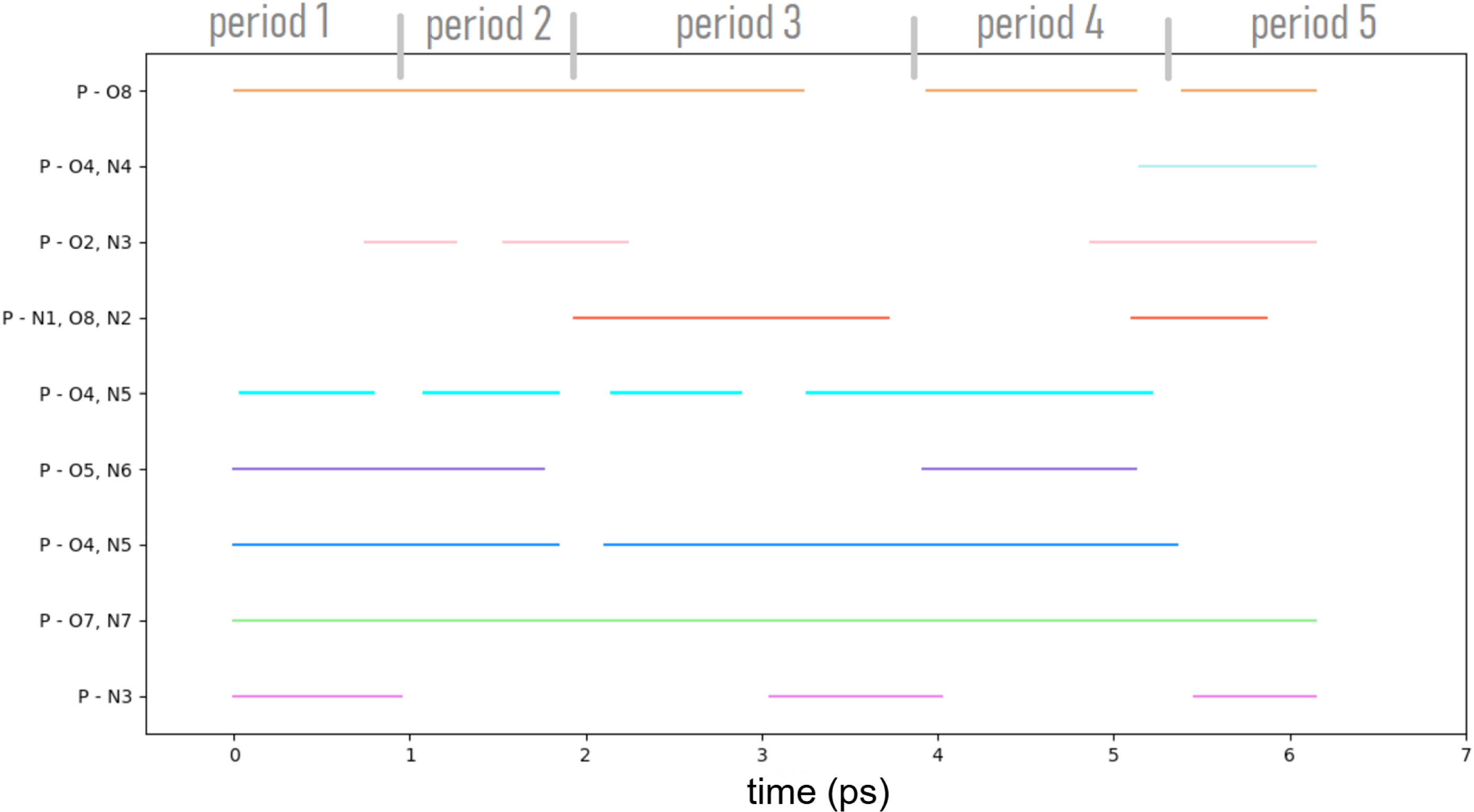
Beyond the time evolution, one further crucial information extracted from the chronogram is which polycycles can be formed simultaneously and which ones cannot be present simultaneously in the 3D conformation of the peptide. For example, it is possible to form the polycycle P-O4,N4 (light blue) at the start of period 5 only if none of the P-O4,N5 (cyan) and P-O5,N6 (purple) polycycles are present. P-O4,N4 seems to coexist only with P-O2,N3 (light pink) and P-N1,O8,N2 (dark orange). Polycycles P-O4,N4, P-O2,N3, P-N1,O8,N2, P-O5,N6, and P-N3 need hence certain structural conditions for them to be exist. This can be explained by the location of H-bonded polycyle P-O4,N4 in regard to polycycles P-O4,N5 (both of them) and P-O5,N6 within the 3D structure of Z-Ala6–COOH.
The polygraph made of nine vertices and their pairwise connected edges in Figure 10 gives the global/statistical view of the whole 6 ps trajectory in terms of a “global metastructure” of the peptide. However, the actual details of the dynamics are lacking in this global polygraph. This could be inferred from the chronogram in Figure 11 where we already saw that not all the polycycles/vertices of the global polygraph could coexist simultaneously over time.
Figure 12 now presents one illustration of the evolution with time of the sub-polygraphs from the global polygraph over a short time period, i.e., between times 2.19 ps and 2.51 ps (period 2 and period 3 in Figure 11). The sequence of sub-polygraphs is reported with the following conventions of colors: the polycycles that are present among the nine possible polycycles are colored in green while the ones that are absent are colored in dark gray. The arrows between the sub-polygraphs can be colored in black, in blue, or in red. The two arrows in red mark the sequence of starting time of the period under scrutiny (2.19 ps) and ending time (2.51 ps), respectively. The arrow in black marks “simple transitions” between sub-polygraphs/3D-structures/conformations of Z-Ala6–COOH. These arrows can be found forward (→) and backward (←), as there are multiple forward/backward isomerisations over time. Marking each one of these transitions over the “real time” would be too messy and would make the plot too cumbersome. The blue arrow marks a distinct transition in the sequence of sub-polygraphs, i.e., in the time sequence of the 3D conformations adopted by the peptide over this period of time. There is indeed no transition observed back to structures adopted previously (in time). Therefore, we marked the whole chart by two distinct rectangles, one outlined with red dots (top of the figure) and one with gray dots (bottom). In the gray rectangle, one can now see the sequence between the sub-polygraphs by following the dark arrows, some of them going in one direction only, others with back/forth directions. Some of the key moments in time are indicated in blue over certain dark arrows.
Sequence in time of the sub-polygraphs of the H-bonded polycycles of Z-Ala6–COOH. See text for all details and comments of this chart.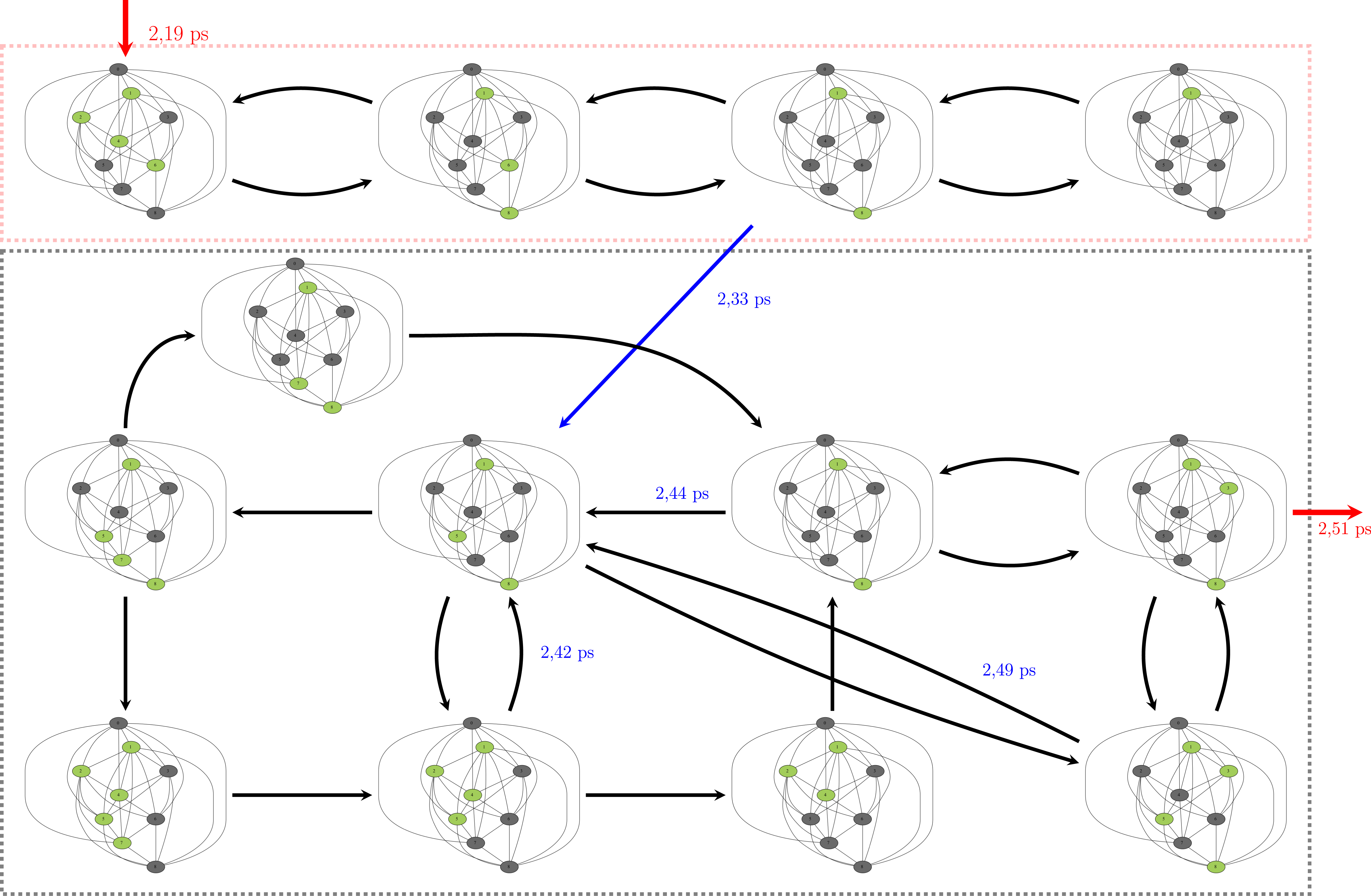
The conformation dynamics seen in this figure over a very short period of time nicely illustrates the complex dynamics in the H-bonds of Z-Ala6–COOH at 450 K, and the high flexibility of the peptide that we have already discussed several times above. Figure 12 also nicely shows the fast exchange between polycycles.
3.2. Topological 2D-MolGraphs easily capture complex condensed phase H-bonded networks
Condensed phase, where liquid water is present, is another area where the 2D-topological graphs can be of great help in understanding H-bond networks. Here we present the use of the atomistic 2D-MolGraphs in order to unravel the structure of water in inhomogeneous molecular systems made of an interface between liquid water and another medium. We specifically focus on three hydrophobic aqueous interfaces, i.e., air/liquid water, graphene/liquid water, and boron nitride BN/liquid water, for which we want to characterize the organization of liquid water at the interface with air or the solid. To that end, our methodology of atomistic topological 2D-MolGraphs is applied on AIMD trajectories of these three aqueous interfaces (∼50 ps time-length MD). These three interfaces have been shown to be hydrophobic by independent molecular analyses in [36] based on a molecular descriptor of hydrophobicity developed in this latter paper and in the follow-up paper [37].
We have previously shown in [38, 10, 36] that liquid water in contact with hydrophobic surfaces forms a two-dimensional (2D) highly collective H-bonded network made by the water molecules in the layer in direct contact with the hydrophobic surface (i.e., water located in the BIL–Binding Interfacial Layer– as defined in [39, 36]), in which the water–water H-bonds are formed parallel to the surface. This water-collective 2D-Hbonded-Network is the molecular signature of surface hydrophobicity [36, 37].
Here, we illustrate the recognition of this 2D-HBonded-Network using topological 2D-MolGraphs, and how these graphs can provide details on the organization of water molecules in this collective H-bond network. Three DFT-MD trajectories have been analyzed using our graph theory algorithm: air/liquid water as the prototype of hydrophobic surfaces, graphene/liquid water, and BN/liquid water. For each trajectory, 400 snapshots were extracted and analyzed (from a total of 50 ps trajectory per system). This corresponds to roughly one snapshot every 0.1 ps of dynamics, which represents a good statistical sampling regarding the dynamics of H-bonds. The graph analyses are carried out on the BIL-interfacial region only, in which there is roughly an average of 48 water molecules (all simulation boxes are roughly equivalent in sizes).
The 2D-MolGraphs in Figure 13 show the very specific structural property of the water molecules in the BIL of the hydrophobic interfaces: a collective arrangement of the water molecules in terms of H-bonded polygons (or rings) adjacent to each others. This collective arrangement is called the 2D-HBonded-Network [38, 10, 36].
Illustration of one 2D-MolGraph per hydrophobic aqueous interface: air/liquid water (left), graphene/liquid water (middle), BN/liquid water (right). Only the water molecules located in the BIL [39, 36] are taken into account for the 2D-MolGraph analysis. Vertices of the graph represent the oxygen atoms of the water molecules (red); the dashed red arcs represent the H-bonds between two water molecules oriented from donor to acceptor.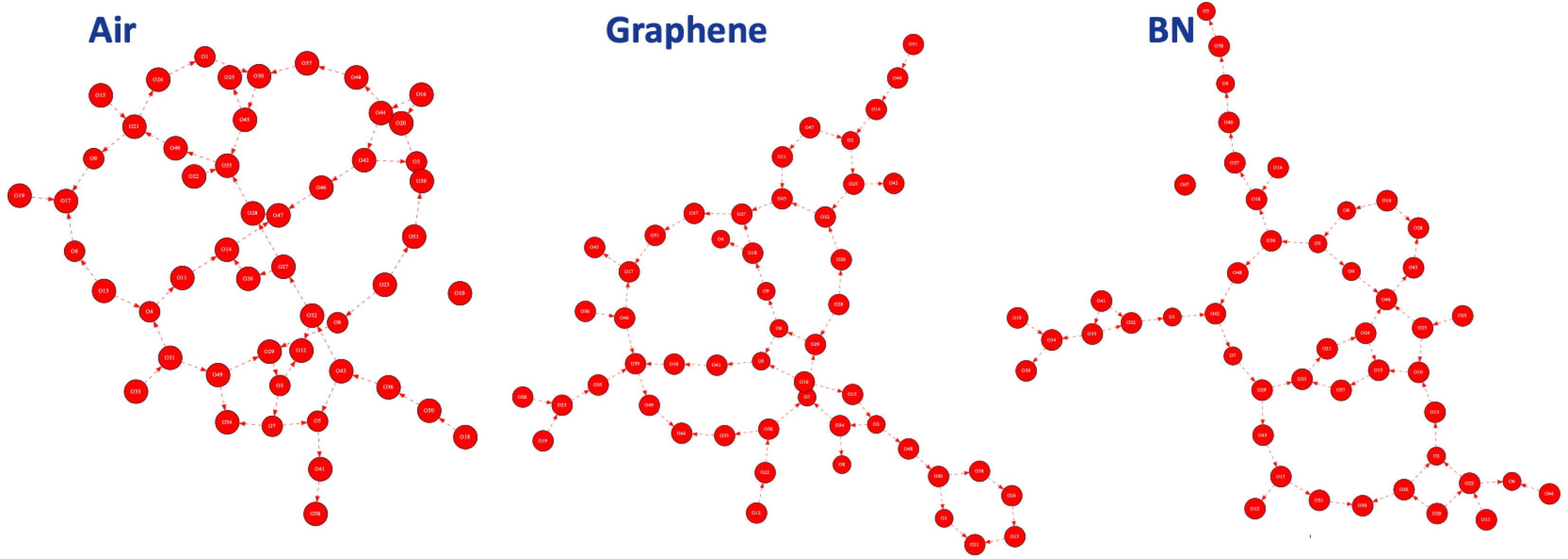
To obtain the statistical view on the number of water molecules that are interconnected within the 2D-HBonded-Network, the (identified non-isomorphic) 2D-MolGraphs can be analyzed in terms of the size of the connected components, i.e., the set of subgraphs in which all vertices are connected to each others without interruption. Figure 14 illustrates the distribution of the connected components for the 400 2D-MolGraphs extracted for each trajectory of the three interfaces.
Distribution of the connected components of the 2D-MolGraphs (see text for details) for the air/liquid water interface (left), the graphene/liquid water (middle), and the BN/liquid water (right), obtained over ∼50 ps AIMD trajectories.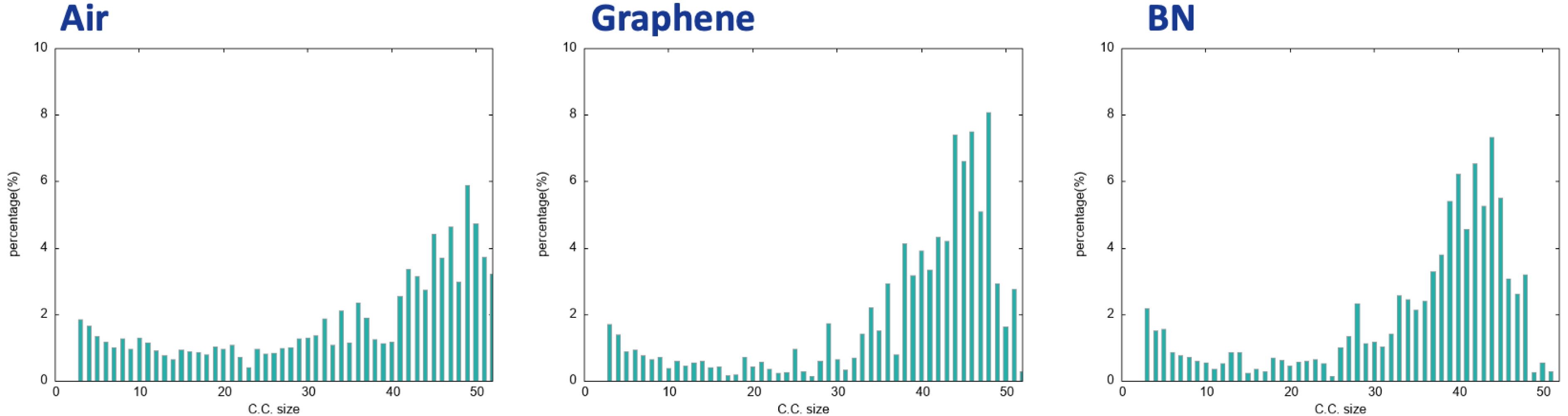
One can immediately see that the 2D-HBonded-Network is extended over ∼90–95% of the water molecules located in the BIL for the three interfaces, hence with a high degree of interconnectivity (very collective network between the water molecules). One can thus conclude that the water molecules in the BIL are statistically organized with the same collective HB-Network in all these hydrophobic interfaces.
The 2D-MolGraphs provide further details on the organization of water molecules in this collective H-bonded network. One can see from the 2D-MolGraphs shown in Figure 13 that water molecules are organized in polygons/rings formed by H-bonds. Using the Horton algorithm [40], we analyzed the 2D-MolGraphs in terms of the size of H-bonded polygons/rings formed by the water molecules in the BIL for the three hydrophobic interfaces. The results are presented in Figure 15.
Distribution of the size of H-bonded rings/cycles formed by the water molecules in the 2D-MolGraphs. (left): air/water interface; (middle): graphene/water interface; (right): BN/water interface.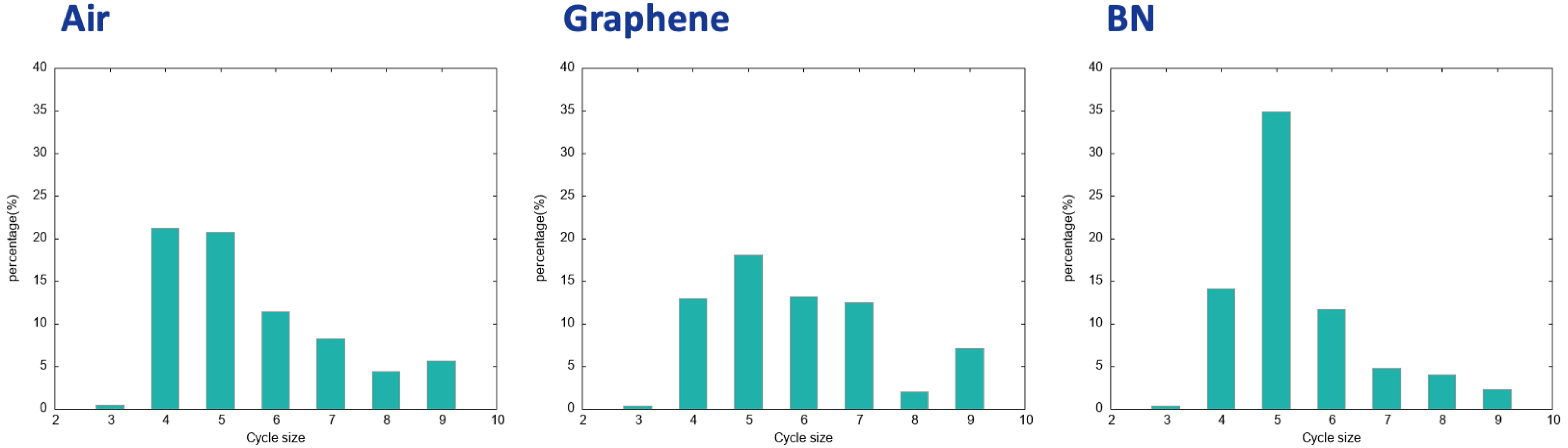
Very interestingly, though the water molecules in the three investigated BILs are assembled with the same collective 2D-Hbonded-Network, the distribution of sizes of the H-bonded polygons that build these networks are non-identical between the three hydrophobic interfaces. On the one hand, the sizes of the H-bonded polygons are centered on four to six for the air/water and BN/water interfaces. There is a clear dominant component related to H-bonded pentagons made by the water molecules at the interface with the BN surface while the formation of H-bonded tetragons and pentagons is found equivalent at the interface with air. On the other hand, the 2D-Hbonded-Network made by the water molecules at the surface of graphene is more homogeneous in terms of sizes of the polygons, where tetragons, hexagons, and heptagons have roughly the same probability of appearance, and H-bonded pentagons dominate slightly more. We hence see that water molecules predominantly form five-membered H-bonded rings/polygons at the interface with the BN surface, which can be associated to the hexagonal-templated structure of BN. The length of the C–C covalent bonds in BN is shorter than the O⋯ H hydrogen bonds: the best arrangement for water molecules is thus into five-membered H-bonded rings rather than six-membered rings.
Moreover, we find that the percentage of water molecules giving rise to the polygons within the 2D-HBonded-Network is around 30–40% for the three interfaces, with the following interesting ranking: one finds a larger percentage of water in the 2D polygons for the air/water interface (∼43%) than for the graphene/water interface (∼36%) interface, and the BN/water interface (∼34%). Such percentages might explain the strength of the 2D-HBonded-Network found at each interface. The work in [36] indeed showed that the strength of the 2D-HBonded-Network can be ranked as air > graphene > BN. In other words, the more water molecules forming rings within the 2D-Hbonded-Network (i.e., the more rings being formed), the stronger the 2D-HBonded-Network, and the more hydrophobic the interface.
3.3. Integration of 2D-MolGraphs in workflows in high-throughput in silico chemical reactivity
We further explored the utility of our 2D-MolGraph approach as the core for automated reaction network analysis workflows suitable for implementation in high-throughput in silico reactivity screening of complex multicomponent homogeneous catalytic systems [41]. We implemented the 2D-MolGraph approach in the computational catalytic reaction space exploration method ReNeGate [5] (see the workflow in Figure 16) and in the high-throughput reactivity screening HiREX workflow [11] specifically designed to explore realistic catalytic systems and identify thermodynamically feasible chemical transformations, corresponding to secondary catalyst deactivation and inhibition paths.
Schematic representation of the ReNeGate workflow from [5] involving the sequential reactive space exploration, the structure analysis using the 2D-MolGraphs in the fingerprinting and network construction parts, with the reaction network generation and refinement steps (trimming).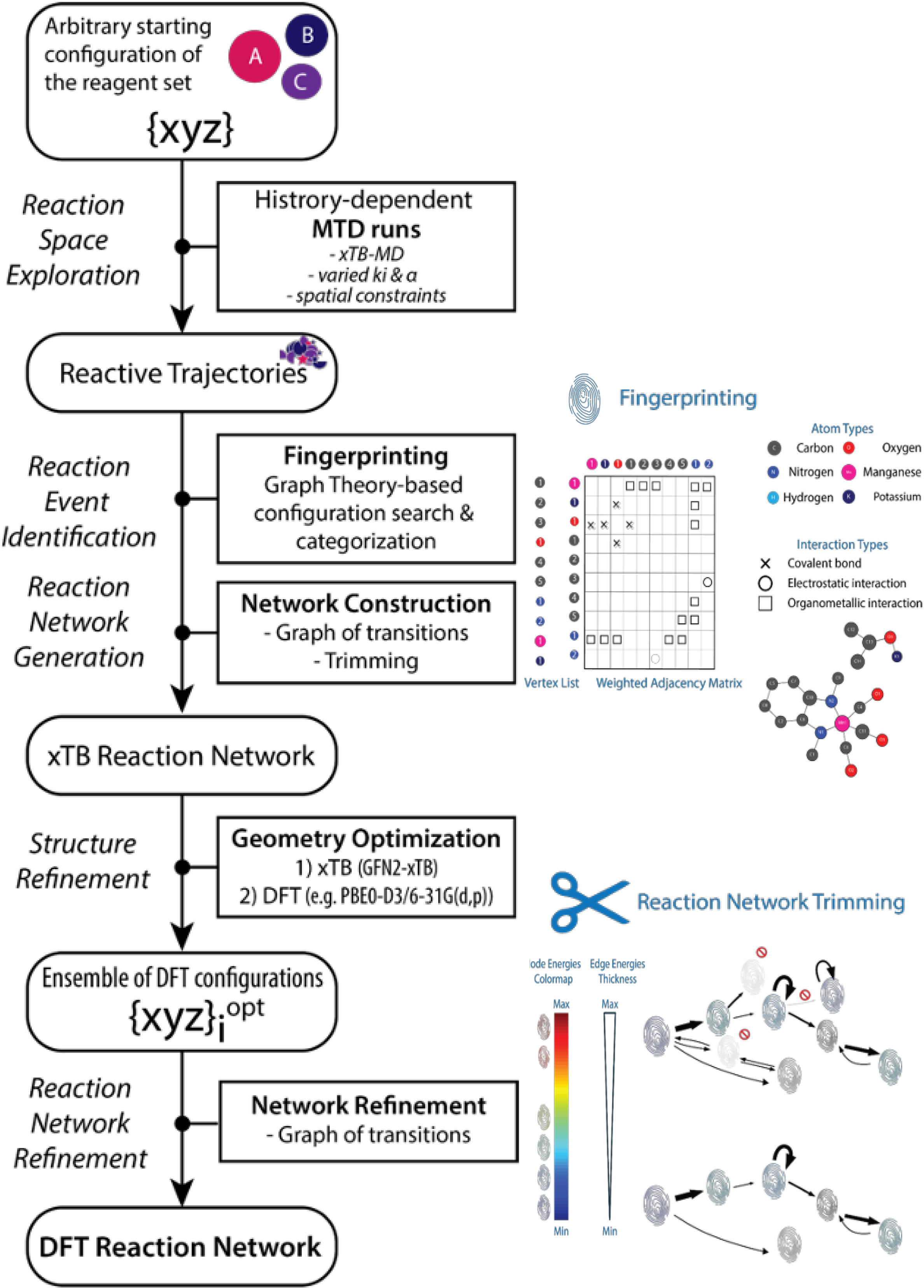
The method was validated by case studies on representative multicomponent (de)hydrogenation catalytic systems based on Mn(I) coordination complexes with a special focus on probing unconventional and less expected reaction channels, which could be responsible for loss of catalytically potent species during the initial pre-catalyst activation. An illustrative example is our computational analysis of the activation of manganese pentacarbonyl bromide (Mn(CO)5Br) with inorganic alkoxide base KOiPr that is a common protocol for the experimental screening and in situ generation of Mn-based homogeneous catalysts [42]. The reactivity exploration was carried out with parallel metadynamics simulations on a minimal model constituted by the two main reagents only (Figure 17a) using the CREST functionality (metaD/CREST) at the GFN2-xTB level [43]. The reactive trajectories were populated using the root-mean-square-deviation (RMSD) in Cartesian space as a metric for the collective variables [43], while the pushing and pulling strengths (k and 𝛼) were systematically varied over the parallel simulations.
(a) Metadynamics simulations of the reaction between Mn(CO)5Br and KOiPr yield reactive trajectories, from which (b) a reaction network has been constructed with the respective three representative 2D-MolGraphs presented in (c). Colors for the 2D-MolGraph vertices: dark gray for carbons, red for oxygens, dark blue for postassium, pink for the manganese, and green for the bromide. Solid black edges in the graphs represent covalent bonds, the red dashed edges represent the organometallic interactions.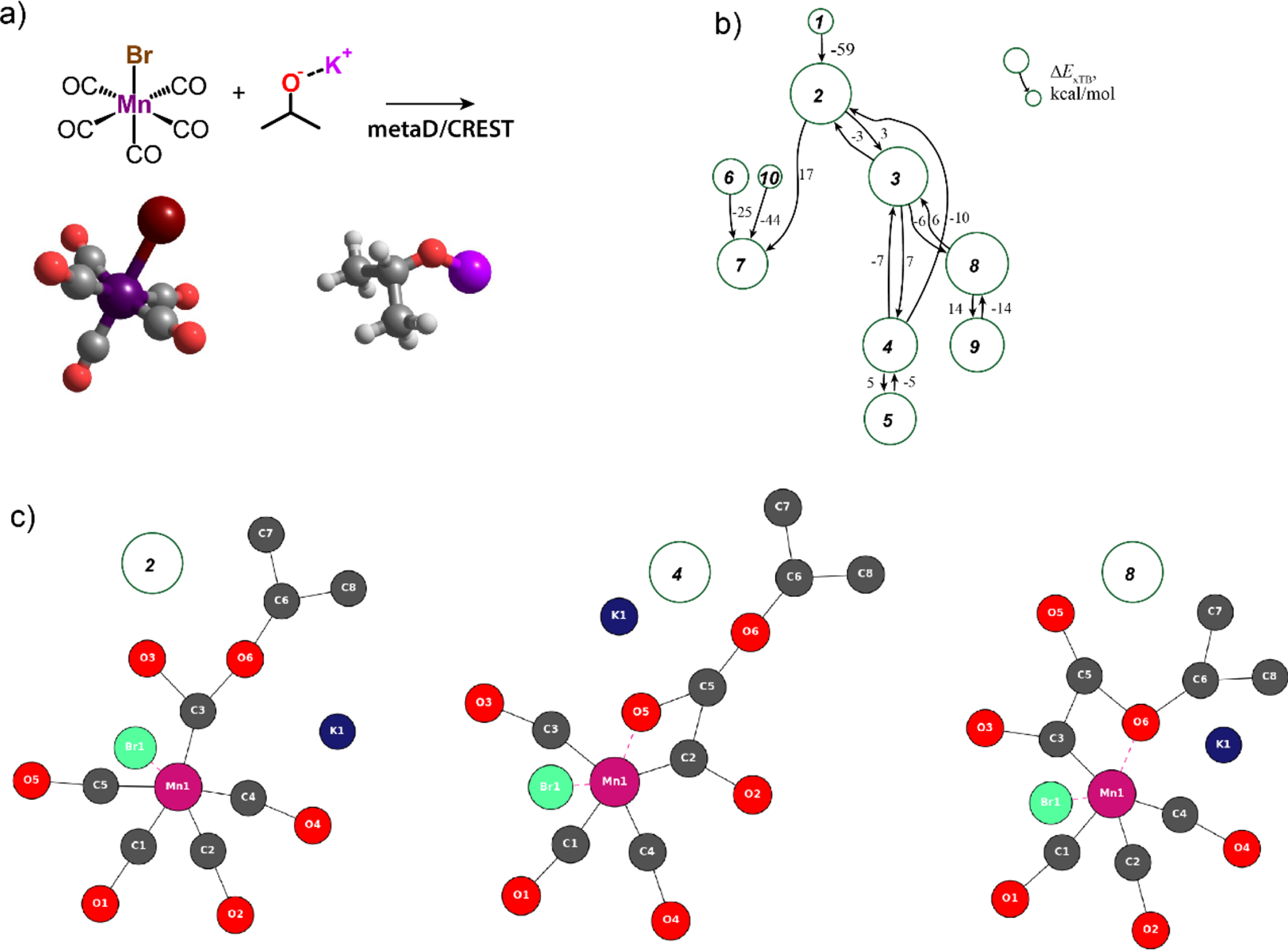
The analysis of the reactive trajectories with the 2D-MolGraphs yielded a reaction network containing 12 conformers, which after trimming the edges exceeding an arbitrary threshold of 25 kcal/mol, produced the reaction network shown in Figure 17b. State (1) corresponds to the starting configuration with unreacted Mn(CO)5Br and KOiPr, which can transform to one of the new species identified by the 2D-MolGraphs from the reactive trajectories (Figure 17c).
Our automated procedure revealed that all reaction paths involve the reaction of the alkoxide nucleophile with the Mn(I)-bound carbonyl ligand to form a Mn–acyl complex (2). Due to its approximate nature, the GFN2-xTB method incorrectly predicts further migratory insertion of CO with the –C(O)OiPr species yielding species (4) and (8) to be also thermodynamically favorable. Subsequent energy refinement at the DFT level restores the agreement with the experimental observations. Similar reaction paths were identified for more complex catalytic model containing the molecularly defined Mn(I)-catalyst stabilized by a bidentate diamino ligand, the alkoxide base, two isopropanol solvent molecules and acetophenone as a model substrate. Simulations suggested that the nucleophilic attack of the alkoxide anion by the Mn-bound carbonyl ligand may initiate reaction paths resulting in a (partial) decoordination of the organic ligand, which can be considered the onset of catalyst deactivation [5].
These computational insights have inspired the experimental finding on the stabilizing role of Lewis acid additives mediating the nucleophilicity of the alkoxide base allowing to considerably extend the lifetime of the homogeneous Mn(I) catalysts [44] and the discovery of new Mn-mediated C–C coupling chemistry [45].
The application of our reaction network analysis approach was further extended towards high-throughput computational reactivity exploration and automation identification of the classes of reactivity patterns within specific catalyst groups (Figure 18a) [11]. We have applied this workflow to a virtual library containing 576 Mn-pincer complexes corresponding to four distinct pincer families with varied functionalization of the ligand backbone (R1 and R2 functionalities) and Mn coordination (X) (Figure 18b). The 2D-MolGraphs were used to analyze the reactive trajectories, as well as to featurize and label the discovered new configurations and intermediates following the changes in the interaction patterns observed during the transformations. K-mode clustering analysis on the resulting labeled database (Figure 18b) has provided new insights into the reactivity of Mn(I) pincers and how it is affected by the structural modification of the ligand backbone.
(a) A perspective workflow for the chemical space exploration and automated reactivity analysis of virtual catalyst libraries involving 2D-MolGraphs as the core component of the dynamic trajectory analysis and structure featurization. The method was used for (b) the reactivity screening of a virtual library of 576 Mn(I) pincer complexes followed by K-mode clustering analysis of the resulting data. The figure presents top 10 clusters showing the most frequent types of interaction changes as a function of different functionalization at R1 site for each pincer class. The color coding is given at the bottom of the figure.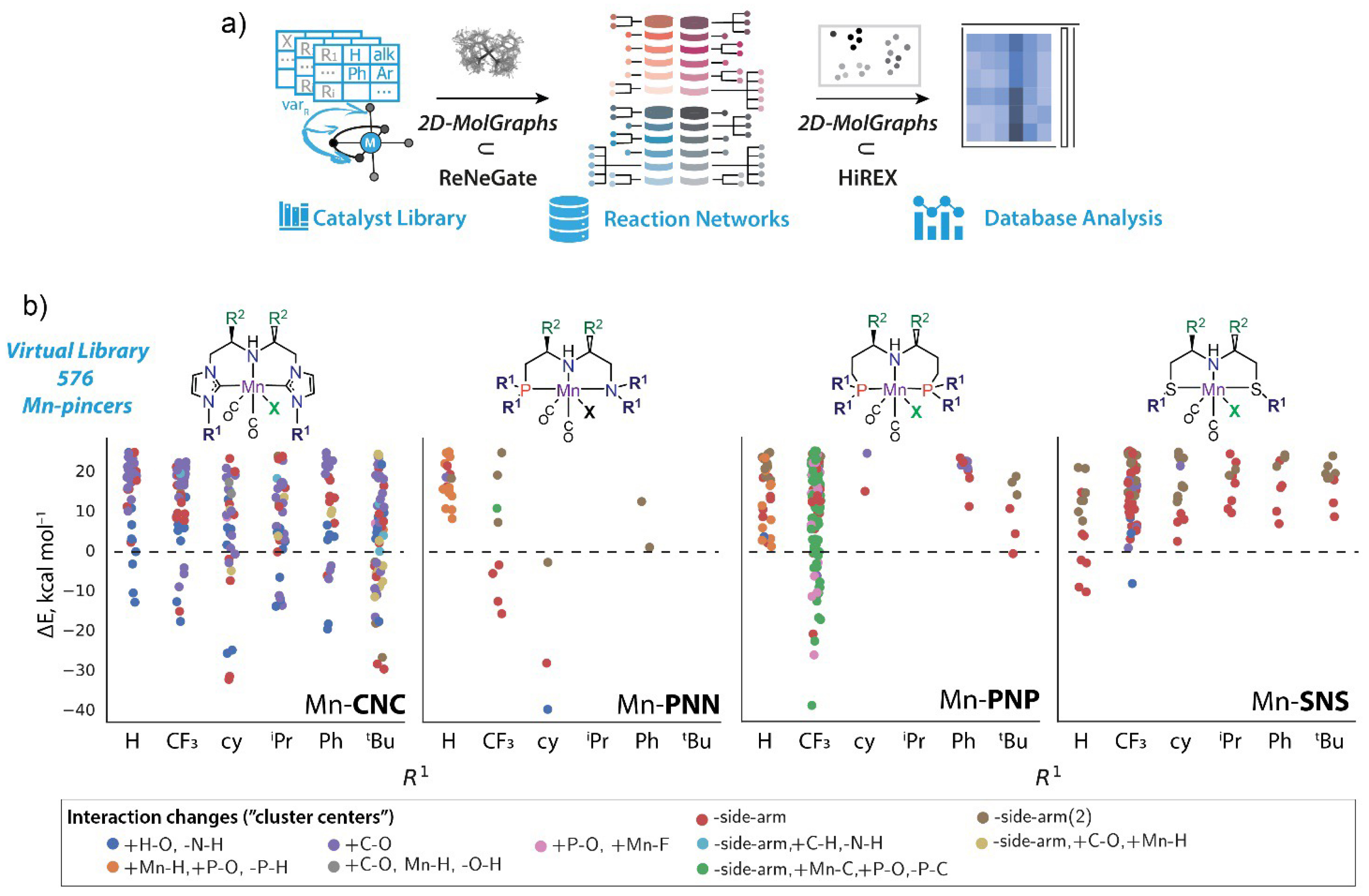
Specifically, the calculations indeed revealed multiple paths involving the nucleophilic attack on the carbonyl ligand and decoordination of the pincer ligand. Depending on the ligand’s nature and structure, the thermodynamic favorability of such secondary conversion paths varies greatly providing thus an opportunity to tune the stability and reactivity of the transition metal catalyst, and guide the exploration of new chemical conversion paths.
4. Prospects and new developments in progress
With this review, we believe that the topological 2D-MolGraphs and associated graph algorithms have been shown to be powerful tools for analyzing atomistic molecular dynamics trajectories and extracting the actual conformations sampled over time. Demonstrations were carried out on gas phase flexible molecules and inhomogeneous aqueous interfaces in the condensed phase. We have also shown the relevance of different levels of granularity to be used in the topological graphs. In particular, the coarse-grained approach of graphs of polymorphic H-bonded cycles was shown decisive in order to rationalize the dynamics of a flexible hexapeptide. The “metastructures” over which the dynamics of this peptide is built could be found only at this level of topology representation.
We have also shown that the 2D-MolGraph approach can be easily coupled to global workflows that include several theoretical methods to sample conformational and reactive chemical spaces. The topological graphs were inserted in high-throughput in silico chemical reactive workflows in homogeneous catalysis. The conformational fingerprinting provided by the 2D-MolGraphs was decisive in several steps of these workflows. The outcome of these reactive workflows would not have been as easy and successful without the topological graphs. These works continue.
Ongoing works and developments also include for instance the use of the 2D-MolGraphs to extract the knowledge of structural motifs at aqueous interfaces. For instance, it is of utmost importance to reveal the motifs formed between the sites at the surface of a solid (for instance silica oxide as in [46, 47]) and the water molecules located at the interface with the solid in the Binding Interfacial Layer (BIL). These motifs are not only responsible for the spectroscopic signatures recorded at aqueous interfaces, typically by SFG (Sum Frequency Generation) spectroscopies, they are also involved in the chemical reactivity of these aqueous interfaces. Motifs and their vibrational fingerprints have already been discussed in [47] for aqueous silica interfaces. We are developing algorithms that can automatically recognize and classify these motifs from the 2D-MolGraphs, for instance in terms of the sizes of the H-bonded cycles formed between surface sites and water molecules and in terms of their statistical distribution in space within the BIL. The same algorithms will also be applied to the water molecules in the BIL of biomolecules. This is also ongoing work, using the atomistic 2D-MolGraphs and the coarse-grained polygraphs of H-bonded cycles.
Naturally, databases of 2D-MolGraphs and coarse-grained polygraphs can be built up and connected to AI (Artifical Intelligence) and machine learning techniques. This is where our next step will take us.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.




 CC-BY 4.0
CC-BY 4.0