1. Introduction
Indole derivatives are prominently and extensively distributed in diverse ecosystems within the natural environment [1, 2, 3]. They play a pivotal role in numerous biological and clinical applications. These versatile compounds exhibit a spectrum of activities, including antiviral [4], anti-inflammatory, and analgesic properties [5]; anticancer potential [6, 7, 8, 9, 10]; anti-HIV activity [11, 12, 13]; antioxidant effects [14]; antimicrobial attributes [15, 16, 17, 18]; antitubercular functions [19]; and anticholinesterase capabilities [20, 21]. Additionally, they demonstrate noteworthy antimalarial activity [22, 23].
In the pursuit of designing innovative organic compounds featuring atropisomers, a strategic approach involves, among others, the synergistic coupling of indole moieties with phthalonitrile derivatives [24, 25, 26, 27]. This method not only increases the structural diversity of the resultant compounds but also holds significant promise for expanding the repertoire of bioactive molecules [28].
The impact of chirality on a drug’s biological activity is exemplified by the significant complications arising from enantiomers in racemic mixtures. A classic illustration of this phenomenon is thalidomide. Consequently, atropisomerism manifests when a rotational barrier takes place due to steric hindrance, leading to the separation of individual conformers when axial chirality is established [29, 30]. Atropisomerism emerges in various molecular frameworks in drug discovery, encompassing biaryls, diaryl ethers, and other structural motifs [31]. This emphasizes the relevance of considering atropisomerism in the design and development of pharmaceutical compounds with enhanced biological efficacy and reduced complications associated with stereochemistry. According to LaPlante et al., atropisomers are classified into three categories based on the amount of energy required for their racemization by rotation of the chiral axis [32, 33]. Class 1 atropisomers have barriers of rotation, around the chiral axis, of <20 kcal/mol and racemize in a minute or faster; class 2 atropisomers have a barrier to rotation between 20 and 28 kcal/mol and racemize in 1 h to a month; and class 3 atropisomers possess a barrier to rotation >28 kcal/mol and racemize in 1 year or greater.
An intriguing observation emerges concerning atropisomerism in small-molecule drugs, where the prevalence is notably dominated by unstable class 1 atropisomers. Despite these molecules possessing distinct biological functions and exhibiting atroposelective binding to proteins, they are frequently categorized as achiral [33, 34].
In fact, rapidly interconverting atropisomers or class 1 atropisomers interact with their biological receptors in configurations that are biologically irrelevant, which can cause side effects [35, 36]. Interconverting atropisomers are shown to bind their respective targets atroposelectively [37, 38, 39]. Therefore, atropisomers should be taken into account when designing new medicinal drugs.
In a previous work [24], we have synthesized an atropisomeric phthalonitrile-3-yl (PN3) substituted indole derivative with a N–C chiral axis. A dihedral angle of 42.17(8)′′ exists between the indole and the phthalonitrile due to steric repulsion. Theoretical studies revealed that the rotational barrier of PN3 was 8.82 kcal⋅mol−1 at room temperature (RT) and, according to LaPlante et al. [34], PN3 is classified as a class 1 atropisomer.
In this study, we report the synthesis of a new indole derivative, 3-(2-methyl-1H-indol-3-yl)-6-nitrophthalonitrile (1). Compound 1 was synthesized, and theoretical calculations were performed to investigate the structure of the transition state of 1 and its activation energy as well as its rotational transition states. Additionally, highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) analyses were conducted. Compound 1 exhibits axial chirality. It was structurally characterized and has been studied theoretically and spectroscopically.
2. Results and discussion
2.1. Synthesis and characterization of compound 1
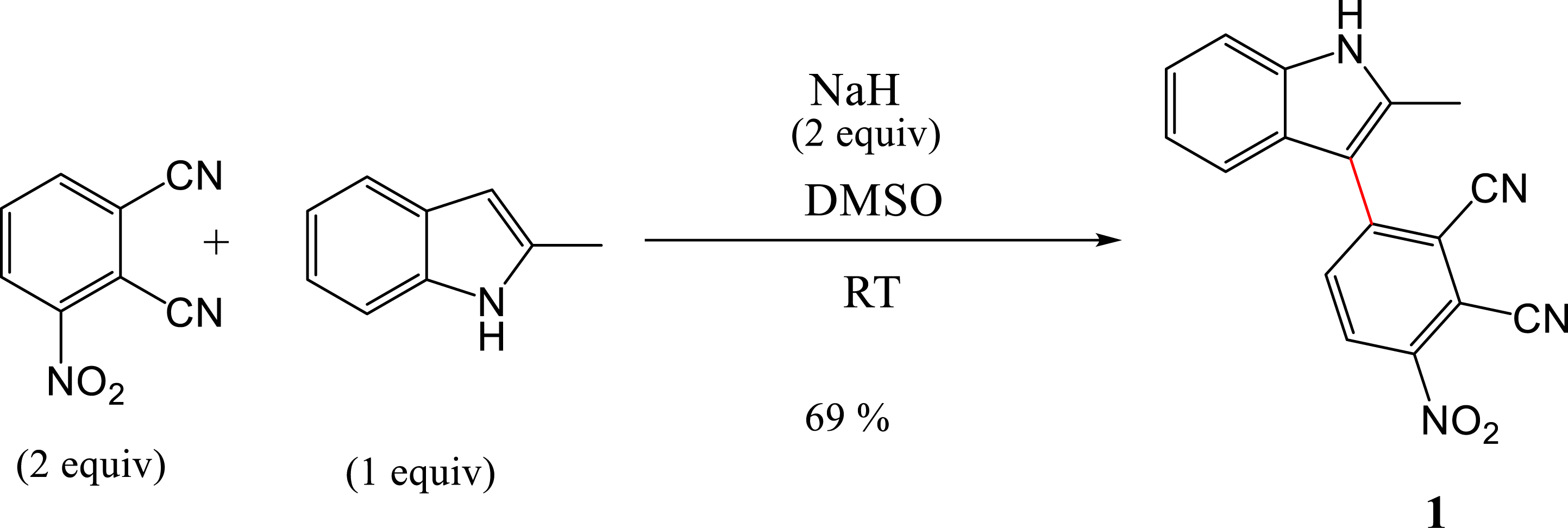
A transition-metal-free nucleophilic attack to form a C–C bond between phthalonitrile-3-yl (PN3) and 2-methylindole in the presence of NaH as the base, in DMSO at room temperature, was achieved. The α- and β-position are suitable for C–N and C–C cross-coupling, but the presence of the methyl group in the α-position makes the β-position favorable for the C–C coupling. No reaction occurred when using K2CO3 as the base and DMF as the solvent. To achieve the coupling reaction, NaH was used as the base and DMSO as the solvent at RT. The reaction provided compound 1 in 69% yield. The mechanism of the coupling reaction is presented in Scheme 1.
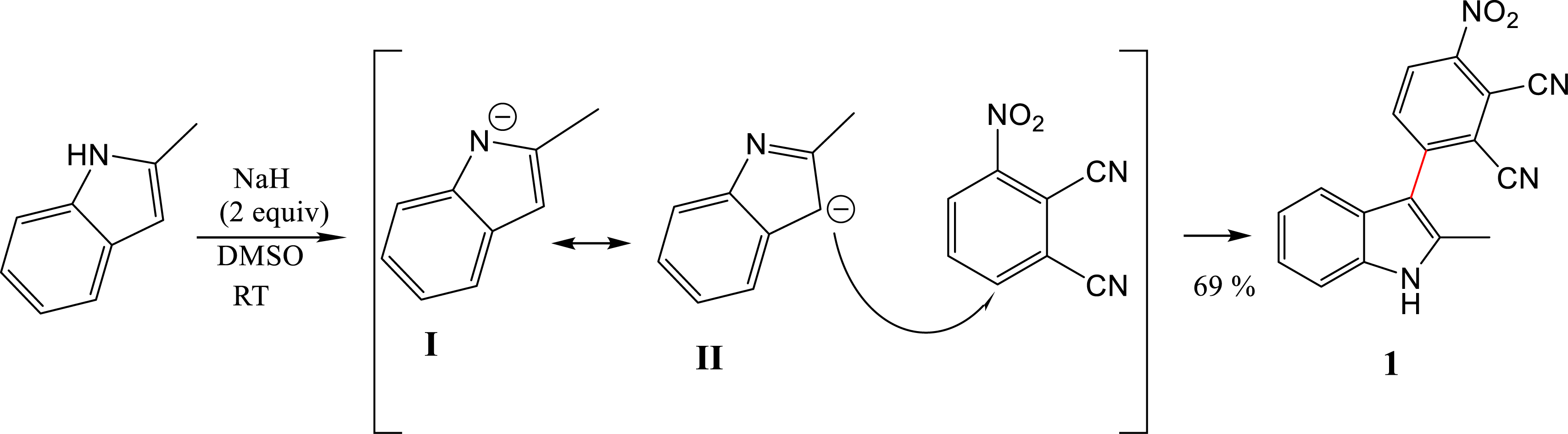
Mechanism for coupling reaction of 3-nitrophthalonitrile with 2-methylindole.
The electron-withdrawing nitro group orients the addition to the ortho position. This molecule presents three mesomeric forms, with form IV being the most stable and least sterically congested. For this reason, 2-methylindole in its form II preferentially adds to the nitro group (Scheme 2).
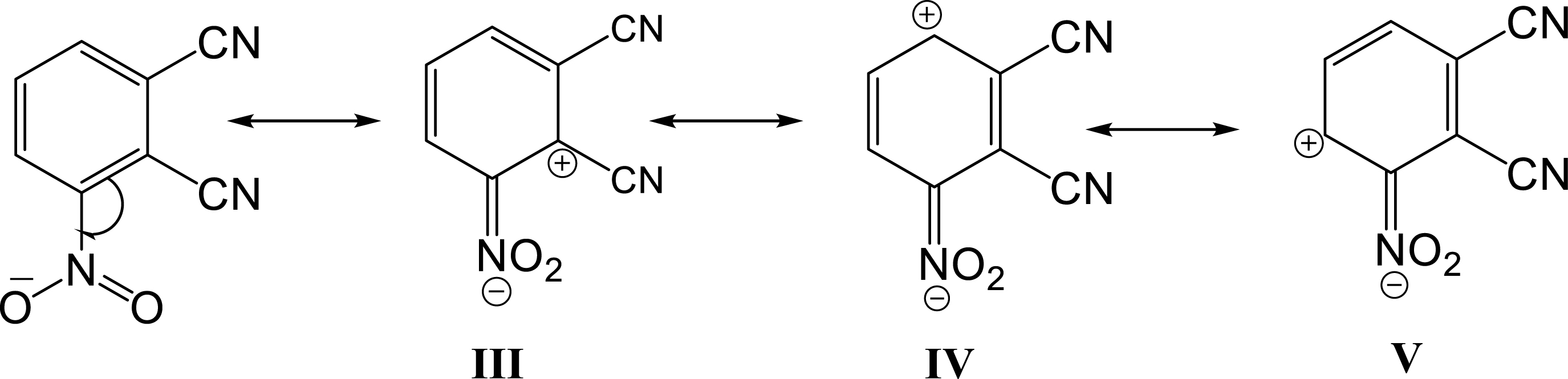
Mesomeric forms of 3-nitrophthalonitrile.
The protonation of indole occurs at C3 rather than N1. The deprotonation of the indole moiety starts when the N–H group reacts with NaH leading to 2-methylindol-1-ide I, which was converted to 2-methylindol-3-ide II via resonance (Scheme 1). The nucleophilic attack of II on 6-nitrophthalonitrile would lead to compound 1 [40]. Nuclear magnetic resonance (NMR, 1H and 13C) and mass spectroscopy spectra analysis were used to confirm the structure of target compound 1. As shown in the Supporting Information, the analyses were consistent with the predicted structures (SI, Figure 1–3).
2.2. Transition state energy
As shown in Figure 1A, K2CO3 is used as a weak base while in Figure 1B, NaH is used as a strong base to remove the proton from the N–H group of the indole moiety.
The geometries of the transition states of the studied reaction with different bases.
The activation energy, Ea, of 3-nitrophthalonitrile and 2-methylindole was studied to understand the factors that control their reactivity. Deprotonation of the nitrogen atom of the indole moiety reduces the activation energy, facilitating the coupling of 2-methylindole with 3-nitrophthalonitrile via the C–C bond. The structure of the transition state was determined by the Beckes three parameter hybrid B3 and the nonlocal correlation of the Lee–Yang–Parr (B3LYP) method, DFT/B3LYP/6-311+G(d,p). The location of the transition states was confirmed by the presence of only one imaginary frequency in the Hessian matrix. All calculations were performed with Gaussian 09 programs [41]. A comparison of the activation energies was carried out to assess the influence of deprotonation on the indole moieties. The geometries of the transition states corresponding to reaction 1 using DFT/B3LYP 6-311+G(d,p) [42] are shown in Figure 1.
The calculation of the transition states and their activation energies are shown in Table 1 with the maximum barrier. It is worth mentioning that the lower transition state energy is the stable state and promotes the coupling reaction.
Transition state and activation energies (kcal⋅mol−1)
| React1 | TS1B | Product1B | React2 | TS2B | Product2B | |
|---|---|---|---|---|---|---|
| △E | 0.00 | 36.23 | 1.55 | 0.00 | 10.03 | −1.43 |
| △E+Zero-Point Energy (ZPE) | 0.00 | 36.29 | 1.34 | 0.00 | 10.21 | 0.37 |
| △H | 0.00 | 35.13 | 1.57 | 0.00 | 9.31 | −0.60 |
| △G | 0.00 | 43.16 | 3.54 | 0.00 | 13.64 | 4.10 |
The geometries of the reagents, products, and transition states have been optimized. The intrinsic reaction coordinate computations were performed in order to verify the geometry of the transition states. The calculations were carried out without and with the removal of the proton, that is, with the use of a weak base and with the use of a strong base. As indicated in Table 1, we found that the energy barrier for the formation of product 1B is 36.23 kcal⋅mol−1 while that for the formation of product 2B is 10.03 kcal⋅mol−1.
The weak base results in relatively high energy barriers, which prevent the reaction from taking place, while a strong base leads to weak energy barriers, allowing the reaction to proceed more rapidly.
2.3. Optimized geometry parameters
To determine the configuration of the intermediate that has the minimum energy, geometry optimizations were performed. The DFT/B3LYP optimized geometry at the 6-311+G(d,p) level of 1 is shown in Figure 2. The structure of the molecule is nonplanar. In terms of energy, the global minimum is −1023.453090 (u.a) and the dipole moment is 15.282 D.
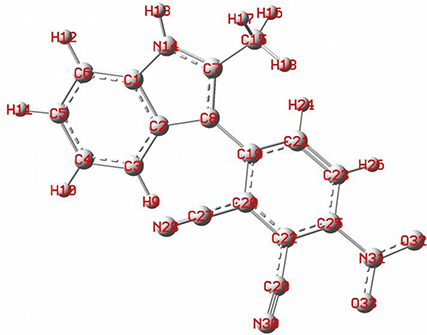
The optimized structure of 1 based on DFT B3LYP/6-311+G(d,p) basis set.
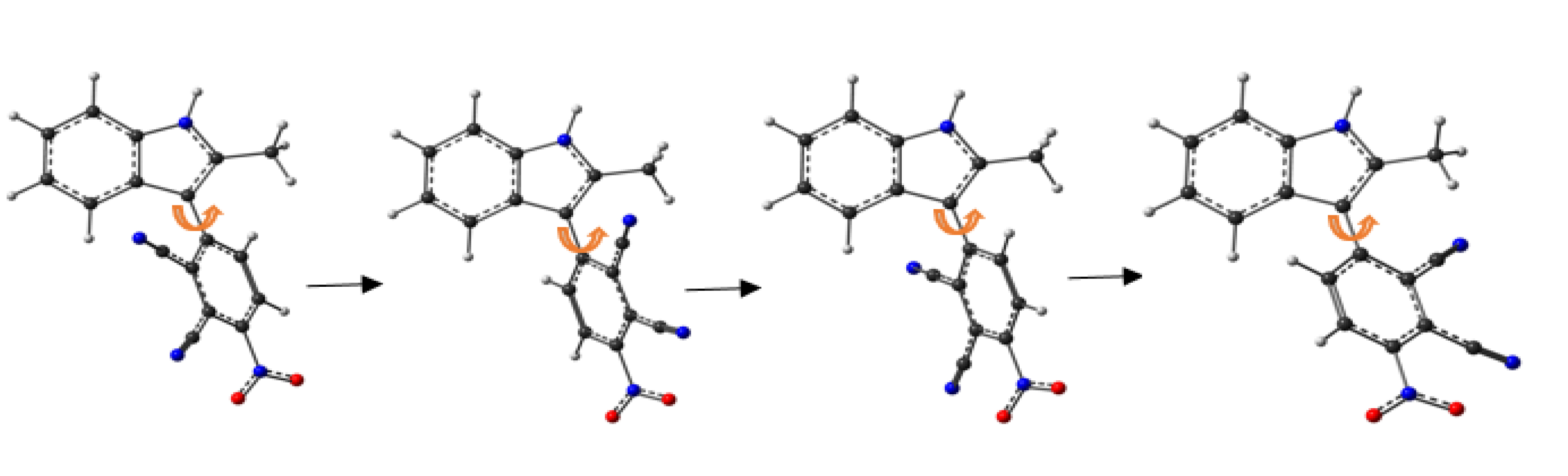
Rotation of 1 through the C–C bond axis.
Table 2 shows the bond length and the dihedral angles of compound 1. The bond length of C8–C19 was 1.460 Å and the calculated dihedral angle of C2–C8–C19–C20 was 7.68°.

HOMO and LUMO of 1.
The calculated bond length (Å) and dihedral angles (°) by B3LYP/6-311+G(d,p) of 1
| Parameters | 1 |
|---|---|
| Bond length (Å) | |
| C8–C19 | 1.460 |
| Dihedral angles (°) | |
| C3–C2–C8–C19 | 52.24 |
| C2–C8–C19–C20 | 7.68 |
2.4. Chirality analysis
In racemic 1, the molecular structure contains a chiral axis, whose isomers—an (S)-isomer and an (R)-isomer—are generated by the symmetry operation in their space groups. A theoretical study was conducted to determine the rotational transition state of the stereochemistry. A scan dihedral angle calculation was performed for C2–C8–C19–C20. Structural optimization indicated that the most stable structure has an angle of 52.24°. The eclipsed form having 𝜃 = 0° and 𝜃 = 180° should be the transition state for 1. The rotational barrier of 1 is 16 kcal⋅mol−1.
According to LaPlante et al., 1 is classified as a class 1 atropisomer that possesses a barrier of rotation around the chiral axis <20 kcal/mol and racemizes in less than 1 min or faster.
2.5. Frontier molecular orbital analysis
The energy gap between the HOMO and the LUMO can be used to calculate intramolecular charge transfer activity [40]. Molecular interactions with other species can be determined by frontier molecular orbitals (FMOs). The transition from the HOMO to the LUMO corresponds to electronic absorption. The HOMO energy represents the ionization potential (IP) while the LUMO energy is related to electron affinity (EA). The energy difference between the HOMO and LUMO orbitals is called the energy gap. Figure 4 shows the 3D plots of the HOMO and LUMO frontier orbitals computed at the B3LYP/6-311+G(d,p) level of 1. The red color represents the positive phase and the green color the negative phase. According to theory, the energy gap for 1 is 2.53 eV (Table 3).
2.6. Density of states
Theoretical HOMO, LUMO, and gap energies (in eV) for 1
| EHOMO | ELUMO | Eg |
|---|---|---|
| −6.12 | −3.59 | 2.53 |
The electronic density of states (DOS) of 1 comes from the difference of energy between the HOMO and the LUMO. An FMO energy level is related to its ionization potential and electron affinity according to the Koopmans theorem [43]. In order to evaluate the global indices of activities like IP, EA, global hardness (η), and global softness (G) of 1, theoretical calculations were made and are summarized in Table 4. The IP is the minimum amount of energy required to remove an electron from the least bound level in the gaseous phase. The IP of 1 is 6.12 eV. In the gaseous state, the EA is 3.59 eV. The hardness (η) represents the resistance of an atom to a charge transfer that was 1.27 eV. Generally, the softest material has the smallest band gap. The global softness is calculated as 0.79 eV−1. The IP, EA, η, and G are defined as follows:
The quantum chemical parameters of 1
| IP (eV) | EA (eV) | η (eV) | G (eV−1) | |
|---|---|---|---|---|
| 1 | 6.12 | 3.59 | 1.27 | 0.79 |
3. Conclusion
In this study, we have demonstrated that 2-methylindole and 3-nitrophthalonitrile can be coupled at RT using NaH as the base without utilizing a transition metal catalyst. The theoretical studies confirmed the nucleophilic attack of 2-methylindol-3-ide on the mesomeric form IV of 6-nitrophthalonitrile. This leads to the formation of a C–C bond in DMSO. This is verified by calculating the activation energies of 1 and its transition state structure as well as its rotational barrier to demonstrate the axial chirality of 1 and its corresponding atropisomerism characteristic. Calculations were made to determine the optimized geometry parameter values (bond length, bond angle, and dihedral angle). FMO and DOS analysis were also conducted, and the energy gap for 1 was determined to be 2.53 eV.
4. Experimental section
4.1. Synthesis of 3-(2-methyl-1H-indol-3-yl)-6-nitrophthalonitrile
A preliminary assay revealed that the reaction of 3-nitrophthalonitrile with 2-methyl indole using K2CO3 as the base did not result in a nucleophilic aromatic substitution—which is not the case for the second reaction with NaH as the base—but rather results in a C–C coupling reaction (Table 5 and Scheme 3).
Reaction conditions between 3-nitrophthalonitrile and 2-methylindole
| Base | Solvent | T (°C) | Time (h) | Yield (%) |
|---|---|---|---|---|
| K2CO3 | DMF | 70 | – | NR |
| NaH | DMSO | RT | 4 | 69 |
Synthesis pathway of 1.
To a solution of 2-methylindole (302.4 mg, 2.3 mmol, 1 equiv) in anhydrous DMSO (9 mL), NaH (110.4 mg, 4.58 mmol, 2 equiv) was added under a nitrogen atmosphere. The solution was stirred for 5 min. To this solution, 3-nitrophthalonitrile (800 mg, 4.62 mmol, 2 equiv) was then added. The reaction mixture was stirred at RT under a nitrogen atmosphere. After 4 h, the reaction mixture was poured into a saturated aqueous NaHCO3 solution (15 mL). The resulting mixture was extracted with ethyl acetate (3 × 20 mL). The organic layers were combined, dried over anhydrous Na2SO4, filtered, and concentrated in vacuum. The crude product was purified by column chromatography using EtOAc/hexane (20:80) as an eluent. A solid reddish color compound was obtained. Yield: 69% (480 mg). 1H NMR (500 MHz, DMSO-d6) δ: 11.85 (s, 1H), 8.65 (d, J = 8.8 Hz, 1H), 8.17 (d, J = 8.8 Hz, 1H), 7.44 (ddd, J = 8.2, 2.8, 1.8 Hz, 2H), 7.18 (ddd, J = 8.2, 7.1, 1.2 Hz, 1H), 7.11 (ddd, J = 8.0, 7.0, 1.0 Hz, 1H), 2.47 (s, 3H). 13C NMR (500 MHz, DMSO-d6) δ: 146.3, 146.0, 137.0, 136.3, 135.3, 129.1, 126.1, 121.9, 120.3, 117.7, 116.8, 115.3, 113.6, 112.5, 111.3, 108.1, 12.8. APCI MS (m/z) calculated for C17H10N4O2: 302.080; found: 302.079.
4.2. Computational details
Theoretical calculations were performed using the density functional theory method to optimize the considered structure of 1 with hybrid B3 [42], with B3LYP method [44], and the 6-311+G(d,p) basis set. Software package and GaussView 06, a molecular visualization program package, were used [45]. The HOMO–LUMO analyses were conducted to explain the charge transfer that takes place in 1. The chemical hardness and chemical potential were also calculated using the HOMO and LUMO. The structure optimization of the transition states was performed by the DFT B3LYP method using 6-311+G(d,p) as the basis. The corresponding energies were calculated at the same level with B3LYP/6-311+G(d,p).
Declaration of interests
The authors do not work for advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.





 CC-BY 4.0
CC-BY 4.0