1. Introduction
Dichlorosilane (H2SiCl2) is a highly reactive and toxic gas that is commonly used in microelectronics for fabricating semiconducting silicon layers. H2SiCl2 readily hydrolyzes and reacts with oxidizing agents [1], while it has a very strong repulsive odour and is highly flammable [2], giving off irritating/toxic fumes upon burning. At the same time, it is also a poisonous gas and thus is considered a severe health concern [3]. Inhalation of H2SiCl2 could lead to sore throat, cough, burning sensation, shortness of breath, and labored breathing. It may also cause blisters, burns, and frostbite on the skin, whereas contact with the eye may potentially cause loss of vision. As a result, highly strict measures for preventing exposure must be taken when handling H2SiCl2 [4]. In addition to these measures, we urgently need to develop sensitive cost-effective sensors for detecting and measuring the concentration of the gas at the workplace in case of accidental release in the breathing air.
A highly promising type of cost-effective gas sensor relies on the adsorption of the target gas (H2SiCl2 in our case) on nanostructured materials consisting of nanoparticle building blocks [5] and nanotubes [6]. In 1994, Rubio et al. [7] theoretically predicted the existence of stable boron nitride nanotubes (BNNT), which were later synthesized by Chopra et al. [8, 9]. BNNTs are electrically insulating but thermally conductive, and therefore can be used in heat dissipation in electronics [10]. However, their poor dispersibility hinders fabrication and thus their potential for material enhancement, subsequently excluding it from many industrial applications [10, 11]. Using solvents such as N,N-dimethylformamide (DMF), dimethylacetamide (DMAc), acetone, N-methyl-2-pyrrolidone (NMP), ethanol, and 2-propanol may improve the dispersion of BNNT nanocomposites [10, 11]. For a more detailed description of various interparticle forces such as van der Waals, magnetic and electrostatic, repulsive steric, confining or jamming, solvation, structural and depletion, capillary, convective, and friction and lubrication, acting in nanoparticle assembly such as BNNT, the authors encourage the reader to consult a review article by Min et al. [12].
Through first-principles calculations, Deka et al. [13] explored the adsorption of drug molecule isoniazid (INH) on various BNNT. They found that adsorption on (5,5) BNNT is more favorable than (10,10) BNNT. For the adsorption of tryptophane (a nonpolar amino acid), aspartic acid, and arginine (polar amino acid) on BNNTs, strong bonding energy between polar amino acids on the surface of boron nitride nanotubes have been observed [14]. Peyghan et al. [15] investigated the adsorption and electrical structure of the BNNT (6,0) imidazole complex in gaseous and soluble phases. They found that the imidazole adsorption had no significant effect on the electronic structure of BNNT. Yang [16] studied the interaction between BNNTs with biological molecules using DFT calculations. Anota et al. [17] investigated the interaction between BNNTs and metformin using DFT methods. More recently, the interaction between the uracil molecule with BNNT (n,0) has been investigated by Mirzaei et al. [18]. Along with the widespread use of boron nitride nanotube, there are also several reports of theoretical investigations on the adsorption of different molecules, such as aluminum nitride and silicon carbide, onto the surface of nanostructures [19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34].
Different methods have been used in theoretical studies to improve the effectiveness of adsorption onto nanomaterials, including metal doping [35, 36, 37], surface defect formation [38, 39, 40], transition metal decoration [41, 42], etc. Impurities introduced into the nanomaterial change the energy gap and can thus dramatically change its morphology. A recent study has shown that even the introduction of nonmetals such as oxygen can activate the surface of nanomaterials [43]. In fact, decorated nanomaterials exhibit different resistivity compared to their pure counterparts, a parameter that can be tuned to achieve high sensitivity when used in gas sensors [44]. Aluminum, gallium, and germanium are the elements that have been mostly investigated theoretically for activating the surface of nanotubes [45, 46, 47, 48]. Lin et al. [49] provide a comprehensive study on the effect of transition metal doping to sheets of BNNTs. They found that the doped nanomaterial is stable at high temperatures and explored its effect on CO oxidation. Doping of BNNT with Al atoms (BNAlNT) may significantly alter the electronic structure of the nanotubes, which can, in turn, facilitate the adsorption of gaseous molecules such as methane and hydrazine [50, 51]. Ga atom doping (BNGaNT) can also enhance the adsorption of rare gases, such as halomethanes and SF4, compared to pure BNNT [52, 53, 54].
In this paper, we investigate the intermolecular interactions between the H2SiCl2 gas molecule and pristine or BNNTs doped with Al and Ga elements. The computational details are provided in Section 2. Section 3 discusses the results of our study in four subsections: the first provides insights on the optimized bond lengths and energies of H2SiCl2 adsorbed on BNNT, BNAlNT, and BNGaNT; the second discusses the various electronic properties and Density of States (DOS) of the system; the third and fourth illustrate the nature of intermolecular interactions between the two fragments. A brief discussion on the underlying theory of the calculated electronic properties has been provided in each subsection of Section 3. Lastly, Section 4 summarizes the most important conclusions of this study.
2. Computational details
The structures of the nanotubes investigated here have been optimized using one-dimensional periodic boundary condition Kohn–Sham density functional theory [55, 56, 57, 58] (PBC-DFT) formalism. We have chosen four different functionals in this study to best estimate the accuracy of the calculations in combination with a split-valence triple-zeta basis set with d-type Cartesian–Gaussian polarization functions (6-311G(d)). The functionals include the PBE0 [59], M06-2X [60], 𝜔B97XD [61], and B3LYP-D3 schemes of Grimme [62, 63, 64]. As reported in a benchmark study by Grimme et al. [65], the choice of the basis set is appropriate for the systems under consideration. In this study, the full-dimensional geometry optimization calculations have been carried out with Berny’s [66] optimization procedure and without imposing any symmetry.
For all calculations, sampling in the Brillouin zone [67] has been performed with a 5 × 5 × 1 k-points. The kinetic energy cutoff has been set to 450 eV. In this approach, when the number of unit cells increases, the total energy decreases. The ab initio electronic structure calculations have been performed with the Gaussian 16 Rev. C.01 [68] package. The optimization calculations have been carried out using the default Gaussian convergence criteria. The optimization calculations are followed by harmonic frequency analysis to determine the nature of the stationary points. Population analysis has been carried out by calculations using the NBO v 3.1 software included within the Gaussian 16 Rev. C.01 package. The Multiwfn [69] package has been employed for the natural bond orbital (NBO), non-covalent interaction (NCI), and quantum theory of atoms in molecule (QTAIM) analyses, while DOS diagrams have been created with the GaussSum [70] program.
The energy of adsorption (Eads) between two fragments (nanotube and H2SiCl2) can be considered as follows:
| (1) |
| (2) |
One can easily verify from (1) that a negative value of (i.e. corresponding to exothermic adsorption) would indicate that the nanotube and H2SiCl2 complex is stable. In contrast, positive values would signify that the adsorption of H2SiCl2 on the nanotubes is not favored.
The bond length (Å) obtained from 𝜔B97XD/6-311G(d) calculations for (a) BNNT, (b) BNAlNT, and (c) BNGaNT.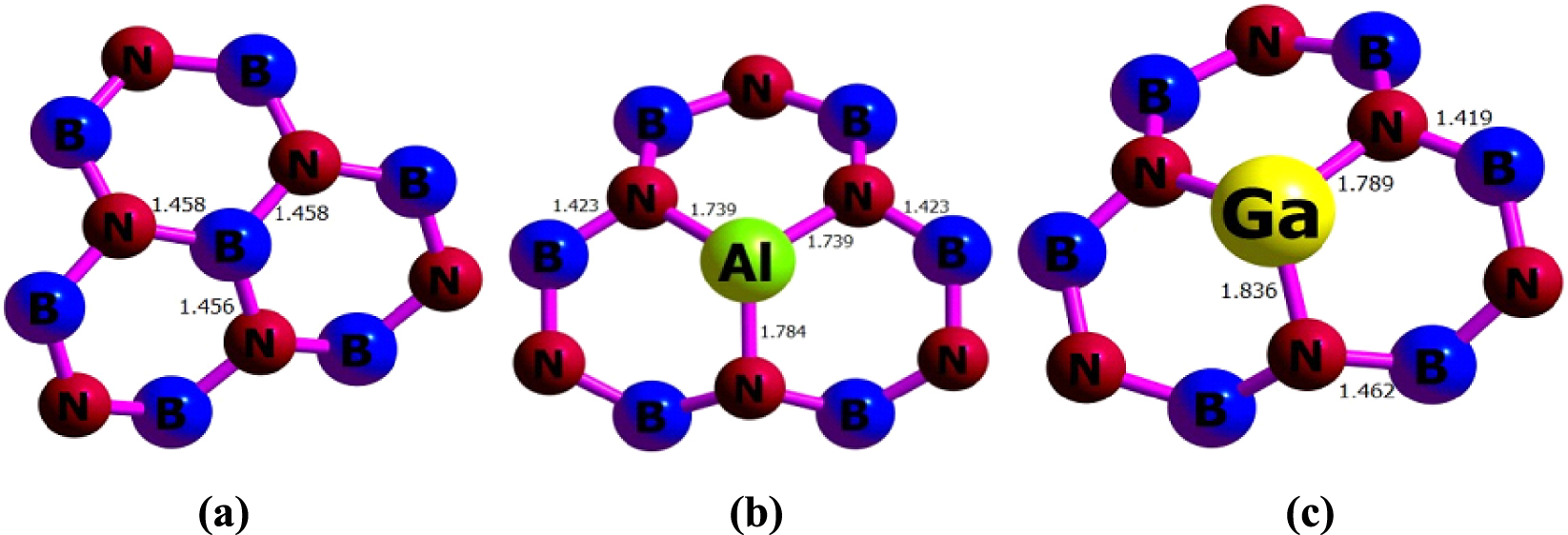
Unit cells of the BNNT used for density functional theory calculations. Tx positions are shown for the boron atom (T1), the nitrogen atom (T2), between the boron and the nitrogen atoms (T3), and for the hexagonal ring (T4).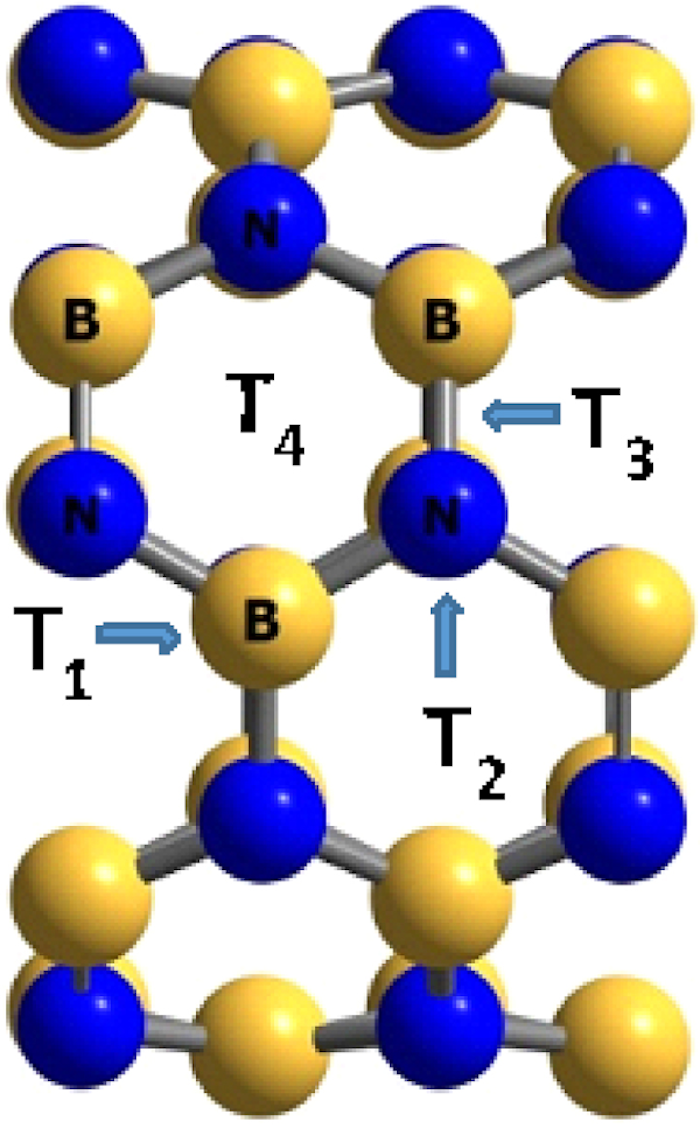
3. Result and discussion
3.1. Geometric surveys
The initial geometry calculations of the isolated nanotubes, H2SiCl2 molecule, and the adsorbed complex have been performed with PBE0 functional using a 6-311G(d) basis set. The estimated structures are further optimized with more accurate functionals, including M06-2X, 𝜔B97XD, and B3LYP-D3. Within the Minnesota 06 suite, the global hybrid functional with double nonlocal exchange (M06-2X) is a high-performance method to study the non-covalent interactions [60], whereas the latest version of B3LYP-D3 (GD3BJ) developed by Grimme et al. [62, 63, 64] takes account of the dispersion effect. On the other hand, the 𝜔B97XD functional includes both long-range interactions and dispersion corrections [61].
The PBE0/6-311G(d) calculations have been carried out on a pristine unit cell of a B40N40 nanotube having a length of 5.38 Å and diameter of 6.95 Å within the PBC-DFT framework. The optimized parameters of BNNT, BNAlNT, and BNGaNT obtained from 𝜔B97XD/6-311G(d) calculations are provided in Figure 1. From these calculations, it is evident that in BNAlNT and BNGaNT, X–N bonds (where X = B, Al or Ga) are longer than the other bonds in the nanotube. For example, in pristine BNNT, the average B–N bond length is around 1.46 Å. In contrast, the X–N bond length increases to 1.74 Å (or 1.78 Å) and 1.79 Å (or 1.84 Å) in BNAlNT and BNGaNT, respectively. Due to the inner stress, the B–N bond length in the vicinity of Al and Ga dopant atoms decreases to 1.42 Å.
Adsorption energies (Eads) for H2SiCl2 on BNNT, BNAlNT, BNGaNT and nanotubes complexes at the T1 site
| Systems | PBE0 | M06-2X | 𝜔B97XD | B3LYP-D3 |
|---|---|---|---|---|
| H2SiCl2/BNNT | − 0.055 | − 0.085 | − 0.155 | − 0.199 |
| H2SiCl2/BNAlNT | − 0.455 | − 0.642 | − 0.681 | − 0.790 |
| H2SiCl2/BNGaNT | − 0.707 | − 0.996 | − 0.960 | − 1.077 |
All values are in eV and obtained from geometry optimization calculations using PBE0, M06-2X, 𝜔B97XD, and B3LYP-D3 functional in combination with the 6-311G(d) basis set.
The adsorption of the H2SiCl2 gas molecule on the surface of BNNT, BNAlNT, and BNGaNT has been initiated by placing the gas molecule on top of the nanotube in different positions and orientations. There are four different sites in the BNNT for adsorption: (i) on top of boron atom (T1), (ii) on top of nitrogen atom (T2), (iii) on top of the bond between boron and nitrogen atom (T3), and (iv) on top of the hexagonal ring (T4) (see Figure 2). From these calculations, the local minima have been identified.
The H2SiCl2 molecule has two different heads, H and Cl, through which they can interact with the nanotubes (see Figure 3). The adsorbate molecule has been put on top of each Tx site at different distances, having the freedom to interact with the nanotube through each of its heads. The distances of these heads from the four different adsorption sites of the nanotube have been varied vertically from 0.5 Å to 5.0 Å (with 0.5 Å intervals). Overall, there are 80 initial configurations (2 × 4 × 10) for which the interaction energies between the gas molecules and the pristine or the doped BNNTs have been calculated. Initially, the interaction energies were calculated at the semi-empirical PM7/6-311G(d) level. The eight minimum energy structures of each H2SiCl2–nanotube complex were then further optimized through the PBE0/6-311G(d) calculations. The most stable complexes for each BNNTs found at the PBE0 level were reoptimized using M06-2X, 𝜔B97XD, and B3LYP-D3 functionals. The optimized structures for gas–nanotube complexes are depicted in Figure 4.
The optimized structure of the H2SiCl2 gas molecule obtained from 𝜔B97XD/ 6-311G(d) calculations.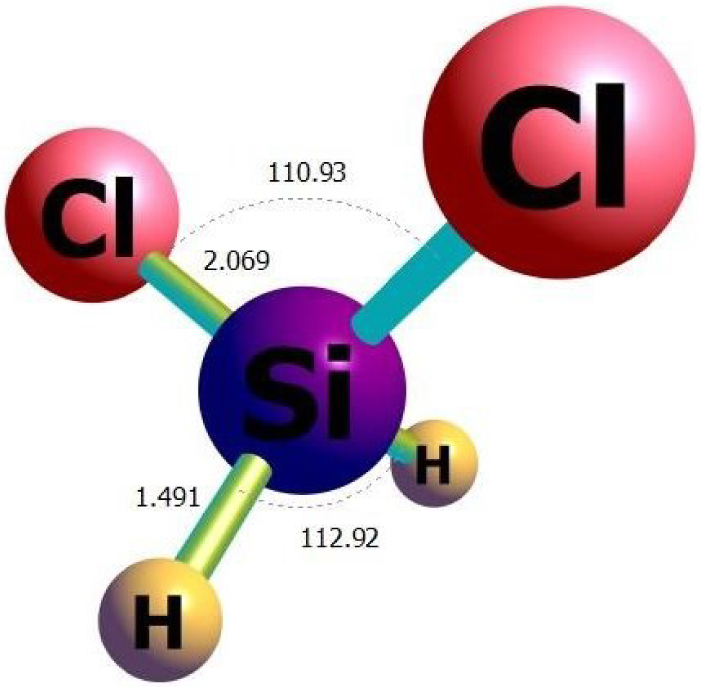
Optimized structures of (a) H2SiCl2/BNNT, (b) H2SiCl2/BNAlNT, and (c) H2SiCl2/BNGaNT obtained from 𝜔B97XD/6-311G(d) calculations.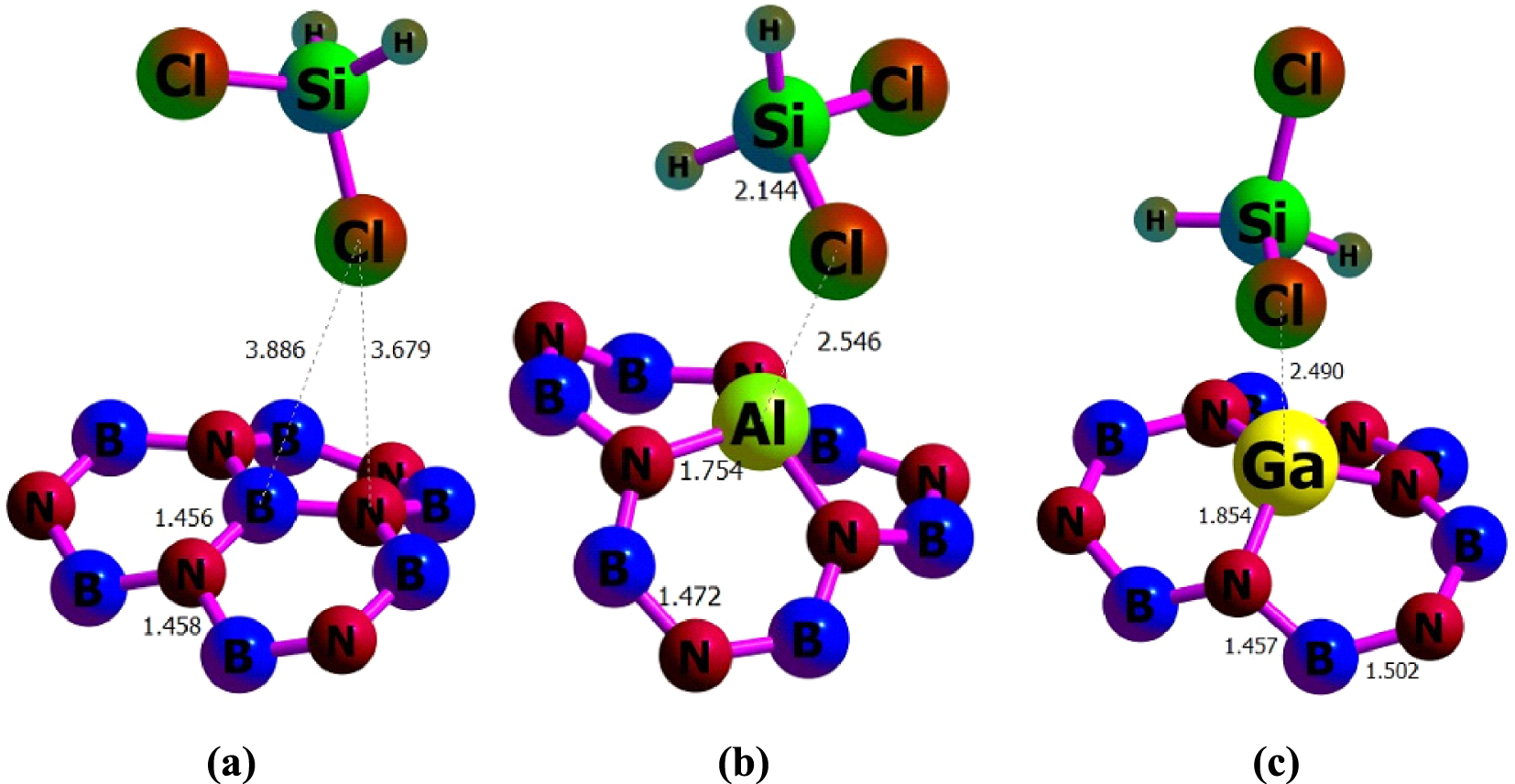
We found that the adsorption at the T1 site (i.e., on top of the B atom for BNNT, the Al atom for BNAlNT, and the Ga atom for BNGaNT) with the Cl head of the adsorbate releases maximum negative Eads in comparison to other adsorption sites. Table 1 provides the associated adsorption energies calculated with four different functionals. Evidently, the maximum negative Eads value is obtained for the B3LYP-D3 functional, whereas the adsorption energy values obtained from the 𝜔B97XD and the B3LYP-D3 functionals are very close to each other. The Eads obtained by the PBE0 functional corresponds to the lowest adsorption energy among all functionals considered in this study. The above statements are true for each of the three nanotubes.
Another common feature of the Eads values is that they tend to be more negative (more exothermic) for doped nanotubes, and with the increasing size of the dopant atom. For example, if we consider calculations performed with the 𝜔B97XD functional, the Eads value decreases from − 0.15 eV for the BNNT, to − 0.68 eV for the BNAlNT and further to − 0.96 eV for the BNGaNT. In general, there is a larger gain in adsorption energy when a pristine BNNT is doped by Al (0.40 eV–0.59 eV) than switching from BNAlNT to BNGaNT (0.25 eV–0.35 eV). Comparing Eads values among the functionals, PBE0 functional generates the least gain in adsorption energy when successively doping BNNT and BNAlNT, while 𝜔B97XD functional reports intermediate values in comparison to M06-2X and B3LYP-D3 functionals.
At the T1 site, the interaction primarily occurs between the Cl head of the adsorbate and the group 13 element (X) of the nanotube, whose ionization potential (IP) decreases when going from B to Al (IP of Al and Ga are comparable). Therefore, it is increasingly possible that there is a charge transfer from the nanotube to the H2SiCl2 molecule driving the exothermic adsorption, particularly for the doped nanotubes. To evaluate the likelihood of this phenomenon, we have further investigated the changes in the electronic structure for the adsorption processes. In order to reduce computational time, and given that results obtained with the 𝜔B97XD/6-311G(d) calculations has the best agreement with the experimental structure of the adsorbate, the calculations presented in the rest of this paper only corresponds to the 𝜔B97XD/6-311G(d) functional. Additionally, we have carried out further analysis where the unit cell of the nanotube has been expanded five times along its central axis. It should also be noted that to minimize the boundary effects, we use H as the terminal atoms.
Density of state diagrams for (a) BNNT, (b) H2SiCl2/BNNT, (c) BNAlNT (d) H2SiCl2/BNAlNT (e) BNGaNT, and (f) and H2SiCl2/BNGaNT. Data were obtained from 𝜔B97XD/6-311G(d) calculations.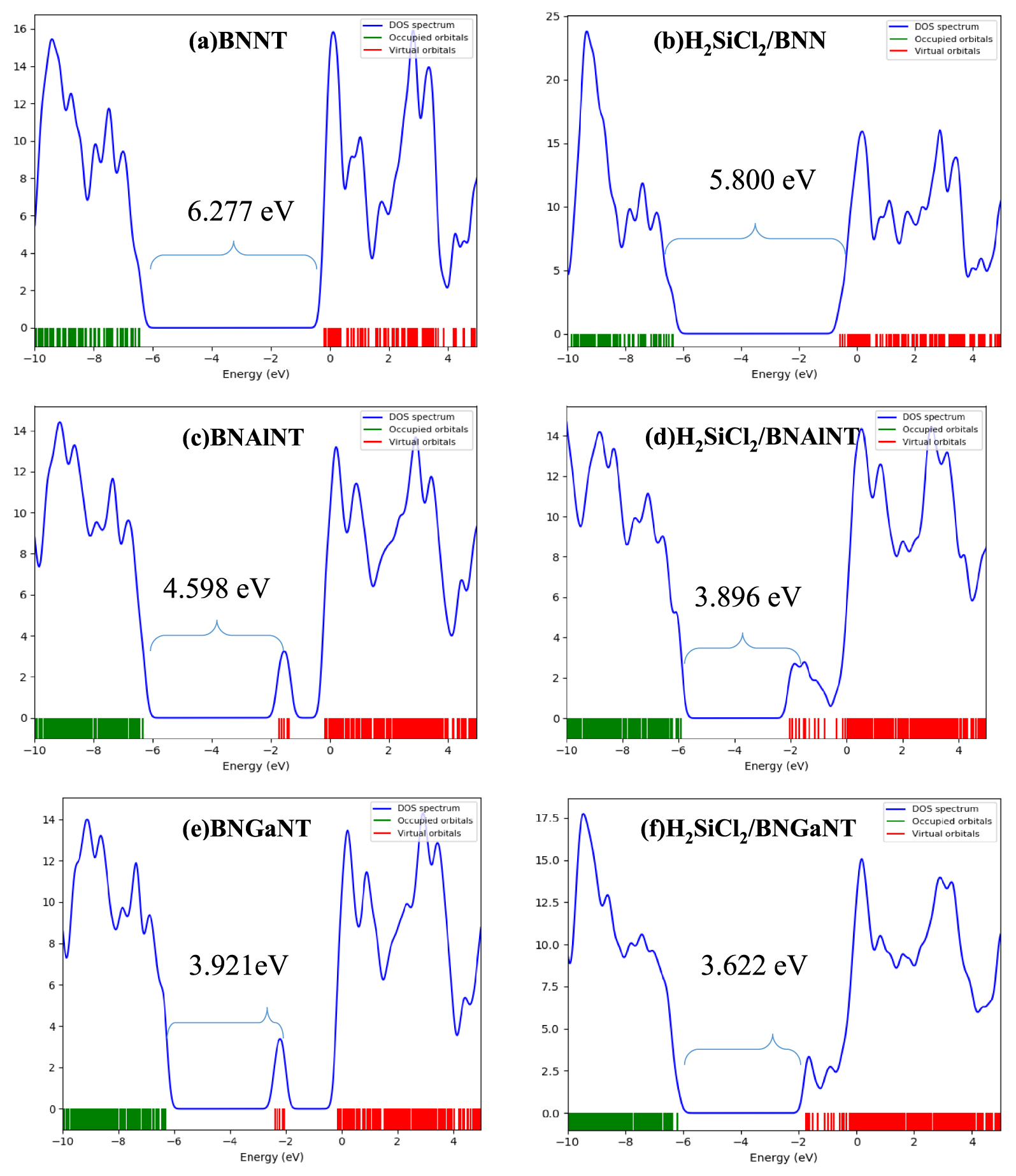
3.2. Electronic structure
The Highest Occupied Molecular Orbital (HOMO)–Lowest Unoccupied Molecular Orbital (LUMO) energy gap (HLG) calculated from the DFT calculation may serve to further evaluate the electronic properties of a molecular system [73]. Some of these properties, such as the IP, electron affinity (EA), electronegativity (𝜒), chemical hardness (𝜂), electrophilicity (𝜔) are directly linked to the HOMO–LUMO energy gap. From the Koopmans’ theorem, the energy of the HOMO can be considered as the vertical IP, while the LUMO energy represents the vertical EA. The negative electronegativity (𝜒) is equal to the chemical potential of a complex given by:
| (3) |
| (4) |
| (5) |
The HOMO is destabilized, while LUMO is stabilized upon adsorption of on the nanotubes. Maximum destabilization of HOMO is obtained for the adsorption on BNAlNT (0.41 eV), while the maximum stabilization of LUMO is calculated to be for the pristine BNNT (0.40 eV). Adsorption of H2SiCl2 on the doped nanotubes is accompanied by a decrease in HLG compared to their pristine counterpart. This decrease is more pronounced on BNAlNT (0.70 eV) than other nanotubes and is attributed to the large destabilization of HOMO, as discussed previously. DOS map is useful in intuitively revealing the density of distribution of molecular orbitals in different energy regions. The HOMO–LUMO gap is clearly visible from this DOS map (Figure 5). For a resistance-based sensor, the resistivity will be diminished when the HLG is reduced as it is proportional to the reciprocal of the conducting electron population. Hence, the resistivity of the nanotube after adsorption is low, and the electric current passed through it will face the lowest resistance. Similarly, 𝜇 and 𝜂 values also decrease upon adsorption. However, electrophilicity 𝜔 decreases for the doped nanotube but increases for the pristine one.
HOMO energy (𝜖H), LUMO energy (𝜖L), HOMO–LUMO energy gap (HLG), chemical potential (𝜇), chemical hardness (𝜂), and electrophilicity (𝜔) of pristine BNNT, BNAlNT, and BNGaNT (top three rows) and at their H2SiCl2 adsorbed optimized structures (bottom three rows)
| Systems | 𝜀H | 𝜀L | HLG | 𝜇 | 𝜂 | 𝜔 |
|---|---|---|---|---|---|---|
| BNNT | − 6.460 | − 0.183 | 6.277 | − 3.321 | 3.139 | 17.312 |
| BNAlNT | − 6.330 | − 1.732 | 4.598 | − 4.031 | 2.299 | 18.679 |
| BNGaNT | − 6.310 | − 2.390 | 3.921 | − 4.350 | 1.960 | 18.547 |
| H2SiCl2/BNNT | − 6.381 | − 0.581 | 5.800 | − 3.481 | 2.900 | 17.571 |
| H2SiCl2/BNAlNT | − 5.923 | − 2.027 | 3.896 | − 3.975 | 1.948 | 15.393 |
| H2SiCl2/BNGaNT | − 6.192 | − 2.571 | 3.622 | − 4.382 | 1.811 | 17.383 |
All values reported are in eV and have been obtained from the 𝜔B97XD/6-311G(d) calculations.
3.3. Natural bond orbital (NBO) analysis
The NBO method, developed by Weinhold et al. [74, 75, 76], is one of the robust population analysis methods widely used in the scientific community. One of its main advantages is that the results do not vary with respect to changes in the basis set. The NBO method calculates the electron density distribution between two atoms. The density matrix, which is required for NBO analysis, can usually be obtained from DFT calculation. In addition to the density matrix, an atomic charge is used to define natural bonding orbitals. The valence space is spanned by bonding NBO (𝜎) and antibonding NBO (𝜎∗). The bonding and antibonding NBOs between atom A and B can be defined as:
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
Mulliken, Mayer, and Wiberg bond orders determined by the interactions of the molecule with BNNT, BNAlNT, and BNGaNT
| Systems | Xa…Yb | Mulliken | Mayer | Wiberg |
|---|---|---|---|---|
| H2SiCl2/BNNT | Cl…B | 0.004 | 0.007 | 0.005 |
| H2SiCl2/BNAlNT | Cl…Al | 0.094 | 0.252 | 0.459 |
| H2SiCl2/BNGaNT | Cl…Ga | 0.223 | 0.425 | 0.717 |
All values have been obtained from 𝜔B97XD/6-311G(d) calculations.
a X atom belongs to H2SiCl2.
b Y atom belongs to the nanotubes.
QTAIM topological parameters for electron density 𝜌(r), Laplacian of electron density 𝛻2𝜌(r), kinetic electron density G(r), potential electron density V (r), bond ellipticity (𝜀), and eta index (𝜂) at the BCPs of the optimized H2SiCl2/BNNT, H2SiCl2/BNAlNT, and H2SiCl2/BNGaNT complexes
| Systems | Bond | 𝜌 | 𝛻2r | G(r) | V (r) | G(r)∕|V |(r) | 𝜀 | 𝜂 |
|---|---|---|---|---|---|---|---|---|
| H2SiCl2/BNNT | Cl…B | 0.0036 | 0.0124 | 0.0024 | − 0.0018 | 1.3878 | 0.1256 | 0.1280 |
| H2SiCl2/BNAlNT | Cl…Al | 0.0253 | 0.0727 | 0.0209 | − 0.0237 | 0.8838 | 0.2751 | 0.1950 |
| Si…Al | 0.0096 | 0.0265 | 0.0059 | − 0.0051 | 1.1476 | 0.1028 | 0.1900 | |
| Si…N | 0.0079 | 0.0231 | 0.0050 | − 0.0042 | 1.1820 | 1.7608 | 0.1427 | |
| H2SiCl2/BNGaNT | Cl…Ga | 0.0439 | 0.1129 | 0.0378 | − 0.0473 | 0.7985 | 0.0352 | 0.2070 |
| Si…Ga | 0.0222 | 0.0333 | 0.0106 | − 0.0128 | 0.8250 | 0.8185 | 0.2359 | |
| Si…N | 0.0080 | 0.0253 | 0.0053 | − 0.0043 | 1.2328 | 1.0981 | 0.1686 | |
All the values have been obtained from 𝜔B97XD/6-311G(d) calculations and NBO analysis.
In the above equations, P and S represent the density and overlap matrix, respectively. Mulliken and Mayer’s bond orders are sensitive to the basis set, especially for the basis sets that include diffuse functions. In comparison, the Wiberg bond index has a lower basis set dependence. Table 3 provides the various bond orders calculated in this study. As the size of the group 13 element (X) increases, the Cl–X bond order increases, indicating that the interaction is stronger. This is valid for each of the three methods considered in this study. Taking also into consideration the adsorption energies, one may conclude that the BNAlNT and BNGaNT adsorbents are more active materials for adsorbing H2SiCl2 rather than the pristine BNNT. Therefore, the interaction between the gas molecule and BNNT can be considered as physisorption rather than chemisorption.
Bond critical points for (a) H2SiCl2/BNNT, (b) H2SiCl2/BNAlNT, and (c) H2SiCl2/BNGaNT systems. The orange dots represent the BCPs.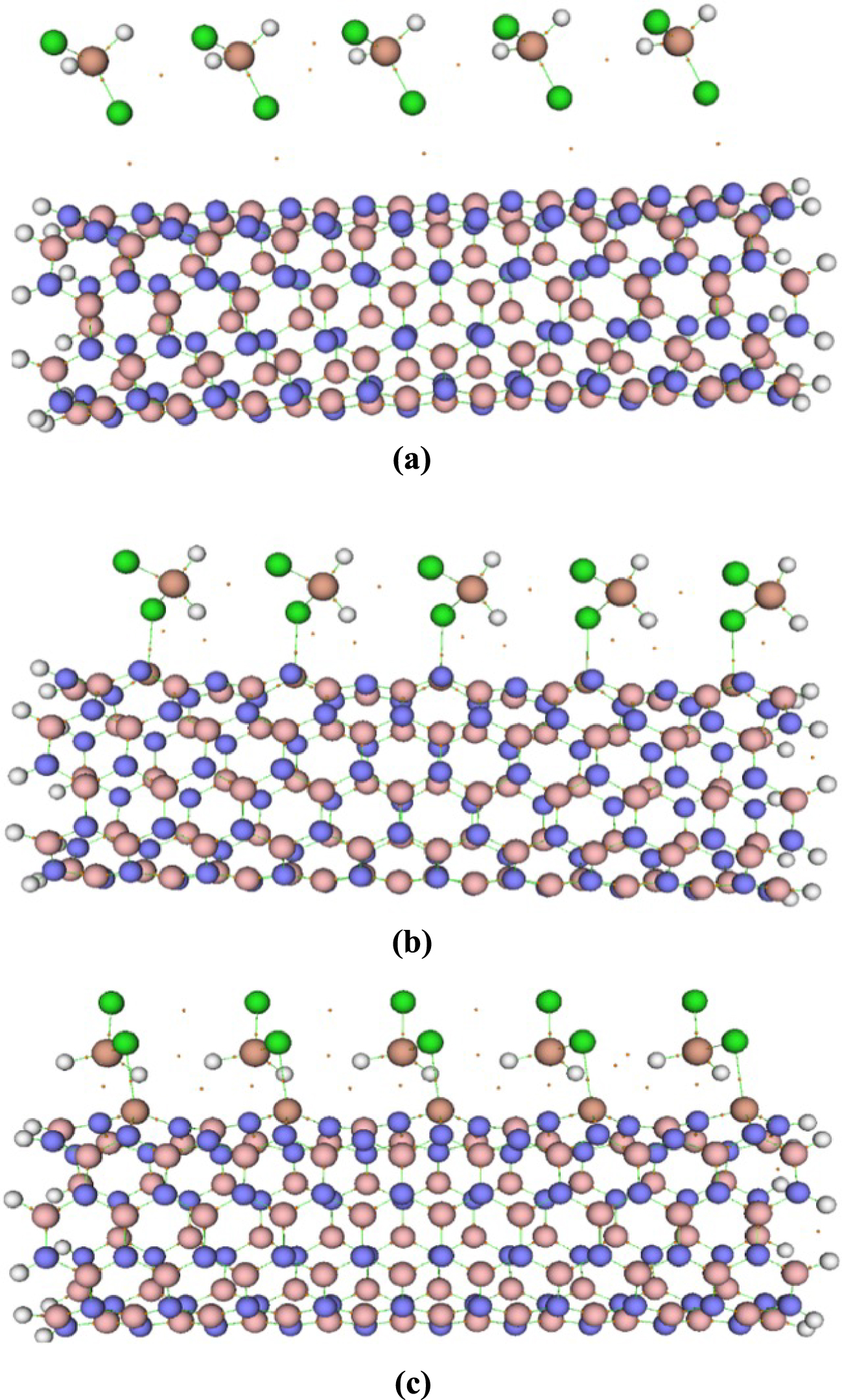
3.4. Quantum theory of atoms in molecules (QTAIM) analysis
QTAIM analysis has been performed to deduce the bond types and intermolecular interactions of the adsorbed complex. In QTAIM analysis, a bond critical point (BCP) is derived from the topological analysis of the electron densities to the chemical bonds. BCP is a saddle point of electron density with a maximum electron density in the two mutually perpendicular directions of space and a minimum in the third one. Therefore, the electron density 𝜌(r) and the Laplacian electron density 𝛻2𝜌(r) play a pivotal role in the QTAIM analysis. From the values of 𝜌(r) and 𝛻2𝜌(r) one can divide the electrostatic interactions into different sectors and assign them to different critical points, such as atomic critical point (ACP), BCP, ring critical point (RCP), and cage critical point (CCP). The BCPs of the H2SiCl2/BNNT, H2SiCl2/BNAlNT, and H2SiCl2/BNGaNT complexes at their optimized geometry are illustrated in Figure 6.
A covalent bond occurs when a BCP has a negative value of 𝛻2𝜌(r) and large values of electron density (𝜌(r) > 10−1 a.u.). Conversely, a positive value of 𝛻2𝜌(r) corresponds to a nonsubstrate closed-shell type that includes ionic and van der Waals interactions [83]. On the other hand, one can also characterize the intermolecular interaction from the Lagrangian kinetic energy G(r) and potential energy density V (r) values. When G(r)∕|V |(r) < 0.5, the nature of the interaction is covalent. If G(r)∕|V |(r) > 1, the interaction may be assumed as non-covalent. However, if G(r)∕|V |(r) lies between 0.5 and 1.0, then the nature of bonding must be correlated with the values of 𝜌(r) and 𝛻2𝜌(r), and the bonds may be denoted as partially covalent or partially non-covalent. Table 4 reports the values 𝜌(r), 𝛻2𝜌(r), G(r), |V |(r) and the G(r)∕|V |(r) ratio. In all cases, we can clearly see that 𝛻2𝜌(r) values for Cl–X bond (where X is a group 13 element) are all positive. Therefore, the Cl–X interactions can be considered as non-covalent. With the exception of the H2SiCl2/BNNT complex, G(r)∕|V |(r) ratio falls close to 0.8, indicating that the interactions between the doped nanotubes with the Cl atom of the adsorbent are partially non-covalent. Furthermore, the interaction of the nanotubes with the Si atom of the adsorbent also appears to be mostly of the non-covalent type.
Additionally, 𝜂 at the BCP is also a good indicator to illustrate bond type. The value of 𝜂 is less than 1 for closed-shell interactions and increases with increasing covalent character [84]. The value of 𝜂 is equal to the |𝜆1|∕𝜆3 ratio, where 𝜆i corresponds to the eigenvalues of the Hessian matrix. In this study, each of the calculated values of 𝜂 falls below unity (see Table 4), so, in accordance to the previous analysis, we can assign the H2SiCl2 nanotube interactions as non-covalent. Finally, the bond ellipticity, defined as 𝜀 = 𝜆1∕𝜆2 − 1, is a measure of the preferential accumulation of electron density in a given plane containing the bond path at the BCP; in essence, it quantifies the deviation from a cylindrical shape, i.e., π characteristics [85]. If a bond is cylindrically symmetrical, then 𝜀 = 0. From the values reported in Table 4, we can see that the Si–X bond largely deviates from the cylindrical symmetry, while, Cl–Ga has the lowest bond ellipticity.
A 2D plot of the reduced density gradient (atomic units) versus the electronic density multiplied by the sign of the second Hessian eigenvalue sign 𝜆2(r)𝜌(r) (atomic units) for (a) BNNT, (b) H2SiCl2/BNNT, (c) BNAlNT, (d) H2SiCl2/BNAlN, (e) BNGaNT and (f) H2SiCl2/BNGaNT. The diagrams were obtained from 𝜔B97XD/6-311G(d) calculations.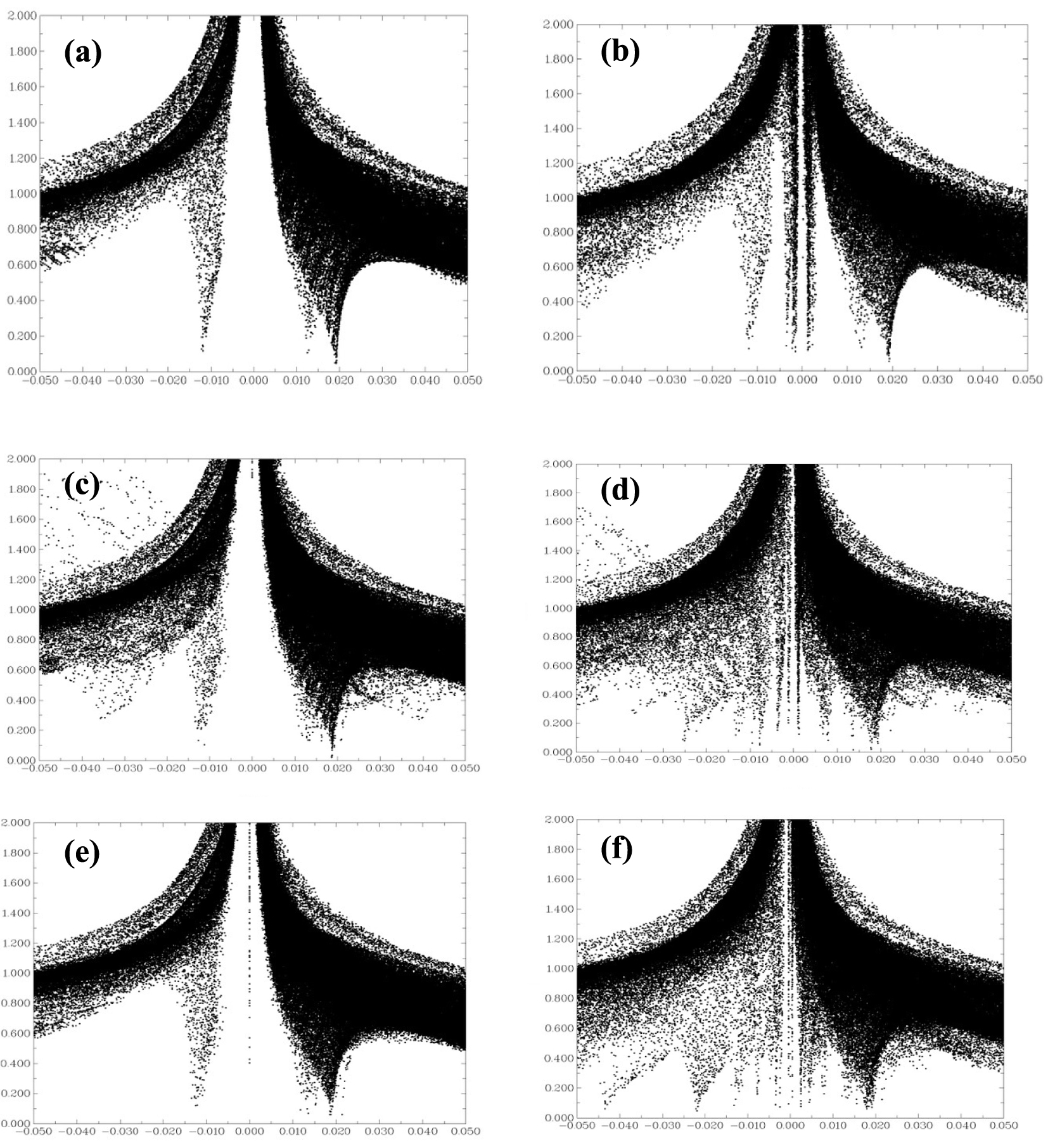
As H2SiCl2 adsorbs on the nanotubes via non-covalent interactions, we have further investigated their nature from a purely Non-Covalent Interaction (NCI) perspective [86]. A plot of the Reduced Density Gradient (RDG) against sign 𝜆2(r)𝜌(r), can be visualized to interpret the type of NCI that exists in the adsorbed complexes. RDG is defined as follows [86, 87]:
| (11) |
Figure 7 provides RDG versus sign 𝜆2(r)𝜌(r) plots for the pristine BNNT, BNAlNT, BNGaNT, and the adsorbed H2SiCl2 species on its surface. If we consider the RDG = 0.5 isosurface as a reference, it is evident that many points emerge within the sign 𝜆2(r)𝜌(r) ≈ 0 zone for the adsorption of H2SiCl2 on the BNNT. Therefore, the interaction between BNNT and H2SiCl2 is of weak van der Waals type, validating earlier assumptions. However, on BNAlNT and BNGaNT, there is an accumulation of points within the sign 𝜆2(r)𝜌(r) < 0 region, suggesting a strong non-covalent ionic interaction.
Drawing conclusions from adsorption energies, Cl–X bond order, and QTAIM analysis, one can clearly visualize a pattern caused by doping the BNNTs. As the size of the dopant increases, there is an increase in the adsorption energy, apparently due to a stronger non-covalent ionic interaction between the Cl atom of the adsorbent and the element of group 13. Therefore, to further facilitate the adsorption of H2SiCl2, it would be highly desirable to use a larger and heavier group 13 element dopant such as In and Tl. An effort along this line is already underway in our group.
4. Conclusion
In this work, we have evaluated the prospect of using boron nitride nanotubes (BNNT), and their doped variants BNAlNT and BNGaNT for enhancing adsorption of gaseous dichlorosilane (H2SiCl2). The adsorption energy H2SiCl2 on the surfaces of the nanotubes has been determined within the DFT formalism. Overall, we have utilized four functionals (i.e., PBE0, 𝜔B97XD, M06-2X, and B3LYP-D3) together with a 6-311G(d) basis set in order to find trend convergence in intermolecular interactions. We find that adsorption on top of the B atom of the BNNT (as well as on the Al and Ga atom in the case of BNAlNT and BNGaNT, respectively) is energetically most favorable compared to other sites. Adsorption energy increases with the size of the dopant atom, i.e., the energy of adsorption follows the trend BNNT < BNAlNT < BNGaNT. For example, adsorption energy on BNNT calculated with the 𝜔B97XD functional is around ∼0.5 eV smaller than that obtained on BNAlNT, which in turn is ∼0.3 eV smaller than on BNGaNT.
Optimized structures obtained from 𝜔B97XD/6-311G(d) have been chosen for further electronic structure analysis. The amount of adsorption energy can be closely correlated with the bond strength between the Cl atom of the gas and the nanotube, following the order: BNNT < BNAlNT < BNGaNT. The results can be explained from the QTAIM analysis, where the nature of the interaction between two moieties can be deduced. We find that adsorption on pristine BNNT is governed by weak van der Waals forces, while those on doped nanotubes are driven by stronger non-covalent ionic interactions. The adsorption phenomenon is accompanied by a decrease in HOMO–LUMO energy gaps in the nanotubes.
Overall, doping pristine BNNT by Al and Ga atoms can activate its surface for a greater tendency of adsorbing H2SiCl2 gas. Accordingly, these doped nanomaterials could provide excellent means for designing nanomaterials for dichlorosilane sensors.




 CC-BY 4.0
CC-BY 4.0