1. Introduction
The technology of hydraulic fracturing monitoring with microseismic signals is used to judge the form and extension trend of fracturing through an analysis of recorded microseismic data [Maxwell and Urbancic 2001]. However, low-amplitude microseismic signals are usually submerged by a strong noise [Zhang and Van der Baan 2018a]. Likewise, increasingly difficulties arise in desert seismic signals detection because of the similarity between signal and noise [Li and Li 2016]. Thus, we need to develop an accurate and fast low-amplitude seismic signal detection method. Various approaches have been proposed: the STA/LTA method detects signals based on the ratio variation of the amplitude or energy in the time domain [Allen 1982]. Although the computation cost of the STA/LTA is low, its quality decreases when the signal-to-noise ratio (SNR) of the record is low. The Akaike information criterion (AIC) proposed here is based on an autoregressive model used to determine the boundary points of two stationary sequences with different statistical properties for signal detection [Leonard 2000]. AIC does not work well for low-amplitude seismic signal detection, either. Methods based on convolutional neural network (CNN) signal detection have attracted much attention [Yuan et al. 2018; Samaneh et al. 2018; Xiong et al. 2018], but their performances depend on the existence of large training datasets.
The wavelet transform is widely used for seismic signal detection [Wang 2009]. It is a method based on time-frequency analysis, which has high flexibility and fast calculation [Mallat and Hwang 1992]. There are two types of signal detection methods using wavelet transform: one uses the wavelet transform for pre-processing in order to suppress the noise [Wang 2009]; the other makes use of some signal features in the wavelet domain such as energy entropy, multi-scale entropy [Jia et al. 2016]. However, the wavelet transform cannot perform multi-directional decomposition. Multi-directional analysis methods such as the shearlet transform are proposed to treat this issue [Lim 2010]. The shearlet transform has a lower approximation error for signals than other multiscale and multidirectional analysis methods [Zhang and Van der Baan 2018b, 2019].
In this paper, we propose a method combining shearlet energy entropy with SVM to detect a microseismic and seismic signal. The signal can achieve a sparser representation in the shearlet domain due to the multi-direction characteristic of the shearlet transform, which favours signal feature extraction. Furthermore, we do the correlation processing across scales to enhance the difference between signal and noise in the shearlet domain. Then we calculate the shearlet energy entropy as a signal feature. Compared with the traditional features such as amplitude and energy, SVM can give a more accurate classification result with shearlet energy entropy. The SVM has higher accuracy for small training datasets compared with methods of deep-learning signal detection [Zhang et al. 2004]. We use SVM instead of a threshold to obtain an automatic detection. It avoids misjudgments caused by threshold selection. Tests show that the proposed method can effectively detect microseismic and seismic signals at low SNR.
2. Shearlet energy entropy
2.1. Shearlet
Guo and Labate [2006, 2007] combined the complex wavelet theory with multi-scale geometric analysis to construct a sparse representation of a multidimensional function: the shearlet representation. The shearlets 𝜓j,k,m are a special example of composite wavelets in , which can be constructed by applying dilations, shear transformations, and translations to an appropriate mother function. In dimension 2, the shearlets can be written as the following form:
| (1) |
The shearlet transform of a function for a certain scale, direction and position is defined as follows:
| (2) |
2.2. Shearlet energy entropy
The shearlet transform can decompose the data into different scales and directions which yields the shearlet coefficients Sf(j,k,m). The signals energy is concentrated in only a few directions due to their spatial correlation at those dips only [Zhao et al. 2016; Zhang and Van der Baan 2019]. We define the energy of the shearlet coefficient as:
| (3) |
The difference between signal and noise becomes small when the SNR is low. Thus, we determine to do the correlation between two adjacent scales to highlight the features of the signals. The correlation energy between two adjacent scales is defined as follows:
| (4) |
Through (4), we can get the signal’s direction by largest energy distribution. Then we do the correlation to the signal’s direction coefficients between two adjacent scales to further enhance the coefficients associated with signals. Finally, We divide the enhanced coefficients into some segments, the energy of these segments is expressed as E1,E2,…,E𝜀. The total energy E is equal to the sum of E1,E2,…,E𝜀. Set p𝜏 = E𝜏∕E, and . Shearlet energy entropy is defined as:
| (5) |
The entropy is used to measure the randomness of signals. In the process of signal detection, randomness causes noise to have larger entropy values than the signals [Rezek and Roberts 1998]. Since signal and noise present different characteristics in the shearlet domain, the proposed shearlet energy entropy can further enhance the difference between signal and noise.
3. Signal detection based on shearlet energy entropy and SVM
SVM is a classifier and its basic theory is margin-maximization. It has a simple structure and low computation cost [Adankon and Cheriet 2009; Hu et al. 2013]. For signal detection, we get a SVM classifier through the training set, and then we can use this trained SVM classifier to determine if the input represent signals. The specific theories of SVM are as follows:
The main principle of SVM classification is to find the optimal classification surface. The optimal classification surface can be transformed into solving the following equation [Widodo and Yang 2007]:
| (6) |
| (7) |
After solving the above equation, the final decision function is given by:
| (8) |
| (9) |
The penalty parameter 𝛾 and the parameter 𝜎 in the kernel functions are two key factors affecting the accuracy of the SVM classifier. If the penalty parameter 𝛾 is set too small or too large, the learning algorithm will be under-fitting or over-fitting. When 𝜎 is set too small, the radius of the area of influence of the support vectors only includes the support vector itself and no amount of regularization with 𝛾 will be able to prevent over-fitting. Conversely, if 𝜎 is too large, the model cannot capture the complexity or “shape” of the data. Therefore, in this paper, we use leave-one-out cross-validation to get some pairs of 𝛾 and 𝜎 which can achieve a high accuracy.
To train a SVM classifier, first, we choose some signal and noise samples to create the training dataset, where the number of noise samples and signal samples is the same. The signal samples are generated by using Ricker wavelets with different amplitudes and dominant frequencies. The noise samples are generated using by a combination of white Gaussian noise (WGN) and real noise with different levels. Then we calculate the shearlet energy entropies of these samples and put them into SVM to train a final classifier. When we have obtained a SVM classifier, the signal detection is done in two steps:
Step 1: We decompose the input data into a shearlet domain to find the shearlet coefficients in signal’s direction. Then we correlate them with a adjacent scale to enhance the signal coefficients.
Step 2: We calculate the energy entropies of the enhanced shearlet coefficients obtained from step 1. Then, the energy entropies are used as input into the trained SVM classifier for signal identification.
4. Experiments
4.1. Synthetic microseismic data
To verify the reliability of this method, we simulated the microseismic signal containing the P wave and the S wave. The amplitude of the P wave is smaller than that of the S wave, as shown in Figure 1. The frequency of the microseismic signal is high and the dominant frequency of the actually received wavelet is about 200 Hz. [Gao et al. 2018; Maxwell and Urbancic 2001]. We set the dominant frequencies of two microseismic signals to 200 Hz [Zhu et al. 2016] which is close to the real situation. The sampling frequency is 1000 Hz. The amplitudes of the P wave and S wave are 0.5 and 0.2. Figure 2 is the noisy record where white Gaussian noise (WGN) was added with the SNR of −8 dB.
Synthetic microseismic record.
Noisy record contaminated by WGN with the SNR of −8 dB.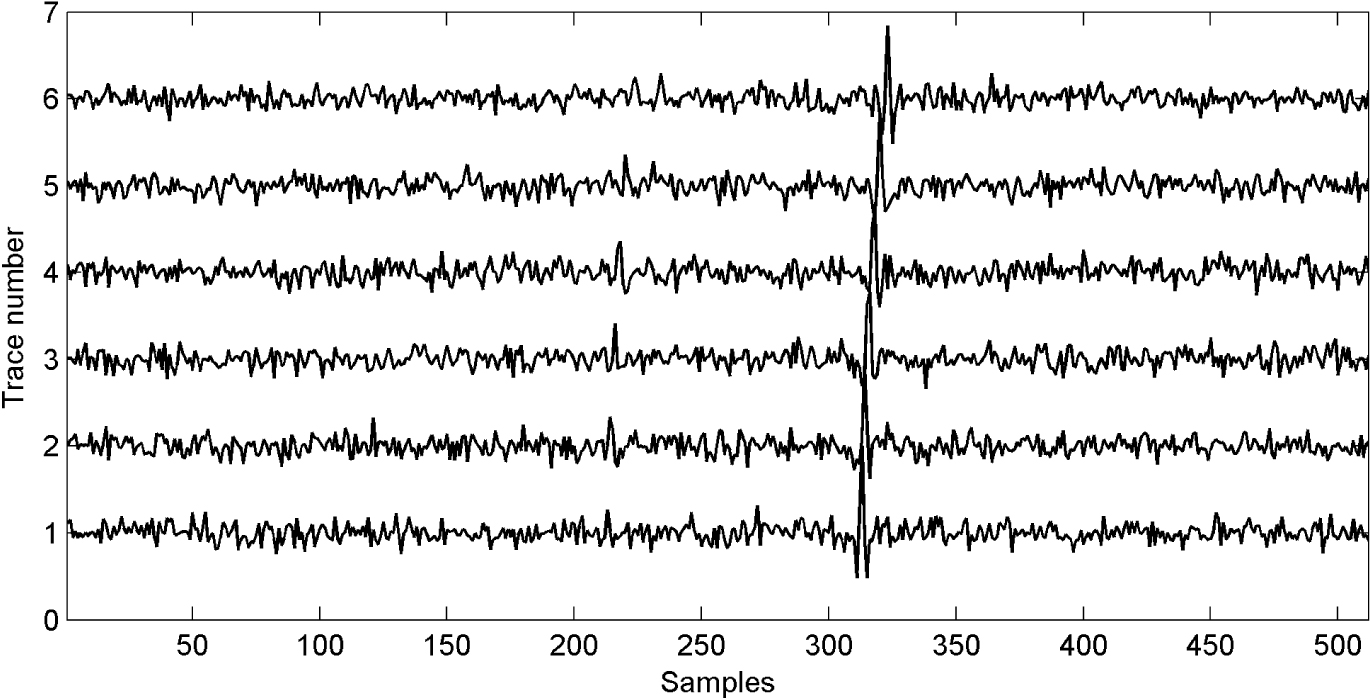
The record is decomposed into 4 scales by the shearlet transform. Since most microseismic signals concentrate on the high frequency scales, and the larger scales correspond to higher frequencies, we choose the larger scales for detection. In this paper, we divide records into 4 scales and we process the two largest scales: 3rd and 4th scale. Figure 3 shows the shearlet coefficients in different directions at the 3rd scale. We can see that most signals are concentrated in the 4th direction, while noise is distributed in all directions. The correlation energy of the first trace between adjacent scales is shown in Figure 4. We can see that the correlation energy in the 4th direction is obviously larger than the others. This indicates that we can obtain more accurate signal directions through correlation processing. Figure 5(a) shows the waveform of the first trace. We can see that the front low-amplitude microseismic signal is submerged by noise which is difficult to identify. The shearlet coefficients after the correlation processing is shown in Figure 5(b), the shearlet coefficients associated with microseismic signals are all distinguished from the noise, which facilitates the subsequent energy entropy feature extraction and SVM detection.
(a)–(f) Correspond to the shearlet coefficients from the first to the sixth directions at the 3rd scale.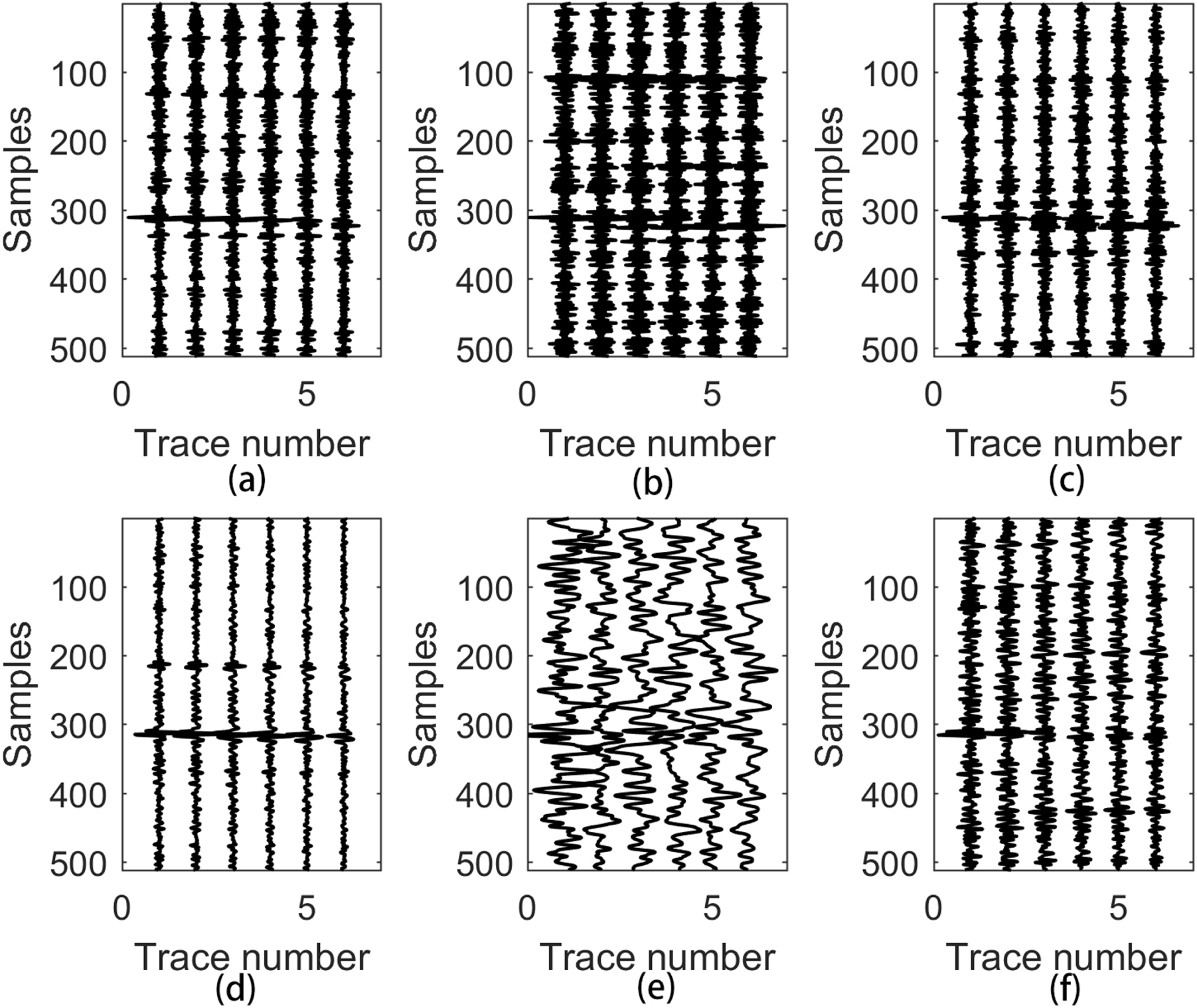
The correlation energy of first trace between adjacent scales (j = 3 and j = 4).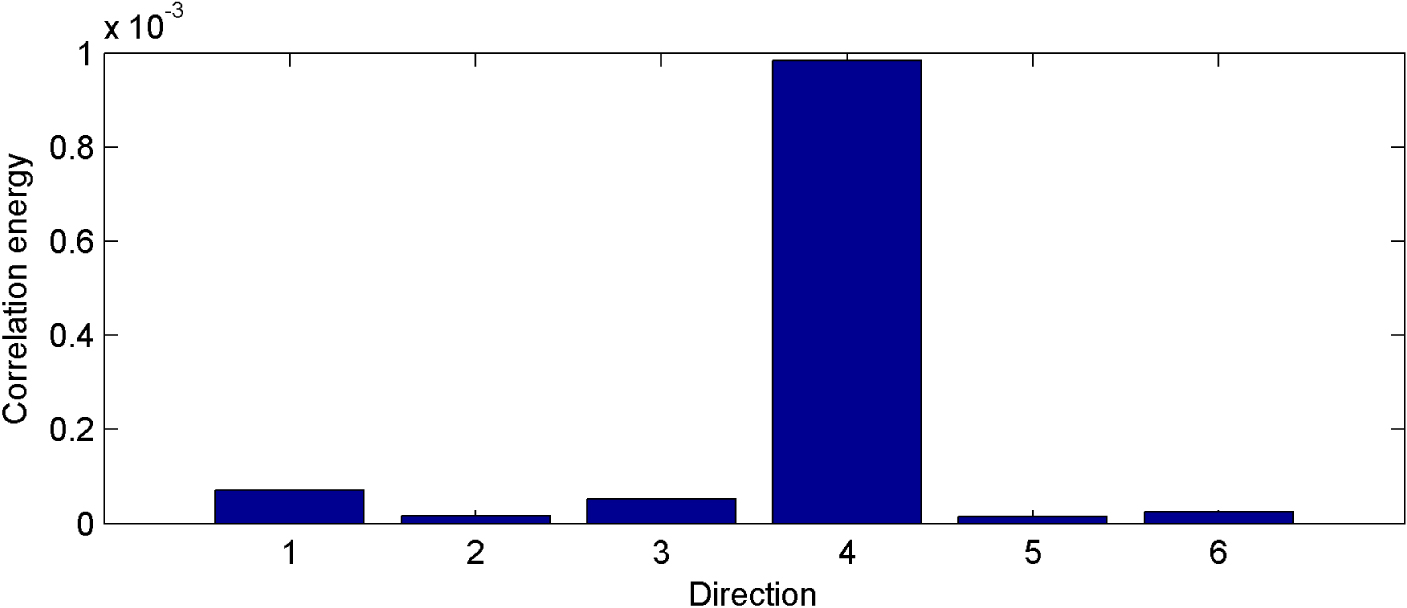
(a) The waveform of the first trace from Figure 2. (b) Shearlet coefficients of the first trace after correlation processing.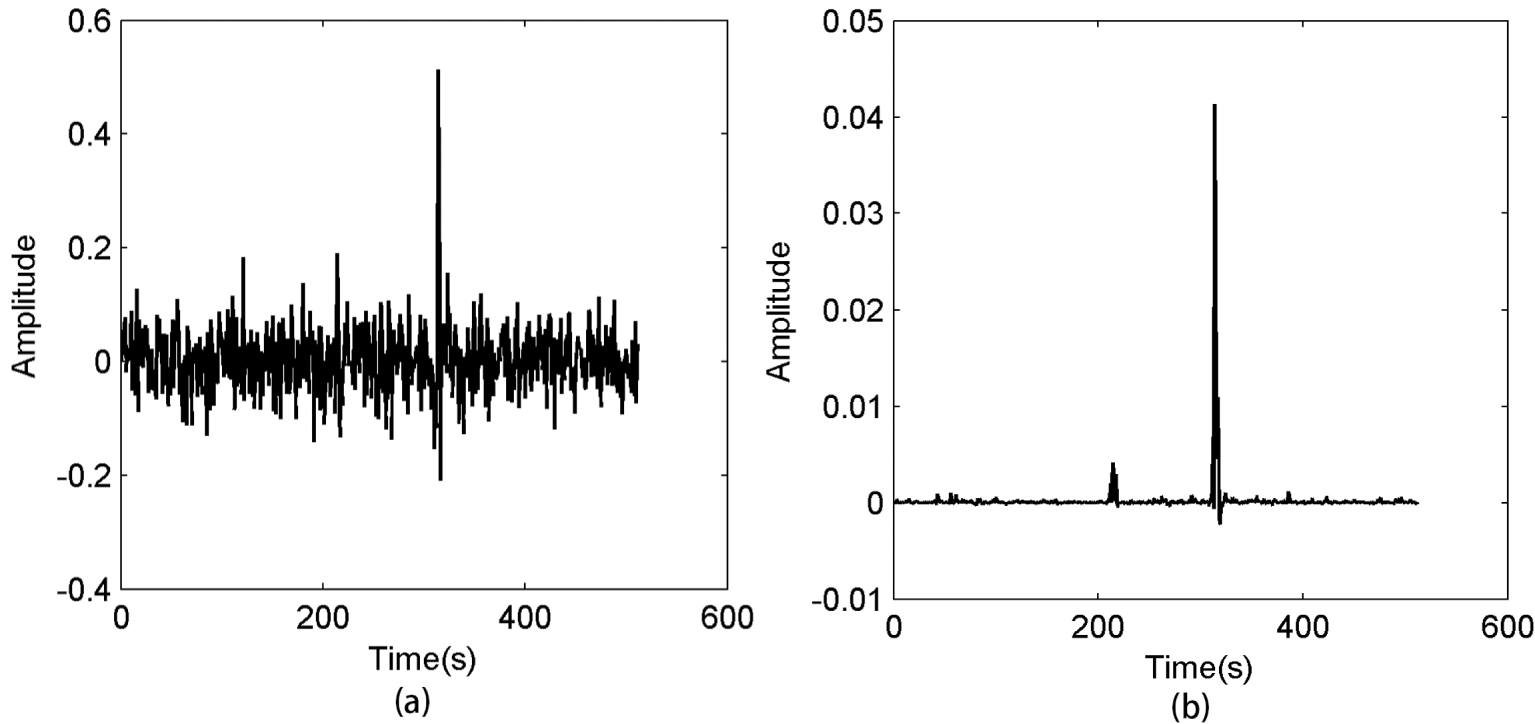
Next comes the training process of the SVM. For the training set of the SVM classifier, we chose here 1000 groups of signal samples and 1000 groups of noise samples to form the training set. The signal samples are were randomly generated by using Ricker wavelets with the amplitudes ranging from 0.1 to 1 and frequencies ranging from 100 to 500 Hz. The noise samples were randomly generated with WGN and real noise with different levels. Through training, we can obtain the trained SVM classifier.
We compared the proposed method with the STA/LTA and CNN, and the detection results are shown in Figure 6. The proposed method can accurately detect two microseismic signals and there is no misjudgment. In the case of low SNR, we can still accurately detect the microseismic signals, while there are many detection errors with the STA/LTA and CNN methods. It is difficult to choose a suitable threshold for the STA/LTA method especially when the SNR is low. CNN achieves accurate detection at high SNR, but it does not work well for low SNR either. In contrast, the proposed method avoids threshold setting and the detection result of the proposed method is accurate at low SNR.
Detection results of Figure 2 by the proposed method, STA/LTA and CNN.
4.2. Statistical experiments
In order to verify the validity of the proposed method, we pick 500 groups of samples to make the experiment. A Ricker wavelet is used to simulate the signal. The dominant frequency of Ricker wavelets is 200 Hz. The sampling frequency is 1000 Hz. We add different WGNs to pure Ricker wavelets and change the amplitudes of the Ricker wavelets. The detection results of the proposed method, STA/LTA and CNN are listed in Tables 1, 2 and 3, respectively.
Accuracy of synthetic signal detection by the proposed method
| Amplitude | SNR | |||
|---|---|---|---|---|
| −5 dB | −6 dB | −7 dB | −8 dB | |
| 1 | 100% | 99.2% | 92.4% | 87% |
| 0.5 | 100% | 98.6% | 92.2% | 85% |
| 0.2 | 99.8% | 98.2% | 91.4% | 80% |
Accuracy of synthetic signal detection by STA/LTA
| Amplitude | SNR | |||
|---|---|---|---|---|
| −5 dB | −6 dB | −7 dB | −8 dB | |
| 1 | 97% | 90.2% | 86.4% | 70% |
| 0.5 | 90% | 89.5% | 85.6% | 69% |
| 0.2 | 87% | 87% | 83.4% | 63.4% |
Accuracy of synthetic signal detection by CNN
| Amplitude | SNR | |||
|---|---|---|---|---|
| −5 dB | −6 dB | −7 dB | −8 dB | |
| 1 | 97.8% | 94% | 89% | 76% |
| 0.5 | 92.5% | 89.6% | 85% | 73.1% |
| 0.2 | 91% | 88% | 84.6% | 68.2% |
ROC curves of the proposed method, STA/LTA and CNN.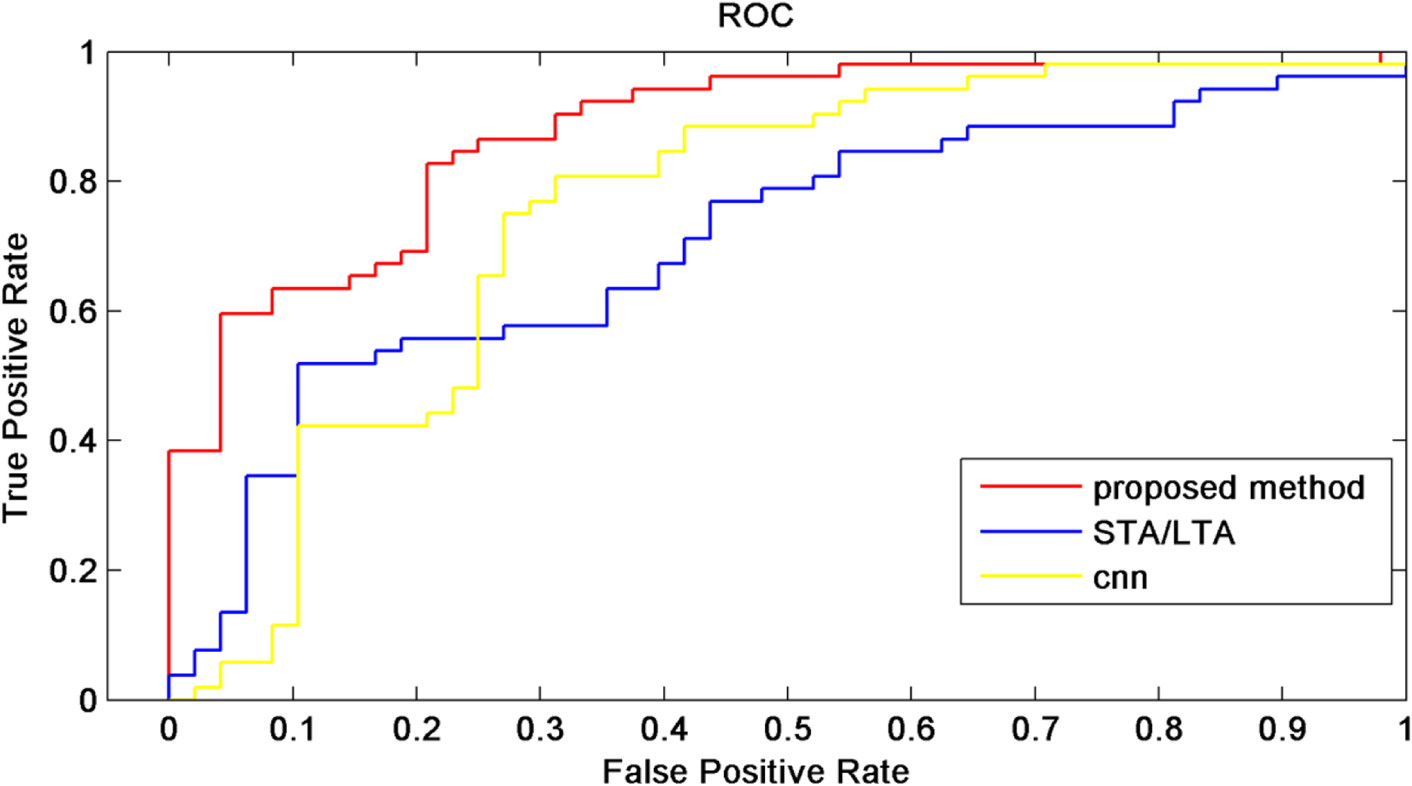
The field microseismic record.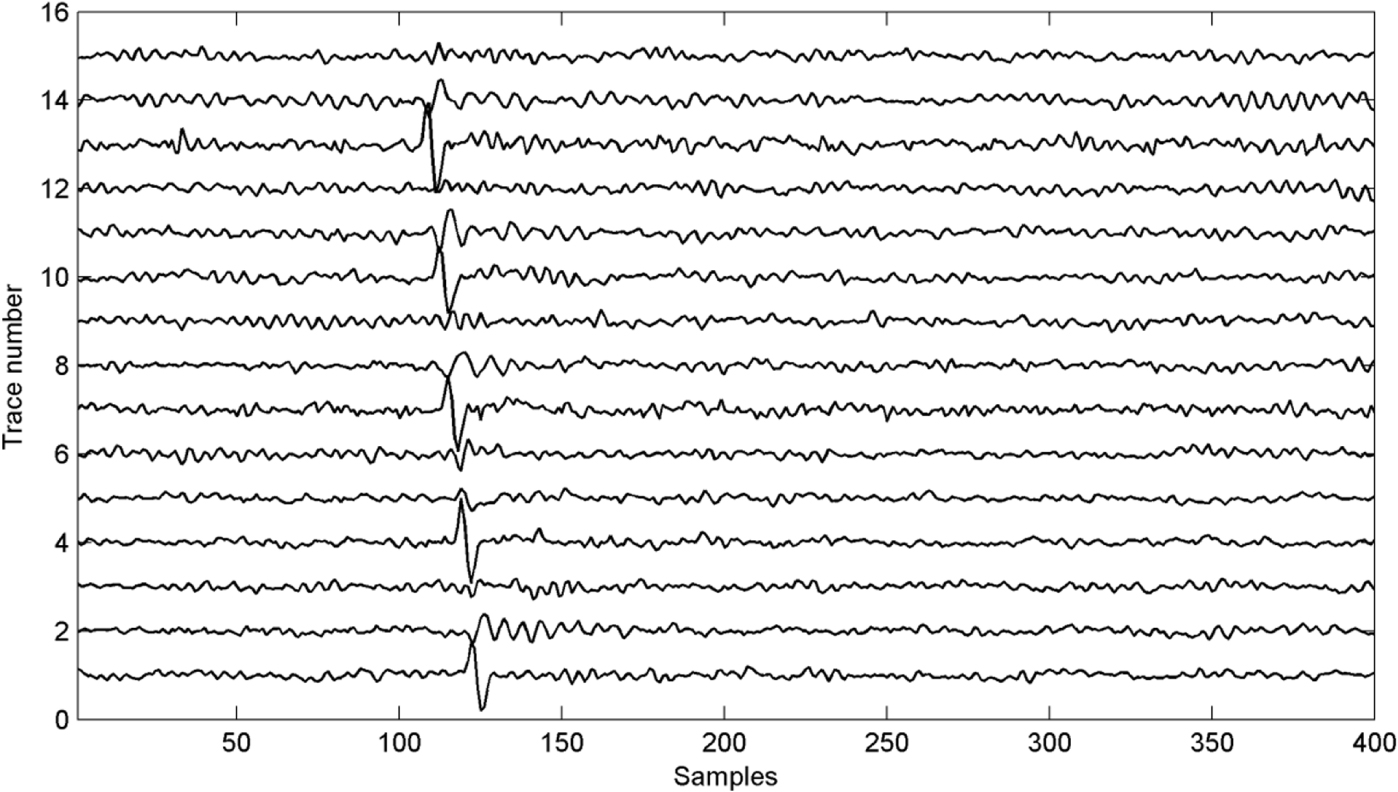
From Tables 1, 2 and 3, we can see that the detection accuracy decreases as the SNR and signal amplitude decrease. The proposed method achieves higher accuracy at low SNR compared with the STA/LTA and CNN. The accuracy of the proposed method is 80% when the SNR is −8 dB. The accuracy of STA/LTA and CNN is only 60%–76%. We draw receiver operating characteristic (ROC) curves of 100 groups of samples when SNR is −8 dB and the amplitude of the Ricker wavelet is 0.2 as shown in Figure 7. A method works more accurately if its ROC curve is closer to the upper left corner. The AUC is the value of the area under the ROC curve which is used to conclude whether a classifier is excellent. When an AUC value of a method is larger, this method has higher accuracy. The AUC values of the proposed methods, STA/LTA and CNN, are 0.8570, 0.7091 and 0.7536, respectively. As shown by Figure 7, the ROC curve of the proposed method is closer to the upper left upper corner and its AUC value is larger than that of the other two methods. Thus the proposed method has higher accuracy than the other two methods. To further verify the effectiveness of the proposed method, we add real noise with different levels to the above synthetic microseismic signals to compose 300 group samples: the amplitude of synthetic microseismic signals is 1 in the first 100 groups, 0.5 in the second 100 groups, and 0.2 in the last 100 groups. The detection results of the proposed method, STA/LTA and CNN are listed in Table 4. We can see that the proposed method still has the highest accuracy in all cases.
Detection accuracy of synthetic signal contaminated with real microseismic noise
| Amplitude | 1 | 0.5 | 0.2 |
|---|---|---|---|
| The proposed method | 100% | 95% | 82% |
| STA/LTA | 93% | 71% | 60% |
| CNN | 95.6% | 77% | 70% |
Detection results of Figure 8 by the proposed method, STA/LTA and CNN.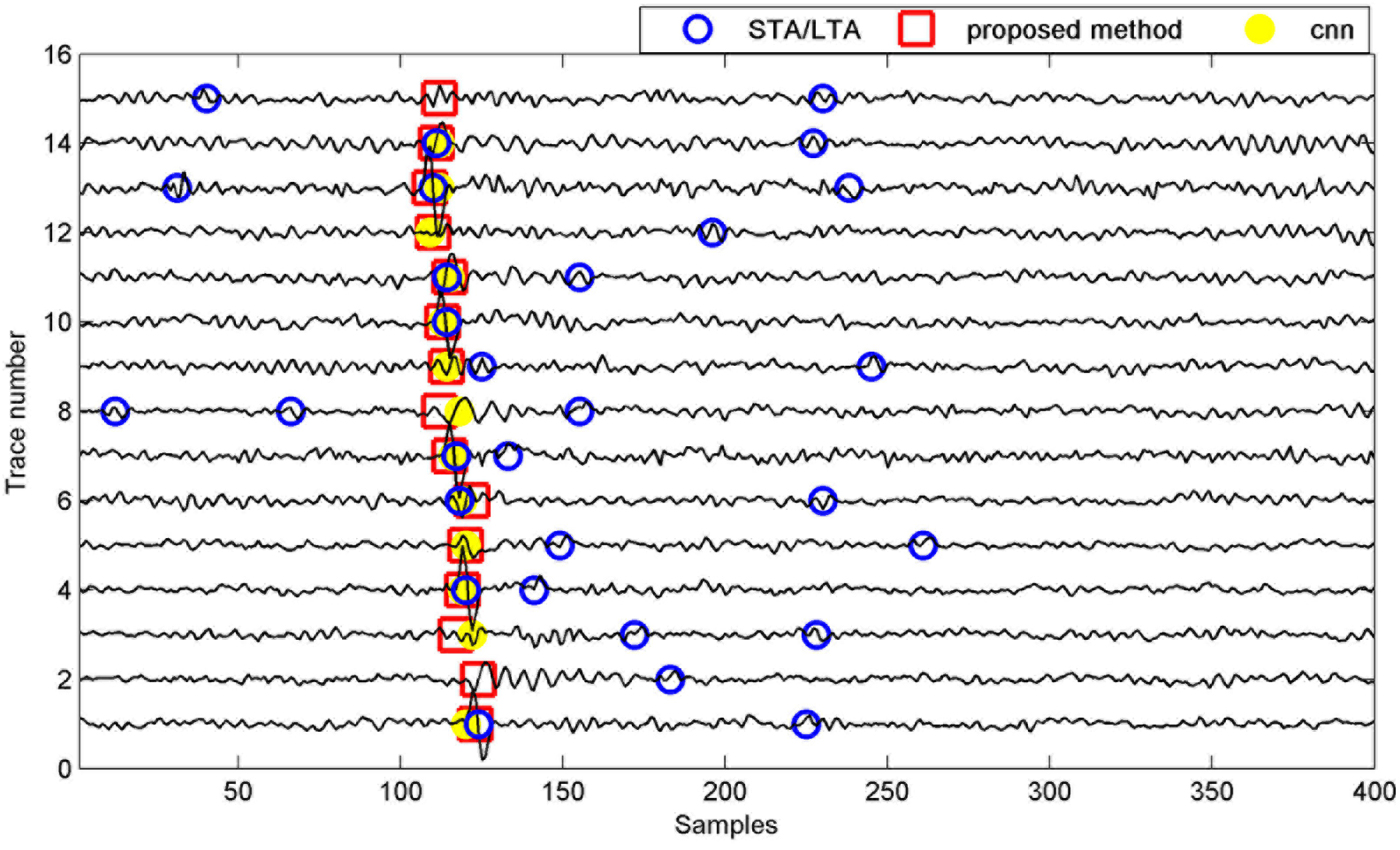
4.3. Real microseismic and desert seismic data
In order to prove the validity of the proposed method in dealing with real data, we selected for analysis and processing a real microseismic record with 15 traces in a certain area of China, as shown in Figure 8 (this record is also used in some published papers such as Li et al. [2018], Zhu et al. [2016]). We can see that the amplitudes of signals in some traces are too weak to detect. These weak signals also have waveforms similar to those of the noise. The detection results of the proposed method, STA/LTA and CNN are shown in Figure 9. The STA/LTA method does not work well for this situation. Some noise with a similar amplitude and waveform is identified as a signal by the STA/LTA method. CNN identifies the low-amplitude signals as noise and thus they cannot be detected. High-frequency weak microseismic signal detection is very challenging for methods based on energy or deep learning. These weak signals can be accurately detected by the proposed method which performs well in low SNR.
This challenge also appears in the desert record. The random noise in a desert seismic record is concentrated to the low frequency bands which often overlaps with the seismic signal. It causes great difficulty in desert seismic signal detection. Figure 10 shows a real desert record with 30 traces. We can see that desert noise has a low frequency and a waveform similar to that of the signal. In this example, we also compare the proposed method with the STA/LTA and CNN, and their detection results are shown in Figure 11. The performance of the STA/LTA dramatically decreases for weak desert seismic signal detection. Most signals can be detected by the CNN, but some noise sequences are also identified as signals. The proposed method has the highest accuracy compared with the STA/LTA and CNN.
The field desert record.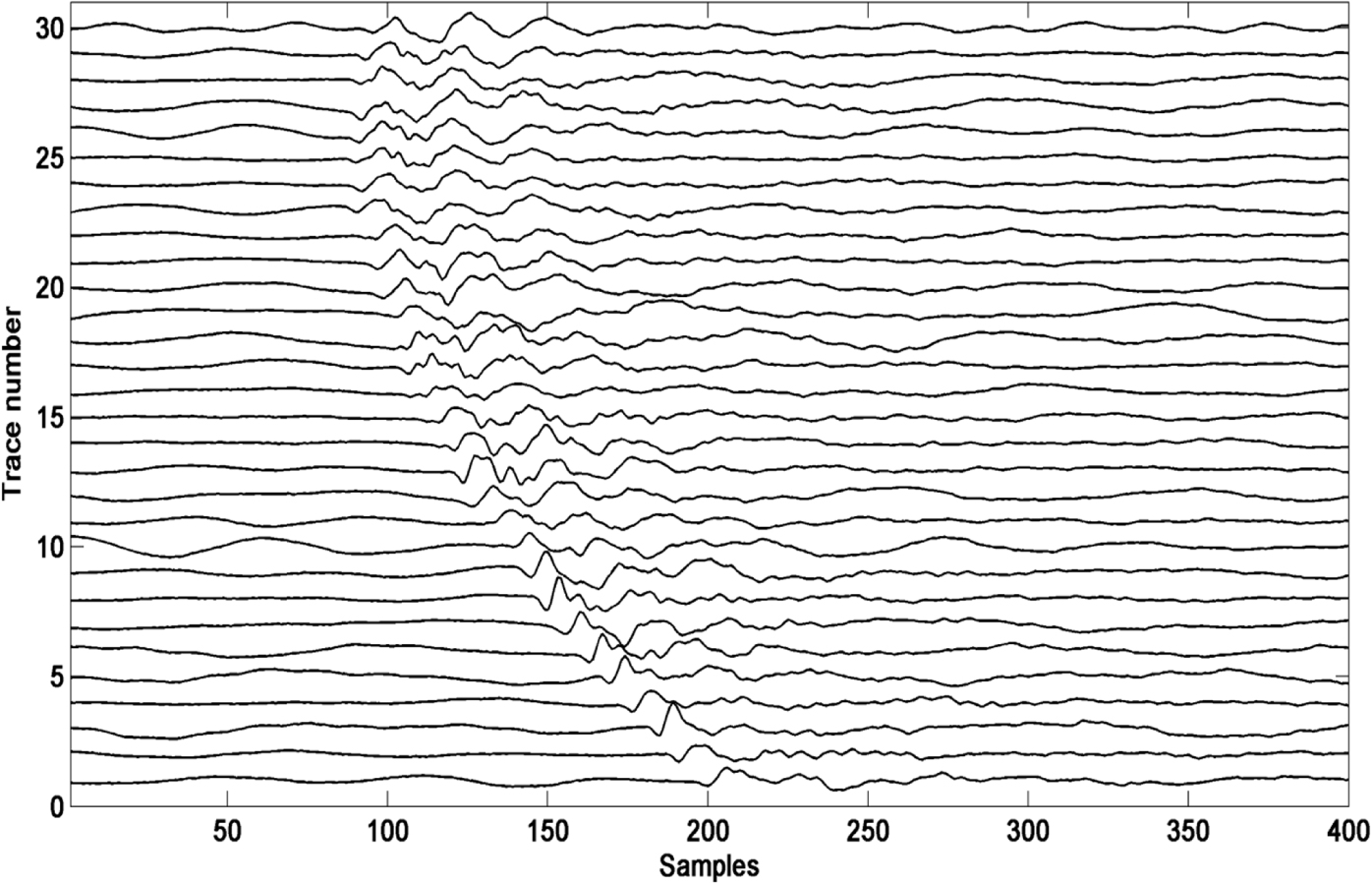
Detection results of Figure 10 by the proposed method, STA/LTA and CNN.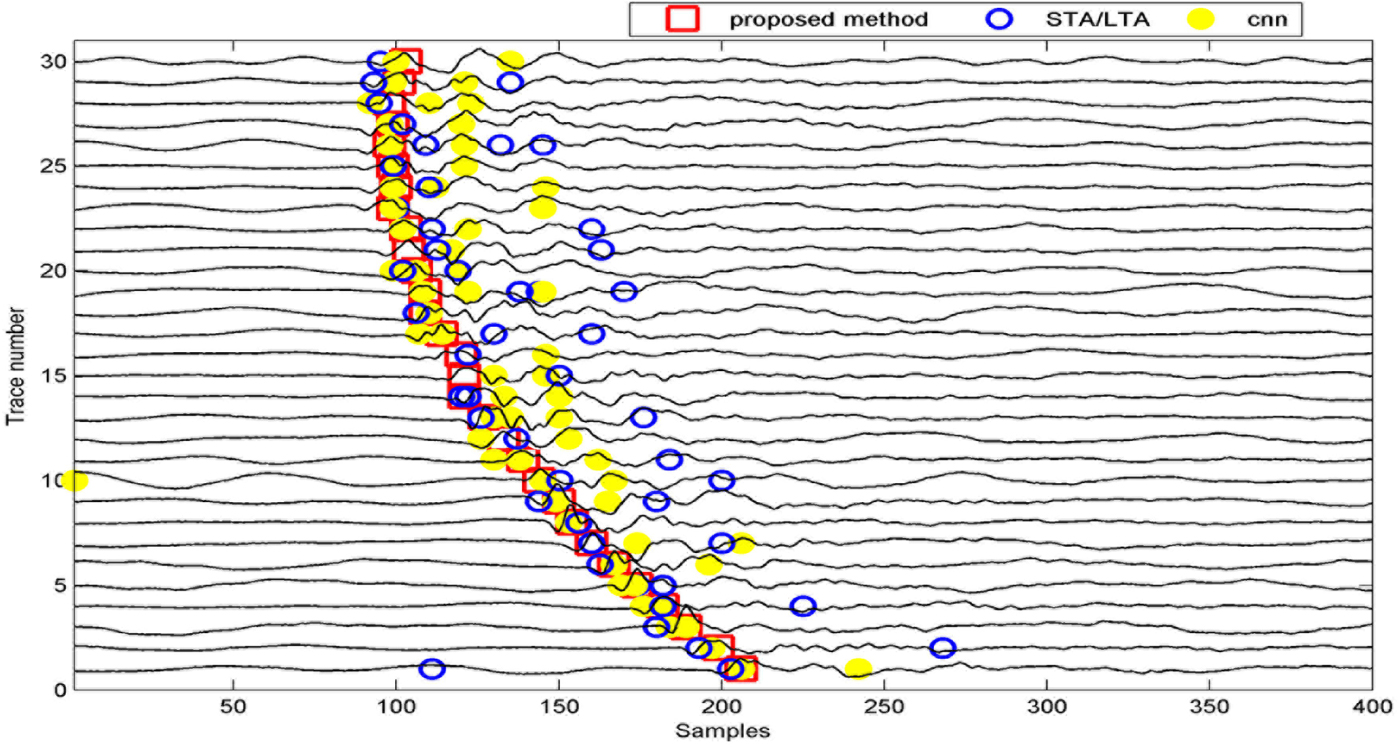
5. Conclusion and discussion
In this paper, shearlet energy entropy is used as a signal feature to detect effective signals. This feature can better differentiate the signal from the noise than a simple energy computation. The SVM classifier is trained with the extracted feature. There is no need to select a reasonable signal detection threshold with the use of SVM. The detection errors due to inappropriate threshold selection can be reduced. The signal is detected in an intelligent way by the proposed method. A large number of experiments demonstrate the potential and superiority of this proposed method for low-amplitude microseismic and seismic signal detection. It requires much fewer training datasets than the CNN- based signal detection methods.
In the proposed method, shearlet energy entropy is used as a feature to train a SVM classifier for signal detection. A more effective classifier can be obtained by combining more features. In addition, a more refined kernel-function selection in the SVM such as a mixed-kernel function can further increase the classification accuracy.
Acknowledgements
This research is financially supported by the National Natural Science Foundations of China (under grants 41730422, 41974143, 41574096). We thank the efforts made by Professor Ghislain de Marsily. We also thank the anonymous reviewers for their comments and suggestions.



 CC-BY 4.0
CC-BY 4.0