Plan
Comptes Rendus
no. 9-10

A molecular orbital study of C–H···Cl– and N–H···Cl– hydrogen bonds. Inferences on selected metal complexes and on protein ClC Cl– channels
Sandra Defazio1  ; Gabriella Tamasi1  ; Renzo Cini1
1 Department of Chemical and Biosystem Sciences and Technologies, University of Siena, Via Aldo Moro 2, 53100 Siena, Italy
Comptes Rendus. Chimie, Volume 8 (2005) no. 9-10, pp. 1584-1609.

Résumés

Hydrogen bond type interactions X–H···Y– (X: C, N, O; Y: Cl) for systems that contain 1,3-imidazole (IM), 1,3-pyrimidine (PYM), N-methylacetamide (MAA), methylammonium (MA), methylamine (MAB), 1-hydroxy-4-methylbenzene (HMB), N-methylguanidinium (MGU), methanol (MeOH), have been investigated via the methods of density functional theory (DFT) at the B3LYP functional level and ab initio MP2, by using mostly the standard 6-31G** and 6-31+G** basis sets. The study helps in understanding structural aspects of at least Re/Ru-imidazole, Ru-pyrimidine and Ru-arene complexes and allows to evaluate the adduct formation energy (electronic), for species of the type M(IM)N–H···Cl–, M(IM/PYM)C–H···Cl–, whose upper limits are ca. –24 and –10 kcal at gas phase. Computed structural and energy parameters help also in evaluating the mechanism of extrusion of Cl– anions in certain ClC Chloride channels from membrane proteins. The hydrogen bond formation energy for selected aminoacid residues with Cl– ranges ca. –106 to –15 kcal mol–1. Owing to the predominance of CONH peptide bonds in every protein system, the formation of the C(=O)–N–H···Cl– hydrogen bond (ΔEel ≈ –21 kcal) is often revealed in X-ray structures of protein···chloride adducts. .

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

Les interactions de type liaison hydrogène X–H···Y– (X: C, N, O; Y: Cl) dans les systèmes contenant les composés 1,3-imidazole (IM), 1,3-pyrimidine (PYM), N-méthylacetamide (MAA), méthylammonium (MA), méthylamine (MAB), 1-hydroxy-4-méthylbenzène (HMB), N-méthylguanidinium (MGU), méthanol (MeOH) et, ont été explorées à l'aide des méthodes de fonctionnelle de densité (DFT) au niveau B3LYP et ab initio MP2, en utilisant le plus souvent les bases standards 6-31G** et 6-31+G**. Cette étude permet de comprendre les aspects structuraux des complexes Re/Ru-imidazole, Ru-pyrimidine et Ru-arene au moins et permet d'évaluer l'énergie de formation (électronique) des adduits, pour des espèces de type M(IM)N–H···Cl–, M(IM/PYM)C–H···Cl–, dont les limites supérieures en phase gazeuse sont d'environ –24 et –10 kcal. Les calculs sur les paramètres structuraux et d'énergie amènent à comprendre le mécanisme d'extrusion des anions Cl– dans certains canaux ClC chlorure des membranes protéiniques. L'énergie de formation de la liaison hydrogène des résidus sélectionnés d'acide aminé avec Cl– est de l'ordre de –106 à –15 kcal mol–1. En raison de la prédominance de liaisons peptide CONH dans tous les sytèmes protéiniques, la formation de la liaison hydrogène C(=O)–N–H···Cl (ΔEel ≈ –21 kcal), est souvent révélée dans les structures aux rayons X des adduits protéine clorure. .

Compléments :
Des compléments sont fournis pour cet article dans le fichier séparé :

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2004.11.042
Keywords: Molecular orbital, DFT, Hydrogen bond, Pyrimidine, Imidazole, Aminoacid, Ruthenium
Mots clés : Orbitale moléculaire, Fonctionnelle de densité, Liaison hydrogène, Pyrimidine, Imidazole, Acide aminé, Ruthénium
Sandra Defazio 1 ; Gabriella Tamasi 1 ; Renzo Cini 1

1 Department of Chemical and Biosystem Sciences and Technologies, University of Siena, Via Aldo Moro 2, 53100 Siena, Italy 
@article{CRCHIM_2005__8_9-10_1584_0,
     author = {Sandra Defazio and Gabriella Tamasi and Renzo Cini},
     title = {A molecular orbital study of {C{\textendash}H{\textperiodcentered}{\textperiodcentered}{\textperiodcentered}Cl\protect\textsuperscript{{\textendash}}} and {N{\textendash}H{\textperiodcentered}{\textperiodcentered}{\textperiodcentered}Cl\protect\textsuperscript{{\textendash}}} hydrogen bonds. {Inferences} on selected metal complexes and on protein {ClC} {Cl\protect\textsuperscript{{\textendash}}} channels},
     journal = {Comptes Rendus. Chimie},
     pages = {1584--1609},
     publisher = {Elsevier},
     volume = {8},
     number = {9-10},
     year = {2005},
     doi = {10.1016/j.crci.2004.11.042},
     language = {en},
}
TY  - JOUR
AU  - Sandra Defazio
AU  - Gabriella Tamasi
AU  - Renzo Cini
TI  - A molecular orbital study of C–H···Cl– and N–H···Cl– hydrogen bonds. Inferences on selected metal complexes and on protein ClC Cl– channels
JO  - Comptes Rendus. Chimie
PY  - 2005
SP  - 1584
EP  - 1609
VL  - 8
IS  - 9-10
PB  - Elsevier
DO  - 10.1016/j.crci.2004.11.042
LA  - en
ID  - CRCHIM_2005__8_9-10_1584_0
ER  - 
%0 Journal Article
%A Sandra Defazio
%A Gabriella Tamasi
%A Renzo Cini
%T A molecular orbital study of C–H···Cl– and N–H···Cl– hydrogen bonds. Inferences on selected metal complexes and on protein ClC Cl– channels
%J Comptes Rendus. Chimie
%D 2005
%P 1584-1609
%V 8
%N 9-10
%I Elsevier
%R 10.1016/j.crci.2004.11.042
%G en
%F CRCHIM_2005__8_9-10_1584_0
Sandra Defazio; Gabriella Tamasi; Renzo Cini. A molecular orbital study of C–H···Cl– and N–H···Cl– hydrogen bonds. Inferences on selected metal complexes and on protein ClC Cl– channels. Comptes Rendus. Chimie, Volume 8 (2005) no. 9-10, pp. 1584-1609. doi : 10.1016/j.crci.2004.11.042. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2004.11.042/

Version originale du texte intégral

1 Introduction

Hydrogen bonds are key forces in molecular recognition and play important roles in the stability of biological systems [1–6], of organic, inorganic, and coordination aggregates [7–10]. These features have been taken into account to design new drugs [11] and to design new high affinity ligands for neutral, anionic, cationic molecules [12–15]. Recently, the X-ray structures of channels that conduct chloride (Cl–) ions across cell membranes have been published on journals (see Ref. [16]) and/or deposited in the Protein Data Bank, PDB [17]. Several other X-ray structures of proteins/Cl– adducts are reachable via PDB (January 2004), by searching ‘chlorine’ (ca. 10). It has to be noted that amide type N–H, C–NH3+, C–OH, C=NH2+, imidazole type N–H functions are all involved in the interactions to Cl–. The ClC channel-containing proteins play a role in governing the electrical activity of muscle cells, of certain neurons, the transport of electrolytes, the acidification of intracellular vesicles, etc. [16]. Recently an extensive theoretical study on bacterial ClC Cl– pores as performed through the methods of molecular mechanics and dynamics, was published [18].

The classic H-bonds (X–H···Y) involves a neutral molecule able to ‘donate’ a hydrogen atom covalently linked to an electronegative atom (X), to an acceptor molecule which contains an electronegative atom carrying at least a lone electron pair (Y) [19]. The investigations on conventional H-bonds consist of the general understanding of the requirements for their formation and of the analysis of their geometrical and electronic properties. Some frequently mentioned requirements for strong H-bonds are the following. (a) A short distance between the X and Y atoms. If this is the case and in the absence of any structural constraints the interaction is often referred as ‘short strong H-bond’, SSHB [20]. (b) A relatively non-polar environment. The strength of SSHB decreases rapidly as the polarity of the medium increases [20–24]. (c) Identical pKa (or proton affinity in the gas phase) of the two hydrogen bonded molecules. It has been proposed that the strongest SSHB is formed when the pKas are identical for X and Y [25–27].

Even though the conventional H-bonds have attracted a large amount of research efforts, recent studies have shown the importance of interactions for which Y is Cl, S, π-systems and X may sometimes be a carbon atom [1,2,19,28]. These linking forces are often named as ‘H-bond type interactions’ (here after HBTIs) mostly because they are not accepted by the majority of chemists as real H-bonds and also because their nature is largely unknown. Recently, a new type of H-bond termed as anti-hydrogen bond (anti-H-bond) has been proposed by Hobza et al. [29]. As opposite to the features observed in the accepted H-bonds, the anti-H-bonds show a shortening of the X–H (usually C–H) bond distance and a blue shift of the C–H stretching frequency.

In addition to the issues just mentioned it recently happened to us to find that (pyrimidine)C–H···N(pyrimidine) and (imidazole)C–H···Cl interactions play important structural roles in metal complexes [30,31]. Those findings reinforced in our mind the plans to perform a theoretical analysis of the forces that pair several types of N–H/C–H donors and Cl– or MCl acceptors, as well as those that pair imidazole molecules and pyrimidine molecules. Further calculations aimed to analyze HBTIs like O–H···Cl and C–H···N, have been carried out. All the computations have been performed through both DFT and ab initio methods. We wish to report here on the selected results from this work.

2 Computational methods

All the calculations were carried out through the Gaussian98 package [32] implemented on SGI Origin 2000 and Origin 3800, and on IBM SP4 machines located at CINECA (North–East Inter-University Consortium for Advanced Computing, Casalecchio di Reno, Italy). The ab initio analysis was performed on the isolate molecules or aggregates via the RHF, MP2, MP4, CCSD(T) methods by using the 6-311G, 6-31G*, 6-31+G** or 6-311++G (3df, 3pd) basis sets [33]. In the cases the full structure optimizations were carried out by taking into account the electron correlation and diffuse basis sets, the starting structures came from pre-optimization procedures through lower basis sets or through density functional methods. The optimizations were carried out to reach the criteria of convergence implemented in Gaussian98 (maximum force, 0.000450 mdyne; root mean square (rms) force 0.000300 mdyne; maximum displacement 0.001800 Å; rms displacement 0.001200 Å). Minima were considered correct when no imaginary frequency was found from the hessian analysis (see below). The treatment of the solvent effects was performed on the selected previously optimized structures through the procedure by Tomasi (PCM, polarized continuum model, see [33] and references therein).

The density functional analysis was carried out on the isolate molecules at the B3LYP/6-31G*, /6-31G** and /6-31+G** levels [33]. The corrections for the basis set superposition error were carried out via the Massage procedure of Gaussian98. The analysis of the natural bond orbitals (NBOs) was carried out through the Gaussian-NBO program Version 3.1 [34].

3 Results and discussion

The selected molecules and molecular aggregates studied in this work along with the respective level of theory and electronic energies (Eel) are listed in Table 1. The selected geometrical parameters are shown in Tables 2–11. The electronic ΔEel (kcal) formation energies for aggregates are reported in Table 12. Not all the parameters discussed in the text are reported in the corresponding Tables and vice-versa. More comprehensive listing of geometrical parameters and orthogonal coordinates for refined systems are reported in the Supporting Material. Drawings of formulas for selected systems are reported in Figs. 1 and 2.

Table 1

Total electronic energy (Eel, hartrees) for the selected isolate molecules and adduct systems as computed through Gaussian98 via ab initio and DFT methods. IM = 1,3-imidazole, PYM = 1,3-pyrimidine, MePYM = 4-methyl-1,3-pyrimidine, AA = acetamide, MA = methylammonium, MAA = N-methylacetamide, MAB = methylamine, HMB = hydroxyl-4-methylbenzene, MeOH = methanol, MGU = methylguanidinium

TheoryIon, Molecule, Aggregate/Eel
Isolate monoatomic ions
Cl–F–
B3LYP/6-31G**–460.25223–99.75409
B3LYP/6-31+G**–460.27473–99.85969
MP2/6-31+G**–459.67115–99.62385
MP4(SDTQ)/6-31+G**–459.68584
Isolate molecules
HFHClH2OIMIMH+PYMMePYM
B3LYP/LANL2DZ–303.58179
B3LYP/6-31G**–100.42746–460.80078–76.41974–226.22309–264.32949–303.65460
B3LYP/6-31+G**–100.45137–460.80321–76.43405–226.23538–226.60810–264.34081–303.66670
B3LYP/6-31++G**–460.80327–76.43412
RHF/6-31G*–100.00291
MP2/6-31+G**–100.21581–460.20762–76.23311–225.56846–225.93974–263.55699
–263.55675 a
MP3/6-31+G**–100.21481–263.57221 a
–263.57221 b
MP4(SDTQ)/6-31+G**–100.22298–225.62499 a
CCSD(T)/6-31G**–100.20115–460.22457–76.23158–225.60592–263.60579 a
CCSD(T)/6-31+G**–100.22158–460.22691–76.24439
CCSD(T)/6-31++G**–460.22706–76.24468
RHF/6-31G* c–100.00291–460.05998–76.01075
RHF/6-31+G* c–100.01487–460.06102–76.01774
MP2/6-311+G(3df, 2p) d–460.29699
AAMAAMAMABMeOHMGUHMB
B3LYP/6-31+G**–209.23796–248.54874–96.22822–95.87185–115.73487–245.10152–346.81408
MP2/6-31+G**–208.62882–247.80372–95.91782–95.55901–115.39352–244.36477–345.75024
Isolate molecules in reaction field e
HFHClIMPYMMAAMAMGU
B3LYP/6-31G**–100.43778–460.80467–226.24360
B3LYP/6-31+G**–460.80722–226.25228–264.35997–284.56778–96.34109–245.21067
–226.25172 f
Molecular aggregates
ClH···Cl–FH···F–ClH···OH2FH···OH2
B3LYP/6-31G**–921.10225–200.28999–537.23341–176.86369
B3LYP/6-31+G**–537.24779–176.90146
B3LYP/6-31++G**–537.24795
B3LYP/6-311++G**–921.17766–200.44523–537.30278
RHF/6-31G*–176.02806
CCSD(T)/6-31G**–536.46694–176.44793
CCSD(T)/6-31+G**–536.48157–176.48140
CCSD(T)/6-311++G**–921.01781–200.03573–536.56057
(IM)N1–H···Cl–(IM)C2–H···Cl–(IM)C4–H···Cl–(IM)C5–H···Cl–(IM)N1–H···F–(IM)C2–H···F–(IMH+)N1···H+···Cl–
B3LYP/6-31G**–686.51920–686.49297–686.48135–686.49686–326.10935–326.05063
B3LYP/6-31+G**–686.54793–686.52402–686.51315–686.52803–687.05590
MP2/6-31+G**–685.28240–685.79360
MP4(STDQ)/6-31+G**–685.35262 a
(IM)N–H···N(IM) (coplanar)(IM)N–H···N(IM) (free)(IM)C2–H···N(IM) (C2–H2···N1′ 180°)
B3LYP/6-31+G**–452.48378–452.48484–452.47518
MP2/6-31+G**–451.15334 b
(PYM)C2–H···Cl–(PYM)C5–H···Cl–(PYM)C6–H···Cl–(MePYM)C7–H···Cl–
B3LYP/6-31G**–763.93089
B3LYP/6-31+G**–724.62089724.63635–724.63042
MP2/6-31+G**–723.23546 b–723.25304 b–723.24565 b
(PYM)C2–H···N1(PYM)(PYM)C2–H···N1(PYM)/(PYM)C6′–H···N3(PYM)(PYM)C5–H···N1(PYM)
B3LYP/6-31G**–528.66489–528.66342
B3LYP/6-31+G**–528.68391–528.68541–528.68480
MP2/6-31+G**–527.11836 b–527.12085 b–527.11969 a
–527.11972 b
MP3/6-31+G**–527.14999 a
–527.14995 b
(AA)NH···Cl–(MAA)NH···Cl–(MA)N···H–Cl–(MAB)NH···Cl–(HMB)OH···Cl–MeOH···Cl–
B3LYP/6-31+G**–669.54618–708.85704–556.69493–556.15988–807.12115–576.03341
MP2/6-31+G**–668.33620–707.51306–555.78458–555.24522–805.45789–575.09019
(MGU)NH2···Cl–(MGU)(CH3)NH···Cl–(MAA)NH···F–
B3LYP/6-31+G**–705.54452–705.54606–348.46996
MP2/6-31+G**–704.20801–704.21068–347.48901

a Single-point calculation with the coordinates optimized at B3LYP/6-31G** level.

b Single-point calculation with the coordinates optimized at B3LYP/6-31+G** level.

c Refs. [35–37].

d Ref. [38].

e Dielectric constant for water unless otherwise specified.

f Dielectric constant for methanol.

Table 10

Selected geometrical parameters for computed PYM···PYM systems

(PYM)C2–H···N1'(PYM)(PYM)C2–H···N1'(PYM)/(PYM)C6′–H···N3(PYM)(PYM)C5–H···N1'(PYM)
B3LYP 6-31+G**B3LYP 6-31G**B3LYP 6-31+G**B3LYP 6-31G**B3LYP 6-31+G**
Length (Å)1.395
C2–N11.3411.3391.339C5–C41.3941.395
C2–N31.3421.3421.342C5–C61.3941.086
C2–H21.0881.0881.087C5–H51.0851.340
N1′–C2′1.3391.3371.338N1′–C2′1.3391.341
N1′–C6′1.3401.3421.338N1′–C6′1.3402.501
C6′–H6′1.0881.0891.088H5···N1′2.4433.587
H2···N1′2.4622.5412.647C5···N1′3.529
C2···N1′3.5513.4603.573
H6′···N32.5122.559
C6′···N33.4403.514
Angle (°)
C2–H2···N1′180141.5142.7C5–H5···N1′180180
C6′–H6′···N3142.5146.0C2′–N1′–C6′115.9116.1
N1–C2–N3126.5126.7126.6C4–C5–C6116.0116.1
C2–N3–C4116.2116.1116.2
C2′–N1′–C6′116.6116.1116.2
N1′–C6′–C5′122.16121.8121.8
Table 11

Selected geometrical parameters for computed AA···Cl–, MAA···X– (X = Cl, F), MA···Cl–, HMB···Cl–, MGU···Cl–, MAB···Cl–, MeOH···Cl– systems at B3LYP/6-31+G** and MP2/6-31+G** levels

(AA)N–H···Cl–(MAA)N–H···Cl–(MAA)N–H···F–(MA)N···H–Cl–
B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**
Length (Å)
N1–C21.3481.3491.3471.3451.3371.337N1–C21.4771.472
C–O1.2421.2491.2441.2531.2541.263H–Cl1.4161.336
C–C1.5221.5151.5221.5151.5271.519H···N1.5151.683
N–H1.0381.0321.0381.0341.1391.131Cl···N2.9303.015
H···X2.1432.1292.1362.0951.3261.330Cl–H···N177.8175.4
N···X3.1813.1583.1743.1282.4652.461
Angle (°)
N–H···X177.4175.4176.9178.1179.4179.0
(HMB)O–H···Cl–(MGU)NH2NH2···Cl–(MGU)NH2N–H···Cl–
B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**
Length (Å)
O1–C21.3471.355C1–N21.3381.339C1–N21.3391.344
C2–C31.4061.405C1–N31.3291.328C1–N31.3611.365
C2–C71.4091.407C1–N41.3561.355C1–N41.3251.318
O1–H11.0040.999N2–H2a1.0491.041N2–H2b1.0471.037
C7–H71.0861.082N3–H3a1.0551.051N4–H41.0561.057
H1···Cl12.0932.090H2a···Cl2.0672.067H2b···Cl2.0852.118
O1···Cl13.0703.062N2···Cl3.0393.036N2···Cl3.0503.069
H7···Cl12.5542.490H3a···Cl2.0221.995H4···Cl2.0081.945
C7···Cl13.4253.367N3···Cl3.0092.985N4···Cl3.0102.954
Angle (°)
O1–H1···Cl1163.8163.8N2–H2a···Cl153.0153.6N2–H2b···Cl152.1151.4
C7–H7···Cl1136.5137.4N3–H3a···Cl154.4155.9N4–H4···Cl157.0159.4
(MAB)N–H···Cl–(MeOH)O–H···Cl–
B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**
Length (Å)
N1–C21.4641.463C–O1.4081.415
H–N11.0301.025O–H0.9940.989
H···Cl2.4012.369H···Cl2.1332.128
N···Cl3.4033.362O···Cl3.1173.102
Angle (°)
N–H···Cl164.0163.0O–H···Cl170.1168.1
Table 2

Bond lengths (Å) and bond angles (°) for the small molecules computed through Gaussian98 via ab initio and DFT methods

H2O
H–OH–O–HH–ClH–F
B3LYP/6-31G**0.965103.71.2860.925
B3LYP/6-31+G*0.969 c105.5 c
B3LYP/6-31+G**0.965105.81.2870.928
B3LYP/6-31++G**0.965105.71.2870.930 a
RHF/6-31G*0.911 a
RHF/6-31+G**0.913 a
CCSD(T)/6-31G**0.962103.81.2730.921
CCSD(T)/6-31+G**0.963105.31.2740.925
CCSD(T)/6-31++G**0.964105.31.274
MP2/6-31+G**0.963105.41.270 b
MP2/6-3111+G(3df, 2p)1.281 b
MP4(SDTQ)/6-31+G**0.926

a Refs. [35–37].

b Ref. [38].

c Ref. [39].

Table 3

Selected geometrical parameters for the optimized structures of 1,3-imidazole (IM) and 1,3-imidazolium (IMH+) at B3LYP level. The structural parameters optimized at the CCSD(T) and MP2 levels are also reported for comparative purposes. Self-consistent reaction field (SCRF) [33] means that the treatment of the solvent has been carried out

IMIMH+
B3LYP 6-31G**B3LYP 6-31+G**CCSD(T) 6-31G**MP2 6-31+G**B3LYP 6-31G** SCRF (water)B3LYP 6-31+G** SCRF (water)B3LYP 6-31+G** SCRF (methanol)B3LYP 6-31+G**MP2 6-31+G**
Length (Å)
N1–C21.3671.3681.3691.3621.3631.3621.3621.3371.341
C2–N31.3151.3171.3221.3251.3231.3251.3251.3371.341
N3–C41.3781.3791.3871.3841.3851.3831.3841.3841.377
C4–C51.3721.3741.3761.3761.3741.3761.3761.3641.372
C5–N11.3801.3811.3841.3791.3791.3781.3791.3841.377
N1–H11.0081.0091.0061.0211.0191.0211.0211.0141.014
Angle (°)
N3–C2–N1111.8111.6112.0111.6111.6111.6111.6107.0106.5
C2–N3–C4105.2105.4104.7105.2105.1105.2105.2110.0110.4
C5–C4–N3110.8110.7111.0110.4110.5110.4110.4106.5106.4
C4–C5–N1105.0105.1105.0105.3105.2105.3105.3106.5106.4
C2–N1–C5107.2107.3107.2107.5107.5107.5107.5110.0110.4
H1–N1–C2126.5126.4126.4126.1126.5126.2126.1124.4124.1
H1–N1–C5126.3126.3126.4126.3125.9126.3126.3125.6125.5
Table 4

Selected geometrical parameters for the optimized structures of 1,3-pyrimidine (PYM) and 4-methyl-1,3-pyrimidine (MePYM). SCRF [33] means that the treatment of the solvent (water) has been carried out

PYMMePYM
B3LYP 6-31G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G** SCRFB3LYP LANL2DZB3LYP 6-31G**B3LYP 6-31+G**
Length (Å)
N1–C21.3371.3381.3441.3381.3561.3361.336
C2–N31.3381.3391.3441.3401.3571.3381.339
N3–C41.3391.3401.3451.3461.3641.3431.344
C4–C51.3931.3951.3941.3961.4151.4011.403
C5–C61.3931.3951.3941.3961.4041.3891.390
N1–C61.3391.3401.3461.3461.3621.3411.342
C4–C71.5101.5061.506
H2–C21.0881.0871.0831.0951.0861.0891.088
H5–C51.0851.0851.0821.0971.0861.0861.086
Angle (°)
C2–N1–C6115.7115.9115.7116.7115.9115.1115.3
N1–C2–N3127.4127.1127.2126.1126.3127.5127.2
C2–N3–C4115.7115.9115.7116.7117.6116.7117.0
N3–C4–C5122.4122.3122.2121.9120.0120.6120.4
C4–C5–C6116.5116.5116.9116.6118.0117.4117.5
N1–C6–C5122.4122.2122.2121.9122.2122.6122.5
H2–C2–N1116.3116.5116.4117.0116.9116.4116.5
H2–C2–N3116.3116.4116.4116.9116.8116.1116.2
Table 5

Selected geometrical parameters for computed acetamide (AA), N-methylacetamide (MAA), methylamine (MAB), methylammonium (MA), N-methylguanidinium (MGU), methanol (MeOH), 1-hydroxy-4-methylbenzene (HMB). SCRF [33] means that the treatment of solvent (water) has been carried out

AAMAAMGU
B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G** SCRFB3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G** SCRF
Length (Å)
N1–C21.3691.3731.3691.3681.346C1–N21.3431.3421.345
C–O1.2251.2331.2281.2371.244C1–N31.3391.3381.338
C–C1.5201.5131.5201.5141.515C1–N41.3351.3321.334
N–H1.0081.0071.0091.0071.026N4–C51.4681.4651.459
N2–H1.0101.0081.019
N3–H1.0101.0081.019
N4–H1.0111.0101.032
Angle (°)
N–C–O121.9121.9122.8122.9122.3N2–C1–N3119.5119.4119.3
N3–C1–N4120.4120.3121.3
N4–C1–N2120.2120.3119.3
MeOHHMBMAMAB
B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31+G** SCRFB3LYP 6-31+G**MP2 6-31+G**
Length (Å)
O/N–H1.4251.4290.9660.9671.0261.0231.0321.0161.013
C–O/N0.9650.9641.3741.3801.5161.5071.4971.4671.464
Table 6

Selected geometrical parameters for the H2O···HX (X = Cl, F) systems computed through Gaussian98 via ab initio and DFT methods

FH···OH2
RHF 6-31G**CCSD(T) 6-31G**CCSD(T) 6-31+G**B3LYP 6-31G**
Length (Å)
O···H1.8091.7661.7411.721
O···F2.7292.6972.6792.659
F–H0.9200.9310.9380.939
O–H0.9480.9610.9630.964
Angle (°)
H···O–H126.4126.9126.4126.7
H–O–H107.2106.2107.2106.7
ClH···OH2
CCSD(T) 6-31G**CCSD(T) 6-31+G**CCSD(T) 6-31++G**CCSD(T) 6-311++G**B3LYP 6-31G**B3LYP 6-31+G**B3LYP 6-31++G**B3LYP 6-311++G**
Length (Å)
O···H1.9161.9401.9391.9451.7991.8551.8551.864
O···Cl3.2013.2243.2243.2323.1083.2243.1603.168
Cl–H1.2851.2841.2851.2871.3091.3051.3051.305
O–H0.9620.9640.9640.9600.9640.9650.9650.962
Angle (°)
H···O–H127.3126.9126.9127.6126.7126.3126.3126.6
H–O–H105.5106.3106.3104.8106.5107.3107.3106.9
Table 7

Selected bond distances (Å) for computed IM···X– (X = Cl; F) and IMH+···Cl–. SCRF [33] means that the treatment of solvent (water) has been carried out

(IM)N1···Cl–(IMH+)N1···H+···Cl–(IM)N1···F–
B3LYP 6-31G**B3LYP 6-31+G**MP2 6-31+G**B3LY 6-31G** SCRFB3LYP 6-31+G**MP2 6-31+G**B3LYP 6-31G**B3LYP 6-31G** SCRF
N1–C21.3551.3561.3571.3571.3191.3291.3521.353
C2–N31.3281.3291.3391.3251.3601.3631.3421.335
N3–C41.3781.3781.3781.3861.3821.3771.3741.381
C4–C51.3781.3811.3861.3761.3721.3791.3851.381
C5–N11.3711.3711.3691.3761.3781.3771.3731.376
N1–H11.0601.0531.0491.034
X–H1.3681.3171.0021.135
H···X2.0042.0422.0002.099
N···H1.6251.7511.5311.266
N···X3.0643.0953.0503.1322.9933.0682.5322.401
(IM)C2···Cl–(IM)C4···Cl–(IM)C5···Cl–(IM)C2···F–
B3LYP 6-31G**B3LYP 6-31+G**B3LYP 6-31G** SCRFB3LYP 6-31G**B3LYP 6-31+G**B3LYP 6-31G**B3LYP 6-31+G**B3LYP 6-31G**
N1–C21.3701.3701.3651.3691.3701.3671.3681.391
C2–N31.3231.3231.3221.3141.3161.3171.3191.349
N3–C41.3791.3801.3821.3871.3861.3851.3851.381
C4–C51.3731.3761.3741.3731.3751.3751.3771.372
C5–N11.3801.3811.3791.3861.3861.3801.3801.386
N1–H11.0081.0091.0181.0071.0081.0081.009
X–H1.088
H···X2.3172.3922.7022.4702.5622.3112.398
H···C1.471
C···X3.4183.4873.7853.5653.6533.4103.4912.559
Table 8

Selected bond lengths (Å) for computed IM···IM systems at B3LYP/6-31+G** level

(IM)N1–H···N3′(IM)coplanarfree(IM)C2–H···N1′(IM)coplanar
N1–H11.0261.027C2–H21.083
N1···N3′3.0142.989H2···N3′2.406
H1···N3′1.9881.962C2···N3′3.489
N1–C21.3641.364N1–C21.368
N1–C51.3781.378N3–C21.319
N3′–C2′1.3191.319N3′–C2′1.318
N3′–C4′1.3801.380N3′–C4′1.381
Table 9

Selected bond lengths (Å) for computed PYM···Cl– systems at B3LYP/6-31+G** level

(PYM)C2–H···Cl–(PYM)C5–H···Cl–(PYM)C6–H···Cl–
N1–C21.3481.3381.337
N1–C61.3361.3451.346
C2–N31.3481.3381.340
N3–C41.3361.3451.344
C5–C61.3951.3951.401
C2–H1.0971.0891.089
C5–H1.0861.0981.085
C6–H1.0901.0881.099
H···Cl2.4552.3582.388
C···Cl2.5533.4563.456
Table 12

Adduct formation energy (ΔEel; kcal) for the selected formal reactions, as calculated from the total electronic energies. Values are uncorrected (nco) or corrected (corr) for the basis set superposition errors

Theory/reactionΔEel
ncocorrncocorrncocorrncocorr
HF + H2O → FH···OH2HCl + H2O → ClH···OH2
B3LYP/6-31G**–10.3476–8.0886
B3LYP/6-31+G**–10.0652–6.6077
RHF/6-31G*–9.0361–8.3535
CCSD(T)/6-31G**–9.5382–8.0070–6.7708–5.2836
CCSD(T)/6-31+G**–9.6825–8.0886–6.4445–4.6373
IM + Cl– → (IM)N1–H···Cl–IM + Cl– → (IM)C2–H···Cl–IM + Cl– → (IM)C4–H···Cl–IM + Cl– → (IM)C5–H···Cl–
B3LYP/6-31G**–27.5351–11.0756–3.7839–13.5166
B3LYP/6-31+G**–23.7324–8.7287–1.9076–11.2450
MP2/6-31+G**–26.8511–24.7302
MP4(STDQ)/6-31+G**a–26.2236–24.3160
IM + F– → (IM)N1–H···F–IM + F– → (IM)C2–H···F–(IMH+)N1–H+ + Cl– → (IMH+)N1···H+···Cl–
B3LYP/6-31G**–82.9568–46.1094
B3LYP/6-31+G**–108.6031
MP2/6-31+G**–114.6523–112.7949
IM + IM → (IM)N1–H···N(IM) (coplanar)IM + IM → (IM)N1–H···N(IM) (free)IM + IM → (IM)C2–H···N(IM) (C2–H2···N1′ 180°)
B3LYP/6-31+G**–8.1702–8.8353–2.7734
MP2/6-31+G**–10.3037 b–8.9546 b
PYM + Cl– → (PYM)C2–H···Cl–PYM + Cl– → (PYM)C5–H···Cl–PYM + Cl– → (PYM)C6–H···Cl–
B3LYP/6-31+G**–3.3572–13.0585–9.3373
MP2/6-31+G**–4.5933 b–3.0654 b–15.6250 b–13.2969 b–10.9877 b–9.1679 b
PYM + PYM → (PYM)C2–H···N(PYM)PYM + PYM → (PYM)C2–H···N(PYM)/C6′–H···N3(PYM)PYM + PYM → (PYM)C5–H···N(PYM)
B3LYP/6-31G**–3.7086–2.7861
B3LYP/6-31+G**–1.4370–2.3783–1.9955
CCSD(T)/6-31G**–3.3195 a
MP2/6-31+G**–2.7485 b–1.9327 b–4.3110 b–3.2128 b–3.5831 a–2.6795 a
–3.6019 b–2.6795 b
MP3/6-31+G**–3.4952 a–2.3532 a
–3.4701 b–2.3845 b
(AA)N–H + Cl– → (AA)N–H···Cl–(MAA)N–H + Cl– → (MAA)N–H···Cl–(MA)N–H + Cl– → (MA)N···H–Cl(MAB)N–H + Cl– → (MAB)N–H···Cl–
B3LYP/6-31+G**–21.0153–21.0655–120.4694–8.3459
MP2/6-31+G**–22.7347–20.7957–23.9646–21.3542–122.7472–121.2398–9.4503–8.2517
(HMB)O–H + Cl– → (HMB)O–H···Cl–(MeOH)O–H + Cl– → (MeOH)O–H···Cl–(MGU)NH2 + Cl– → (MGU)NH2···Cl–(MGU)(CH3)N–H + Cl– → (MGU)(CH3)N–H···Cl–
B3LYP/6-31+G**–20.2937–14.9410–105.5911–106.5575
MP2/6-31+G**–22.9041–20.6639–16.0140–14.1817–107.9882–106.8963–109.6636–108.7789
(MAA)N–H+F– → (MAA)N–H···F–
B3LYP/6-31+G**–38.6107
MP2/6-31+G**–38.5542

a Single point calculation with the coordinates optimized at B3LYP/6-31G** level.

b Single point calculation with the coordinates optimized at B3LYP/6-31+G** level.

Fig. 1

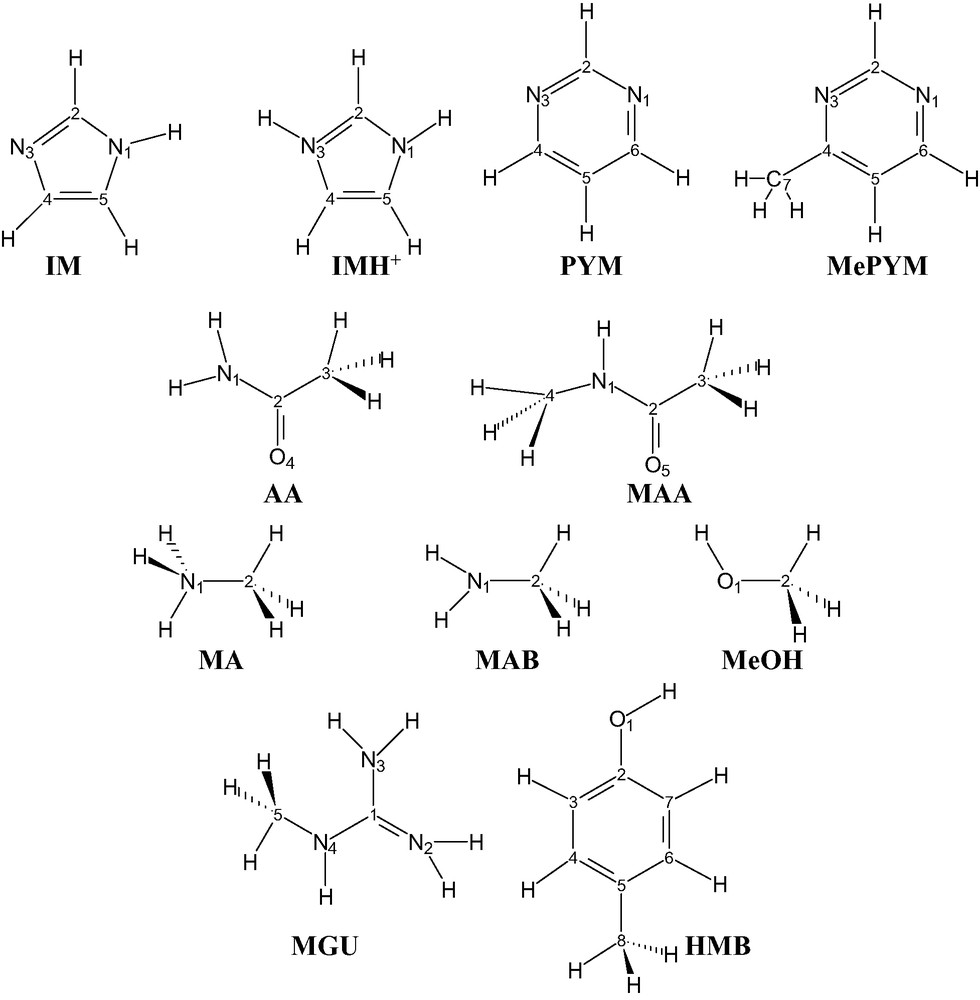
Structural formulae for selected isolate molecules: imidazole (IM), protonated imidazole (IMH+), pyrimidine (PYM), 4-methylpyrimidine (MePYM), acetamide (AA), N-methylacetamide (MAA), methylammonium (MA), methylamine (MAB), N-methylguanidinium (MGU), methanol (MeOH) and 1-hydroxy-4-methylbenzene (HMB). The numbering of the atoms used throughout the paper is also reported, whereas the symbol for carbon atoms is not typed.

Fig. 2

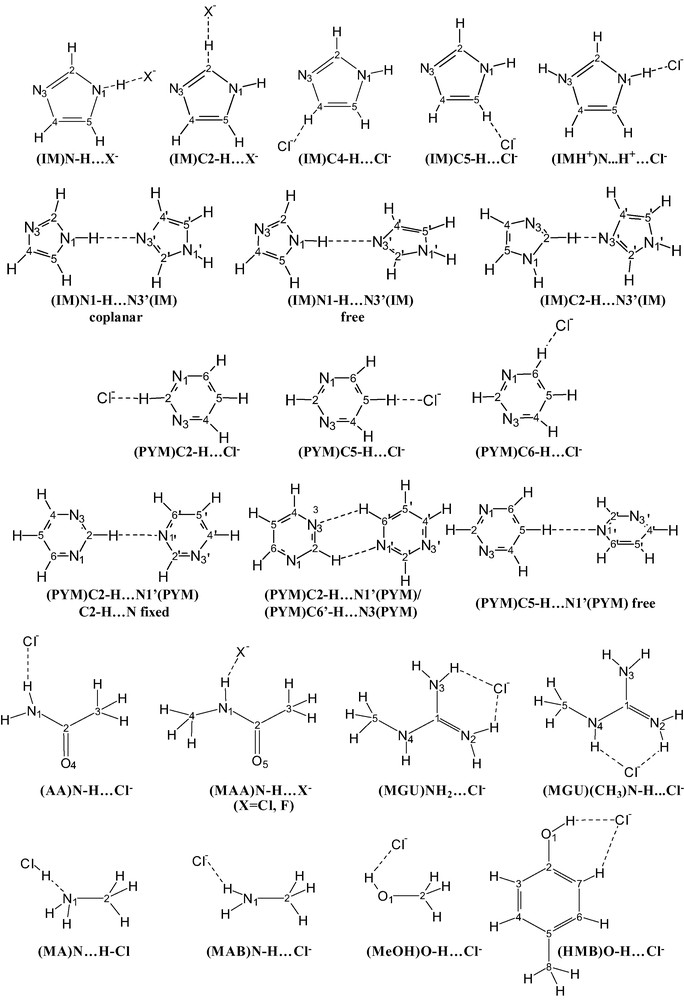
Structural formulae for selected two-particle systems investigated in this paper. The numbering of the atoms used throughout the paper is also reported, whereas the symbol for carbon atom is omitted.

3.1 Structures

3.1.1 Isolate molecules

3.1.1.1 Calibration of the methods on small molecules

This paragraph contains a comparative analysis of computations at several levels of theory and basis sets. Small particles such as HF, HCl, H2O, even though already extensively investigated and reported by others (see for instance Refs. [1,2] and references cited therein), were first investigated to check the reliability of the methods and to select accurate and possibly fast methods for larger systems.

The HF molecule was optimized at the RHF/6-31G*, MP4(SDTQ)/6-31+G**, CCSD(T)/6-31G**, B3LYP/6-31G** and B3LYP/6-31+G** levels and the computed F–H bond distances are 0.911, 0.926, 0.921, 0.925 and 0.928 Å, respectively (see Table 2). It has to be noted that previously reported calculations at the RHF/6-31G* and RHF/6-31+G*, and B3LYP/6-31++G** levels gave F–H bond distances of 0.911, 0.913 and 0.930 Å [35–37].

The HCl molecule as optimized at the CCSD(T)/ and B3LYP/6-31G** levels has Cl–H distance of 1.273 and 1.286 Å. By using the diffuse basis sets 6-31+G** and 6-31++G** the computed distance at B3LYP does not change (1.287 Å). Cl–H bond distances computed at the MP2/6-31+G** and MP2/6-311+G(3df, 2p) levels were 1.270 and 1.281 Å [38].

The H2O molecule as optimized at the CCSD(T)/ and B3LYP/6-31G** levels has O–H distance of 0.962 and 0.965 Å, whereas the computed bond angle is 103.8 and 103.7°, respectively. On introducing diffuse 6-31++G** basis set the bond distance (0.964 and 0.965 Å) does not change; whereas the bond angle undergoes an increase up to 105.3 and 105.7°, respectively, for the ab initio and DFT methods. Previously reported computed parameters at B3LYP/6-31+G* for H2O are 0.969 Å and 105.5° [39].

The results for the bi- and tri-atomic molecules above reported show that 6-31G** and 6-31+G** basis sets are enough accurate for the purpose of the present work. Therefore the optimization on larger molecules were performed mostly with the Dunning–Huzinaga basis sets expanded with polarized p functions for H atoms and d functions for heavy atoms, and with diffuse functions added to heavy atoms [33].

3.1.1.2 Imidazole and pyrimidine

Previous computations at lower levels were in part previously reported from this laboratory, in cooperation with other research groups or from other laboratories ([31,40] and references cited therein).

IM was investigated at deeper levels of computations in the present work (all the internal coordinates were relaxed, unless the torsion angles that were constrained to fix the planarity of the molecule). When optimized at the CCSD(T)/6-31G** level the molecule has selected computed distances C2–N1 1.369, N3–C2 1.322, N1–H 1.006 Å (Table 3) in excellent agreement with those for the geometry optimized structure at the B3LYP/6-31G** level: C2–N1 1.367, N3–C2 1.315, N1–H 1.008 Å. On introducing the diffuse functions (6-31+G** basis set) the selected bond parameters do not change much. As a consequence of this analysis, the structures of even larger molecules were usually optimized by using the 6-31G** and 6-31+G** basis sets, and the B3LYP and MP2 methods, unless otherwise specified.

The N3 protonated imidazole molecule (IMH+) has selected bond lengths N1–C2 1.337 and 1.341, and N1–H 1.014 and 1.014 Å at B3LYP/ and MP2/6-31+G**, respectively. The computed bonding parameters IM and IMH+ are in agreement with corresponding values obtained in other works and previously reported (see Ref. [40] and works cited therein).

The PYM and MePYM molecules optimized at B3LYP/6-31+G** have selected bond distances N1–C2 1.338 and 1.336, N3–C2 1.339 and 1.339, N3–C4 1.340 and 1.344, and C4–C5 1.395 and 1.403 Å, respectively (see Table 4). The selected endocyclic computed bond angles for PYM and MePYM at N1, C2, N3, C4 and C5 are 116.0 and 115.3, 127.1 and 127.3, 115.9 and 117.0, and 122.3 and 120.4, 116.5 and 117.5°, respectively. These parameters agree very well with the corresponding ones from experiments (see for instance Ref. [41]). From the comparative analysis with the 6-31G** basis set it can be stated that the usage of diffuse functions does not appreciably change things. The computed geometrical parameters for PYM at MP2/6-31+G** agree very well with those computed via B3LYP/6-31+G**.

3.1.1.3 Other molecules: acetamide, N-methylacetamide, methylamine, methylammonium, N-methylguanidinium, methanol, 1-hydroxy-4-methylbenzene

Acetamide (AA) was optimized at B3LYP/ and MP2/6-31+G** levels and it was considered as a model for the side branch for glutamine and asparagine. The refined molecules has C–O (1.225 and 1.233 Å) (see Table 5), C–N (1.369 and 1.373 Å), and N–H distances (1.008 and 1.007 Å) that show a good agreement between the two methods. It has to be noted that the X-ray structure of l-glutamine showed corresponding distances of 1.228, 1.331 and 1.005 Å [42]. Therefore C–O and N–H bond lengths are well reproduced by theory, whereas the C–N bond distance is overestimated by ca. 0.04 Å. A similar trend was observed for –CONH2 grouping of asparagine [43]. Packing forces and intermolecular hydrogen bonds may cause the discrepancies.

N-Methylacetamide (MAA) was optimized at B3LYP/ and MP2/6-31+G** levels and it was considered as a general model for the –NH–C(O)– peptide bond. The computed (H)N–C(O) bond distances are almost the same (1.369 Å, B3LYP; 1.368 Å, MP2) for the two levels of theory. The computed C–O bond distances differ by 0.009 Å (1.228 Å, B3LYP; 1.237 Å, MP2). All other distances differ by 0.008 Å or less. The corresponding computed bond angles at B3LYP/ and MP2/6-31+G** have a very good agreement; the selected values at B3LYP/6-31+G** being: C–N–C(O) 123.2, H–N–C(O) 118.3, N–C(O)–C 114.8°. The comparative analysis with the X-ray structure of free N-methylacetamide (as co-crystallized with 3,5-diiodo-l-tyronine-N-methylacetamide) shows that the C–N bond distance is overestimated by ca. 0.025 by theory; whereas the C=O bond length is underestimated by ca. 0.040 Å [44]. As for AA intermolecular forces at solid state may cause the differences with theory.

Methylammonium (MA) was optimized as a model for a protonated terminal amine group like that of lysine. The computed C–N and N–H bond distances are 1.516 and 1.026 Å at B3LYP/6-31+G** and 1.507 and 1.023 Å at MP2/6-31+G**, respectively. The computed values agree excellently with those found at the solid state for l-lysine sulfate [45].

Computed methylamine (MAB) at B3LYP/ and MP2/6-31+G** has C–N and N–H lengths of 1.464 and 1.013 Å, and 1.465 and 1.013 Å, respectively.

N-Methylguanidinium (MGU) was optimized as a model for the side chain of arginine that is suitable to link anions as a hydrogen bond donor. Computed C5–N4, N4–C1, C1–N3 and C1–N2 are 1.468, 1.335, 1.339, 1.343 Å, whereas computed N4–C1–N3, N4–C1–N2 and N3–C1–N2 bond angles are 120.4, 120.2 and 119.5° (B3LYP/6-31+G**). Corresponding computed parameters at MP2/6-31+G** level are 1.465, 1.332 1.338, 1.342 Å, and 120.3, 120.3 and 119.4°, respectively. The corresponding bond lengths and bond angle found at solid state in the structure of dl-arginine dihydrate [46] are 1.461, 1.320, 1.333, 1.335 Å and 118.7, 122.5, 118.8°. This shows that the levels of theory are accurate to compute reliable structures for this type of molecules.

Methanol (MeOH) was optimized as a model for a terminal fragment of serine or threonine. The computed C–O and O–H bond distances are 1.425 and 0.965 Å at B3LYP/6-31+G** and 1.429 and 0.964 Å at MP2/6-31+G**.

1-Hydroxy-4-methylbenzene (HMB) was optimized as the model for the side chain of tyrosine able to link chloride anions (as hydrogen donor). The computed C–O and O–H bond lengths are 1.374 and 0.966 Å, respectively, at B3LYP/6-31+G**, and 1.380 and 0.967 Å at MP2/6-31+G**. The C–O and O–H distances in the X-ray structure of tyrosine [47] are 1.374 and 0.988 Å. The C–O and O–H bond distances found via X-ray diffraction for para-cresol in bis(para-cresol)-N,N,N′,N′-tetraisopropyloxamide where the O–H function is the hydrogen donor to a carbonyl group are 1.369 and 1.023 Å [48].

3.1.1.4 Solvent effect on the structure of selected molecules

The analysis of solvent effects was performed by using mostly the parameters for water. The molecules studied in this work may undergo complex protonation equilibria in aqueous systems which were not taken into account in the computations. The study was limited to evaluate the changes on the geometrical parameters caused by the solvent.

Upon the treatment of the solvent effects, at the B3LYP/6-31G**/PCM level, the optimized F–H and Cl–H bond lengths for hydrogen fluoride and chloride molecules were 0.939 and 1.293 Å (increased by 0.014 and 0.007 Å, respectively, with respect to gas phase). The solvent effect on the structure of H2O causes lengthening of O–H bonds from 0.965 up to 0.972 Å and a narrowing of H–O–H angle from 103.7° down 103.0°.

The effect of the treatment of the solvent (water) on the structure of IM at the B3LYP/6-31G** is usually small; the largest changes on bond lengths being those relevant to N1–H, C4–H and C5–H (increasing by ca. 0.012 Å) (see Table 3). The bond angles are almost unaffected. In the case the diffuse function are added (B3LYP/6-31+G**) the effect of solvent treatment is small too, i.e. N1–H increases by 0.012 Å both for water and methanol.

The PYM molecule as optimized at B3LYP/6-31+G** and under the effect of solvent (water) has lengthenings for C2–H, C4–H and C5–H bond distances by 0.008, 0.010 and 0.012 Å (see Table 4); whereas the internal bond angles at N1, C2, N3 undergo an increase by 0.8, 1.0 and 0.8°, respectively.

It has to be noted that the treatment of solvent on MAA has significant changes on the (H)N–C(O) bond length 1.346 Å (1.370 Å, gas phase (see Table 5)), so that a very good agreement with experimental values from X-ray diffraction is reached. This analysis shows that the potential of surrounding particles at solid state has significant influence on bond parameters for MAA as predicted above (see Section 3.1.1.3). In the present case the potential of crystal lattice and that simulated by the PCM have equivalent effects.

The computed C–N and N–H bond distances for MA under the effect of solvent are 1.497 and 1.033 Å (B3LYP/6-31+G**) showing small changes with respect to the corresponding parameters computed for isolate molecules. Similarly, the optimization of the MGU molecule upon treatment of solvent effect (B3LYP/6-31+G**/PCM) gave small effects on the structural parameters (see Table 5).

3.1.2 Two-particle systems

3.1.2.1 Small particle systems

The structure of the F–H···OH2 (Fig. 3) system as optimized at the CCSD(T)/6-31G** level, with the atoms constrained to be coplanar and the F–H···O angle fixed at 180°, has optimized F–H and O–H bond lengths of 0.931 and 0.961 Å (increased by 0.01 and 0.001 with respect to the isolate molecules) (see Table 6), and the (F)H···O distance was 1.766 Å. The refined H···O–H and H–O–H angles were 126.9 and 106.2° (103.9° free H2O). The same system as optimized at the B3LYP/6-31G** level has F–H and O–H distances 0.939 and 0.964 Å. The (F)H···O distance is 1.721 Å. The H···O–H and H–O–H angles are 126.7 and 106.7°. Therefore the DFT method computes geometrical parameters for the adduct that are in good agreement with the ab initio method except for the H···O distance (that is 0.046 Å shorter at DFT than at CCSD(T)).

Fig. 3

Ortep-style representations of F–H···OH2 (a) and Cl–H···OH2 (b) as optimized at B3LYP/6-31+G**. The adduct formation energy (ΔEel; kcal mol–1) was computed at B3LYP/6-31+G**, CCSD(T)/6-31+G** () and CCSD(T)/6-31+G** after basis set superposition error (BSSE) correction [ ]. See text for values computed at different levels.

The Cl–H···OH2 adduct (Cl–H fixed in the plane of H2O and Cl–H···O, 180°) has computed Cl–H, H···O, O–H distances of 1.309, 1.799 and 0.964 Å at B3LYP/6-31G** (see Table 6). Things do not change much upon introduction of the diffuse functions (B3LYP/6-31+G**) as regards the intramolecular distances; however the (Cl)H···O distance changes significantly (increasing to 1.855 Å, by 0.056 Å). Upon enlarging the diffuse set (6-31++G**) and using the triple ξ functions (6-311++G**) (Cl)H···O does not change significantly.

The calculation of Cl–H···OH2 at CCSD(T)/6-31G** gives (Cl)H···O of 1.916 Å; by introducing the diffuse set (6-31+G**) the bridging H···O distance increases up to 1.940 Å; finally the introduction of the triple ξ set (6-311+G**) gives H···O 1.945 Å.

In conclusion the DFT methods underestimate the (Cl)–H···O distance by ca. 0.1 Å.

3.1.2.2 Imidazole···X– (X: Cl, F) systems

The (IM)N1–H···Cl– (Fig. 4) system as optimized at the B3LYP/6-31G** level by fixing the N1–H···Cl angle at 180° has a H···Cl distance of 2.004 Å (see Table 7). It has to be noted that on freely refining the (IM)···Cl system (by fixing the coplanarity of Cl– and IM plane, only) the N1–H···Cl– angle converged to 180.0°, no matter the initial position of Cl– with respect to IM (three different initial structures were used; the Cl– anion was set in a region between: (a) N1 and C2 at ca. 2.99 Å from H2; (b) N1 and C2 at ca. 2.40 Å from H2; (c) C4 and C5 at ca. 2.47 Å from H5). As expected the (N)H1···Cl– contact in the refined structure is much shorter than that relevant to H2···Cl– (2.317 Å when the (IM)C2–H···Cl– angle is constrained to 180°). The lengthening effect by hydrogen bond formation on N–H (1.060 Å) is large, 0.052 Å, when compared to the corresponding effect on C2–H (0.019 Å). The C4–H···Cl– hydrogen bond formation (C–H···Cl– angle constrained to 180°) behaves similarly to the C2–H···Cl– one, as regards the effects on bond distances for the IM molecule. The H4···Cl– distance is 2.470 Å, significantly larger than the corresponding one for C2–H···Cl–. Interestingly, the C5–H···Cl– adduct (C–H···Cl– angle constrained to 180°) has a short H···Cl distance of 2.311 Å. The lengthening effect on C5–H is 0.020 Å. Therefore, the analysis of the geometrical parameters shows that the strength of H-bond type interactions decreases in the order N1–H···Cl– > C5–H···Cl– ≥ C2–H···Cl– > C4–H···Cl–. The computed adduct (IM)N1–H···Cl– at B3LYP/6-31+G** has H···Cl distance of 2.042, longer by 0.038 Å than that computed without diffuse functions. Even larger lengthening effects caused by the introduction of diffuse functions have been found also for (IM)C2–H···Cl– (IM)C4–H···Cl– and (IM)C5–H···Cl– adducts (by 0.075, 0.092 and 0.087 Å).

Fig. 4

Ortep-style representations of the (IM)N1–H···Cl– (a), (IMH+)N1···H+···Cl– (b) and (IM)C2–H···Cl– (c) systems as optimized at B3LYP/6-31G** level. The adduct formation energy (ΔEel, kcal mol–1) was computed at B3LYP/6-31+G**, MP2/6-31+G** () and MP2/6-31+G** after basis set superposition error (BSSE) correction [ ].

It has to be noted that N–H···Cl– interactions play important roles for metal complexes at solid state and in solution. As a first example, Re-BIMH2 (BIMH2 = bisimidazole) complexes and Cl– [49] form very stable aggregates of the type [ReOCl3(BIMH2···Cl)]– both at the solid state and in solution. The observed N···Cl bond distance 3.090(5) Å (average) is in excellent agreement with the value computed at B3LYP or MP2 level of theory in this work (3.095 and 3.050 Å, respectively, see Table 7). An estimation of adduct formation energy for (IM)N–H···Cl– is reported below (see Section 3.3.2). As a second example, N–H···Cl– adducts are much stable in Pt-aminoacridine complexes as shown in Ref. [50], the N···Cl– distance is 3.14(1) Å (the adduct is stable even in the solution phase). Third the (IM)C–H···Cl interaction is important for legions of metal-IM complexes that contain Cl– ligands cis-to IM both in solid and solution state (see Refs. [31,51] and references therein). Experimental C···Cl distances are ca. 3.37 Å for [RuCl2(MeIM)2(SbPh3)2] [31]. The data compare well with computed C2···Cl– and C5···Cl– distances (3.49 Å) from this work. Therefore (IM)C–H···Cl– systems appear to be good models for (IM)C–H···Cl(M) interaction as far as the C···Cl distance are concerned. This analysis suggested to approximately estimate the stabilizing effects by (IM)C–H···Cl hydrogen-bond-type interactions in metal complexes from the computed electronic formation energy of (IM)C–H···Cl– (see below, Section 3.3.2).

The (IMH+)N1–H···Cl– system (as optimized at B3LYP/6-31+G**) has the bridging hydrogen closer to Cl– than to N1 (H···Cl, 1.368; N···H, 1.625 Å). It has to be noted that N–C2 distances undergo shortening (by 0.018 Å, N1) and lengthening effects (by 0.023 Å, N3) upon adduct formation. The X-ray structure of glycyl-l-histidinium chloride dihydrate [52] has the imidazolium moiety as a hydrogen donor to the Cl– anion via an N–H function. The normalized H···Cl– distance is 2.16 Å. A stronger (N)H···Cl– interaction occur at the solid state for l-histidyl-l-tyrosinium dichloride dihydrate [53], the normalized H···Cl– distance being 2.07 Å. Notwithstanding, the adduct formations for the two solid state structures have less dramatic effects than that computed in this work as regards the fate of the N–H bond. The N···Cl distances found for the glycyl-l-histidinium chloride and for the l-histidyl-l-tyrosinium dichloride are 3.126 and 3.105 Å, respectively, some 0.1 Å larger than for IMH+···Cl– computed at the gas phase. It must be recalled that the chloride anions are hydrogen acceptors also from water molecules at the solid state; this justifies a weaker accepting ability towards N–H. Furthermore, a comparative analysis between the present results for (IM)N–H···Cl– hydrogen bond, as computed at gas phase (B3LYP/6-31+G**, N···Cl, 3.095 Å) and the X-ray structure of dehalogenase from Xanthobacter Autotrophicus [54] that has two (tryptophan)N–H···Cl– hydrogen bonds (N···Cl: 3.13, 3.37 Å) shows a good agreement.

The gas phase optimization at B3LYP/6-31G** of a model for the (IM)N1–H···F– adduct converged to (IM)N–···H–F. The refined H–F and H···N1 distances are in fact 1.002 and 1.531 Å. The effects on bond angles for the imidazole system are large, as expected. The C2–N1–C5 bond angle in the adduct is 103.3°, smaller by 3.9° than that for free IM. On the contrary the N1–C2–N3 angle is enlarged by 4.1° upon deprotonation and adduct formation. The optimization of the (IM)C2–H···F– adduct also brings to an almost complete dissociation of the C2–H bond in the gas phase.

3.1.2.3 Imidazole···imidazole systems

The formation of IM···IM adduct (Fig. 5) formed via N–H···N hydrogen bond was analyzed via DFT-B3LYP/6-31+G** level (the two IM molecules were constrained to be coplanar, the arrangement of the two IM molecules is head-to-tail). The H1···N3′ length and N–H..N′ angle are 1.988 Å and 179.5° (N–H···N′ freely refined, initial value 180.1) (see Table 8). In the case the dihedral angle between the two IMs is let free the optimized structure has almost perpendicular bases (dihedral angle is 89.7°). In this case the H1···N3′ bond and N–H···N′ angle are 1.962 Å and 179.9°, respectively. It has to be noted that the biologically significant structure as determined via NMR in solution of GAACTGGTTC/tri-imidazole polyamide complex [55] has an N–H···N hydrogen bond between the imidazole moiety (donor) and N3 of a guanine base. In this case the N···N distance is 3.34 Å (computed N···N distance for N1–H···N3′ paired imidazole from this work, 2.989 Å).

Fig. 5

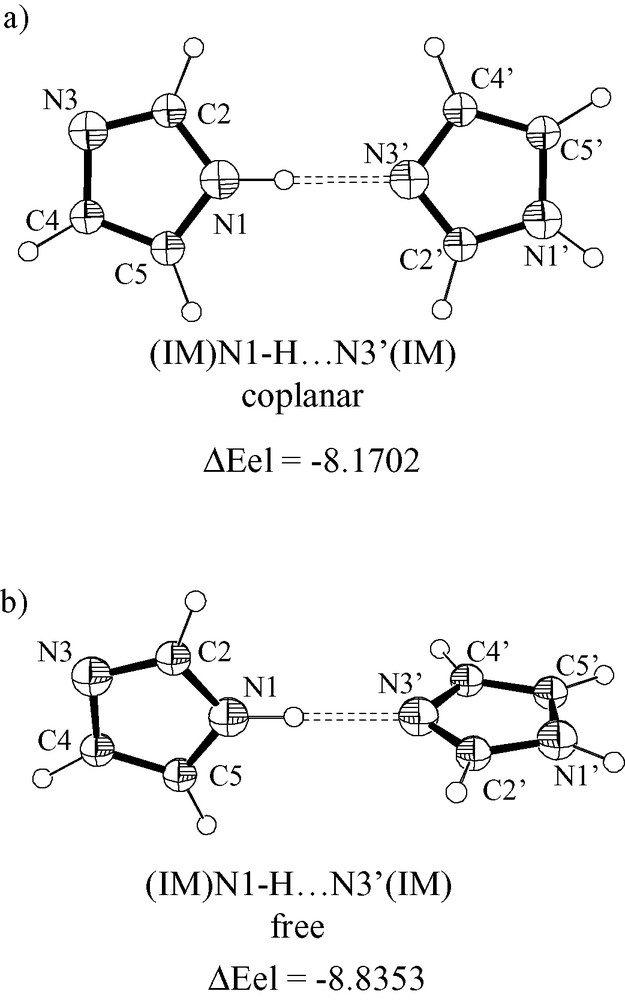
Ortep-style representations of (IM)N1–H···N3′(IM) systems as optimized at B3LYP/6-31+G**. The C2′–N3′–N1–C5 torsion angle was constrained at 0° (a) and let free (b) during optimization cycles. The adduct formation energy (ΔEel, kcal mol–1) was computed at B3LYP/6-31+G**.

Several optimization attempts to optimize IM···IM adducts formed via a C2–H···N3′ hydrogen bond did not fully reach the threshold criteria implemented on Gaussian98; notwithstanding, a partially optimized structure (C2–H···N3′, fixed at 180°) has a C2–H···N3′ hydrogen bond type interaction (H···N, 2.406 Å), whereas H4′ points towards N3 (H4′···N3, 3.760 Å).

3.1.2.4 Pyrimidine···Cl– systems

The optimized structure of (PYM)C2–H···Cl– (Fig. 6) (B3LYP/6-31+G**, C–H···Cl angle constrained at 180°) has H···Cl distance of 2.455 Å (see Table 9), larger than the corresponding distances for the (PYM)C6–H···Cl– and (PYM)C5–H···Cl– systems, 2.388 and 2.358 Å. It is reasonable that attraction from H5 contributes in shortening the (C6)H···Cl– distance with respect to the (C2)H···Cl– one.

Fig. 6

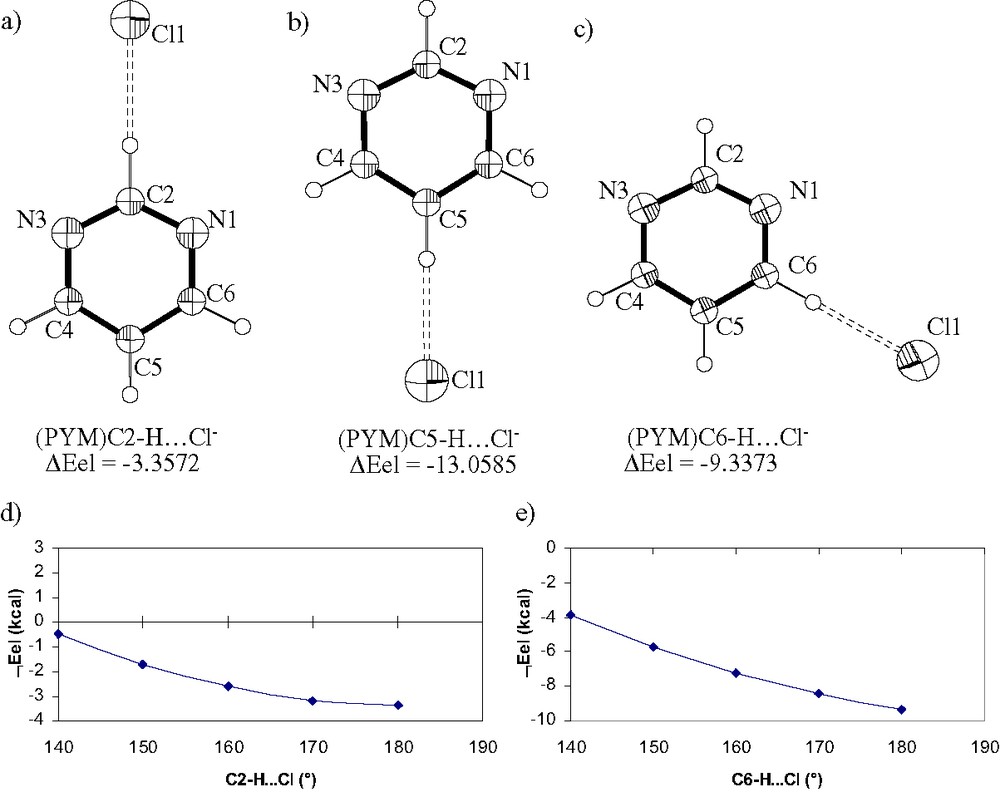
Ortep-style representations of (PYM)C2–H···Cl– (a), (PYM)C5–H···Cl– (b) and (PYM)C6–H···Cl– (c) systems as optimized at B3LYP/6-31+G**. The adduct formation energy (ΔEel, kcal mol–1) was computed at B3LYP/6-31+G**. The C–H···Cl– angles were fixed at 180°. The trend for the adduct formation energy as a function of C–H···Cl angles (Cl– approaching the N1 side) is also reported for C2–H (d) and C6–H (e).

It has to be noted that the (Ru)Cl···H contact distances found at the solid state for trans,cis,cis-[RuCl2(MePYM)2(SbPh3)2] [31] are 2.738 (H(C6), average) and 2.639 Å (H(C2) average). In this structure the chlorides are not free but linked to Ru(II) (trans each other) so that the Cl···H(C5) interaction is negligible. The (Ru)Cl···H–C6 and (Ru)Cl···H–C2 angles are 120.7 and 117.0°. The analysis of ca. 6600 X-ray structures previously reported by others showed that metal–Cl moieties are good hydrogen bond acceptors and form interaction similar to those of chloride anion [56].

3.1.2.5 Pyrimidine···pyrimidine systems

The structure of the (PYM)C5–H···N1(PYM) adduct (Fig. 7) has been optimized at the B3LYP/6-31G** and /6-31+G** levels. The C5–H···N bond angle and the dihedral angle between the molecules were freely refined. The geometrical parameters of each PYM moiety of the adduct do not change significantly upon adduct formation for both the basis sets. However, the H···N1 distance is sensitive to the type of basis set, and is 2.443 (6-31G**) and 2.501 Å (6-31+G**) (see Table 10).

Fig. 7

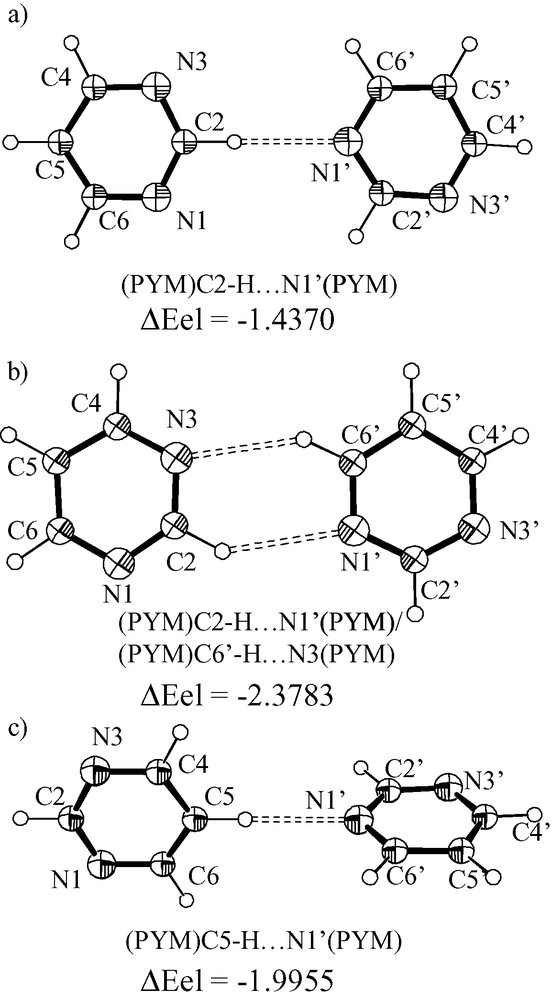
Ortep-style drawings for the (PYM)C2–H···N1′(PYM) system (a) and (PYM)C2–H···N1′(PYM)/(PYM)C6′–H···N3(PYM) system (b); the N3–C2–N1′–C6′ torsion angle was fixed at 0° for (a) and (b), whereas the C2–H···N1′ angle was fixed at 180° and let free for (a) and (b), respectively. The (PYM)C5–H···N1′(PYM) system (c) was optimized by fixing the C5–H···N1′ angle at 180° and by leaving free the dihedral angle between the rings. The adduct formation energy (ΔEel, kcal mol–1) was computed at B3LYP/6-31+G**.

It has to be recalled that a similar PYM···PYM pairing was found between pyrimidine ligands in the solid state structure of trans,cis,cis-[RuCl2(MePYM)2(SbPh3)2] [31] where the N···H and N···H–C distance and angle are 2.729(2) Å and 153(1)° (H atom set in calculated position with a H–C distance of 0.93). The dihedral angle between the two pyrimidines are 89° (theory, 6-31+G**) and 70(1)° (found) [31]. The introduction of diffuse function improve significantly the agreement.

In the case the two PYM molecules are constrained to be coplanar and C2–H···N1′ fixed at 180° the H2···N1 distance converges to 2.462 Å (B3LYP/6-31+G**). Interestingly a PYM···PYM base pair stabilized by C2–H···N1′ (H···N, 2.647 Å) and C6′–H···.N3 (H···N, 2.559 Å) forms in the case the constraint on the C2–H···N1′ angle is removed (coplanarity maintained).

3.1.2.6 Other molecule···Cl– systems

The fully relaxed adduct (MAA)N–H···Cl– (Fig. 8a) as optimized at the B3LYP/6-31+G** level converged nicely, and the refined (N)H···Cl– and N···Cl– distances are 2.136 and 3.174 Å (see Table 11). The N–H length increases by 0.029 Å (1.038 from 1.009 Å) upon hydrogen bond formation, whereas the N–C(O) distance decreases by 0.023 Å (1.347 from 1.370 Å) and the C–O length increases by 0.027 Å (1.255 from 1.228 Å). All the other distances do not change much. The N–H···Cl angle converges to 176.9°. The selected optimized geometrical parameters at MP2/6-31+G** are (N)H···Cl 2.095, N–H 1.034, N–C(O) 1.348, C–O 1.253 Å.

Fig. 8

Ortep-style representations of (MAA)N–H···Cl– (a), (HMB)O–H···Cl– (b), (MGU)NH2NH2···Cl– (c), (MGU)NH2N–H···Cl– (d), systems as optimized at B3LYP/6-31+G**. The adduct formation energy (ΔEel, kcal mol–1) was computed at B3LYP/6-31+G**, MP2/6-31+G** () and MP2/6-31+G** after basis set superposition error (BSSE) correction [].

The experimental N···Cl distances for N–H···Cl hydrogen bonds for selected complexes are 3.234 Å ([(η6-C6H6)RuCl(N,N′-triglycine)] [57]) and 3.273 Å ([PtCl2(η2-allylglycine)] [58]).

As far as the structure of an Ec–ClC protein [16] is concerned the N···Cl– distance found for the three chloride anions in the open conformation of a channel ranges 3.04–3.73 Å (average 3.30 Å).

The interaction of methylammonium (MA) and Cl– is dramatic at the gas phase, as expected. In fact, on refining a starting structure that has Cl– in the proximity of NH3+ and no constraints on internal coordinates, the CH3NH2·HCl adduct formed. The refined N···H(Cl) distance is 1.515 Å (B3LYP/6-31+G**), whereas the H–Cl and C–N bond distances converged to 1.416 and 1.477 Å. The C–N bond distance for free CH3–NH3+ and CH3–NH2 is 1.516 and 1.467 Å, respectively. It is interesting to note that the optimization of the adduct at MP2/6-31+G** gives H–Cl and N···H(Cl) distances of 1.336 and 1.681 Å, respectively; i.e. the virtual dissociation of a N–H bond is more effective when computed at MP2 than at B3LYP.

The refined (MAB)N–H···Cl– adduct is characterized by H···Cl, N–H(Cl) and C–N distances of 2.401, 1.030 and 1.464 Å. The optimized (HMB)O–H···Cl– adduct (Fig. 8b) has H···Cl, O–H and C–O distances of 2.093, 1.004 and 1.347 Å (B3LYP/6-31+G**). The O–H and C–O bonds undergo an increase by 0.038 Å and a decrease by 0.027 Å, respectively, upon adduct formation. It has to be noted that the X-ray structure of l-histidyl-l-tyrosinium dichloride dihydrate has a O–H···Cl– hydrogen bond characterized by H···Cl 2.23 Å (2.07 Å, normalized value) [53] values that compare well with theory.

The (MGU)N–H···Cl– adducts converge nicely to the structures represented in Fig. 8c,d. One of the structures has the chloride anion as hydrogen acceptor from (CH3)N–H group and a NH2 group. The optimized (CH3N)H···Cl distance is 2.001 Å, whereas the (NH2)H···Cl distance is 2.090 Å. This shows that the amide type NH group is a stronger hydrogen donor than the NH2 grouping for this system. The lengthening effects on amide type N–H and on (NH2)N–H are 0.047 and 0.038 Å, respectively. The second adduct has the Cl– anion chelated by the two NH2 groups. The H···Cl distances are 2.022 and 2.067 Å with lengthening effects on N–H bonds by 0.046 and 0.040 Å, upon adduct formation. The X-ray structure of l-arginine hydrochloride monohydrate [59] has the chloride anion as hydrogen bond acceptors from water molecules and from NH, NH2+ and NH3+ functions from arginine. The shortest (N)H···Cl contact distance is 2.249 Å and involve the function NH3+.

3.1.2.7 Solvent effects on the structure of selected two-particle systems

The treatment of solvent (water) for the (IM)N1–H···Cl– adduct causes a lengthening of the H···Cl distance up to 2.099 Å at B3LYP/6-31G** (i.e. by 0.095 Å), a shortening of the N1–H bond length (0.026 Å), and a small increasing of the N3–C4, C4–H and C5–H vectors (by 0.008, 0.007 and 0.011 Å).

The treatment of the solvent effects for the IMH+···Cl– system at B3LYP/6-31+G** gives H···Cl and N···H distances of 1.317 and 1.751 Å. It is interesting to note that the magnitude of the formal dissociation of the N–H bond increases when the solvation is taken into account.

The treatment of solvent for the (IM)N1–H···F– adduct does not change the pattern much, as the F–H bond (1.135 Å) is still shorter than the N1–H linkage (1.266 Å), even though longer (by 0.133 Å) than that for the gas phase system. The strengthening on the N1–H bond upon the inclusion of the solvent effects causes an enlarging of the C2–N1–C5 bond angle by 1.7°.

3.2 NBOs analysis for selected systems

With the aim to get further insights of the nature of X–H···Cl– hydrogen bonds, the analysis of NBOs for selected systems was performed.

3.2.1 Imidazole···X– (X: Cl, F) systems

The IM molecule (gas phase, B3LYP/6-31G**) has characters of 27.45% (H) and 72.55% (N1) for the N1–H NBO. Things do not change significantly in the case the diffuse function are added (26.93% (H) at B3LYP/6-31+G**). The analysis of the NBOs in the case the solvent effects are treated shows that the N1–H bonding orbital has 25.44% (H) characters.

The (IM)N1–H···Cl– (gas phase) adduct has a N1–H NBO with 22.27% (H) characters.

The (IM)N1–H···F– system once the solvent effect is treated has N1–H bonding orbital with 14.11% (H) and 85.89% (N) characters, respectively. This shows that F– is more effective in labilizing the N1–H bond even in the reaction field of water, than Cl– in the gas phase. The selected delocalizing electron density acceptor orbitals on N1 and H1 associate with donor orbitals from fluoride NBOs are anti-bonding N1–H, N1–C5 and N1–C2 in agreement with a lengthening of N–H and therefore with a classical H-bond [60]. In the case the solvent effect is not taken into account, the (IM)N···H···F– system has a relatively strong H–F bond with 17.14% (H) character, and H–F length 1.135 Å.

3.2.2 X–H···Cl– (X: N, O) systems

The MAA molecule has 28.34% (H) character for the amide N–H bond at gas phase, whereas the (MAA)N–H···Cl– system has 23.22% (H). For the AA molecule the H character for N–H bond undergoes a decrease by 3.5% only. This predicts a larger ΔEel formation energy for MAA···Cl– than for AA···Cl–. The H character for amide N–H NBO is 22.32% for the (MGU)···Cl– adduct that has (CH3)N–H and a NH2 group as H-donors, and decreases by ca. 4.4% upon adduct formation.

The (HMB)O···H···Cl– adduct consists of almost Cl– ion (HMB)O and H particles. A lone pair orbital of Cl– is mostly delocalized on the bridging H atom and at a lesser extent on the O1- and C2-Rydberg orbitals. The natural charge on the atoms of HMB (isolate) and of (HMB)O···H···Cl– are reported in Fig. 9. The electron density transfer (EDT) from Cl is ca. 0.11e and is mostly spread out on the oxygen atom and many carbon and hydrogen atoms of the CH3–C6H4 system. The bridging H atom (O···H···Cl) has a small EDT (0.02 e) towards the ring.

Fig. 9

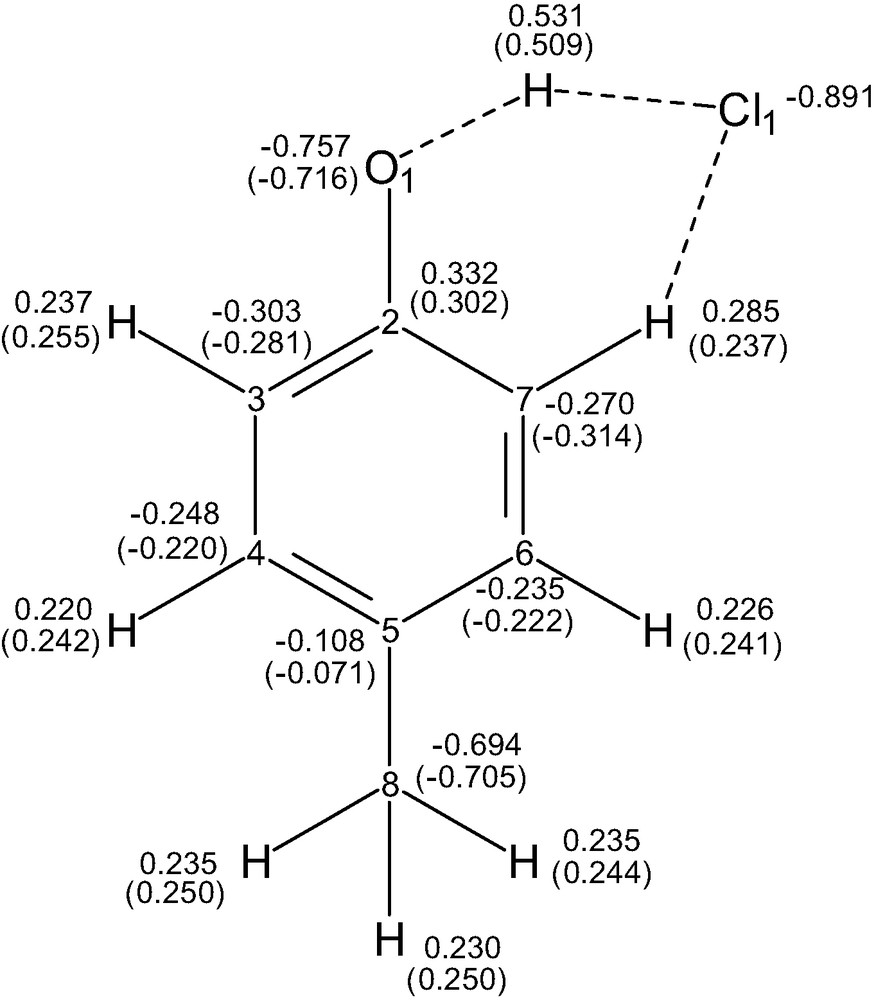
Natural charges from NBO analysis at B3LYP/6-31+G** level for (HMB)O–H···Cl– adduct, and for free HMB in parenthesis.

3.3 Energy

3.3.1 Small particles

The computed electronic formation energy for the FH···OH2 adduct at the RHF/6-31G* level is –9.0361 and –8.3535 kcal (Table 12) without and with the correction for the basis set superposition error (BSSE). Once the computations has been carried out at the coupled cluster CCSD(T)/6-31G** level the corresponding electronic formation energies are –9.5382 and –8.0070 kcal showing that the introduction of electron correlation effects and improving the basis set type contribute by less than 10% to the formation energy of such adduct. The computed formation energy at CCSD(T)/6-31+G** level is –9.6825 kcal (Fig. 3), in excellent agreement with the value computed at MP2 (see [1] and references cited therein). The introduction of diffuse functions has a small effect on the adduct formation energy. The computed formation energy for FH···OH2 at the B3LYP/6-31G** level is –10.3476 kcal (no BSSE correction) a value some 8% higher than that from the ab initio-electron correlation calculations.

The Cl–H···OH2 system (Fig. 3) has a formation energy at CCSD(T)/6-31G**, CCSD(T)/6-31+G**, B3LYP/6-31G** and B3LYP/6-31+G** of –6.7708, –6.4445, –8.0886 and –6.6077 kcal without any correction for BSSE. So, from the comparative analysis it can be stated that the introduction of diffuse functions influences the computed adduct formation energy by ca. 5% for Cl–H···OH2 adducts at CCSD(T)/6-31+G** but by ca. 20% at B3LYP, a value significantly higher than for the corresponding F–H···OH2 adduct. For this reason the diffuse functions were usually included in calculations aimed to estimate adduct formation energies for system that contain chlorine atoms. The correction for BSSE effects at CCSD(T)/6-31+G** level gives ΔEel –4.6373 kcal.

3.3.2 Imidazole···X– (X: Cl, F) systems

The adduct formation energy ΔEel for (IM)N1–H···Cl– at MP4(SDTQ)/6-31+G** (single point from coordinates obtained from B3LYP/6-31G** level) is –26.2236 and –24.3160 kcal, uncorrected and corrected for BSSE effects. The formation energy at B3LYP/6-31G** and B3LYP/6-31+G** (fully optimized) are –27.5351 and –23.7324 kcal (Fig. 4). The affinity of IM for Cl– via N–H···Cl– hydrogen bond formation as computed in this work is therefore comparable with the GC–Watson–Crick base pairing energy [1] and help estimating the formation energy for the adduct between Re(V)-bisimidazole complexes and Cl– [49]. The value of this latter can be taken as ca. two times the ΔEel pairing energy for (IM)N–H···Cl– i.e. ca. –48 kcal. The adduct formation energies for (IM)C2–H···Cl– (IM)C4–H···Cl– and (IM)C5–H···Cl– are –11.0756 and –3.7839 and –13.5166 kcal (no correction for BSSE) at B3LYP/6-31G**. The corresponding values computed at B3LYP/6-31+G** level are –8.7287, –1.9076 and –11.2450 kcal. These values are in agreement with the trend of (C)H···Cl distances (see above), and show that introduction of diffuse function has significant effects on formation energies.

The (IMH+)N1···H···Cl– system (see above, Section 3.1.2.2) has ΔEel –108.6031, and –114.6523 and –112.7949 kcal at B3LYP/, and MP2/6-31+G** without and with correction for BSSE.

3.3.3 Imidazole···imidazole systems

The ability to form adducts via N–H···N and C–H···N interactions for two imidazole molecules has been analyzed at the B3LYP/6-31+G** level in the gas phase. The adduct formation energy for the head-to-tail N1–H···N3′ fully optimized structure (planar system) is –8.1702 kcal (Fig. 5) without any BSSE correction, whereas, the formation energy for the C2–H···N3′/N3···H–C4′ adduct is –2.7734 kcal. The formation energy at MP2/6-31+G** (for the structure optimized at B3LYP) is –10.3037 and –8.9546 kcal (without and with correction for BSSE). In the case the dihedral angle between the two IM moieties is refined the adduct formation energy at B3LYP/6-31+G** is –8.8353 kcal. For comparative purpose it has to be recalled that ΔEel for the formation of H2N–H···NH3 dimer as computed at MP2 level is –2.86 kcal (corrected for BSSE) [1] and ΔEel for the formation of HO–H···N(H)=CH2 as computed at MP2/6-31G** is –8.20 kcal (uncorrected) [1].

3.3.4 Pyrimidine···Cl– systems

The adduct formation energies (no correction for BSSE) for (PYM)C2–H···Cl– (PYM)C5–H···Cl– and (PYM)C6–H···Cl– at B3LYP/6-31+G** (C–H···Cl angle fixed at 180°) are –3.3572 (Fig. 6), –13.0585 and –9.3373 kcal, in agreement with the trend of C–H···Cl distances. The corresponding values obtained via MP2/6-31+G** (single point for structures optimized at B3LYP) are –4.5933, –15.6250, –10.9877 kcal (uncorrected) and –3.0622, –13.2969, –9.1679 kcal (corrected). With the aim to estimate the energy surface for the (PYM)C2–H···Cl– and (PYM)C6–H···Cl– adducts as a function of the C–H···Cl angle, several structure optimizations were performed with Cl– in the plane of PYM (range 180–130°, by steps of 10°) and the respective ΔEel values were computed (see Fig. 6d, e). The results show that the value of adduct formation energy charges to –0.4832 kcal (C2–H) and to –3.8780 kcal (C6–H) for C–H···Cl 140°. In the case C–H···Cl is 120° (as found in the solid state for [RuCl2(MePYM)2(SbPh3)2] [31]) the estimated adduct formation energy values are ca. +3 and +1 kcal for H2 and H6, respectively. This means that the formation of (PYM)C–H···Cl– adduct with C6/C2–H···Cl angles ≤ 130° (N1–C6–/C2–H–Cl torsion angle, 0°) is not a stabilizing event unless N1(PYM) acts as donor to a M–Cl function that sits in the plane of the base and is endo with respect to the C–H hydrogen donor. It has to be noted that X–H···Cl– (X = O, C) hydrogen bonds in Ru(II)-complexes have recently been reported by other workers [61] and an extensive investigation from the Cambridge Data Base have also been carried out [62]. These works show that C–H···Cl– and C–H···Cl(M) interactions play important roles in inorganic and coordination chemistry. While the computed formation energies for C–H···O have been reported and commented in Ref. [61], the C–H···Cl– ones have been briefly commented for their structural parameters, only. The computed formation energy for C6–H···Cl– from the present work can be considered as an upper limit for the (arene)C–H···Cl– described in [61].

3.3.5 Pyrimidine···pyrimidine systems

The formation energy for the (PYM)C5–H···N1′(PYM) aggregate, computed at B3LYP/6-31G** is –2.7861 kcal without any correction for BSSE; once the calculation is performed at CCSD(T)/6-31G** on the coordinates obtained at B3LYP/6-31G** the formation energy is –3.3195 kcal (no BSSE correction) [31]. In the case the diffuse basis set is taken into account for the optimization (B3LYP/6-31+G**) the formation energy is –1.9955 kcal. The computed formation energies at MP2/6-31+G** on the structure optimized at B3LYP/6-31+G** is –3.822 and –2.6795 kcal without and with the correction for BSSE.

The optimized (PYM)C2–H···N1′(PYM) adduct with the C–H···N angle fixed at 180° and the two molecules constrained to be coplanar has a formation energy of –1.4370 kcal (B3LYP/6-31+G**). On leaving the C2–H···N angle free, the optimization (B3LYP/6-31+G**) converged to an adduct that consists of a C2–H···N1′ interaction and a C5′–H′···N3 interaction. The adduct formation energy is –2.3783 kcal (uncorrected). The corresponding value at MP2/6-31+G** is –3.2128 kcal (single point; corrected).

3.3.6 Other X–H···Y– (X: N, O; Y: Cl, F) systems

The adduct formation energy for (AA)N–H···Cl– at B3LYP/6-31+G** without any correction for BSSE effect is –21.0153 kcal, whereas the corresponding values computed at MP2/6-31+G** are –22.7347 and –20.7957 kcal, without and with BSSE correction. Computations at B3LYP without corrections for BSSE compare well with energy of formation computed at MP2 after the counter-poise correction.

The adduct formation energy for (MAA)N–H···Cl– at B3LYP/6-31+G** without any correction for BSSE effect is –21.0655 kcal, whereas the formation energy at MP2/6-31+G** without and with BSSE correction is –23.9646 and –21.3542 kcal. Therefore the N–H function of the peptide bond and terminal amide group (as that of asparagine) give adducts with chloride anions of ca. the same stability than N–H from imidazole (see above).

It has to be recalled that N–H groups from the peptide bonds are much more favored as hydrogen donors than N–H imidazole systems (histidine) or indole system (tryptophan), or than CONH2 groupings in protein systems, on the basis of statistical reasons. On examining X-ray structures of protein···chloride adducts, Cl– is often hydrogen acceptor from N–H peptide bond but very rarely from N–H imidazole type groups [16,17,54].

As expected, the adduct formation energy for (MA)NH2–H+···Cl– (that converge to (MA)NH2···HCl) is very high (–120.4694 kcal, B3LYP/6-31+G**, no BSSE correction). This means that lysine residues, even though not statistically favored, are energetically preferred by chloride anions. In fact, some protein/Cl– systems have short lysine···Cl– interaction when studied via X-ray diffraction [63]. It has to be noted that in these cases the bridging proton should be almost midway between Cl– and the aminic nitrogen. The adduct formation energy at MP2/6-31+G** before and after BSSE correction is –122.7472 and –121.2393 kcal.

In the case the aminic NH2 group is the hydrogen donor, the donating ability to chloride is much smaller than for alkyl ammonium cations. The adduct formation energy for (MAB)NH–H···Cl– is –8.3459 kcal. The adduct formation energy at MP2/6-31+G** before and after BSSE correction is –9.4503 and –8.2517 kcal. It has to be noted that the computed formation energy for NH2–H···Cl– at MP2/aug-cc-pVTZ is –7.7 kcal after correction for BSSE [64].

The methylguanidinium system (MGU) is very versatile as hydrogen donors to chloride and two types of monoadduct can be formed, both containing chelate Cl– anions (see above, structures). The adduct formed from the amide N–H and one of the C–NH2 functions has a formation energy of –106.5575 kcal (B3LYP/6-31+G**). The second type adduct, formed from the H2N–C–NH2 grouping has a formation energy of –105.5911 kcal. The adduct formation energies at MP2/6-31+G** are –109.6636 (uncorrected), –108.7789 (corrected), and –107.9882 (uncorrected), –106.8963 (corrected) kcal for the two types of adduct.

The (HMB)O···H···Cl– adduct as computed at B3LYP/6-31+G** has a formation energy of –20.2937 kcal, whereas the values at MP2/6-31+G** are –22.9041 and –20.6639 (corrected).

Finally, the (Me)O–H···Cl– adduct has computed formation energy of –14.9410 at B3LYP/6-31+G** and of –16.0140 (uncorrected) and –14.1817 (corrected) kcal at MP2/6-31+G**.

Therefore, the order of magnitude for X–H···Cl– adduct formation energy is C–NH3+ (lysine like) > (IMH)N–H+ (histidinium like) ≅ NH–C(NH2)2 (arginine like) > C(=O)–NH– (peptide like) ≅ C(=O)–NH2 (asparagine like) ≅(IM)N–H (histidine like) ≅ (C6H4)OH (tyrosine like) > (MeOH) O–H (serine like).

3.4 Vibration frequencies

The values commented are those computed at B3LYP/6-31+G** unless otherwise specified.

3.4.1 Selected small particle adducts

The computed frequency for HF is 4084 cm–1 (force constant, 10.4043 mdyne Å–1; IR intensity, 61.0551 km mol–1). The value compares well with the computed one at MP2/6-31+G** (3941 cm–1) [65] and even better with the experimental value (4139 cm–1) [66]. The value is red-shifted to 3884 cm–1 (9.4224; 59.3220) upon inclusion of solvent (water) effects and to 3660 cm–1 (8.3697; 976.5180) upon the formation of the F–H···OH2 adduct.

The H–Cl molecule in the gas phase has vibration frequency of 2943 cm–1 (5.2869 mdyne Å–1; 22.0887 km mol–1); whereas the corresponding value for the Cl–H···OH2 adduct is 2710 (4.4863; 646.1660). In the case the reaction field is applied (water) the vibration data for HCl alone are 2881 (5.0660; 21.8644).

3.4.2 Imidazole systems

The (IM)N1–H···Cl– adduct has νN–H of 2920 cm–1 (5.5594 mdyne Å–1; 2578.5933 km mol–1); the wavenumber decreases extensively and intensity increases with respect to free IM (3667.5 cm–1; 8.5729 mdyne Å–1; 57.7220 km mol–1). At MP2/6-31+G** level the νN–H frequency is 2979.6 cm–1 (5.8032; 2652.9469) in agreement with the values obtained via DFT.

The effect of adduct formation (IM)N1–H···N3′(IM) (dihedral angle between the rings refined freely) on the N–H stretching vibration frequency is much smaller than that due to the N–H···Cl– H-bond interaction. In fact the computed values for IM···IM is 3261 cm–1 (6.8638 mdyne Å–1; 3.0271 km mol–1), so that the red shift is ca. 400 cm–1 instead of ca. 750 cm–1 (for N–H···Cl–) and the IR intensity decreases by ca. 45 times.

3.4.3 Pyrimidine systems

The computed νC2–H stretching vibration for free PYM has wavenumber 3192 cm–1 (6.5531 mdyne Å–1; 15.6651 km mol–1), whereas the corresponding value for (PYM)C2–H···Cl– is 3059 cm–1 (6.0987 mdyne Å–1; 320.5396 km mol–1).

The (PYM)C2–H···N1′(PYM)/(PYM)N3···H–C6′(PYM) system (two C–H···N bonds) has a small negative frequency (–21.9 cm–1) and corresponds to motion out of plane for all the atoms. The νC2–H stretching vibration has wavenumber 3190 cm–1 (6.5623 mdyne Å–1; 5.6287 km mol–1). The adduct formation has therefore a negligible effect on νC2–H motion.

With the aim to summarize the computed results on the analysis of adducts that involve imidazole and pyrimidine one can say that N–H···Cl– and even C–H···Cl– interactions give significant red shifts (in the range 100–500 cm–1) at the gas phase. It is expected that IR techniques are valuable tools to detect such a type of interactions for solution systems whose solvents have low dielectric constants or for hydrophobic pockets of macromolecular systems even if dispersed in water. On the contrary, the C–H···N interactions could probably not be detected via IR at least for adduct between imidazole and pyrimidine molecules.

These observations suggested to extend the analysis of the frequency to several models that mimic N–H···Cl– and O–H···Cl– interactions for aminoacids.

3.4.4 Other X–H···Y– (X: N, O; Y: Cl, F) interactions as model for protein···Cl– systems

The vibration of the N–H bonds for AA occurs at 3601 cm–1 (7.9897 mdyne Å–1; 36.2015 km mol–1) and 3744 cm–1 (9.1285; 41.4036), that are red-shifted to 3126 cm–1 (6.2615; 1067.0896) and 3656 cm–1 (8.5225; 29.8931), respectively, upon (AA)N–H···Cl– adduct formation.

The optimized structure for the adduct (MAA)N–H···Cl– (MAA = N-methylacetamide), has computed vibration of the N–H bond at 3145 cm–1 (6.3694 mdyne Å–1; 1074.2019 km mol–1); the motion is combined with a C–H vibration syn to N–H. The frequency for N–H vibration in free MAA is 3652 cm–1 (8.4719 mdyne Å–1; 22.8543 km mol–1). Thus N–H···Cl– hydrogen bond formation has a large effect both on IR frequency and intensity as far as primary and secondary amide N–H are concerned.

The computed νN–H frequencies for free MAB (methylamine) are 3513 cm–1 (7.6285 mdyne Å–1; 0.4991 km mol–1) and 3601 cm–1 (8.3606 mdyne Å–1; 1.7444 km mol–1) and undergo a red shift to 3326 cm–1 (6.9481 mdyne Å–1; 408.1720 km mol–1) and 3526 cm–1 (7.8923 mdyne Å–1; 17.9341 km mol–1) upon the formation of (MAB)N–H···Cl– hydrogen bond. These data confirm that the effects of N–H···Cl– bond formations are larger for amides than for corresponding amines. Notwithstanding, even for amines the infrared technique is a suitable tool to detect N–H···Cl– bond formation at least for environments with low dielectric constant values or in the gas phase.

The computed frequency for (CH3)N–H stretching motion of methylguanidinium (MGU) is 3635 cm–1 (8.3907 mdyne Å–1; 70.8345 km mol–1) whereas the values for amine/imine NH2N–H vibrations are in the range 3602–3729 cm–1 (8.0060–9.0657 mdyne Å–1; 192.2091–96.3697 km mol–1).

Upon adduct formation with the Cl– anion chelated by (CH3)NH and NH2NH, the ν(CH3)N–H vibration is shifted down to 2819 cm–1 (5.1232; 722.3038 km mol–1) and the νN–H (imine type) is decreased to 3028 cm–1 (5.7889; 1549.2417). Similar red shifts and intensity effects have been found for the adduct that contains the Cl– anion as chelated by the two NH2 groupings. These large red shifts (when compared to amides) can be explained on the basis of the stronger electrostatic contribution for MGU.

The computed frequency for (HMB)O–H stretching motion is 3830 cm–1 (9.2149 mdyne Å–1, 56.6372 km mol–1) and undergoes also very large effect upon adduct formation with Cl– ((HMB)O–H···Cl–, 3114 cm–1, 6.1343 mdyne Å–1, 1899.1950 km mol–1). This is related to the high H-donating ability for oxygen atoms combined to the formation of a chelate that involves both O–H and the ortho C–H group. It is interesting to note that the frequency for C–H (ortho to OH) upon adduct formation is 3191 cm–1 (6.5638; 141.1089) i.e. some 10 cm–1 higher than the corresponding value for free HMB. This is a small effect but it agrees with the criteria of anti-H-bond as defined by others [29].

4 Further discussion and conclusion

The work allowed the computations of structural, energetic and IR parameters for the formation of pyrimidine···chloride, imidazole···imidazole and pyrimidine···pyrimidine adducts that play subtle and interesting roles in biological as well as in bio-coordination chemistry. The formation of (PYM)C5–H···N(PYM) chains in the structure of trans,cis,cis-[RuCl2(4-MePYM)2(SbPh3)2] [31] contributes by ca. –3 kcal mol–1 to the stabilization of crystal packing. It is reasonable that this type of interaction between pyrimidine ligands are extensively present in solution of low dielectric constant media at low temperature.

Furthermore, the upper limit of C–H···Cl(M) intramolecular hydrogen bond formation energy (ΔEel) for complexes of the type MCln(IM/PYM) (see Fig. 10) can be estimated as ca. –8 and –10 kcal for C2/C5–H functions of IM, and ca. –3 and –9 kcal for C2–H and C6–H groups of PYM. In the case of adducts such as M(IM)N–H···Cl– the stabilizing effect is much higher, ca. –24 kcal in the gas phase.

Fig. 10

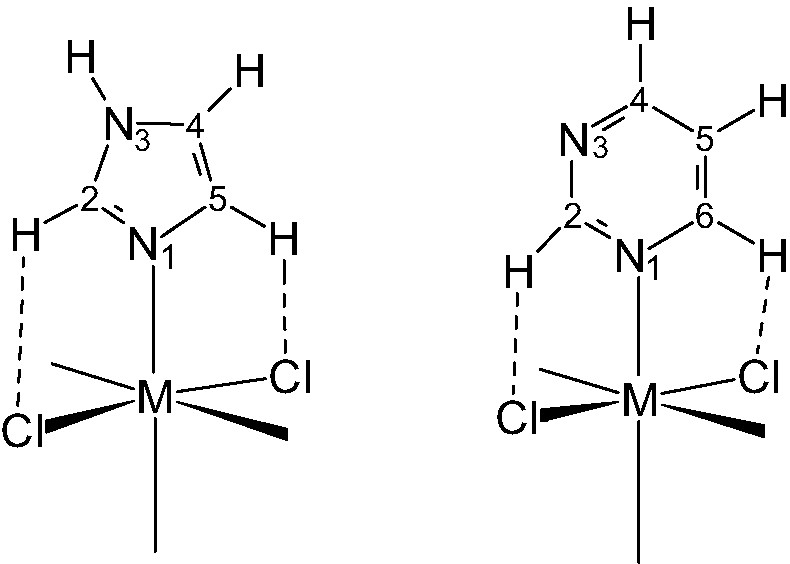
The drawings represent C–H···Cl intramolecular hydrogen bonds that often occur in octahedral metal-imidazole and -pyrimidine complexes. Those H-bonds are important to determine the orientation of the base-plane with respect to M–Cl vectors and the value of M–N–C bond angles [31].

This work computed also several structural, energetic and spectroscopic parameters for hydrogen bonds that involve chloride anions, and help finding a rationale for protein/Cl– adduct formations especially those related to ClC Cl– channels. The H-donors are mostly N–H groupings from peptide bonds, but O–H grouping from tyrosine and serine intervene, too. No water molecules are located within 7 Å from the channel boundaries. So the effect of solvent can be excluded in the computations for the models. On the basis of this assumption and in the case the structural model for the open-channel reported in [16] (see also the analysis in [18]) is taken into account, hydrogen bond formation energy (from electronic energy contribution, only) on moving from the first to the third site increases significantly. In fact the structural data [16] reveals two (MAA)N–H···Cl– type H-bonds for first site (Fig. 11); two (MAA)N–H···Cl– type H-bonds, one (HMB)O–H···Cl– type H-bonds and one (Me)O–H···Cl– type H-bonds for second site; and finally, five (MAA)N–H···Cl– type H-bonds for third site. The formation of X–H···Cl– hydrogen bonds is not the only driving event that causes the movement of chloride anions through the channel. The electrostatic surface potentials of the conducts and the mobility of channel boundaries, play an important role [18]. More accurate modeling should be performed to obtain a full rationale for the extrusion of chloride anions from the cell.

Fig. 11

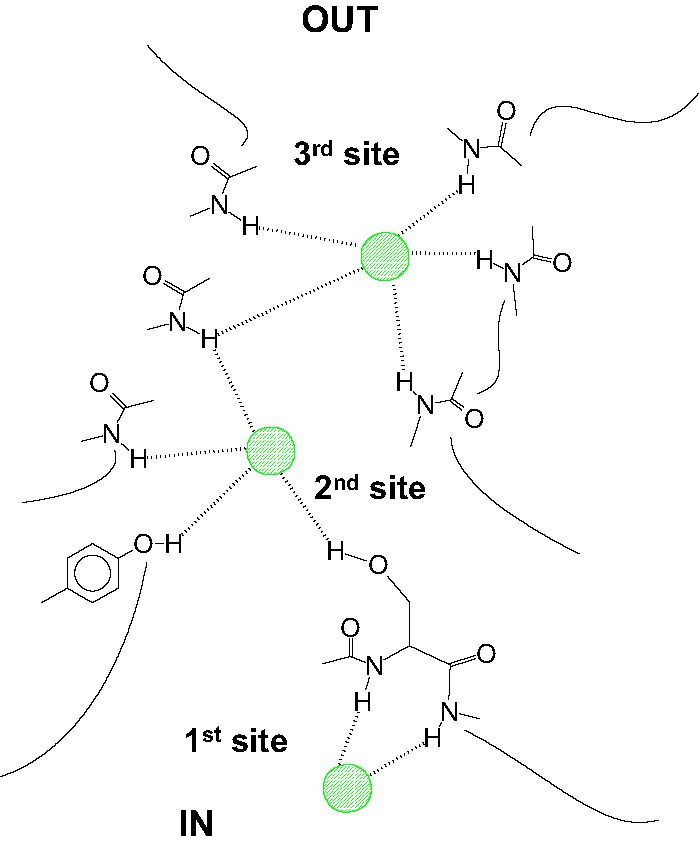
Approximate representation of the ClC Cl– system as drawn on the basis of the X-ray structure reported in Ref. [16].

Acknowledgements

The authors gratefully acknowledge Consorzio Interuniversitario per il Calcolo Automatico dell'Italia Nord-Orientale (CINECA, Casalecchio di Reno, Bologna, Italy) for a Grant 2002 03 06/2003 03 06, and MIUR (Ministero dell'Istruzione, dell'Universtà e della Ricerca, Roma) for funding under the PRIN 2004 Project.

Bibliographie

[1] S. Scheiner Hydrogen Bonding, a Theoretical Perspective, Topics in Physical Chemistry, a Series of Advanced Textbooks and Monographs (D.G. Truhlar, ed.), Oxford University Press, Oxford, 1997 (and references therein)

[2] G.R. Desiraju, T. Steiner, The Weak Hydrogen Bond In Structural Chemistry and Biology, International Union of Crystallography Monographs on Crystallography, P. Coppens (IUCr Book Series Committee Chairman), International Union of Crystallography Oxford Science Publications, Oxford University Press, Oxford, 1999 (and references therein).

[3] M. Nishio CH/pi hydrogen bonds in crystals, Cryst. Eng. Commun., Volume 6 (2004) (130)

[4] M. Nishio; M. Hirota; Y. Umezawa The CH/π Interaction. Evidences, Nature, and Consequences, Methods in Stereochemical Analysis, A.P. Marchand, Series Editor, Wiley-VCH, Weinheim, 1998

[5] The CH/π Institute, 3-10-7 Narusedai, Machida, Tokyo 194-0043, Japan, and references listed in its home-page, last update August 6, 2003, http://www.tim.hi-ho.ne.jp/dionisio/.

[6] T.A. Wesolowski; J. Weber Molecular Orbital Calculations for Biological Systems (A.-M. Sapse, ed.), Oxford University Press, Oxford, UK, 1999 (Ch. 4, p. 85)

[7] E. Cubero; M. Orozco; P. Hobza; F.J. Luque J. Phys. Chem. A, 103 (1999), p. 6394

[8] Y. Wang; P.B. Balbuena J. Phys. Chem. A, 105 (2001), p. 9972

[9] W.-L. Zhu; X.-J. Tan; C.M. Puah; J.-D. Gu; H.-L. Jiang; K.-X. Chen; C.E. Felder; I. Silman; J.L. Sussmann J. Phys. Chem. A, 104 (2000), p. 9573

[10] A. Ricca; C.W. Bauschlicher J. Phys. Chem. A, 106 (2002), p. 3219

[11] J.S. Sun; T. Garestier; C. Hélène Curr. Opin. Struct. Biol., 6 (1996), p. 327

[12] G.A. Jeffrey; W. Saenger Hydrogen Bonding in Biological Structures, Springer, Berlin, 1991

[13] T.S. Balaban; R. Goddard; M. Linke-Schaetzel; J.-M. Lehn J. Am. Chem. Soc., 125 (2003), p. 4233

[14] M.-P. Teulade-Fichon; C. Carrasco; L. Guittat; A. David; J.-M. Lehn; W.D. Wilson J. Am. Chem. Soc., 125 (2003), p. 4732

[15] M.J. Krische; J.-M. Lehn; E. Cheung; G. Vaughn; A.L. Krische C.R. Acad. Sci. Paris, t.2, Ser. IIc 2 (1999), p. 549

[16] R. Dutzler; E.B. Campbell; R. MacKinnon Science, 300 (2003), p. 108

[17] H.M. Berman; J. Westbrook; Z. Feng; G. Gilliland; T.N. Bhat; H. Weissig; I.N. Shindyalou; P.E. Bourne Nucleic Acids Res., 28 (2000), p. 235

[18] G.V. Miloshevsky; P.C. Jordan Biophys. J., 86 (2004), p. 825

[19] M.L. Huggins Angew. Chem. Int. Ed. Engl., 10 (1971), p. 147

[20] L.C. Remer; J.H. Jensen J. Phys. Chem. A, 104 (2000), p. 9266

[21] S. Schan; S. Loh; D. Herschlag Science, 270 (1996), p. 97

[22] M.A. McAllister Can. J. Chem., 75 (1997), p. 1195

[23] A.J. Mulholland; P.D. Lyne; M. Karplus J. Am. Chem. Soc., 122 (2000), p. 534

[24] Y. Pan; M.A. McAllister J. Am. Chem. Soc., 120 (1998), p. 166

[25] W.W. Cleland; M.M. Creevoy Science, 264 (1994), p. 1887

[26] W.W. Cleland; P.A. Frey; J.A. Gerlt J. Biol. Chem., 273 (1998), p. 25529

[27] G.A. Kumar; M.A. McAllister J. Org. Chem., 63 (1998), p. 6968

[28] M. Brandl; M. Meyer; J. Sühnel J. Biomol. Struct. Dyn., 18 (2001), p. 545

[29] P. Hobza; V. Spirko; H.L. Selzle; E.W. Schlag J. Phys. Chem. A, 102 (1998), p. 2501

[30] R. Cini; M. Corsini; A. Cavaglioni Inorg. Chem., 39 (2000), p. 5874

[31] R. Cini; C. Bellucci; G. Tamasi; M. Corsini; M. Fontani; P. Zanello Inorg. Chim. Acta, 339 (2002), p. 89

[32] M.J. Frisch, G.W. Trucks, H.B. Schlegel, G.E. Scuseria, M.A. Robb, J.R. Cheeseman, V.G. Zakrzewski, J.A. Montgomery Jr., R.E. Stratmann, J.C. Burant, S. Dapprich, J.M. Millam, A.D. Daniels, K.N. Kudin, M.C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G.A. Petersson, P.Y. Ayala, Q. Cui, K. Morokuma, D.K. Malick, A.D. Rabuck, K. Raghavachari, J.B. Foresman, J. Cioslowski, J.V. Ortiz, A.G. Baboul, B.B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R.L. Martin, D.J. Fox, T. Keith, M.A. Al-Laham, C.Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P.M.W. Gill, B. Johnson, W. Chen, M.W. Wong, J.L. Andres, C. Gonzalez, M. Head-Gordon, E.S. Replogle, J.A. Pople, Gaussian98, Revision A.7, Gaussian, Inc., Pittsburgh PA, 1998.

[33] A. Frish, M.J. Frisch, Gaussian98, User's Reference, second ed., Gaussian, Inc., Carnegie Office Park, Building 6, Pittsburgh, PA, USA, 15106.

[34] E.D. Glendening; A.E. Reed; J.E. Carpenter; F. Weinhold Natural Bond Orbital, Natural Population Analysis, Natural Localized Molecular Orbital Programs, NBO 3.1 Program Manual, University of Wisconsin, Madison, WI, 1998

[35] M.J. Frisch; J.A. Pople; J.E. Del Bene J. Phys. Chem., 89 (1985), p. 3664

[36] J.C. Jiang; M.-H. Tsai J. Phys. Chem. A, 101 (1997), p. 1982

[37] P.M. Esteves; A. Ramirez-Solis; C.J.A. Mota J. Am. Chem. Soc., 124 (2002), p. 2672

[38] A. Rauk; D.A. Armstrong J. Phys. Chem., A 106 (2002), p. 400

[39] S. Re; K. Morokuma J. Phys. Chem., A 105 (2001), p. 7185

[40] R. Cini; D.G. Musaev; L.G. Marzilli; K. Morokuma J. Mol. Struct. Theochem., 392 (1997), p. 55

[41] O. Teichert; W.S. Sheldrick; Z. Anorg Allg. Chem., 625 (1999), p. 1860

[42] T.F. Koetzle; M.N. Frey; M.S. Lehmann; W.C. Hamilton Acta Crystallogr., B 29 (1973), p. 2571

[43] J.J. Verbist; M.S. Lehmann; T.F. Koetzle; W.C. Hamilton Acta Crystallogr., B 28 (1972), p. 3006

[44] V. Cody; W.L. Duax; D.A. Norton Acta Crystallogr., B 28 (1972), p. 2244

[45] S. Capasso; C.A. Mattia; L. Mazzarella; A. Zagari Acta Crystallogr., C 39 (1983), p. 281

[46] S. Suresh; S. Padmanabhan; M. Vijayan J. Biomol. Struct. Dyn., 11 (1994), p. 1425

[47] M.N. Frey; T.F. Koetzle; M.S. Lehmann; W.C. Hamilton J. Chem. Phys., 58 (1973), p. 2547

[48] F. Toda; Y. Tagami; T.C.W. Mak Bull. Chem. Soc. Jpn, 59 (1986), p. 1189

[49] S. Fortin; A.L. Beauchamp Inorg. Chem., 39 (2000), p. 4886

[50] E. Ceci; R. Cini; J. Konopa; L. Maresca; G. Natile Inorg. Chem., 35 (1996), p. 876

[51] M. Iwamoto; E. Alessio; L.G. Marzilli Inorg. Chem., 35 (1996), p. 2384

[52] T. Steiner Acta Crystallogr., C 52 (1996), p. 2266

[53] T. Steiner Acta Crystallogr., C 52 (1996), p. 1845

[54] K.H.G. Verschueren; B.W. Dijkstra Biochemistry, 32 (1993), p. 9031

[55] X.-L. Yang, R.B. Hubbard IV, M. Lee, Z.-F. Tao, H. Sugijama, A.H.-J. Wang, Protein Data Bank Code 1CYZ, Release Date 14-Sept-1999.

[56] G. Aullòn; D. Bellamy; L. Brammer; E.A. Bruton; A.G. Orpen Chem. Commun. (1998), p. 653

[57] W.S. Sheldrick; S. Heeb J. Organomet. Chem., 377 (1989), p. 357

[58] L.E. Erickson; P.D. Bailey; T.L. Kimball; B.R. Morgan Inorg. Chim. Acta, 346 (2003), p. 169

[59] J. Dow; L.H. Jensen; S.K. Mazumdar; R. Srinivasan; G.N. Ramachandran Acta Crystallogr., B 26 (1970), p. 1662

[60] B.J. van der Veken; W.A. Herrebout; R. Szostak; D.N. Shchepkin; Z. Havlas; P. Hobza J. Am. Chem. Soc., 123 (2001), p. 12290

[61] L. Scaccianoce; D. Braga; M.J. Calhorda; F. Grepioni; B.F.G. Johnson Organometallics, 19 (2000), p. 790

[62] The Cambridge Crystallographic Data Base version 5.24; The Cambridge Crystallographic Data Center, Cambridge, UK, November 2002.

[63] J.J. Wilson; O. Matsushita; A. Okabe; J. Sakon EMBO J., 22 (2003), p. 1743

[64] P.S. Weiser; D.A. Wild; P.P. Volynec; E.J. Bieske J. Phys. Chem., A 104 (2000), p. 2562

[65] M.J. Frisch; J.E. Del Bene; J.S. Binkley; H.F. Schaefer J. Chem. Phys., 84 (1986), p. 2279

[66] U. Dinur Chem. Phys. Lett., 192 (1992), p. 399

Commentaires - Politique

Ces articles pourraient vous intéresser

The remarkable ability of B3LYP/3-21G(*) calculations to describe geometry, spectral and electrochemical properties of molecular and supramolecular porphyrin–fullerene conjugates

Melvin E. Zandler; Francis D’Souza

C. R. Chim (2006)

Computational and experimental approaches to the molecular structure of the HCl adduct of Me3PO

Andreas Orthaber; Ferdinand Belaj; Rudolf Pietschnig

C. R. Chim (2010)

Pseudo-tetrahedral semi-sandwich cycloruthenated compounds: 1H NMR data and DFT-calculations about the racemisation process of the ruthenium atom

Mike Robitzer; Vincent Ritleng; Claude Sirlin; ...

C. R. Chim (2002)