1 Introduction
Density Functional Theory (DFT) has been remarkably successful to accurately evaluate a variety of ground state properties of large systems and, in particular, of complexes containing transition metals [1–3]. More recently, several papers have shown the potentialities of DFT, through the so-called time-dependent DFT approach (TD-DFT), for the study of excited states properties and, in particular, for the calculation of vertical electronic excitation spectra (see for instance references [4–9]). While DFT approaches have been successfully applied to the study of several Ru(II) and Os(II) polypyridyl complexes [10–17], few applications were devoted to the analysis of excited states, the limiting factor being the size of the systems under investigation [18–21]. As a matter of fact, semi-empirical approaches, with all own intrinsic limitations are still commonly used [22,23]. Unfortunately, the reliability of these methods is strictly bound to the quality of the parameters used, thus preventing routinely applications.
This paper is aimed at using theoretical tools to gain insights into the physical chemistry and more specifically the electronic properties of complex of photochemical interest especially when the interpretation of the experimental data is not clear or subject to debate.
In fact, the recent developments in the design, synthesis and characterization of supramolecular architectures [24–27] allowed the construction of fairly sophisticated systems capable of selectively reacting to a given external input and behaving as devices at the molecular level [28]. In the case of photosensitized functional assemblies, so-called photochemical molecular devices (PMDs') [27], the input is light and the response can be either a change in the structural features (photo-triggered isomerization, PTI) or a change in the physico-chemical properties. Amongst the basic light-triggered processes, the most widely studied are, by far, photoinduced electron transfers (PET) due to the prominent part they take in biological systems [29], as well as in the intermingled research fields of molecular electronics [24–28,30–32] and photochemical conversion (and storage) of solar energy [24,26,32–34].
It's a matter of fact that when dealing with such complex systems, associated experimental behavior are not always straightforwardly rationalized. This is particularly true of the determination of the nature of excited-states involved in the photoinduced processes.
In this context, theoretical methods constitute a valuable means to interpret and even anticipate the photochemical behavior of PMDs.
In this account, we will focus more specifically on the capacity of DFT and TD-DFT for predicting and analyzing ground and excited state properties of inorganic chromophores by collecting the results we recently obtained for two different types of systems:
- • a compound undergoing a PTI process, namely the [Ru(bpy)(tpy)dmso]2+ complex (bpy = 2,2′-bipyridine; tpy = 2,2′:6′,2″-terpyridine; dmso = dimethyl sulfoxide);
- • an inorganic acceptor dyad (P1–A/Os; with P1 = [Os(ptpy)]2+, ptpy = 4′-phenyl-tpy and A = H3TP+ = 2,4,6-triphenyl-pyridinium) designed to photo-produce charge separated states (CS) actually corresponding to the transient conversion of light into an electrochemical potential.
In both cases, even if a thorough experimental study has been carried out, theoretical insights are needed to understand the detailed mechanism of the photoinduced processes. The theoretical information contributes to further substantiate or amend the interpretation of observed phenomena only based on experimental issues, and provides a deeper understanding of the nature of the excited states.
Although the two systems herein investigated are clearly different photochemical devices, they are both based on closely affiliated photoactive inorganic chromophores, namely pseudo-octahedral d6 transition metal (Ru(II) or Os(II)) complexes with oligopyridyl ligands (bpy and tpy). Owing to their ubiquitous use throughout the multifarious field of modern Inorganic Chemistry, these types of co-ordination compounds constitute a particularly interesting benchmark to test our computational procedure. However, beyond the shared chemical features of examples examined in this account, it is worth emphasising that the common denominator of importance here actually lies in the computational set-up we have chosen to use and validate.
2 Computational methods
A schematic representation of the complexes studied together with their nomenclature is given in Fig. 1 ([Ru(bpy)(tpy)dmso]2+) and Fig. 2 (P1/M with M = Os, Ru; P1–A/Os). Computational details for the calculations performed for the two systems are reported in Sections 2.1 and 2.2.
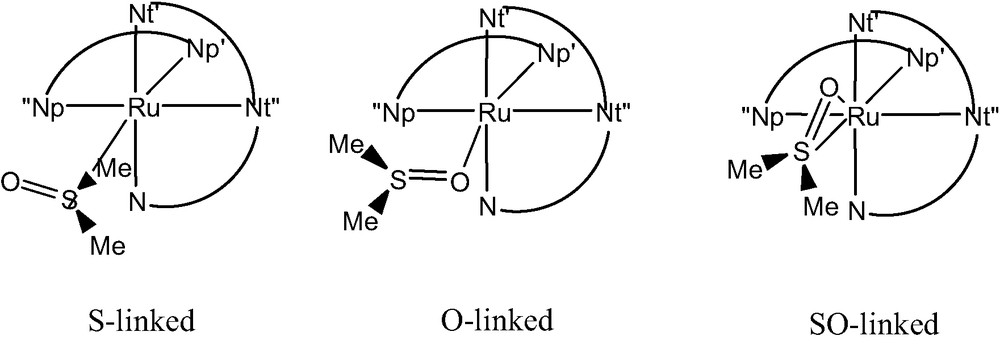
Schematic sketch and labeling scheme for [Ru(bpy)(tpy)dmso]2+.
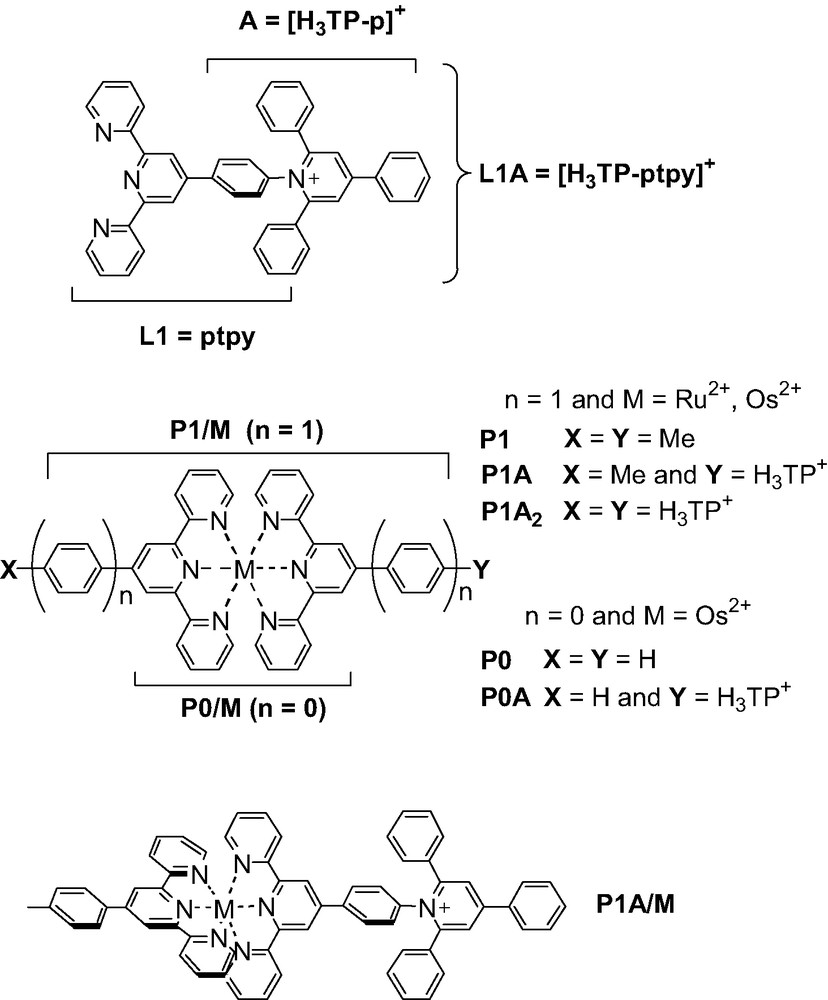
Schematic structures of P1–A/Os and related compounds.
2.1 [Ru(bpy)(tpy)dmso]2+
All calculations were performed using the Gaussian98 program package [35]. The Becke three-parameter hybrid exchange [36] and the Lee Yang Parr correlation [37] functionals (B3LYP) were used. A double-ζ quality LANL2DZ basis [38,39] was used for all atom but oxygen and sulfur, which were described by a split valence Pople basis plus one polarization function (6-31G* [40]). The inner core electrons of Ru(II) were described by the corresponding scalar relativistic electron core potential (ECP) [39]. Structural optimization were performed without symmetry constraints unless otherwise specified. The stationary points found on the potential energy surface (PES) were characterized by subsequent frequency calculations. Absorption spectra were computed as vertical excitations from the minima of the S0 PES using the TD-DFT approach. Emissions from the triplet states were computed as vertical decay using the ΔSCF procedure, i.e. the singlet energy was computed at the triplet geometry. All calculations of the triplet states were performed within a spin-unrestricted formalism and spin contamination, monitored by the expectation value of S2, was found to be negligible.
2.2 Inorganic dyads
All calculations were carried out using a development version of the Gaussian code [41]. A recent hybrid Hartree Fock/Density Functional model, referred to as PBE0, was used [42]. This approach was obtained by casting the PBE exchange and correlation functional [43] in a hybrid DFT/HF scheme, where the HF/DFT exchange ratio is fixed a priori to 1/4 [44].
In the case of open shell systems, unrestricted calculations were performed and spin contamination, monitored by the expectation value of S2, was found to be negligible.
A double ζ quality LANL2 basis [38], and corresponding pseudo-potentials for the metal atoms (Os and Ru) [39], was used for all atoms both for the structural optimizations and the calculation of electronic properties. The molecular structure of each native and one-electron reduced compound was fully optimized. Only in the case of reduced P1–A/Os, the optimized structure of the corresponding native form was used when computing the electronic absorption spectrum. Optical transitions were computed using the time-dependent DFT approach. To make the direct comparison with the experimental data easier, the spectra were simulated from the computed energy of the electronic transitions () and their corresponding oscillator strength (f), by using Gaussian functions with one adjustable parameter only (the full-width at half-maximum, fwhm). A satisfactory matching of the computed spectra with the experimental traces was found using rather small fwhm parameters ranging between 0.1 and 0.2 eV.
3 Photo-triggered isomerization of [Ru(bpy)(tpy)dmso]+: experimental evidences
Within the large class of Ru-polypyridyl complexes, the recently synthesized [Ru(bpy)(tpy)dmso](CF3SO3)2 (Fig. 1) [45] is a typical example of system undergoing a PTI process. In fact, Rack and co-workers [45] showed that, starting from the S–linked isomer (in film or crystal), an immediate change in color from yellow to red is observed upon irradiation at 441.6 nm. This phenomenon is accompanied by a shift of the absorption from 412 to 490 nm, the corresponding photo-product being stable for days. Upon light excitation, the complex also display a weak luminescence (λem = 720 nm) at ambient temperature while an additional new emission feature appears at 625 nm upon cooling down to 170 K [45].
These observations led to the experimental conclusion that the absorption at 412 nm was related to the transition from the singlet ground state (S0) to the first singlet excited state (S1) of the S-linked form. Irradiation was then postulated to induce a S–O linkage isomerization and the new feature appearing at 490 nm was ascribed to the same S0→S1 transition but associated to the O-linked species. The photo-product was therefore assumed to directly convert into the native S-linked species in dmso (solvent) only while in other coordinating solvents (e.g., CH3CN) this transformation was precluded by ligand-exchange involving solvent molecules [45]. The emission at 720 nm was assigned to a triplet to singlet decay (T1→S0) of the O-linked species, while the band at 625 nm was attributed to a similar T1→S0 transition from a hypothetical η2 species, characterized by concomitant S- and O- linkages to the metal cation [45].
Experimentally, both the S-linked [46] and the O-linked [47] isomers have been previously characterized but in none of these studies, all carried out in solution, evidences of S/O (or O/S) linkage isomerization were found.
All these experimental data were supporting the hypothesis that the energy barrier for the S/O linkage isomerization in the ground state of [Ru(bpy)(tpy)(dmso)]2+ was rather large and could not be cleared at room temperature. Therefore, the linkage isomerization was necessarily involving the population of an excited state, either of a Metal-to-Ligand Charge-Transfer (MLCT) or of a Ligand-Field (LF) character. At the same time, available experimental evidences from solid-state (including film materials) properties suggested that the linkage isomerization, contrary to other related Ru-dmso complexes such as [Ru(bpy)2(dmso)2]2+ [48], was an intramolecular process as the dmso ligand was kept confined within the direct coordination sphere of the metal atom [47].
For these reasons, the linkage isomerization of dmso within [Ru(bpy)(tpy)dmso]2+ is an unique case and can be considered as an extremely intriguing system for photoactive materials due to the possibility of switching the optical properties.
3.1 Insight from theory: structure and thermochemistry
In order to characterize the system, we first computed the minimum energy structures corresponding to the S- and O-linked forms both for the ground-state singlet (S0) and for the first excited triplet state (T1). The results are reported in Table 1 and compared to available X-ray data. Concerning geometrical parameters, an overall satisfactory agreement between experimental and computed data for the S-linked S0 form (1) is found, all the computed distances but the Ru–S one being within the experimental error (±0.03 Å). This accuracy is the one expected for the method used, taking also into account experimental factors (e.g. crystal packing forces), which occasionally can be responsible for apparent discrepancies (as for the Ru–S distance, overestimated by 0.13 Å). Two other local minima were found for the S0 S-linked isomer (see reference [49] for details) corresponding to a rotation of the dmso molecule around the Metal–S bond. Nevertheless, due to steric interactions between hydrogen atoms of the dmso and bpy ligands, the inter-conversion barrier was computed to be relatively high (40 kcal/mol). Thus, only the spectroscopic properties of most stable conformer (1) will be discussed. The same finding holds for the S0 O-linked species. Surprisingly, we found the S0 O-linked conformer (3) lying 11 kcal/mol lower in energy than the corresponding S0 S-linked one (1). This issue seems contradictory to the experiment where only the S-bound form has been crystallized [45]. Nevertheless, the main reason for the formation of the S-linked isomer is most likely of kinetic nature rather than thermodynamic. In fact, a smaller volume computed for the S-linked molecules with respect to the O–linked one (3754 bohr3/mol vs. 3785 bohr3/mol) justifies the preferential crystallization observed since better packing is possible.
Main geometrical parameters (in Å and degrees) and the relative energies (in eV) computed for [Ru(bpy)(tpy)dmso]2+, both in the ground singlet (S0) or in first triplet (T1) state. In parenthesis the available experimentala data are reported. For labeling refer to Fig. 1
| S-linked | O-linked | ||||
| S0 (1) | T1 (2) | S0 (3) | T1 (4) | ||
| Relative energy | 0.0 | 2.2 | –0.05 | 1.83 | |
| Ru–S | 2.419 (2.282) | 2.509 | Ru–O | 2.192 | 2.102 |
| S–O | 1.505 (1.467) | 1.504 | S–O | 1.564 | 1.591 |
| Ru–N′t | 2.113 (2.079) | 2.099 | Ru–N′t | 2.104 | 2.087 |
| Ru–N′′t | 2.007 (1.975) | 2.035 | Ru–N′′t | 2.000 | 2.008 |
| Ru–N′′′t | 2.113 (2.072) | 2.098 | Ru–N′′′t | 2.109 | 2.112 |
| Ru–N′′p | 2.142 (2.101) | 2.122 | Ru–N′′p | 2.098 | 2.117 |
| Ru–N′p | 2.103 (2.085) | 2.089 | Ru–N′p | 2.065 | 2.071 |
| a(O–S–Ru) | 114.5 (115.7) | 114.2 | a(S–O–Ru) | 126.5 | 124.3 |
| d(Npcis–Ru–S–O)b | –31.0 (-42.6) | –8.0 | d(Npcis–Ru–S–O) | –21.0 | 154.1 |
| SO-linked | |||||
| S0 (5) | T1 (6) | ||||
| Relative energy | 0.60 | 2.32 | |||
| Ru–O | 3.156 | 2.949 | |||
| Ru–S | 3.089 | 3.094 | |||
| S–O | 1.526 | 1.518 | |||
| Ru–N′t | 2.113 | 2.115 | |||
| Ru–N′′t | 2.008 | 2.023 | |||
| Ru–N′′′t | 2.107 | 2.116 | |||
| Ru–N′′p | 2.113 | 2.175 | |||
| Ru–N′p | 2.029 | 2.138 | |||
| a(S–O–Ru) | 73.4 | 80.2 | |||
| d(Npcis–Ru–S–O)b | –36.0 | –4.4 |
The lowest triplet state, T1, has been analyzed by carrying out calculations using both the corresponding S0 geometries and the fully optimized triplet structures. In all the considered complexes, the triplet state corresponds to an excitation from the HOMO to the LUMO.
The optimized T1 state for the S-linked isomer lies 2.1 eV higher than the corresponding ground state. The optimized structure (2) was obtained starting from the optimized singlet structure 1 without imposing of symmetry constrains. By comparison with the S0 structure (1) a significant elongation of the Ru–S bond (+0.09 Å) and smaller contraction of the Ru–Nt and Ru–Np bonds can be noticed, while the internal dmso parameters are not significantly affected. A slight rotation (+23°) of dmso towards a Cs orientation can also be noted. In general, the variation of the geometrical parameters is in line with the nature of the transition. In fact the S0→T1 transition formally corresponds to the transfer of one electron from the HOMO (Ru dπ orbital, slightly antibonding with bpy) to a MO with mainly π* tpy contribution and a smaller Ru–dmso antibonding character. Since an electron has been removed from a Ru–L antibonding orbital (L = bpy, tpy), the main structural consequences expected are a contraction of Ru–Nt and Ru–Np bond-lengths, which are indeed observed. This is qualitatively confirmed by the corresponding TD-DFT calculations (vide infra) and by the computed Mulliken spin population of the optimized S-linked T1 state. It is also interesting to note the small energy difference between the S0 to T1 gaps computed using the optimized T1 structure (2.1 eV) and the frozen S0 geometry (2.2 eV), thus underlying a small structural relaxation.
The structural optimization of the O-linked triplet state, starting from the optimized S0 O-linked structure (3), leads to two different minima, the most stable corresponding to structure 4 in Table 1. The main structural variations with respect to 3 (i.e. a shorter Ru–O distance, 2.10 Å, and a longer S–O bond-length, 1.59 Å) suggest an increase of the dmso–metal interactions (donation and back-donations), due to the depletion of the HOMO orbital, with a significant Ru–O antibonding contribution, upon excitation. As for the S-linked isomer, there is an overall coherence in the results obtained using frozen or fully relaxed structures.
Noteworthy, another minimum energy structure has been computed for the O-linked T1 state (Cs symmetry, not reported in Table 1), lying at a slightly higher in energy (0.11 kcal/mol). In fact this new minimum corresponds to a LF state, as confirmed by the computed Mulliken spin density on the Ru atom (1.84 e–), which is practically dissociative for dmso as suggested by the longer Ru–O distance (about 2.55 Å). Due to the small energy gap between the two states, the LF one could be easily populated at room temperature and thus be responsible for the exchange mechanism experimentally observed in solution [45].
Experimentally, the formation of a stable intermediate, namely a SO η2-linked species, along the linkage S→0 isomerization path both in the S0 and T1 electronic states is postulated to explain the emission at 625 nm [45]. For this reason, we tried to locate a η2-linked species both on the S0 and on the T1 potential energy surfaces. With this procedure, a first order transition state (TS) (ν = 157i cm–1) was localized on the S0 surface and characterized by an imaginary frequency corresponding to the isomerization pathway. This structure (5 in Table 1) lies 13.9 kcal/mol higher than the S-linked structure (1). The geometrical parameters indicate that the S and O atoms of dmso are at almost the same, relatively large, distance from the Ru atom (3.09 vs 3.16 Å, respectively). At the same time, the internal geometrical parameters of the dmso are close to those of the free ligand. The weak interaction of dmso with the [Ru(bpy)(tpy)]2+ fragment is confirmed by the small computed interaction energy of the two moieties: only 17.4 kcal/mol, significantly lower than in the S-linked (1) (30.3 kcal/mol) or in the O-linked (3) (42.1 kcal/mol) isomers.
Starting from the TS localized on the S0 surface (5), the corresponding intermediate structure has been localized on the T1 surface (6). This structure is characterized by one imaginary frequency (ν = 101i cm-1) and is higher in energy than the S–isomer (2) and the O-linked form (4) by about 3.0 kcal/mol and 13.1 kcal/mol, respectively. The small barrier for the S→O interconversion (3.0 kcal/mol) well evidences the possibility of an isomerization in the T1 state, going through a direct, single step reaction. These results invalidate the two-step mechanism proposed by experimentalists, where the SO η2 structure is a minimum on the T1 surface and where two energy barriers have to be overcome for the complete isomerization [45]. Furthermore, from our calculations, the emission at 625 nm cannot be attributed to the SO-linked form since the non-adiabatic emission of the TS 6 (i.e. a hypothetical decay to the corresponding TS on the S0 surface (5)), is computed at 761 nm (1.7 eV). Of note, an adiabatic transition would appear at even lower energy. The observed transition can be assigned, instead, to the decay of the triplet state of the S-bonded isomer (vide infra).
The calculated geometrical parameters of the SO–linked TS (6) are close to those computed for the S0 TS (5), the only appreciable differences concerning the Ru–O distance, which is shorter in the T1 state, and the rotation angle of the dmso with respect to the bpy. The first variation is particularly important since it suggests a more compact structure of the TS in the T1 state, as also confirmed by the greater interaction energy of the dmso with [Ru(bpy)(tpy)]2+ fragment (21.3 kcal/mol). These latter values strongly suggest that the isomerization mechanism implies a more associative character (A or Ia) in the triplet state than in the singlet ground state.
In summary, our calculations suggest that the isomerization reaction is highly probable in the triplet state, due to the small barrier that can be easily overcome under experimental conditions. At the same time, the reaction mechanism is a single step, the transition structure corresponding to the SO η2 arrangement.
3.2 Computed emission and absorption spectra
Finally, for comparison purposes with experimental data, we have computed the UV-vis. absorption spectra, at the minimal energy structures reported in Table 1, by using the TD-DFT approach. All these electronic transitions were evaluated at the corresponding ground state (S0) geometries (1 and 3) i.e. vertical. The results are collected in Table 2. In the experiments performed both in films and in solution, the most intense MLCT transition occurs at 412 nm in the case of the S-linked complexes and is shifted to 490 nm in case of the O-linked one. Both transitions are well described by our calculations, even if they are slightly and systematically overestimated. In particular, we have found three intense transitions for the S-linked isomer at 416, 402 and 396 nm. The corresponding ones for the O-linked species are at 462, 445 and 444 nm. All these transitions are basically one electron excitations from MOs centered on the d orbital of Ru(II) to empty π* MOs localized on the tpy/bpy moieties, the ligand centered transitions (involving bpy and tpy) normally occurring at higher energy. From these results, it is clear that these most intense bands, rather broad, cover several transitions in the experimental spectra. It is also interesting to note that the red shift observed in going from the S-linked to the O-linked complex is qualitatively reproduced by our calculations. Vertical S0→T1 transition allows identifying the character of the first excited triplet state. These first transitions have been computed using both TD-DFT and ΔSCF approaches. In the former case, we found a transition at 547 and 653 nm for the S- and O-linked forms, respectively. Both for the S- and the O-linked isomers, the first S0→T1 transition involves mainly a MLCT transition. Nevertheless a substantial difference is found: while the S-inked triplet has contribution only from MLCT transitions (essentially HOMO→LUMO), in the O-linked form a relatively small (10%) contribution arises from a LF transition. This corresponds to the promotion of an electron from a dπ orbital of Ru(II) to the dz2 pointing towards the O atom of dmso. This is the reason why, when relaxing both the geometry and the electronic state of the T1, two minima have been found (depending on the population of the LUMO or LUMO + 8 orbital), one for each state. Emission is most probably occurring from the MLCT state (4) since the T1-LF state leads to dissociation in solution.
Computed TD-DFT vertical excitation energies (λ in nm) and oscillator strengths (f in au) for the most stable S-linked (1) and O-linked (3) S0 isomers
| S-linked | O-linked | |||
| Transitions | λ | F | λ | f |
| S0→Sn | 486 | 0.010 | 593 | 0.0110 |
| 416 | 0.0260 | 490 | 0.0039 | |
| 402 | 0.0541 | 462 | 0.0093 | |
| 396 | 0.0481 | 445 | 0.0661 | |
| 378 | 0.0027 | 444 | 0.0287 | |
| 376 | 0.0267 | 443 | 0.0474 | |
| 335 | 0.0016 | 410 | 0.0239 | |
| S0→Tn | 547 | — | 653 | — |
While absorption spectra involve vertical transition from the ground (S0) to the excited states, the emission spectra represent the vertical decay from the minima on the triplet potential energy surface (T1) to the ground state (S0). Therefore, in order to compute the emission spectra it is important to have a full description of the T1 PES. Emissions from the S- and O-linked forms were computed by using the ΔSCF procedure, on the basis of the T1 relaxed geometries (2 and 4). The emission decay for the S-linked form was computed at 697 nm, rather close to the experimental value (625 nm) of the band measured at low temperature [45]. This transition has been previously attributed to the decay of the SO-intermediate (6), but as described in the previous section, this transition is computed to occur at lower energy (761 nm). In the case of the O-linked form, the emission decay was computed at 1130 nm for the LF state while the 3T1 MLCT state (4) is predicted to result in the emission at 744 nm. This latter value is in good agreement with the experimental finding (720 nm) thus confirming the nature of the first excited triplet state as a MLCT one. The overall photochemical behavior of the system can thus be summarized with the sketch depicted in Fig. 3.
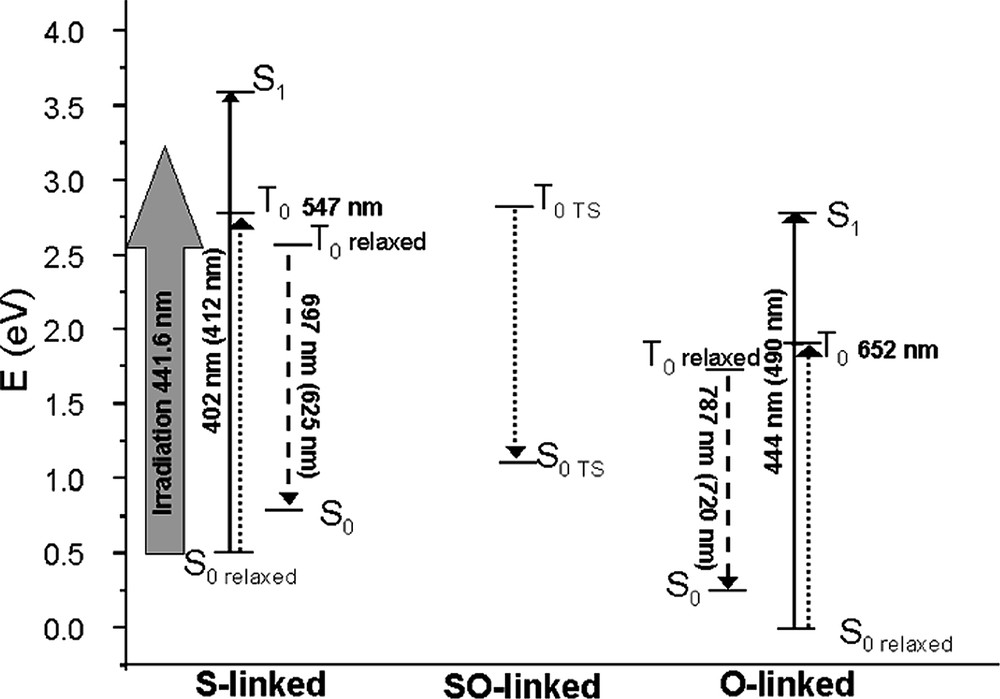
Schematic representation of the computed (TD-DFT) relative energy of the ground (S0), first singlet (S1) and first triplet (T1) excited states of the different conformers of [Ru(bpy)(tpy)dmso]2+ and computed absorption/emission energies. Full lines arrows correspond to computed allowed transitions, dotted to non-allowed ones; dashed arrows to the computed emission. Experimental values are reported in parenthesis; relaxed stands for computed at the corresponding optimized structure and TS indicates a transition state.
In summary our calculation allowed us to confirm the experimental hypothesis of a linkage isomerization through the population of the first triplet excited state but, at the same time, they rule out the experimental inference of the formation of an SO–linked species and, as a consequence, provided a new interpretation of the emission spectra at low temperature.
4 PMD: inorganic dyads
In the context of researches devoted to artificial photosynthesis and related functional model compounds capable of monitoring PET processes at the molecular level, specifically developed PMDs are generally referred to as polyad systems. These polyads are typically constituted by electron donating (D) and/or accepting (A) components together with a photosensitizing unit (P). The building blocks, preferably arranged in a linear fashion [33] according to the D–P–A sequence, are usually held together by covalent links, hydrogen bonding or even mechanical contacts. [50] Subsequent to light excitation of the P unit (the primary donor), a cascade of intramolecular electron transfers takes place, leading to the lower-lying CS state, *[D+–P–A–]. This state is then intended to be employed before charge recombination (CR) occurs. A great deal of synthetic works have been carried out by experimentalists in the last decades to identify and select the different P, A and D building blocks as well as to propose satisfactory intercomponent bridging units [24,26,27,33,50]. Recently [51], an electron-acceptor group (A) of the triphenylpyridinium type, [H3TP]+, was for the first time linked to the complex photosensitizer (P), [M(tpy)2]2+ (M = Ru(II), Os(II); tpy = 2,2′:6′,2″-terpyridine), both directly (P0–A/M) and via a phenyl spacer (P1–A/M, see Fig. 2). These dyad systems are showing appealing structural [52] and photochemical properties [53,54]. They derive from a new family of triarylpyridinio–functionalized [4′-(p–phenyl)n]terpyridyl ligands, R12R2TP+-(p)ntpy (here, R1 = R2 = H and n = 0, 1), that has the valuable advantages, when complexed, of being structurally well-defined (rigid assembly) and, at the same time, of being chemically flexible (R1, R2). The synthetic versatility, which includes the metal cation (M) of P, allows the fine tuning of the electronic and electrochemical properties of polyad systems. In fact, these triarylpyridinio-derivatized bis-terpyridyl complexes of Ru(II) and Os(II) have been designed to satisfy two of the major criteria required for an efficient charge separation: (i) a rod-like shape and (ii) a controlled overall architecture. Both factors allow to avoid untimely withdrawal of the molecule that could favor charge recombination (intramolecular “short circuit”) [55]. Furthermore, the two bulky phenyl substituents ortho to the Npyridinio atom of the electron-acceptor group (A) prevent the pyridinium ring from adopting a coplanar conformation with the covalently linked photosensitizer unit (P1) and warrant the disruption of the conjugation between the two connected subunits. In other words, the necessary intercomponent electronic decoupling is expected to be produced by a geometrical decoupling [56], which is playing the role usually fulfilled by saturated spacers. Experimentally, the effectiveness of such a correlation between structure and electronic properties has been demonstrated in the relaxed ground state for the acceptor-dyads in their native form, P1–A/M. [52,53] Nonetheless, the behavior of the electrochemically reduced forms, [P1–A/M]-, to some extent mimicking the targeted CS state, was remaining somewhat unclear [53]. The photophysical properties of the Os(II)-based dyad as well appeared a little disappointing even if thermodynamics for the charge-separation process was borderline (slightly endoergonic) [53].
In order to correctly account for these phenomena, a full theoretical analysis of the ground-state properties of the various species both in their native and reduced forms (i.e. [P1/M]–, [A]– and [P1–A/M]–), including the simulation of their electronic absorption spectra, has been carried out [57]. Here we will give only a brief review on the theoretical insights on the photochemical behavior of the dyad, both in its native and reduced forms, referring to reference 57 for further information.
4.1 Spectral signatures of the native P1/M and P1–A/Os Complexes
The calculated energies and oscillator strengths (f) of the principal electronic transitions together with the corresponding experimental values [51] for P1/M (M = Ru, Os) and P1–A/Os are reported in Table 3.
Principal computed electronic transitions (λ, in nm) and associated oscillator strength (f) along with absorption maxima (in nm) for simulated (λsim) and experimental (λexp) absorption bands for the native forms of the P1/M and P1–A/Os complexes
| λ | f | λsim (fwhm) | λexpa | |
| S0→Sn transitions | ||||
| P1/Ru | 464 | 0.49 | 461(0.15) | 490 |
| 408 | 0.22 | |||
| P1/Os | 501 | 0.34 | 471 (0.20) | 490 |
| 444 | 0.34 | |||
| P1–A/Os | 500 | 0.34 | 468 (0.20) | 492 |
| 435 | 0.38 | |||
| 353 | 0.28 | 349 (0.20) | 314 | |
| 347 | 0.60 | |||
| S0→T1 transitions | ||||
| P1/Os | 710 (615)b | — | — | 668 |
| 645 | ||||
| P1–A/Os | 736 (650)b | — | — | 668 |
| 645 |
Concerning the most intense transitions for both Os and Ru compounds (at ca. 460 and 500 nm, see Table 3), a good agreement between the computed and the experimental data can be found, the largest difference being of ca. 30 nm. Moreover, the shapes of simulated bands also closely reproduce the experimental profiles (see [57] for a more detailed discussion on band shapes).
For all systems, transitions calculated in the spectral region ranging from 400 nm to 500 nm are of MLCT character. They are ascribed to one-electron excitations from doubly occupied mainly metal-centered orbitals to empty π* orbitals of the tpy ligands. The first main transition (at lower energy) has a dominant contribution of the HOMO-LUMO type. In the case of symmetric compounds (P1/M), the empty π* orbital has contribution from both tpy systems, similarly to other symmetric Ru complexes such as [Ru(bpy)3]2+. In the case of P1–A/Os, the symmetry breakdown due to presence of the acceptor group on one of the two tpy ligands causes a localization of the LUMO. Indeed, the largest contributions of ligand-centered molecular orbitals to the MLCT bands are found to mainly originate from H3TP+-ptpy. Thus, the first intense transition at 500 nm (f = 0.34) is mainly centered on the tpy fragment of the H3TP+-derivatized ligand. More interestingly, optical electronic transitions corresponding to the direct charge transfer from the metal center to the acceptor moiety (A) are also computed to occur at higher energy (at 353 nm), but with a smaller intensity (f = 0.28). They could not be detected in the experimental spectrum due to the closely lying much stronger transition computed at 347 nm (f = 0.6) and other LC transitions.
Spin-forbidden singlet-to-triplet transitions have been computed only for P1/Os and P1–A/Os and compared to the available experimental data. These bands are not experimentally detected for Ru(II) bis-terpyridyl chromophores, due to the small spin orbit coupling of Ru. A ΔSCF procedure, that is the calculation of the singlet–triplet transition as the difference in energy of the triplet and singlet states, was also applied in order to compute the first transition energy (Table 3). It was found that the transition energies are systematically underestimated when using the TD-DFT approach (up to 68 nm i.e. 0.17 eV) whereas the ΔSCF procedure provides overestimated energies of transitions (up to 53 nm i.e. 0.16 eV).
4.2 Spectral signatures of the mono-reduced [P1/M]– and [P1–A/Os]– complexes
Experimentally, the spectroelectrochemical study of the various compounds was undertaken in order to record their electronic spectra when reduced at such a controlled potential that only the corresponding mono-reduced species were expected to be generated. From both computational and experimental results it appears that, upon reduction, the spectroscopic properties of the chromophores are strongly modified. Namely, besides the overall decrease in the intensity of the various transitions, which was already noticed for the reduced model acceptor, the theoretical calculations are also anticipating the rising of a broad new band in the NIR region. These main features are found to be in good agreement with the experimental data [53].
More precisely, in the case of the [P1/Ru]– and [P1/Os]– reduced model photosensitizers (Table 4), new transitions are computed between 600 nm and 800 nm. The most intense simulated band (fwhm = 0.1 eV) in this range is predicted at 671 nm for [P1/Ru]– and 634 nm for [P1/Os]– and is ascribed to a SOMO to π*, ligand centered, transition. Noteworthy, time-resolved transient absorption difference spectra recorded for the photo-excited *[P1/M] systems exhibit a positive feature at around 600 nm, which is usually ascribed to the spectroscopic signature of the reduced ligand [ptpy]–. This assignment was made by analogy to the spectral absorption of both the chemically produced radical anion of the para-substituted ptpy ligand [58] [R-ptpy]– and the features of [bpy]- within photo-excited *[Ru(bpy)3]2+ [26a].
Principal computed electronic transitions (λ, in nm) and associated oscillator strength (f) along with absorption maxima (in nm) for simulated (λsim) and experimental (λexp) absorption bands for the reduced form of the P1/M and P1–A/Os complexes
| λ | f | λsima | λexp | |
| [P1/Ru]– | 818 / 671 | 0.01 / 0.08 | 671 | 760 / 723b |
| 480 | 0.15 | 477 | 515b | |
| 434 | 0.24 | 434 | 457b | |
| [P1/Os]– | 960 | 0.03 | nd | nd |
| 740 | 0.01 | 740sh | 760c | |
| 635 | 0.06 | 634 | 600c | |
| 515 | 0.06 | 515 | 505c | |
| 467 | 0.37 | 469 | 455c | |
| [P1–A/Os]– | 779 | 0.06 | 775 | 760c |
| 539 | 0.07 | 525sh | idc | |
| 531 | 0.07 | |||
| 475 | 0.12 | 468 | ||
| 461 | 0.22 |
Thus, in this case, theory allowed to show how reduced species are expected to absorb in this region and suggests that the broad bands around 600–700 nm are their first characteristic signature.
The other more intense bands, in the different spectra, are situated in the spectral region ranging from 400 nm to 500 nm. As previously discussed in the case of the native species, these bands, of MLCT character, are actually resulting from several transitions, two of them being predominant. It's also noteworthy that these data are in agreement with the experimental spectra, for both band shapes and transition energy shifts.
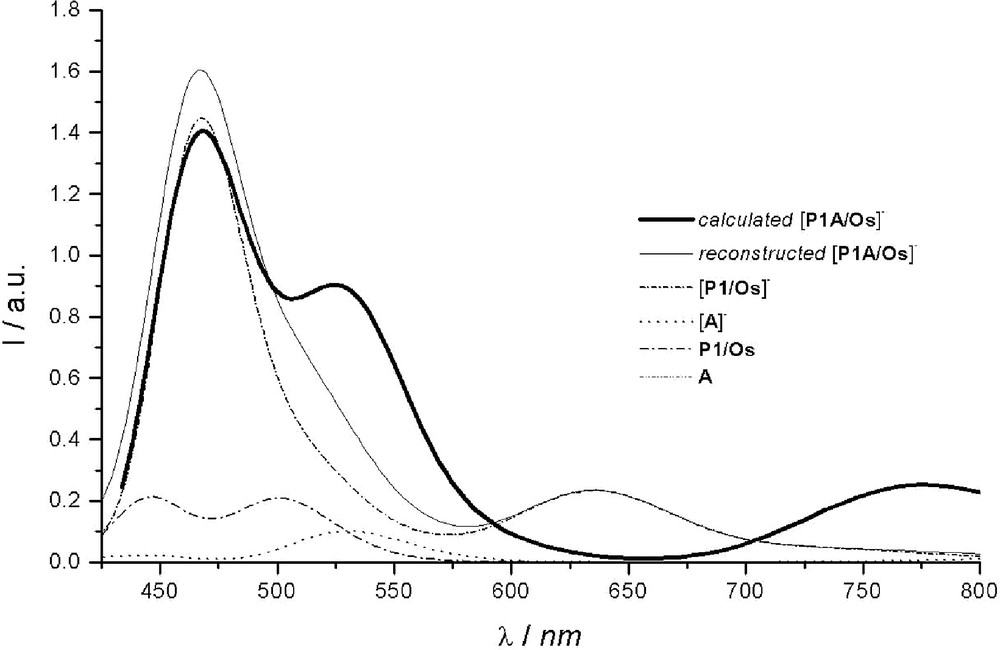
The computed spectrum of [P1–A/Os]– is reported in Fig. 4. For comparison purposes, the spectrum was also reconstructed starting from the weighted contributions of the reduced parent chromophores. It was built up from the different proportions deduced from the spin density map of [P1–A/Os]– (see [57]): 86% of [P1/Os]– and 14 % of [A]– for the reduced forms, together with 14 % of P1/Os and 86 % of A (not absorbing in the visible range) for the complementary contribution of the native forms. As can be noted, the sum of the weighted contributions (reconstructed spectrum) does not match the simulated spectrum computed for the reduced dyad. This indicates that [P1–A/Os]– should no longer be considered as a supramolecular species [24,27,33] as was the case for its native form [52,53]. Upon reduction, the initially rather independent P1/Os and A components are coming on electronically – and noticeably – interact through the phenyl ‘spacer’, as previously revealed by spin density maps [57]. Such an inference could actually be experimentally substantiated from spectroelectrochemistry performed on the dyad and more precisely from the incongruent presence of the reduced photosensitizer1. Although partial delocalization of electrons added onto A over the P1 unit has been postulated [53], its significance was, at that time, underestimated.
Within the 430–850-nm spectral range, two intense bands are predicted: an almost symmetrical one at ca. 775 nm and another one at 468 nm, roughly three times more intense, with a shoulder outlined at about 525 nm. These bands originate from the three sets of intense transitions reported in Table 4. The first absorption band around 775 nm is mainly resulting from a SOMO-to-π* transition computed at 779 nm, the involved π* molecular orbitals being mainly localized on the phenyl (spacer) of the H3TP+-ptpy ligand. As a matter of fact, the presence of A on the ptpy ligand strongly affects the energy of this first transition. The same SOMO-to-π* transition was actually also computed in absence of the acceptor, for [P1/Os]–, but at significantly higher energy (634 nm). However, contrary to [P1/Os]– for which the two Me–ptpy ligands have a share to the π* orbital involved in the transition, in the case of the reduced dyad [P1–A/Os]–, the implicated π* MO is only localized on the phenyl of the ptpy bearing the acceptor. The second set of intense transitions participates to the shoulder (outlined at 525 nm) of the band situated at 468 nm. Although the concerned transitions are MLCT in nature (the most intense ones being computed at 539 nm and 531 nm), the metal–centered orbital has nevertheless a significant contribution from the phenyl spacer that connects the acceptor. From the sole experimental data, it would be tempting to ascribe this shoulder to acceptor-centered transitions, by analogy with the absorption spectrum recorded for the reduced model acceptor (see [57]). However, this attribution would not be consistent with the results of the present calculations. Actually, the transitions from SOMO to the higher virtual MOs of the acceptor are found to occur at higher energy, the most intense ones being typically located at 475 nm and 461 nm (third set of intense transitions). The resulting band is simulated at 468 nm (fwhm = 0.1 eV).
4.3 Insights into Vis.–NIR spectro-electrochemical and transient absorption features
Both the rather large contribution and the unusual profile determined for the absorption band initially ascribed [53] to pure [A]– within [P1–A/Os]– and revealed by the visible-NIR spectroelectrochemical study of P1–A/Os, may be explained by the additional ‘tainting’ contribution of above-identified transitions from SOMO to phenyl spacer centered π* orbitals. Indeed, the absorption spectrum of the reduced acceptor embedded within the reduced dyad was obtained by deducting the contributions of the various other identified parent chromophoric species, in that case not correctly considered as electronically independent entities. [53]
Similarly, in the light of gained new theoretical insights, together with the characteristic spectral features experimentally well established for both the reduced ligand [ptpy]– (also theoretically confirmed [57]) and the oxidized metal center [59], transient difference absorption spectra recorded for P1–A/Os [53] could therefore be qualitatively re-analyzed as follows (Fig. 5).
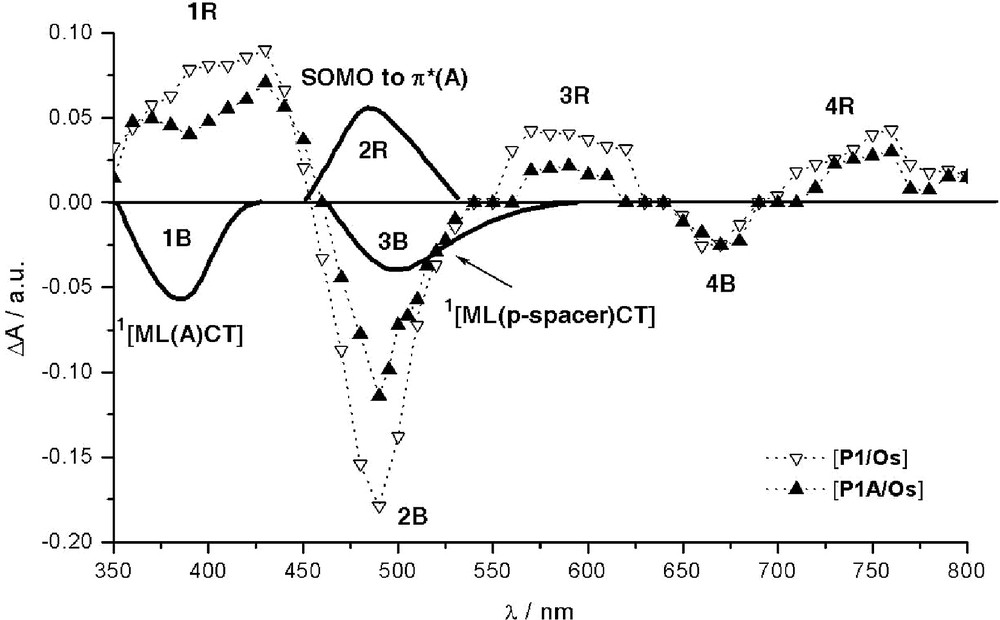
Schematic illustration of various identified contributions to transient absorption difference spectra of P1–A/Os and reference P1/Os recorded at 20 ns after laser excitation (λexc = 308 nm) for isoabsorptive acetonitrile solutions. [53] Dotted lines: experimental features. Bold solid lines: new computed features specific to the dyad. For clarity, the computed bands schematically represented were subject to slight offsets along the λ axis to match the experimental spectra.
The absorption (2R) of the chromophoric reduced acceptor, [A]– (SOMO-to-π*(A) transitions) embedded within the dyad is computed to be accidentally situated in the same region as the 1MLCT transitions (2B) of the native dyad P1–A/Os, at about 468 nm (Tables 3 and 4), in accordance with experimental inference [53]. Ceteris paribus, it is then not surprising that the photoinduced formation of [A]–, if occurs, cannot be easily observed except via an apparent abnormally pronounced attenuation (instead of the usual effect) of the overall bleaching of the more intense 1MLCT band (2B), as compared to the corresponding 2B feature of reference isolated *P1/Os. The uneven profile of the latter bleaching feature, with outlined shoulder at ca. 503 nm, is found to be consistent with the bleaching of a rather intense new 1MLCT band computed at ca. 525 nm, 3B, specifically involving the phenyl spacer. This band (3B) is not present in the parent photosensitizer P1/Os and is maybe also partly responsible for the attenuated absorption feature observed for the band 3R, which is ascribed to the spectroscopic signature of the reduced ptpy ligand. This noticeable weakening of feature 3R is also consistent with the possible capture of the photoexcited electron by the acceptor. Bleaching features recorded around 670 nm (4B) correspond to the disappearance of the 3MLCT band. In the near UV region, another particular feature can be noted when comparing the behavior of *P1/Os to that of *P1–A/Os. A significant depletion at ca. 390 nm is observed for the dyad, which is formed within the time of the laser excitation (pulse duration of ca. 10 ns; λexc = 308 nm), [53] in the region where positive features normally dominate (1R). Indeed, this excited-state absorption, 1R, corresponds to the well-established rising of the LM(Os3+)CT band [59] (correlated with the disappearance of the main 1MLCT band, 2B) together with some absorption (associated with features 3R and 4R) [59] characteristic of the formation of the radical anion of the phenyl-substituted tpy ligand. [53] In the present case, the additional bleaching of the new band (1B) computed at 353 nm (see Table 3) and resulting from a direct optical charge transfer from Os(II) to the acceptor moiety of the derivatized ptpy ligand well accounts for the depletion of 1R features observed for P1–A/Os.
The overall picture drawn out of the time-resolved transient absorption spectroscopy is compatible with the formation of the reduced acceptor although not straightforwardly observable due to unfavorable spectroscopic features. These findings are therefore consistent with the transient formation of the targeted charge-separated state, *[P1/Os+–A–]. To reach this hypothetical CS state, an alternative pathway to the classical stepwise photoinduced ET, involving the triplet MLCT state of *P1, is proposed: the direct optical electron transfer from the ground state to the CS state. This theoretical issue is found to be consistent with available experimental data. Nonetheless, although slightly endoergonic by ca. 0.12 eV [53], the photoinduced pathway seems to remain operative, as suggested, for instance, by the above-noticed sizable consumption of the photo-promoted electron onto ptpy ligand.
In summary the most important outcomes of this work can be summarized as follow:
- • role of the phenyl spacer in providing intercomponent coupling in the parent and reduced (and, presumably, excited) species;
- • direct optical excitation into the charge-separated state;
- • increasing of the intercomponent coupling and electronic delocalization upon reduction;
- • involvement of the phenyl-spacer-to-π* excitations in the spectral transitions of reduced and excited species;
- • re-interpretation of the transient spectrum demonstrating the formation of the CS state.
This overall picture drawn out from the present theoretical study prepares general guidelines for forthcoming supramolecular engineering of the promising potentialities of triarylpyridinio-derivatized polypyridyl complexes of Ru(II) and Os(II).
5 Conclusions
In this contribution, thanks to the analysis of two complex prototype systems of different types of PMDs, we have given some insights on the potentialities of ab-initio theoretical approaches for the description of complex photochemical/photophysical behaviors.
In particular, we have shown that modern computational techniques like DFT and TD-DFT are not only able to give a proper description of the ground and first excited states of the systems but they also constitute valuable tools for the interpretation and comprehension of the experimental data, especially when intermingled contributions are operative.
Acknowledgements
C. A. and I. C. are grateful to CNRS for financial support in the framework of the ACI ‘Jeune Équipe 2002’ project and to the French National Computer Center (IDRIS) for a generous grant of computer time (project 41703).
1 Electrochemical reduction of P1–A/Os has been carried out at such a potential (E = -1 V vs. SCE) that the P1 subunit was not expected to be concerned (E1/2(P1/Os0/-) = -1.21 V) but only redox processes attached to the TPH3+ group (E1/2(TPH3+/0) = -0.91 V and E1/2(TPH30/-) = -1.00 V).