Slow dynamics of water in reverse micelles

Ghazi Kassab; Dominique Petit; Jean-Pierre Korb; Tahar Tajouri; Pierre Levitz

doi:10.1016/j.crci.2005.06.022

Résumés

Anglais
Français

We present the magnetic-field dependence of the proton and deuteron spin–lattice relaxation rate (R₁) of water confined in reverse micelles of bis (2-ethylhexyl) sodium sulfosuccinate (AOT) dispersed in isooctane. After a plateau at very low fields, R₁ decreases as a power law when the Larmor frequency increases. These typical relaxation features have been interpreted according to a model of molecular reorientations coupled with translational diffusion in spherical confinement. A numerical simulation of Brownian dynamics of water molecules confined in a sphere is proposed to support this model. We aim at extending the proposed study to allow a better understanding of the slow dynamics of biological systems in confinement. .

Nous présentons les variations avec le champ magnétique des vitesses de relaxation spin–réseau (R₁) des protons et deutérons de l'eau confinée dans des micelles inverses formées par le mélange d'un tensioactif bis (2-éthylhexyl) sodium sulfosuccinate (AOT), de l'isooctane et de l'eau. Après un plateau à très bas champs, R₁ diminue en loi de puissance lorsque la fréquence de Larmor augmente. Nous avons interprété ce comportement en fréquence à l'aide d'un modèle de relaxation de spin impliquant une réorientation moléculaire couplée à une translation en confinement sphérique. Une simulation numérique de dynamique brownienne de molécules d'eau confinées dans une sphère est proposée et comparée aux résultats expérimentaux. Cette étude constitue une étape préliminaire vers une meilleure compréhension de la dynamique lente de systèmes biologiques en confinement. .

1 Introduction

Surfactants such as sodium bis(2-ethylhexyl) sulfosuccinate (AOT) aggregate in apolar solvents have the remarkable property of solubilizing large quantities of water. These systems have been studied by a great number of physicochemical methods [1]. It is now well established that AOT reverse micelle in isooctane consists of an approximately spherical water core surrounded by closed AOT aggregates [1]. An important property of AOT reverse micelles is to confine various amounts of solubilized water. There is an almost linear relationship between the molar ratio W₀ = $[H_{2} O] / [AOT]$ and the radius R_mic of the water core [2]. Reverse micelles and water in oil micro emulsions can be used to solubilize biopolymers such as proteins, enzymes and genetic material in apolar solvents and to study their physicochemical properties in the presence of a limited amount of water. The guest molecules are either dissolved in the water core or oriented to the AOT–water interface. They may acquire properties and reactivities that are different from those measured in the bulk aqueous phase.

It is known that by using a variety of physical techniques, the part of the water present in the water core of reverse micelles is bound to the AOT polar group as well as to the sodium counter-ions. Spectroscopic techniques, such as NMR [3,4], IR and Raman spectroscopies [5], have shown that the physicochemical properties of AOT reverse micelles change at low water content up to molar ratio W₀ = 10. In this regime, water is structured by its interaction with Na⁺ counter-ions and the strong dipole of the polar AOT. Above this threshold, the properties of the solubilized water approach progressively those of the bulk water.

Only few experimental tools are actually able to probe, on a very large extent, the liquid dynamics in confinement. A promising way is to measure the nuclear magnetic resonance dispersion (NMRD) of the proton spin–lattice relaxation rate (R₁) on a large range of Larmor frequencies [6]. The dynamical information is thus drawn out from these NMRD data according to a dynamical model. Several basic models and experiments have been proposed either for reorientational [7,8] or translational [9,10] molecular diffusion in porous media.

In this paper, we report experimental results that have been obtained for the proton and deuteron magnetic resonance dispersion (NMRD) of water confined in reverse micelles of bis (2-ethylhexyl) sodium sulfosuccinate (AOT) dispersed in isooctane. For the confined water, the relaxation features have been successfully interpreted according to an original model of molecular reorientations coupled to translational diffusion in spherical confinement. A preliminary simulation of Brownian dynamics of water molecules, in fast exchange between surface and bulk, is proposed to support such a model.

2 Experiments

Sodium bis (2-ethylhexyl) sulfosuccinate, i.e. AOT and trimethyl-2,2,4 pentane (isooctane) have been purchased from Sigma Aldrich. Both compounds have been used without further purification. H₂O water has been double distilled and de-ionized (resistivity of 18 MΩ) and was used at pH 6. D₂O water (99.9%) has been provided by CEA (Saclay). The appropriate amounts of H₂O and D₂O (for ²H NMR) have been injected into AOT solutions in isooctane by means of Hamilton syringe. The amount of water incorporated into AOT reverse micelles corresponds to W₀ = 50 and a micellar radius of R_mic = 80 Å (Fig. 1).

Fig. 1
Schematic diagram of a reverse micelle and examples of dynamical water loops of various extensions.

NMRD measurements have been performed, at a stabilized temperature of 298 K, on a fast-field-cycling spectrometer from Stelar Company. High-resolution proton NMR spectroscopy was realized on a Bruker spectrometer operating at 360 MHz. This has allowed to check the proton ratio (AOT/isooctane) = 0.085 in the (W₀ = 50, D₂O) sample and (water/isooctane) = 0.22 in the (W₀ = 50, H₂O) sample.

Two proton NMRD profiles have been performed for the (W₀ = 50, D₂O) (Fig. 2) and (H₂O) (triangles in Fig. 3). In these experiments, the longitudinal magnetizations exhibit a two-exponential decay in all the studied Larmor frequency range (10 kHz–7 MHz). These magnetization time evolutions have been sampled on a logarithmic time scale. Moreover, the number of accumulations has been chosen sufficiently large to reach an accuracy of the data to discriminate the two-exponential magnetization components. One observes a mono-exponential magnetization decay for the deuteron water ²H NMRD data (squares in Fig. 3). In the case of (W₀ = 50, D₂O) ¹H NMRD profiles (Fig. 2), the slowest R₁ curve (circles) is attributed to the isooctane liquid and the fastest R₁ curve (triangles) is attributed to the AOT molecules. The weight factor ratio corresponds to the NMR spectroscopy ratio (AOT/isooctane) in all the frequency range. In the case of (W₀ = 50, H₂O) ¹H NMRD profiles (Fig. 3), we note that there is still a two-exponential magnetization decay even if the system has three different spin populations. The ratio of the slow magnetization component compared to the total magnetization corresponds to the proton ratio of isooctane compared to all protons. Moreover, the slowest R₁ data ¹H NMRD (not displayed in Fig. 3) is the same as those of the isooctane dispersion curve in Fig. 2. As a consequence, the slow component of the magnetization decay is attributed to isooctane. On the other hand, the fastest R₁ curve (triangles) is attributed to the two populations of proton of water and AOT. The weight factor ratio corresponds here to the NMR spectroscopy ratio ((AOT + water)/isooctane) in all the frequency range.

Fig. 2
¹H spin–lattice relaxation rate recorded as a function of the magnetic field strength plotted as the ¹H Larmor frequency for D₂O water confined in spherical reverse micelles of molar ratio W₀ = 50 at T = 298 K. Relaxation rates AOT (triangles) and isooctane (circles).

Fig. 3
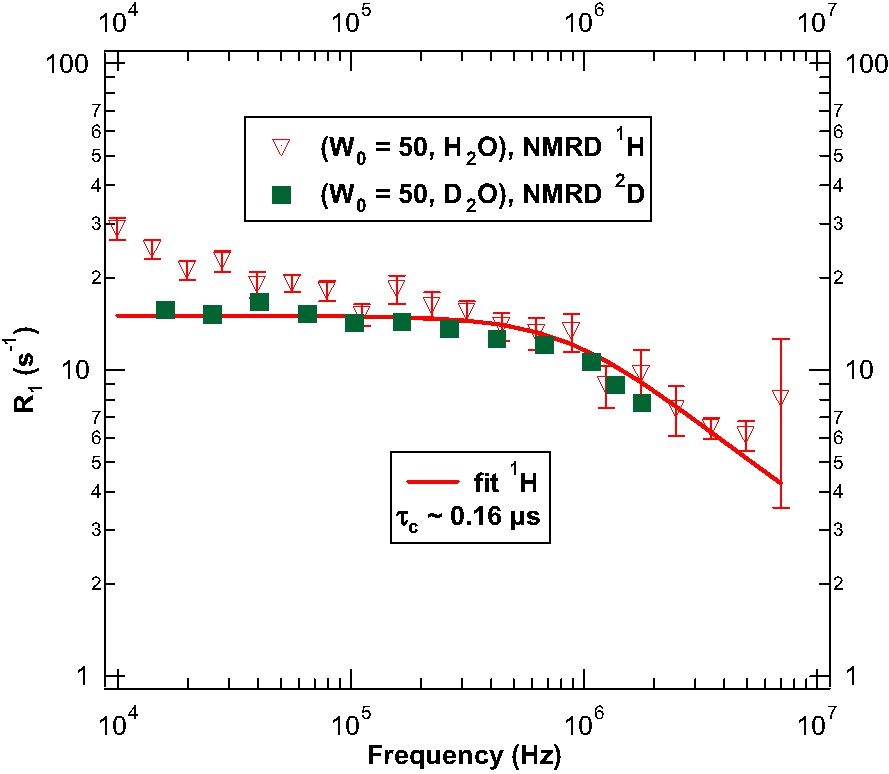
¹H water-AOT (triangles) and ²H water (squares) spin–lattice relaxation rates recorded as a function of the magnetic-field strength plotted as the Larmor frequency for water confined in spherical reverse micelles of molar ratio W₀ = 50 at T = 298 K. The R₁ of ²H NMRD have been rescaled to show the similarity behavior at high frequency with the ¹H R₁.

For convenience, the relaxation rates of deuteron NMRD have been renormalized in amplitude ( $\frac{R_{1} ({}^{1}H)}{R_{1} ({}^{2}H)} \approx 3 .7$ ) in Fig. 3. There is still an ambiguity concerning the separation of the low frequency dependencies of proton water and AOT because the two-exponential decay for a three-spin system could be interpreted either by a biphasic exchange process or a cross relaxation between proton of water and AOT molecules. However, the similarity in Larmor frequency (¹H, ²H) dependencies above 0.2 MHz between the ²H and the ¹H NMRD proves that the relaxation process is mainly driven by an intramolecular (dipolar for ¹H or quadrupolar for ²H) fluctuations. So, we focus in the following on a possible model interpreting only the high frequency behavior of confined water.

3 Model and discussion of the slow water confined dynamics

Concerning the data shown in Figs. 2 and 3, the relevant following observations can be made. In fact the ¹H spin–lattice relaxation dispersion exhibits a specific evolution below a very low frequency (0.1 MHz). This evolution is not observed in ²H experiments. This fact is clearly related to the surfactant slow dynamics inside the ionic/apolar corona coupled with the Brownian rotational diffusion of the entire reverse micelle (f_rot ~ 0.5 MHz obtained with η_isooctane = 0.5 cp). Above this low-frequency range, the proton and deuterium NMRD have a similar frequency dependence, mainly, a plateau up to a cut-off frequency around 1 MHz followed by an algebraic decay running as $1 / \sqrt{ω}$ . The confined water dynamics inside a spherical ‘pocket’ is then specifically probed. In this frequency regime, the reverse micelle can be considered as a non rotating object where the spin–lattice relaxation rate is mainly due to a reorientation modulation coupled with translational diffusion of either an intramolecular dipole–dipole interaction for ¹H or a quadrupolar interaction for ²H. As shown in [11–13], a two step model can be considered to describe the magnetic relaxation of the aqueous fluid nearby the interface. This model involves the superposition of fast motions (local rotations...) and slow dynamics depending on the time correlation of the spherical surface director probed by the molecule during its self-diffusion nearby the interface. We consider that fast and slow motions, in this two step model, are statistically independent. At low frequencies, the spin–lattice relaxation rate can be decomposed into a fast and a slow contribution such as $R_{1} (ω) = R_{1}^{slow} (ω) + R_{1}^{fast}$ . For the slow contribution, the fluid trajectories are modeled as an alternate successions of adsorption steps (A) where interaction I(t) is acting and Brownian loops (L) in the confined bulk media where I(t) = 0. A time cut-off (τ_c) appears naturally at long time (low frequency). This cut-off is associated with the appearance of a maximal end to end extension of Brownian loops, estimated to be equal to the sphere diameter 2 R_mic (Fig. 1). A basic approximation is τ_c = 4 R_mic²/(6D_w) where D_w is the water self-diffusion coefficient inside the confining sphere. For a time much smaller than τ_c, water molecule probes the spherical interface on a length scale lower or on the same order than the interface director persistence length. In this regime (above the cut-off frequency ω_c = 1/τ_c), the Fourier transform of the time correlation function $G (τ) = < I (0) \cdot I (τ) >$ noted J(ω) can be written as [8]:

J (ω) \propto 1 / [{(ω / ω_{0})}^{1 / 2} + (ω / ω_{0}) + 1 / 2 {(ω / ω_{0})}^{3 / 2}]

(1)

with the characteristic frequency ω₀ given by:

ω_{0} = \frac{Γ^{2} (1 / 2)}{2} \frac{τ_{L}}{τ_{A}^{2}}

(2)

where τ_L is the minimal loop duration, τ_A is the average adsorption time on the interface and Γ is the Gamma function. Looking at Eq. (1), three algebraic evolutions can be observed with a characteristic exponent ranging from 1/2 to 3/2. The value of this exponent (1/2 in our case) will be imposed by a proper choice of ω₀. In fact, the characteristic exponent, in the high field regime, is directly imposed by the value of the adsorption time on the surface. To introduce the finite size of the reverse micelle in the model, we have fitted our data using a simplification. As the dominant contribution of Eq. (1) behaves as ω^−1/2 at high frequency, we use the following expression:

J (ω) \propto F T {\frac{\exp (- | τ | / τ_{c})}{\sqrt{ω_{0} τ}}}

. It is then possible to estimate the slow part of spin–lattice relaxation rate as

R_{1}^{slow} (ω) \propto J (ω) + 4 J (2 ω)

. This gives the continuous line in Fig. 3.

Let us recall that our model depends essentially on two independent parameters: (i) a characteristic frequency ω₀, which imposes the ‘‘high-frequency’’ algebraic dispersion and its characteristic exponent; (ii) a cut-off frequency ω_c = 1/τ_c, which imposes the low-frequency cut-off below which a plateau is predicted. An extended analysis of a quite similar theoretical model is presented in [13], with another frequency cut-off mechanism.

In order to check this proposed relaxation process, we present a Brownian dynamics simulation. Our aim is to analyze the long-term dynamics of the confined water pools as probed by NMRD. Numerical details can be found in [12]. The sphere radius is set to R_mic = 8 nm corresponding to the inverse micelle size found for W₀ = 50. In order to get a cut-off frequency about f_c = 1 MHz, we set the self-diffusion coefficient to D_w = 2.5 × 10⁻¹⁰ m²/s. The only unknown parameter is the average adsorption time τ_A that defines the algebraic regime. In this preliminary work, we present a numerical simulation performed with τ_A = 0.3 ns and τ_L = 10 ps corresponding to ω₀ = 175 10⁶ rd/s according to Eq. (2). As shown in Fig. 4, we obtain a spin–lattice relaxation rate dispersion exhibiting a plateau up to 1 MHz, followed by an algebraic decay evolving as 1/ω^0.7. The former exponent is slightly above the experimental one, but can be lowered using a smaller τ_A value. This first simulation captures the main experimental features relative to the water slow confined dynamics. We are now extending our study to analyze the particular influence of the reverse micelle size (W₀).

Fig. 4
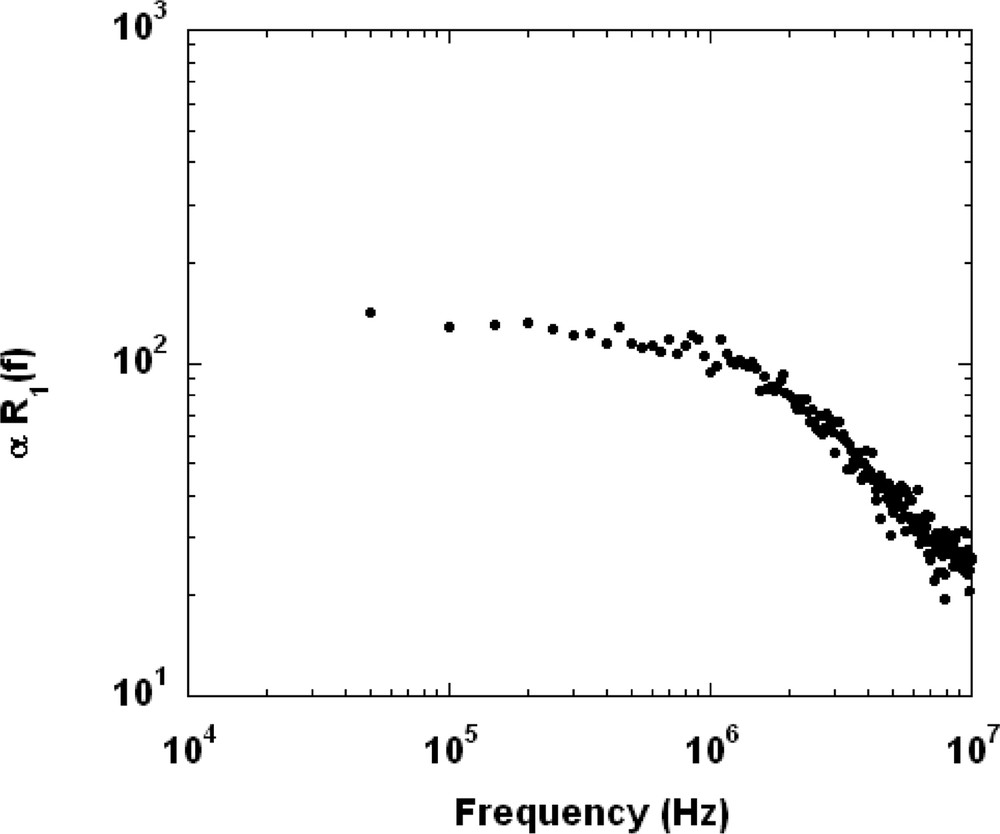
Numerical simulations of the frequency dependence of proton spin–lattice relaxation rate of water molecules that present Brownian dynamics.

4 Conclusion

The proton and deuteron field-cycling relaxometry have allowed us to characterize the slow dynamics of water confined in reverse micelles of nanometric sizes. The typical relaxation features have been interpreted according to a model of molecular reorientation coupled with translation diffusion in spherical confinement. A numerical simulation of Brownian dynamics of water molecules confined in a sphere is proposed to support this model. We aim at extending the proposed study to allow a better understanding of the slow dynamics of biological systems in confinement.