Plan
Comptes Rendus
no. 3-4

DYNAMOF : un programme pour l'analyse dynamique de données de relaxation obtenues à champs magnétiques multiples
Philippe Barthe1  ; Virginie Ropars1  ; Christian Roumestand1
1 Centre de biochimie st ructurale, UMR CNRS 5048–Inserm 554–UMI, faculté de pharmacie, 15, avenue Charles-Flahault, BP 14491, 34093 Montpellier cedex 05, France
Comptes Rendus. Chimie, Volume 9 (2006) no. 3-4, pp. 503-513.

Résumés

Cet article décrit un programme écrit en langage MATLAB utilisable pour l'analyse dynamique de données de relaxation enregistrées à différentes valeurs d'induction magnétique B0. Suivant l'approche de l'échantillonnage réduit des densités spectrales — fondée sur l'approximation des hautes fréquences — ce programme calcule les valeurs des densités spectrales J(0), J(ωX) et < J(ωH) > à partir des vitesses de relaxation hétéronucléaire (15N ou 13C) R1, R2 et de la valeur du NOE hétéronucléaire. Un ajustement des densités spectrales avec différentes variantes du modèle de Lipari–Szabo est alors proposé, permettant l'obtention des paramètres du mouvement (temps de corrélation et paramètres d'ordre) ainsi que de la contribution d'échange Réch. Le choix du modèle approprié peut alors être réalisé par une analyse statistique (test du χ2, F-test). Un exemple d'application est donné sur l'analyse de données de relaxation 15N mesurées à 9,4, 11,75 et 14,1 Tesla (correspondant à des fréquences protons de 400, 500 et 600 MHz) sur la protéine P13MTCP1. .

DYNAMOF: a program for the dynamics analysis of relaxation data obtained at multiple magnetic fields. This manuscript describes a MATLAB program devoted to the analysis of relaxation data obtained at different values of magnetic induction B0. Using Reduced Spectral Density Mapping (based on the High-Frequency Approximation), J(0), J(ωX) and < J(ωH) > are calculated from heteronuclear (15N ou 13C) R1, R2 relaxation rates and heteronuclear NOE ratio values. In order to obtain the motion parameters (correlation times and order parameters), spectral densities are then fitted with the different variants of the Lipari–Szabo model. Then, the choice of the right model can be chosen through a statistical analysis (χ2, F-test). As an application, the dynamics analysis of the 15N relaxation data obtained at 9.4, 11.75 and 14.1 Tesla (corresponding to proton frequencies of 400, 500 and 600 MHz) on the protein P13MTCP1 is given. .

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crci.2005.06.023
Mot clés : Relaxation hétéronucléaire, Analyse dynamique, Modèle de Lipari–Szabo, MATLAB
Mots clés : Heteronuclear relaxation, Dynamics analysis, Lipari–Szabo model, MATLAB
Philippe Barthe 1 ; Virginie Ropars 1 ; Christian Roumestand 1

1 Centre de biochimie st ructurale, UMR CNRS 5048–Inserm 554–UMI, faculté de pharmacie, 15, avenue Charles-Flahault, BP 14491, 34093 Montpellier cedex 05, France 
@article{CRCHIM_2006__9_3-4_503_0,
     author = {Philippe Barthe and Virginie Ropars and Christian Roumestand},
     title = {DYNAMOF~: un programme pour l'analyse dynamique de donn\'ees de relaxation obtenues \`a champs magn\'etiques multiples},
     journal = {Comptes Rendus. Chimie},
     pages = {503--513},
     publisher = {Elsevier},
     volume = {9},
     number = {3-4},
     year = {2006},
     doi = {10.1016/j.crci.2005.06.023},
     language = {fr},
}
TY  - JOUR
AU  - Philippe Barthe
AU  - Virginie Ropars
AU  - Christian Roumestand
TI  - DYNAMOF : un programme pour l'analyse dynamique de données de relaxation obtenues à champs magnétiques multiples
JO  - Comptes Rendus. Chimie
PY  - 2006
SP  - 503
EP  - 513
VL  - 9
IS  - 3-4
PB  - Elsevier
DO  - 10.1016/j.crci.2005.06.023
LA  - fr
ID  - CRCHIM_2006__9_3-4_503_0
ER  - 
%0 Journal Article
%A Philippe Barthe
%A Virginie Ropars
%A Christian Roumestand
%T DYNAMOF : un programme pour l'analyse dynamique de données de relaxation obtenues à champs magnétiques multiples
%J Comptes Rendus. Chimie
%D 2006
%P 503-513
%V 9
%N 3-4
%I Elsevier
%R 10.1016/j.crci.2005.06.023
%G fr
%F CRCHIM_2006__9_3-4_503_0
Philippe Barthe; Virginie Ropars; Christian Roumestand. DYNAMOF : un programme pour l'analyse dynamique de données de relaxation obtenues à champs magnétiques multiples. Comptes Rendus. Chimie, Volume 9 (2006) no. 3-4, pp. 503-513. doi : 10.1016/j.crci.2005.06.023. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2005.06.023/

Version originale du texte intégral

1 Introduction

L'utilité de l'analyse de la dynamique interne des macromolécules biologiques pour la compréhension des processus impliqués dans leurs mécanismes d'action n'est plus à démontrer. De ce fait, les mesures de relaxation hétéronucléaire — plus spécialement celles des noyaux 15N — se sont particulièrement développées au cours de cette dernière décennie (pour une revue récente, voir : [1]). L'analyse de ces données en termes de dynamique interne peut se faire par différentes approches, allant de l'interprétation directe de l'allure des fonctions de densités spectrales (Spectral density mapping) [2–6], jusqu'à une analyse plus élaborée par divers formalismes, permettant l'obtention des paramètres du mouvement. Dans cette dernière approche, le formalisme de Lipari–Szabo (Model Free) [7] est probablement le modèle le plus populaire et le plus utilisé. La relevance des résultats obtenus par cette approche repose néanmoins sur la qualité et la quantité des données expérimentales recueillies (R1, R2 et NOE hétéronucléaires, en général). Bien que relativement simple, l'ajustement du modèle aux données expérimentales sera d'autant plus précis et fiable que les données expérimentales fournies seront plus nombreuses, surtout dans le cas de mouvements complexes nécessitant l'ajustement de nombreux paramètres (modèle de Lipari–Szabo étendu) [8,9]. De ce fait, une analyse des données de relaxation mesurées à plusieurs intensités de champ magnétique paraît être une approche souhaitable [10,11]. Nous présentons ici un programme MATLAB (DYNAMOF, pour DYNamics Analysis with MOdel-Free) permettant l'analyse de telles données. Ce programme permet de calculer les densités spectrales réduites J(0), J(ωN) et < J(ωH) > à partir des données expérimentales précitées, puis de les ajuster avec le(s) formalisme(s) de Lipari–Szabo. Nous présenterons un exemple d'application sur des données de relaxation mesurées à trois inductions B0 différentes sur la protéine oncogène P13MTCP1 [12,13].

2 Matériels et méthodes

Théorie : quand la relaxation d'un hétéronoyau X dépend essentiellement de l'interaction dipolaire avec un proton directement lié et de l'anisotropie de son déplacement chimique, les données de relaxation peuvent être interprétées en termes de mouvement du vecteur X–1H [14]. Sachant que les trois paramètres de relaxation mesurés expérimentalement (RX(Xz) ou R1, RX(Xxy) ou R2, et X{1H}NOE) dépendent des valeurs des fonctions de densité spectrale à cinq fréquences différentes [2,3], le calcul des densités spectrales peut être approché par l'approximation des hautes fréquences permettant un échantillonnage « réduit » de la fonction de densité spectrale. L'approximation des hautes fréquences implique une quasi égalité des valeurs des densités spectrales à haute fréquence (J(ωH – ωN) ≈ J(ωH + ωN) ≈ J(ωH) = < J(ωH) >, ce qui impose un temps de corrélation relativement important (> 1 ns) et des valeurs d'inductions de champ magnétique relativement élevées pour réaliser les mesures de relaxation (en général ≥ 9,4 T). Ces conditions sont généralement réalisées lors de l'étude de la dynamique interne d'une protéine en solution. Si ces conditions sont réunies, les vitesses de relaxation sont directement traduites en densités spectrales à trois fréquences [4–6] par la relation :

[J(0)J(ωX)J(ωH)]=[−34(3d2+c2)32(3d2+c2)−910(3d2+c2)1(3d2+c2)0−75(3d2+c2)0015d2]×[RX(Xz)RX(Xx,y)RX(Hz→Xz)](1)
dans laquelle d2=(µ04π)2(hγHγX4πrXH3)2 et c2=13(γXB0)2(Δσ)2
où μ0 est la perméabilité du vide, h la constante de Planck, γH (2.6752 × 108 rad T−1 par seconde) le rapport gyromagnétique du proton, γX les rapports gyromagnétiques des noyaux X (2.711 × 107 et 6.726 × 107 rad T−1 par seconde pour 15N et 13C, respectivement), ωH et ωX les fréquences de Larmor 1H et X, et rXH la distance internucléaire X–1H (1,02 et 1,07 Å pour 15N–1H et 13Cα–1H, respectivement), B0 l'intensité du champ magnétique, et Δσ la différence entre les composantes parallèles et perpendiculaires du tenseur de déplacement chimique de symétrie axiale (–170 ppm pour 15N [15], 25 ppm pour 13Cα [22]). La vitesse de corrélation croisée RX(Hz→Xz) entre le noyau X et le proton lié est corrélée au NOE hétéronucléaire et calculée par la relation : NOE = 1 + (γH/γX) RX(Hz→Xz)/RX(Xz). La fréquence de la densité spectrale moyenne < J(ωH) >, a été prise égale à 0,87 ωH [16].

Cette approche, dite de « cartographie », de la fonction de densité spectrale permet de juger rapidement de la dynamique interne de la protéine. En effet, une protéine en solution est soumise aux lois de la thermodynamique : elle représente un système à l'équilibre dont l'énergie est conservée. Cela se traduit par la conservation de la quantité de mouvement pour chacun des vecteurs (15N–H ou 13C–H) caractéristiques de chacun de ses résidus, et donc la conservation de l'aire sous la courbe des fonctions de densité spectrale propres à chacun de ces vecteurs (voir Fig. 2). Ainsi, les zones flexibles de la protéine sont caractérisées par des valeurs faibles de J(0) (fréquence représentative des mouvements lents), contrebalancées par des valeurs élevées de < J(ωH) > (fréquence représentative des mouvements rapides). À l'inverse, les zones rigides présentent des valeurs élevées de J(0) et faibles de < J(ωH) >. Certains résidus peuvent déroger à cette règle à cause d'une contribution adiabatique à leur relaxation, généralement apportée par des phénomènes d'échange chimique ou conformationnel s'établissant sur une échelle de temps supérieure à celle du temps de corrélation de la molécule (μs–ms). Bien que parfaitement rigoureuse, cette analyse des fonctions de densité spectrale n'apporte qu'une information qualitative sur la dynamique de la protéine étudiée : aucune information sur les échelles de temps caractéristiques des mouvements qui animent chaque résidu ne peut être obtenue. Néanmoins, elle peut être facilement complétée par l'utilisation d'un modèle de mouvement permettant d'ajuster aux mieux les densités spectrales des différents vecteurs. L'approche model-free de Lipari et Szabo [7] peut être ainsi utilisée pour ajuster les valeurs expérimentales des fonctions de densités spectrales et obtenir les paramètres du mouvement. Du fait de la différence importante de leur domaine de temps respectif, ce formalisme fait l'hypothèse d'une contribution indépendante du mouvement global (ou des mouvements globaux) et des mouvements internes à la fonction d'autocorrélation des vecteurs X–1H. Pour une protéine qui se réoriente de façon isotrope, on obtient :

J(ω)=25{S2τc1+(ω τc)2+(1−S2)τ1+(ω τ)2}(2)
où τc est le temps de corrélation global du vecteur X–1H, τ la somme harmonique des temps de corrélation global et interne (rapide) relatif à chaque résidu : τ−1 = τc−1 + τf−1. Les mouvements rapides internes sont caractérisés par le paramètre d'ordre généralisé S2, relié aux amplitudes relatives de ces mouvements et variant entre 0 (mouvement non contraint) et 1 (absence de mouvement), et le temps de corrélation τf.

Fig. 2

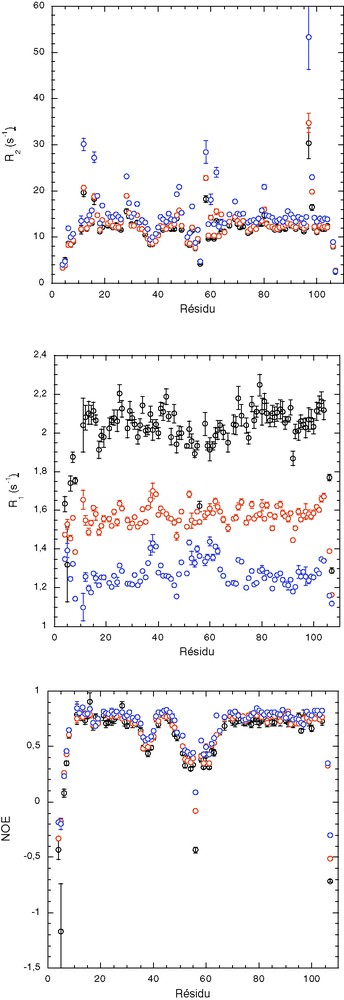
Vitesses de relaxation hétéronucléaire 15N (de haut en bas) R2, R1 et {1H,15N}NOE (I/I0) en fonction de la séquence de la protéine P13MTCP1. Ces paramètres de relaxation ont été mesurés à 400 (symboles noirs), 500 (symboles rouges) et 600 MHz (symboles bleus). Les valeurs de R1 et R2 ont été obtenues pour chaque acide aminé à partir de la décroissance mono-exponentielle de l'intensité du pic de corrélation 1H–15N correspondant sur les expériences hétéronucléaires 2D classiques (voir § Matériel et méthodes).

Pour certains résidus, l'équation [2] s'avère insuffisante pour ajuster les valeurs expérimentales des densités spectrales : cela notamment pour des résidus qui présentent des mouvements internes sur un domaine de temps proche de 1 ns. Dans ce cas, l'expression de la fonction de densité spectrale est étendue à [8,9] :

J(ω)=25{Sf2Ss2τc1+(ωτc)2+Sf2(1−Ss2)τ1+(ωτ)2+(1−Sf2)τ′1+(ωτ′)2}(3)
où τ−1 = τc−1 + τs−1 et τ′−1 = τc−1 + τf−1. Sf2 et Ss2 sont respectivement les carrés des paramètres d'ordre partiel pour les mouvements internes rapides (τf, échelle de la picoseconde) et lents (τs, échelle de la nanoseconde). Le carré du paramètre d'ordre généralisé S2, defini comme Sf2Ss2, constitue une mesure de l'amplitude totale des mouvements internes. En général, on peut négliger la contribution des mouvements internes les plus rapides, si bien que l'expression de la fonction de densité spectrale devient :
J(ω)=25{Sf2Ss2τc1+(ωτc)2+Sf2(1−Ss2)τ1+(ωτ)2}(4)

Enfin, certains résidus présentent des valeurs de J(0) anormalement élevées, signant la présence d'une contribution adiabatique à la fonction de densité spectrale. Cette contribution est due à la présence de mouvements sur une échelle de temps allant de la micro- à la milliseconde (plus lent que le temps de réorientation de la molécule), généralement reliés à un échange conformationnel et essentiellement perçus par la mesure de R2. Pour de tels résidus, la valeur de J(0) doit être corrigée de cette contribution d'échange (Réch) avant d'ajuster la fonction de densité spectrale par le modèle de Lipari–Szabo. Cette correction peut être apportée grâce à une relation linéaire existant entre la valeur de 2 R2 – R1 et les fréquences de Larmor hétéronucléaires ωX2 [17,23] :

2R2−R1=d2[J(0)+32J(ωH)]+[4c29J(0)+2ϕ]ωX2(5)
la valeur du facteur d'échange ϕ (Réch = ϕ ωX2 [Eq. (6)]) est obtenue d'après la valeur de la pente. La valeur de J(0) peut alors être corrigée en utilisant la relation :
J(0)obs=J(0)cor+λϕωX2(7)
où λ est un facteur d'échelle dépendant de la fréquence de mesure et égal à (3/2) [1/(3 d2 + c2)]. Alternativement, la valeur de ϕ peut être obtenue par l'ajustement direct de la fonction de densité spectrale par le modèle de Lipari–Szabo, en utilisant la fonction suivante pour J(0), obtenue en combinant les équations [2] et [7] :
J(0)=25{Sf2τc+(1−Sf2)τ}+λϕωX2(8)

La complexité croissante de ces différents modèles entraîne une augmentation très significative du nombre de paramètres permettant leur description. Ainsi, généralement deux paramètres sont à ajuster pour une analyse avec le modèle de Lipari–Szabo simple, contre trois — voire quatre ! — avec le modèle de Lipari–Szabo étendu. Or, les données de relaxation classiquement enregistrées à un seul champ magnétique ne permettent d'obtenir que seulement trois valeurs de densité spectrale : J(0), J(ωN) et <J(ωH)>.

Le problème devient très vite sous-estimé (du moins partiellement), et le recours à un meilleur échantillonage de la fonction densité spectrale nécessaire. La simulation reportée sur la Fig. 1 montre bien qu'en effet, si l'analyse à une fréquence est suffisante pour détecter la contribution d'un mouvement interne au mouvement global d'un vecteur, seul le recours à une analyse à plusieurs fréquences est capable de révéler la relative complexité de ce mouvement interne.

Fig. 1

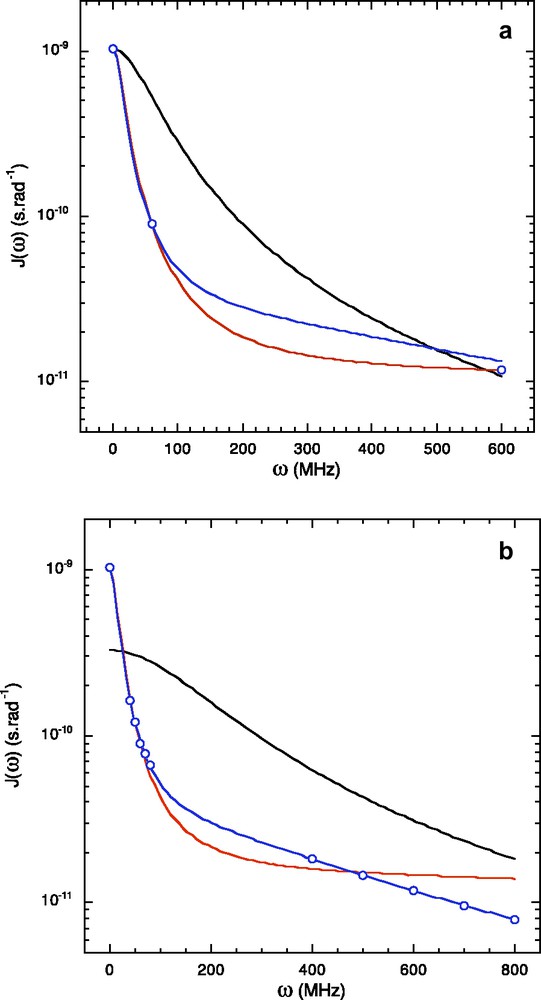
Les valeurs de densité spectrale réduite reportées sur cette figure ont été calculées pour cinq inductions de champ magnétique différentes (correspondant à des fréquences protons de 400, 500, 600, 700 et 800 MHz) avec le modèle de Lipari–Szabo étendu (équation [3] : τc = 10 ns, τs = 0,3 ns, τf = 3 ps, Sf = Ss = 0,5). Elles décrivent le mouvement complexe d'un vecteur tel que celui formé par exemple par le groupement 15N–H d'un résidu dans une protéine en solution animée d'un mouvement Brownien global (τc = 10 ns, concevable pour une protéine d'environ 10 kDa), et porté par un segment peptidique animé d'un mouvement interne complexe (également diffusif), peu contraint (S2 = 0,25), et comprenant deux composantes caractérisées par les temps de corrélation τs = 0,3 ns, τf = 3 ps. Ces différents mouvements sont répartis sur des échelles de temps très différentes et peuvent être considérés comme non corrélés. Seules les valeurs à 600 MHz (a) ou la totalité de ces valeurs de densité spectrale (b) ont été ajustées avec le modèle « sphère rigide » (J(ω) = 2/5{τc/(1 + (ω τc)2}) (courbe noire), le modèle de Lipari–Szabo [éq. (2)] et le modèle de Lipari–Szabo étendu [éq. (4)]. Si le temps de corrélation τc représente la variable ajustable dans le cas du modèle rigide, sa valeur a été fixé à 10 ns lors des ajustements avec les différentes variantes du modèle de Lipari–Szabo.

Le programme DYNAMOF présenté dans ce manuscrit utilise cette stratégie pour analyser les données de relaxation enregistrées à plusieurs intensités de champ magnétique. Une procédure de type SIMPLEX a été adoptée pour ajuster les valeurs de densités spectrales expérimentales aux différentes variantes du modèle de Lipari–Szabo, dont la convergence est assurée par la minimisation d'un χ2 calculé entre les valeurs expérimentales et les valeurs théoriques obtenues avec les différents modèles. Le choix du modèle pertinent se fera ensuite en comparant les valeurs de χ2 obtenues pour les différents ajustements grâce à un test de Fischer–Snedecor (F-test).

Mesures expérimentales : Les expériences de RMN ont été réalisées à 9,4, 11,75 et 14,1 Tesla sur des spectromètres Bruker Avance 400, 500 et 600 équipés de sondes 5 mm triple résonance 1H–13C–15N munies de gradient-z, et sur un échantillon de protéine P13MTCP1 uniformément enrichie en 15N dissoute à une concentration de 1 mM dans 500 μl de tampon Tris-HCl 10 mM pH 7,0 (5% 2H2O pour le lock). La température de mesure a été soigneusement calibrée à 20 °C sur chacun des spectromètres. Les séquences d'impulsions utilisées pour déterminer les valeurs des vitesses de relaxation 15N RN(Nz) (R1), RN(Nxy) (R2), et de 15N{1H}NOE sont similaires à celles déjà décrites [2,3], et les paramètres expérimentaux utilisés ainsi que le traitement des données ont déjà été reportés en détail pour d'autres protéines étudiées au laboratoire [13,18]. La vitesse de relaxation longitudinale 15N (RN(Nz)) a été obtenue à partir de dix expériences d'inversion–récupération, avec des délais de relaxation allant de 18 à 1026 ms. La vitesse de relaxation transverse 15N (RN(Nxy)) a été obtenue à partir de dix expériences CPMG, avec des délais de relaxation allant de 16 à 144 ms. La valeur du NOE hétéronucléaire 15N{1H} a été déterminée à partir du rapport de deux expériences réalisées avec et sans présaturation des protons. Les spectres RMN ont été traités à l'aide du logiciel Gifa (version 4.4) [21]. Le résultat de ces mesures expérimentales est reporté sur la Fig. 2.

3 Résultats

La Fig. 3 présente l'organigramme général du programme DYNAMOF. Le programme débute en demandant un suffixe (par exemple out), qui sera attribué à tous les fichiers de sortie (fichier out) créés lors de son utilisation. Après avoir offert la possibilité de changer en cours d'utilisation certaines valeurs de constantes entrées en valeurs par défaut (Δσ, valeurs de départ utilisées dans les procédures SIMPLEX...), l'utilisateur doit entrer le type de noyau utilisé pour l'analyse (15N ou 13C), puis le nombre de champs magnétiques utilisés. Après avoir laissé le choix entre l'analyse classique (Spectral density mapping) et celle récemment proposée par Roumestand et al. (Fast spectral density mapping, soumis à publication) que nous ne développerons pas ici, l'utilisateur doit entrer les différentes fréquences de mesures protons en ordre croissant (400, 500, puis 600) ainsi que le nom générique (gnam) des fichiers d'entrée correspondant à ces fréquences de mesure. Ces fichiers d'entrée consistent en trois fichiers textes pour chaque fréquence de mesure (R1, R2 et NOE (I/I0)), correspondant aux fichiers directement obtenus par l'analyse des données RMN par le module « Relaxation » du programme de traitement des données Gifa 4 [21]. Ces fichiers sont des tableaux à trois colonnes, chacune contenant respectivement le numéro du résidu (position dans la séquence), la valeur du paramètre de relaxation, et l'erreur mesurée sur ce paramètre. À chacun de ces fichiers, on attribue un suffixe (en général la fréquence de mesure) qui constituera son nom générique (par exemple : R1_400, R2_400 et NOE_400 correspondent aux mesures de relaxation effectuées sur P13MTCP1 à 400 MHz (generic name = 400)). Pour chaque fréquence, le programme calcule les valeurs des densités spectrales réduites en utilisant l'équation (1) ainsi que les erreurs correspondantes, qui seront stockées dans deux fichiers sortie différents (par exemple : J 400.out et dJ 400.out). Une sortie graphique reportant, pour chaque champ de mesure, les valeurs de densités spectrales réduites en fonction de la séquence de la protéine permet d'apprécier rapidement la qualité des données (Fig. 4).

Fig. 3

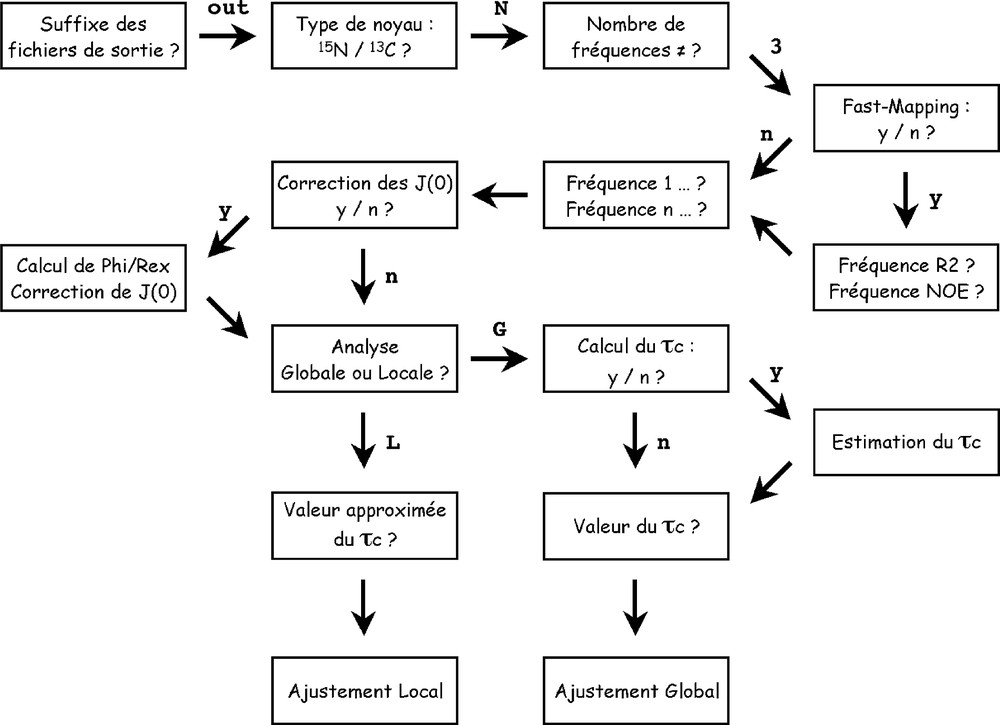
Organigramme général du programme DYNAMOF.

Fig. 4

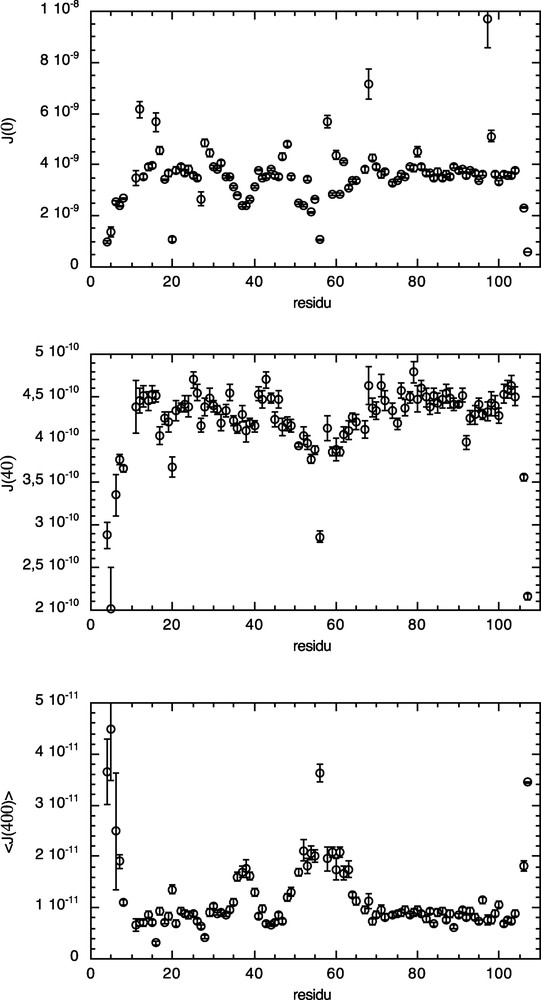
Représentation graphique du résultat du calcul des densités spectrales à partir des données de relaxation R1, R2 et NOE obtenues à 400 MHz (gnam : 401) sur la protéine P13MTCP1 [Eq. (1)].

À partir de cette étape, le programme propose de corriger les valeurs de J(0) d'une éventuelle contribution d'échange. Si l'utilisateur accepte ce choix, le facteur d'échange ϕ sera calculé par régression linéaire en utilisant l'équation [5] : un affichage graphique des données pour chaque résidu est proposé (Fig. 5a), puis le programme va afficher la valeur de ϕ en fonction de la séquence (Fig. 5b) et créer deux fichiers (PHI_R.out et Rex_R.out), correspondant l'un aux valeurs de ϕ par résidu, l'autre aux valeurs de Réch calculées à partir de ϕ [éq. (6)] pour chaque champ de mesure. Les erreurs sur ϕ seront calculées par une procédure Monte-Carlo (nombre d'itérations choisies par l'utilisateur). Le fichier PHI_R.out contient également les valeurs corrigées de J(0) (et dJ(0)) : ces valeurs sont introduites dans deux nouveaux fichiers, contenant les valeurs de densités spectrales et les erreurs correspondantes : J_gnamcorR.out et dJ_gnamcorR.out (ex J_400corR.out et dJ_400corR.out pour la fréquence 400 MHz). Ce sont dès lors ces fichiers qui seront utilisés par défaut pour l'ajustement avec les différents modèles de mouvement.

Fig. 5

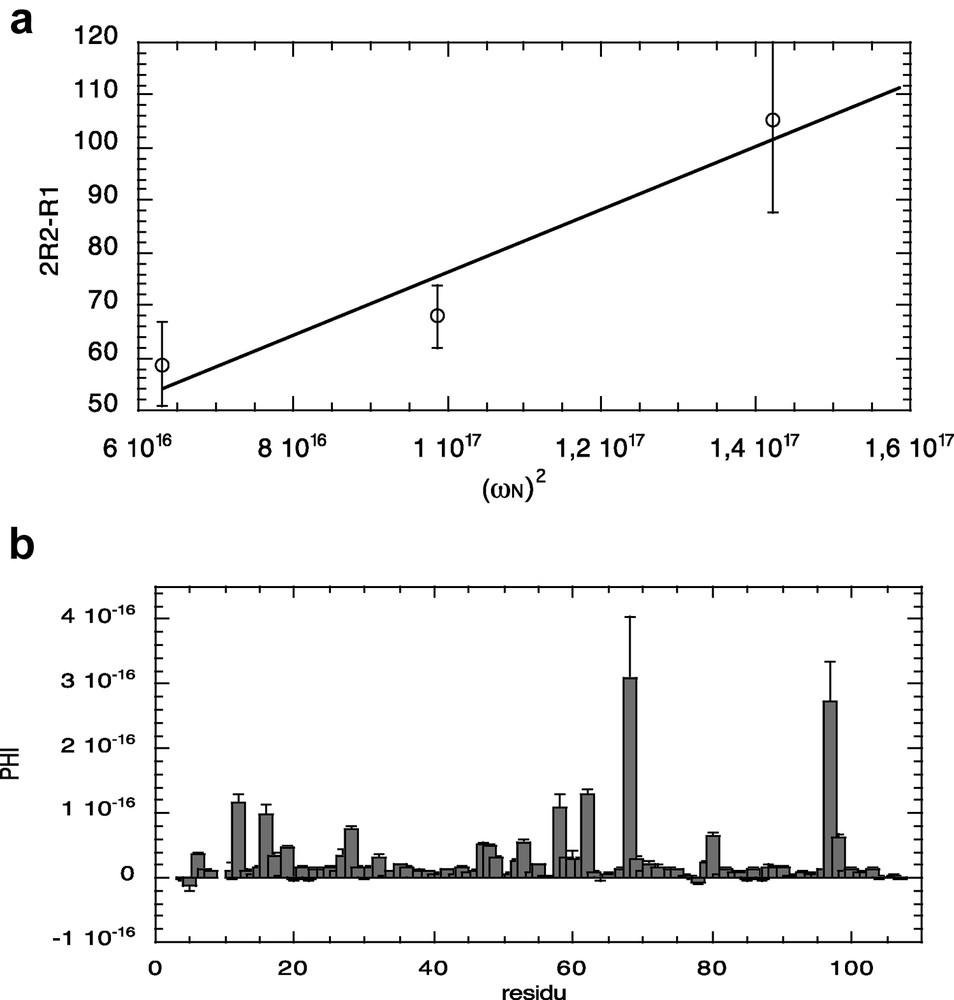
(a) Obtention du facteur d'échange ϕ par régression linéaire à partir de l'équation [5] (résidu 97). (b) Facteur d'échange ϕ en fonction de la séquence de la protéine P13MTCP1.

Cette étape de calcul (et éventuellement de correction) des fonctions densités spectrales effectuées, le programme va débuter l'ajustement des données avec les différents modèles de mouvement décrits dans la partie Matériel et méthodes. En premier lieu, le programme va demander à l'utilisateur de choisir entre un ajustement « local » (un τc par résidu) ou « global » (le même τc pour tous les résidus de la protéine) des données : l'ajustement local des données peut s'avérer judicieux lorsque la protéine présente des domaines avec des comportements dynamiques très différents, ou lorsque la réorientation de la protéine en solution ne peut plus être considérée comme isotrope [11,19,20].

  • • Ajustement Local (une valeur de τc par résidu). Avant de démarrer la procédure d'optimisation, le programme offre encore à l'utilisateur la possibilité d'ajuster la contribution d'échange (ϕ : Eq. (8)) si la correction proposée à l'étape précédente n'a pas été réalisée : les paramètres τc, τf, S2 et éventuellement ϕ seront alors obtenus résidu après résidu par ajustement des 2 n + 1 (n étant le nombre de champs magnétiques utilisés) valeurs expérimentales de densité spectrale (J(0), J(40), J(50), J(60), < J(400) >, < J(500) > et < J(600) > dans le cas de p13MTCP1) par le modèle de Lipari–Szabo (Eq. (2), légèrement modifiée : la contribution haute fréquence au mouvement est supposée indépendante de la fréquence et, de ce fait, ω τ négligé [11]). Une sortie graphique est proposée pour chaque résidu, permettant d'apprécier la qualité de chacun des ajustements. Deux fichiers sont créés à la fin de la procédure, contenant le résultat de chacun des ajustements (LOCAL.out, optimisation de τc, τf et S2–LOCALREX.out, optimisation de τc, τf, S2 et ϕ). Un χ2 expérimental est calculée pour chaque modèle et pour chaque résidu, dont le résultat est également contenu dans le fichier correspondant : ces valeurs de χ2 pourront être utilisées pour sélectionner le modèle optimum grâce à une analyse statistique. Enfin, un calcul de type Monte-Carlo va permettre de déterminer les erreurs sur chacune des variables (nombre d'itérations choisi par l'utilisateur) : ces erreurs seront contenues dans deux fichiers « définitifs », à côté des valeurs des variables τc, τf, S2 et ϕ (LOCAL_MC.out et LOCALREX_MC.out). Cette étape crée également deux fichiers supplémentaires contenant pour chaque résidu les valeurs de χ2 obtenues après chaque itération et ce pour chacun des deux modèles (χ2_CAN_MC.out et χ2_CANREX_MC.out). Ces fichiers pourront être utilisés pour une analyse statistique plus poussée (en cours d'implémentation dans le programme).
  • • Ajustement global (une valeur de τc commune à tous les résidus). Dans une première étape, le programme va tenter de déterminer la valeur commune du τc en ajustant résidu par résidu les valeurs des densités spectrales expérimentales par le modèle de Lipari–Szabo [Eq. (2)] et en tentant d'optimiser pour chaque résidu les valeurs de τc, τf et S2. Une sortie graphique est proposée pour chaque résidu, permettant d'apprécier la qualité de l'ajustement (Fig. 6a). En fin de procédure, un fichier LS3.out est créé, contenant les résultats de l'ajustement pour chaque résidu. La terminologie LS3 signifie que ce fichier a été obtenu à partir du modèle de Lipari–Szabo (LS), en optimisant trois paramètres : τc, τf et S2. Une sortie graphique présente les valeurs de τc en fonction de la séquence et propose une valeur moyenne (± 2σ) utilisable comme valeur de τc « global » (Fig. 6b). Cette valeur de τc pourra être alors utilisée comme constante dans le reste de la procédure qui va consister à ajuster les 2 n + 1 valeurs expérimentales de densités spectrales avec le modèle de Lipari–Szabo simple [Eq. (2)] (LS2, deux variables à optimiser : τf et S2), le modèle de Lipari-Szabo simple avec contribution d'échange [Eq. (2) et (8)] (LSREX, trois variables à optimiser : τf, S2 et ϕ), et les modèles de Lipari–Szabo étendus [Eq. (3) et (4)] (LSE3, trois variables à optimiser : S2s, S2f et τs – LSE4, quatre variables à optimiser : S2s, S2f, τs et τf). Comme précédemment, une sortie graphique est proposée résidu par résidu, permettant de juger la qualité de l'ajustement par chaque modèle (Fig. 7). Quatre fichiers sont alors créés (LS2.out, LSREX.out, LSE3.out et LSE4.out), contenant les résultats obtenus avec les modèles respectifs. Tout comme pour l'approche « locale », un χ2 expérimental est calculée pour chaque modèle et pour chaque résidu, dont le résultat est également contenu dans le fichier correspondant : ces valeurs de χ2 pourront être utilisées pour sélectionner le modèle optimum grâce à une analyse statistique. De même, les erreurs sur chacun des paramètres peuvent alors être calculées par une procédure Monte-Carlo (l'utilisateur choisit le nombre d'itérations) : cette étape conduira à la création de quatre nouveaux fichiers contenant à la fois les valeurs des paramètres optimisés et les erreurs calculées sur ces paramètres (LS2_MC.out, LSREX_MC.out, LSE3_MC.out et LSE4_MC.out). De même, quatre fichiers (correspondant aux quatre modèles) seront créés contenant les valeurs de χ2 obtenues à chaque itération du calcul de Monte-Carlo pour chaque résidu (χ2_LS2_MC.out, χ2_LSREX_MC.out, χ2_LSE3_MC.out, χ2_LSE4.out) : ces derniers seront utilisés pour une analyse statistique plus poussée qui est en cours d'implémentation dans le programme.

Fig. 6

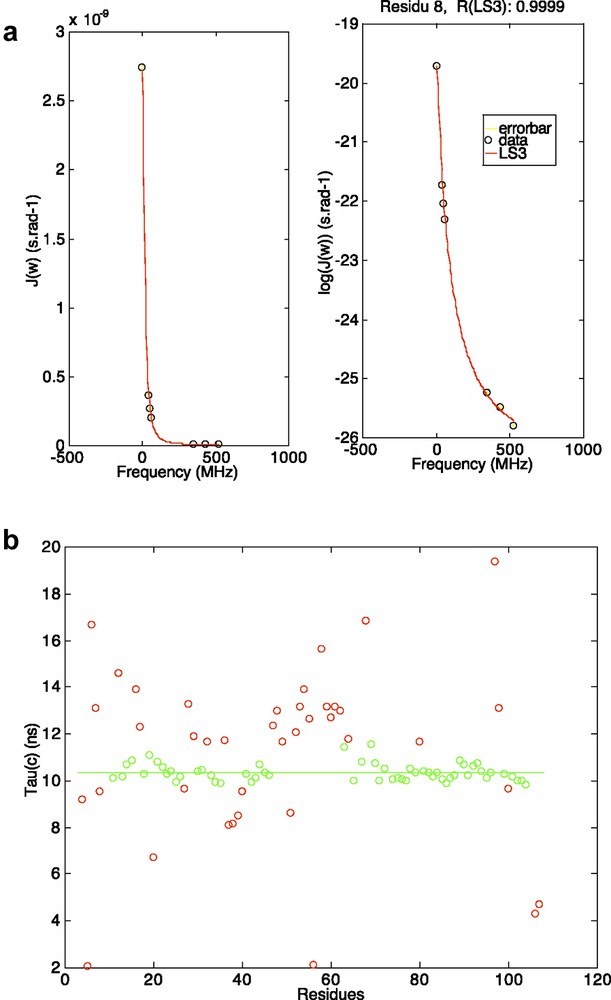
(a) Ajustement des valeurs de densité spectrale obtenues pour le résidu 46 de la protéine P13MTCP1 par le modèle LS3 (voir texte) ; ces valeurs sont reportées sur un axe arithmétique (gauche) ou logarithmique (droite). (b) Valeurs de τc en fonction de la séquence. La ligne verte représente la valeur moyenne du τc calculée sur les résidus représentés en cercles verts (τc ± 2 σ).

Fig. 7

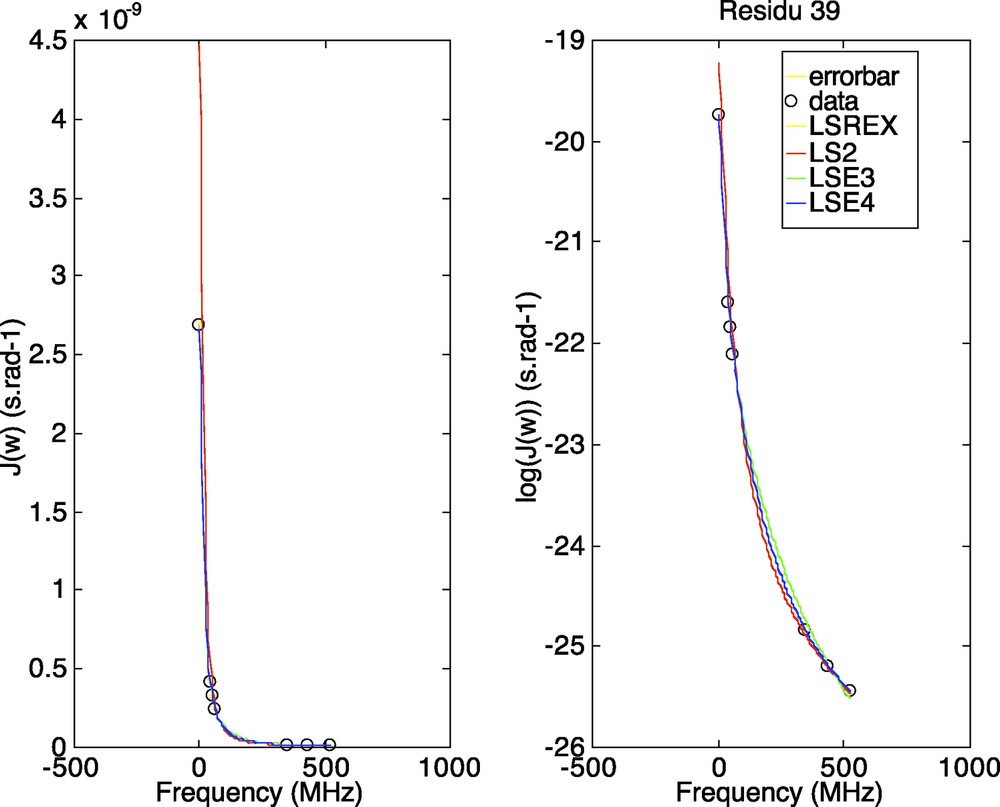
Ajustement des valeurs de densité spectrale calculées pour le résidu 39 de la protéine P13MTCP1 par les différents modèles proposés dans l'approche « globale » (LS2, LSREX, LSE3, et LSE4) (voir texte) ; les valeurs de densité spectrale sont reportées sur un axe arithmétique (gauche) ou logarithmique (droite).

On notera que chaque fois qu'un ajustement par un modèle est effectué, que ce soit dans la procédure « locale » ou « globale », un fichier contenant les valeurs des densités spectrales théoriques (et, après un calcul Monte-Carlo, un fichier contenant les erreurs sur les densités spectrales théoriques) est créé, du type Jtheo_nomdumodèle.out (ou jtheo_nomdumodele_MC.out, dJtheo_nomdumodele_MC.out). Ces fichiers pourront être également utilisés dans une analyse statistique.

4 Discussion

Le programme décrit dans ce manuscrit permet d'analyser des données de relaxation enregistrées à une ou plusieurs intensités de champ magnétique B0. Il a été écrit en langage MATLAB (version 4.2c.1) sur un ordinateur MacIntosch (MacOS9) : la portabilité de ce langage le rend utilisable sur tout autre type de plateforme et système d'exploitation (MacOS X, Windows, Linux, UNIX). Une version en langage OCTAVE a été testé notamment sur des données de relaxation mesurées à trois intensités de champ magnétique sur la protéine P13MTCP1 : les résultats de l'analyse dynamique sont présentés sur la Fig. 8. Pour cette protéine relativement globulaire et de symétrie quasi-sphérique, l'approche « globale » (une valeur de τc commune à tous les résidus) est pertinente. Notre analyse nous a permis de déterminer un temps de corrélation global de 10,4 ns, compatible avec la taille de la protéine (107 résidus, 13 kDa) et la température à laquelle ont été réalisées les mesures (20 °C). Elle montre également des mouvements internes relativement contraints dans le tonneau β (modèle LS2), alors que la longue boucle, qui relie les deux motifs de feuillet β constituant le tonneau, est animée par des mouvements internes relativement complexes, avec des temps de corrélation proches de la nanoseconde (modèle LSE3, l'utilisation du modèle LSE4 n'apportant pas une amélioration statistiquement significative de l'ajustement). De tels mouvements ont été également identifiés sur l'une des deux boucles « plissées » qui émergent sur une face du tonneau β. Comme le montrait déjà la relative dispersion des valeurs de J(0), des contributions d'échange significatives ont été mesurées pour de nombreux résidus, répartis sur des zones bien particulières de la protéine : une face du tonneau β, autour de l'hélice présente dans la longue boucle, sur l'autre boucle « plissées » émergeant du tonneau β… Des valeurs similaires pour ces contributions d'échange ont été obtenues par correction des valeurs de J(0) [17] ou par ajustement direct des valeurs expérimentales (modèle LSREX).

Fig. 8

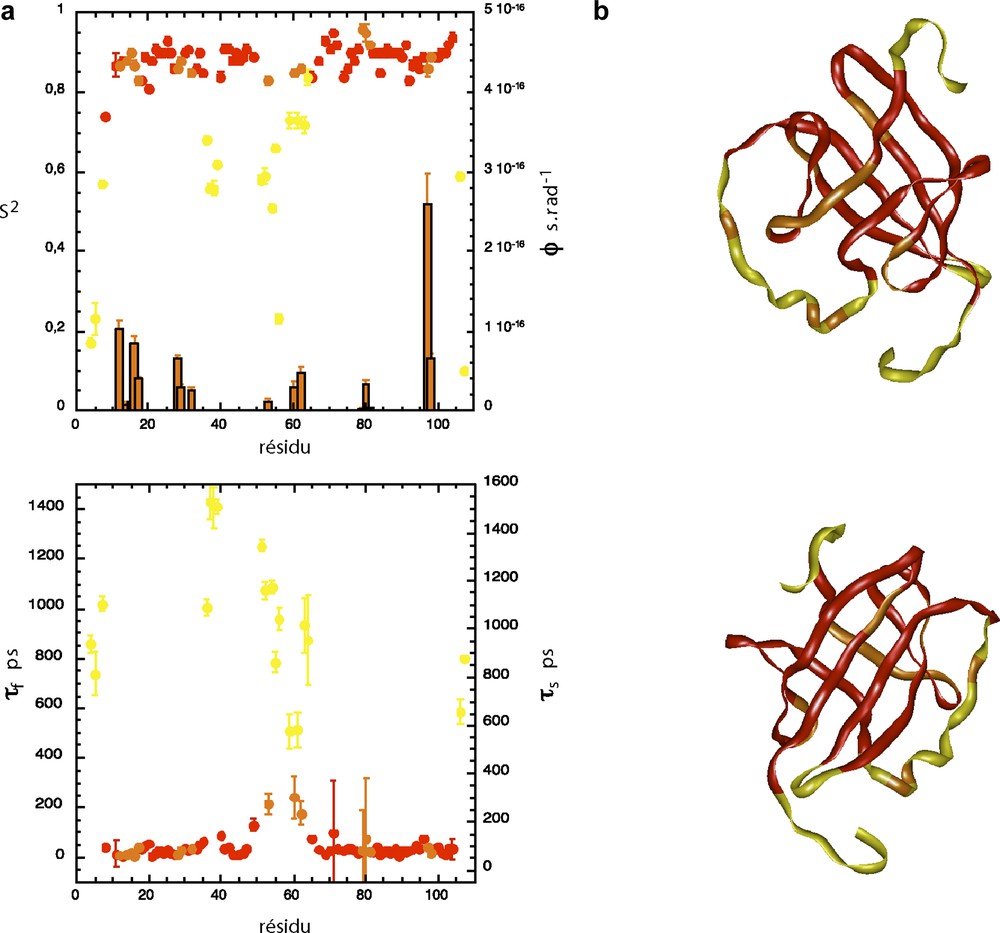
Résultats de l'analyse dynamique des données de relaxation mesurées sur P13MTCP1 à trois intensités de champ magnétique. (a) paramètres dynamiques (S2, τf, τs et ϕ) obtenus en ajustant les données expérimentales avec les modèles LS2 (rouge), LSREX (orange) et LSE3 (jaune). (b) deux vues à 180° d'une représentation en ruban de la protéine P13MTCP1 montrant la restriction des mouvements internes : le ruban a été colorée avec le même code de couleur qu'en (a).

Si des résultats similaires peuvent être obtenus en analysant les données de relaxation obtenues à une seule fréquence de mesure (résultats non montrés), l'analyse à plusieurs fréquences permet une bien meilleure discrimination entre les différents modèles par les tests statistiques utilisés, et augmente ainsi notre confiance dans les résultats de notre analyse dynamique.

Le programme DYNAMOF est téléchargeable à partir du serveur du Centre de biochimie structurale (ftp://ftp.cbs.cnrs.fr/pub/DYNAMOF_1.0.zip).

Remerciements

Le travail de Virginie Ropars est financé par une bourse de la Ligue contre le cancer. L'étude des protéines oncogéniques de la famille TCL1 constitue un projet du laboratoire soutenu par l'Association pour la recherche contre le cancer. La conversion des données de relaxation en valeurs de densité spectrale utilise une routine MATLAB écrite par J.-F. Lefèvre : Philippe Barthe et Christian Roumestand remercient cet ami, malheureusement trop tôt disparu, qui a su leur communiquer sa passion pour l'étude de la dynamique interne des protéines et la relation entre les propriétés dynamiques des protéines et leur activité.

Bibliographie

[1] R.A. Atkinson; B. Kieffer Prog. Nucl. Magn. Reson. Spectrosc., 44 (2004), p. 141

[2] J.W. Peng; G. Wagner J. Magn. Reson., 98 (1992), p. 308

[3] J.W. Peng; G. Wagner Biochemistry, 31 (1992), p. 8571

[4] N.A. Farrow; R. Muhandiram; A.U. Singer; S.M. Pascal; C.M. Kay; G. Gish; S.E. Shoelson; T. Pawson; J.D. Foreman-kay; L.E. Kay Biochemistry, 33 (1994), p. 5984

[5] R. Ishima; K. Nagayama J. Magn. Reson., B108 (1995), p. 73

[6] J.-F. Lefèvre; K.T. Dayie; J.W. Peng; G. Wagner Biochemistry, 35 (1996), p. 2674

[7] G. Lipari; A. Szabo J. Am. Chem. Soc., 104 (1982), pp. 4546-4559

[8] G.M. Clore; A. Szabo; A. Bax; L.E. Kay; P.C. Driscoll; P.T. Wingfield; A.M. Gronenborn J. Am. Chem. Soc., 112 (1990), p. 4989

[9] G.M. Clore; P.C. Driscoll; P.T. Wingfield; A.M. Gronenborn Biochemistry, 29 (1990), p. 7387

[10] J.W. Peng; G. Wagner Biochemistry, 34 (1995), p. 16733

[11] D. Canet; P. Barthe; P. Mutzenhardt; C. Roumestand J. Am. Chem. Soc., 123 (2001), p. 4567

[12] Y.-S. Yang; L. Guignard; A. Padilla; F. Hoh; M.P. Strub; M.-H. Stern; J.-M. Lhoste; C. Roumestand J. Biomol. NMR, 11 (1998), p. 339

[13] L. Guignard; A. Padilla; J. Mispelter; Y.-S. Yang; M.-H. Stern; J.M. Lhoste; C. Roumestand J. Biomol. NMR, 17 (2000), p. 215

[14] A. Abragam Principles of Nuclear Magnetism, Oxford Science Publication, Clarendon Press, Oxford, UK, 1961

[15] N. Tjandra; A. Szabo; A. Bax J. Am. Chem. Soc., 118 (1996), p. 6986

[16] N.A. Farrow; O. Zhang; A. Szabo; D.A. Torchia; L.E. Kay J. Biomol. NMR, 6 (1995), p. 153

[17] J. Habazettl; G. Wagner J. Magn. Reson., B109 (1995), pp. 100-104

[18] P. Barthe; L. Chiche; N. Declerck; M.A. Delsuc; J.-F. Lefèvre; T. Malliavin; J. Mispelter; M.-H. Stern; J.-M. Lheste; C. Roumestand J. Biomol. NMR, 15 (1999), p. 271

[19] S. Bouguet; P. Mutzenhardt; C. Roumestand; D. Canet Concepts Magn. Reson., 24 (2005), p. 1

[20] S. Bouguet; P. Mutzenhardt; C. Roumestand; D. Canet Concepts Magn. Reson., 24 (2005), p. 9

[21] J.L. Pons; T.E. Malliavin; M.A. Delsuc J. Biomol. NMR, 8 (1996), p. 445

[22] C. Ye; R. Fu; J. Hu; L. Hou; S. Ding Mag. Reson. Chem., 31 (1993), p. 699

[23] H. Vis; C.E. Vorgias; K.S. Wilson; R. Kaptein; R. Boelens J. Biomol. NMR, 11 (1998), p. 265

Commentaires - Politique

Ces articles pourraient vous intéresser

Analysis of the C12A-p8MTCP1 protein internal motions using fast spectral density mapping at multiple magnetic fields

Virginie Ropars; Julien Roche; Philippe Barthe; ...

C. R. Chim (2008)

Bases structurales de l'inhibition de la kinase Akt (PKB) par le peptide inhibiteur Akt-in : une étude RMN

Virginie Ropars; Jean-François Guichou; Daniel Auguin; ...

C. R. Chim (2006)

Détermination de l'état d'oligomérisation du domaine homologue à la pleckstrine de la protéine AKT2 par des techniques RMN

Daniel Auguin; Thierry Gostan; Marc-André Delsuc; ...

C. R. Chim (2004)