1 Introduction
Conversion of solar light into electrical energy occurs both, during the primary process of photosynthesis in the photosynthetic membrane and in a single crystalline silicon solar cell devices, which already have a history of 50 years of intensive development towards higher efficiency and economic feasibility. The materials and the charge separation principle in both cases are drastically different. Photosynthetic charge separation occurs by kinetic mechanisms, which are practically unexplored for technical applications, while inbuilt electrical fields dominate silicon and related semiconductor junction solar cells. It is by no means clear what type of solar cell will, at the very long-term, dominate the market. It is obvious now that, in spite of half a century of research the prices for silicon solar cells are still too high for a wide commercialization, especially in third-world countries. A key target should be the implementation of a solar cell technology, which involves cheap and rapid production methods like screen-printing or deposition by reactive sputtering. The progress in recent years of nano-composite solar cells such as liquid [1] and solid dye sensitization solar cells [2] and composite polymer fullerene solar cells [3] indicates that alternative solar cell strategies as compared with traditional silicon cell technology are feasible. This paper will show that they are based on kinetic charge separation. It will also show that they all are faced with photo-degradation problems. The aim of this contribution is to look into the fundamentals of the solar cell principle and to explore the possibility of preparing improved and reasonably stable solar cells just by mixing and self-assembling nano-particles and chemicals. The basic question raised will be what fundamental principles will have to be respected and guaranteed to get efficient charge separation and energy conversion.
2 Experimental
The experimental procedures used in the laboratory of the author to produce liquid and solid dye sensitization cells as well as composite polymer fullerene solar cells have been described in specialized articles [4–6]. Experimental results obtained with these solar cells will be used to elaborate fundamental principles and to identify specific problems, which have to be addressed in the future.
2.1 What is the simplest solar cell?
As Fig. 1 visualizes, the simplest solar cell is a membrane, which, upon illumination, is selective for the passage of photo-generated electrons and holes. No additional restrictions are given with respect to further properties of such a membrane. In silicon photovoltaic technology such a membrane has developed in direction of highly sophisticated electronic devices based on crystallized silicon. As a specific charge-separating feature, imprinted electrical fields obtained by joining p- and n-conducting layers or by using selective and optimized interfaces have been applied. Efforts to develop silicon-based solar cells look back at a history of 50 years. At present, such cells reach 24% efficiency in the laboratory and efficiencies in production, which are approximately one third lower. However, the electricity produced is still 10 times higher in costs than the electricity available from fossil fuel technology.
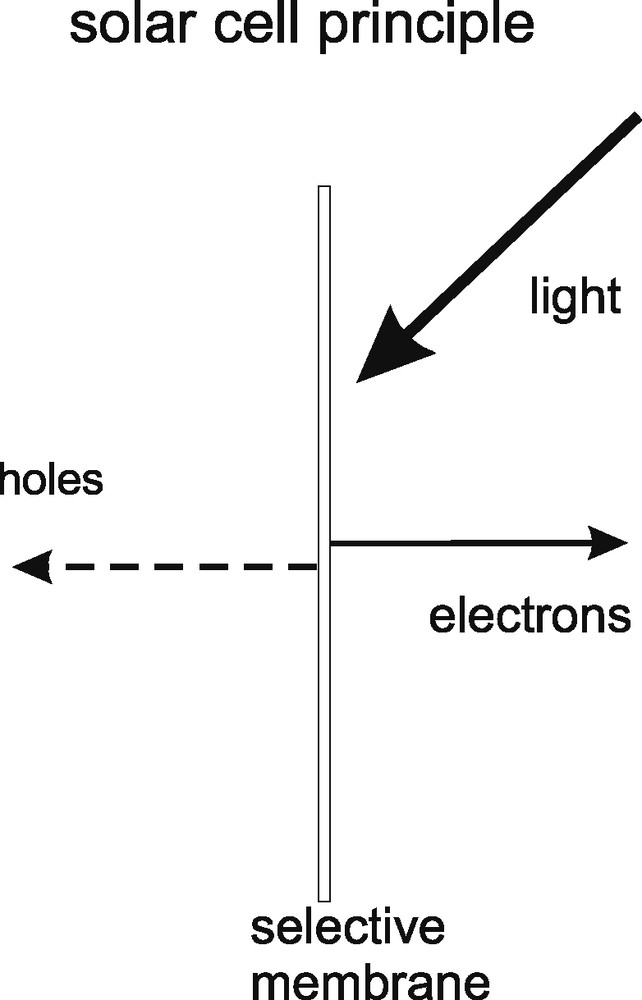
Visualization of the simplest solar cell. It is a membrane, which is selective for charge separation. The origin of selectivity involves mostly inbuilt electrical fields and selective contacts in classical solar cells and kinetic selectivity in the photosynthetic membrane.
In contrast to the strategy adopted in semiconductor photovoltaics, generation of electrical energy from light in the photosynthetic membrane does not rely on imprinted electrical fields for charge separation. Charge separation in the reaction center is based on irreversible chemical kinetics, that is on electron transfer processes, which are much more efficient in one direction than in the opposite one. The key elements, allowing charge separation, are in this case molecular electronic mechanisms, which give excited charges a high probability for charge separation while recombination and reverse processes are significantly suppressed. A remarkable feature of charge separation in the photosynthetic membrane is that the electron transfer particles engaged in charge separation and transport are self-organizing within the bilipid layer and can be extracted and re-added without irreversibly destroying the energy conversion process. It is obvious that a technology, in which chemical particles can just be mixed together, in order to achieve a solar cell function, would constitute a significant advantage for solar cell fabrication and an entirely different approach to solar cell technology as it is understood now. Is such a strategy based on kinetic charge separation technically feasible?
Interestingly, during the last decade, nano-structured and nano-composite solar cells, such as liquid and solid dye solar cells and polymer fullerene solar cells have developed [1–8]. Fig. 2 visualizes the essential structural differences as compared to the classical silicon solar cells or cells made from other crystallized inorganic semiconductor materials. As Fig. 2 (top) shows, the classical solar cell relies on contacting electronic materials with different free energy for electrons. In this way electrical fields are generated for charge separation. In contrast, nano-structured dye solar cells or injection solar cells are based on a cheap and easy to fabricate nano-structured oxide (e.g., TiO2) into which excited molecules inject electrons. Since the electrolyte or the electric contact penetrate this nano-structure, electrical fields can no longer build-up significantly so that charge separation has essentially to occur on the basis of kinetic irreversibility. Just by trial and error, dye sensitization solar cell research has identified the redox system iodide/iodine to be especially favorable for the achievement of high-energy conversion efficiencies [8]. As to be discussed later, this redox system happens to be irreversible to a significant degree, that means electrons are easily donated by iodide but the electron is not easily returned to iodine due to a complex electrochemistry. For this reason the electrons photo-injected into TiO2 nano-particles can migrate across a network of nanoparticles, with abundant traps, to the front contact without significantly reverse reacting with the electrolyte [9]. Solar cell efficiencies for dye sensitization solar cells of up to 10% have been reported [1].

Comparison of the structure of a classical silicon solar cell with an injection solar cell (dye solar cell) and a polymer fullerene composite solar cell. Innovative nanostructrured cells rely on irreversible electron transfer kinetics for efficiency: in the dye-solar cell, it is essentially that of the: I–/I3 redox system. In the polymer cell, it is the electron exchange with the fullerene molecule.
The composite polymer fullerene solar cell works by mixing polymer with fullerene and placing this mixture, which can segregate by self-organization, between two contacts, ITO and aluminum, respectively. Solar cell efficiencies of 3–5% have been reported, while stability problems are still significant, so that the cells have to be sealed against access of oxygen and humidity [3]. In this cell the fullerene molecule has been identified, again by trial and error, to be most efficient for electron capture and transport via percolation. Also in this case, kinetic irreversibility is a key element. The fullerene can easily accept electrons but it cannot easily re-donate them. In discussions of the mechanism of the composite polymer fullerene solar cell, this irreversibility is not yet sufficiently considered, even though it is established that replacing the fullerene molecule for another arbitrary polymer with similar energy band positions will not yield comparable energy conversion efficiencies. This implies that the energy diagram used for explaining this type of solar cell is insufficient and does not characterize the main phenomenon involved.
2.2 Kinetic irreversibility in nano-structured solar cells
Fig. 3 shows a photocurrent image of a 2.6% efficient composite polymer PPV fullerene solar cell prepared in our laboratory [3]. Even though a homogeneous performance is expected from reflectance measurements quite dramatic inhomogeneities in charge separation and percolation of charge carriers are observed. This indicates further improvement possibilities for this type of solar cells. But the key element determining the efficiency of this cell is charge separation between the PPV polymer and the C60 fullerene. Neither the exciton trapping ability of the fullerene nor the favorable relative energy band position for charge separation, as indicated in Fig. 3, is the most critical aspect for the performance of this type of solar cells, but the fact, that the forward reaction of the electron is orders of magnitude faster than the reverse reaction (10−13 s, as compared to 10−6 s). The reason why the fullerene turned out to be such a successful component in this type of solar cell, which was a chance discovery, is simply the high degree of kinetic irreversibility of charge separation. This means, that a typical energy band diagram shown for composite polymer fullerene solar cells is merely showing the necessary but not the sufficient conditions for reasonably high energy conversion efficiency.
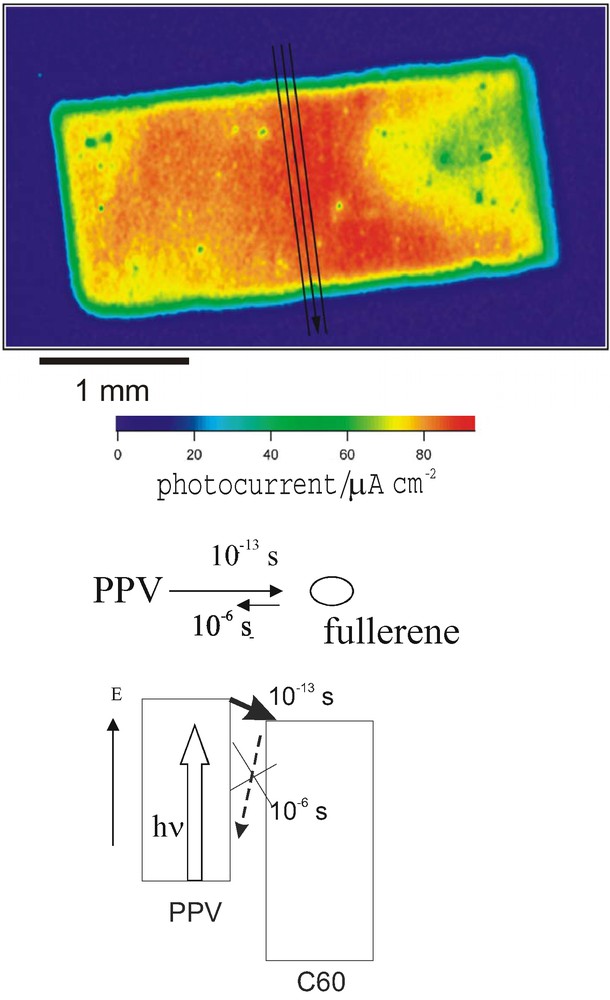
Photocurrent image (top) of a composite polymer fullerene solar cell (2.6% solar cell efficiency). Inhomogeneities within the cell are clearly seen. Below the principle of charge separation between polymer and fullerene as well as the origin of selectivity is explained via an energy scheme.
A similar situation of kinetically determined mechanisms exists in the dye solar cell. As Fig. 4 (right) shows, electrons excited by light in the sensitizer are injected and migrate across an array of TiO2-nano-particles. The oxidized dye is regenerated by a redox system, which can also penetrate to the front fluorinated tin oxide (FTO)-contact of the solar cell. Fig. 4 (a), which depicts a photocurrent image of a cell, selectively illuminated for 59 days, shows, that there are also problems of photo-electrochemical degradation. Irreversible processes slowly tend to degrade the system. Since the onset of research on nano-crystalline dye sensitization solar cells the advantage of using the iodide/iodine redox system became apparent. If this redox system is exchanged by other redox systems with comparable redox potential (i.e. hydroquinone/quinone, Fe2+/3+, Fe (CN)63–/4–) the solar cell efficiency of this cell essentially collapses. This suggests that the significant kinetic irreversibility of the iodide/iodine system, permitting an easy transfer of electrons from the iodide, but guaranteeing a suppressed reverse reaction with the iodine is a critical and very important factor also in this case. This can further be supported by simple experiments involving the front FTO contact. If this front contact would just act as a metal, as frequently assumed [10], it should not matter to deposit small islands of platinum or of another catalytically active metallic conducting ruthenium oxide. In both cases, however, the efficiency of the solar cell dramatically decreases. The explanation is quite simple: both deposited metals catalyze the reverse reaction of electrons with the iodine, thus making the iodide/iodine redox system much more reversible. Using photocurrent imaging techniques in combination with selective illumination and combinatorial techniques as shown as an example in Fig. 4a, the discussed kinetic aspects of dye solar cell function can be elaborated and tested quite convincingly [11]. In Fig. 4b an energy scheme for the dye solar cell function is shown together with the structure of the cell. The sites of kinetic irreversibility, both at the nano-particles and at the front contact, are indicated.
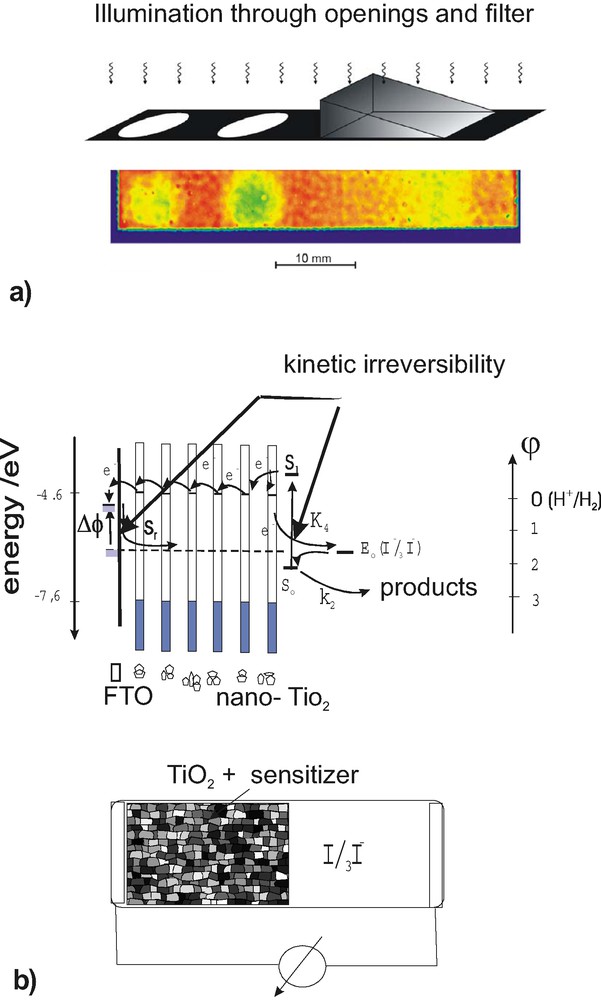
(a) Photocurrent image of selectively illuminated dye solar cell. Below (b) the energy scheme is depicted together with the kinetic pathway indicating the origin of selectivity at the nano-particles and the front contact.
Also solid-state dye sensitization solar cells, which reach an efficiency of up to 4% are critically determined by kinetic processes. However, interpenetration of the solid electrical contact with the nano-structured absorber is much less efficiently achieved than with a liquid electrolyte. This is the main reason for the still moderate efficiency reached with this type of solar cell, which is schematically explained in Fig. 5 (top). Photocurrent imaging of a locally illuminated solar cell showed a quite remarkable rate of photo-degradation (Fig. 5 (center)). It is, surprisingly, more than 100 times higher than that observed for liquid dye sensitization solar cells, using the same sensitizing ruthenium complex (N3) [12]. It turned out that the hydro-thiocyanate-group contained in an organic chemical, which was supposed to provide small grain-size of the contact forming copper iodide only, also works as bridge for the electron transfer and regeneration of the oxidized sensitizer molecule. Reverse reacting electrons electrochemically destroy this bridge and thus deteriorate solar cell efficiency (Fig. 5 (bottom)). Thin over-layers of oxides (e.g., zinc oxide) on the TiO2 nano-particles can both improve efficiency and photochemical stability of the cell as these layers still allow efficient electron injection but apparently suppress the reverse reaction of the electrons. It is evident that kinetic factors are critically involved in solid state dye solar cell performance.
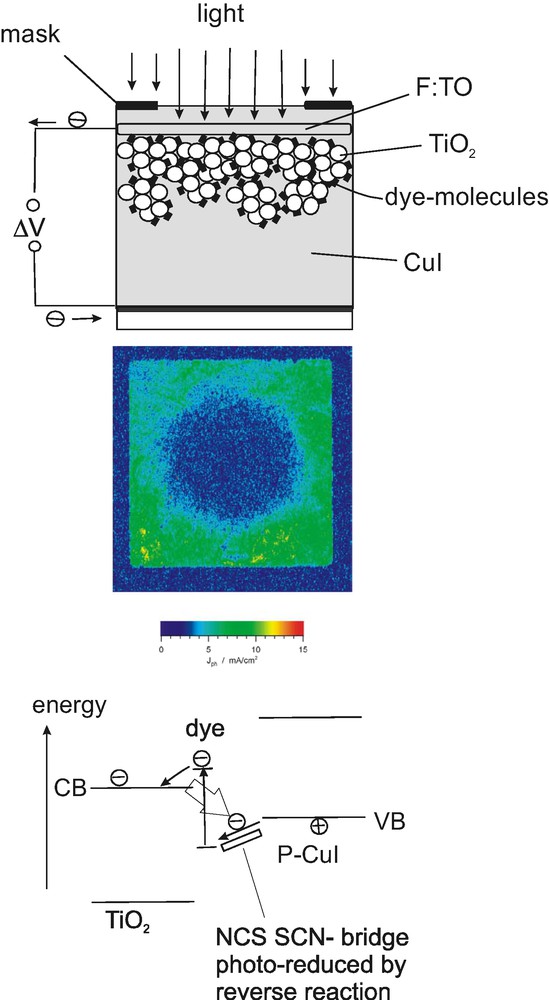
Properties of solid-state TiO2/Ru-N3/CuI dye solar cells. Above. Top: Scheme of solar cell structure. Center: effect of selective illumination (circular spot) during the time period of 72 h. Below, the cell structure and the energy scheme are depicted for discussion of selectivity. (C2H5)3NHCNS acts as a bridge-forming chemical.
In a parallel publication in this journal [13], a new kind of nano-structured solar cell is presented, which works without a solid or liquid electrolyte contact but with a lipid (detergent) medium containing a micro heterogeneous suspension of ionically and electronically conducting particles. The system was modeled on the basis of the photosynthetic membrane in which electron conducting and ion conducting macromolecular particles are floating in a lipid environment. When replacing the liquid electrolyte of a dye sensitization solar cell with such a lipid based medium reasonably high photocurrents (1.5 mA cm−2) and photovoltages (0.5 V) could still be maintained. This indicates that solar energy conversion is working in such a lipid environment. The ion-conducting particles, while conducting electricity, are expected to be poor acceptors for electrons, thus apparently, suppressing the reverse reaction from the TiO2 nano-particle interface. A photopotential can thus build up and electrons flow in one direction. The lipid closes the circuit apparently via electron or ion shuttles. This new lipid-based solar cell may therefore also be considered to be a kinetically determined solar cell. While its detailed mechanism is still to be explored, this example suggests that, to some extent, kinetically determined solar cells may be designed by tailoring kinetic processes.
3 Kinetic irreversibility in electron-transfer; what could it be?
Mechanisms for electron transfer in which electrons are proceeding efficiently into one direction, reluctantly, however, into the other direction may be chemically very complex and composed of many reaction steps. There are, however, also modern and only partially explored strategies involving molecular electronic rectifiers and far from equilibrium electron transfer mechanisms. Especially since the I–/I3– redox system has been mentioned as a source of directionality and selectivity in liquid dye sensitization solar cells, it is reasonable to start with electrochemical and classical electron transfer considerations.
3.1 Selectivity via classical electrochemistry and electron-transfer theory
The well known Butler–Volmer equation of electrochemistry already considers the possibility of an asymmetrical energy barrier via the parameter α. It can vary between 0 and 1 and reflects a symmetrical barrier when amounting to 0.5. Strong asymmetry is found with α close to zero or one as seen from the structure of the Butler–Volmer Eq. (1). The current I, depending on the over-potential η = E − E° is proportional to the exchange current i0 and critical dependent on α in the exponent for the forward reaction and on (1 − α) in the exponent for the reverse reaction (N = charges turned over, f = F/RT).
| (1) |
The kinetic barrier thus undergoes a strong lowering when the over-potential η = E − E° is increased in one direction and a weak lowering in the opposite direction. In a photoreaction the over-potential may be created by the free energy change induced by the photo-activation of electrons, and, for the reverse reaction, by a still present excess free energy of reverse reacting electrons. But the skill to tailor α-values on nano-particles for values close to 0 or 1 has still to be developed.
Similar considerations can be put forward on the basis of electron transfer theory. The classical approach to electron transfer is the Marcus [14] theory which has also been specifically applied to interfaces [15,16]. In the picture of this Marcus theory the relation of energy and bond length (along the nuclear coordinate x) due to nuclear vibrations follows a parabola as described by Hooke's law. It has the well known structure:
| (2) |
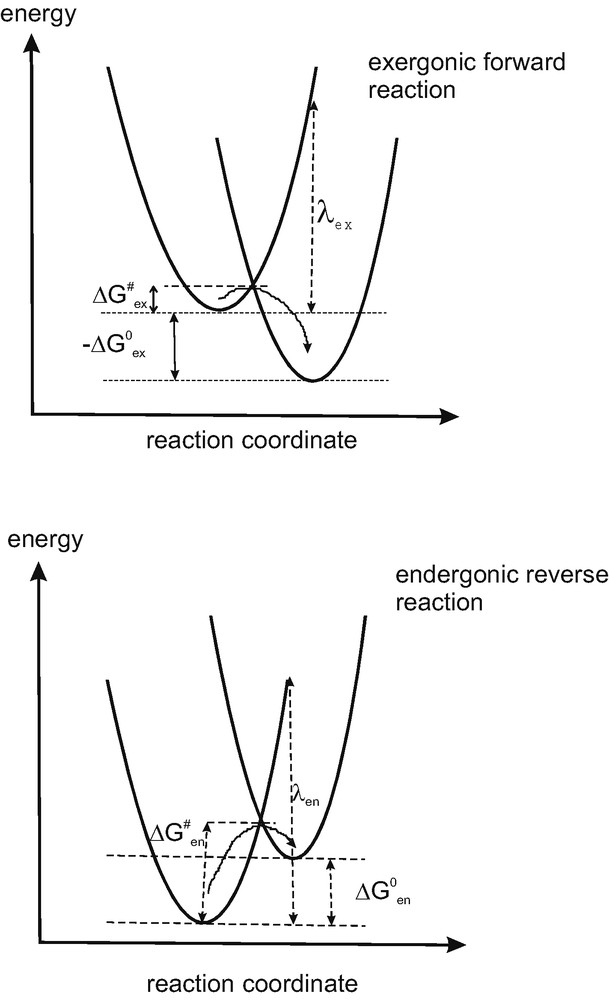
Energy-nuclear coordinates showing the reaction parabolas describing an exergonic forward and an endergonic reverse reaction of electrons according to Marcus theory. Both reorganization energies and concavity parameters, which depend on nuclear dynamics, may give rise to a certain asymmetry between forward and reverse reaction (compare arguments in the text).
The distance is replaced by a nuclear coordinate, which lumps together the distances in all the bond so that a single parabola is used to present the parabolas of all bonds, which is a drastic, but very useful simplification. The crossing points between the parabola of reactant and product fulfills, as well known, the Frank–Condon principle and the energy conservation requirements for electron transfer. To this level the reactant state must be raised to progress to the product state, with somewhat different boundary conditions for diabatic and adiabatic conditions. The reorganization energy λ is the energy required to transfer the electron from the bottom of the energy profile of the donor state up to the energy of the acceptor state in the same nuclear configuration as the energy minimum of the donor state. It consequently depends on the relative positions of the parabolas in both reaction coordinate and energy dimensions. Let us now compare the electron transfer kinetics for an exergonic forward reaction of an electron from the donor (excited state) to an acceptor and subsequently an endergonic reverse reaction back to the donor (excited) state (Fig. 6). For the exergonic reaction (Fig. 6a), where the free energy gain for the electron transfer is the activation barrier amounts to
| (3) |
For an endergonic reaction, the reverse reaction, during which a free energy change of has to be surmounted, the activation barrier for electron transfer is
| (4) |
Relations (3) and (4) have been derived assuming identical relations between energy and bond length for acceptor and donor. This means identical k values (relation (2)) or identical concavity for the corresponding parabola (compare Fig. 6). This of course does not correctly reflect reality and the mechanistic possibilities for generating anisotropy for electron transfer. If different values for k are assumed, k1 for the electron donor, and k2 for the electron acceptor, significantly more complex expressions are obtained for the activation energies (3) and (4). Simplified formulas are obtained when k1 and k2 are considered not to be too different, so that some terms can be dropped. For this case at least the tendency of the influence of the concavity of the parabola on the activation energy for electron transfer is found. For the exergonic reaction, one obtains:
| (5) |
| (6) |
In order to provide a low activation energy for the forward reaction (5) and a high activation energy for the reverse reaction (6), while keeping the energy loss for solar cells low ( low) one has only the options to optimize the reorganization energies (λex, λen) and the k factors (k1, k2) describing the concavity of the parabolas. When the k factors are different for the donor and the acceptor system they affect reversibility since their ratio is found to be inverted in the activation energies for the exergonic forward and the endergonic reverse reactions. The reorganization energies and the concavity parameters are of course interrelated. An electron reverse reaction is suppressed, if the ratio k1/k2 as well as the reorganization energy λen in the activation energy term (6) are selected to be large. This is apparently found in the iodide/triiodide system which is predominantly used in dyesensitization cells.
It should be mentioned that activation energy formulas (5) and (6) leave another option for making the reverse reaction of an electron much more improbable than the forward reaction. It is found in the entropy term of the activation energy in (6):
| (7) |
It expresses the need for molecular order (negative entropy) within the activation complex to make the reaction possible. This requirement could be maximized to suppress the reverse reaction. The transferred electron would immediately be passed on to states from where a reverse reaction would be improbable. The Marcus approach is essentially a reversible, close-to-equilibrium theory based upon molecular dynamics subject to Boltzmann statistics (Fig. 7a). It is expected to provide the necessary preconditions for allowing electrons to get involved in reversible quantum tunneling processes between donor and acceptor on equivalent energy levels. As discussed above, irreversibility can be introduced by tailoring reorganization energies and the concavities of the nuclear reaction parabola. A complementary possibility to induce anisotropy exists in pushing the reverse reaction into the Marcus inverted region, which involves a large free energy change, when referred to the donor's ground state, and results in a low reaction rate.
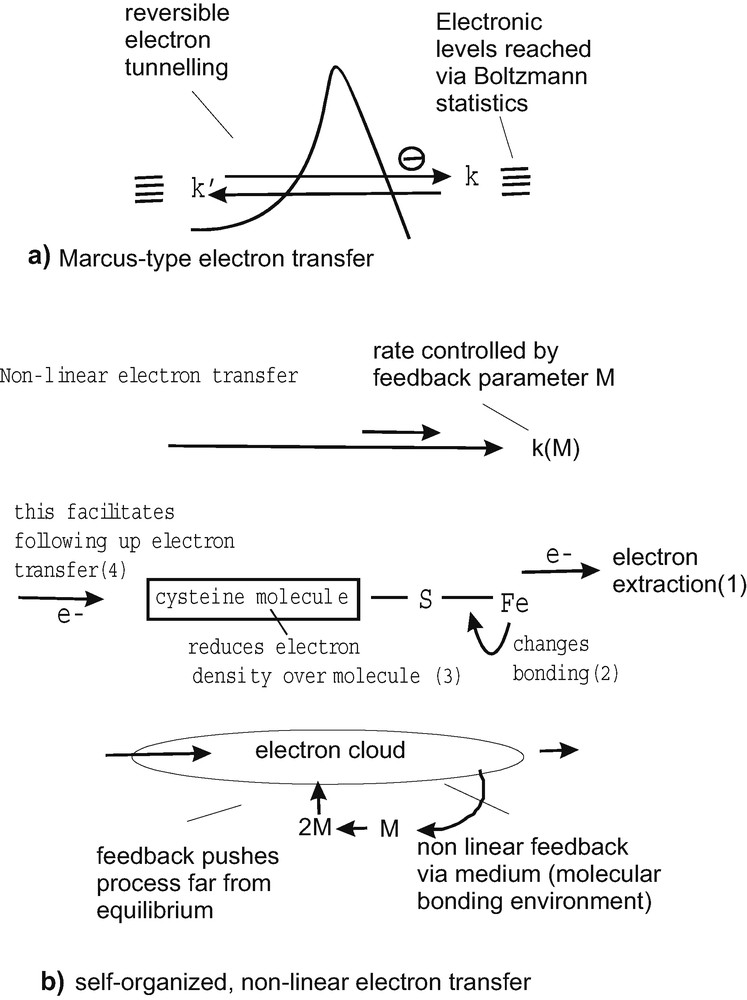
Figure explaining Marcus-type (a) and self-orgaized electron transfer (b). In case (a), only asymmetries in nuclear dynamics may contribute to a certain degree of suppression of the reverse reaction, while the electron exchange itself, via tunneling, is reversible. The self-organized electron transfer (b), on the other hand, involves an autocatalytic (feedback) reaction, which is pushing the electron transfer process itself far from equilibrium to generate new phenomena. This is qualitatively explained using the example of cysteine bound to iron via sulfur (thiol-group). When an electron (or electron density) is taken away from the iron, then the bonding of the molecule will change, decreasing the electron density over the molecule. This will strongly facilitate the uptake of a new electron. The feedback loop involved is shown below, emphasizing the non-linear nature of the electron transfer process.
3.2 Selectivity via non-equilibrium mechanisms
Inducing selectivity and directionality by considering a fundamentally reversible theory has its limitations. It is therefore reasonable to also invoke fundamentally irreversible phenomena. A straightforward mechanism for irreversible electron capture would be an electron tunneling process to a transient acceptor state from which a very fast relaxation to energetically lower states is possible. To get rapidly rid of the surplus energy via vibration quanta (phonons), it is in this case necessary that a reasonably high density of electronic states is present for rapid relaxation in subsequent small energy steps. New far from equilibrium mechanisms, as allowed by irreversible thermodynamics are also imaginable for electron transfer. The following arguments may underline this conclusion: It is an important fact that Marcus theory does not consider polarization effects while the electron is being transferred from the donor to the acceptor. Only polarization effects relating to the initial and final state may be considered. The consideration of polarization however allows to exert electronic feedback, which is critical for obtaining inter-linked electronic processes as well as new far from equilibrium phenomena and synergetic electron transfer processes. Far from equilibrium electron transfer can be mathematically described in a phenomenological way. It involves electronic feedback, which drives the system far from equilibrium and enables new mechanisms, which can be considered as belonging to irreversible thermodynamics [17,18]. It is not difficult to understand the principle intuitively, when the following model situation is considered: Electron transfer, which affects the molecular environment, may have an impact and feedback on the subsequent electron transfer rate and on following-up electron transfer steps. This is shown in Fig. 7b on the basis of the amino acid cysteine bound to iron via its sulfur (thiol) group. It is well known that cysteine acts as an electron bridge to numerous ferredoxin (Fe2S2, F4S4) clusters in biology. Comparative studies of gene sequences for these ferredoxins have shown that electron transfer via cysteine bridges has been conserved for 2 billion years starting from most primitive bacteria [32]. Cysteine must therefore be very efficient for electron transfer. However it contains no double bond or another feature (e.g. aromatic ring) favoring electron transfer. The key to its electron transfer abilities is its highly non-linear behavior. When electrons are extracted from the iron, the bonding with the cysteine molecule undergoes a quite significant change. The consequence is that the electron density over the cysteine molecule is decreased. This enables the efficient transfer of an electron from the opposite side. All together the electron (density) extraction from the iron has a feedback effect on the electron density of the molecule which greatly facilitates the transfer of a following up electron. Calculating such a mechanism phenomenologically clearly shows that the non-linear feedback can stimulate self-organization and leads to a slaving of electrons. Mathematically this means that the equations for subsequent electron transfer steps can be reduced to one equation in which the first electron controls the behavior of the following ones. A real multi electron transfer, as it is known from theoretical electrochemistry, is in this way possible without defined intermediate states. The Marcus theory cannot explain such multi electron transfer processes, as they are thermodynamically considered, for example in the four-electron transfer reaction involving the decomposition of water into oxygen and hydrogen near an electrochemical potential of E° = 1.23 V (NHE). The reason is that it does not consider polarization effects along the route of electrons. Now it should be explained why these considerations of a multi-electron transfer can help us understanding irreversible one-electron transfer mechanisms. Instead of considering individual electrons in a feedback reaction, also electron density within an electron cloud can be used to calculate the feedback reaction exerted and experienced by a single electron. Using a similar mathematical approach it can be shown that self-organized electron transfer is also feasible for an individual electron transfer via an electron density cloud in suitable molecular environments (e.g., a cysteine molecule) [17]. Because of the feedback processes or the polarization effects involved, the electron transfer mechanisms are highly irreversible and as far from equilibrium processes clearly different from those electron transfer mechanisms calculated via the Marcus [14] formula. Due to the mere nature of the feedback-stimulated process, because action is ahead of reaction, an inversion of the mechanism is not possible. Calculations also show that feedback significantly enhances forward electron transfer.
3.3 Examples from molecular electronics and biology
There are two science disciplines which can experimentally underline the existence of directional, selective electron transfer. These are molecular electronics and biological electron transfer. Molecular electronics aims at using molecular structures for microelectronic applications. Many examples for molecular rectifiers or molecular switches have been proposed and discussed [19–29]. In the classical paper by Aviram and Ratner [19] the rectifying molecules consisted of an electron donor (D) and an electron acceptor (A), connected by an alkyl bridge through an insulating saturated sigma (σ) bond to form a D-σA molecular structure. The first really working rectifying molecular bridge was apparently however a ground state zwitterion D+-π-A– configuration, connected by a twisted π-bridge [24,25]. Also a molecular structure working like a Schottky diode has been presented, the high forward electron flow of which is probably induced by a field induced electron transfer from an iodide anion to a pyridinium ring with a rectification factor of up to 90 [26]. Diode function has also been observed in di-block oligomer molecules with built-in electronic asymmetry [27,28]. Electronic rectification and p/n junction type behavior could, for example, be obtained by joining electron rich oligo-thiophene segments with electron-poor oligo-thiazole segments [27]. Molecular systems with strongly non-linear behavior have been compiled in a recent book [29]. A molecule which conducts an electron just in one direction, but not in the reverse one must be a molecule in which the electron communicates with the molecular environment and does it differently when the electron is arriving from one direction compared to the other. This typically involves feedback mechanisms. Theories on rectifying molecules are still in their infancy. But it should be claimed here that the highly non-linear behavior of these systems must involve same kind of feedback during electron transfer, as phenomenologically calculated in [17,18]. Bi-stability and rectifying properties can directly be demonstrated as consequences of feedback which in some way will also have to be considered in molecular electronic mechanisms as they are now considered in microelectronic devices. It should be mentioned that also interfaces of semiconductors can involve far from equilibrium processes [30].
Also in biology non-linearly behaving molecules have been discussed. Among electron transfer proteins from biological electron transfer chains, examples may be identified where such far from equilibrium mechanisms prevail. When, for example, an electron is transferred to cytochrome C3, which contains four-heme groups, the redox potential of all four heme groups will be affected. The transfer of an additional electron is expected to lower its electron affinity. But when the next electron is transferred to C3, the electron transfer is more easily accomplished than the transfer of the first one. The reason is that the transfer of the first electron has changed the molecular environment so as to easier accommodate the next electron. This electron will consequently have a low chance of getting involved in a reverse reaction. Molecular electronic feedback processes could thus, as calculations show [17,18], provide the tool for obtaining directional electron transfer. With a better understanding of these mechanisms molecules with rectifying properties for electron transfer could 1 day probably be tailored. They could have a decisive function in kinetically determined solar cells.
4 Near equilibrium versus far from equilibrium mechanisms
The fundamental difference between classical electron transfer according to the Marcus theory and self-organized, rectifying electron transfer, is explained in Fig. 7. In the Marcus picture near equilibrium nuclear configuration changes put the electron exchanging systems into a state where reversible electron tunneling may occur. Only differences in the configuration dynamics between donor and acceptor states leave room for a certain degree of asymmetry. In the case of molecular mechanism involving polarization and feedback the situation is different (Fig. 7b). Feedback from the electronic-molecular environment pushes the system far from equilibrium, where entirely new phenomena may occur. They also involve one-directionality as implemented by the orientation of the feedback reaction, which cannot be inverted [19,20]. Rectifying molecules may thus result, or molecules which allow bistable (multiple) states.
These considerations relating to self-organized electron transfer with highly non-linear behavior are not only a theoretical speculation. Experience from molecular electronics with rectifying and switching molecules shows that such systems exist and can practically be used. The theoretical knowledge for the description and tailoring of such molecular electronic systems is, however, modest. Electron transfer considerations, including those aimed at understanding photosynthetic mechanisms, can definitively take advantage from considering such non-linear self-organizing processes. This may be shown by discussing the mechanism of charge separation proceeding in the photosynthetic reaction center. It has to be emphasized that all the electron transfer steps involved there have already been interpreted on the basis of the near reversible classical Marcus theory (Fig. 7a). However, a more elegant and logic understanding can easily be achieved on the basis of self-organized, far from equilibrium electron transfer (Fig. 7b). It is well known, that the photosynthetic reaction center involves a symmetric molecular structure allowing two independent electron transfer pathways from the bacterio-chlorophyll pair via monomeric bacterio-chlorophyll to the pheophytine and further electron transfer elements (Fig. 8). Only one pathway is, however, efficiently used so that the other one is considered to be an unnecessary, forgotten relict from evolution, which just happens to still be present. The self-organized electron transfer model, on the other hand, takes an existing amino acid pair linking monomeric chlorophyll with the bacterio-chlorophyll pair (Fig. 8) as essential for a feedback function between the electron density cloud induced by excitation, transforming the linear system into a self-organizing one [31]. The arriving electron density exerts a feedback on itself. As Fig. 8 shows, the function of the reaction center could be described as a mechanism occurring near a bifurcation point, distant from equilibrium, where typically a high degree of instability occurs. The two electron transfer pathways of the reaction center correspond to the two reaction possibilities offered. Only one direction is, however, favored because feedback and self-organization is in play. It leads to a very efficient far-from equilibrium charge separation, because the starting position is very unstable [31]. The double structure of the photosynthetic reaction center is, in this picture, therefore, a strictly needed organization to allow efficient far from equilibrium charge separation. This discussed model demonstrates the possible relevance of irreversible electron transfer concepts for energy conversion in photosynthesis. Such fundamentally irreversible mechanisms may also be needed for designing molecular complexes, for tailoring electronically rectifying molecules, to operate kinetically determined solar cells. It is important to emphasize here that far from equilibrium processes of energy conversion will energetically never be as efficient as close to equilibrium ones could theoretically be. However the modest energy consumption which has to be sacrificed for operating the feedback loops may help to significantly improve a sluggish kinetics of energy conversion. It may happen by favoring the forward reaction and suppressing the reverse reaction (photosynthetic reaction center), by providing bi-stable states or by allowing synergetic multi-electron transfer (oxygen evolution in photosynthesis, other biological catalysts). Biology appears to have taken advantage of self-organization of kinetic processes to function at ambient temperature. Nano-structured solar cells with their complex micro-heterogeneous structure should also be developed along this line. To give one possible example of a research target we may again mention the structural-electronic properties of thiol (SH) groups in electron transfer. The molecule 4-thioacetatebiphenyl, interacting via the thiol group with Au to form an –S-link and with Ti at the opposite phenyl-end showed excellent current rectification in molecular electronic experiments [20]. The only amino acid carrying a thiol group, cysteine, has become a prominent electron transfer bridge in numerous biological enzymes and it has been, as already mentioned, shown that electron transfer pathways in ferredoxins may have conserved cysteine mediated pathways through evolutionary mutations [32]. This demonstrates that cystein is performing extraordinarily well. The remarkable thing is that the structure of cysteine, with an absence of double bonds or aromatic rings, does not seem at all to favor classical electron transfer. Also the comparable small size of the molecule does not provide an explanation. The amino acids glycine, alanine or serine are even smaller or comparable in size. But they are not known at all for good electron transfer properties. What is then special with the thiol group and the sulfur bond in such complexes? When removing or adding an electron the electronic structure of the molecule is drastically changing, as shown with model systems such as thiolate ligated to iron [33]. This means the changes induced by electron transfer only make electron transfer efficient. There is a feedback and electron transfer process becomes self-organized.
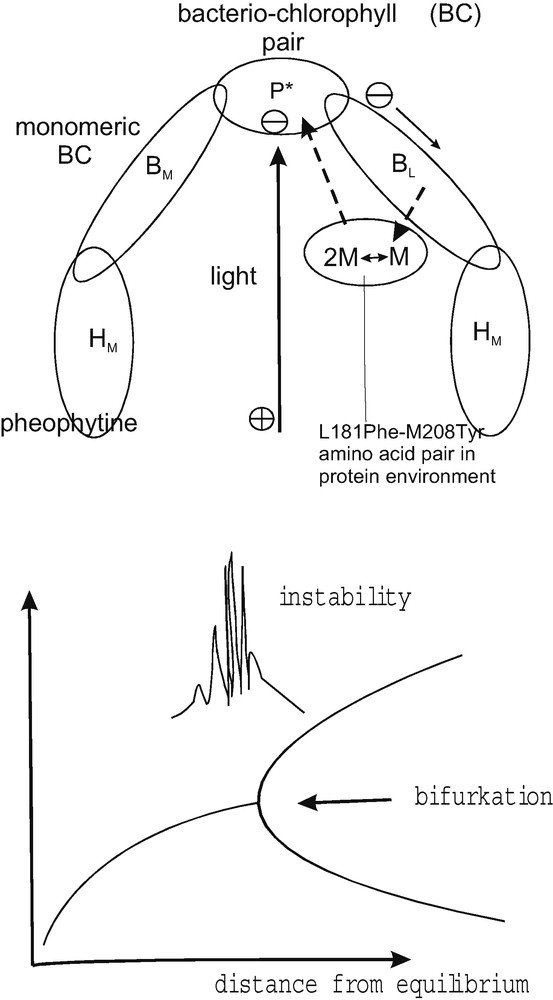
Simplified visualization of vectorial charge separation in the bacterial reaction center (top). The two electron transfer branches are considered to be an inherent structure of an autocatalytic charge separation mechanism (pathway M→ 2 M) operating near a bifurcation point (shown at the bottom) where the system is critically unstable. The conventional view, based on reversible electron transfer theory, considers the second branch an unnecessary relict from the evolutionary history.
5 Discussion and conclusions
This contribution emphasizes that the new nano-structured solar cells, solid and liquid dye sensitization solar cells as well as composite polymer fullerene solar cells, owe their already reasonable efficiency to a kinetically determined irreversibility of electron transfer. These elements of kinetic irreversibility, the iodide/iodine redox system in the dye sensitization solar cell, the fullerene in the polymer–fullerene composite solar cell have emerged by trial and error. They have unintentionally been integrated experimentally at an early stage of nanocomposite solar cell development and, because they were well functioning, have been conserved and maintained while other parameters were further optimized. At the moment there is no sufficient fundamental knowledge and experience with chemically determined irreversibility available to replace these elements for more stable and convenient ones. Both the iodide/iodine system and the fullerene, have problems with photochemical and chemical instability, but they cannot be replaced because no better functioning systems are presently known or can be designed. This constitutes a difficulty for the nano-structured cells concerned (e.g. [8]), but at the moment no better functioning alternatives can be identified because of a lack of knowledge. The same is true for solid dye solar cells using copper iodide contacts. The thiocyanate electron transfer bridge which is critical for the cells high efficiency is equally the source of irreversible photo-degradation [12]. We conclude that a better understanding and handling of kinetic charge separation and electronic rectification towards new frontiers is needed. We have to learn how to tailor rectifying electronic systems on a molecular scale. Here the experience of molecular electronics with rectifying and switching molecules could be very helpful. For both initiatives it will however be necessary to develop theories for irreversible charge separation as a precondition for understanding and designing stable electronic current rectifying molecular compounds and aggregates. Electronically rectifying molecules may be used to surface modify nano-particles for improved selectivity in electron transfer processes. The development of alternative rectifying elements is a big challenge since all nanocomposite solar cells are not only suffering from moderate energy conversion efficiencies but also from instability problems which are somehow related to molecules involved in rectifying charge separation (the iodide-iodine system, the fullerene). Multiple approaches towards kinetic irreversibility seem to be possible. The opportunities offered by classical molecular electronic approaches have been discussed. But far from equilibrium self-organized electron transfer [17,18] based on autocatalysis (feedback) and demonstrated by rectifying molecules from molecular electronics, suggest very appealing new mechanistic possibilities, which should specifically be explored. Kinetically determined nano-composite solar cells open the way towards fundamentally simple solar cells with a prospect of cheap production. One day it may be possible to produce reasonably efficient solar cells just by mixing and self-organizing chemically modified nano-particles with electronically rectifying interfacial properties and processing them by printing techniques on plastic contact membranes. They would follow the most basic solar cell principle, as shown as energy scheme in Fig. 3 (right). One just needs an efficient charge separation involving a kinetically determined restriction for a reverse reaction, together with a certain degree of self-organization, towards drastically simplified solar energy conversion devices. But the scientific challenge ahead is significant.


