1 Introduction
The extent to which fullerene cages can be described as aromatic continues to be debated [1–8], and indeed ‘aromatisation’ of the C60 cage has been proposed as a driving force in fullerene chemistry [9]. A widely accepted criterion of aromaticity for a cyclic system is its ability to sustain a diatropic ring current induced by the presence of a perpendicular external magnetic field [10–16]. Such currents can be inferred indirectly from their effects on observable magnetic properties (exaltation of magnetisability [17–19], downfield chemical shifts of external hydrogen nuclei [20]) and properties that are sub-observables, in Hirschfelder's sense [21], such as the characteristically negative NICS value at the ring centre or some other chosen point [22]. Inferences of this type all have difficulties associated with masking of ring-current effects by other contributions to the property [23–27], but ring-current aromaticity can in fact be deduced directly from calculation of the induced current itself, by solution of the Schrödinger equation for the molecule immersed in the magnetic field, using an appropriate distributed-origin method [28–31]. The present paper is concerned with the application of this technique to fullerenes and similar curved-carbon molecules.
The ipsocentric approach [32,33] offers well tested procedures for the accurate and relatively economical calculation of current density maps at an ab initio level, and provides a theoretical framework for their interpretation in terms of chemical concepts of orbital symmetry, node-count and energy [32,33]. Full ab initio calculation rapidly becomes expensive for large systems, or for problems in which there are large numbers of cases, such as the comparisons amongst the many [34] conceivable isomeric forms of a fullerene, or the truly vast numbers [35] of possible isomers of a fullerene derivative. Fortunately, the advantages of the ipsocentric approach can be retained in a simplified version of the calculation that is much less costly: the pseudo-π model [36]. As will be explained below, this model relies on a matching in symmetry between the carbon π orbitals responsible for ring currents and the σ orbitals of a set of hydrogen atoms that has the same connectivity. In previous work, the pseudo-π model has been shown to reproduce qualitatively and even semi-quantitatively the patterns of induced current density in planar and near-planar aromatic, antiaromatic and non-aromatic systems, giving yes/no answers to the question of aromaticity and an account of the origins of the ring current (if any) in terms of orbital contributions, all at a tiny fraction of the cost of a full ab initio treatment [36–40].
However, carbon is a versatile element, and its π bonding patterns are not restricted to two dimensions. ‘Curved graphite’ entered chemistry with the appearance of the fullerenes and nanotubes. Our discussion of ab initio and model methods in terms of strict σ/π separation reveals their origins in the treatment of the properties of planar arrays of carbon atoms. This separation is absent, or at least blurred, in curved arrays. In spherical and cylindrical systems, the specification of aromaticity in terms of a ring current is also less well defined in principle, as it is no longer possible for one given external field to be simultaneously perpendicular to all rings. However, we can still expect to find some situations in which currents induced by locally perpendicular fields are localised in bonds and others where these currents are delocalised over faces or over larger circuits. For example, calculations on [60]-fullerene have shown (paratropic) ring currents in pentagons and localised (diatropic) currents in the formal double bonds of the hexagons; the strong paratropic currents in the pentagons appear to act as a set of driving cogwheels [41]. This idea was taken up in the ‘pentagon-proximity’ model for NICS(0) values in faces of leapfrog fullerenes [42]. Currents may also extend over larger circuits: calculations on the functionalised fullerene derivative C60F15X3 (X = [CBr(CO2Et)2]), for example, show a global (diatropic) current delocalised over a [18]trannulene π-subsystem of the cage, which has the typical two-orbital, four-electron signature of the (4n + 2) monocycle [38]. From the existing results it is clear that there are patterns here that can often be rationalised using simple mechanical or orbital arguments.
The three-dimensional version of the pseudo-π model offers a tool for a systematic approach to exploration of the aromaticity of curved carbon. The symmetry analogy is now even closer than in the two-dimensional case, as in 3D the model set of ‘σ’ s orbitals on hydrogen atoms spans exactly the same symmetry as the set of radially directed ‘π’ p orbitals of the carbon cage. Such a model would not be capable of recovering radial effects—differences in ring currents between the inner and outer sides of the curved surface—but it could be expected to reproduce the other significant features of the current–density map, and in fact does so for the case in hand, C120 archimedene, as we will show.
To test these expectations, we have performed a study of an icosahedrally symmetric 120-vertex fullerene analogue, a cage based on the largest Archimedean polyhedron, the great rhombicosidodecahedron, and known by the trivial name archimedene [43,44] (Fig. 1). As a generalisation of the phenylenes, archimedene is a synthetic target [45], and its face sizes of 4, 6 and 10 suggest varied possibilities for ring currents.
C120, archimedene.
The high symmetry of archimedene allows a complete comparison of full ab initio and pseudo-π calculations. The success of the pseudo-π model shows that σ−π separability does not cause major complications in archimedene, and this is not surprising in view of the small departure from planarity and hence from pure sp2 hybridisation [46] implied by the angle-sum defect of only 6°, half that of C60, where π-only models have good success in describing current patterns [47]. As a prologue to wider application of the pseudo-π model for fullerenes, nanotubes and analogues, calculation of pseudo-π maps for fullerenes C60 and C70 and a C60 derivative are presented here.
2 Calculations
The geometry of archimedene was optimised in two stages. First an RHF calculation with the minimal STO-3G basis was performed in full icosahedral symmetry with Gaussian 98 [48], yielding bond lengths r(4/6) = 1.482 Å, r(4/10) = 1.497 Å and r(6/10) = 1.340 Å (where r(i/j) is the length of the 60 edges common to faces of sizes i and j), in agreement with the results of Schulman and Disch [44]. This structure was confirmed as a local minimum by diagonalisation of the Hessian, and was then refined at the B3LYP/6-31G level, retaining icosahedral symmetry. Bond angles are fixed by the symmetry: the 4-, 6- and 10-rings have internal angles 90°, 120° and 144°, respectively, leading to a defect from 360°-planarity of just 6° in the angle sum at each vertex. The final bond lengths are r(4/6) = 1.491 Å, r(4/10) = 1.483 Å and r(6/10) = 1.363 Å. The 4-membered ring has uniform bond lengths (Δr = 0.008 Å), whereas the 6- and 10-membered rings show strong bond alternation (Δr = 0.128, 0.120 Å). A straightforward exhaustive enumeration shows that archimedene has 21,956,126,976 = 28 × 36 × 76 Kekulé structures, with Pauling π bond orders p(4/6) = 1/6 ≈ 0.167, p(4/10) = 31/84 ≈ 0.369 and p(6/10) = 13/28 ≈ 0.464. Of this huge number, just three of the Kekulé structures are totally symmetric: the optimised geometry corresponds to one of these, in which all 120 edges of 4-membered rings are formal single bonds, and the 20 6-membered rings and 12 10-membered rings contain alternate formal single and formal double bonds. The 360 doubly occupied orbitals of Ih C120 span
(the regular representation of the Ih group) account for the 120 1s2 cores and
Current density was calculated at the CHF/6-31G* level in the ipsocentric approach using the SYSMO program [49]. That part of the total current arising from the 60 π-like orbitals was visualised in a set of maps, displayed in Fig. 1. Separate maps were calculated for magnetic fields oriented along each of the three high-symmetry directions in turn, i.e. along a C2, C3 and C5 axis perpendicular to a 4- 6- and 10-membered ring, respectively. For each orientation, current was plotted in planes parallel to the respective face at heights –1, 0 and +1 a0. This gave a picture of the pattern of current density inside, on the surface and outside the cage. Contours show the magnitude of the current density vector and arrows the direction and relative magnitude of its in-plane component. Diatropic/paratropic currents are represented by anticlockwise/clockwise sets of arrows. Filled circles in each plot represent projections of the atomic positions into the plotting plane. Magnitudes of the different circulations can be gauged by the value of jmax, the locally largest value of the current density per unit inducing magnetic field. The quantity jmax is calculated as an absolute value in atomic units, but is more helpfully quoted as a ratio to the corresponding quantity in the 1a0 plane for benzene, calculated using the same level of theory (this ‘standard’ benzene value is 0.08 a.u. [41]).
Starting from the maps for the inside of the cage (Fig. 2, top row), we see that the four-membered ring supports a strong paratropic circulation. This is a surprising observation if we compare with the known planar phenylene, tris(benzocyclobutadieno)benzene, where the maps [50,51] show diatropic currents in 6-rings but no strong paratropic currents in the 4-rings. This difference is a consequence of the C120 connectivity rather than its curvature, as illustrated by the fact that the 4-rings still acquire no strong paratropic current in the maps for a tris(benzocyclobutadieno)benzene subunit held at the geometry of archimedene—the maps for this curved fragment (not shown) are instead dominated by the diatropic circulations in the outer hexagonal rings, as are those for the planar geometry of the tris(benzocyclobutadieno)benzene molecule itself.
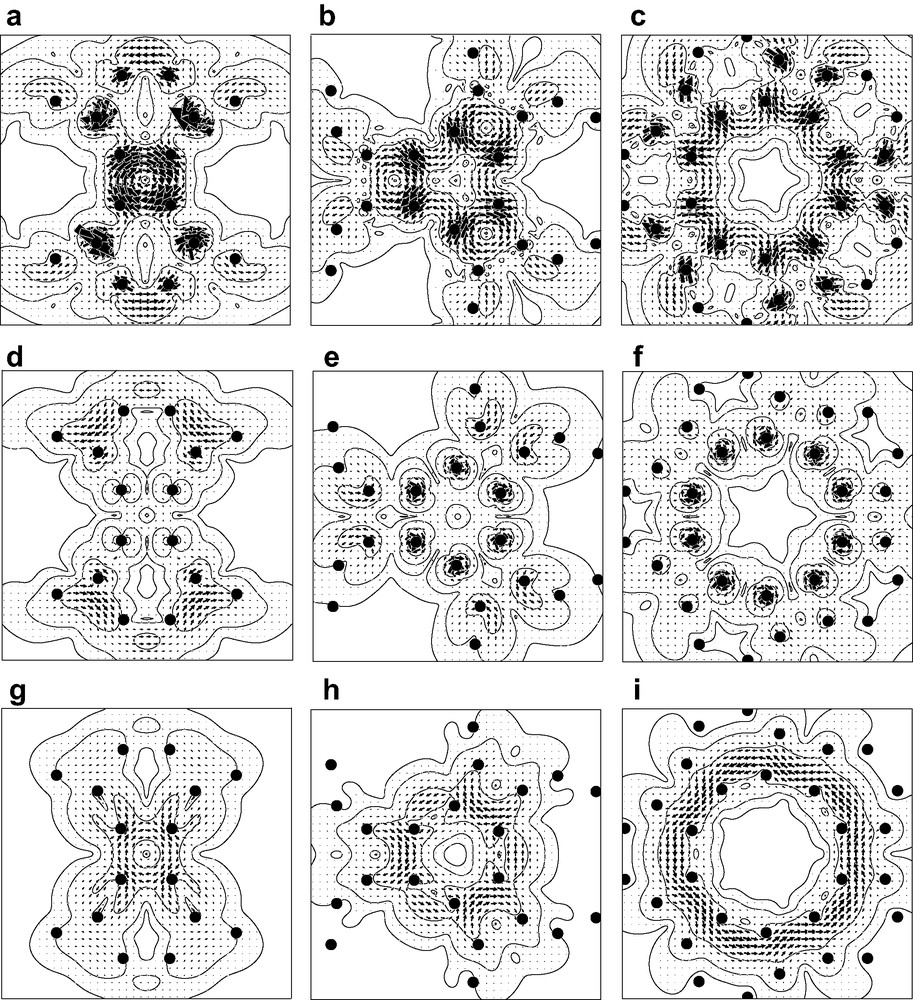
Maps of current density induced in the archimedene molecule by an external magnetic field. The maps are calculated at the CTOCD-DZ/6-31G*//B3LYP/6-31G level, and show only the current density arising from the 60 π-like molecular orbitals of the cage. Each column of maps shows the effect of a field directed along an axis perpendicular to a face of the C120 polyhedron (left, C2 axis through a 4-membered ring; centre C3 axis through a 6-membered ring; right C5 axis through a 10-membered ring). Each row of maps refers to a plotting plane at a different height (top row, (a)–(c), inside the cage, 1a0 below the plane of the face; centre row, (d)–(f), in the plane of the face; bottom row, (g)–(i), outside the cage, 1a0 above the plane of the face). Contours show the magnitude of the total π current density vector and arrows show the direction and relative magnitude of its in-plane component. Diatropic/paratropic currents are represented by anticlockwise/clockwise sets of arrows. Filled circles represent projections of nuclear positions into the plotting plane.
Hexagonal and decagonal faces of the polyhedron, in contrast, show no coherent global circulation, in spite of their formal 4n + 2 π-counts. Rather, the current in both 6- and 10-membered rings shows alternation of intensity and results from superposition of two effects: strong currents associated with the formal single bonds arising from the true ring currents in the adjacent 4-membered rings, and local diatropic currents centred on the formal double bonds. The closed character of the double-bond centred circulations at the 6/10 fusions can be seen by inspecting the two sides of a given bond as it appears for two different field directions (Fig. 2b and c). The current for the tetragonal ring is the most intense: its maximum of jmax = 0.079 is essentially the same as the (diatropic) benzene standard value [32].
The maps for the surface of the cage (Fig. 2, centre row) show tightly localised circulations associated with the atomic cores but, as would be expected for π contributions plotted in the vicinity of their nominal nodal surface, show no significant current elsewhere.
The maps for the outside of the cage (Fig. 2, bottom row) show circulations that are weaker than those seen inside the cage, a trend that would be expected from consideration of orbital overlap. The four-membered ring supports a paratropic circulation, weaker by a factor of 2.5 than in the –1a0 plane, and so only 40% as intense as the (diatropic) current of benzene. The current in the region over the hexagon is a weaker version of the alternating superposition pattern seen for the cage interior. At first glance, the pattern for the 10-membered ring seems radically different from that for the interior of the cage in that the map (Fig. 1(i)) appears to show a global circulation connected with the decagon. However, this is again a superposition of local currents, though difficult to recognise as such in this planar projection of the three-dimensional currents. In fact, over all the double bonds on the 6/10 edges, what we are seeing in Fig. 2i is the outer part of the local diatropic bond circulation, and over the single bonds on the 4/10 edges what we are seeing is part of the paratropic ring current of the adjacent 4-membered ring. This analysis is backed up by the map of the current in the external 1a0 plane induced by an field normal to a 4/10 edge (Fig. 3), which makes it clear that the apparently concerted circulation breaks up into local 6/10 bond and 4-gonal ring circulations There is thus an essential difference between the three types of face of the archimedene polyhedral cage: only the 4-membered rings support a true ring current, and that current is paratropic, indicating local anti-aromaticity. The 4-membered rings have uniformly long bonds. In contrast, the hexagonal and decagonal rings are non-aromatic, their magnetic response being a consequence of superpositions of the true ring currents and localised bond circulations. Both 6- and 10-membered rings are strongly bond-alternated according to the geometry optimisation. It is apparent from this analysis that the induced currents of archimedene indicate global antiaromaticity for this molecule. In this connection, it is interesting to note that the simplest π-electron models predict C120 archimedene to have a lower π-resonance energy per atom than C60 [43].
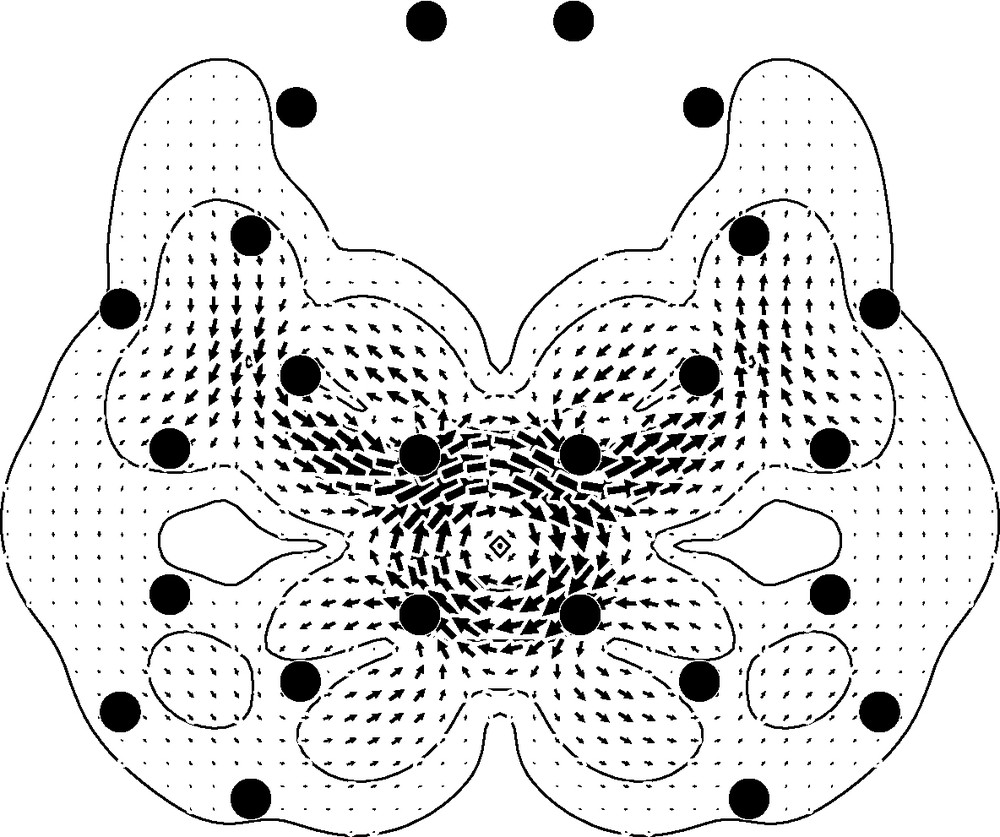
Map of current density induced by a radial external magnetic field normal to the 4/10 bond, in a plotting plane outside the cage, 1a0 above and parallel to the selected bond. Plotting conventions as in Fig. 2.
3 The pseudo-π model
Pseudo-π modelling of a planar π system has two stages [36]. First, the conjugated carbon centres of the π system are replaced by a set of hydrogen atoms on the same positions, each consisting of a unit positive charge, bearing a single 1s (STO-3G) basis function and contributing a single electron. Then, the map of the current density induced in the HN-system by a perpendicular magnetic field is calculated self-consistently and ipsocentrically, i.e. with the full coupled Hartree–Fock CTOCD-DZ (continuous transformation of origin of current density–diamagnetic zero) approach [30]. The first stage rests on the one-to-one correspondence between the Hückel molecular orbitals of a π system and the σ orbitals of an array of hydrogen atoms with the same connectivity. Both are defined by eigenvectors of the same adjacency matrix, representing the same linear combinations of the respective basis functions, with the same energy eigenvalue expressions, adjusted appropriately for scale and origin. The symmetries of the orbitals are also related. In a planar system, each π molecular orbital of symmetry Γ(π) is converted on switching pπ and s basis functions to a σ molecular orbital of symmetry Γ(σ) = Γ(π) × Γz, where Γz is the symmetry of a translation perpendicular to the plane. In a system embedded in a curved surface, each radial π molecular orbital is converted to one of the same symmetry Γ(σ) = Γ(π).
In the ipsocentric approach there is a clear partition of the total current density into easily interpretable orbital contributions [32]. Each occupied molecular orbital makes a contribution that depends on the availability of formal excitations to empty orbitals, which is in turn governed by the energies and symmetries of the manifold of the unoccupied orbitals. The symmetry of the excitation determines the sense of the ring current: in a monocyclic system diatropic current arises from a translational excitation, paratropic from a rotational excitation [33].
The correspondence of unperturbed π orbitals of CN and σ orbitals of HN implies that there should also be a one-to-one correspondence of orbital contributions to the total current density induced by a perturbing magnetic field. As the pπ-to-s switch corresponds in both planar and curved systems to multiplication of the orbital symmetry by a one-dimensional representation (in one case Γz, in the other Γ0, the totally symmetric representation), the symmetries of π→π* transitions are preserved, and the selection rules carry over unchanged. As a consequence, the pseudo-π model reproduces overall patterns and specific features of the current density maps for a wide range of planar systems; it also captures the breakdown of total π current into orbital contributions [36]. Qualitative questions about aromaticity of specific systems can therefore often be settled without recourse to expensive ab initio calculations.
The model also benefits from an unexpectedly precise numerical coincidence [36]. It turns out that when STO-3G hydrogen 1s orbitals are used with typical carbon–carbon distances, there is a close numerical match between the σ currents calculated in the nuclear plane of HN and the π currents calculated for CN in the usual 1a0 plotting plane. The degree of agreement is surprisingly high: the difference in pseudo-π and true π currents for benzene is less than 1%, for example.
Performance of the pseudo-π model for fullerenes and similar closed curved carbon networks is unexplored, but on the general grounds described above would be presumed to be good. The application to archimedene described in the following section provides a test and validation of this presumption.
4 Pseudo-π maps for archimedene and fullerenes C60 and C70
Taking the calculated B3LYP/6-31G geometry of the archimedene cage, the pseudo-π model was applied directly: all carbon centres were replaced by hydrogen atoms bearing STO-3G 1s functions and current density was calculated in the ipsocentric approach for the three high-symmetry orientations of the external field. Fig. 4 shows the maps of current density plotted in the planes of the tetragonal, hexagonal and decagonal faces, respectively.
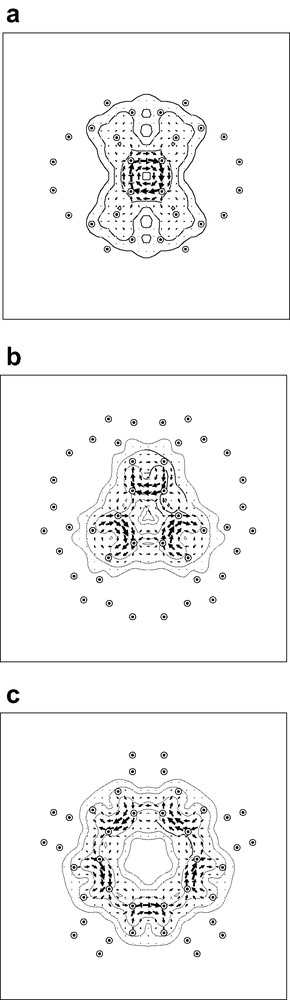
Pseudo-π maps of current density induced in the archimedene molecule by an external magnetic field: with the external field directed along (a) a C2 axis through a 4-membered ring; (b) a C3 axis through a 6-membered ring; (c) a C5 axis through a 10-membered ring. Contours show the magnitude of the total current density vector and arrows show the direction and relative magnitude of its in-plane component. Diatropic/paratropic currents are represented by anticlockwise/clockwise sets of arrows. Dotted circles represent projections of nearby pseudo-atom positions into the plotting plane, which in each case is the plane of the face.
The derived maps give a clear qualitative picture of the magnetic response of this molecule: the tetragonal face supports a strong paratropic ring current, and the other faces do not support ring currents, but instead show only localised bond circulations and currents derived from the neighbouring 4-membered rings. In other words, the model reproduces all the essential features of π current density shown by the full ab initio maps of Fig. 1. By construction, the model cannot identify specific radial effects, and so does not address any differences in ring currents between the inner and outer surfaces of the cage, but as these are questions of magnitude rather than overall pattern, the model can be considered to be highly successful in this first application to a fullerene analogue.
In the light of this success, application to the fullerenes themselves seems justified. Fig. 5 shows the pseudo-π maps for the distinct faces of the C60 and C70 fullerenes.
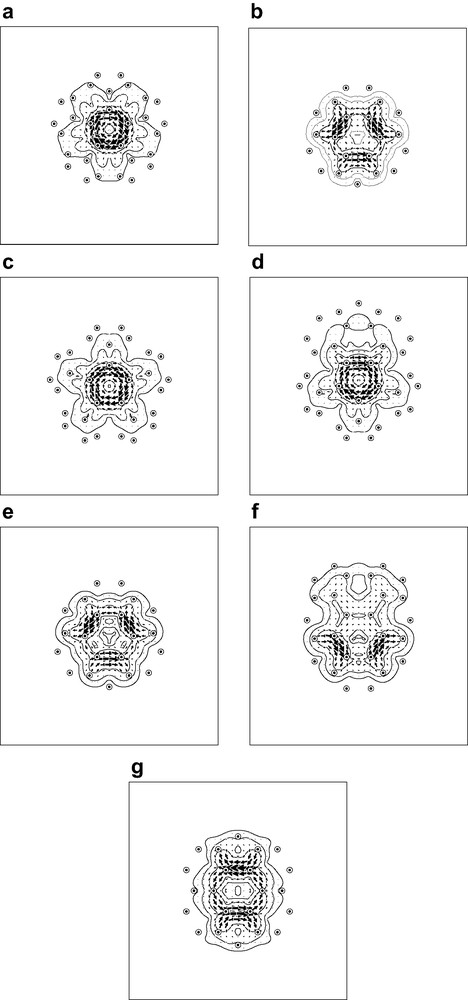
Pseudo-π maps of current density induced in the C60 and C70 fullerene cages by an external magnetic field. All symmetry-distinct faces of the two polyhedral cages are shown, with the external field directed in each case perpendicular to the median plane of the face. Maps (a) and (b) refer to C60: (a) the unique pentagonal face; (b) the unique hexagonal face. Maps (c) to (g) refer to C70: (c) the ‘polar’ pentagonal face; (d) the ‘non-polar’ pentagonal face; (e) the ‘equatorial’ hexagonal face; (f) the hexagonal face abutting a polar pentagon, (f) the hexagonal face abutting two equatorial hexagons. Plotting conventions as in Fig. 4.
In each case the external magnetic field is directed normal to the face, and the current valuated in the median plane of the face. The results are in full accord with the evidence from previous work on magnetic properties of these two fullerenes.
In C60, the pseudo-π maps show a paratropic ring current on the pentagonal face, and only local double-bond and pentagon-derived circulations arising on the hexagons. This is in agreement with the early Hückel–London calculations [2,46] and ab initio current density maps [41]. Pseudo-π maps are able to recover finer features of the current map arising from the through-space nature of the current flow [36], whereas Hückel–London maps confine all current to the geometrical lines of the bonds. There is no evidence in the maps of global aromaticity of C60.
C70 has two distinct pentagonal and three distinct hexagonal faces. The pseudo-π maps show both pentagonal faces behaving as in C60, each supporting a characteristic paratropic ring current. The hexagonal faces away from the equator also behave magnetically as in C60, with only localised and consequential currents, but the equatorial hexagon of C70 supports its own identifiable diatropic current. The maps are consistent with those calculated in the Hückel–London model [47], which show ring currents in both pentagons and equatorial hexagons, but not elsewhere, and with the pattern of NICS values for individual rings [52]. Thus, broadly speaking, C70 has magnetic properties consistent with a simple picture in which this elongated fullerene consists of two halves of C60 separated by a benzenoid equatorial belt [53,54]. Given their paratropic pentagonal ring currents, neither C60 nor C70 should be considered as especially aromatic on the magnetic criterion. The paratropicity of the pentagons in C60 and C70 is consistent with the diatropic-rim, paratropic-hub pattern of current found in bowl-shaped corannulene [55], which is itself part of a more general pattern in which the central ring of an [n]circulene is paratropic and the perimeter diatropic [56].
The pseudo-π model will also be useful in the evaluation of aromaticity of fullerene derivatives. Functionalisation of C60 in the ‘octahedral’ (more properly, centrosymmetric tetrahedral, Th) C60X12 pattern characteristic of derivatives such as [(Et3P)2M]6C60 (M = Pt, Pd) [57] where each organometallic moiety adds η2-fashion across a formal double bond of the [60]-fullerene cage, produces a closed, conjugated and π-alternant network of 48 carbon centres, which has been proposed to be aromatic [57,58] and less strained than C60 itself [59]. The network consists of eight equivalent hexagonal rings, each linked 1,3,5 to three others (Fig. 6a). Bond alternation within the hexagons is reduced to just over half the value for C60 itself [57]. A pseudo-π map for the unique symmetry-distinct hexagonal ring of this network (Fig. 6b and c) indicates that it supports a self-contained ring current and is indeed therefore aromatic in the same way as benzene on the magnetic criterion.
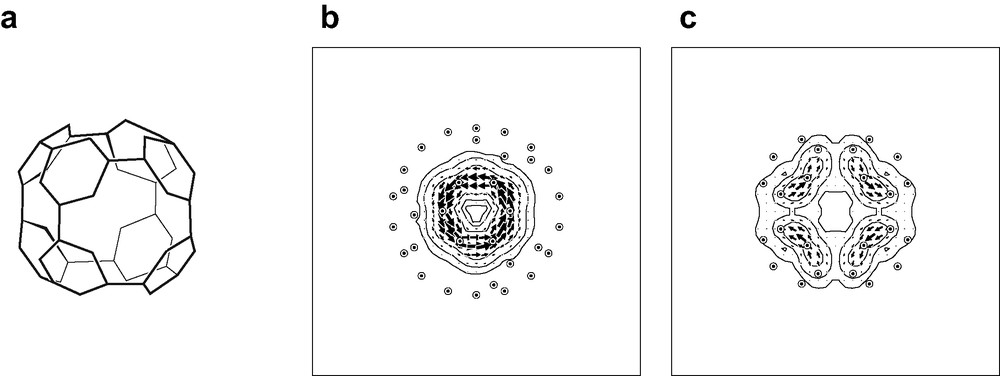
Pseudo-π treatment of the Th-symmetric C60X12 derivative of [60]-fullerene. The 48-centre conjugated system is illustrated in (a). Coordinates for the pseudo-π model of this network are taken from an RHF/6-31G** optimisation on C60(CH2)6. with −CH2− groups inserted in an octahedral array of formal double bonds of the fullerene cage. Pseudo-π maps of current density induced in the 48-centre system by an external magnetic field are shown, with the external field directed (b) along a C3 axis through one of the eight equivalent ‘bare’ hexagonal rings and (c) along a C2 axis through one of the six 12-gonal ‘holes’ in the conjugated system. Current is plotted in the plane of the hexagon and the median plane of the 12-gonal hole. Plotting conventions as in Fig. 4.
Given the advantages in simplicity and transparency of the pseudo-π model, its success in accounting for current density distributions in three-dimensional carbon networks suggests a useful future in screening large numbers of fullerenes and fullerene derivatives for aromaticity. Applications to nanotubes can also be envisaged.
Acknowledgements
The Royal Society/Wolfson Research Merit Scheme is thanked for an award to P.W.F. and the EU is thanked for financial support under RTN contracts HPRN-CT-2002-00177 (A.S., P.W.F.) and HPRN-CT-2002-00171 (P.W.F.). Financial support from Ministero dell'Istruzione, dell'Università e della Ricerca (MIUR) and Università di Salerno via 60% funds is gratefully acknowledged.


