It is well known that the problem of right or left classification of chiral objects, important in chemistry and the bio-sciences, has subtleties even for objects as basic to stereochemistry as the tetrahedron [1,2]. The history of attempts to devise measures of chirality and symmetry has recently been reviewed comprehensively by Petitjean [3]. In the present note we briefly review some theoretical difficulties and suggest one scheme by which chiral tetrahedra may be classified as right or left handed on the basis of their geometry.
Ruch [4] famously introduced the analogy of potatoes and shoes to illustrate a distinction between two types of chiral objects that we might wish to classify. Imagine two boxes. We are given a set of chiral objects and asked to assign each object to a box. In the weak version of the assignment problem, we must ensure that objects are assigned subject only to the condition that no two enantiomers end up in the same box. In the stronger version, we are asked to put all ‘right’ enantiomers in one box (R) and all ‘left’ enantiomers in the other (L). As Ruch points out, we could expect to perform the second task easily enough for shoes, despite the many differences between two arbitrary right shoes, but not for potatoes, where we can easily see that each individual object is chiral (non-superimposable on its mirror image) but we have no obvious way of labelling it R or L. “Any classification would be very artificial” [4]. Ruch also notes that other objects such as screws belong to the shoe-like category in that they too can be split into disjoint right and left forms; in this case, according to the direction of motion when the screw is turned in a clockwise sense.
This distinction between the two types of objects, with shoe-like and potato-like chirality, corresponds to the difference that is drawn between chirality and handedness [5]. Shoes have a natural assignment to R or L and are therefore said to be handed. Potatoes do not have this natural assignment and so, though they are chiral, they are said not to be handed. This distinction is potentially significant in chemistry: chiral molecules have a huge variety of shapes, with no obvious correspondence to left or right shoes, and so in general they are potato-like and not handed.
However, a distinction based on a notion of what is natural is not clear-cut. For instance, one can easily imagine an innovative fashion designer, or the effects of extreme wear and tear, producing shoes that would puzzle the classifier. Similarly, it is conceivable that a principle accepted as ‘natural’ by some cohort of researchers could be derived for potatoes. Perhaps this could be based on a chiral effect reflecting the chirality of the cause, in line with Curie's Principle. An example might be a hydrodynamic effect such as the sense of rotation of a sinking object in a conveniently chosen fluid under standard conditions, or, on the microscopic level, the pitch induced in a nematic liquid crystal by doping with one enantiomer of a molecule to be tested. In the molecular domain, optically active molecules of any shape have long been classifiable in a 'natural' way, by reference to the sign of the optical rotatory power under specific conditions. At the present time, the Cahn–Ingold–Prelog (CIP) rules [6–10] constitute another definition of what is considered by chemists to be natural in the molecular context, and give an algorithmic procedure for solution of the classification problem by assignment of labels to chirality elements inside a molecule, although the list of labels is not normally condensed to a single whole-molecule descriptor. These examples suggest that, given a sufficiently flexible notion of what is natural, it should be possible to attribute handedness to any class of chiral objects.
Even when handedness is uncontested, there are difficulties. Although the test proposed for the handedness of a screw is reasonable and objective, and may appear natural to a right-handed person in a tool-using culture, there is no necessary connection between R and L shoes and R and L screws. This depends on a convention. Thus even within the domain of recognisably handed objects, we are inexorably faced with the situation described by Cahn, Ingold and Prelog, where “systems for the specification of asymmetric configuration […] have grown like islands of local government in a large semi-civilized country” [6]. A convention is inevitably local to some class of ‘similar’ objects.
A distinct fundamental, problem with any definition that relies on a continuously variable property such as rotatory power arises from a general property of three-dimensional geometrical objects, their chiral connectedness [11,12]. Consider the formal interconversion of the two enantiomers of a chiral object by some continuous structural deformation. If it is possible to find such a pathway that consists entirely of chiral configurations, then the enantiomers are said to be chirally connected. Suppose that we have defined a chirality index ψ, i.e. a continuous pseudo-scalar function of structure that by definition takes equal and opposite values for enantiomers. A smooth connection between the enantiomer with positive ψ and the partner with negative ψ then demands the existence of a ‘false zero’ [1,4,13], i.e. a vanishing value of ψ for some chiral configuration, rendering the sign of ψ effectively useless as a global means of assigning left and right labels to structures. This problem surfaces repeatedly in the literature, and has recently been discussed in connection with a measure originally devised for liquid crystals [14], where chiral zeroes can be identified for particular choices of parameters [15].
Thus, at least some chiral structures will have an undefined chirality for any continuous pseudo-scalar function ψ [16]. This mathematical fact has physical counterparts. For example, the Kuhn zero-sum rule for rotational strengths [17] guarantees that the optical rotation for a given enantiomer of a chiral molecule will have changes in sign as a function of wavelength and so, by varying the conditions of the test (hence changing the definition of the function ψ) a false zero can be produced. In principle, this objection applies to any test based on a single continuous physical property, and has induced some authors to state that it is impossible to assign handedness to chirally connected objects [1]. To be less pessimistic, it would appear that the problem can be side-stepped, after a fashion, at the cost of sacrificing continuity, by adopting an open-ended hierarchy of chirality indices, each to be checked only when predecessors yield false zero results [13,18].
A chirally connected set of labelled vertices must contain at least five points [11]. A centred tetrahedral molecule such as the penta-atomic substituted methane C(XYZW) is chirally connected, whereas the empty tetrahedral cage XYZW is not. Chiral tetrahedra considered as sets of unlabelled vertices are chirally connected [1,19]; our subject here is the chiral tetrahedron, free of labels, considered as a geometrical object. In spite of their chiral connectedness, all such tetrahedra can be assigned a handedness. The CIP approach can be adapted to demonstrate this point. In the CIP system, absolute configuration labels R,S are assigned to chiral centres using a set of priority rules based on the chemical nature of the neighbours. We will use priorities based on relative edge lengths to assign R,S labels to vertices and, by convention, transfer them to the tetrahedron as a whole. With one addition, an analogy of the P,M helicity rule of the CIP system, all possible cases of chiral tetrahedra are covered.
The basis of the classification is geometric: the set of edge lengths. A tetrahedron is specified up to enantiomorphism once the set of six side lengths is given, up to similarity once the set of five relative lengths is given. Considering all possible combinations of side lengths, and excluding degenerate planar, linear or point configurations, there are 25 different cases, spanning the achiral groups Td, C3v, D2d, C2v, Cs (10 cases) and the chiral groups D2, C2, C1 (15 cases) [2]. The 15 chiral cases are those shown in Fig. 1, where the first entry for each point group indicates the maximum possible number of distinct edge lengths, with different line styles for different lengths. In D2 symmetry, there are three pairs of equivalent edges, and no further equalities between them are allowed. In C2 symmetry, there are two pairs of equivalent edges, and up to three of the six edges may have the same length. In C1 symmetry, there can be from six to three distinct lengths in various arrangements.
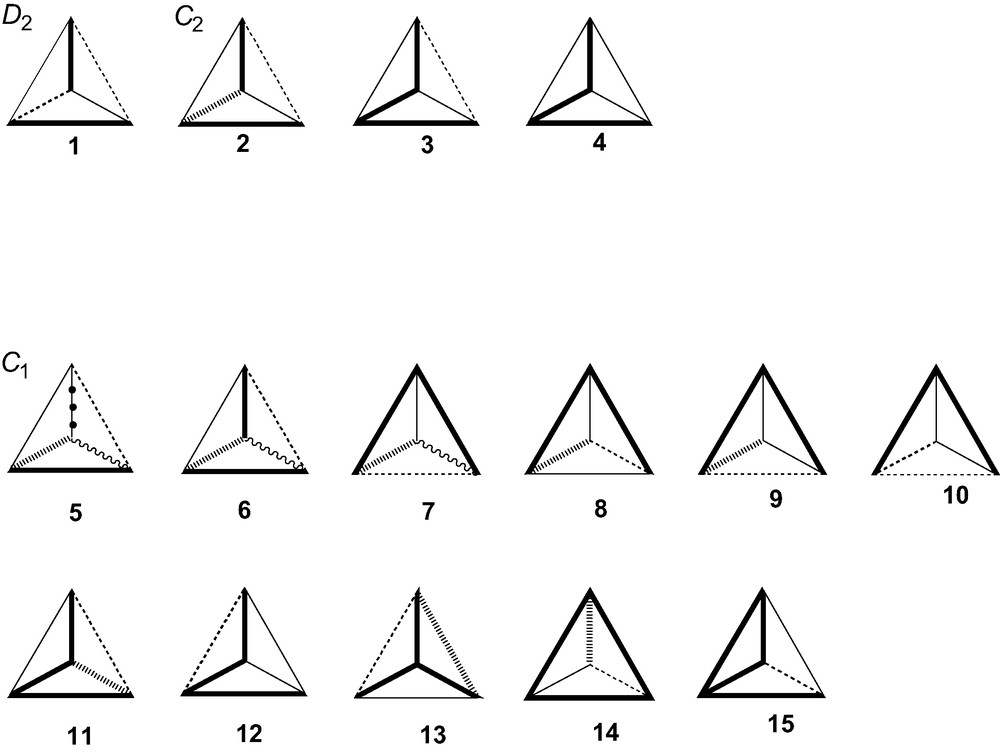
The 15 chiral tetrahedra, classified according to the pattern of edge lengths. The line styles bold, feint, dashed, hatched wavy and bobbled indicate edges of different lengths.
The original CIP ‘steering wheel’ rule assigns labels R,S to a tetrahedrally coordinated atom as follows: assign priorities a > b > c > d to the four neighbouring groups; imagine a steering wheel with the steering column going from the central atom down the bond to the group of lowest priority d; if the priorities a, b, c run clockwise on the wheel, when inspected from above, the absolute configuration is R, if they run anticlockwise it is S (Fig. 2). In the adaptation for geometric tetrahedra, we attach R,S labels to a vertex of a tetrahedron based on the lengths of the edges that meet at that vertex, assigning priorities a > b > c to the long, medium and short edges, respectively, and taking the steering column to run from the vertex down into the centroid of the tetrahedron. Of course, only vertices that are the meeting points of edges of three different lengths can be labelled in this way. The four vertices of a chiral tetrahedron fall into 1, 2 and 4 orbits of sizes 4, 2 and 1 in the groups D2, C2, C1, respectively, the number of orbits giving the maximum number of candidates that need to be considered for labelling in each group. Thus, at most 1, 2 and 4 inequivalent vertices qualify for labelling in D2, C2, C1 symmetries. Degeneracy amongst the edge lengths may reduce the number of vertices that can be labelled at first order (see Fig. 1), but, in every case bar one (4, C2), there is at least one vertex that can be labelled. Leaving this exception aside for the moment, Rule I for assigning an R,S label to the tetrahedron is as follows (Fig. 3a):
- ● (I.1) label all vertices that can be labelled by the steering-wheel rule;
- ● (I.2) identify the ‘senior’ vertex as the labelled vertex that has the longest Long edge, and if more than one have the same longest edge, select from these the one with the longest Medium edge, and, if necessary, decide between these by requiring the longest Short edge;
- ● (I.3) the R,S label for the tetrahedron as a whole is that of the senior vertex.
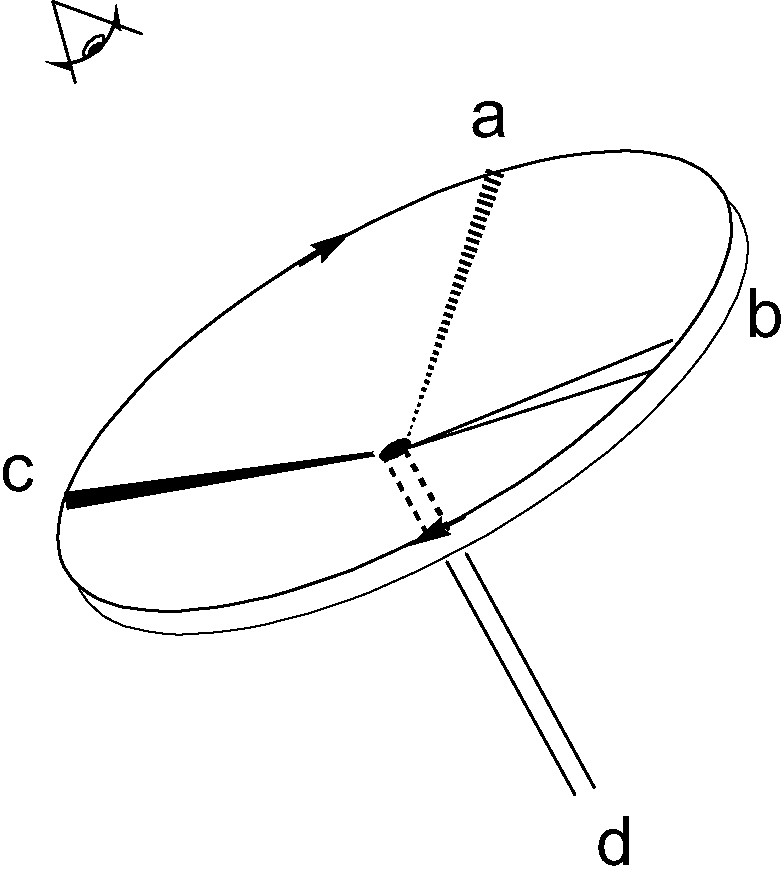
Steering-wheel mnemonic for the CIP R/S convention.
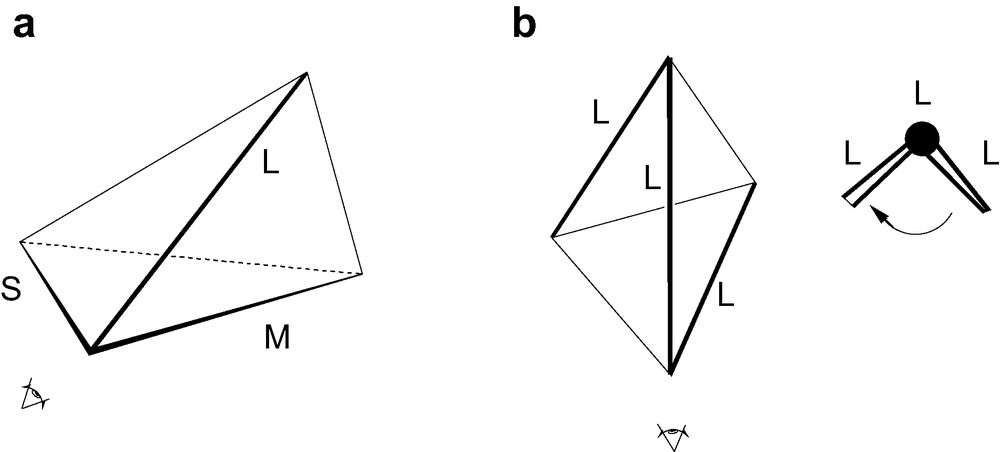
(a) Inspection of a vertex for application of Rule I. (b) Alignment of the helix of a type-4 tetrahedron for application of Rule II.
Sometimes the full order of precedence in (I.2) must be invoked. Case 8 with bold edges longer than feint longer than dashed and hatched presents an example where comparison of short edges is needed to decide the identity of the senior vertex.
The one exception to Rule I as a complete decision procedure is 4, C2 where step (I.1) yields no candidate vertices, and yet the tetrahedron is clearly chiral. In this case, the tetrahedron has two paths comprised of three equal edges, forming two oppositely directed helices in 3D space. We can use the helix of longer edges to assign an R,S label to the tetrahedron by Rule II as follows (Fig. 3b):
- ● (II.1) view the tetrahedron down the direction of the central edge of the helix of longer edges. One of the two remaining edges of the helix will be at the front, and the other at the back;
- ● (II.2) bring the front edge into coincidence with the projection of the back edge by a minimum rotation of the front edge around the viewing direction: if a clockwise rotation were required, the helix would have label P; otherwise the label is M;
- ● (II.3) by convention, this label is applied to given an R/S label to the tetrahedron as a whole, by converting P to R and M to S;
The two rules can be cast in terms of a purely mathematical calculation without direct reference to the CIP rules. It is equivalent to Rule I to make use of a triple product L ● M × S where L, M and S are the vectors from the vertex of interest along the long, medium and short edges, respectively. For each vertex, this pseudoscalar product is six times the signed volume of the tetrahedron: if the product is positive for the senior vertex the tetrahedron is labelled R, if negative S. Likewise, to replace Rule II, the triple product can be evaluated for the three vectors in the path AB, BC, CD of long edges going from vertex A through vertices B and C to vertex D, again leading to a label R for a positive sign, S for negative. [AB ● BC × CD is equal to the product, DC ● CB × BA, so the sign is unique]. This calculation automates and simplifies the determination of clockwise and anticlockwise senses at vertices, which are not always easy to see from drawings.
By either approach, all 15 types of chiral tetrahedra are therefore classified into R and S ‘right’ and ‘left’ classes, in a solution to the strong form of Ruch's classification problem. Of course, we have not avoided the problem of chiral connectedness by this classification. An R tetrahedron in the present classification can be transformed continuously to its S enantiomer without necessarily passing through an achiral intermediary (Fig. 4). Nor have we obtained an index that partitions the shape space into homochiral sub-spaces separated by achiral boundary surfaces: in the five-dimensional shape-space of chiral tetrahedra, a given R tetrahedron may be surrounded by S tetrahedra. A tetrahedron could also jump epimer class under a small change in the detailed ordering of bond lengths. However, any given chiral tetrahedron receives a label, and it is therefore possible to communicate a precise prescription for its reconstruction in the same absolute configuration by giving only a set of lengths and that label. We have therefore applied to geometrical objects the philosophy used for molecules in organic chemistry, where it is considered to be more important to define absolute configuration than to worry about continuity between closely similar species. Although couched in terms of lengths, Rules I and II are essentially combinatoric, and in their application we must be prepared to tolerate jumps in labelling where some small physical change produces a change in combinatorial type, just as the CIP rules can allow the labels to jump as a consequence of small chemical changes to ligands. Finally, we note that although the case of the tetrahedron has special claims to be considered fundamental (Td is isomorphic to the group of permutations of four elements), the principle of assignment of assignment of vertex-handedness could be extended to other geometrical bodies.
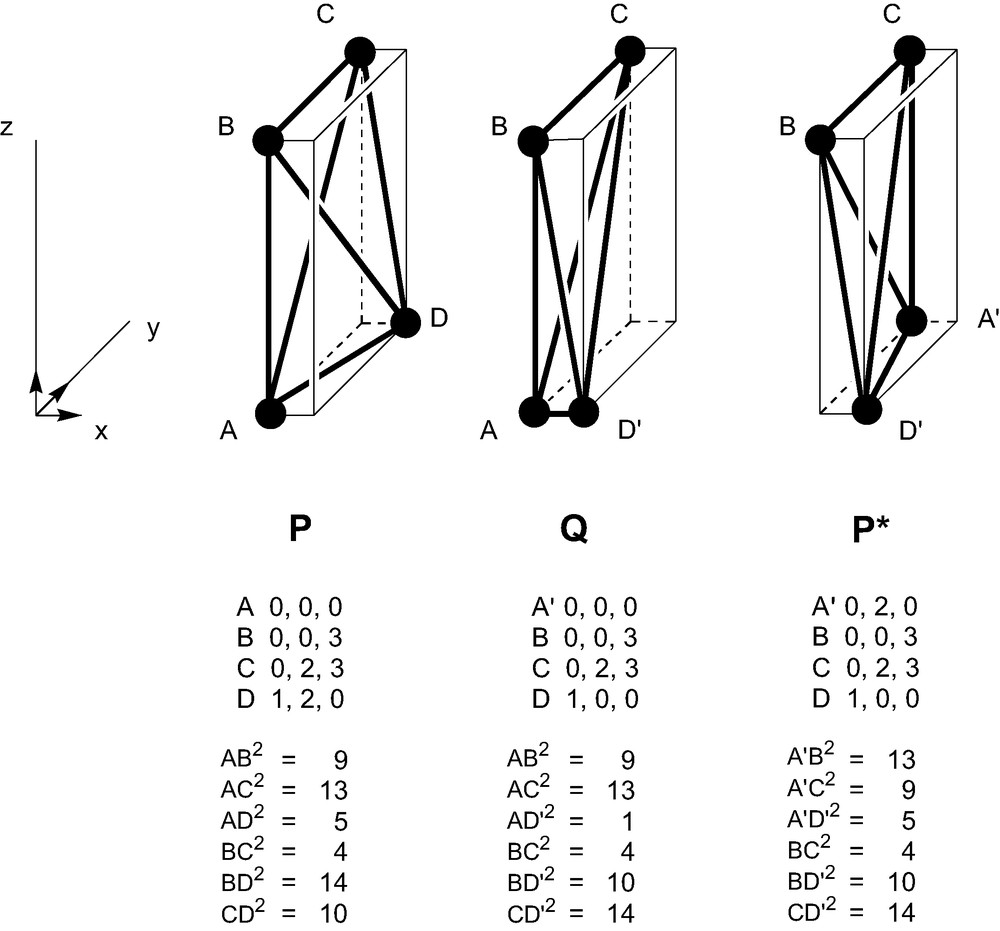
Chiral connectivity of geometric tetrahedra. P and P* are mirror images, linked by an entirely chiral pathway through Q. In the R,S classification, all vertices of P are R and all vertices of P* are S; in Q, A and B are R, C and D′ are S. The senior vertex is D (D′) in P (P*) and C in Q. All three tetrahedra are of unit volume and the triple product is therefore ± 6.
Acknowledgements
P.W.F. thanks the École normale supérieure (Paris, France) and Royal Society/Wolfson Research Merit Award Scheme for support. An anonymous referee is thanked for thought-provoking comments.


