1 Introduction
The discovery, by Albert Fert and Peter Grünberg, of the effect of giant magnetoresistance (now used commercially in the hard disk drive industry) is widely recognized as the starting point of the field of spintronics. It represents the first example of electric currents controlled efficiently by spin structures. The complementary process of so-called spin transfer torques, where magnetic structures and textures are manipulated by electric currents, appears to be even more promising [1]. Nanowires are candidates for enabling the exchange of quantum information between light and matter. The rapid control of a single electron spin by solely electrical means brings this possibility closer [2]. Over the past 10 years, the search for compounds combining properties of semiconductors and Ferro magnets has evolved into an important field of material science [3,4]. Also, oxide films and interfaces have become a key ingredient for new concepts of electronic devices [5]. Often completely different from those of the corresponding bulk materials, they bring about novel functionalities to be exploited in spintronics and electronics architectures. In order to obtain finite-temperature properties, Sato et al. [4] used statistical methods in order to solve a classical Heisenberg Hamiltonian that describes the magnetic ordering of the system. The simplest solution to this Hamiltonian is to treat the spins as classical quantities. This is expected to be a reasonable approximation, able to give a typically large moment for each substituted magnetic moment. Moreover, reliable estimates of the Curie temperature in Dilute Magnetic Semiconductors (DMS) require going beyond the simple mean field approximation. Indeed, the often used mean field combined with virtual crystal approximation led to an overestimated Curie temperature or overestimated stability of ferromagnetic states. Sato et al. [4] pointed out that one of the reasons of the discrepancy between theoretical and experimental approaches is a bad treatment of thermal fluctuations within a mean field approximation. Moreover, the ferromagnetic state strongly competes with a number of other spin wave states which have almost the same energy. This indicates that a realistic picture is more complex than the one following total energy calculations and assuming a collinear magnetic structure. Thus, one of the purposes of the present contribution is to mainly focus on the description of magnetic nanostructures within a semi-empirical Periodic Anderson Model (PAM) approach for non-collinear magnetism developed by Uzdin and Yartseva [6]. In this short review, we discuss (Section 1) the general problem of calculating non-collinear magnetism in nanostructures. In Sections 2 and 3, we apply the PAM to two specific situations: respectively to vacancy effect on Spin Density Waves (SDW) and to Cr Mono-Layer (ML) magnetic behaviour on a Fe (110) film. Then (Section 4), we point out M.M. Rohmer's work related to similar magnetic problems in connection to the University of Mascara. Finally (Section 5), we outline a few recent developments in the field of magnetic nanostructures. Section 6 is devoted to our conclusion.
2 Non-collinear approach for magnetism in nanostructures: general considerations
Oda et al. [7] proposed a description of small free-standing Fe clusters in a fully unconstrained approach to non-collinear magnetism. They develop a plane-wave pseudo potential based on a generalized local spin density theory in which the direction of the magnetization is a continuous variable of position. They allow atomic and magnetic structures to relax simultaneously and self-consistently. This calculation is clearly the first application of a fully unconstrained scheme for non-collinear magnetism. Later, Uzdin et al. [8] presented the very first non-collinear magnetic structure calculations of supported Cr and Fe trimers. Within a vector PAM and according to the ratio between hopping parameters, the trimer ground state was found to be collinear or non-collinear. Actually, the dependence of the angles between magnetic moments, with respect to hopping integrals, was shown to be different, when going from Cr to Fe, although these angles are equal to 120° in the ground state of an equilateral triangle situation.
Crystallography and Magnetization of bulk Fe strongly depend on temperature. Fe is bcc with a magnetic moment of 2 Bohr Magnetons at T = 0 K, and fcc without polarization above the Curie temperature. Non-collinear magnetic structures were obtained by Oda et al. [7] for Fe clusters with a small atom number (3 or 5). Usually, there is a strong connection between magnetism and dimensionality for the considered systems. Very interesting from this point of view is the evolution of Cr magnetic properties with the size of the sample. Bulk Cr has complex magnetic structure comprising an uncommensurate antiferromagnetic SDW [9]. Inspection of the Fermi surface of Cr led to the conclusion that the nesting condition is fulfilled and that, consequently, the wave-modulated antiferromagnetic state should have a lower energy than the paramagnetic state. However the available versions of the Density Functional Theory (DFT) do not predict the experimentally observed SDW to be the ground state of bulk Cr. Quite recently, a so-called “nodon model” was proposed as an alternative way to reconcile theory and experiment [10]. In that model, the Cr ground state is truly antiferromagnetic, whereas SDW appears due to low-lying thermal excitations. Uzdin and Demangeat [10] used a PAM model, while Vanhoof et al. [11] were able to reproduce these nodons by ab initio calculations. Furthermore, SDW in epitaxial films can be manipulated by the choice of magnetic cover, interfacial roughness or Cr film thickness. Indeed for films with thickness less than the SDW period, magnetic structure is determined by the interface region. In Fe/Cr MLs, thin Cr spacer interface defects, such as steps or pinholes, are responsible for the non-collinear coupling of Fe magnetic moments through Cr layers [12]. For thicker Cr spacer however, SDW takes place. Its total energy is of course in competition with basic layered antiferromagnetic coupling. More precisely, there is a possibility of tailoring SDW in Fe/Cr (001) MLs through a selective inclusion of Sn, V and Mn MLs [13]. This study has been recently complemented by investigating X/Cr (001) MLs (X = Sn, V and Mn). Then, without having the polarization effect of Fe any more, it is possible to get insight on the proximity effects of these X elements on the SDW of the Cr slabs [14].
3 Case of vacancy effect on SDW in Fe/Cr
Also recently, within PAM, Parlebas et al. [15] discussed the effect of vacancies on the SDW onset in Fe/Cr superlattices. For a Cr spacer made of 36 or 37 layers, in general, two solutions were obtained. One solution is a layered antiferromagnetic structure where magnetic moments are ferromagnetic in each layer with an antiferromagnetic coupling between two nearest neighbouring layers. The second solution (with a total energy almost equal to the preceding case: quasi degeneracy) presents in some planes (one or two) a cancellation of the magnetic moments. Those planes are called “nodes”. Details can be found in the paper by Parlebas et al. [15]. In Fig. 1, we just report results for a superlattice with an odd number of Cr MLs, containing randomly located 4% of vacancies in the central Cr ML. Fig. 1 displays an increase of the Cr magnetic moments near the vacancies. This is pretty reasonable because it is well known that the magnetic moments of a given Cr atom drastically depend on its surrounding. For an even number of Cr MLs, for the same vacancy concentration of 4%, a shift to the right is depicted for the position of the SDW node (Fig. 2).

Distribution of magnetic moments in a Fe/Cr (001) superlattice for an odd number of Cr MLs with 4% of vacancies in the middle of the Cr spacer.
Taken from [15].
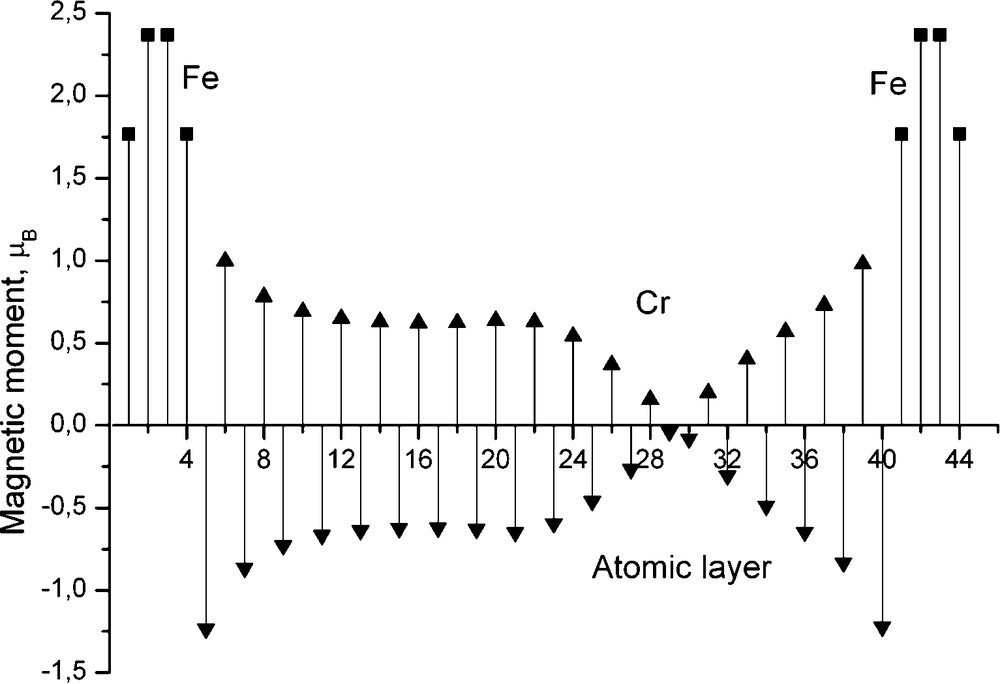
Distribution of magnetic moments in a Fe/Cr (001) superlattice for an even number of Cr MLs with 4% of vacancies in the two middle Cr MLs.
Taken from [15].
The role of vacancies is twofold: (1) they tend to increase Cr magnetic moments at neighbouring sites; and (2) in the case of an even number of Cr layers, they shift the node from the central layer, to the right (Fig. 2), or symmetrically, to the left (not shown here) of this central layer. Indeed, due to the presence of vacancies in the central layer, the node cannot survive because of a strong increase of magnetic moments on the surrounding Cr atoms. Therefore, two degenerate solutions with respectively one node to the right (respectively to the left) are obtained. Very recently, Soulairol et al. [16] also presented interesting results concerning the effect of vacancies on SDW in Fe/Cr superlattices.
4 Case of a Cr monolayer on a Fe (110) film
Most of the calculations concerning Fe/Cr interfaces are restricted to (001) interface. In this case, a simple collinear model is sufficient. This is related to the fact that both Fe and Cr are bcc materials so that, in (001) interfaces, there is only one non-equivalent atom per plane. Fe being clearly of ferromagnetic type, all Fe atoms are aligned in a same given direction. Cr, on the other hand, presents antiferromagnetic coupling for small Cr spacer (SDW for bigger spacer). At Fe/Cr (001) interfaces, the first Cr layer adjacent to Fe is antiferromagnetically coupled to it [17]. However, in the case of (011) interfaces, it is difficult to restrict to collinear magnetism as has been performed recently by Bose et al. [18]. The reason is as follows. Fe being ferromagnetic, in all surfaces of low or high Miller indices, all Fe atoms point in the same direction, although for high Miller indices, some Fe atoms could be canted due to non-symmetrical environments. In the case of a (011) Cr ML, we are concerned with an in-plane antiferromagnetic configuration, i.e. each Cr atom is surrounded by four Cr atoms in the opposite direction. From symmetrical considerations, it can be stated that each Cr atom does present a same magnetic moment, with nearest neighbouring atoms showing opposite magnetic directions. Within PAM, we first performed spin-polarized collinear calculations for one Cr ML on Fe (011), in order to check if our semi-empirical PAM approach was able to reproduce Bose et al.’s DFT result. Two values (Cr1 and Cr2) for the Cr moments were obtained: (i) Cr1 moment which points in the same direction as the Fe substrate magnetic direction and presents a smaller modulus than Cr2; (ii) Cr2 moment which is in opposite direction with respect to the Fe substrate magnetic direction. Again, this is easy to understand. It should first be remembered that, at Fe/Cr interfaces, the Fe and Cr atoms prefer to be antiferromagnetically coupled. This is indeed the ground state. However, for a Cr monolayer adsorbed on Fe (011), the coupling is much trickier. Uzdin et al. [8] already pointed out that, for the Cr trimer adsorbed on a noble metal, an antiferromagnetic coupling between Cr atoms cannot survive. Coupling is frustrated and the considered system does minimize its total energy only by introducing a non-collinear polarization. For a Cr monolayer on Fe (011), in order to minimize its total energy, the Cr1 and Cr2 magnetic moments will present a canting angle with the Fe-bulk magnetic direction. Due to this canting angle, a torque is exercised on the Fe (011) surface, so that the Fe1 and Fe2 surface atoms too will be canted (Table 1). Contrary to the collinear calculation of Bose et al. [18], where Cr magnetic moments are different, here, the magnetic moments of Cr1 and Cr2 atoms are almost equivalent, but there is now a canting angle between Cr1 and Cr2. This canting angle between Cr atoms induces dissymmetry in Fe subsurface layers. That leads straightforwardly to canting angle between Fe1 and Fe2 magnetic moments in the Fe layer in contact to Cr [19]. Results are reported in Fig. 3.
Self-consistent results corresponding to a stable non-collinear solution and concerning a Cr Mono Layer (ML) surface and three successive Fe MLs.
| Layer | Moment value on Cr1 atoms | Moment value on Fe1 atoms | Moment value on Cr2 atoms | Moment value on Fe2 atoms | Angle between Cr1 and Cr2 moments | Angle between Fe1 and Fe2 moments |
| Surface Cr ML | 1.86 | 1.86 | 157 | |||
| Interface Fe ML | 2.08 | 2.08 | 25 | |||
| Second Fe ML | 2.25 | 2.25 | 4 | |||
| Third Fe ML | 2.23 | 2.23 | 0 |
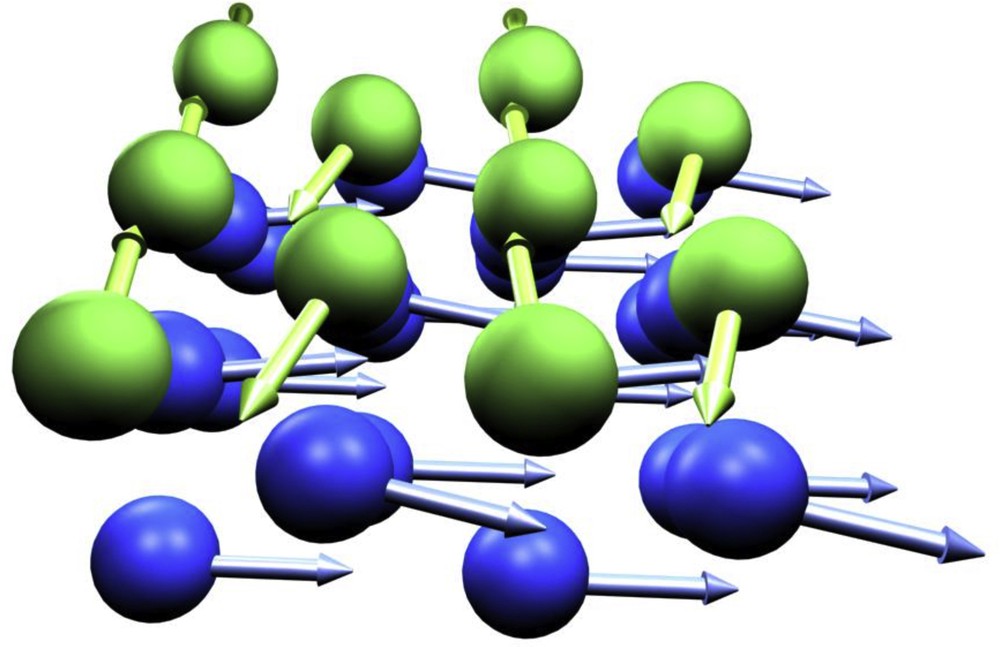
Distribution of Cr (green balls) and Fe (blue balls) moments for the top Cr ML and three successive Fe MLs. Both moments on Cr1 and Cr2 atoms present a mutual angle of 157°. The corresponding Fe1 and Fe2 atoms are also canted to each other by an angle of 25°.
Taken from [19].
One may wonder about the effect of spin-orbit on the onset of non-collinearity in the present approach. Like in the paper by Soulairol et al. [20], we ignore it because it is far beyond the purpose of the present communication. Let us, however, point out that our calculation is a very first attempt concerning the onset of non-collinearity for a Cr monolayer on a Fe (011) surface.
5 Marie-Madeleine Rohmer's contribution to the University of Mascara
With Marie-Madeleine Rohmer and Marc Bénard of the University of Strasbourg (France) and Claude Daul of the University of Fribourg (Switzerland), a conference was organized at the University of Mascara (Algeria) [21]. This meeting was entitled: “Journées de Simulation Numérique de Mascara” (JSNM’06). Magnetism was one of the main topics and Marie-Madeleine presented a communication on “Linear trimetallic complexes with 24 electrons” [22]. The sequence of metal orbitals arising from various linear triatomic chains of metal atoms was obtained from DFT and the population of these orbitals was sketched according to the nature of the transition metal M under investigation, for M = Cr, Co, Ni and Cu. For example, in the case of Ni, the high spin state gave rise to an antiferromagnetic interaction between the considered Ni atoms. For more details, see ref. [23]. Furthermore, at this meeting and after a discussion with local scientific professors, a Master degree in Physical Chemistry was supposed to be built up by Mohammed Sahnoun with the help of Marie-Madeleine Rohmer and Claude Daul. Very unfortunately, this Master degree was stopped by Marie-Madeleine's death.
6 Recent news about magnetic nanostructures: state of the art
Progress in nanoscale physics depends, on one hand, on the development of a more sophisticated version of the exchange-correlation term in DFT, and on the other hand, on versatile devices to measure tiny magnetization. The Superconducting Quantum Interference Device (SQUID) magnetometer is one of the most sensitive experimental techniques to characterize samples with high sensitivity. However, this technique is not free from possible artefacts and pitfalls present in commercial SQUIDs [24].
Quite recently, Demangeat and Parlebas [25] reported on electronic, magnetic and spectroscopic properties of vanadium, chromium and manganese nanostructures. In their review paper, and especially in the case of trimers, they pointed out that collinear magnetization was definitively a metastable state. The ground state is obtained when the direction of magnetization is non-collinear. This situation appears because of frustration on a triangular lattice. Although, for Ni and Co trimers, a ferromagnetic configuration could survive, in the case of basic antiferromagnetic bulk systems, like Cr or Mn, antiferromagnetism in a trimer cannot survive. Therefore, in order to diminish the total energy of the considered system, a non-collinear approach is worthy and necessary. Carbone et al. [26] reported on recent experimental approaches to build zero-, one-, and two dimensional magnetic particle arrays. The investigation of self-assembled sub-nanometer magnetic particles leads to significant progress in the design of fundamental and functional aspects. Tung et al. [27] determined the onset of spin-spiral wave in V, Cr and Mn atomic chains on Cu (001) surface. They display the formation of a non-collinear spin-spiral structure in Mn linear chains and also in V linear chains upon atop sites on Cu (001) surface, due to frustrated magnetic interactions in these systems. Schubert et al. [28] focused on non-collinear magnetism in free-standing chains of Cr-Mn-Fe alloys. For a pure Cr chain, an antiferromagnetic configuration was shown to be the ground state. Increasing the number of “d-electrons” drastically modifies the magnetic map, going from a purely antiferromagnetic configuration for a pure Cr chain to a pure ferromagnetic configuration for a Fe chain, through a regime of non-collinear magnetization for Mn-rich chains. Calculations were also performed for Mn linear chains deposited on metallic surfaces. Even weak chain-surface hybridization could be sufficient to dramatically change the magnetic map of the chain. Deposited on Pd (110), Mn chains are antiferromagnetic while, for Cu (110) and Ag (110) substrates, a weak non-collinear order survives. Moreover, it is worth mentioning Negulyaev et al.’s very recent work [29], where electric field has been displayed as a switching tool for Mn dimers deposited on metal.
Theoretically, a Mn dimer on Ni can take a non-collinear, a ferrimagnetic or a ferromagnetic configuration, the non-collinear configuration being the ground state. The ferrimagnetic state is shown to be a few meV above whereas the ferromagnetic configuration is the least stable. However, as pointed out by Munoz et al. [30] the Mn dimer on Au (111) is unstable as compared to isolated Mn atoms adsorbed on this gold-surface. This conclusion is perhaps not worthy because Munoz et al. have restricted their approach to collinear configuration although Negulaev et al. pointed out that the non-collinear Mn dimer on Ni is really the ground state.
7 Conclusion
The present short review paper focuses on Cr and Mn in chains, free or adsorbed monolayer of Cr in contact with Fe. We are involved in the description of non-ferromagnetic nanomaterials. Particular focus is on non-collinear magnetism. This non-collinear magnetism arises intrinsically in free-standing monoatomic chains. Non-collinear magnetism arises also in some triangular clusters, free-standing or deposited. This is due to the fact that antiferromagnetism cannot survive in this configuration. More and more calculations do not rely anymore on classical collinear approaches, but are trying to take full account of the non-symmetrical environment of a given atom. Due to this absence of symmetry, one cannot anymore determine the magnetic map of a given nanostructure by constraining magnetization. This latter approach only leads to metastable configurations. However, the difficulties of those non-collinear treatment approaches are tremendous and, up to now, only very few calculations have been performed within an unconstrained version of the spin-polarized approach.
We are presently investigating a possible minimization of the interlayer exchange coupling [31] by considering spin-spiral like configurations for the Cr spacer in Fe/Cr superlattices. Indeed, we believe that spin-spiral could remove the frustration present in the metastable solution.
Acknowledgments
The authors of the present communication would like to thank Marc Bénard for giving them the opportunity to contribute to the present “Festschrift” in memory of Marie-Madeleine Rohmer.


