1 Introduction
Process design benefits from understanding the various steps involved in the chemical conversion of a given feedstock into the desired products so that each step can be:
- • promoted by a suitable catalyst and/or;
- • carried out under appropriate operating conditions as to push away the limiting conversion associated with the thermodynamics of the system.
Thermodynamics is thus routinely used as a tool to determine favorable reaction conditions so that high yields into the products of interest can be achieved. It is yet far less common to relate the proportions of reactants and products present in a reactor to thermodynamic equilibrium constants pertaining to the system to unravel the details of the reaction mechanism. Three examples are described thereafter emphasizing the power of this approach, which is then applied to the condensation of ethanol to butanol.
2 Unraveling reaction mechanisms through thermodynamics
The hydroisomerisation of n-butane to isobutane over reduced molybdena provided an example in which thermodynamics enabled one to positively determine both the reaction mechanism and the rate-determining step (RDS) [1]. The concentration of butenes, potential reaction intermediates in a bifunctional mechanism, could be accurately measured, despite being present at levels more than three orders of magnitude lower than that of butane. The proportions of butenes corresponded to those at the hydrogenation/dehydrogenation thermodynamic equilibrium with the corresponding saturated compound. On the contrary, the skeletal isomerisation between butenes and isobutene had not reached equilibrium and was proposed as being the RDS. The cases of n-pentane and n-hexane were also addressed and it was shown that the same bifunctional mechanism operated, with the main difference that the dehydrogenation/hydrogenation steps were rate-determining for these longer alkanes [2].
The steam reforming of methanol (Eq. (1)) over a Cu–Zn–Zr–Al–O catalyst provided an example of a system in which a combination of kinetics and thermodynamics enabled discarding a reaction mechanism [3]. A critical question was whether or not CO was a primary reaction product, which would be formed prior to CO2 (Eq. (2)) and would then be converted into CO2 via the water-gas shift reaction (forward Eq. (3)).
| CH3OH + H2O → CO2 + 3H2 | (1) |
| CH3OH → CO + 2H2 | (2) |
| (3) |
CO only appeared after the other reaction products H2 and CO2 as the contact time was increased. Moreover, the proportions of H2 and CO2 first matched the thermodynamic composition associated with a CO-free system, being in excess with respect to the proportion associated with a system containing CO. Therefore, these data unambiguously and surprisingly proved that CO was not the precursor of CO2, but that CO was rather formed from CO2 as a result of a reverse water-gas shift reaction (backward (3)).
Finally, the selective catalytic reduction of NO with propene over alumina provided another example in which the long-thought-crucial reaction step described by Eq. 4 was actually found to be irrelevant [4]:
| NO + 0.5 O2 → NO2 | (4) |
This was demonstrated by noting that the NO2/NO ratio obtained during the reaction was far greater than that associated with the thermodynamics of the reaction described by Eq. 4. Several other catalysts based on Ag- or Co-alumina led to similar observations [5,6]. These observations were rationalized by realizing that NO2 was formed through a more complex pathway, probably involving the formation and combustion of organo-nitrogen species. It was concluded that one of the major roles of Ag was to oxidize NO to adsorbed NOx species (but not to gas-phase NO2), which then reacted with hydrocarbon-derived species to form the organo-nitrogen species eventually leading to N2 [5]. Having a dedicated catalyst and/or additional reactor to oxidize NO to NO2(g) was therefore shown not to be a requirement to improve the process.
The examples above underline the potential of thermodynamics in understanding the mechanistic details of a reaction and suggest better catalyst and/or process design. In the present contribution, a similar approach was used to unravel the mechanism of the (metal-free) high-temperature condensation of ethanol to butanol over one of the best catalysts reported for this reaction, a hydroxyapatite (noted “HAP”) [7,8]. In particular, the role of acetaldehyde was investigated, since this compound was often proposed as being a crucial reaction intermediate, through its self-aldolization [7,9–11].
3 Experimental
The hydroxyapatite (noted “HAP”) was supplied by Acros Organics (Ca3(PO4)2Ca(OH)2, batch A0312711) and exhibited a surface area of 82 m2·g−1. The limits of concentration of the main impurities given by the supplier were as follows: sulfate ≤ 5000 ppm, Cl ≤ 1500 ppm, Fe ≤ 400 ppm, F ≤ 50 ppm, Cu ≤ 20 ppm, Zn ≤ 20 ppm, As ≤ 2 ppm, Hg ≤ 1 ppm.
Powder X-ray diffraction patterns were recorded using a PANalytical X’Pert Pro diffractometer equipped with a copper radiation source (λ = 1.5406 Å). The diffraction pattern of HAP (Fig. 1) perfectly matched that associated with the hydroxylapatite reference pattern 00-024-0033 and that reported by Costentin and co-workers (see Ca-HAP-1 in Fig. 1 of this reference) [8].
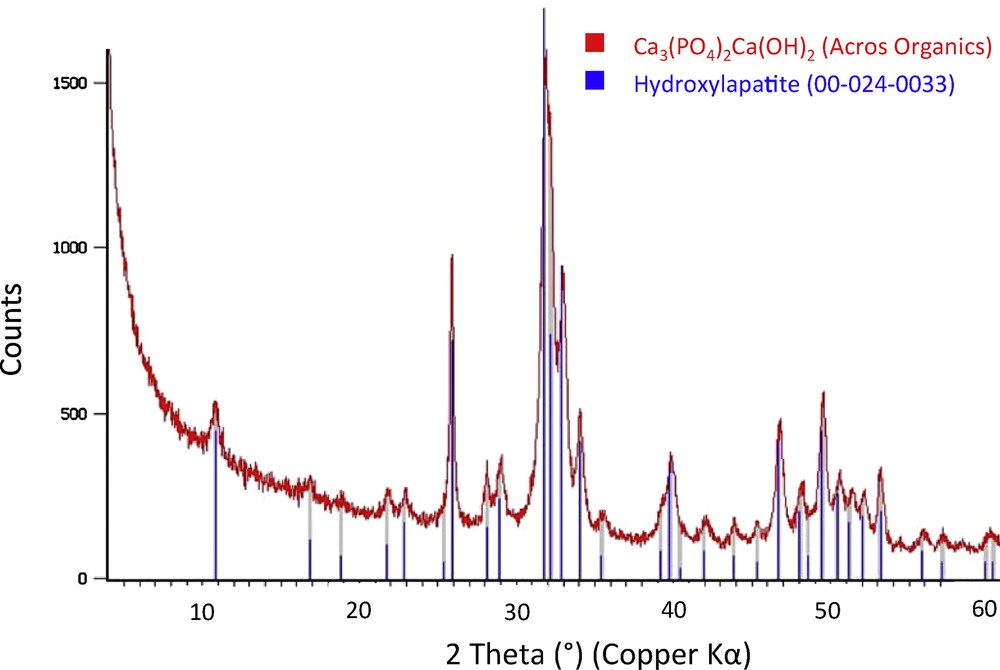
Red line: X-ray diffraction pattern of the hydroxyapatite supplied by Acros Organics. Blue bars: Reference pattern 00-024-0033: hydroxylapatite. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper).
Ethanol (from Prolabo 99.5%, the main impurity being water) was fed using a saturator kept at 45 °C into a heat-traced stainless steel flow setup. The sample was activated under Ar at 480 °C for one hour before introducing the ethanol/Ar feed at the reaction temperature. The catalyst was placed in a quartz tube reactor and held between quartz wool plugs. The reactor was located in a tubular furnace. Ar was used as the carrier gas. A combination of mass spectrometry, gas chromatography, and gas-phase FT-IR spectroscopy was used to determine the concentration of ethanol and the main products of interest (including H2O and H2).
The gas chromatograph (Bruker 450-GC) was fitted with Zebron ZB-Bioethanol column (30 m, 0.25 mm, film thickness: 1.00 μm). A flame ionization detector (FID) was used and a precise quantification of all the detectable products was realized through the use of an internal standard (i.e. toluene) added to the analyzed stream before injection in the column. The concentration of most reaction products, including H2, could also be monitored by online mass spectrometry (Pfeiffer Omnistar 320). The contribution of large molecules to the fragment m/z = 2 was taken into account to determine H2 concentration, also using calibration curves. The concentration of some reaction products, in particular acetaldehyde and water, was also monitored by online FT-IR gas analysis using a 27-cm-long single path gas cell fitted in a Nicolet 560 spectrometer. Calibration curves were drawn to relate IR band signal intensity to concentrations.
The thermodynamic calculations were done with the HSC Chemistry® software (version 6.2, by Outotec). For the calculation of the reaction quotient Q, the pressure P of the various products was measured at different temperatures over the HAP. The pressures were derived from the compounds concentration determined from the various analytical measures, assuming that the ambient pressure was 101.3 kPa. P° refers to the standard pressure = 100 kPa. All the compounds were taken as ideal gases (fugacity coefficient = 1), which is a reasonable assumption in view of the low pressures considered.
4 Kinetic results
The HAP activity was measured between 350 and 440 °C and the highest selectivity to butanol was obtained at around 400 °C (Fig. 2). The ethanol conversion was always lower than 30% and the selectivity to C6+ products was negligible. The main other product was acetaldehyde. The apparent activation energies for product formation were measured over the 360–410 °C temperature range and were 133 kJ/mol for butanol and 88 kJ/mol for acetaldehyde (Fig. 3). These values were significantly different and indicate that different rate-determining step occurred for the formation of these compounds and, possibly, that different mechanism were involved. The butanol Arrhenius plot shows a bend at the higher temperature (Fig. 3), which could possibly be related to the onset of mass transport limitations.

(Color online.) Selectivities to the main reaction products during ethanol reaction over the hydroxyapatite catalyst as a function of temperature. Feed: ethanol = 15.2% in Ar; WHSV = 14 h−1.
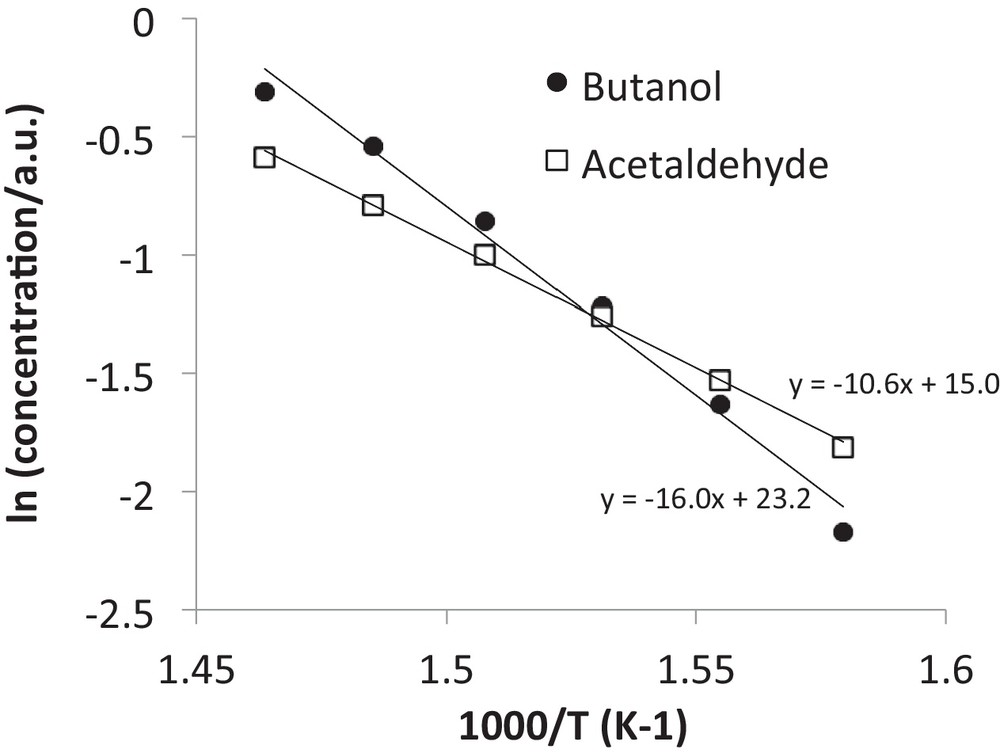
Arrhenius-like plot giving the logarithms of butanol and acetaldehyde concentrations vs. the reciprocal temperature. Feed: ethanol = 15.2% in Ar; WHSV = 14 h−1.
The effect of the contact time was investigated at 400 °C and have been reported elsewhere [12]. Both butanol and acetaldehyde concentration increased in a linear fashion with a non-zero slope, indicating that both products could be considered as primary reaction products. This observation supports the hypothesis that both products could possibly be formed independently.
5 Thermodynamic equilibrium of relevant systems
The formation of butanol and water from ethanol (Eq. 5) is a reaction that is strongly favored on a thermodynamic point of view between 100 and 500 °C (Fig. 4).
| (5) |

Composition at the thermodynamic equilibrium of a system containing ethanol, butanol, and water as a function of temperature. The total pressure is 1 bar. The initial state of the system corresponds to an equivalent 11 mol.% of ethanol (balanced by Ar).
Essentially full conversion to butanol could be expected if a suitable catalyst, which would not lead to any other side-products, were to be found.
The formation of butanol from ethanol at low temperature in the liquid phase apparently proceeds through acetaldehyde self-aldolization (Scheme 1) [13]. Bifunctional catalysts are typically used, comprising a metallic component active for the dehydrogenation of ethanol to acetaldehyde and the hydrogenation of intermediates leading to butanol (steps 1, 3 and 4). An acido-basic component is also present to carry out step 2, i.e. the self-aldolization of acetaldehyde and the dehydration of the corresponding intermediate to butenal (i.e. crotonaldehyde).

Ethanol condensation mechanism based on the self-aldolization of acetaldehyde (from reference [9]).
The thermodynamic equilibrium of a system containing most of the species present in Scheme 1 was calculated over the 100–500 °C temperature range (Fig. 5). The thermodynamic data of 3-hydroxybutyraldehyde were not available and this molecule was therefore omitted from the system. Its equilibrium concentration is yet expected to be very low and should not change the values associated with other species. The striking feature of the data reported in Fig. 5 is that the equilibrium concentration of butanol drops dramatically with increasing temperature and becomes negligible above 300 °C. Butanol is replaced at high temperature by butanal (and H2) and then acetaldehyde and butenal (i.e. crotonaldehyde). The equilibrium distribution of products above 300 °C (Fig. 5) is clearly at odds with the catalytic data collected in the 350–440 °C temperature range reported in Fig. 2, in which butanol was clearly the main reaction product obtained over the HAP material.
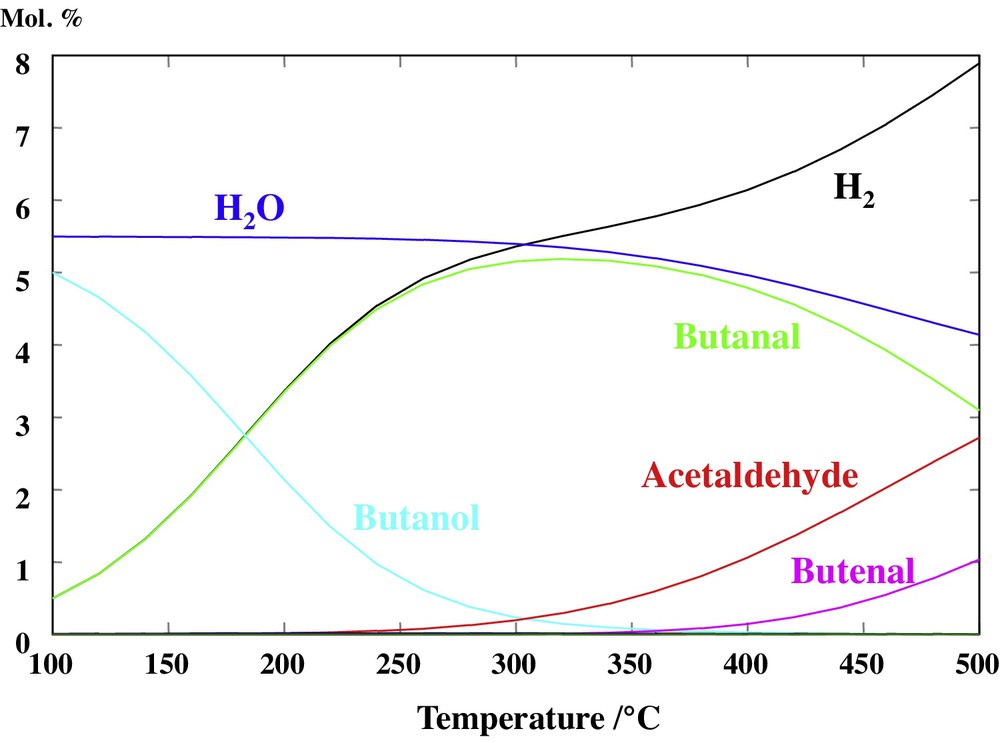
(Color online.) Composition at the thermodynamic equilibrium of a system containing ethanol, butanol, acetaldehyde, butenal (= crotonaldehyde), butanal, 2-buten-1-ol, H2 and water as a function of temperature. The total pressure is 1 bar and the initial state of the system corresponds to an equivalent 11 mol.% of ethanol (balanced by Ar). The molar fractions of ethanol and 2-buten-1-ol were always lower than ca. 0.01 mol and cannot be seen on the graph.
Other thermodynamic systems were also considered, for instance one in which the intermediates in the hydrogenation of butenal to butanol were omitted, that are butanal and 2-buten-1-ol (Fig. 6). This system led to a markedly higher proportion of butanol above 300 °C, but the corresponding concentration was still lower than that of acetaldehyde above 350 °C. Similar conclusions were obtained for a system free of butenal (Fig. 7).
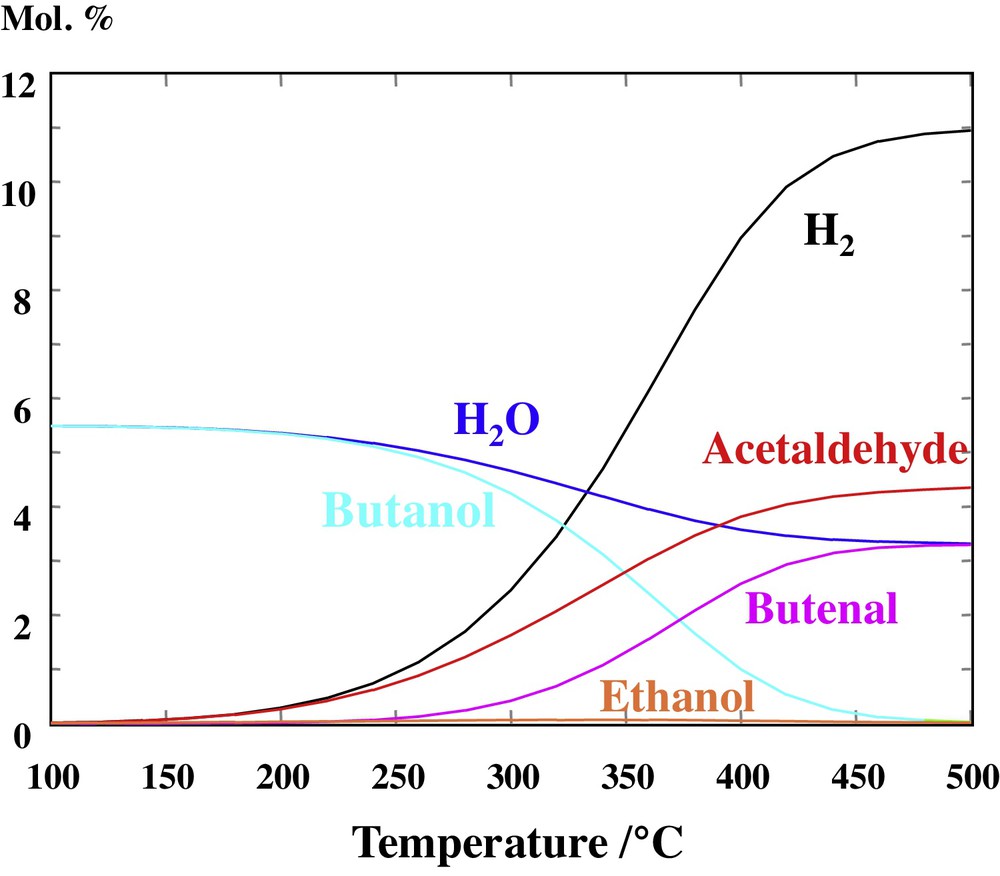
(Color online.) Composition at the thermodynamic equilibrium of a system containing ethanol, butanol, acetaldehyde, butenal (= crotonaldehyde), H2 and water as a function of temperature. The total pressure is 1 bar and the initial state of the system corresponds to an equivalent 11 mol.% of ethanol (balanced by Ar).

(Color online.) Composition at the thermodynamic equilibrium of a system containing ethanol, butanol, acetaldehyde, H2 and water as a function of temperature. The total pressure is 1 bar and the initial state of the system corresponds to an equivalent 11 mol.% of ethanol (balanced by Ar).
The combination of the thermodynamic analysis and the kinetic data suggests that the reaction scheme as proposed above (Scheme 1) is irrelevant because it would violate the rules of thermodynamics. In simple terms, if butanal and acetaldehyde were to be reaction intermediates in the formation of butanol, then the concentration of these compounds should remain higher than that of butanol when operating above ca. 350 °C, because those are more favored thermodynamically.
6 Comparison of thermodynamic equilibrium constant K and reaction quotient Q
The comparison of reaction quotients (Q), which are calculated directly using the concentrations of compounds measured at the reactor exit, and equilibrium constants (K) is required to be able to draw a definitive conclusion on the relevance of the pathway described by Scheme 1. There are indeed many other by-products (e.g., butadiene, ethylene, H2) that affect the various reaction equilibria involved and alter the concentration of the products of interest. For a given reaction, the value of Q should always remain lower than K or, at the most, equal to K as the system reaches equilibrium. The approach to equilibrium “η” is actually defined by η = Q/K.
The simplest system based on acetaldehyde self-aldolization that can be computed (i.e. having intermediates of accurately measurable concentrations and available thermochemical data) is given by the following reactions:
| (6) |
For this reaction, the reaction quotient Q is simply expressed as (7):
| (7) |
P(acetaldehyde) = 0.47 kPa
P(butanol) = 0.60 kPa
P(water) = 1.4 kPa (note: some of the water was already present in the ethanol supply)
P(H2) = 0.67 kPa, leading to Q = 8.8 × 104. It must be stressed that our study, to the best of our knowledge, is the first in which water and dihydrogen concentrations were also quantitatively measured, alongside those of the other carbon-containing products. It is indeed compulsory to quantify the concentration of these molecules to be able to calculate the reaction quotient.
The ratios between the reaction quotient Q and the equilibrium constant K were calculated at various temperatures and for different experimental conditions (Table 1). Since the reaction quotient would be higher than the equilibrium constant (in fact, Q >> K), the reaction given by Eq. (6) is irrelevant to describe the mechanism taking place over our HAP under our experimental conditions. In other words, butanol is not formed via a reaction scheme involving acetaldehyde self-aldolization (Eq. 6).
Ratio between the reaction quotient Q and the equilibrium constant K for the reaction: 2 acetaldehyde + 2 H2 = butanol + water (Eq. 6), obtained under various reaction conditions.
| Temperature /°C | Ethanol inlet Concentration /% | WHSV h−1 | Q/K |
| 350 | 15.2 | 28 | 623 |
| 360 | 15.2 | 28 | 484 |
| 370 | 15.2 | 28 | 536 |
| 380 | 15.2 | 28 | 1103 |
| 390 | 15.2 | 28 | 1780 |
| 400 | 15.2 | 28 | 2430 |
| 410 | 15.2 | 28 | 2533 |
| 420 | 15.2 | 28 | 2704 |
| 430 | 15.2 | 28 | 2832 |
| 440 | 15.2 | 28 | 2732 |
| 400 | 7.6 | 1.4 | 8443 |
| 400 | 7.6 | 2.1 | 7449 |
| 400 | 7.6 | 4.2 | 6787 |
| 400 | 7.6 | 7.0 | 4559 |
| 400 | 7.6 | 9.8 | 5209 |
| 400 | 7.6 | 14 | 4427 |
The work reported here unambiguously proves that over our hydroxyapatite catalyst, at temperatures between 350 and 440 °C, the condensation of ethanol to butanol does not proceed via acetaldehyde self-aldolization. This observation is in contrast with low-temperature catalytic systems, which typically include a metallic phase, and which were shown to operate through aldol self-condensation [14]. The metallic phase is crucial for the low-temperature system to enable alcohol dehydrogenation and the hydrogenation of reaction intermediates (Scheme 2).
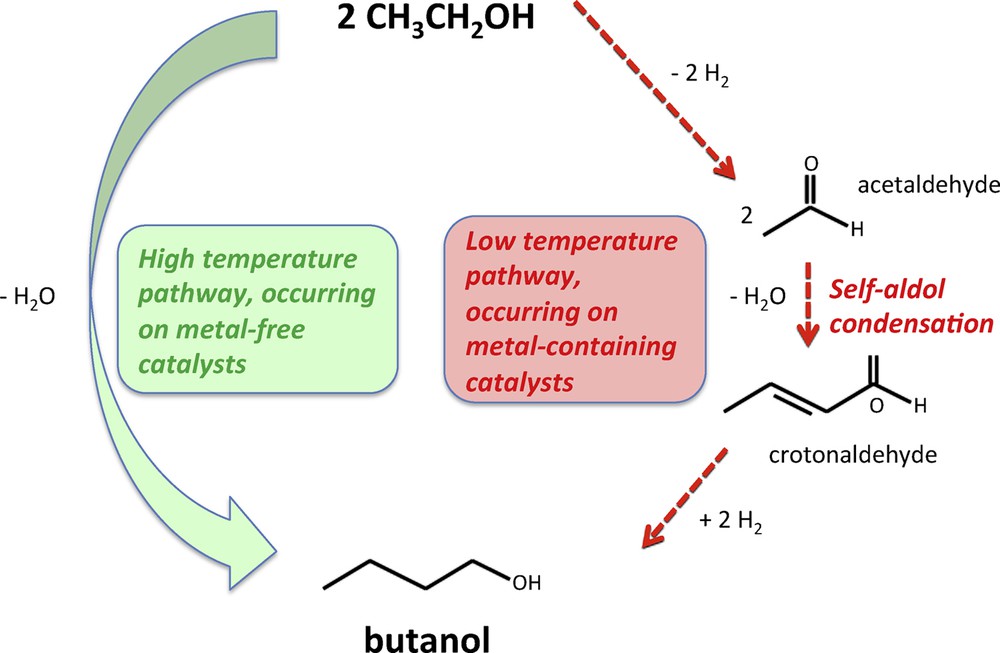
(Color online). The ethanol condensation mechanism prevailing at high temperatures over metal-free catalysts (left) is different from that occurring at low temperatures on metal-containing systems (right).
Basic oxides are well known to readily dehydrogenate alcohols since the conversion of isopropanol to acetone is routinely used as a means to measure oxide basicity [15,16]. However, the propensity of oxides to activate molecular hydrogen (H2) to hydrogenate unsaturated compounds is far less effective. To our opinion, the absence of any metallic phase to catalyze step 3 of the self-aldolization pathway (Scheme 1) makes highly doubtful this route in the case of metal-free basic oxides. Other reaction pathways must be considered (that may involve acetaldehyde, but not via the self-aldolization route) in the case of our HAP at temperatures above 350 °C, which are discussed elsewhere [12].
7 Conclusions
In the present work, the concentrations of the main gas-phase reaction products formed over a hydroxyapatite were monitored in the reactor effluent, including H2O and H2. Our results, based on thermodynamic analyses, rigorously showed that a mechanism based on the self-condensation of acetaldehyde, formed as a gaseous intermediate, has a negligible contribution to butanol formation at temperatures higher than 350 °C over our metal-free basic hydroxyapatite.


