1 Introduction
The π-conjugated organic compounds have gained significant attention for use as biological active compounds [1], sensors [2], organic light-emitting diodes (OLEDs) [3,4], organic field-effect transistors (OFET) [5,6], and photovoltaics [7–9]. In the present study, we have selected trans-3-(3,4-dimethoxyphenyl)-2-(4-nitrophenyl)prop-2-enenitrile (DMNPN) (Fig. 1) with the goal of investigating the structural, electronic (highest occupied molecular orbitals [HOMOs], lowest unoccupied molecular orbitals [LUMOs], and total/partial density of states [TDOS/PDOS]), optical (absorption [λabs] and fluorescence [λfl] spectra) and charge-transport properties (vertical/adiabatic ionization potentials [IPsv/a], vertical/adiabatic electron affinities [EAsv/a], hole/electron reorganization energies [λ(h)/λ(e)], hole/electron-transfer integrals [Vh/Ve] and hole/electron intrinsic mobilities). Moreover, it is well known that a low hole/electron-injection barrier would lead to efficient charge-transport materials. We have shed light on the hole/electron-injection barrier with respect to gold electrodes, and we have discussed the corresponding injection behavior. To the best of our knowledge, no computational study has previously been performed on DMNPN. This is the first in-depth investigation of DMNPN. The paper is structured as follows: Section 2 presents an outline of density functional theory (DFT) and time-dependent density functional theory (TDDFT), including the rationale for choosing the hybrid functional and the basis set; Section 3 presents the frontier molecular orbitals and the electronic, optical and charge-transport properties; and Section 4 presents the major conclusions of the present investigation.

(Color online.) The optimized labeled structure of trans-3-(3,4-dimethoxyphenyl)-2-(4-nitrophenyl)prop-2-enenitrile.
2 Computational details
Previously, it has been proven that DFT and TDDFT are reliable approaches to optimize and elucidate electro-optical and charge-transport properties and that they offer an accurate way to reproduce experimental data [10–17]. It has been shown in previous studies that B3LYP is a suitable and consistent functional to calculate the properties of interest for both small and large π-conjugated organic compounds [18–20]. In particular, it has reproduced the experimental data for compounds such as azo dyes [21,22], triphenylamine dyes [23], chemosensors [24], phthalocyanines [25], chromene derivatives [26] and oxadiazoles [27]. Preat et al. optimized the geometries at the B3LYP/6-31G** level of theory to investigate charge injection and found that this level of theory is adequate [28]. Huong et al. studied the electronic and charge-transport properties of naphtho[2,3-b]thiophene derivatives at the B3LYP/6-31G** and PBE0/6-31G** levels of theory and concluded that B3LYP/6-31G** is a decent method to replicate the experimental data [29]. Recently, experimental data on the electronic and charge-transport properties of dianthra[2,3-b:20,30-f]thieno[3,2-b]thiophene was reproduced using the B3LYP/6-31G** level of theory [30]. Additionally, geometric, electro-optical and charge-transport properties have been studied at the B3LYP/6-31G** level of theory, and it was proven that this level of theory is a reliable approach [31]. Scalmani and co-workers calculated the absorption and emission wavelengths by TDDFT [32].
In the present study, ground-state geometries have been optimized at the DFT/B3LYP/6-31G** level of theory. The excited state geometries have been optimized at TDDFT using the TD-B3LYP/6-31G** level of theory. The absorption and emission spectra have been computed by TDDFT, which has been proven an efficient approach. The absorption spectra were calculated by the TD-CAM-BLYP/6-31G** and TD-LC-BLYP/6-31G** levels of theory at the optimized geometry at the B3LYP/6-31G** level, and the fluorescence wavelengths were computed at the same levels of theory, as were the absorption spectra at the optimized geometry at the TD-B3LYP/6-31G** level.
The intrinsic mobility (μ) can be calculated by the Einstein equation as:
| μ = eD/KBT, | (1) |
The charge transfer rate can be described by Marcus theory via the following equation [33]:
| W = V2/h (π/λkBT)½ exp(–λ/4kBT), | (2) |
where the electronic coupling constant/transfer integral (V) and reorganization energy (λ) are the main parameters that determine the self-exchange electron-transfer rates and, subsequently, the charge mobility. For efficient charge transport, higher V and lower λ values are necessary.
The λ term can be divided into an inner λ (the molecular geometry relaxation when an electron is added or removed from a molecule) and outer λ (the alterations in the surrounding medium due to polarization effects). We calculated the inner λ, which reveals the geometric variations in the molecules. The λ term can be divided into two parts: correspond to the geometry relaxation energy of a molecule from neutral to a charged state, and from charged to a neutral state, respectively [5].
| (3) |
These terms were calculated from the adiabatic potential energy surfaces [34]:
| (4) |
In 2006, Valeev et al. concluded that the site-energy correction should be taken into account [36]. This can be achieved using single-crystal V values that have been computed by a direct approach [37–42] by our homemade code [43–46]. The hole as well as electron-transfer integrals (Vh and Ve) have been computed using the following equation:
| (5) |
| F0 = SCɛC−1, | (6) |
To compute the total and partial densities of states (T/PDOS), the initial molecular structure has been used, optimized at the B3LYP/6-31G** level of theory. The DOS have been computed using the generalized gradient approximation GGA/PW91 [49] functional and the DNP basis set [50] by DMol3 code [51], which is implemented in the Accelrys package of Materials Studio [52].
3 Results and discussion
3.1 Geometries
In Fig. 2, we presented the selected bond lengths and bond angles of the neutral (both ground and excited states), cation and anion states of DMNPN. The experimental geometrical parameters were reproduced by the computed bond lengths and bond angles at the B3LYP/6-31G** level of theory [53]. The maximum deviation was observed for the C11N1 bond length, i.e., the calculated bond distance of 0.017 Å overestimated the experimental data. We observed that the C3O1, C4O2, and C15N2 bond lengths decreased to 0.031, 0.030, and 0.058 Å, respectively, whereas the N2O3 and N2O4 bond lengths increased to 0.051 and 0.050 Å, respectively, from the ground to excited states.

(Color online.) Selected optimized bond lengths in angstroms (Å) and bond angles (degrees) of the ground state (neutral, cation and anion) and first excited state for DMNPN at the B3LYP/6-31G** and TD-B3LYP/6-31G** level of theory, respectively.
Experimental data from [53].
The major bond–length decreased was observed in C3O1 and C4O2 from the neutral ground to cation state, i.e., 0.030 Å and 0.039 Å, respectively. The increase/decrease in the bond lengths from the neutral ground to anion state is 0.025/0.050 Å for C4O2/C15N2. The largest changes were found in the O3N2O4 and C4O2C8 bond angles, −2.12° for the anion and +2.62° for cation, respectively (here, the negative and positive signs indicate decreases and increases compared to the values for the neutral state).
3.2 Electronic and optical properties
The distribution patterns for the HOMOs and LUMOs for the ground and first excited states of DMNPN are presented in Fig. 3. In Table 1, we tabulated the HOMO energies (EHOMO), LUMO energies (ELUMO), HOMO–LUMO energy gaps (Eg) in eV, and absorption (λa) and fluorescence wavelengths (λfl) in nm for the ground and first excited states of DMNPN calculated at the B3LYP/6-31G** and TD-B3LYP/6-31G** levels of theory, respectively. To overcome the electron-injection barrier energy in DMNPN, 2.41 eV (2.41 = −2.69 − (−5.1)) would be required; the work function of gold is −5.1 eV, and the ELUMO level of DMNPN is −2.69 eV (Table 1). The electron-injection barrier of DMNPN is smaller than those for the 4,6-di(thiophen-2-yl)pyrimidine [54] and dianthra[2,3-b:2,3-f]thieno[3,2-b]thiophene [30]. It is expected that 0.75 eV = −5.10 eV − (−5.85 eV) would be required to overcome the hole-injection barrier energy from the DMNPN to a gold electrode, which is smaller than the value for 4,6-di(thiophen-2-yl)pyrimidine. It is anticipated that DMNPN would be a superior charge-transport material than the reference compound. The lower-lying ELUMO of DMNPN than those of 4,6-di(thiophen-2-yl)pyrimidine and dianthra[2,3-b:2,3-f]thieno[3,2-b]thiophene reveal that DMNPN may be thermodynamically more stable and that charge-transport cannot be quenched by losing the electron.

(Color online.) Distribution patterns of the frontier molecular orbitals contributing to the major transitions.
The HOMO energies (EHOMO), LUMO energies (ELUMO) and HOMO-LUMO energy gaps (Eg) in eV for the ground and first excited states, computed at the B3LYP/6-31G** and TD-B3LYP/6-31G** levels of theory, respectively, and the absorption (λa) and fluorescence wavelengths (λfl) in nm, computed at the aLC-BLYP/6-31G** and bCAM-B3LYP/6-31G** levels of DMNPN.
| Ground state | |||||
| EHOMO | ELUMO | Eg | λa | f | Transitions (% configuration) |
| –5.85 | –2.69 | 3.16 | 316 | 1.1179 | HOMO→LUMO (61%)a |
| 235 | 0.0970 | HOMO–2→LUMO (41%)a | |||
| 198 | 0.1084 | HOMO–2→LUMO (35%)a | |||
| 348 | 1.0249 | HOMO→LUMO (66%)b | |||
| 220 | 0.0735 | HOMO→LUMO+2 (53%)b | |||
| Excited state | |||||
| EHOMO | ELUMO | Eg | λfl | f | Transitions (% configuration) |
| –5.57 | –2.99 | 2.58 | 295 | 0.8254 | HOMO←LUMO+1 (67%)a |
| 243 | 0.2141 | HOMO–2←LUMO (62%)a | |||
| 213 | 0.1616 | HOMO←LUMO+4 (52%)a | |||
| 319 | 0.6761 | HOMO←LUMO+1 (69%)b | |||
| 268 | 0.3321 | HOMO–1←LUMO+1 (59%)b | |||
| 228 | 0.1137 | HOMO←LUMO+4 (59%)b |
The computed absorption (λa) and fluorescence (λfl) wavelengths of DMNPN at the TD-CAM-B3LYP/6-31G** and TD-LC-BLYP/6-31G** levels of theory are presented in Table 1 and Fig. S1, Supporting information. In a detailed depiction of the ground state, the HOMO–2 is distributed across the entire backbone, the HOMO is delocalized on the dimethoxyphenyl and nitrile moieties, the LUMO is delocalized over the (nitrophenyl)prop-2-enenitrile and the LUMO+2 is delocalized over the benzene of nitrophenyl. The main transitions for DMNPN are the HOMO→LUMO and HOMO→LUMO+2, which contribute to charge-transport with the f(λa) values 1.0249 and 0.0735 (348 and 220 nm, respectively), at the TD-CAM-B3LYP/6-31G** level of theory. At the TD-LC-BLYP/6-31G** level of theory, the main transitions are the HOMO→LUMO and HOMO–2→LUMO, which contribute with the f (λa) values 1.1179, 0.0970 and 0.1084 (316, 235 and 198 nm, respectively). At the TD-CAM-B3LYP/6-31G** level of theory for the excited state, two main transitions, HOMO←LUMO+1 and HOMO–1←LUMO+1, with f values of 0.6761 and 0.3321 for λa of 319 and 268 nm, respectively, and one shoulder peak for HOMO←LUMO+4 with an f value of 0.1137 at λa of 228 nm are observed. In contrast, at the TD-LC-BLYP/6-31G** level of theory, three main transitions, HOMO←LUMO+1, HOMO–2←LUMO and HOMO←LUMO+4, with f values of 0.8254, 0.2141 and 0.1616 at λa, 295, 243 and 213 nm, respectively, are observed. The charge density in the HOMO, HOMO–1 and LUMO+1 is distributed on the dimethoxyphenyl and nitrile unit, whereas that in the LUMO+4 exists at the dimethoxyphenyl moiety. At the LC-BLYP/6-31G** level of theory, Stokes shifts for three major peaks are observed, with values of 21 nm (blue shift), 8 and 15 nm (red shift), respectively. At the CAM-B3LYP/6-31G** level of theory, Stokes shifts for the two major peaks are observed, with values of 29 nm (blue shift) and 48 nm (red shift), respectively. It is possible that the blue Stokes shifts are observed because the charge is distributed at the dimethoxyphenyl and nitrile moieties in the occupied and unoccupied orbitals (HOMO and LUMO+1) involved in the maximum emission wavelengths.
The total and partial densities of states of DMNPN are illustrated in Fig. 4. In DMNPN, the p states occur from 0.0 to –0.85 Hartrees. The p states dominate between 0.0 and –0.40 Hartrees, whereas the s states prevail from –0.45 to –0.87. The major contribution in the total densities of states is due to the p states in the conduction band from 0.0 to 0.16 Hartrees. No significant contribution is observed for the d states.

(Color online.) The total and partial density of states of DMNPN, calculated by DMol3.
3.3 Ionization potentials, electron affinities and reorganization energies
The IP, EA, λ (h), and λ (e) are significant factors that contribute to the charge-transport behavior. A smaller/larger IP/EA value means that a material is expected to be an efficient hole/electron transporter. Smaller λ (h) and λ (e) values indicate efficient hole- and electron-transport materials, respectively. We have tabulated the IPa, IPv, EAa, EAv, λ (h) and λ (e) values in Fig. 5. The smaller IPa and IPv values of DMNPN than of 4,6-di(thiophen-2-yl)pyrimidine, i.e., 0.43 and 0.38 eV, respectively, indicate that DMNPN should be a better hole-transport material. [4–6,17]. The larger EAa and EAv values of DMNPN than of 4,6-di(thiophen-2-yl)pyrimidine, i.e., 0.97 and 0.84 eV, indicate that DMNPN should also be a superior electron transporter. The smaller computed λ (h) than λ (e) for DMNPN indicate that it would be better hole-transport material.

(Color online.) The vertical and adiabatic ionization potentials (IPv/IPa), vertical and adiabatic electronic affinities (EAv/EAa) and hole/electron reorganization energies (λ (h)/λ (e)) of DMNPN (in eV) at the B3LYP/6-31G** level of theory.
The DMNPN neutral bond lengths for C3O1 and C4O2 changed to 0.030 and 0.039 Å, respectively, compared to the values for the cation state. The variations in the C4O2 and C15N2 bond lengths are 0.025 and 0.050 Å, respectively, from the values for the neutral to anion states. We observed that the geometry relaxation between the neutral and anion states is greater than that for the cations, resulting in greater polarization in the former, which results in a larger value of λ (e) than λ (h).
3.4 Transfer integrals
We have evaluated five discrete nearest neighboring hopping pathways (Fig. 6) at the DFT/pw91pw91/6-31G** level of theory for DMNPN. The packing and orientation of the crystal structure is important considered during calculation of the transfer integrals. Changing the packing would lead to different values for the transfer integrals, resulting in misleading intrinsic mobilities. Thus, the transfer integrals were calculated by selecting the dimer from the experimental crystal structure, which was then used to compute the values of the hole- and electron-transfer integrals without further optimization. It is well known that optimization of the dimer results in entirely different, and false, mobility values compared to the experimental data, due to a change in geometry (thus, a packing change can also lead to a different mobility). To ensure accurate results when calculating the transfer integrals, the crystal packing must not be altered. The transfer integrals for the electron and hole were evaluated using the method expressed in Eq. (5) and are presented in Table 2 for all five pathways. The strongest hole/electron-transfer integrals are –2.1/–4.7,–1.1/4.2, 1.58·10−5/3.35·10−7,–27.9/4.8, and 5.55·10−5/–4.54·10−5 meV, respectively. The highest hole- and electron-transfer integral values were observed for d4, even though the mass center for this pathway is 8.48 Å which is more than for d1 and d2. It is expected that the larger transfer integrals of the former pathway may arise from the side benzene rings, which are face-to-face as well as parallel. The greater hole-transfer integral values reveal that DMNPN might be a better hole-transport material.
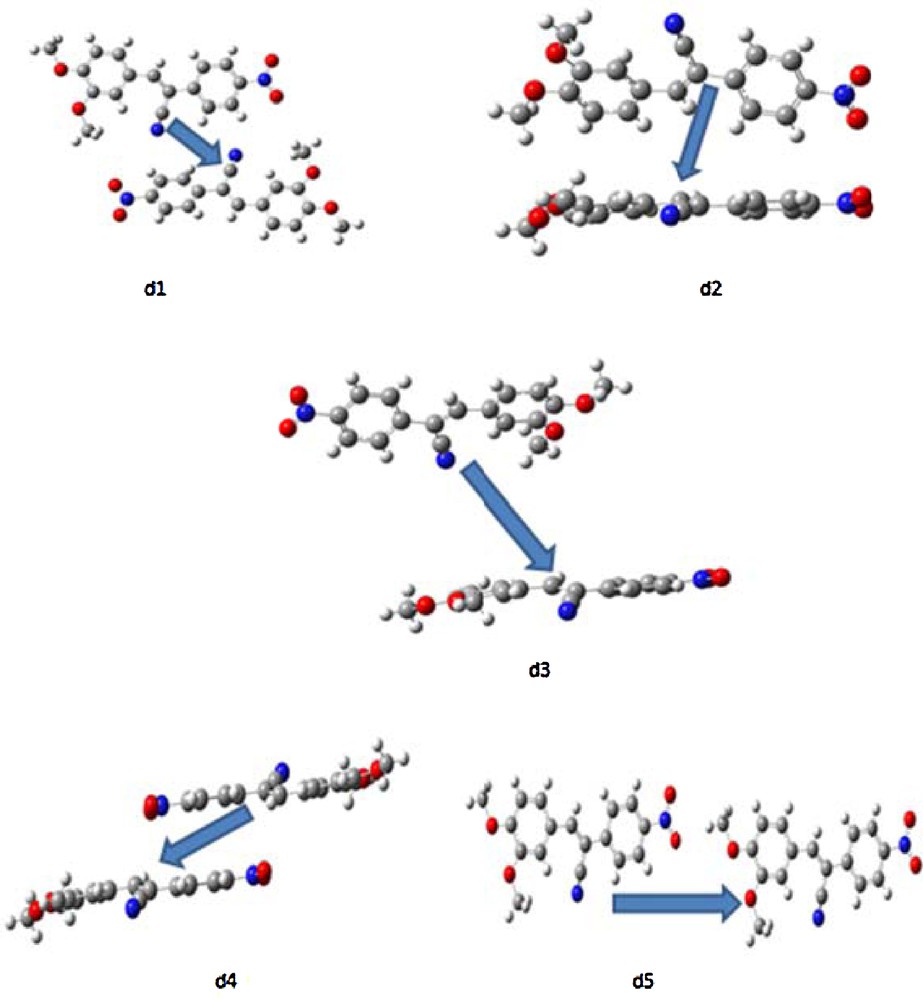
The dimers and pathways investigated in this study.
The transfer integrals (meV), mass centers (Å) and mobilities (cm2/V·s) for holes and electrons for DMNPN at the PW91PW91/6-31G** level of theory.
| Pathways | Transfer integrals | Mass centers | Mobility | ||
| Vh | Ve | μh | μe | ||
| 1 | –2.1 | –4.7 | 7.94 | 9.29·10−6 | 1.21·10−3 |
| 2 | –1.1 | 4.2 | 5.88 | 3.84·10−7 | 4.23·10−4 |
| 3 | 1.58·10−5 | 3.35·10−7 | 9.81 | 4.55·10−14 | 4.75·10−20 |
| 4 | –27.9 | 4.8 | 8.48 | 0.33 | 1.50·10−3 |
| 5 | 5.55·10−5 | –4.54·10−5 | 17.04 | 2.10·10−11 | 4.84·10−11 |
3.5 Intrinsic mobilities
The intrinsic mobility of DMNPN for five pathways was calculated and is tabulated in Table 2. The hole (μh) and electron (μe) intrinsic mobilities for DMNPN of pathways ‘1–5’, respectively, are 9.29·10−6 and 1.21·10−3, 3.84·10−7 and 4.23·10−4, 4.55·10−14and 4.75·10−20, 0.33 and 1.50·10−3 and 2.10·10−11and 4.84·10−11 cm2/V·s. The average μh/μe value is 5.50·10−2/5.22·10−4 cm2/V·s. From the average μh and μe values, it is predicted that DMNPN may be a good hole-transport material. Moreover, for a good humidity sensor, its affinity for H2O molecules is very important. It is expected that the dimethoxy and phenyl sites would be favorable for humidity sensing [55]. Further work on this topic is being explored.
4 Conclusions
The present quantum chemical study illustrates a theoretical framework through which we obtained the following conclusions:
- • the B3LYP/6-31G** level is a precise and optimal level of theory to replicate the experimental bond lengths and bond angles of sulfanylidene-5-(thiophen-2-ylmethylidene)imidazolidin-4-one (DMNPN);
- • the smaller electron- and hole-injection barriers for DMNPN than for 4,6-di(thiophen-2-yl)pyrimidine reveal that the former compound may be a superior charge-transport material;
- • the distribution of charge density at the dimethoxyphenyl moiety in the HOMO and that at the (nitrophenyl)prop-2-enenitrile in the LUMO indicates intramolecular charge transfer in the ground state;
- • the smaller ionization potential and larger electron affinity values for DMNPN than for 4,6-di(thiophen-2-yl)pyrimidine indicate that the former may be a better hole- and electron-transport material;
- • the smaller hole-reorganization energy and superior hole-transfer integral values than electron analogues for DMNPN indicate that it should be an efficient hole-transport material;
- • the greater geometry relaxation between neutral/anion than between neutral/cation causes greater polarization for the former, which ultimately results in a larger electron reorganization energy;
- • the parallel and face-to-face side benzene rings increase the values of the transfer integrals, resulting in enhanced mobility;
- • the computed hole intrinsic mobility is one hundred times greater than the electron value, indicating an efficient hole-transport material.
Acknowledgments
The authors would like to acknowledge the support of the Ministry of Higher Education, Kingdom of Saudi Arabia for this research through a grant (PCSED-005-14) under the Promising Centre for Sensors and Electronic Devices (PCSED) at Najran University, Kingdom of Saudi Arabia. A. Irfan acknowledges the technical and computational support of Prof. Zhang Jingping regarding Materials Studio calculations.


