1. Préambule
J’ai d’abord pensé qu’il était saugrenu d’évoquer dans une revue scientifique mes souvenirs de ma formation en radio cristallographie à l’université de Nancy entre 1985 et 1993. En réalité, c’est bien plus que des souvenirs, c’est un hommage et une expression de ma gratitude dont il s’agit. C’est certes inhabituel mais dans le cadre d’une approche transdisciplinaire de la connaissance et des sciences en particulier, cela prend tout son sens pour nous rappeler que nous sommes aussi liés par des sentiments, une manière d’être avec nos instructeurs et cette dimension relationnelle (ou émotionnelle) n’est pas incompatible avec la transmission des connaissances et recherche. Bien au contraire, elle l’humanise !
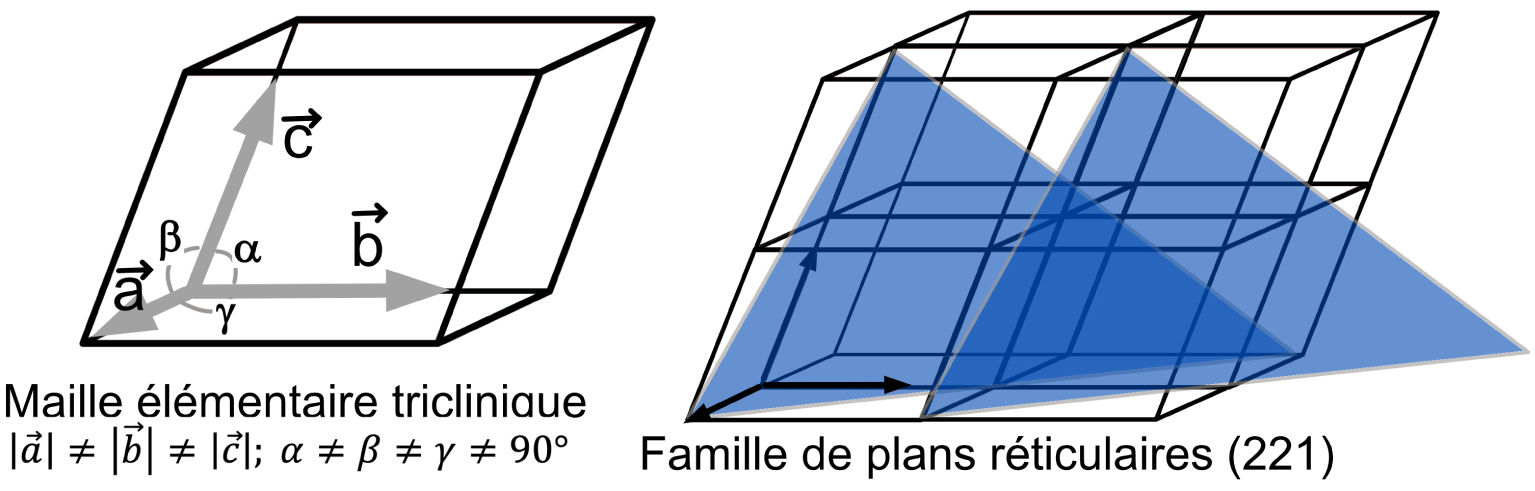
Représentation d’une maille élémentaire triclinique construite sur les trois vecteurs de base
C’est le décès récent du Professeur Yves Dusausoy, mon premier enseignant de la cristallographie, qui m’a donné l’envie de rédiger ce court article en hommage à l’école de Nancy. J’ai connu le Professeur Yves Dusausoy dès ma première année à l’université et immédiatement j’ai été interpellé par cette science des structures : la cristallographie géométrique. Le Professeur Dusausoy parlait doucement, posément, respectueusement et il construisait tous les schémas au tableau noir, avec 4 couleurs judicieusement choisies. Dans la première partie de cet article, j’expliciterai comment le Professeur Yves Dusausoy décrivait la cristallographie géométrique, depuis les lois basiques des réseaux tridimensionnels jusqu’aux groupes d’espace en passant par les opérateurs de symétrie compatibles.
Deux autres professeurs ont ensuite marqué ma formation (en licence et master) et m’ont permis d’être bien formé dans ce vaste domaine de la radiocristallographie : il s’agit des Professeurs Jean Protas et Niels Hansen et je montrerai, sur quelques exemples simples, la pertinence de leurs enseignements respectifs. Avant d’entrer dans le vif du sujet, je souhaite exprimer encore ma plus sincère gratitude au Professeur Bernard Malaman qui m’avait accepté en 1990 dans son équipe de recherche autour des composés « Intermétalliques », ainsi que son compagnon de route Dr. Gérard Venturini [1]. Je les remercie car ils ont cru en moi et m’ont donnée la passion de la recherche en chimie du solide, passion qui a trouvé écho à Strasbourg en septembre 2000 auprès des Professeurs Pierre Braunstein et Jean-Pierre Sauvage, que je remercie pour leur accueil, leur confiance et leur amitié sans faille.
1.1. La cristallographie géométrique avec le Professeur Yves Dusausoy
Ce qui caractérise l’état cristallin, c’est le concept d’ordre ou « d’agencement » spatial tridimensionnel d’atomes ou de molécules. Le support mathématique pour représenter cet ordre spatial tridimensionnel est donc tout naturellement les réseaux mathématiques de type 3D (D pour dimensions), définis par 3 vecteurs (Figure 1) non-colinéaires
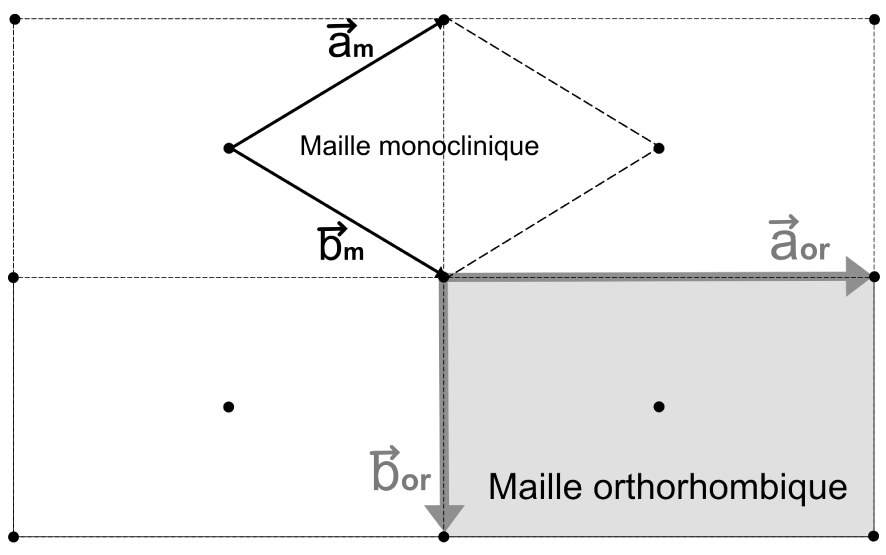
Représentation bidimensionnelle d’un réseau de Bravais orthorhombique C (face
Liste des 14 réseaux de Bravais répartis dans les 7 systèmes cristallins. P, S, I et F signifie respectivement : maille primitive (P), 1 face centrée (S), maille centrée (I) et toutes faces centrées (F)
| Système cristallin | Modes de réseau possibles |
|---|---|
| Triclinique | P |
| Monoclinique | P et S |
| Orthorhombique | P, S, I et F |
| Rhomboédrique | P |
| Quadratique | P et I |
| Hexagonal | P |
| Cubique | P, I et F |
Le Professeur Dusausoy m’a permis de comprendre que la présence de certains opérateurs de symétrie spécifiques (et leur éventuelle combinaison) dans un réseau 3D conduit à un type de maille particulier. On en connait 7, ce sont les 7 systèmes cristallins : triclinique, monoclinique, orthorhombique, rhomboédrique, quadratique, hexagonal et cubique (Tableau 1). Par exemple un réseau triclinique ne peut pas contenir un axe de rotation de type 2 (rotation de 180°) car ceci implique deux directions perpendiculaires, qui est la signature des réseaux monocliniques ou orthorhombiques. Et avec une construction relativement simple et utilisant des concepts de la trigonométrie basique, le Professeur Dusausoy aimait faire cette démonstration de la limitation du nombre d’opérateurs de symétrie possible dans les réseaux. Sans passer par la théorie des groupes (souvent moins « digeste » pour nos étudiants !), il montrait que les opérateurs de symétrie compatibles sont au nombre de 9 : l’identité — noté 1, pas de symétrie —,
A partir de ces bases claires, le Professeur Dusausoy nous amenait comme dans un voyage au cœur des réseaux et de leur symétrie. En combinant ces opérateurs dans les 7 systèmes cristallins, on génère 32 groupes de symétrie ponctuelle (on reste pour le moment dans des réseaux mathématiques). Et il nous faisait remarquer que parmi ces 32 groupes, il y en avait une majorité (21) qui ne possèdent pas de centre d’inversion, pourtant une condition fondamentale de la symétrie des réseaux mathématiques ! Il y a en effet 11 groupes centrosymétriques (les groupes dits de Laue) et 21 groupes non-centrosymétriques qui ne sont pas une anomalie mathématique mais qui vont servir à décrire des symétries cristallines (la symétrie dans les « vrais » cristaux), lorsqu’on va associer à notre réseau mathématique un motif atomique. Cette explication était très éclairante pour moi car elle montrait enfin pourquoi la cristallographie géométrique permet finalement de décrire des cristaux, et avant cela, de déterminer leur structure. Je reviendrai sur ce point plus avant dans cet article.
Notre voyage vers les groupes d’espace en cristallographie n’est pas encore achevé. A cette étape du raisonnement, le Professeur Dusausoy introduisait le concept de réseau de Bravais qui s’appuient sur le fait qu’il existe des mailles particulières (multiples) qui possèdent plus que 1 nœud (par maille) et qu’il convient de choisir pour des raisons de symétrie : ce sont les 14 modes de réseau de Bravais dans les 7 systèmes cristallins (voir Tableau 1). Prenons l’exemple d’un réseau orthorhombique non primitif tel que représenté sur la Figure 2. On voit clairement que ce réseau peut être décrit par la maille orthorhombique (grisée) mais il peut aussi être décrit par la maille élémentaire monoclinique (l’angle entre les vecteurs
Le Professeur Dusausoy montrait comment calculer le volume de toutes les mailles ainsi que les distances entre deux points des réseaux à partir du « tenseur métrique », une matrice 3 × 3 qui se construit par une combinaison simple des paramètres de la maille. Puis enfin il expliquait comment relier les valeurs dhkl (distances entre deux plans consécutifs d’une famille de plans réticulaires) à ces mêmes paramètres de la maille et aux indices de Miller. Cet ensemble me donnait une vision cohérente et finalement assez simple de cristallographie. Le calcul des valeurs dhkl me faisait par ailleurs entrevoir les premières étapes de l’interprétation des diffractogrammes aux rayons X via la célèbre relation de Bragg : 2 × dhkl ×sin𝜃 =𝜆. J’invite le lecteur à se reporter à l’article passionnant — The birth of X-ray crystallography — du Professeur John Meurig Thomas à propos de la découverte de la fameuse relation que l’on doit à Lawrence et William Bragg, article publié à l’occasion de l’année internationale de la cristallographie en 2014 [2].
Il nous manque encore un outil avant de pouvoir construire les groupes d’espace. Ce sont les opérateurs de symétrie ponctuelle. De quoi s’agit-il ? Un cristal réel n’est pas un réseau mathématique, c’est un motif composé d’atomes que l’on trouve à l’intérieur de la maille. En réalité on devrait exprimer les choses en sens inverse, à savoir un motif atomique se construit (par les lois complexes des liaisons chimiques fortes et faibles) dans l’espace et on peut alors définir une maille qui représente cet ordre tridimensionnel, en accord avec les lois mathématiques des réseaux. Mais les motifs eux-mêmes peuvent présenter des éléments de symétrie, c’est-à-dire qu’il doit exister des opérateurs spécifiques qui lient deux, trois (ou plus) atomes dans la maille élémentaire (Figure 3). Ce sont les opérateurs de symétrie de position en cristallographie, et ils doivent être en phase avec les opérateurs de symétrie du réseau. Sans en faire la démonstration ici, on peut montrer que tous les opérateurs « classiques » sont aussi potentiellement des opérateurs de position et deux supplémentaires sont mis en évidence lorsqu’on examine les possibles combinaisons de ces opérateurs « classiques » avec des translations de type
Représentation partielle du motif constitutif d’un polymère de coordinateur inorganique, en projection dans le plan
1.2. La description originale des groupes d’espace en cristallographie
J’en arrive à présent au point qui m’a le plus marqué dans l’enseignement du Professeur Dusausoy, à savoir la construction des groupes d’espace en s’appuyant sur une lettre majuscule « non symétrique » en 2 dimensions, le F. Mais tout d’abord, c’est quoi au juste un groupe d’espace ? La manière de l’expliquer me vient là aussi du Professeur Dusausoy ! Si on combine, dans les 7 systèmes cristallins tous les groupes ponctuels possibles, si on ajoute à cela les 14 modes de réseau de Bravais « autorisés » et finalement les opérateurs de symétrie ponctuels, alors on construit (ce travail a été fait par nos prédécesseurs cristallographes) très exactement 230 groupes d’espace. Ils représentent les possibilités mathématiques de l’ordre cristallin, ni plus, ni moins, mais c’est impressionnant ! Cela signifie que lorsque on a entre les mains un cristal, on peut décrire sa structure dans un des groupes d’espace répertorié (il y a quelques exceptions mais cela sort du cadre de cet article).
Comment construire un groupe d’espace en cristallographie ? Dans un système cristallin donné, il s’agit donc de combiner un type de réseau de Bravais, un groupe de symétrie ponctuelle et les possibles opérateurs de symétrie de position associés. Ainsi, dans le système triclinique, il n’existe que 2 groupes d’espace P1 et P −1, puisque dans ce système seul des réseaux de Bravais primitifs sont permis et il y a 2 groupes de symétrie ponctuelle possibles : 1 et −1. Dans le système monoclinique, on voit bien que le nombre de combinaison sera plus important puisqu’il existe 2 types de réseaux de Bravais possibles (P et C), 3 groupes de symétrie ponctuelle (2, m et 2/m) et la possibilité de trouver aussi des axes hélicoïdaux 21 ou des miroirs translatoires (c ou n). Ceci amène à 13 groupes monocliniques : P2, P21, C2, Pm, Pc, Cm, Cc, P2/m, P21/m, C2/m, P2/c, P21/c et C2/c. La construction rigoureuse et le dénombrement montrent qu’ils existent respectivement 59, 25, 68, 27 et 36 groupes d’espace dans les systèmes orthorhombique, rhomboédrique, quadratique, hexagonal et cubique. Ces 230 groupes d’espace sont regroupés, explicités et représentés en projection dans les Tables Internationales de Cristallographie [4]. Les premiers groupes sont faciles d’accès (je veux dire que même le néophyte comprend le jeu des opérateurs de symétrie) puis, au fur et à mesure, les combinaisons des opérateurs conduisent aux groupes de haute symétrie dans lesquels le nombre de positions équivalentes peut aller jusqu’à 192 dans le groupe cubique Fm −3m ! Placer toutes ses positions dites équivalentes, c’est construire le groupe d’espace. Le « jeu » consiste à examiner comment un objet situé dans la maille se retrouve à d’autres endroits de la maille par symétrie, du fait de la présence des opérateurs que j’ai cités plus haut (voir par exemple Figure 5, le groupe monoclinique P21/c).
Lorsque j’ai appris ces constructions avec le Professeur Dusausoy, je ne savais pas qu’il utilisait sciemment un autre symbole que le symbole « officiel » des Tables Internationales [4]. Il dessinait un F (F majuscule), notait un + juste à côté et nous montrait comment cet objet (ou cette molécule si vous voulez) se comportait vis-à-vis des opérateurs de symétrie dudit groupe. Dans les tables internationales de cristallographie le choix s’est porté sur un symbolisme différent, un cercle et un cercle avec une virgule à l’intérieur, comme je le montre sur la Figure 4. Personnellement, je continue à préférer le F pour les cours de base en cristallographie géométrique et depuis des années mes étudiants comme les visiteurs de ma chaine Youtube1 trouvent ce choix pertinent. Sur la Figure 5, j’ai représenté le groupe P21/c avec le symbole F, à la manière dont me l’a enseigné le Professeur Dusausoy, il y a plus de 30 ans déjà.
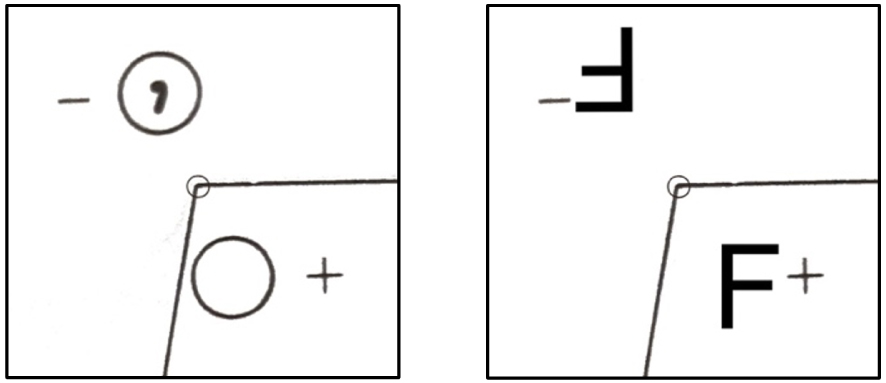
Représentation comparée du symbolisme utilisé pour la position générale dans les groupes d’espace. A gauche, la représentation des tables internationales de cristallographie, à droite celle enseignée par le Professeur Dusausoy à l’université de Nancy. Le petit cercle en centre des images représente un centre d’inversion. Les notations + et − représentent les coordonnées fractionnaires de la position générale dans la troisième direction (+z ou −z par exemple).
1.3. Comprendre la diffraction avec le Professeur Jean Protas
Lorsque j’ai rencontré le Professeur Jean Protas pour la première fois, je fus impressionné par sa prestance. C’était un homme grand, droit, large d’épaule et toujours bien habillé (costume, cravate). J’ai suivi son enseignement en Maîtrise de Chimie du Solide (aujourd’hui Master 1) et j’ai apprécié la manière qu’il avait de reprendre les bases de la cristallographie pour nous permettre de saisir le mieux possible les phénomènes de diffraction, dans le cadre de l’interaction rayonnement/matière.
Sans entrer dans le détail de ce grand domaine de la physique qu’est l’étude de l’interaction rayonnement/matière, le Professeur Protas m’a permis très tôt de comprendre un point clé du phénomène de diffraction : l’analyse d’un diffractogramme (Figure 6) se fait d’abord d’un point de vue géométrique puis du point de vue des intensités relatives des tâches (ou pics) de diffraction. L’analyse géométrique — la position des pics de diffraction — s’appuie principalement sur la relation de Bragg [5] et des relations mathématiques des réseaux 3D, l’analyse des intensités diffractées s’appuie quant à elle sur le facteur de structure qui est un nombre complexe (au sens mathématique) et dont la transformée de Fourier représente la densité électronique au sein même de la maille élémentaire.
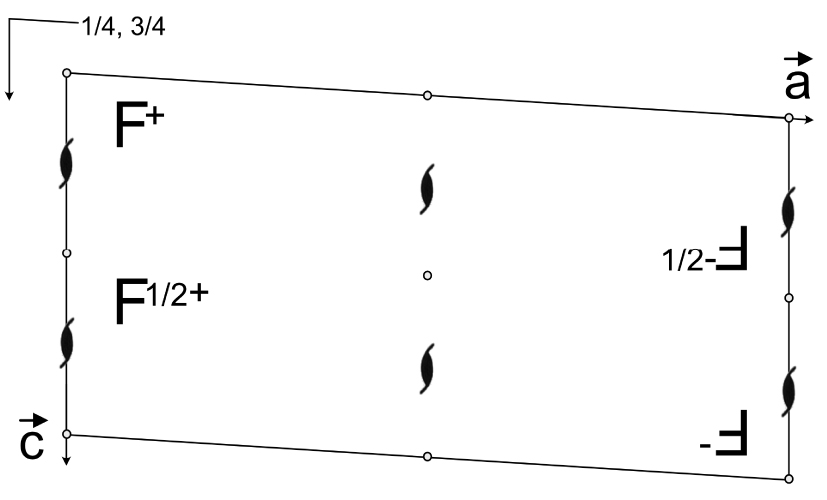
Représentation du groupe d’espace monoclinique P21/c avec le centre d’inversion (petit cercle) placé à l’origine de la maille élémentaire. Les « lentilles » verticales représentent les axes hélicoïdaux de type 21 qui sont dans la direction de
Représentation du groupe d’espace monoclinique P21/c avec le centre d’inversion (petit cercle) placé à l’origine de la maille élémentaire. Les « lentilles » verticales représentent les axes hélicoïdaux de type 21 qui sont dans la direction de Lire la suite
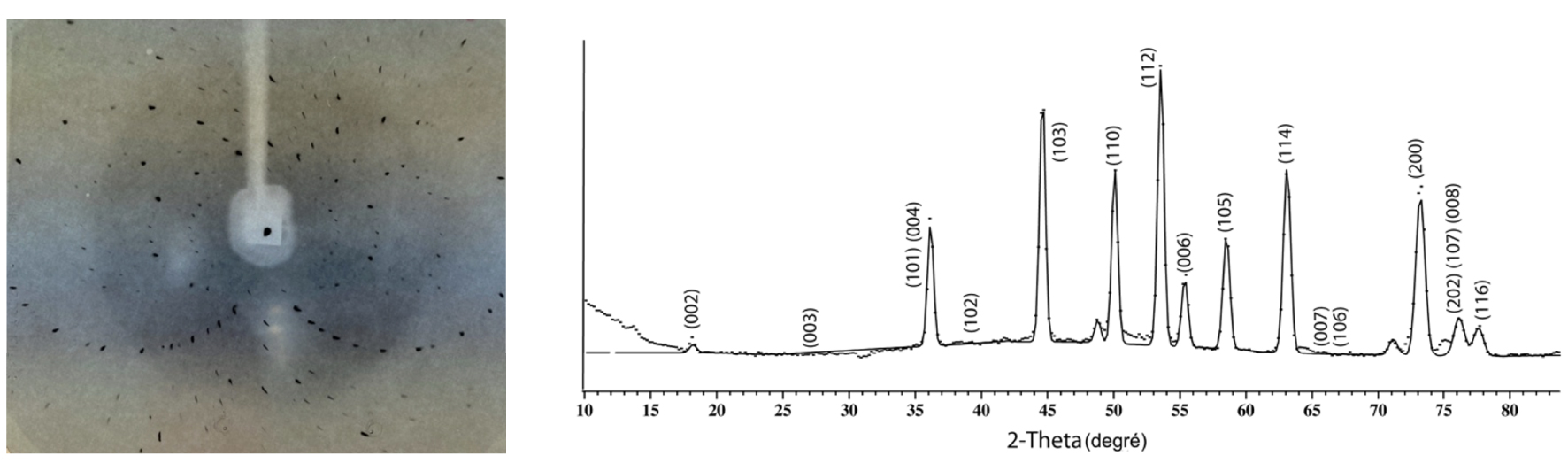
A gauche : diffractogramme aux rayons X (faisceau monochromatique de longueur d’onde 1,54059 Å) d’un monocristal organométallique (enregistrement sur une pellicule argentique, années 1980). A droite : diffractogramme neutronique de poudre d’un composé intermétallique avec indexation partielle (indices de Miller hkl) des pics de diffraction (longueur d’onde des neutrons utilisés : 2,52 Å).
1.4. La relation de Bragg et le facteur de structure : l’alpha et l’oméga de la diffraction
Lorsque j’écoutais le Professeur Protas, je comprenais progressivement pourquoi « les Bragg » père et fils avaient obtenu le prix Nobel en 1915. La relation qui porte leur nom est magnifique. Elle permet de relier une mesure macroscopique (l’angle 𝜃) à une dimension infiniment petite, la valeur dhkl, la distance entre 2 plans consécutifs dans une famille de plans réticulaires (𝜆 est la longueur d’onde des rayons X utilisés).
Dans les années 1990, le travail de résolution puis d’affinement structural prenait encore plusieurs jours (quelques fois des semaines), le facteur limitant étant la manipulation des facteurs de structure et le calcul de leurs « Transformées de Fourier ». En 30 années de carrière, j’ai vécu la révolution informatique que nous connaissons toutes et tous, et aujourd’hui, sur un ordinateur portable d’entrée de gamme, il est possible d’affiner des structures complexes (possédant plus de 500 atomes dans la maille élémentaire) en quelques secondes par cycle d’affinement. Je suis convaincu que le Professeur Protas serait heureux et excité de voir cela.
Pour conclure sur cet hommage au Professeur Jean Protas, je souhaite encore évoquer un enseignement que j’ai reçu et qui m’a été très utile quelques années plus tard. Il s’agit de la diffraction des neutrons et des électrons.
1.5. Quelques mots sur la diffraction des électrons et des neutrons : aux origines de la dualité onde/particule
Lorsqu’on parle de diffraction, on pense à l’expérience de la double fente et de la figure d’interférence. Pour une onde électromagnétique comme la lumière (et son photon sans masse), c’est tout à fait « naturel » oserais-je dire mais lorsqu’il s’agit de particules massiques comme l’électron (9,11 × 10−31 kg) ou encore le neutron (1,67 × 10−27 kg) c’est beaucoup plus surprenant. En 1923, Louis De Broglie [8] formula une hypothèse qui allait révolutionner la physique : la dualité onde/particule ou exprimé autrement, toute particule en mouvement est associée à une onde, l’onde dite de De Broglie (la longueur d’onde 𝜆 de l’onde de De Broglie [8] se calcule à partir de la formule simple : 𝜆 = h∕(mv) où h est la constante de Planck 6,626 × 10−34 J⋅s, m la masse de la particule et v sa vitesse). Cette idée révolutionnaire fut confirmée 4 années plus tard par les expériences de diffraction électronique de Clinton Davisson et Lester Germer [9]. Les observations faites par Davisson et Germer cadraient parfaitement avec le modèle de Bragg établi pour la diffraction des rayons X. On a dû attendre 1945 pour observer ce phénomène de diffraction de Bragg avec un flux de neutrons, c’était au Laboratoire National d’Oak Ridge (dans l’état du Tennessee aux États-Unis), expériences menées sous la direction d’Ernest O. Wollan [10]. Quels sont les intérêts principaux de la diffraction électronique et des neutrons ? Pour répondre à cette question, et sans entrer dans le détail physique de l’interaction rayonnement-matière, il faut examiner le terme « facteur de diffusion » noté 𝜞j dans l’expression du facteur de structure rappelé ci-contre.
Dans le cas de la diffraction des électrons, le terme 𝜞j est également lié à l’interaction avec le nuage électronique des atomes, sa valeur est forte en comparaison avec le Fj aux rayons X mais il n’est plus directement proportionnel à Z (numéro atomique). De plus, on peut montrer que ce terme décroît encore plus rapidement avec l’angle de Bragg et, compte tenu du pouvoir de pénétration faible des électrons dans la matière, il est beaucoup plus difficile de remonter à la densité électronique (et donc de déterminer des structures cristallines). Le lecteur trouvera les détails de ces calculs et les explications complémentaires de ces limitations dans l’usage de la diffraction électronique dans le livre du Professeur Protas [7]. La diffraction électronique sera cependant très précieuse pour l’étude des couches minces par incidence rasante ou encore pour avoir un premier accès à la structure de très petits échantillons, les nanoparticules en particulier.
Dans le cas de la diffraction des neutrons, les choses se compliquent un peu mais cela ouvre des champs d’étude nouveaux ! En effet, le terme 𝜞j devient une « section efficace de capture » pour ce qui concerne la diffraction atomique, mais cette fois, c’est l’interaction avec le noyau qui est prépondérante. La section efficace varie de façon discontinue avec le numéro atomique, permettant, par exemple, de repérer avec précision la position de 2 atomes très proches en termes de numéro atomique (manganèse et fer, par exemple), chose impossible par la diffraction des rayons X. De plus, la section efficace aux neutrons varie peu avec l’angle de Bragg, permettant de collecter des intensités fortes même aux grands angles. La technique est très efficace pour résoudre des structures cristallines, sur monocristal ou sur poudre.
Enfin, dès 1946, il a été montré l’existence d’une diffraction d’origine magnétique [11] qui trouve son origine dans le fait que le neutron possède un moment magnétique intrinsèque. Lorsqu’il existe un ordre magnétique à longue distance au sein d’un matériau, sa mise en évidence est possible par diffraction magnétique des neutrons à l’instar de la mise en évidence de l’ordre des atomes dans un cristal par diffraction des rayons X. Les premières expériences [12] dans ce domaine ont en particulier confirmé de manière spectaculaire l’ordre antiferromagnétique théorisé par Louis Néel en 1932 [13]. Les études portaient en particulier sur l’oxyde de manganèse MnO qui est le « modèle » de l’ordre antiferromagnétique.
J’aimerais souligner ici l’importance de ces domaines de la physique expérimentale comme une illustration magistrale des bases de la physique quantique (la dualité onde/particule), telle que nous l’enseignons à l’université. Lorsque je suivais les cours du Professeur Protas en maîtrise de chimie du solide puis en DEA à Nancy, je n’imaginais pas à quel point ses connaissances seraient importantes pour mes travaux de recherche (95% de mes publications sont liées directement à la diffraction des RX sur monocristaux, sur poudre ou encore liées à la résolution de structures magnétiques par diffraction des neutrons !) puis dans mes enseignements de la radiocristallographie mais aussi de la chimie générale.
Pour conclure cet hommage au Professeur Jean Protas, je souhaite encore partager une anecdote surprenante. Quelques jours après avoir été nommé sur mon premier poste permanent à l’université de Nancy (Maître de Conférences en Chimie du Solide, en 1995), je rencontre par hasard le Professeur Protas dans un couloir et je lui annonce la bonne nouvelle me concernant. Il me dit alors qu’il se réjouit de cela mais que c’est simplement une étape. Il me prédit alors que je serais Maître de Conférences pendant 5 ans puis je pourrais être nommé professeur ici ou ailleurs en France ! Je le regarde surpris, incrédule et flatté, puis nous continuons nos chemins. J’ai été nommé professeur de chimie inorganique à l’université de Strasbourg en septembre 2000, en particulier grâce à mon expérience et ma formation à la radiocristallographie ! Étonnante prédiction vous en conviendrez.
1.6. Niels Hansen, des modèles en bois aux cartes de densité électronique par diffraction haute résolution
Le 3
Niels Hansen avait un accent marqué et j’avais du mal à savoir d’où il venait. J’ai su plus tard qu’il était originaire du Danemark et qu’il avait effectué sa thèse à New-York, sous la supervision du Professeur Coppens, une sommité dans le domaine de la cristallographie.
Niels Hansen semblait nonchalant, comme un peu détaché de l’enseignement qu’il nous donnait. Et pourtant, lorsqu’une question lui était posée, il cherchait à répondre de façon complète, approfondie, souvent trop complexe d’ailleurs pour nous autres étudiants de licence de chimie. Ceci entraina une réputation d’un professeur « tournesol », un peu farfelu.
Quelques années plus tard, lorsque j’étais déjà en poste d’enseignant chercheur au laboratoire de chimie du solide minéral à Nancy, un projet de recherche m’a permis de démarrer une collaboration avec le Professeur Hansen. Il s’agissait d’explorer la possibilité d’établir des cartes de densité électronique dans des composés intermétalliques, pour mieux comprendre la nature des liaisons chimiques dans ce type de matériaux. Ce type d’étude n’avait jamais été menée et le Professeur Hansen était le plus à même de nous aider à atteindre cet objectif. Mon travail a été de préparer des cristaux de ces composés intermétalliques CaMnSi, CaMnGe, CaNi2Si2 [14] avant de partir quelques jours à Hambourg avec le Professeur Hansen (1997), pour réaliser les mesures de diffraction haute résolution sur l’un des Synchrotrons allemands. C’est là que j’ai découvert qui était Niels Hansen: un homme d’une grande humanité, toujours souriant et pourtant ultra concentré sur les mesures et leur traitement. On peut dire que je me suis lié d’amitié avec lui lors de ce séjour. J’étais admiratif de sa simplicité et de sa grande compétence, et malgré les difficultés (les cristaux que j’avais préparés n’étaient pas de très grande qualité), il était optimiste.
Il prenait le temps d’expliquer comment il convient de corriger l’absorption, les extinctions secondaires, etc. (voir Figure 7). Finalement il pouvait appliquer son modèle et son logiciel d’affinement multipolaire de la densité de charge [15], travail initié à Hambourg et qui a été achevé lors de notre retour à Nancy. Ces études ont donné lieu à l’une de mes plus belles publications scientifiques [14] (la Figure 8 montre une coupe bidimensionnelle de la répartition de la densité électronique dans le composé intermétallique CaNi2Si2, avec la mise en évidence de la liaison métallo–iono–covalente entre les atomes de nickel et de silicium).
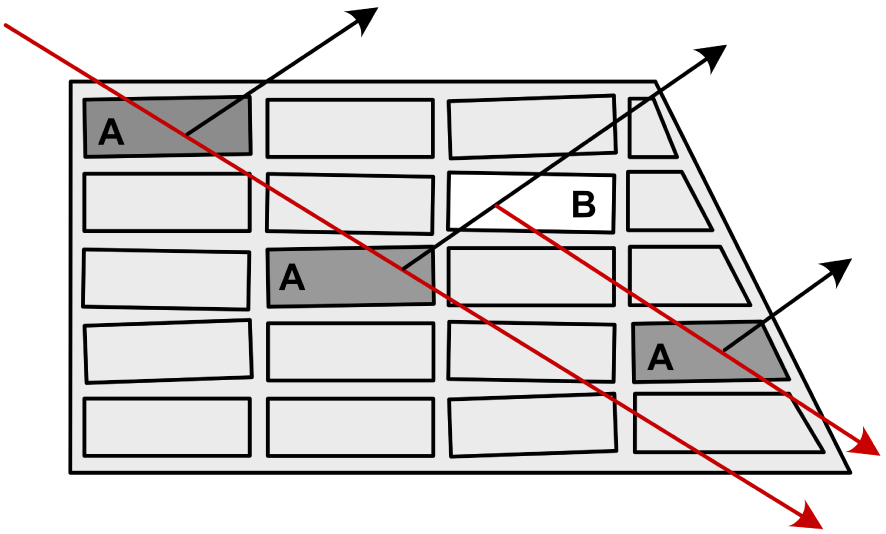
Principe de l’extinction secondaire dans le cadre de la théorie du cristal mosaïque. En rouge le faisceau incident et en noir les faisceaux diffractés. Les « micro-cristallites » A ont la même orientation et le « micro-cristallite » B est orienté de telle manière à diffracter à son tour le faisceau diffracté, abaissant ainsi l’intensité théorique. La connaissance précise des dimensions du cristal est aussi nécessaire pour une correction rigoureuse de l’absorption.
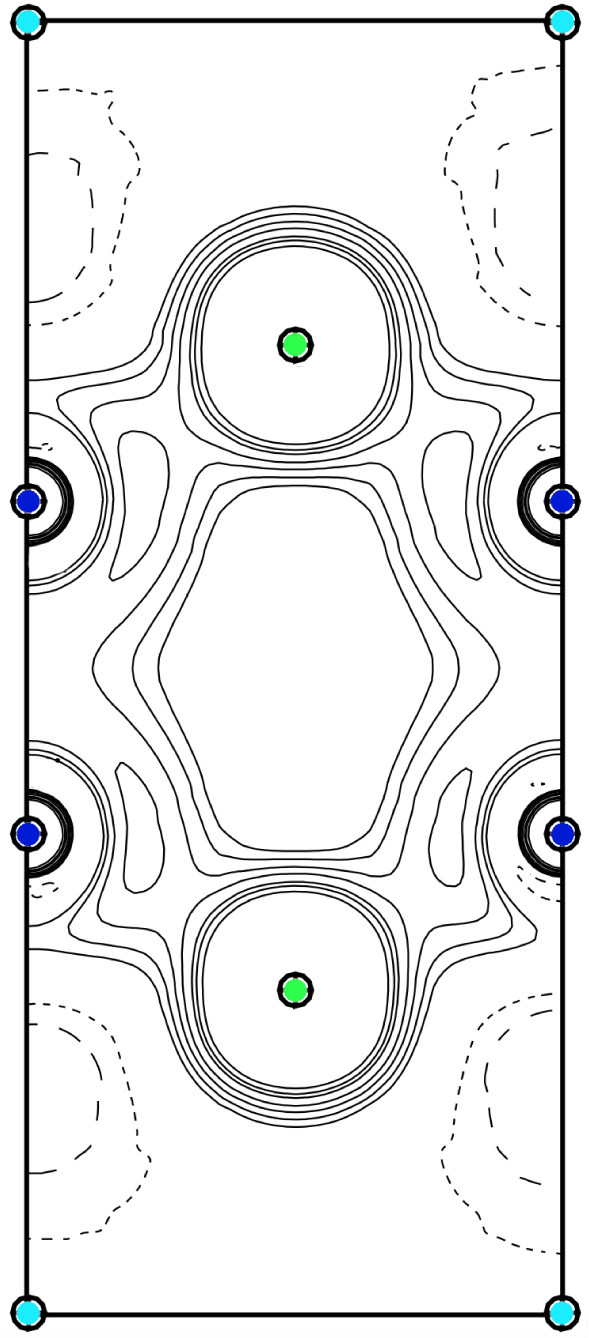
Extrait des cartes de densité électronique dans le composé CaNi2Si2 (coupe dans le plan (a,c) de la maille élémentaire —
Quelques explications sur les conditions de la diffraction haute résolution s’imposent ici, en mémoire avec la manière dont Niels Hansen aimait l’expliquer (une description plus complète est disponible dans l’article original de Hansen et Coppens [15] et aussi dans l’ouvrage du Professeur Protas — Diffraction des rayonnements [7]). Tout d’abord, il est utile de préciser la notion de résolution en diffraction, par un simple calcul qui s’appuie sur la relation de Bragg 2dhkl sin𝜃 =𝜆. Dans le cas d’un rayonnement de longueur d’onde 0,71 Å (K𝛼 du molybdène), si on peut mesurer avec précision des pics de Bragg à un angle 𝜃 de 20°, cela correspond à une distance dhkl de 1,038 Å. Si la collecte s’étend jusqu’à 25°, la résolution sera alors de 0,84 Å. Avec ce type de valeurs, on pourra espérer placer les atomes avec précision dans l’unité asymétrique (même les atomes d’hydrogène), ainsi que l’ajustement des paramètres d’agitation thermique. Mais si on veut « voir » les électrons entre les atomes, une résolution encore plus faible sera visée. Avec un angle 𝜃 de 35° par exemple, on atteint une résolution de 0,619 Å ! (Remarque : les intensités diffractées diminuent rapidement en fonction de l’angle de Bragg 𝜃 en diffraction des rayons X à cause d’une décroissance rapide du facteur de diffusion 𝜞j).
C’est une première base importante pour tenter de remonter, par transformée de Fourier du facteur de structure, à la densité électronique dans la maille élémentaire. Niels Hansen insistait souvent sur l’importance de la qualité des données de diffraction, les intensités diffractées, leur nombre en comparaison avec les paramètres qui vont être ajustés dans la structure puis dans l’établissement des cartes de densité électronique. Au-delà de la résolution et du nombre d’intensités collectées, j’ai appris auprès de Niels Hansen le soin qu’il convient d’apporter à la correction de toutes ces intensités : correction rigoureuse de l’absorption, de la polarisation, des extinctions primaires et secondaires, et bien entendu minimiser autant que possible l’agitation thermique. A partir de données de diffraction « propres », le processus d’affinement peut être mené. En nous rappelant les trois termes principaux du facteur de structure, en comprend aisément qu’une fois la position des atomes connue (le terme hxj + kyj + lzj) et que l’agitation thermique est bien décrite (le terme 8πU…), il reste le terme 𝜞j — facteur de diffusion aux rayons X — qui contient en quelque sorte l’information de densité électronique. Cette fonction « densité de charge » s’obtient par la transformée de Fourier du facteur de structure
Ce modèle multipolaire et les outils associés que Niels Hansen a développés avec le Professeur Coppens reste encore aujourd’hui la référence de la communauté « Charge Spin and momentum density » de l’Union Internationale de la Cristallographie. C’est de fait une des signatures reconnues de l’Ecole de cristallographie de Nancy.
Dans les dernières années de son activité de chercheur à Nancy, Niels Hansen s’était investi dans la diffraction des matériaux piézo-électriques soumis à un champ électrique [18]. C’est un domaine prometteur ouvrant le champ à de nombreuses applications technologiques. J’ai été très chanceux d’avoir pu collaborer avec mon collègue et ami Niels Hansen, avec tant de simplicité et d’enthousiasme. J’ai beaucoup appris à ses côtés. Niels Hansen s’est éteint à l’âge de 57 ans, des suites d’une longue maladie.
2. Conclusion
Tout au long de la rédaction de cet article, c’est un sentiment de gratitude et de reconnaissance qui m’habitait. J’ai eu beaucoup de chance d’avoir pu rencontrer ces 3 professeurs de cristallographie. Ils ont été, à l’instar d’autres bien sûr, des exemples de ce que signifie être un homme de sciences. Il s’agit ici de la cristallographie, mais je suis certain que nombreux ont vécu cela dans leur discipline spécifique. Nous sommes redevables à nos maîtres et professeurs, ils ont contribué à ce que nous sommes et leur rendre hommage quelques fois nous rappelle notre propre responsabilité (droiture, véracité, compétence, bienveillance, etc.) vis-à-vis de nos étudiants et collègues d’aujourd’hui.
Conflit d’intérêt
L’auteur n’a aucun conflit d’intérêt à déclarer.
1Sur Youtube, Welter Teaching : chimie et cristallographie.



 CC-BY 4.0
CC-BY 4.0